Question

In an experiment of mathematics frustum of cones is made up of seven rings, the radius of the uppermost ring is 4cm and the radius increases by 1cm so that radius of the last ring is 10cm, if the width of each ring is 3cm, find the volume of frustum.

Answer 1

Hint: A frustum is a part of a cone that is formed after removing the upper portion of the cone by a plane parallel to its base.

Volume of a frustum= \[\dfrac{1}{3}\pi h\left( {{r^2} + rR + {R^2}} \right)\]

Complete step-by-step answer:
Given that,
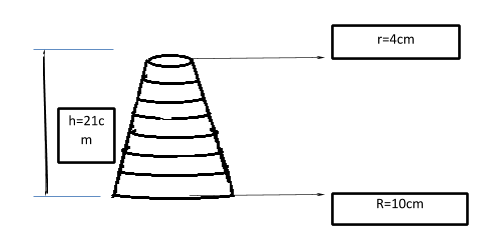
Width of each ring =3cm
Radius of uppermost ring (r) =4cm
Radius of lowermost ring (R) =10cm

Volume of a frustum= \[\dfrac{1}{3}\pi h\left( {{r^2} + rR + {R^2}} \right)\]
  \[
  = \dfrac{1}{3} \times \dfrac{{22}}{7} \times 21\left( {{4^2} + 4 \times 10 + {{10}^2}} \right) \\
   = 22\left( {16 + 40 + 100} \right) \\
   = 22 \times 156 \\
   = 3432c{m^3} \\
\]
Thus, volume of frustum is \[3432 c{m^3}\].

Note: In these types of problems that belong to surface areas and volume first look at the diagram and check for its formula.
The only point where a student can get confused is slant height and normal height of frustum. Here they have asked for volume and for that we need normal height h. This height is the perpendicular distance between the cut plane and the base.
Slant height is written as l.