Question

In an examination, 70% of the students passed in Paper I, and 60% of the students passed in Paper II. 15% of the students failed in both the papers while 270 students passed in both the papers. What is the total number of students?
A. 600
B. 580
C. 560
D. 540

Answer 1

Hint: First of all, find the percentage of students failed in both the papers and hence the percentage of students failed in the examination. Then find the percentage of students passed in both the papers to obtain the required answer as the number of students passed in both the papers.

Complete step-by-step answer:

Let the total number of students attempted the examination \[n\left( U \right) = 100\% \]
And let the total number of students be \[x\].

The percentage of set of students passed in Paper I \[n\left( A \right) = 70\% \]

The percentage of set of students passed in Paper II \[n\left( B \right) = 60\% \]

We know that the complement of \[n\left( X \right)\] is given by \[n\left( {{X^c}} \right) = n\left( U \right) - n\left( X \right)\].

By using this formula, we get

The percentage of set of students failed in Paper I \[n\left( {{A^c}} \right) = n\left( U \right) - n\left( A \right) = 100\% - 70\% = 30\% \]

The percentage of set of students failed in Paper II \[n\left( {{B^c}} \right) = n\left( U \right) - n\left( B \right) = 100\% - 60\% = 40\% \]

Given the percentage of students failed in both Papers I & II is 15%

The Venn diagram for failed students is shown as below:

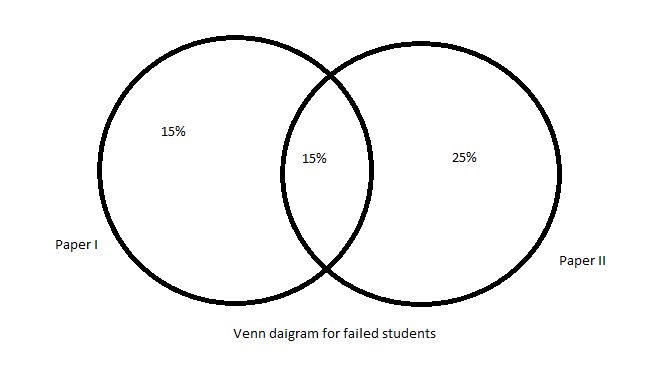
Now, consider the percentage of students failed in the examination.

The percentage of set of the students failed in the examination = percentage of set of students failed in Paper I + percentage of set of students failed in paper II – set of the students failed in both Papers I & II

So, percentage of set of students failed in examination \[ = 30\% + 40\% - 15\% = 55\% \]

The percentage of students passed in both the papers = 100% - percentage of students failed in examination.

So, percentage of set of students passed in both papers \[ = 100\% - 55\% = 45\% \]

Given the number of students passed in both the papers is 270.

So, we have 45% of \[x\] = 270

\[

   \Rightarrow \dfrac{{45}}{{100}} \times x = 270 \\

   \Rightarrow 45x = 270 \times 100 \\

   \Rightarrow x = \dfrac{{27000}}{{45}} \\

  \therefore x = 600 \\

\]

Hence the total number of students is 600.

Thus, the correct option is A. 600

Note: The complement of \[n\left( X \right)\] is given by \[n\left( {{X^c}} \right) = n\left( U \right) - n\left( X \right)\]. In these types of problems try to solve the problem by drawing Venn diagrams and considering the set of objects in their respective areas or fields.