Question

In a parallelogram ABCD, diagonal AC measures 34 m and the perpendicular distance of AC from either of the vertices B and D is 12 m. Area of the parallelogram is
a. 204 ${{m}^{2}}$
b. 408 ${{m}^{2}}$
c. 816 ${{m}^{2}}$
d. 402 ${{m}^{2}}$

Answer 1

Hint: In order to solve this question, we will first visualize the given condition and draw the figure accordingly. We need to remember that the diagonal of a parallelogram divides it in 2 congruent triangles. Also, we need to remember that the area of a triangle is given by the formula, $\dfrac{1}{2}$ (base) (height). By using these concepts we will solve this question.

Complete step-by-step answer:
In this question, we have been asked to find the area of a parallelogram ABCD, whose diagonal AC measures 34 m and the perpendicular distance of AC from either of the vertices B and D is 12 m. To solve this question, we will first consider the given situation and draw the figure accordingly. So, we get,

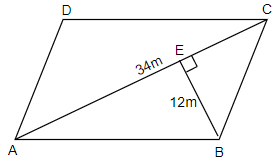
Here, we have considered E as the point of intersection of the perpendicular drawn from B on AC. So, according to the question, we can say that BE = 12 m.
Now, we know that the diagonal of a parallelogram divides it in 2 congruent triangles. So, we can say that,
Area of triangle ABC = Area of triangle ACD
Now, we know that the area of the parallelogram ABCD can be given as,
Area of triangle ABC + Area of triangle ACD
As we know that both the triangles are congruent, their areas will be the same, so we can further write the above expression as,
2 Area of triangle ABC
Now, we know that the area of the triangle = $\dfrac{1}{2}$ (base) (height). So, for triangle ABC, we can say that, area of triangle ABC = $\dfrac{1}{2}\times AC\times BE$. Therefore, we can write the area of parallelogram ABCD as,
$\begin{align}
  & 2\times \dfrac{1}{2}\times AC\times BE \\
 & AC\times BE \\
\end{align}$
Now, we will put the values of AC and BE, that are, AC = 34 m and BE = 12 m. So, we get the area of the parallelogram ABCD as,
$\begin{align}
  & 34\times 12{{m}^{2}} \\
 & 408{{m}^{2}} \\
\end{align}$
Therefore, we get the area of the parallelogram ABCD as $408{{m}^{2}}$. Hence option (b) is the correct answer.

Note: While solving the question, the possible mistakes we can make is by forgetting to multiply the area of the triangle by 2, to get the area of the parallelogram ABCD. So, we will choose the wrong answer. So, we have to be very careful while solving this question.