Question

Given A = ( 1 , 1 ) and AB is any line through it cutting the x – axis in B. if AC is perpendicular to AB and meet the y axis in C, then the equation of locus at the midpoint P on BC is
( a ) x + y = 1
( b ) x + y = 2
( c ) x + y = 2xy
( d ) 2x + 2y = 1

Answer 1

Hint: To solve this question what we will do is first, we will find the coordinates of B and C I terms of h and k. then, we will find the slopes of lines of AB and AC, and then using the condition of slopes when they are perpendicular, we will find the locus equation at point P.

Complete step-by-step solution:

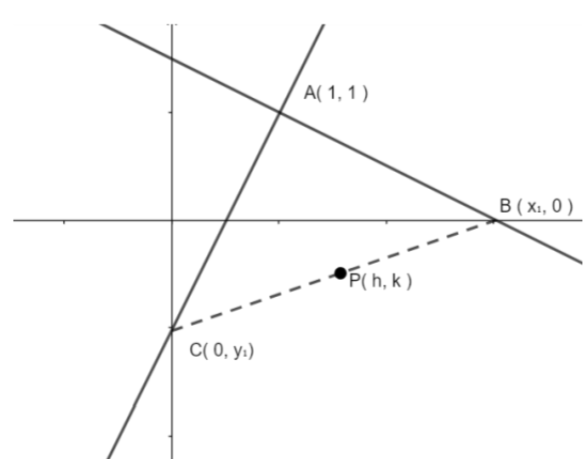
In figure we can see that P is mid point of line joining points $B({{x}_{1}},0)$ and $C(0,{{y}_{1}})$.
So using mid point formula $\left( \dfrac{{{x}_{1}}+{{x}_{2}}}{2},\dfrac{{{y}_{1}}+{{y}_{2}}}{2} \right)$ , we can find out coordinates of point P which is,
$P(h,k)=P\left( \dfrac{{{x}_{1}}+0}{2},\dfrac{0+{{y}_{1}}}{2} \right)$
$P(h,k)=P\left( \dfrac{{{x}_{1}}}{2},\dfrac{{{y}_{1}}}{2} \right)$
On comparing, we get
$h=\dfrac{{{x}_{1}}}{2},k=\dfrac{{{y}_{1}}}{2}$
Or, ${{x}_{1}}=2h,{{y}_{1}}=2k$
So, coordinate of point B will be ( 2h, 0 ) and coordinate of point C will be ( 0, 2k ).
Now, if we have two points say, $({{x}_{1}},{{y}_{1}})$ and $({{x}_{2}},{{y}_{2}})$ lying on same line, then slope of line is equals to $m=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{2}}}$ .
So slope of line AB will be equals to whose two pints are A ( 1, 1 ) and B ( 2h, 0 ),
${{m}_{AB}}=\dfrac{1-0}{1-2h}$
Or, ${{m}_{AB}}=\dfrac{1}{1-2h}$
And, slope of line AC will be equals to whose two pints are A ( 1, 1 ) and C ( 0, 2k ),
${{m}_{AC}}=\dfrac{1-2k}{1-0}$
Or, ${{m}_{AC}}=\dfrac{1-2k}{1}$
We know that when two lines are perpendicular and slope of those two lines are say ${{m}_{1}}$ and \[{{m}_{2}}\]then, ${{m}_{1}}\times {{m}_{2}}=-1$
We are given that AC and AB are perpendicular and slope of line AB is ${{m}_{AB}}=\dfrac{1}{1-2h}$ and slope of AC is ${{m}_{AC}}=\dfrac{1-2k}{1}$ so,
${{m}_{AC}}\times {{m}_{AB}}=-1$
Putting values of ${{m}_{AB}}=\dfrac{1}{1-2h}$ and ${{m}_{AC}}=\dfrac{1-2k}{1}$in ${{m}_{AC}}\times {{m}_{AB}}=-1$, we get
$\dfrac{1-2k}{1}\times \dfrac{1}{1-2h}=-1$
On simplifying, we get
$\dfrac{2k-1}{2h-1}=-1$
Taking 2h – 1 from denominator of left hand side to numerator of right hand side, we get
$2k-1=-(2h-1)$
On simplifying, we get
$2k-1=-2h+1$
On solving we get
$h+k=1$….( i )
In general we can write ( h, k ) in terms of ( x, y ) as
$x+y=1$
Hence, option ( a ) is correct.

Note: To solve such questions, one must know the conditions of perpendicular of two slopes and how to calculate slopes and what is the formula of mid-point. The calculation should be done correctly and accurately as it may give an error in calculation and answers may get wrong.