Question

Calculate the area of a regular pentagon with sides of 2cm and apothem is 12cm.
A. $60c{{m}^{2}}$
B. $61c{{m}^{2}}$
C. $62c{{m}^{2}}$
D. $63c{{m}^{2}}$

Answer 1

Hint: We will first start by drawing a rough diagram of the polygon. Then we will use the fact that apothem is the distance of the centre of the polygon from midpoint to its one side and then we will use the SSS congruence to prove that apothem is perpendicular to the side and finally use the formula for area of triangle to find the answer.

Complete step-by-step answer:
Now, we have been given a regular pentagon with sides of 2cm and apothem is 12cm. Now, we know that apothem is the distance is the distance of the centre of the polygon from its side. So, we have,

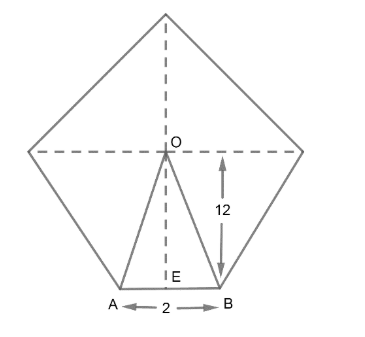
Now, we have in $\Delta OAE\ and\ \Delta OEB$
OA = OB since the pentagon is regular
AE = EB since E is midpoint of AB
OE = OE since OE is common
Now, we have by SSS congruence
$\Delta OAE\cong \Delta OEB$
Now, we know that by corresponding parts of congruent triangle we have,
$\angle AEO=\angle OEB..........\left( 1 \right)$
Now, we have AB as a straight line. So,
$\angle AEB=\angle AEO+\angle OEB=180{}^\circ $
Now, using (1), we have,
$\begin{align}
  & 2\angle AEO=180{}^\circ \\
 & \Rightarrow \angle AEO=\angle OEB=90{}^\circ \\
\end{align}$
Now, we have $OE\bot AB$. So, we can find the area of \[\Delta OAB\ as\ \dfrac{1}{2}\times base\times height\]
 \[\begin{align}
  & =\dfrac{1}{2}\times AB\times OE \\
 & =\dfrac{1}{2}\times 2\times 12 \\
 & =12c{{m}^{2}} \\
\end{align}\]
Similarly, we have the area of all 4 other sub triangles in the pentagon as \[12c{{m}^{2}}\].
Hence, the area of pentagon,
 $\begin{align}
  & =5\times 12 \\
 & =60c{{m}^{2}} \\
\end{align}$
Hence, the correct option is (A).

Note: It is important to note that we have used SSS congruence to prove that apothem is perpendicular to one side of the pentagon. Also, it is important to note that we have divided the pentagon into 5 similar triangles and find the area of one triangle to find the area of the whole pentagon.