Question

All rhombuses are kites.
(a) True
(b) False

Answer 1

Hint: Compare the properties of kite with the properties of rhombus to check whether all rhombus are kites or not. If the properties of rhombus satisfies the properties of kites, then all rhombuses are kites.

Complete step-by-step answer:
We will first see the properties of kites:
Let us consider a kite ABCD, then

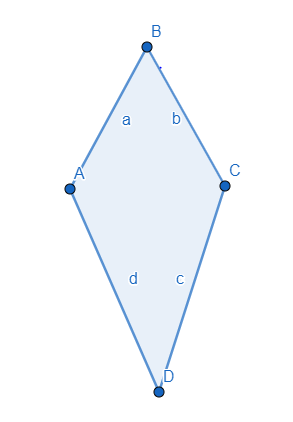
1. Two disjoint pairs of sides known as consecutive sides should be equal or we can say congruent to each other, that means, a=b and c=d.
2. One pair of opposite angles should be equal to each other and such angles are known as congruent angles.
3. Both the diagonals should meet each other at \[{{90}^{\circ }}\], which means they should cut each other orthogonally.
4. Main diagonal of a kite is the angle bisector of the vertices containing the diagonal.
 Now, let us see the properties of rhombus:
A rhombus with dimensions ABCD is taken, then,

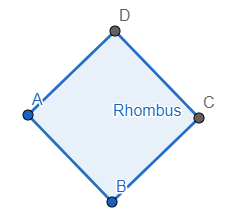
1. All sides of the rhombus are equal.
2. Opposite angles of rhombus are equal.
3. In rhombus, diagonals bisect each other at \[{{90}^{\circ }}\].
4. Diagonal acts as the angle bisector.
5. The two diagonals of a rhombus form four right-angled triangles which are congruent to each other.
Now, let’s check whether properties of rhombus fulfil the condition of kites
As all the sides of rhombus are equal which satisfies the condition of congruent consecutive sides, which satisfies the condition that all rhombuses are kites.
Also, opposite angles of rhombus are equal and satisfy the property of congruent angles of kites.
Now, we can also notice that diagonals of rhombus and kites meet each other at \[{{90}^{\circ }}\].
And, the last property of kite i.e. main diagonal bisects the angles of vertices containing diagonal is also satisfied by the rhombus because all angles are bisected by the diagonals of rhombus.
Therefore, from above all observations we can conclude that all rhombuses are kites.
Hence, option (a) is correct.

Note: We can conclude from the solution that all rhombuses are kites but all kites are not rhombus because diagonals of rhombus bisect each other but diagonals of kites do not. Also, all sides of rhombus are equal to each other but kites have two consecutive pairs of congruent sides.