Question

AB and CD are the two common tangent to circles which touch each other at C. If D lies on AB such that CD = 4 cm, then AB is equal to
A.4 cm
B.6 cm
C.8 cm
D.12 cm

Answer 1

Hint: Before attempting this question remember to construct the diagram using the given information and use Point C is the common point that lie on the circumference of both the circles, use this information to approach towards the solution of the given question

Complete step-by-step answer:
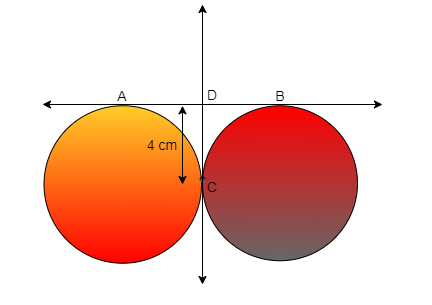
Let’s construct the diagram using the given information
According to the given information we have two circles which touch each other at point C also the circle have 2 common tangents AB and CD
And there is a point D which lie on AB such that CD = 4cm
So the constructed diagram is

To find the value of AB let join Point B and C and point A and C so the diagram we get is

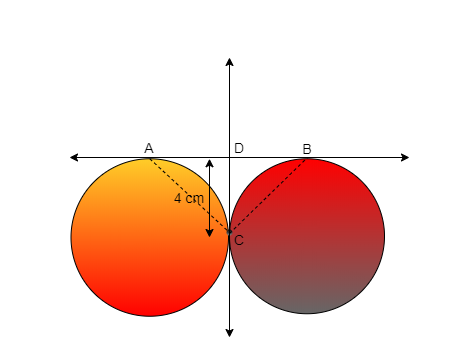
As we know that the two tangent drawn from the same external point from the circle are equal in length
Therefore we can say that CD = DB
Since CD = DB so DB = 4 cm
Similarly for tangent AD and DC by the property of tangent from the same external point form circle
AD = CD
So AD = 4 cm
Since AB is equal to AD + DB i.e. AB = AD + DB
Substituting the given values in the above equation we get
AB = 4 cm + 4 cm
AB = 8 cm
Since the measure of AB is 8 cm.
So, the correct answer is “Option C”.

Note: The concept of tangent played a main role to solve the above problem which can be explained as the line which intersect circle at one point that lie on the circumference of the circle here at the point where tangent intersect the circle, radius of the circle becomes perpendicular to the tangent. There are some basic properties that are shown by the tangent such as: the line of tangent never passes through the circle and the tangent drawn from the external points of the circle are equal to each other.