Question

A rectangular lawn 75 m by 60 m, has two roads 4 m wide each running through the middle of the lawn one parallel to the length and other parallel to the breath as shown in figure. Find the cost of graveling the roads at Rs. 4.50 per sq m.
A. Rs. 2358
B. Rs. 2385
C. Rs. 2300
D. Rs. 2500

Answer 1

Hint: For finding the cost of gravelling, first we have to find the total area of road (area of the rectangle IJLK + area of rectangle EFHG – area of square MNPO). And by multiplying the area of road to the cost of graveling per square meter, we will get the total cost.
The area of rectangle is given by the formula = length \[\times \] breadth
The area of square is given by the formula = side \[\times \] side

Complete step by step solution:
The figure for the given problem is as follows:

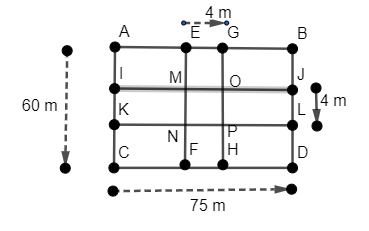
Now in the given question, it is given that
The length of the rectangular lawn is = 75 m
The breadth of the rectangular lawn is = 60 m
We have to find the cost of graveling the road which is inside the rectangle road for which the cost per sq m is 4.50 rupees.
So for that we have to find the area of the road and multiply it with 4.50.
The area of the road is given by
= area of the rectangle IJLK + area of rectangle EFHG – area of square MNPO …….(1)
The area of rectangle is given by the formula = length \[\times \] breadth
The length of JL is given = 4 m
And the length of KL as it is parallel to line AB or CD = 75 m
So the area of rectangle IJLK = length of JL \[\times \] length of KL
\[\Rightarrow 4\times 75=300{{m}^{2}}.......(2)\]
The length of EG = 4 m
The length of EF as it is parallel to line AC or BD = 60 m
So the area of EFHG = length of EG \[\times \] length of EF
\[\Rightarrow 4\times 60=240{{m}^{2}}.........(3)\]
The area of square is given by the formula = side \[\times \] side
The side of square MNPO = 4 m
So the area of square MNPO is equal to
\[\Rightarrow 4\times 4=16{{m}^{2}}......(4)\]
Now using equation (1), (2), (3) and (4), we get
The area of road
= \[300+240-16=524{{m}^{2}}\]
Now we are given that the cost of gravelling for 1 sq m is 4.50 Rs.
Cost of the gravelling for the road is = total area of road \[\times \] cost of gravelling for one sq m
That is
= \[524\times 4.5=2358\]
So the cost for graveling of the road is 2358 Rs.
Hence the correct option is (A).

Note: Students may make the mistake that they do not subtract the area of square MNPO from the area of rectangle IJLK + area of rectangle EFHG. Because square MNPO is common in both rectangles IJLK and EFHG.