Question

A circle is inscribed in a square of side length 6. The area of the region inside the square but outside the circle is
[a] $36\pi $
[b] $26\pi -9$
[c] $26\pi -36$
[d] $36-9\pi $
[e] $9\pi -36$

Answer 1

Hint: Join the centre of the circle with the four points of contact of the four sides of the square with the circle. Use the fact that the chord formed by joining points of contact of two parallel tangents is the diameter of the circle. Hence find the length of the side of the square. Use the fact that the area of the region inside the square but outside the circle is equal to the area of the circle subtracted from the area of the square. Hence find the area of the required region.

Complete step-by-step answer:

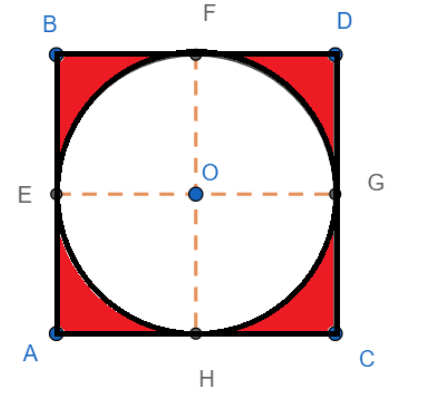
ABCD is a square and a circle with centre O is inscribed in the circle. E, F, G and H are the points of contact of AB, BD, DC and CA with the circle. Join OE, OF, OG and OH.
Since BD||AC, we have F, O and H are collinear, and FH is the diameter of the circle.
Since FH ||AB and BF||AH, we have FHAB as a parallelogram. Hence, we have FH = BA.
Since FH is the diameter of the circle, we have FH = 2r, where r is the radius of the circle.
Hence we have 2r = 6
Dividing both sides by 2, we get
r = 3.
Now the region which is inside the square but outside the circle is shaded in the diagram.
Clearly, the area of the shaded region is equal to the area of the circle subtracted from the area of the square.
Hence, we have
Area of the required region $=ar\left( ABCD \right)-ar\left( circle \right)$
We know that the area of a square of side length a is ${{a}^{2}}$ and the area of a circle of radius r is $\pi {{r}^{2}}$
Hence, we have
$ar\left( ABCD \right)={{6}^{2}}=36$ and $ar\left( circle \right)=\pi {{r}^{2}}=\pi {{\left( 3 \right)}^{2}}=9\pi $
Hence, we have
Area of the required region $=36-9\pi $
Hence option [d] is correct.

Note: In the above question, we have used the property that the distance between two parallel tangents of a circle is equal to the diameter of the circle.
Consider a circle as shown. Lines l and m are two tangents to the circle. Join OA and OB.

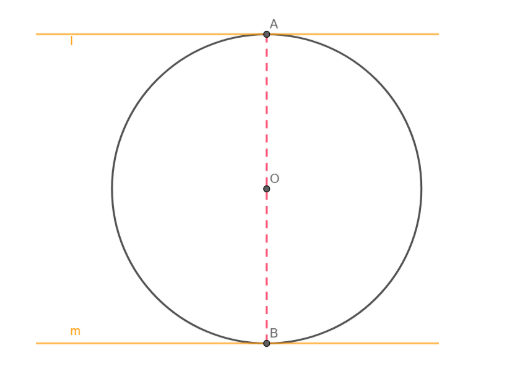
As the tangent and the radius at the point of contact are parallel, we have OA is perpendicular to l and OB is perpendicular to m. Now, since l is parallel to m, we have a line perpendicular to m that is also perpendicular to m. Hence line OA if extended will be perpendicular from. Since perpendicular from the centre of a circle to a tangent of the circle passes through the point of contact, we have OA passes through B. Hence O, A and B are collinear. Hence, we have AB = 2OA.
Also, since AB is perpendicular to both l and m, we have, AB is the distance between the parallel lines l and m.
Hence the distance between the parallel tangents is equal to the diameter of the circle.