What is Division for Kids?

An Introduction to Division Methods

When you divide, you begin to create equal portions of a group of items. Counting objects into equal groups is one method that is commonly applied when learning to divide. For instance, if you had three dolls and needed to place 12 bracelets on each of them, you may distribute the bracelets evenly among the dolls until there are none remaining. Here, each doll would receive 4 bracelets since $\dfrac{12}{3}$ equals 4. The dividend in this instance is 12, the divisor is 3, and the quotient is 4. We must first know the components of a division problem in order to understand how to divide. The significant figure you are dividing is the dividend. The divisor is the quantity into which you are dividing the dividend. When you divide, the result is the quotient. Let's discuss how to divide in the further section.

What is Division?

In mathematics, the division is the process of dividing a number into equal parts and estimating the maximum number of equal parts that may be formed. For example, in this case, dividing 15 by 3 resulted in the division of 15 into 3 groups of 5 each.

The character "$\div$" or often "/" stands for division.

Components of Division

A long division equation is made up of many unique components. Let's understand these components in detail which makes sure your kids recognise what they represent and how to identify them.

1. The number under the line on the right side of the calculation is the dividend. It stands in for the dividing amount.

2. The number on the left, which is doing the dividing, is the divisor.

3. The number at the top is the quotient. When the equation is finished, it indicates the solution or the number of units in each place value.

4. The figure at the bottom is the remaining amount. It stands for the units that remain after being divided into the quotient unevenly.

Components of Division

The following statement shows the relation between these four components:

Dividend = Divisor x Quotient + Remainder

To determine whether or not the solution is right, use this formula, often known as the division formula.

Short Division

A large number can be divided by a one-digit number using the short division, while a two-digit or more number can be divided by a large number using the long division.

Here is an illustration to help us better comprehend this concept.

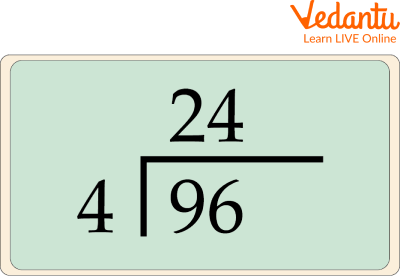
Short Division

In this image, four is multiplied by nine twice, leaving a remainder of one. The remainder is then added to the following number (six), making a total of 16. Four enters 16 four times, resulting in a total answer of 24.

Long Division

Long division is a mathematical technique used to divide big numbers into smaller groups or parts. Dividing a problem into small, straightforward steps can be helpful. There are dividends, divisors, quotients, and remainders in long divisions. Decimal numbers can also be divided into equal groups using long division. It follows the same processes as long division, which are to divide, multiply, subtract, bring down, and repeat or get the remainder.

Let’s see an example of Long division by 10. Here, 621300 is divided by 10.

Long division by 10

And this is how teachers will know how to do division for kids. Let’s see some solved example:

Solved Examples

Example 1: Divide 726 by 4

Solution: Firstly, Put the divisor, or the number you're dividing by another number, outside the long division bar to properly format the problem. The number you will be dividing by the divisor, the dividend should be put inside the long division bar. Your result, or the quotient, will come above the division bar.

Division

As a result, the problem's quotient is 181, and the remainder is 2.

Example 2: Laila's mother gathered every family photo and planned to put them all in an album. How many pages will she need if there are 285 photos if each page of an album can hold 9 pictures?

Solution: Given 285 photos if 9 photos are there on one page the 285 photos require 285 $\div$ 9

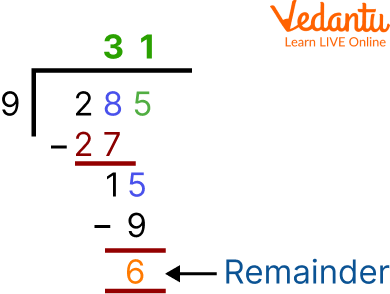
Division

Here the quotient is 31, and the remaining number is 6. She, therefore, requires 32 pages, or 31 + 1 (for the left six photos).

Practice Problems

Q1. If the remainder is 4, the quotient is 71, and the divisor is 8, find the dividend.

Ans: 572

Q2. Five garlands are to be constructed from the 75 flowers. What number of flowers will be in each garland?

Ans: 15

Summary

We have already discussed that we can split up huge numbers into numerous smaller groups or portions with the long division method. The number of groups that can be formed when a dividend is divided by a divisor is given by the quotient, and the number of elements or integers that will remain ungrouped is given by the remainder. Larger numbers can be divided by one-digit numbers using the short division, while larger numbers can be divided by two-digit or more numbers using the long division. Some solved examples and practice questions are also provided in this article. Grab your pen and pencil and start solving these questions.