What are the Factors?

The concept of factors and multiples are interrelated in Mathematics. Factors are the numbers that divide the given number exactly with no remainder left. Here in this article, we will learn what are factors, how to construct a factor tree, and much more.

The factors in simple words are the numbers (dividend) when exactly divided by any number (divisor), then the divisor is said to be a factor of the number i.e dividend. Every number will have '1'as a common factor and for any prime number, '1' and the number itself will be its factors for sure.

Factors and multiples

Factor Tree

A factor tree is a method of factorizing a number that is similar to the way in which the branches of a tree are split. Every branch of the factor tree is split into factors and once the factors cannot be factorized further, the branches come to an end, the final factors are circled and are considered to be the prime factors of the given number.

How to Solve Factor?

Factors are the numbers that divide the given number exactly with no remainder left.

Now let us see how to solve factor questions.

Let us consider the number 8,

$8 =1 \times 8$

$=2 \times 4$

Hence, 8 is a product of 1 and 8 and 2 and 4 . As a result, factors of 8 are 1,2,4 and 8.

Hence, "When finding or solving a factor question, we only consider positive numbers, whole numbers, and non-fractional numbers". Decimal and negative numbers are not considered while solving the factors of the numbers.

Also, the general rule to define factors is, "When we multiply 2 whole numbers, the numbers we multiplied are the factors of the product. Because they are divisible by the product".

In general, if ' $a$ ' and ' $b$ ' are multiplied to give 'ab' we say that ' $a$ ' and ' $b$ ' are the factors of 'ab'.

For example, $7 \times 5=35$. Hence, 7 and 5 are the factors of 35 . Because no remainder is left when $35 \div 7$ or $35 \div 5$, the remainder is zero.

$2 \times 3=6$

Hence, 2 and 3 are the factors of 6 because no remainder is left when $6 \div 2$ or when $6 \div 3$.

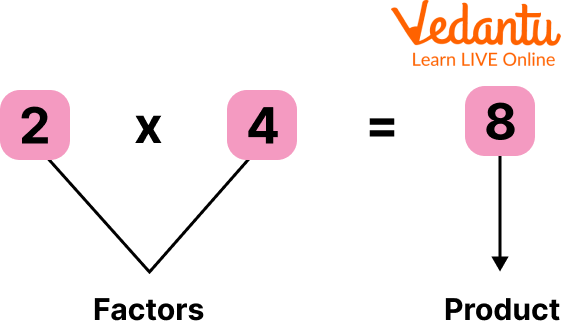
How to find Factors

Properties of Factors

• '1' is the smallest factor a number can have.

• Every number is always a factor in itself.

• The number of factors a number can have is always finite.

Things to Remember

1. '1' is not a prime number, hence it will not appear in the factor tree, but 1 is a factor of all numbers.

2. Factors of a number must be represented with multiplication symbol(×) and not addition while we represent it in index form.

3. The multiplication of factors of a number must always give the number which was factorized.

4. The last branch of the factor tree must always contain a prime number.

5. A factor tree will not contain decimals as we are working with positive factors only.

6. The factor tree of a number is not unique but the product of prime factors is unique.

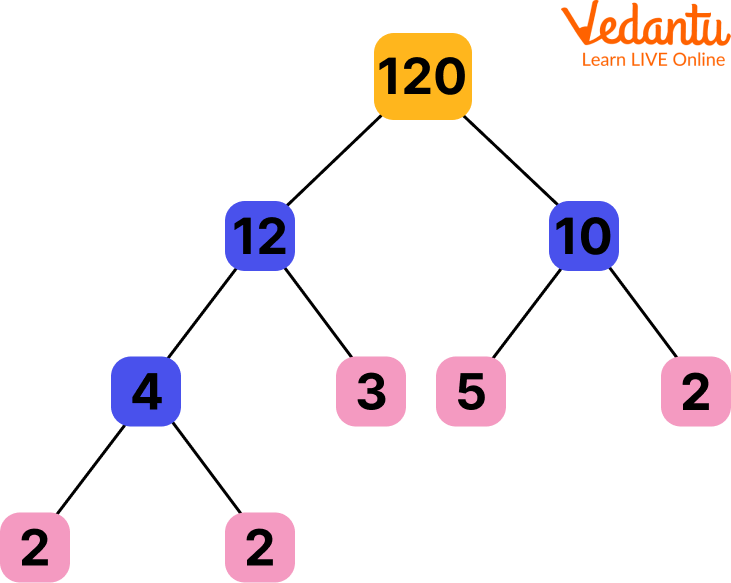
Factor tree

Steps to Construct a Factor tree

Here are some steps to make your factor tree practice easy.

Setp 1: Write the number at the top of the factor tree in a rectangular box.

Step 2: Fill in the branches with factors of the given top number.

Step 3: Factorized the branch number till we get a prime number in the end.

Step 4: Denote the prime number in the last with a circle.

Step 5: Write the solution in the indexed form separately.

Now, let us do some factor tree practice to make the concept easy for kids.

For example, express the factor of 51 in the form of the factor tree.

Here, we have $51=3 \times 17$

Hence the factors of 51 are 3 and 17 only.

Now we write 51 in a rectangular box and 3 and 17 as its branches. Both 3 and 17 are prime numbers. Hence we highlight both 3 and 17 in circles. We can say that 3 and 17 are prime factors of 17.

So, "When there is a prime number at the end of the factor tree we say that we have constructed a prime factor tree".

And, when there are no prime numbers at the end of the factor tree, it means it will be more factorized, we will have to split the branches until we receive prime numbers at the end of the branches.

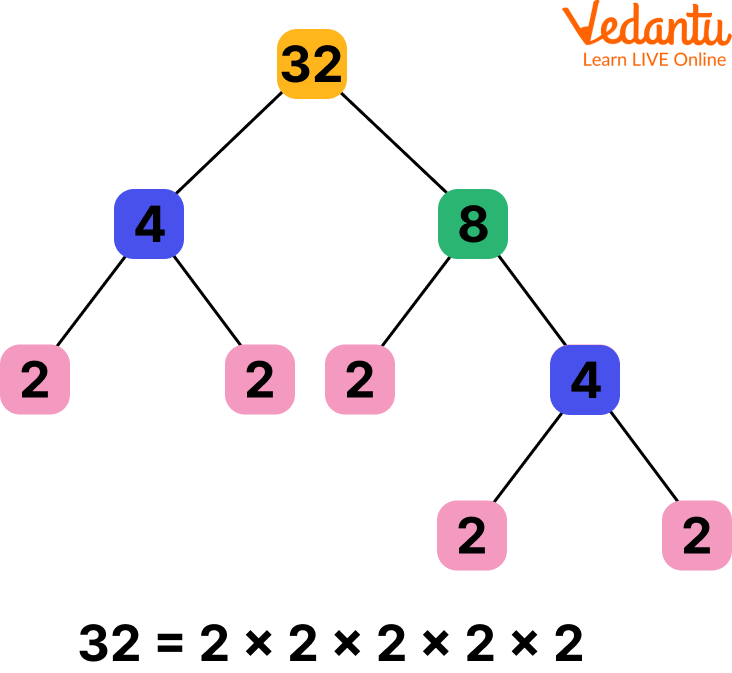
Factor tree example

Solved Examples

Q 1. Find the factors of 27.

Ans: We have $27=3 \times 9$

Hence, the factors of the number 27 are 1,3,9, and 27.

Q 2. Find the factors of the numbers 55 and 81 .

Ans: We have $55=11 \times 5$

Hence, factors of 55 are 1,5,11, and 55 .

Also, we have $81=3 \times 27=3 \times 3 \times 9$

Hence, factors of 81 are $1,3,9,27$ and 81.

Practice Set

Q 1. Find the factors of 20.

Ans: 1,2,4,5,10 and 20

Q 2. Find the factors of 81, 55,190

Ans: Factors are as following:

81= 1,3,9, 27,81

55= 1,5,11,55

190= 1,2,5, 10,19,190

Q 3. What is the smallest factor of 51?

Ans: 1

Summary

So in this article, we learned about factors. A number or algebraic expression which divides another number or expression in a way such that no remainder is left is called a factor. For example, 2 and 5 are the factors of 10 because 10÷2=5 and 10÷5= 2 exactly. We also saw how to make a factor tree to solve examples efficiently. Factors play an important role in day-to-day life. We tried to list factor questions that would help students to practice. Factor tree practice will help kids to factorize any numbers and find their prime factors. We understood how to solve factors and how to construct a factor tree.