




Step-by-Step Proof and Practical Applications for Students
The theorem on the exterior angle of a cyclic quadrilateral is used to state the property of cyclic quadrilaterals and helps us in solving complex problems related to exterior angles in an easy and efficient manner. Cyclic quadrilaterals are the quadrilaterals that are formed when all the vertices of the quadrilateral lie on the circumference of the circle. In this article, we will discuss the detailed proof of the theorem related to exterior angles of the cyclic quadrilateral along with the application of the cyclic quadrilateral in our real life.
History of Euclid

Euclid
Name: Euclid
Born: Mid-4th century BC
Died: Mid-3rd century BC
Field: Mathematics
Nationality: Greek
Statement of Theorem on the Exterior Angle of a Cyclic Quadrilateral
The theorem on the exterior angle of a cyclic quadrilateral states that an exterior angle of a cyclic quadrilateral is equal to the interior angle at the opposite vertex.
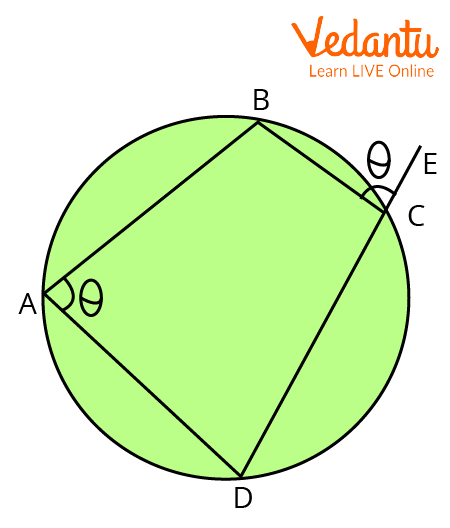
Cyclic Quadrilateral ABCD
Proof of Theorem on the Exterior Angle of a Cyclic Quadrilateral
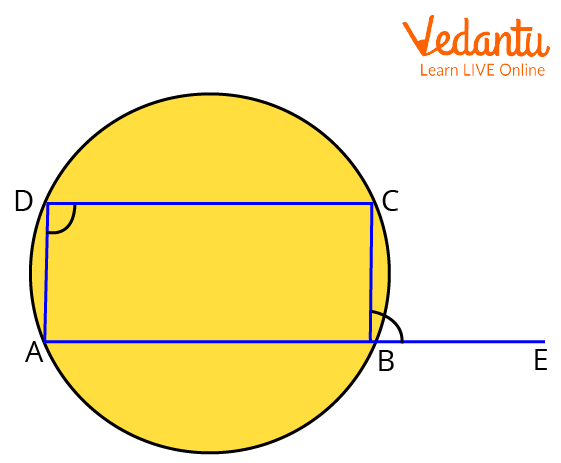
Proof of the Exterior Angle of a Cyclic Quadrilateral
Given: In a cyclic quadrilateral $A B C D$, side $A B$ is produced to a point $E$.
To prove: External $\angle C B E=\angle A D C$
Proof:
$\angle A B C+\angle C B E=180^{\circ}$ (Linear pair)
$\angle A B C+\angle A D C=180^{\circ}$ (Opposite angles of a cyclic quadrilateral)
Equating above both cases, we get
$\angle A B C+\angle C B E=\angle A B C+\angle A D C$
$\angle C B E=\angle A D C$
Hence proved.
Limitations of Theorem on the Exterior Angle of a Cyclic Quadrilateral
The theorem is applicable only in the case of cyclic quadrilaterals.
Applications of Theorem on the Exterior Angle of a Cyclic Quadrilateral
It is used in making paintings, sculptures, etc.
The Cyclic Quadrilateral Theorem is used in computer programming.
It is used in graphic arts, logos, and packaging.
Solved Examples of Exterior Angles of Cyclic Quadrilateral
1. In the cyclic quadrilateral, side $\mathrm{BD}$ is produced to $\mathrm{E}$ and $\angle B A C=75^{\circ}$. What is the value of $\angle C D E$?
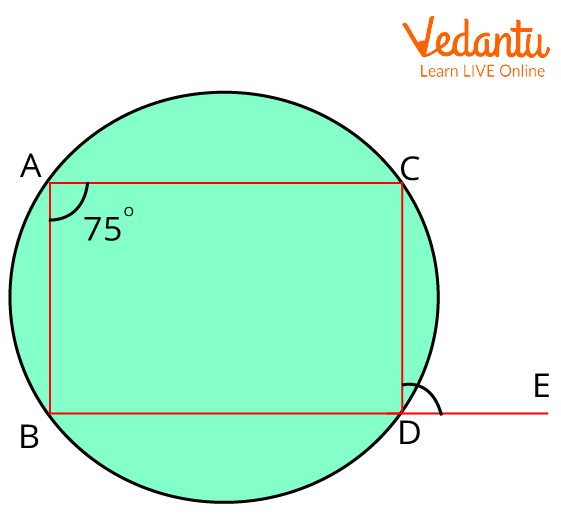
Angle A is given in ABCD is a Cyclic Quadrilateral
Ans:
$\angle B A C=\angle C D E$ (exterior angle of a cyclic quadrilateral is equal to the interior angle at the opposite vertex)
And we are given that $\angle B A C=75^{\circ}$
$\angle B A C=\angle C D E$
Therefore, $\angle C D E=75^{\circ}$
2. In the cyclic quadrilateral, side $\mathrm{BD}$ is produced to $\mathrm{E}$ and $\angle B A C=75^{\circ}$. What is the value of $\angle C D B$?

To Find Angle CDB in the Quad. ABCD
Ans:
$\angle B A C=\angle C D E$ (exterior angle of a cyclic quadrilateral is equal to the interior angle at the opposite vertex)
And we are given that $\angle B A C=75^0$
and $\angle B A C=\angle C D E$
Therefore, $\angle C D E=75^{\circ}$
$\angle C D B+\angle C B E=180^{\circ} \text { (Linear pair) } \\$
$\angle C D B+75^{\circ}=180^{\circ} \\$
$\angle C D B=105^{\circ}$
3. In the cyclic quadrilateral, side $\mathrm{BC}$ is produced to $\mathrm{E}$ and $\angle D C E=95^{\circ}$. What is the value of $\angle D A B$?

To Find Angle DAB
Ans:
$\angle B A D=\angle D C E$ (exterior angle of a cyclic quadrilateral is equal to the interior angle at the opposite vertex)
And we are given that $\angle D C E=95^{\circ}$
and $\angle B A C=\angle C D E$
Therefore, $\angle B A D=95^0$
Important Points to Remember
The exterior angle of a cyclic quadrilateral is equal to the interior angle at the opposite vertex.
Important Formulas to Remember
In a cyclic quadrilateral ABCD, side AB is produced to point E.
Then, External $\angle C B E = \angle A D C$
Conclusion
Cyclic Quadrilaterals are connecting links between polygons and circles. In the article, we have discussed the detailed proof of the exterior angles of the Cyclic Quadrilateral Theorem. Applications of the Cyclic Quadrilaterals are also discussed in this article. And we can conclude that the theorem is a fundamental tool of Euclidean Geometry and is of great significance in solving problems related to Cyclic Quadrilaterals.
FAQs on Theorem on Exterior Angle of a Cyclic Quadrilateral
1. What is a cyclic quadrilateral?
A quadrilateral is called cyclic if all four of its vertices lie on the circumference of a single circle. This means the quadrilateral is inscribed within the circle, a property that gives it unique angular relationships not found in other quadrilaterals.
2. What does the theorem on the exterior angle of a cyclic quadrilateral state?
The theorem on the exterior angle of a cyclic quadrilateral states that if a side of a cyclic quadrilateral is produced (extended), the exterior angle formed is equal to the interior opposite angle. For example, in a cyclic quadrilateral ABCD, if the side AB is extended to a point E, then the exterior angle ∠CBE will be equal to the interior opposite angle ∠ADC.
3. What is the main property of the interior angles of a cyclic quadrilateral?
The most important property of the interior angles of a cyclic quadrilateral is that the sum of each pair of opposite angles is 180° (i.e., they are supplementary). For any cyclic quadrilateral ABCD, this means:
- ∠A + ∠C = 180°
- ∠B + ∠D = 180°
4. How can you prove the theorem for the exterior angle of a cyclic quadrilateral?
The proof for this theorem is straightforward and relies on two basic geometric facts. Consider a cyclic quadrilateral ABCD where the side AB is extended to a point E, creating an exterior angle ∠CBE.
- Step 1: We know that opposite angles of a cyclic quadrilateral are supplementary. Thus, ∠ABC + ∠ADC = 180°.
- Step 2: The angle ∠ABC and the exterior angle ∠CBE form a linear pair on the straight line ABE. Therefore, ∠ABC + ∠CBE = 180°.
5. How is the exterior angle theorem of a cyclic quadrilateral used to solve problems?
This theorem provides a direct and efficient method to find unknown angles. For instance, if a problem gives you a cyclic quadrilateral with an exterior angle measuring 85°, you can immediately conclude that the interior angle at the opposite vertex is also 85°. This acts as a shortcut, saving you from having to calculate other intermediate angles to arrive at the answer, making it very useful in geometry problems under timed conditions.
6. What is the key difference between the exterior angle theorem for a triangle and for a cyclic quadrilateral?
The primary difference is what the exterior angle equals. It's a common point of confusion for students:
- For a triangle, an exterior angle is equal to the sum of the two interior opposite angles.
- For a cyclic quadrilateral, an exterior angle is equal to the single interior opposite angle.
7. Why is it necessary for the quadrilateral to be cyclic for this theorem to be valid?
The theorem's validity is entirely dependent on the foundational property of cyclic quadrilaterals: that their opposite angles sum to 180°. This property only holds true when all four vertices lie perfectly on a circle's circumference. If a quadrilateral is not cyclic, this specific angular relationship does not exist. Consequently, the proof, which equates the exterior angle to the interior opposite angle based on this 180° sum, falls apart. Therefore, the 'cyclic' condition is not optional; it is the reason the theorem works.































