Squeeze Theorem

Squeeze Theorem, also known as Sandwich Theorem, is a theorem used to find the limits of a function that is squeezed between two functions. The modern Squeeze form was given by Carl Friedrich Gauss. In this article, we will discuss the Squeeze theorem and the steps to apply and prove the Squeeze theorem in questions. Squeeze theorem proof and examples will be elaborated in this article in simpler form for better clarity of the topic and how to do Squeeze theorem in function will be discussed here.

History of Carl Friedrich Gauss

Carl Friedrich Gauss

Name: Carl Friedrich Gauss

Born: 30 April 1777

Died: 23 February 1855

Field: Mathematics

Nationality: German

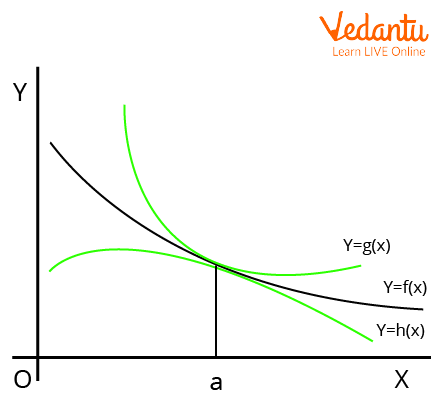
Statement of Squeeze Theorem

According to Squeeze Theorem, if g(x), f(x), h(x) are three functions such that \[g(x) \leq f(x) \leq h(x)\] and at any point a \[\mathop {{\rm{\;}}\lim }\limits_{x \to a} g(x) = \mathop {{\rm{\;}}\lim }\limits_{x \to a} h(x) = L \], then \[\mathop {{\rm{\;}}\lim }\limits_{x \to a} f(x) = L\].

Squeeze Theorem Proof

Assume that $g(x) \leq f(x) \leq h(x)$ and $\mathop {{\rm{\;}}\lim }\limits_{x \to a} g(x)=\mathop {{\rm{\;}}\lim }\limits_{x \to a} h(x)=L$.

Squeeze Theorem

Using the definition of limits,

$\Rightarrow \mathop {{\rm{\;}}\lim }\limits_{x \to a} g(x)=L \text { means that } \forall \in>0, exists \delta_{1}>0$ such that

$\Rightarrow|x-a|<\delta_{1}$

$\Rightarrow |x-a| < \delta_{1}$

$\Rightarrow|g(x)-L|< \epsilon$

$\Rightarrow - \epsilon < g(x)-L< \epsilon \ldots \text { (1) } $(expanding using property of modulus)

$\Rightarrow \lim _{x \rightarrow a} h(x)=L \text { using definition of limits again } \forall \in>0, \exists \delta_{2}>0 \text { such that }$

$\Rightarrow |x-a| < \delta_{2} $

$\Rightarrow |x-a| < \delta_{2} $

$\Rightarrow |h(x)-L| < \epsilon$

$\Rightarrow - \epsilon < h(x)-L < \epsilon \ldots \text { (2) }$ (expanding using property of modulus)

Now, it is given that $g(x) \leq f(x) \leq h(x)$.

Subtracting $L$ from each side of the above expression, we get

$\Rightarrow g(x)-L \leq f(x)-L \leq h(x)-L$

Let us choose $\delta=minimum \left\{\delta_{1}, \delta_{2}\right\}$,

we have, whenever $|x-a| < \delta$,

$\Rightarrow - \epsilon < g(x)-L \leq f(x)-L \leq h(x)-L <\epsilon \text { (using (1) and (2)) }$

So, from the above expression, we have

$\Rightarrow - \epsilon < f(x)-L < \epsilon$

$\Rightarrow \mathop {{\rm{\;}}\lim }\limits_{x \to a} f(x) = L$

Hence, the squeeze theorem is proved.

Limitations of Squeeze Theorem

• The squeeze theorem is not applicable if left and right function limits are not equal.

• The squeeze Theorem does not apply if we know the limits of any of two functions other than both extreme functions.

Applications of Squeeze Theorem

• The squeeze Theorem is used to reduce the tedious calculation of the limits of some functions.

• The squeeze Theorem can be related to the converging power of the lense.

Squeeze Theorem Examples

1. Evaluate the limit $\mathop {{\rm{\;}}\lim }\limits_{x \to 0}\left(x \cdot \cos \left(\dfrac{1}{x}\right)\right)$, if it exists.

Ans: We know that $-1 \leq \cos \left(\frac{1}{x}\right) \leq 1$ for all $x \neq 0$.

Then, $-x \leq x \cdot \cos \left(\frac{1}{x}\right) \leq x$, so

$\Rightarrow \mathop {{\rm{\;}}\lim }\limits_{x \to 0}(-x) \leq \mathop {{\rm{\;}}\lim }\limits_{x \to 0} \left(x \cdot \cos \left(\frac{1}{x}\right)\right) \leq \mathop {{\rm{\;}}\lim }\limits_{x \to 0} x$

Since $\mathop {{\rm{\;}}\lim }\limits_{x \to 0}(-x)=0=\mathop {{\rm{\;}}\lim }\limits_{x \to 0} x$,

we see that

$\Rightarrow \mathop {{\rm{\;}}\lim }\limits_{x \to 0}\left(x \cdot \cos \left(\frac{1}{x}\right)\right)=0$.

2. Evaluate the limit using the Squeeze Theorem:

$\mathop {{\rm{\;}}\lim }\limits_{x \to 0} x^{2} \cos \frac{5}{x}$

Ans: We know that $-1 \leq \cos \frac{1}{x} \leq 1$.

Next, multiplying the inequality by $x^{2}$, we have

$\Rightarrow-x^{2} \leq x^{2} \cos \frac{5}{x} \leq x^{2}$

Take the limit of each part of the inequality.

$\Rightarrow \mathop {{\rm{\;}}\lim }\limits_{x \to 0}\left(-x^{2}\right) \leq \mathop {{\rm{\;}}\lim }\limits_{x \to 0} x^{2} \cos \frac{5}{x} \leq \mathop {{\rm{\;}}\lim }\limits_{x \to 0} x^{2}$

Next, we know that

$\Rightarrow \mathop {{\rm{\;}}\lim }\limits_{x \to 0}\left(-x^{2}\right)=0 \text { and } \mathop {{\rm{\;}}\lim }\limits_{x \to 0}\left(x^{2}\right)=0$.

Thus, we have

$\Rightarrow 0 \leq \mathop {{\rm{\;}}\lim }\limits_{x \to 0} x^{2} \cos \frac{5}{x} \leq 0$

So, $\mathop {{\rm{\;}}\lim }\limits_{x \to 0} x^{2} \cos \frac{5}{x}=0$

3. Evaluate the limit using the Squeeze Theorem:

$\mathop {{\rm{\;}}\lim }\limits_{x \to 0} x^{2} \cos (10 x)$

Ans: We know that $-1 \leq \cos (10 x) \leq 1$.

Next, multiplying the inequality by $x^{2}$, we have

$\Rightarrow-x^{2} \leq x^{2} \cos (10 x) \leq x^{2}$

Take the limit of each part of the inequality.

$\Rightarrow \mathop {{\rm{\;}}\lim }\limits_{x \to 0}\left(-x^{2}\right) \leq \mathop {{\rm{\;}}\lim }\limits_{x \to 0} x^{2} \cos (10 x) \leq \mathop {{\rm{\;}}\lim }\limits_{x \to 0} x^{2}$

Next, we know that

$\Rightarrow \mathop {{\rm{\;}}\lim }\limits_{x \to 0}\left(-x^{2}\right)=0 \text { and } \mathop {{\rm{\;}}\lim }\limits_{x \to 0}\left(x^{2}\right)=0$.

Thus, we have

$\Rightarrow 0 \leq \mathop {{\rm{\;}}\lim }\limits_{x \to 0} x^{2} \cos (10 x) \leq 0$

So, $\mathop {{\rm{\;}}\lim }\limits_{x \to 0} x^{2} \cos (10 x)=0$

Conclusion

In the article, we have discussed the detailed proof of the Squeeze Theorem and its proof. Squeeze Theorem in simple terms says that if you are stuck between two things, then you will go the same way the two things are going. In all, we can say that Squeeze Theorem is a fantastic theorem in calculus and we can say that calculus needs limits and limits needs Squeeze Theorem.

Important Formulas to Remember

If $g(x), f(x), h(x)$ are such that $g(x) \leq f(x) \leq h(x)$, and $\mathop {{\rm{\;}}\lim }\limits_{x \to a} g(x)=\mathop {{\rm{\;}}\lim }\limits_{x \to a} h(x)=L$ then $\mathop {{\rm{\;}}\lim }\limits_{x \to a} f(x)=L$

Important Points to Remember

• Squeeze Theorem is also known as Sandwich Theorem.

• The limit of the Squeeze function has the same value as the limits of the other two functions.