




How to Simplify Math Questions Step by Step
Do you feel lost when it comes to Maths problems? If that's the case, simplification questions happen to be your best friend. Join us as we walk you through this problem-solving technique, giving an example of how they work and how they can help simplify Maths examples that are difficult concepts to solve!
Simplification questions can be useful because they help you to solve more complicated problems with ease. Simplification questions are asked in Maths to help the learner simplify a concept. They can be used to help in getting rid of complications. You are simplifying so they can understand the reasoning behind the question.
What are Simplification Questions?
The word simplification refers to any process of making something as easy as possible. Simplification questions are questions that can simplify Maths examples, like the one below:
Example: Simplify $4(10+15\div\,5\times 4-2\times 2)$
Ans: The answer is: $72$
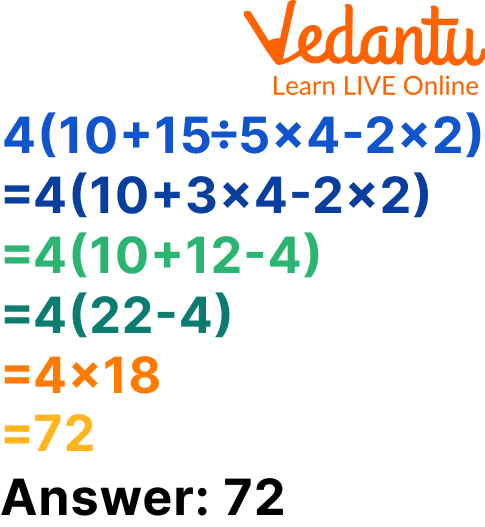
Simplify the Question
The basic idea behind simplifying is that you want to transform your number or expression into its simplest form by reducing the numerical value and getting rid of the signs.
What is the Simplification Formula?
BODMAS: This is an acronym for a set of steps that you should follow when answering a question, which are: Bracket, Order, Division, Multiplication, Addition, and Subtraction. The objective is to reduce the number as much as possible without causing problems with addition or subtraction.
B: Brackets
O: Operation
D: Division
M: Multiplication
A: Addition
S: Subtraction

BODMAS
How Do You Solve Simplification Questions?
To solve simplification problems, you must understand the process behind simplifying.
Step 1: Check for the operations that are equal to each other.
Example: Simplify (a+bc)+(b-d)(a-c)(d+b)-2, using the BODMAS simplification formula.
Step 2: Check for similar operations of the operands. Example: Simplify (ab+cd)(ab-bc)(a-b)+(c-d).
Step 3: If operations are not equal or similar, simplify the one on the right of the equal sign first.
Step 4: Add together (or multiply) all terms using the same or similar operations. Example: Simplify x(x+3)+(x-9)
Step 5: Include any brackets with numbers that have been added together (or multiplied).
How Do You Simplify a Fraction?
You can combine the numerator and the denominator by adding, subtracting, or multiplying them together.
For example, one of the simplification questions with solutions is, $\dfrac{12}{6}$ simplifies to $\dfrac{2}{3}$ by adding 6+12 to get 18 and $\dfrac{18}{3}$=6.
For example, 5x4=20 becomes $\dfrac{20}{10}$= 2 so 5x4 = 20 or 2x5 = 10.
The new number is now divided into 10 parts instead of four parts to get your final answer of two.
How to Simplify Decimals?
If a number is in decimals, you would have to convert it into fractions before simplifying. The simplest form of converting $\dfrac{2}{3}$ into a decimal which is 0.66 or to a fraction with one unit, $\dfrac{6}{1}$=6 becomes the answer.
If it were in fractions, then your number would be easier than doing the multiplication. So try converting them into fractions first, and then simplify while solving simplification problems.
Solved Examples
Q1 Simplify: 37 - [5 + {28 - (19 - 7)}]
Ans: 37 - [5 + {28 - (19 - 7)}]
= 37 - [5 + {28 - 12}] (Removing the innermost bracket ( ))
= 37 - [5 + 16]
= 37 - 21
= 16.
Q2 Simplify: 78 - [24 - {16 (5 - 4 - 1)}]
Ans:-78 - [24 - {16 (5 – 4 - 1)}]
= 78 - [24 - {16(5 - 5)}] (Removing vinculum)
= 78 -[24 - {16 (0)}] (Removing parentheses)
= 78 - [24 – 0] (Removing braces)
= 78 - 24
= 54
Q3. Simplify. $\dfrac{1}{3}+\left[\dfrac{1}{2}-\left\{\dfrac{1}{5}+\left(\dfrac{1}{3}-\dfrac{1}{5}\right)\right\}\right]$
Ans: $\dfrac{1}{3}+\left[\dfrac{1}{2}-\left\{\dfrac{1}{5}+\left(\dfrac{1}{3}-\dfrac{1}{5}\right)\right\}\right]$
$=\dfrac{1}{3}+\dfrac{1}{6}$
$= \dfrac{2+1}{6}$
$=\dfrac{1}{2}$
Practice Questions
Q1. 3 - (5 – 6 ÷ 3)
Ans: 0
Q2. – 25 + 14 ÷ (5 - 3)
Ans: -18
Q3. 25-{5+4-(3+2-1+3)}
Ans: 23
Q4. 27 - [38 - {46 - (15 - 13 - 2)}]
Ans: 35
Q5 36 - [18 - {14 - (15 – 4 ÷ 2 x 2)}]
Ans: 21
Summary
We've covered a lot of different strategies for simplification questions in this article. We've focused on the BODMAS method, which is a helpful way to simplify original equations, and learned to simplify equations by cancelling out factors.
In our opinion, it is one of the ways to learn maths quickly, because you can use this rule over and over again. At first, you do not understand what it truly means, but as you keep applying it in real-life situations and play games, you begin to grasp the meaning of how many even numbers there are in a set of numbers.
FAQs on Simplify Questions Made Easy
1. How to solve a simplify question?
To solve a simplify question in mathematics, you aim to reduce an expression or equation to its most basic or efficient form. This often involves:
- Combining like terms
- Performing arithmetic operations
- Factoring expressions where possible
- Canceling common factors
2. What is an example of a simplification question?
Simplification questions typically ask students to rewrite expressions in their simplest form. For instance:
Example: Simplify $4(a + b) - 2a + 3b$.
Solution:
$4a + 4b - 2a + 3b$
= $(4a - 2a) + (4b + 3b)$
= $2a + 7b$
At Vedantu, students can practice various such examples with expert-verified solutions and concept explanations.
3. What are some examples of simplify?
Here are several examples of simplify questions across different math topics:
- Algebra: Simplify $(x^2 + 2x + 1) - (x^2 - 3x + 2)$
- Fractions: Simplify $\frac{8}{12}$
- Decimals: Simplify $2.50 + 3.150$
- Exponents: Simplify $2^3 imes 2^2$
4. What does it mean to simplify a question?
To simplify a question in mathematics means to make an expression, equation, or problem as straightforward and manageable as possible. The goal is to:
- Eliminate unnecessary complexity
- Combine and reduce terms
- Express the answer in the most concise form
5. How do you simplify algebraic expressions step by step?
To simplify algebraic expressions, follow these systematic steps:
- Remove brackets by applying the distributive property.
- Combine like terms: Add or subtract terms with the same variable and exponent.
- Arrange terms in order, usually descending by exponent.
- Factor the expression if possible for further simplification.
$3x + 12 + 2x - 6$
Combine like terms: $(3x + 2x) + (12 - 6)$
=$5x + 6$
Vedantu’s platform provides interactive examples and doubt-solving classes on such algebraic methods.
6. What strategies can help simplify complex fractions?
To simplify complex fractions:
- Find a common denominator for the numerator and denominator, if needed.
- Simplify both separately.
- If there is a fraction divided by another fraction, apply: $\frac{a}{b} \div \frac{c}{d} = \frac{a}{b} \times \frac{d}{c}$.
For example, simplify $\frac{\frac{3}{4}}{\frac{5}{8}}$:
Invert and multiply: $\frac{3}{4} \times \frac{8}{5} = \frac{24}{20} = \frac{6}{5}$
At Vedantu, tutors break down these steps with visual aids for deeper understanding.
7. Why is simplification important in math examinations?
Simplifying mathematical expressions is crucial in exams for several reasons:
- Saves time, making it easier to handle lengthy questions.
- Reduces errors by minimizing computational steps.
- Clarifies answers as required by marking schemes.
8. How to simplify expressions with exponents and roots?
When faced with exponents and roots, use key properties:
- Product of exponents: $a^m \times a^n = a^{m+n}$
- Power of a power: $(a^m)^n = a^{mn}$
- Root as exponent: $\sqrt[n]{a} = a^{1/n}$
Example: Simplify $\sqrt{16x^4} = \sqrt{16} \times \sqrt{x^4} = 4x^2$
Vedantu's concept notes and problem sets give ample practice with these simplification types.
9. Are there online resources to practice simplification questions?
Yes, Vedantu offers a wide range of online resources for practicing simplification questions, including:
- Interactive quizzes
- Downloadable worksheets
- Live classes with expert teachers
- Video lectures on step-by-step simplification techniques
10. What are common mistakes students make when simplifying?
Common mistakes in simplifying mathematical expressions include:
- Incorrectly combining unlike terms
- Omitting brackets during distribution
- Miscalculating negative signs
- Forgetting exponent or fraction rules























