




How to Identify Point Symmetry: Steps & Tips
In mathematics refers to a specific pattern in which we may draw a centre dividing line on a form or object and it offers two perfectly identical sides termed symmetry, and the shape or thing is referred to as symmetrical when this occurs. Examples of symmetrical figures are butterflies, and honeycombs made by bees. There are different types of symmetry, one of them being point symmetry. Let us now learn about it.
What Is Point Symmetry?
Point symmetry occurs when every part has a mirror portion. It is the same distance as the centre point but in the opposite direction. It is sometimes referred to as "Order 2 rotational symmetry." However, the two conditions listed below can be used to see if a shape possesses symmetry around a point.
Every portion of the defined form must be the same distance from the centre as the others.
The part of the form and its equivalent part must be in opposing directions.
What Is Line Of Symmetry?
The line of symmetry is an imaginary line that divides a form into two precise or identical halves. This line of symmetry in math shows the symmetry in form along only one axis. Many forms can have many lines of symmetry because they can be split into half by more than one line. A location within an object or figure through which any straight line passes, as well as two points on the figure's edge at the same distance from the centre but on opposing sides, is the centre of symmetry.
The following are the attributes of the line of symmetry:
It always travels through the shape's centre.
The halves formed by creating the symmetry line reflect each other. As a result, this sort of symmetry is also known as reflection symmetry.
Because the halves formed by drawing the line of symmetry math are mirror copies of each other, the symmetry is also known as mirror symmetry.
Point Symmetry Is Seen In Alphabet
When you draw a line across the point of symmetry, it will intersect the figure such that one side of the point would be at the same distance from the point. Point symmetry exists when every piece of an item has an equal part and can be seen in the English alphabet. The alphabet O has the centre point, and the equivalent parts are oriented in opposite directions. The uppercase letters H, I, N, O, X and Z all have point symmetry; when you draw a line from the middle of H, I, O and X you will get both upper and lower parts of the same length. The letters H, I, O, and X all have point and line symmetry.
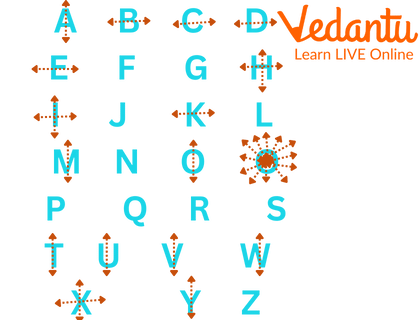
Centre of Symmetry Examples For Alphabets
Point Symmetry In Shapes
If two equal forms are made by putting a point on an object or shape, but they face different directions, the object or shape shows point symmetry. Or in simple words, we can say that the point of origin should be equally distant from the two opposite sides of a shape. Squares and rectangles, for example, have a point of symmetry. We can restore the original form by rotating the shapes square and rectangle 180 degrees.
Conclusion
In conclusion, we can say that every object may or may not be symmetrical depending upon the line of symmetry that passes through it. An object has a centre of symmetry if an imaginary line can be stretched from any point on its surface to its centre and a corresponding point exists along the line equidistant from the centre.
Sample Questions
1. Which alphabet has a point of symmetry?
a. Q
b. O
c. G
d. L
Ans. O
Explanation: A point of symmetry is a point of origin through which a line of symmetry passes. O can be divided into two equal-looking halves making it an alphabet not having a line of symmetry with two parts being placed equally distant from each other.
2. Which shapes do not have a point of symmetry?
a. Equilateral Triangle
b. Circle
c. Square
d. None of the above
Ans. None of the above
Explanation: All the shapes have points of symmetry as they have two opposite parts that are equally placed from the point of origin.
3. A line of symmetry divides the object into two or more parts.
a. True
b. False
Ans. False
Explanation: A line of symmetry divides the object into two equal halves which when placed over one another cover themselves fully.
FAQs on What Is Point Symmetry in Mathematics?
1. What is point symmetry in mathematics?
Point symmetry describes a property of a shape where it looks identical after being rotated by 180 degrees around a central point. This central point is known as the centre of symmetry. For every point on the shape, there is a corresponding point on the opposite side at the same distance from the centre.
2. How can you determine if a shape has point symmetry?
To check for point symmetry, you can perform a simple test: identify the shape's centre and turn it upside down (a 180-degree rotation). If the shape appears exactly the same after the rotation, it possesses point symmetry. If it looks different, it does not.
3. What are some examples of geometric shapes that have point symmetry?
Many common geometric shapes have point symmetry. Some key examples include:
- Circle
- Square
- Rectangle
- Rhombus
- Parallelogram
- Regular hexagon and other even-sided regular polygons
4. Which uppercase letters of the English alphabet exhibit point symmetry?
Several uppercase letters in the English alphabet have point symmetry. When rotated 180 degrees about their centre, they remain unchanged. These letters are H, I, N, O, S, X, and Z.
5. What is the key difference between point symmetry and line symmetry?
The main difference lies in the transformation involved. Line symmetry (or reflectional symmetry) means a shape can be folded along a line, and both halves will match perfectly, like a mirror image. Point symmetry (or rotational symmetry of order 2) involves rotating the shape 180 degrees around a central point to get the same appearance.
6. How is point symmetry related to rotational symmetry?
Point symmetry is a specific type of rotational symmetry. A figure has rotational symmetry if it looks the same after a rotation of less than 360 degrees. Point symmetry is precisely defined as rotational symmetry of order 2, which means the shape maps onto itself after a half-turn (180 degrees).
7. Can a figure have both line symmetry and point symmetry? Provide an example.
Yes, a figure can have both types of symmetry. A square is a perfect example. It has four lines of symmetry (one horizontal, one vertical, and two diagonal) and also has point symmetry around its centre. A rectangle and a circle are other common examples.
8. In coordinate geometry, how is point symmetry about the origin represented mathematically?
In a coordinate plane, a figure has point symmetry with respect to the origin (0,0) if for every point (x, y) on the figure, the corresponding point (-x, -y) is also on the figure. This mathematical rule confirms that each point is reflected through the origin to its opposite position.
9. Are there examples of point symmetry found in the real world or nature?
Yes, point symmetry appears in various real-world contexts. Examples include some playing cards (like the 10 of hearts), the design of many car hubcaps or alloy wheels, certain logos, and the yin-yang symbol. While perfect point symmetry is rare in nature, some flowers or starfish exhibit rotational symmetry that is closely related.
10. How do you draw a figure with point symmetry?
To draw a figure with point symmetry, follow these steps:
- First, mark a central point (the centre of symmetry).
- Draw any point or line segment on one side of the centre.
- To create its symmetrical counterpart, draw a straight line from your original point through the centre.
- Measure the distance from the original point to the centre, and mark the new point at the same distance on the opposite side.
- Repeat this process for all parts of your figure to complete the symmetrical design.

















