Plane Surface

Have you ever noticed which type of surfaces we deal with every day? We deal with both types of surfaces in our everyday life, i.e. plane surfaces as well as curved surfaces. There is nothing possible without the surface in one's life. In the below article, students will acquire knowledge about what surfaces in maths are, types of surfaces, and single curved surfaces. This is one of the most basic topics of geometry, thus, should be on the tips of every student to excel in further mathematics. Now, let's begin with our learning.

What is Surface in Maths?

A surface in maths is defined as the continuous space available for the collection of points that may or may not be two-dimensional. Surface examples are cones, ellipsoids, flat surfaces of 3-dimensional solids, etc.

Types of Surfaces

There are several types of surfaces whose list is given below:

• Minimal Surface

• Ruled Surface

• Quadrics

• Non-orientable Surface

• Pseudospherical Surface

• Algebraic Surface

• Miscellaneous Surface

What is a Plane Surface?

A two-dimensional flat surface extended indefinitely is called a plane surface. In simple terms, a plane surface is a flat surface that can be extended in all possible directions. Plane surface examples are flat surfaces of cubes and cuboids, floors with zero thickness, etc.

Showing Plane surfaces that are parallel

Properties of Planes

• If there are two distinct planes, they are either parallel or intersect in a line.

• A line is either parallel to a plane, intersects at a single point, or exists in the plane.

• If there are two distinct lines, which are perpendicular to the same plane, then they must be parallel to each other.

• If two different planes are perpendicular to the same line, they must be parallel.

What is a Curved Surface?

A curved surface is defined as a surface which is not flat. These surfaces are two-dimensional as well as three-dimensional. For example, water bottles, ice cream cones etc. Curved Surfaces can further be divided into two categories, namely:

1. Single Curved Surface

2. Double Curved Surface

What is Single Curved Surface

A single curved surface represents the curved surface in which only one is curved out of two given curves. This makes the surface developable, the one whose Gaussian Curvature is always zero.

Single Curved Surface

Solved Surface Examples

Q 1. Which three-dimensional geometrical figure has only one curved surface with no plane surface?

Ans: The geometrical figure possessing only one curved surface is a sphere. It has no flat surface due to its round or circular shape.

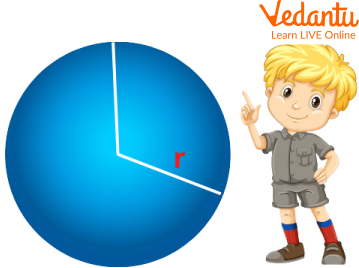
Showing a three-dimensional figure, sphere

Q 2. Which shape represents each flat surface of a cylinder?

Ans: Cuboid is the shape that represents the flat surfaces of a cylinder. Also, the two circular surfaces represent the flat surface of a cylinder. It has three flat surfaces with two circular ends depicted by the circles and one rectangular surface.

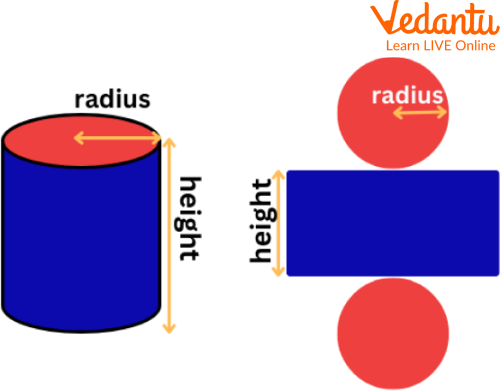
Showing the open sketch of a three-dimensional figure, cylinder

Practice Problems

Q 1. State three plane surface examples that belong to one's environment and real life.

Ans: Top of a table, Wall and Floor.

Q 2. A plane represents the _______ surface with no thickness.

Ans: flat.

Q 3. Which surface is called the developable surface?

Ans: Single curved surface is sometimes called a developable surface.

Summary

Summing up here with the concept of surfaces. This writing covers numerous topics, including surfaces, types of surfaces, plane surface examples, single curved surfaces and solved surface examples. Practice problems are assigned based on these topics to check students’ understanding. The language is kept simple and interesting to grab children's kind attention. In addition, images make the article more engaging for the students. Wishing you enjoyed reading the article. Feel comfortable to ask your problems by writing in the comments.