Perpendicular Formula

In geometry, a pair of lines that meet or intersect at right angles (90°) are referred to as perpendicular lines. To determine if two provided lines are perpendicular to one another or not, apply the perpendicular lines formula. When we know the slope of two lines we want to compare, we can use the perpendicular lines formula. Two lines that are perpendicular to one another form a 90 degree angle.

What is the Perpendicular Line Slope?

A line's steepness can be determined by looking at its slope. Slope is calculated mathematically as "rise over run" (change in y divided by change in x). The letter "m" represents the slope. The ratio of the "vertical change" to the "horizontal change" between any two separate points on a line is used to determine slope. The ratio can also be written as a quotient, where each of the two unique points on the same line is assigned the same integer.

What is the Equation of Perpendicular Line?

Now, We will learn to find the equation of the perpendicular line. It forms a 90-degree angle with a specific place where the line passes. The need for determining the perpendicular line is coordinates and a line equation.

Think about a line with the equation \[ax + by + cz = 0\] and the coordinates \[\left[ {{x_1},{y_1}} \right]\] The slope of this line should be \[\dfrac{-a}{b}\]. The slopes should add up to -1 if one line is perpendicular to this one. Let \[{m_1}{\rm{ and }}{m_2}\] represent the slopes of two lines; their product will be -1 if the lines are perpendicular to one another.

Formula:

\[\begin{array}{l}m = \left( {\dfrac{{ - a}}{b}} \right)\\{m_1} \times {m_2} = - 1\end{array}\]

Where \[{m_1}\] represents the slope of the first line.

\[{m_2}\] represents the slope of the second line.

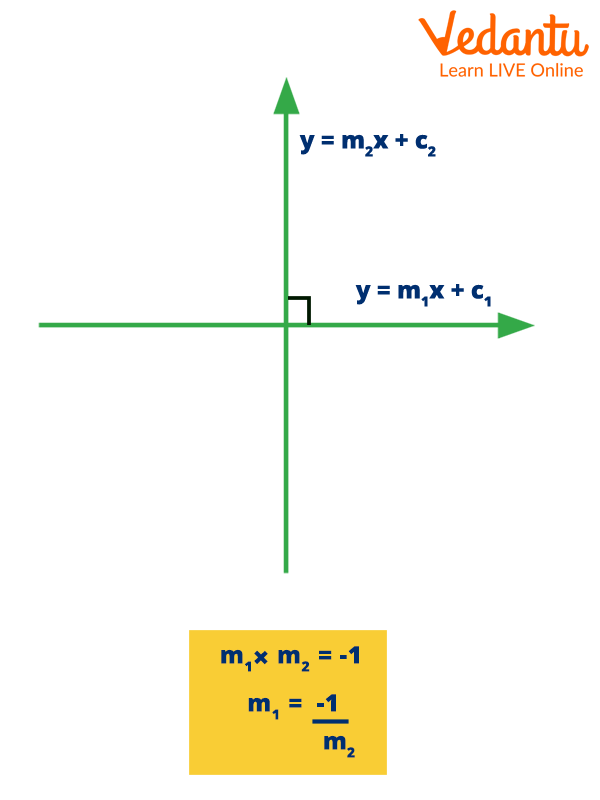
Perpendicular Formula

Applications of Perpendicular Formula in Real Life

Perpendicular lines can be found all around us in everyday life. The following are instances of perpendicular lines in the real world:

• Boundary lines of the Football field.

• Boundary lines of the Medical kit.

• The building of a home with perpendicular walls and floors.

• Boundary lines of the Television.

Conclusion

The original slope's reciprocal will be the opposite of the perpendicular slope. To find the intercept, b, enter the supplied point and the new slope into the slope-intercept form \[\left[ {y = mx + b} \right)\] .Rewrite the following equation in standard form:\[ax + by = c\] .

Solved Examples

Example 1: Verify whether or not the equations \[2x + 3y + 5 = 0{\rm{ and }}3x - 2y + 1 = 0\] are perpendicular.

Ans: Two equations for lines are provided: \[2x + 3y + 5 = 0{\rm{ and }}3x - 2y + 1 = 0\].

Find the slopes of both lines to see if they are perpendicular to one another. These lines are perpendicular to one another if the product of their slopes is a negative one.

The slope is given by \[\begin{array}{l}m = \left( {\dfrac{{ - a}}{b}} \right)\\\end{array}\] .

First line's slope is \[{m_1} = \dfrac{{\left( { - 2} \right)}}{3}\]

Second line slope:\[{m_2} = \dfrac{{\left( { - 3} \right)}}{{\left( { - 2} \right)}}\]

For two lines to be perpendicular, we know that \[{m_1} \times {m_2} = - 1\]

The given lines are perpendicular to one another since the product of slope equals -1.

Example 2: What will the slope of the line perpendicular to the line \[3y - 45x = 12\] be?

Ans: To find: The perpendicular line's slope

Given: Line 1 equation: \[3y - 45x = 12\].

Rearranging and multiplying by three gives us: \[y = 15x + 4\]

When compared to \[{\bf{y}}{\rm{ }} = {{\bf{m}}_1}{\bf{x}}{\rm{ }} + {{\bf{c}}_1}, {{\bf{m}}_1} = {\rm{ }}{\bf{15}}\]

Using the formula for perpendicular lines,

\[{m_1} \times {m_2} = - 1\]

\[{m_2} = \dfrac{{ - 1}}{{15}}\]

As a result,\[\dfrac{{ - 1}}{{15}}\] is the perpendicular line's slope.

Example 3: What kind of equations are perpendicular?

Ans: The definition of a perpendicular line in geometry is a pair of lines that meet or intersect at right angles (90°). For two perpendicular lines we can say that the product of their slope is equal to -1.