




How to Solve Math Problems Using Multiplication and Division Models
Students should have a clear understanding of Mathematical operations and not just memorise steps and procedures. For that, it is essential that students are able to analyse numbers and think about their relations. The algorithms of traditional multiplication and division are important to learn. To gain the full concept of this, we should start with a concrete concept and then move towards the pictorial and finally end with the abstract which will help students develop full mastery. In this article, there are some models that will be discussed which will help students to understand the relationship between multiplication and division.
Examples of Multiplication and Division Models
The multiplication and division models are discussed below with examples.
Arrays
Array Model is one of the earliest models which is helpful in understanding the concept of multiplication and division. In this model, we can observe the connection between the two operations and can visually see the concept of “grouping” or “sharing”. An example of multiplication of 3 and 6 and division of 18 by 3 is given in the array model.
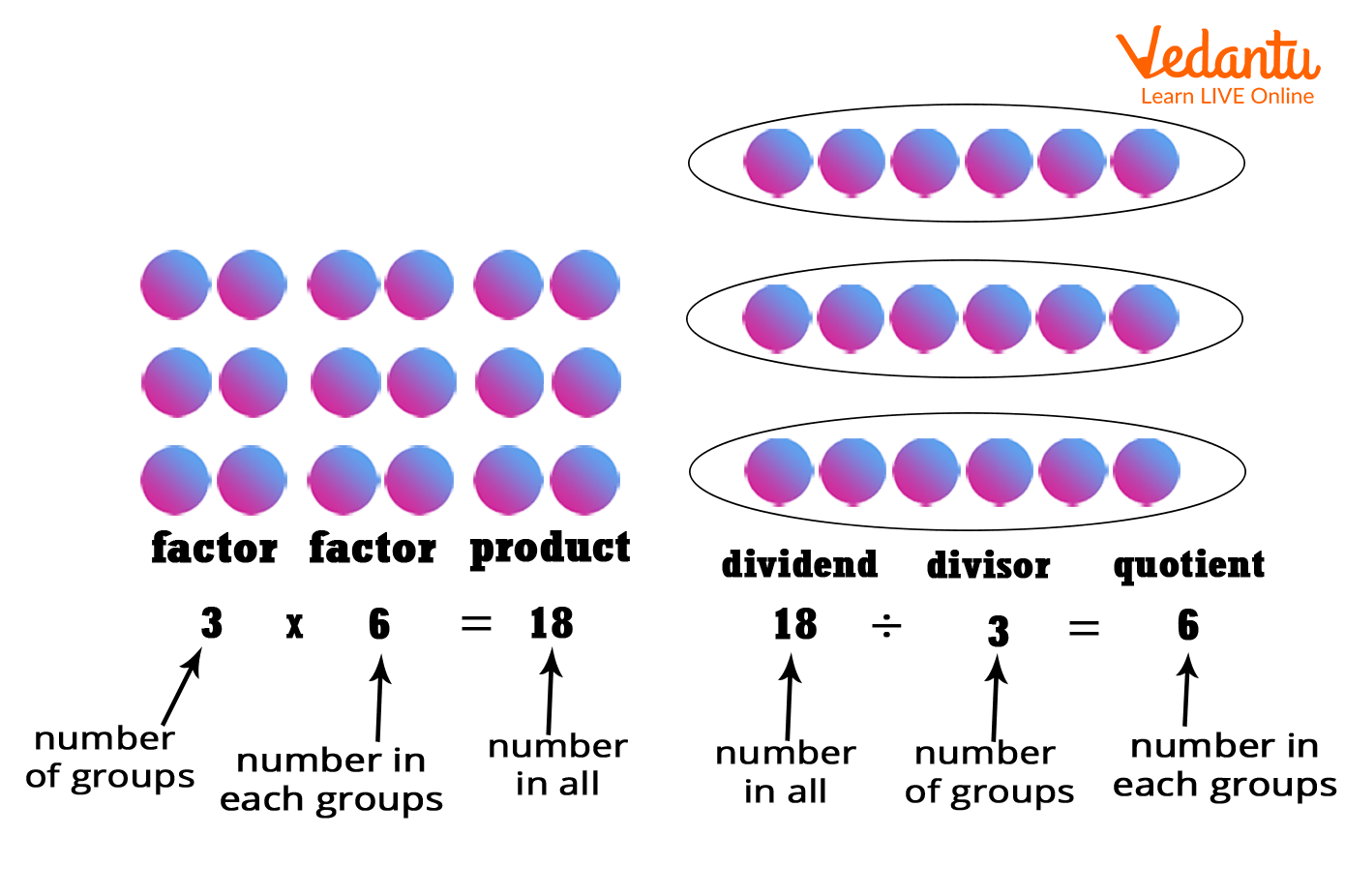
Image: Example of arrays model of multiplication and division
Area Models
The area model is closely related to the computation with the standard algorithm. In this model, the difference is the visual representation and connection to the Base 10 System, and the understanding of place value. We can visually see the actual size of each computation and learn how to interpret the partial products. An example of multiplication of 7 and 16 is given below through the area model.
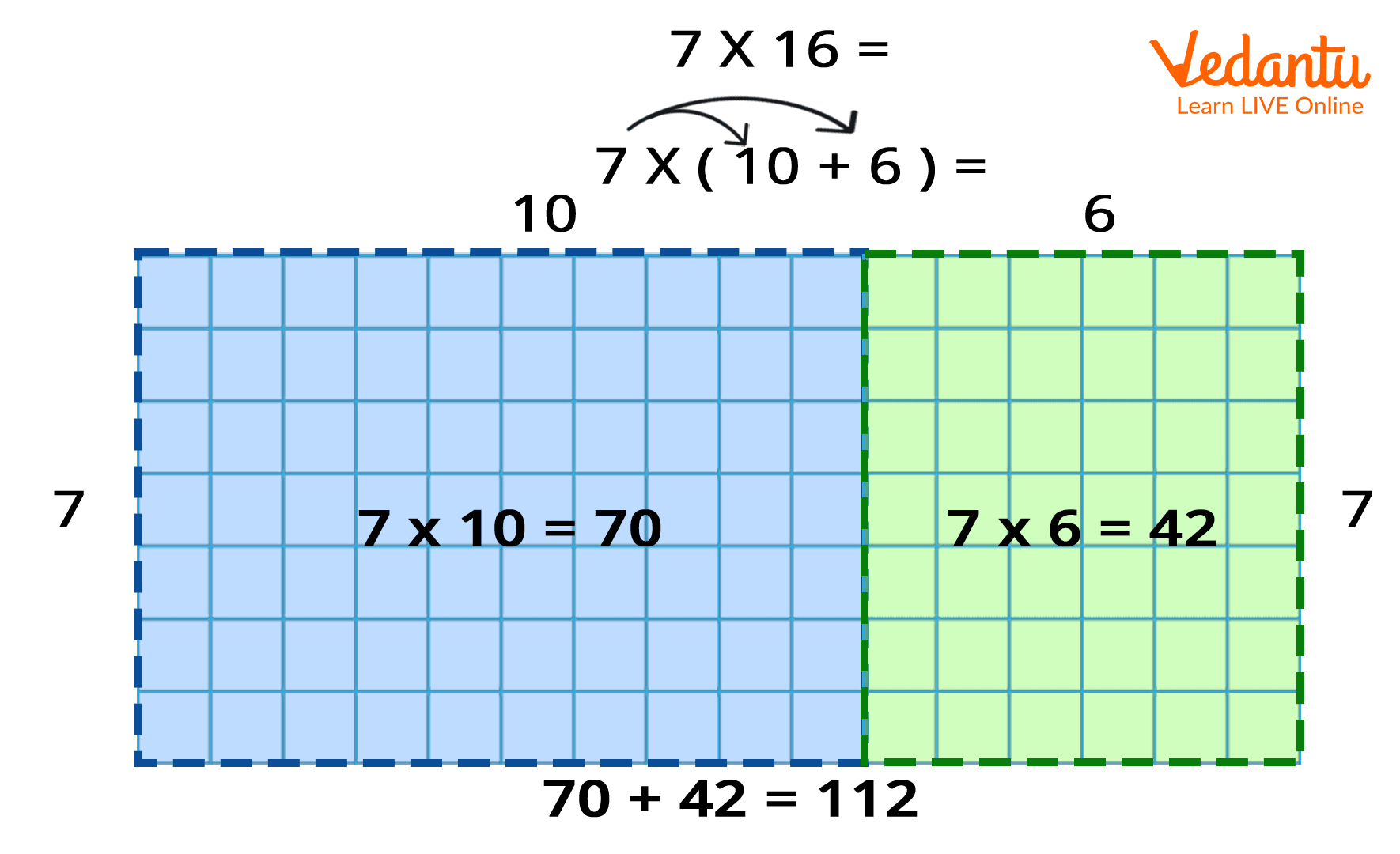
Image: Example of area model
Bar Models
This model is based on the concept of equal groups and part-part-wholes. This model is helpful in moving away from the concrete phase and makes us familiar with the pictorial stage. Bar models are a good method for the students to show their thinking when problem-solving, especially when solving two-step problems. An example of multiplication of 30 and 4 is given below with the help of the bar model.
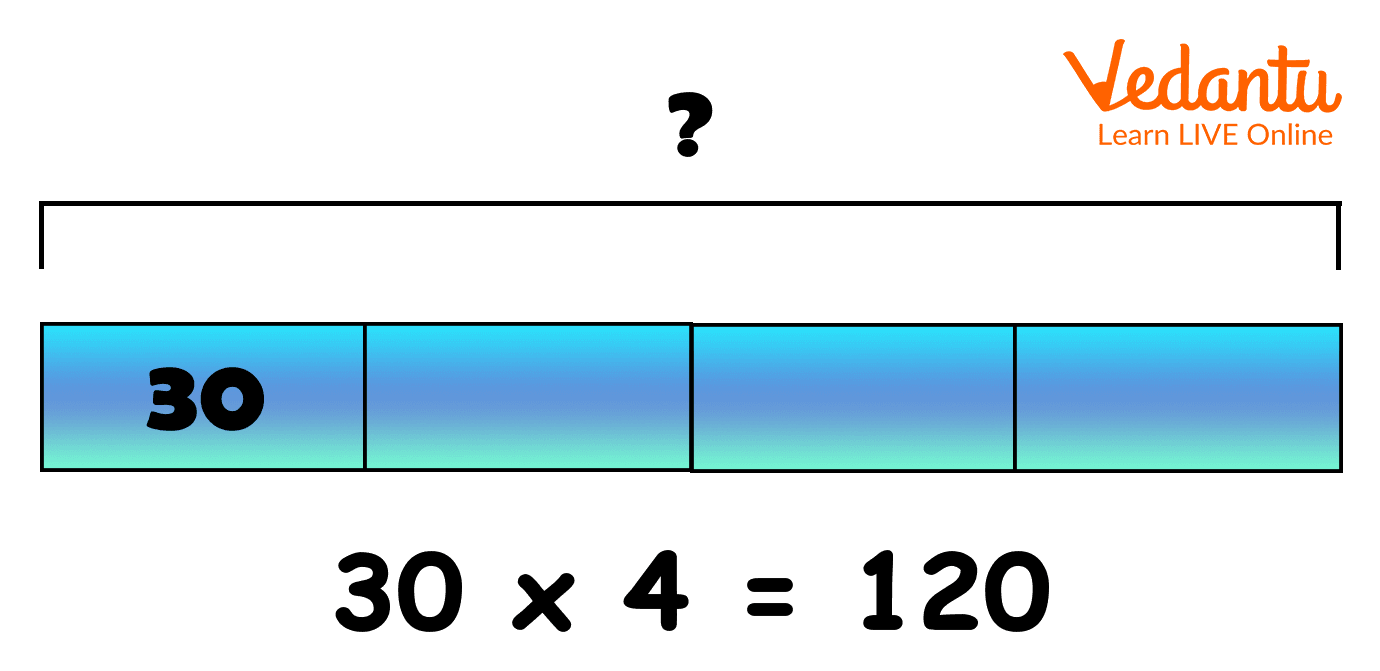
Image: An example of the bar model of multiplication
Number Lines
Number lines help students to know the abstract stage of multiplication and division. They are allowed here to “skip” forwards or backwards direction distances to represent the inverse operation. Number lines are a traditional model which is taught to students to develop their thinking and explain the reasoning of multiplication and division. An example of multiplication of 4 and 5 and division of 20 by 5 is given below with the help of a number line.
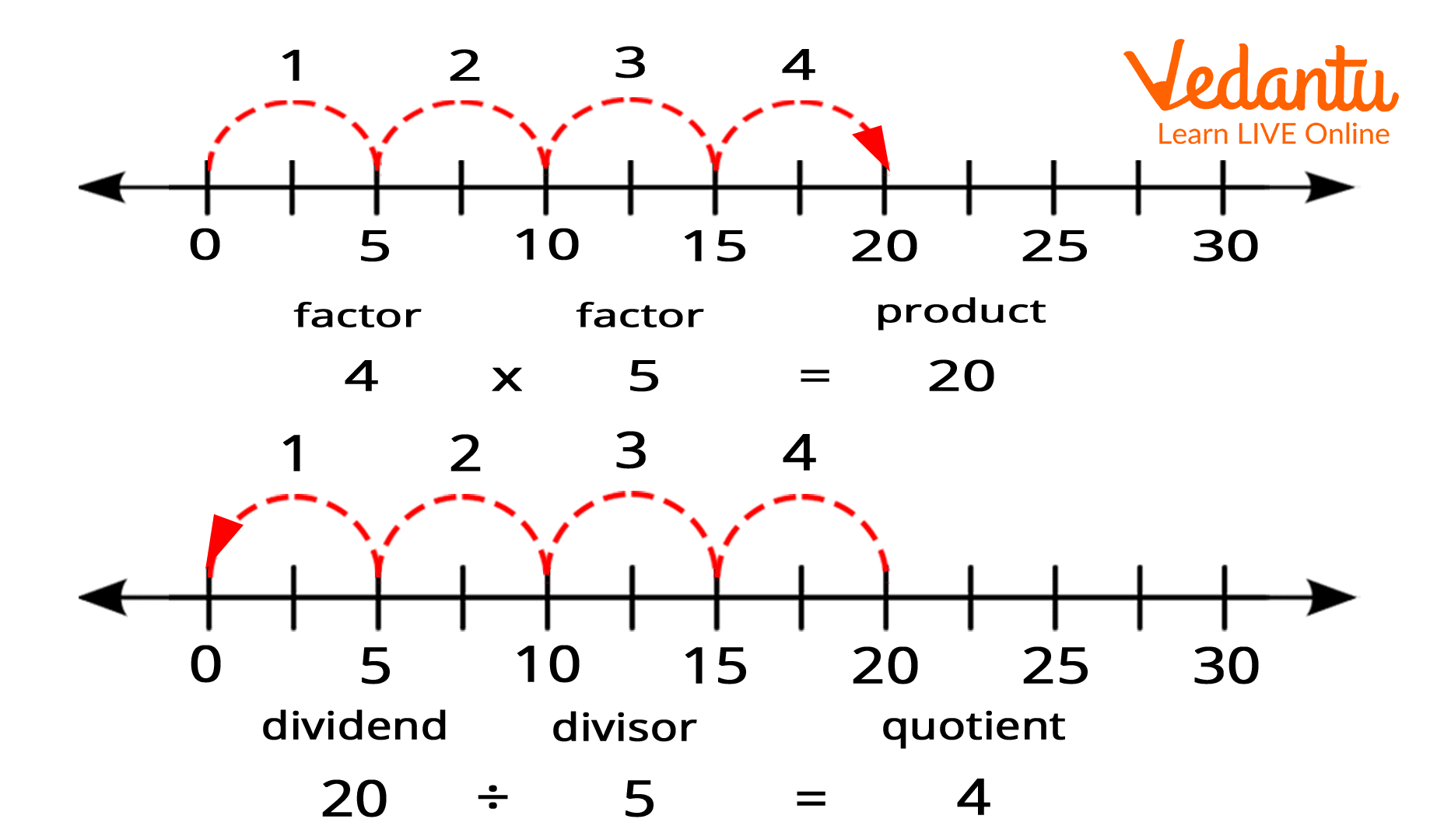
Conclusion
It is very important for the students to understand the actual meaning of the Mathematical operation. Just following the procedure of performing these operations is not enough. Hence, the models that describe the Mathematical operation are essential. In this article, we have discussed multiplication and division models with examples.
FAQs on Multiplication and Division Models Explained
1. What are multiplication and division models in Maths?
Multiplication and division models are visual tools that help students understand the core concepts of these operations. Instead of just memorising facts, these models, such as arrays or area grids, allow students to see what is happening when numbers are multiplied or divided, making the process more intuitive and easier to grasp.
2. How can you explain the basic concept of multiplication and division?
The basic concept of multiplication is repeated addition. For example, 3 x 4 is the same as adding 3 four times: 3 + 3 + 3 + 3 = 12. The basic concept of division is equal sharing or grouping. For example, 12 ÷ 4 means sharing 12 items into 4 equal groups, with 3 items in each group.
3. What are some common models used to explain multiplication?
Some of the most common and effective models for explaining multiplication, as per the NCERT approach, include:
- The Array Model: Arranging objects in equal rows and columns to represent a multiplication problem (e.g., 3 rows of 4 dots for 3 x 4).
- The Area Model: Using a rectangle where the length and width represent the factors, and the total area represents the product.
- The Number Line Model: Showing multiplication as a series of 'jumps' of equal length along a number line.
- The Equal Groups Model: Drawing a specific number of groups with an equal number of items in each group.
4. How does the 'equal grouping' model work for division?
The 'equal grouping' model for division answers the question, "How many groups can you make?" For example, to solve 15 ÷ 3, you would start with 15 objects and circle groups of 3. The total number of circles you can make is the answer, which is 5. This model visually represents division as repeated subtraction.
5. Can you provide a simple example of using the area model for multiplication?
Yes. To multiply 12 x 4 using the area model, you would draw a rectangle. You can break down 12 into (10 + 2). The rectangle's width would be 4, and its length would be split into two parts: 10 and 2. You then calculate the area of each smaller rectangle: (10 x 4 = 40) and (2 x 4 = 8). Adding these areas together (40 + 8) gives you the final product, 48.
6. Why are visual models like the array or area model important for learning multiplication?
Visual models are crucial because they bridge the gap between abstract numbers and concrete understanding. They help students develop number sense by allowing them to see the relationship between factors and products. This foundational understanding is more powerful than simple memorisation and helps in solving more complex problems later on, including those involving fractions and algebra.
7. How are multiplication and division related, and how can models show this relationship?
Multiplication and division are inverse operations, which means one operation undoes the other. An array model shows this relationship perfectly. For example, an array of 3 rows by 5 columns shows that 3 x 5 = 15. The same array also demonstrates that if you have 15 items, you can divide them into 3 equal rows of 5 (15 ÷ 3 = 5) or 5 equal columns of 3 (15 ÷ 5 = 3).
8. What is the main difference between the 'array model' and the 'area model' for multiplication?
The main difference lies in what they represent. The array model uses distinct, countable objects (like dots or counters) arranged in rows and columns, making it ideal for introducing multiplication with whole numbers. The area model uses a continuous space (a rectangle) and is more abstract. Its strength is in visualising the multiplication of larger numbers, decimals, and even algebraic expressions.
9. How can a number line be used to model both multiplication and division?
A number line can model both operations effectively:
- For Multiplication: To show 4 x 3, you would start at zero and make 4 jumps, with each jump being 3 units long. You will land on 12.
- For Division: To show 12 ÷ 3, you would start at 12 and make jumps of 3 units backwards towards zero. The number of jumps it takes to reach zero is the answer, which is 4.
10. Beyond basic calculation, what is a real-world problem that can be solved using a division model?
A division model can solve practical planning problems. For example, if a librarian has 45 new books to place on shelves, and each shelf can hold 9 books, they need to figure out how many shelves are required. Using the 'equal grouping' model to solve 45 ÷ 9, the librarian would find they need exactly 5 shelves for all the new books.























