Overview of the Lines
Have you ever thought about how to measure the length of a line? A line is a figure formed when two points are connected with a minimum distance between them, and both ends extended to infinity. The length of a line can be measured using a ruler. This article gives us complete details about the line and line segment. Reading this article, students will be able to identify the difference between a line and a line segment. This is the most basic topic of geometry, thus, should be at the tips of every child. Let us now begin with the learning about the given topic.
What is a Line?
A line is defined as a one-dimensional figure with no endpoints. In simple words, a line can be defined as a collection of points that can be extended indefinitely.
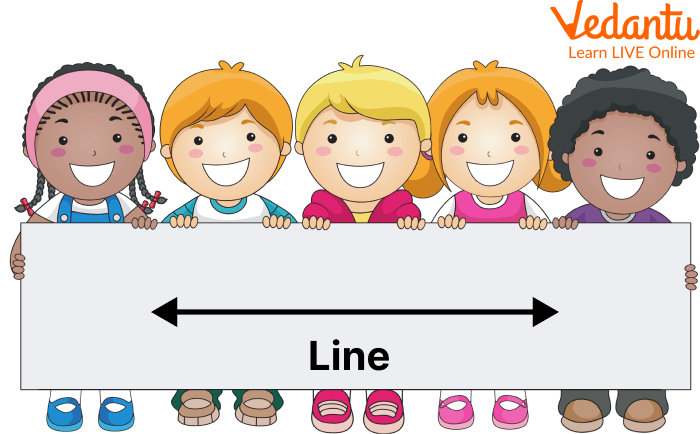
Showing a Line
How long is a Line?
The length of a line is not fixed; it can be extended indefinitely in both directions. The line is measured in terms of units with rules. For example, meters, centimetres, inches etc., i.e., a 5 cm length of a line can be extended in both directions as shown below.
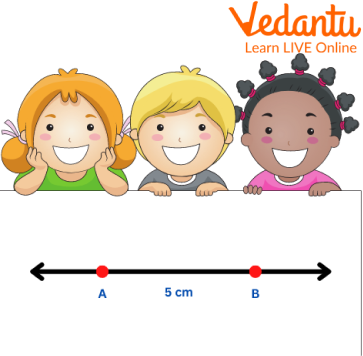
Showing a 5 cm length line
What is a Line Segment?
A line segment is defined as a line with two fixed endpoints that can not be extended in any direction. A line can be converted to a line segment by fixing two points.
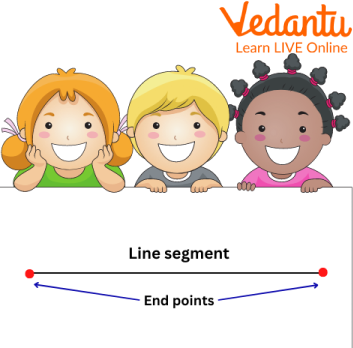
Showing a Line Segment
Length of a Line Segment
The length of a line segment is always fixed, i.e. it can not be changed because it cannot be extended in any direction. Line segment length can be measured in different measurement units, meters, centimeters, inches, etc.
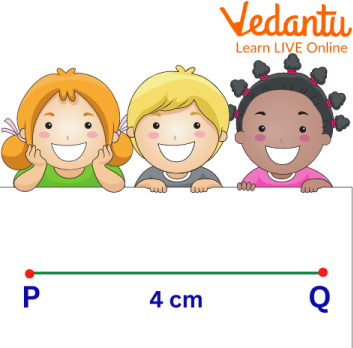
Showing a line segment length of 4 cm
Solved Examples
1. What is the length of the line shown in the image? Note: Measurement in cm
Measure the length of a line by putting the scale over it and noting its value down. Here, the length of the line is 2 inches. Now, it is known that 1 inch = 2.54 cm.
The length of the line in centimetres is converted by multiplying the length of the line by 2.54, i.e. $2.54 \times 2 = 5.08 cm$.
Thus, the length of the line in centimetres is 5.08 cm.
Showing 5.08 cm length of line
Q 2. What is the length of line AB shown in the image?
Line AB
Ans: The length of a line AB is measured using the ruler. Put the ruler on the line and mark the point on the scale as per the length of the line for the given line AB mark at 6 cm. Then, note the point, i.e. 6 cm.
Hence, the length of a line is obtained.
Practice Problems
Q 1. Spot the length of the given line segment.
Showing a line segment length
Ans: 6 cm
Q 2. What is the length of the line in centimetres, given that the line is 10 Inches?
Ans: 25.4 cm
Summary
Summing up the article here, with the concept of lines and the lines segments. This writing has covered the topics of line and line segments in an attractive format using simple language and related images. Some solved examples are also given for the clarification of concepts, and related practice problems are specified for students to master the given topic.
FAQs on Lines and Line Segments
1. How many types of lines are there?
There are four types of lines in geometry, namely:
Horizontal Lines
Vertical Lines
Parallel Lines
Perpendicular Lines
2. What are perpendicular lines?
Perpendicular lines are those lines which are perpendicular to each other, i.e. these bisects or cut each other at $90^{\circ}$. The geometric representation of two perpendicular lines is given by using the perpendicularity symbol, i.e. $\perp$. For example, $A B \perp C D$.
3. What is a ray?
A ray is a line with only one fixed point. The other point in the ray is not fixed, i.e. a ray can be extended to infinite in one direction.
