




How to Find the Incircle and Its Radius in Any Triangle
A triangle in geometry is a three-sided polygon with three edges and three vertices. The fact that a triangle's interior angles add up to 180 degrees is its most crucial characteristic. This characteristic is known as the triangle's angle sum property. If ABC is a triangle, it is written as ABC, where A, B, and C represent the triangle's vertices.
In Euclidean geometry, a triangle is a two-dimensional shape that is represented by three non-collinear points in a single plane. A triangle is a form of a polygon with three sides; the intersection of the two longest sides is known as the triangle's vertex.
Have a look at Incircle of a Triangle
The greatest circle that may fit within a triangle in geometry is known as the incircle or inscribed circle, which touches (or is tangent to) all three sides of the triangle. The triangle's incenter, also known as the triangle's centre, sits at the centre of the incircle. The intersection of the three internal angle bisectors, or the incenter, marks the location of the incircle's centre.
Properties of Incentre
There are several characteristics of a triangle's incenter; let's examine the image below and list each one one by one.
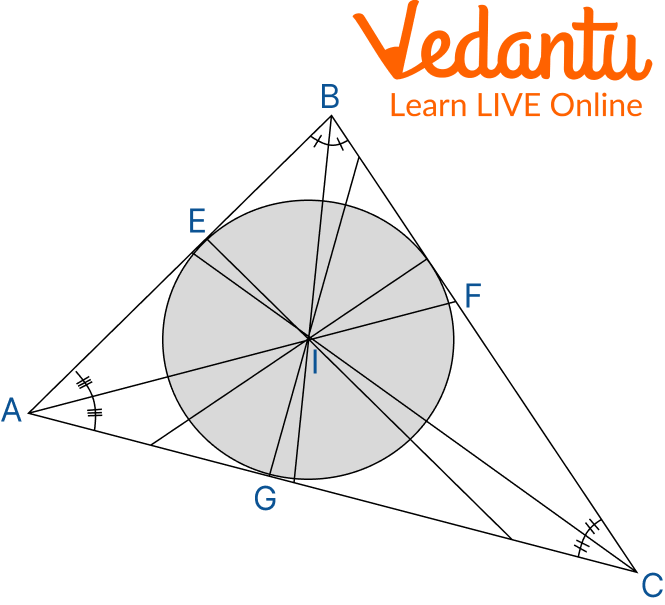
Incentre
Property 1: Line segments AE and AG, CG and CF, BF and BE are equal in length if I is the triangle's incenter.
Proof: As triangles, AEI and AGI are congruent triangles according to the rule of congruence.
Here AI = AI is common
The radius of the circle is IE = IGAnd $90^{\circ}$ angles are $\angle A E I=\angle A G I=90^{\circ}$
Thus, $\Delta AEI\cong \Delta AGI$
So, By CPCT we have AE = AG similarly which implies CG = CF AND BF = BE
Property 2: $\angle \text{BAl}=\angle \text{CAl},\angle \text{ABI}=\angle \text{CBI, }\angle \text{BCl}=\angle \text{ACl}$ if I is the triangle’s incentre.
Proof: According to the rule of congruence by RHS we have AEI and AGI congruent triangles.
Thus, by CPCT, angle BAI is equal to angle CAI.
Property 3: The triangle's sides are tangents to the circle and are referred to as the circle's inradii. Here, OE = OF = OG = r are the inradii.
Property 4: We have $s=\dfrac{a+b+c}{2}$ where ‘s’ is semi perimeter, ‘r’ is inradius then area is A = sr
Property 5: A triangle's incenter, as opposed to an orthocenter, always resides within the triangle.
Incircle of Triangle Formula
Here let E, F, and G be the angle bisectors of C, A, and B which cross the sides AB, AC, and BC respectively.
Now, use the angle sum property for calculating the incentre of a triangle angle.
Thus, we have $\angle AIB=180{}^\circ -\left( \dfrac{\angle A+\angle B}{2} \right)$ where ‘I’ is the incentive.
If we want to calculate it by using three coordinates. Coordinates are
$A{{(x)}_{1}},{{(y)}_{1}},B{{(x)}_{2}},{{(y)}_{2}},C{{(x)}_{3}},{{(y)}_{3}}$ for sides a, b, c.
Thus, incentre formula be $\left( \dfrac{a{{x}_{1}}+b{{x}_{2}}+c{{x}_{3}}}{a+b+c},\dfrac{a{{y}_{1}}+b{{y}_{2}}+c{{y}_{3}}}{a+b+c} \right)$
Solved Examples
Q 1. ‘I’ be the incentre of the triangle in ABC triangle, find the value of ‘x’
Ans. Given that ‘I’ is the incenter.
According to the figure, we have AI, BI, and CI as angle bisectors.
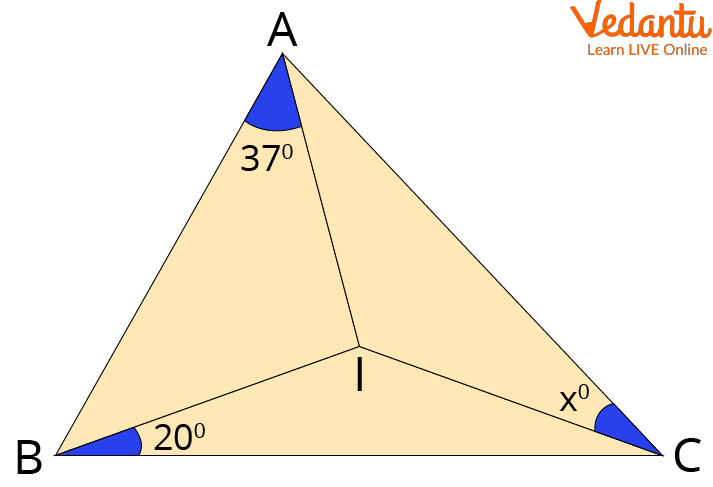
Triangle Showing Incentre
$\angle \text{BAl}+\angle \text{CBI}+\angle \text{ACl }=\dfrac{{{180}^{{}^\circ }}}{2}$
${{37}^{{}^\circ }}+{{20}^{{}^\circ }}+{{x}^{{}^\circ }}={{90}^{{}^\circ }}$
${{57}^{{}^\circ }}+{{x}^{{}^\circ }}={{90}^{{}^\circ }}$
${{x}^{{}^\circ }}={{90}^{{}^\circ }}-{{57}^{{}^\circ }}$
${{x}^{{}^\circ }}={{33}^{{}^\circ }}$
Q 2. Sandeep determined that a triangular sheet has a surface area of 50 feet square. The sheet has a 10-foot radius. Please assist Ram with determining the triangle's semiperimeter if a circle is drawn inside the triangle, touching each side.
Ans. We have given that the area is 50 feet square and the radius is 10 feet.
Area = semiperimeter which is multiplied by the inradius of the triangle.
$50=s\times 10$
$s=\dfrac{50}{10}$
$s=5$
Practice Problems
Q 1. The triangle ABC constructed by the points A(3, 1), B(0, 3), and C(-3, 1) has the following coordinates for its incenter: (p, q). Find (p, q).
Ans: Coordinates = $\left( 0,\dfrac{2\sqrt{13}+18}{6+2\sqrt{13}} \right)$
Q 2. ‘I’ be the incentre of the triangle in PQR triangle, solve for the value of ‘x’ where $P=40{}^\circ , Q=20{}^\circ$
Ans: $x{}^\circ =30{}^\circ$
Q 3. Whichever of the following is true for the triangle's incenter.
The place where the triangle's perpendicular bisectors intersect is known as the incenter.
One of a triangle's sides may be where the triangle's incenter is located.
A triangle's incenter is located at equal distances from its vertices.
None of the above
Ans: Option D i.e. none of the above
Q 4. What is the incentre in the given figure
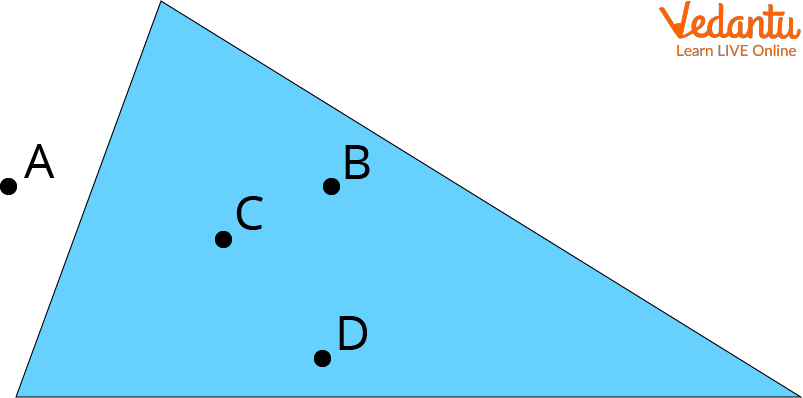
Incentre
Ans: Here, ‘C’ is the incentre in the above figure.
Summary
This article summarizes that a triangle in geometry is a three-sided closed polygon with three edges and three vertices and the greatest circle that may fit within a triangle in geometry is known as the incircle or inscribed circle, which touches (or is tangent to) all three sides of the triangle. The incenter of a triangle is defined as the point at which all three interior angle bisectors intersect. The properties of the Incenter and some solved examples on incenter are also discussed in this article which helps you to get a better understanding of the concept of Incircle.
FAQs on Incircle of a Triangle: Definition, Properties & Steps
1. What is the incircle of a triangle?
The incircle of a triangle is the largest possible circle that can be drawn inside the triangle. A key property of the incircle is that it is tangent to all three sides, meaning it touches each side at exactly one point. The center of this circle is a special point called the incenter.
2. How do you find the incenter of a triangle?
The incenter is found at the point where the angle bisectors of the triangle's three interior angles intersect. An angle bisector is a line that divides an angle into two equal halves. Since all three angle bisectors meet at a single point, this point of concurrency is the incenter. It is uniquely equidistant from all three sides of the triangle.
3. What are the steps to construct the incircle of a given triangle?
To construct an incircle, you first need to find its center (the incenter) and its radius. The steps are as follows:
Step 1: Draw the triangle (e.g., ∆ABC).
Step 2: Construct the angle bisectors for any two of the three interior angles (e.g., ∠B and ∠C).
Step 3: Mark the point where these two bisectors intersect as the incenter, labelled 'I'.
Step 4: From the incenter 'I', draw a perpendicular line to any one of the sides of the triangle (e.g., side BC). The length of this perpendicular line is the radius (r) of the incircle.
Step 5: With the compass centered at 'I' and set to the radius 'r', draw the circle. This circle will be the incircle, touching all three sides.
4. What are the important formulas related to the incircle of a triangle?
There are two primary formulas related to the incircle, crucial for calculations in coordinate geometry and mensuration:
Inradius (r): The radius of the incircle can be calculated using the formula r = A / s, where 'A' is the area of the triangle and 's' is the semi-perimeter (s = (a+b+c)/2).
Incenter Coordinates: For a triangle with vertices A(x₁, y₁), B(x₂, y₂), and C(x₃, y₃) and opposite side lengths a, b, and c, the coordinates of the incenter (I) are given by: I = ( (ax₁ + bx₂ + cx₃)/(a+b+c) , (ay₁ + by₂ + cy₃)/(a+b+c) ). This formula is particularly useful in higher-level mathematics as per the CBSE 2025-26 syllabus.
5. Why is the incenter of a triangle always located inside it?
The incenter is always located inside the triangle because it is defined as the intersection point of the internal angle bisectors. By definition, these bisectors originate from a vertex and extend into the interior of the triangle. Therefore, their point of intersection must logically be within the boundaries of the triangle. This holds true for all types of triangles, whether they are acute, obtuse, or right-angled.
6. How does an incircle differ from a circumcircle?
While both are fundamental circles associated with a triangle, they have distinct properties:
Position: The incircle is drawn inside the triangle, tangent to its three sides. The circumcircle is drawn outside the triangle, passing through its three vertices.
Center: The incircle's center is the incenter (intersection of angle bisectors). The circumcircle's center is the circumcenter (intersection of the perpendicular bisectors of the sides).
Center Location: The incenter is always inside the triangle. The circumcenter, however, can be inside (for acute triangles), outside (for obtuse triangles), or on the hypotenuse (for right-angled triangles).
7. Is there a simpler formula for the inradius of an equilateral triangle?
Yes, for an equilateral triangle, the properties of symmetry lead to a much simpler formula for the inradius (r). If the side length of the equilateral triangle is 'a', the inradius is given by:
r = a / (2√3).
This is a direct result of the fact that in an equilateral triangle, the incenter, centroid, circumcenter, and orthocenter all coincide at the same point.
8. Are the incenter and the centroid of a triangle the same point?
No, the incenter and the centroid are generally two different points with different geometric properties. The only exception is in an equilateral triangle where they coincide. Here's the key difference:
The incenter is the intersection of the angle bisectors and is equidistant from the sides of the triangle.
The centroid is the intersection of the medians (lines from a vertex to the midpoint of the opposite side) and is the triangle's center of mass.








































