




What Is a Fraction? Definitions, Types & Proven Methods
Suppose you and your friends went for a dinner party, after eating the waiter comes with a single bill for everyone and now you want to know the amount that had to be paid by each of your friends, but you find it confusing that how would you calculate the amount so you paid the bill and came home. Then you asked your brother about it and then he told you that it’s all a “fraction”, and now you are curious!! , what is a fraction, “ A fraction is a portion or a part of a whole thing”. If anything as a whole is divided into equal parts then every part is a portion and hence, a fraction.
Now you are curious about the next time when you will go to have dinner and be able to divide the bill equally through “fractions”. In this article, we will learn all about fractions in detail.
Finding the Fractions
To find a fraction of a whole number, we multiply the numerator of the fraction by the provided number and then divide the product by the denominator of the fraction.
For example: $\dfrac{1}{2}, \dfrac{2}{3}, \dfrac{6}{8}$
Fraction Formula
The fraction formula is helpful in executing a number of operations on fractions . When it comes to fractions the basic arithmetic operations are different from those of normal integers.
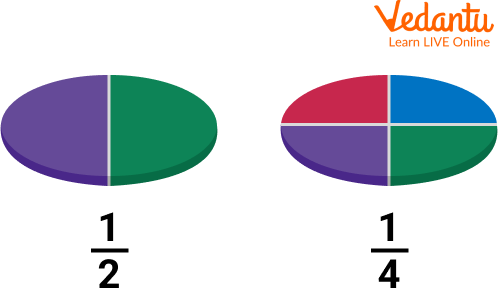
Fraction representation
Formula 1
A fraction associated with a whole number is known as a “mixed fraction” . Then the mixed fraction is converted into an “improper fraction” , how?? , by multiplying the denominator of the fraction with the whole number and adding it to the numerator of the fraction , to form the numerator of the improper fraction.
$A\dfrac{b}{c} = \dfrac{Ac + b}{c}$
Formula 2
The addition of the fractions is quite easy when in the given fractions the denominators are the same , numerators are simply added and the denominator of the answer is equal to the denominators of the given fractions.
$\dfrac{a}{b} + \dfrac{c}{b} = \dfrac{a + c}{b}$
Formula 3
When there are unlike fractions, suitable constant numbers are multiplied to both fractions to make the denominators same and then use ‘formula 2’ , in which simply add the numerators and the denominators remain the same.
$\dfrac{a}{b} + \dfrac{c}{d} = \dfrac{a.d}{bd} + \dfrac{c.b}{db}$
Formula 4
Multiplication in fractions is simply done by multiplying numerators together and then the denominators of both the given fractions. The answer is a single fraction which is further simplified if needed.
$\dfrac{a}{b} . \dfrac{c}{d} = \dfrac{ac}{bd}$
Formula 5
Division of fractions is simplified by reciprocation of numerator and the denominator of the given number and the desired result is achieved by multiplying numerators together and then denominators together.
$\dfrac{\dfrac{a}{b}}{\dfrac{d}{c}}=\dfrac{a}{b} \cdot \dfrac{c}{d}=\dfrac{a c}{b d}$
Fraction to Whole Number
A fraction can be written into a whole number when you divide the numerator by the denominator of the given fraction only if, the numerator is a multiple of the denominator
For example: convert $\dfrac{8}{2}$ into a whole number
$\mathrm{So}, \dfrac{8}{2}=4$
(as ' 8 ' is a multiple of ' 2 ' )
Hence, to convert a fraction to a whole number, divide the numerator by the denominator only if , numerator is a multiple of the denominator.
Dividing Whole Numbers by Fractions
What do we have to do when we divide whole numbers by fractions? when dividing a whole number by a fraction, we find how many numbers of parts can be fitted in a whole.
The most easy method for dividing a whole number by a given fraction is multiplication of the given whole number by the reciprocal of the fraction.
For example, if we have to calculate $7 \div \dfrac{3}{5}$
Step 1:
We will represent 7 as $\dfrac{7}{1}$
Step 2
Now , we will reciprocate the given fraction that means,
the reciprocal of $\dfrac{3}{5}$ will be $\dfrac{5}{3}$
Step 3: Now , we have both the fractions we need which are,
For example, $\dfrac{7}{1} \times \dfrac{5}{3}=\dfrac{35}{3}$
Solved examples
Q 1.Rani took 8 apples from the bucket of 24 apples. Find the fraction of apples taken by theRani?
Ans: The fraction of apples taken by Divya = $\dfrac{8}{24}$ and its simplest form is $\dfrac{1}{3}$.
Q2. Sahana bought $\dfrac{1}{4}$ kg of apples and $\dfrac{1}{2}$ kg oranges from the shop. Total how many fruits she bought?
Ans: The total fruits bought by Sahana= $\dfrac{1}{4}$ +$\dfrac{1}{2}$ = $\dfrac{1+2}{4}$ = $\dfrac{3}{4}$
Practice Questions
Q 1. Write $\dfrac{18}{30}$ in the simplest form. (Ans: $\dfrac{3}{5}$ )
Q 2. Find the simplest form of $\dfrac{53}{8}$? , and write in mixed fraction form if needed. (Ans: $6 \dfrac{5}{8}$)
Summary
In this article, we learn about what fractions are, how often we use them in our real life and how interesting they are!!!! . We also learned about how we can handle and operate in fractions and perform arithmetic operations. Fractions are a very interesting and recurring part of our life. Then we got to know how to convert a fraction into a whole number and vice-versa, along with that we also threw light on how to divide whole numbers by fractions and then how to simplify them further. After completing the article, make sure to understand the solved examples, solve the practice questions and keep FAQs on your tips for better results in an understanding of the concept.
FAQs on How to Find Fractions: Complete Student Guide
1. What is a fraction and what are its main parts?
A fraction represents a part of a whole or any number of equal parts. It is used to describe a quantity that is not a whole number. A fraction has two main parts: the numerator (the top number), which shows how many parts you have, and the denominator (the bottom number), which shows the total number of equal parts the whole is divided into.
2. What are the different types of fractions students should know?
There are several key types of fractions that are fundamental to understanding this topic in Maths:
Proper Fractions: The numerator is smaller than the denominator (e.g., 2/5).
Improper Fractions: The numerator is greater than or equal to the denominator (e.g., 7/4).
Mixed Fractions: A combination of a whole number and a proper fraction (e.g., 1 ¾).
Unit Fractions: Fractions with a numerator of 1 (e.g., 1/8).
Like Fractions: Fractions that have the same denominator (e.g., 1/7 and 3/7).
Unlike Fractions: Fractions that have different denominators (e.g., 2/5 and 3/8).
3. How are fractions used in everyday life?
Fractions are used constantly in real-world situations. For example, when you are sharing a pizza with friends, each person gets a fraction of the whole (like 1/8). When you follow a recipe, you might need to measure 1/2 cup of flour or 3/4 teaspoon of salt. Other examples include tracking time (half an hour), measuring fuel in a car (1/4 tank), or getting a discount (50% off is a 1/2 reduction).
4. What is the key difference between a proper and an improper fraction?
The key difference lies in their value relative to one whole. A proper fraction always has a value less than 1 because its numerator is smaller than its denominator (e.g., 3/4 means you have 3 parts out of 4). An improper fraction has a value that is equal to or greater than 1 because its numerator is equal to or larger than its denominator (e.g., 5/4 means you have more parts than one whole contains).
5. How do you find a fraction of a whole number, for example, 2/3 of 18?
To find a fraction of a whole number, you follow a two-step process. First, you divide the whole number by the denominator of the fraction. Then, you multiply the result by the numerator. For example, to find 2/3 of 18:
- Step 1: Divide 18 by the denominator (3): 18 ÷ 3 = 6.
- Step 2: Multiply the result (6) by the numerator (2): 6 × 2 = 12.
Therefore, 2/3 of 18 is 12.
6. Why is it necessary to find a common denominator when adding or subtracting fractions?
Finding a common denominator is essential because you can only add or subtract things that are of the same size or type. The denominator of a fraction tells you the size of each piece. For example, you cannot directly add 1/2 and 1/3 because 'halves' and 'thirds' are different-sized pieces. By converting them to equivalent fractions with a common denominator (like 3/6 and 2/6), you are essentially cutting the whole into same-sized pieces ('sixths'), which can then be added or subtracted easily.
7. How do you read a fraction like 3/4 out loud?
To read a fraction, you use a cardinal number (like one, two, three) for the numerator and an ordinal number (like third, fourth, fifth) for the denominator. So, the fraction 3/4 is read as "three-fourths." Similarly, 2/5 is read as "two-fifths," and 1/2 is read as "one-half."
8. Can a fraction have zero as its denominator? Explain why or why not.
No, a fraction can never have zero as its denominator. The denominator represents how many equal parts a whole is divided into. Division by zero is undefined in mathematics. You cannot divide something into zero parts. Trying to do so has no meaningful answer, so any fraction with a denominator of 0 is considered mathematically impossible.











