




How to Find HCF Using Long Division-Simple Steps for Students
As we all know, the Highest Common Factor (HCF) as the name itself says, it's the method of finding the highest common factors of two or more than two numbers. It's the highest common number that can divide the given two or more two positive numbers equally.
There are different methods through which we can find out the HCF of given numbers. Of Course, it can be used to find the HCF of small numbers but when it comes to large numbers, then the most suitable method is the Long Division Method. Come on, let us understand HCF by the long division method step by step with a few examples along the way.
What is H.C.F?
HCF stands for Highest Common Factor. HCF of 2 numbers is the highest factor that can divide the two numbers easily. The highest common factor (HCF) can be evaluated for 2 or more than 2 numbers. It is the greatest divisor for any two or more numbers that can equally or completely divide the given numbers.
For Example, the HCF of 60 and 75 is 15 because 15 is the largest number which can divide both 60 and 75 exactly.
Methods for Finding H.C.F
HCF of two or more number can be found by using two methods:
By prime factorization method
By division method
We will discuss the division method in this article.
Steps of HCF by Long Division Method
Step 1: Divide the larger number by the smaller number.
HCF of 18 and 30
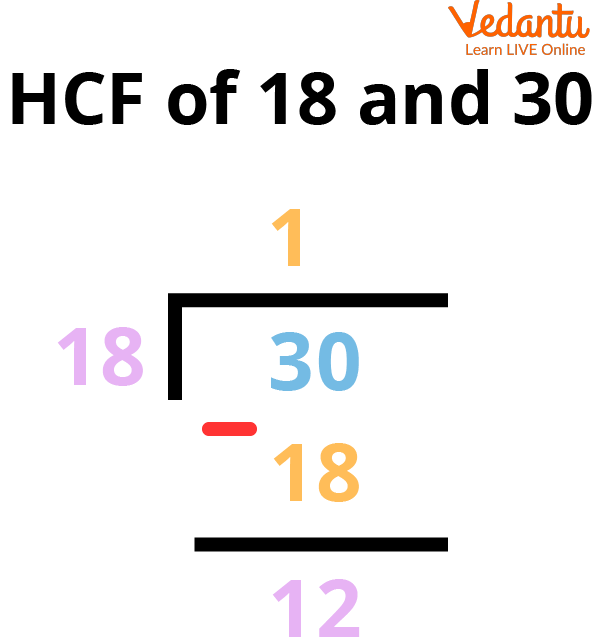
The Long Division Method
Step 2: The remainder becomes the divisor and the divisor becomes the dividend. Therefore, divide the first divisor by the first remainder.
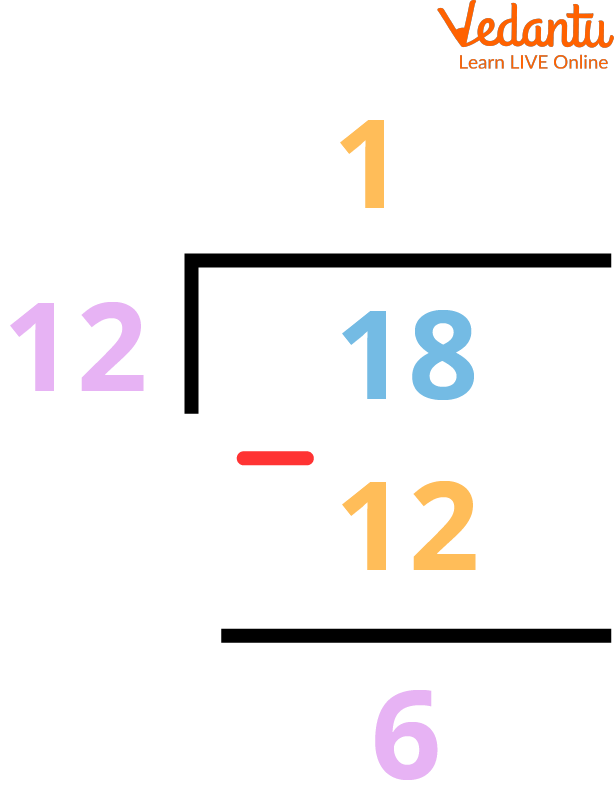
The Long Division Method
Step 3: If the remainder is not 0, then again the remainder becomes the divisor and the divisor becomes the dividend. Therefore, divide the second divisor by the second remainder.
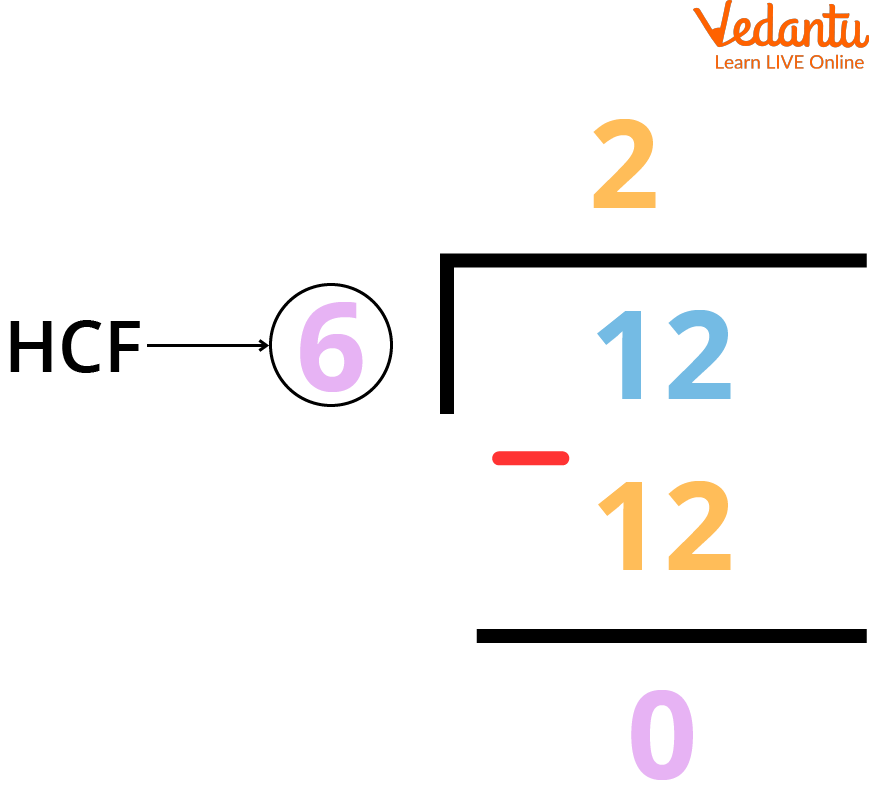
The Long Division Method
Step 4: The divisor which does not leave a remainder is the HCF of the two numbers and thus, the last divisor becomes the HCF of the given two numbers.
Let us try to understand the long division method to find the HCF of given numbers with examples.
Solved Examples
Example 1:Find the HCF of 64 and 144 using the long division method
Step 1: Dividing the larger given number with the smaller given number. So, 144 becomes the dividend and 64 as the divisor.
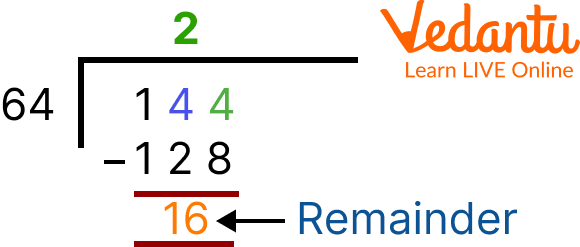
Long Division Method
Step 2: The remainder becomes the divisor and the divisor becomes the dividend.
Step 3: Therefore, we need to divide 64 (dividend) by 16 (divisor).
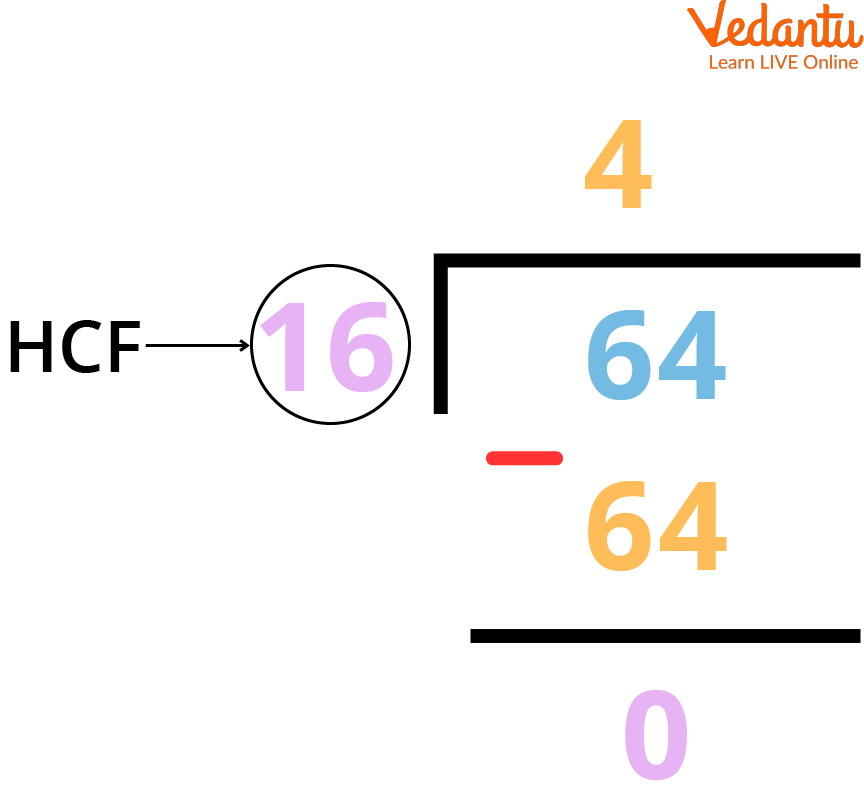
Long Division Method
Once the remainder becomes 0, the divisor of that particular division becomes the HCF.
Therefore, HCF of (64, 144) = 16
Example 2: Find the HCF of 700 and 300 using the long division method.
Step 1: Simply divide the larger given number by the smaller given number. In this case, 300 is the divisor and 700 is the dividend.
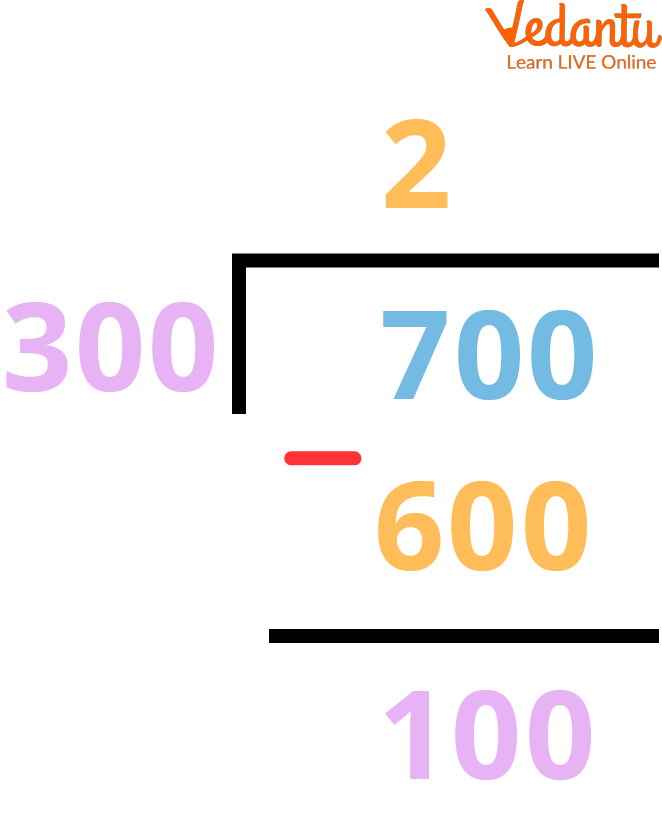
Long Division Method
Step 2: The remainder that we got is 100 therefore the remainder that is 100 becomes the divisor and 300 which was the divisor earlier becomes the dividend.
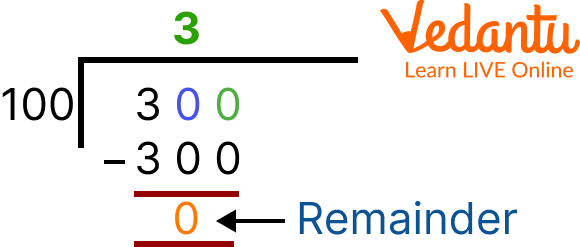
Long Division Method
Step 3: Now, we simply divide the second divisor with the second remainder. Follow the image down below for a better understanding.
=> HCF of 700 and 300 is 100
Practice questions
1. Find the HCF of 30 and 45
Ans: 15
2. Find the HCF of 162 and 180
Ans: 18
3. Find the HCF of 270 and 9
Ans: 9
4. Find the HCF of 78 and 98
Ans: 2
5. Find the HCF of 702 and 405
Ans: 27
Summary
This article has tried to explain the detailed steps of how to find HCF by using the long Division method for 2 positive given numbers. To find the HCF by division method, the first step is to divide the larger number by the smaller number and then the remainder becomes the divisor and divide the smaller number until the remainder is zero. In this article, you have learn about all other different topics related to HCF.
FAQs on HCF by Long Division Method Made Easy
1. How to find HCF using long division?
To find the HCF (Highest Common Factor) using the long division method, follow these steps:
- Divide the larger number by the smaller number.
- Note the remainder.
- Now, divide the previous divisor by this remainder.
- Continue this process until the remainder is zero.
2. What is the HCF of 403 434 and 465 by long division method?
To find the HCF of 403, 434, and 465 using the long division method:
- Step 1: Find the HCF of 403 and 434. Divide 434 by 403.
$434 \div 403 = 1$, remainder $31$. - Now divide 403 by 31.
$403 \div 31 = 13$, remainder $0$. - Thus, HCF of 403 and 434 is $31$.
- Step 2: Find the HCF of $31$ and $465$.
$465 \div 31 = 15$, remainder $0$.
3. What is the HCF of 144 180 and 192 by long division method?
Let’s evaluate the HCF of 144, 180, and 192 by the long division method:
- Step 1: Find HCF of 180 and 144.
$180 \div 144 = 1$, remainder $36$. - 144 ÷ 36 = 4, remainder $0$.
So, HCF of 180 and 144 is $36$. - Step 2: Find HCF of $36$ and $192$.
$192 \div 36 = 5$, remainder $12$. - 36 ÷ 12 = 3, remainder $0$.
So, HCF is $12$.
4. How do you do HCF step by step?
To calculate the HCF step by step using the long division method:
- Divide the larger number by the smaller one.
- Write down the remainder.
- Now, divide the earlier divisor by this remainder.
- Continue until the remainder becomes zero.
- The last divisor (before the remainder becomes zero) is the HCF.
5. What are the advantages of finding HCF by long division method?
The long division method for HCF offers several benefits:
- Efficient for large numbers — Works well even for numbers with multiple digits.
- Systematic process — Reduces mistakes by following a sequence of steps.
- Applicable to multiple numbers — Extendible to more than two numbers by iterative division.
- Widely accepted in exams — Most examination boards, including those aligned with Vedantu’s syllabus, accept this method.
6. Can the HCF by long division method be used for more than two numbers?
Yes, you can use the long division method to find the HCF of more than two numbers. Begin with any two numbers, find their HCF, and then use that result with the next number, continuing the process. For example, to find the HCF of $a$, $b$, and $c$:
- Find HCF($a$, $b$) = $d$.
- Find HCF($d$, $c$), and so on for additional numbers.
7. Is there any difference between HCF by long division method and by prime factorization?
Yes, while both find the HCF, their approaches differ:
- Long division method: Involves repeated division and subtraction steps; efficient for large numbers.
- Prime factorization: Breaks numbers into their prime factors and finds common ones; useful for smaller numbers.
8. What are some real-life uses of HCF found by the long division method?
The ability to find the HCF using the long division method has many practical applications:
- Dividing things into equal parts, such as cutting wires or ribbons of equal length.
- Solving problems on fraction reduction.
- Arranging items in groups with no items left over.
- Scheduling recurring events at minimum intervals.
9. How can students quickly check their HCF answer found by long division method?
To quickly check your HCF answer:
- Confirm that the HCF divides each original number exactly with zero remainder.
- There should be no greater number (other than the HCF) that divides each number without a remainder.
10. What are common mistakes to avoid when finding HCF by long division method?
When using the long division method for HCF, students should avoid:
- Incorrectly arranging numbers (always divide the larger by the smaller).
- Forgetting to divide with the last non-zero remainder.
- Stopping the process before reaching a zero remainder.
- Missing steps in problems with more than two numbers.























