Factors of 240

Factorisation provides us with the factors of any number. It defines the process of determining the factors of a number in a systematic approach so that all of the factors are noticed. A factor of any given integer may be defined as the divisor that divides it completely, leaving no remainder behind. We can employ any of the techniques among the division method, the factorisation method, or the prime factorisation method to identify the factors of any integer.

The factors can be positive integers or negative integers. In common practice, we consider only the positive factors in any factorisation, and usually, they are referred to as factors only. Thus, the words factor and positive factor are synonymous from a mathematical point of view. The factors are responsible directly or indirectly in the real-world scenarios of price comparisons, exchange money, etc.

What is a Factor?

Assume we have a reference to a multiplication operation in which we find that the number X is written equal to the product of another number a and the number b. the mathematical expression looks like the following.

$\begin{align}X= a\times b \end{align}$

Now, if we perform the division operation on the number X by a or b, we find that X is completely divisible by a and b.

$\begin{align} X \div a=b \end{align}$

$\begin{align} X\div b=a \end{align}$

So, it is evident that both a and b are the factors of the number X.

Thus, we get the following definition of a factor.

Whenever an integer divides any number completely, leaving no remainder, the referred integer is the factor of that number.

What is a Multiple?

Inspect another multiplication operation where the number Y is expressed as equal to the product of the numbers b and c, expressed as the following.

$\begin{align}Y= b \times c\end{align}$

Here, it is apparent that by multiplying the number b with another number c, we get the number Y which is greater than both b and c.

So, it is inferred that the number Y is the multiple of both the numbers b and c.

Thus, we get the following definition of a multiple.

Whenever an integer is multiplied by another integer, the resultant product, which is also an integer, is the multiple of the first and the second integers.

What are the Methods of Finding Factors?

We can use any of the following methods of finding factors.

• Factorization

• Prime Factorization

Both these methods end in finding the factors of any number, however small or large, without any miss.

Define the Method of Factorization

In this method of factorisation, split the concerning number in terms of all the possible multiplications between any two integers, such that the obtained product is always the preferred number (whose factors are needed).

The following is an example of factorisation of any arbitrary number 36.

$\begin{align} 36=1\times 36 \end{align}$

$\begin{align} 36=2\times 18 \end{align}$

$\begin{align} 36=3\times 12 \end{align}$

$\begin{align} 36=4\times 9 \end{align}$

$\begin{align} 36 =6\times 6 \end{align}$

Thus, the factorisation method reveals that the factors of 36 are 1, 2, 3, 4, 6, 9, 12,18, and 36.

What are the Methods of Prime Factorisation?

As a matter of practice, prime factorisation employs the following two techniques to determine the prime factors of a given integer.

• The division method

• The factor tree method

Division Method

The division method of prime factorization involves the following steps.

• Divide the given integer by the smallest possible prime number that completely divides the provided integer.

• Write the quotient below the given number.

• Now, divide the quotient by the smallest but divisible prime number and write below it.

• Continue in the same manner until we obtain the quotient as 1.

An example of the division method prime factorisation is as follows.

$\begin{align} 2\underline{\left| 36 \right.}\end{align}$

$\begin{align} 2\underline{\left| 18 \right.} \end{align}$

$\begin{align} 3\underline{\left| \quad 9 \right.}\end{align}$

$\begin{align} 3\underline{\left| \quad 3 \right.}\end{align}$

$\begin{align} \quad 1 \end{align}$

The prime factors of 36, found out by the division method, are 1, 2, 2, 3, and 3.

Factor Tree Method

The factor tree method of prime factorization involves the following steps.

• Assume the given integer to be the base of the supposed factor tree.

• Split the given number into two factors such that one of these two factors is the smallest possible prime number that completely divides the provided number.

• Write these two factors as the two elements of the base number, thus, creating the first set of branches of the factor tree.

• Now, consider the greater factor between the above two factors and split it following the previous rule.

• Continue in the same manner until we obtain the quotient of the prime number as the factor pairs.

• Thus, we end up with a factor tree where each branch contains a pair of factors. a tree with two elements as its branches. Write the quotient below the given number.

• Now, divide the quotient by the smallest but divisible prime number and write below it.

The prime factors of 36, found out by the factor tree method, are 1, 2, 2, 3, and 3.

On writing all the possible combinations of multiplications among the above prime factors, irrespective of the method employed, we get that the factors of 36 are 1, 2, 3, 4, 6, 9, 12,18, and 36.

Identify the Prime Factors Of 240

We can identify the prime factors of 240 by employing any of the following two methods.

Division Method to Identify the Prime Factors of 240

• First, divide the number 240 by the lowest divisible prime number 2 to get the quotient 120.

$240 \div 2 = 120$

• Next, divide the number 120 by the lowest divisible prime number 2 to get the quotient of 60.

$120 \div 2 = 60$

• Again, divide the number 60 by the lowest divisible prime number 2 to get the quotient 30.

$60 \div 2 = 30$

• Now, divide the number 30 by the lowest divisible prime number 2 to get the quotient of 15

$30 \div 2 = 15$

• Subsequently, divide the number 15 by the lowest divisible prime number 3 to get the quotient 5

$ 15 \div 3 = 5 $

• As 5 is a prime number, finally divide it by itself to get 1.

$ 5 \div 5 = 1 $

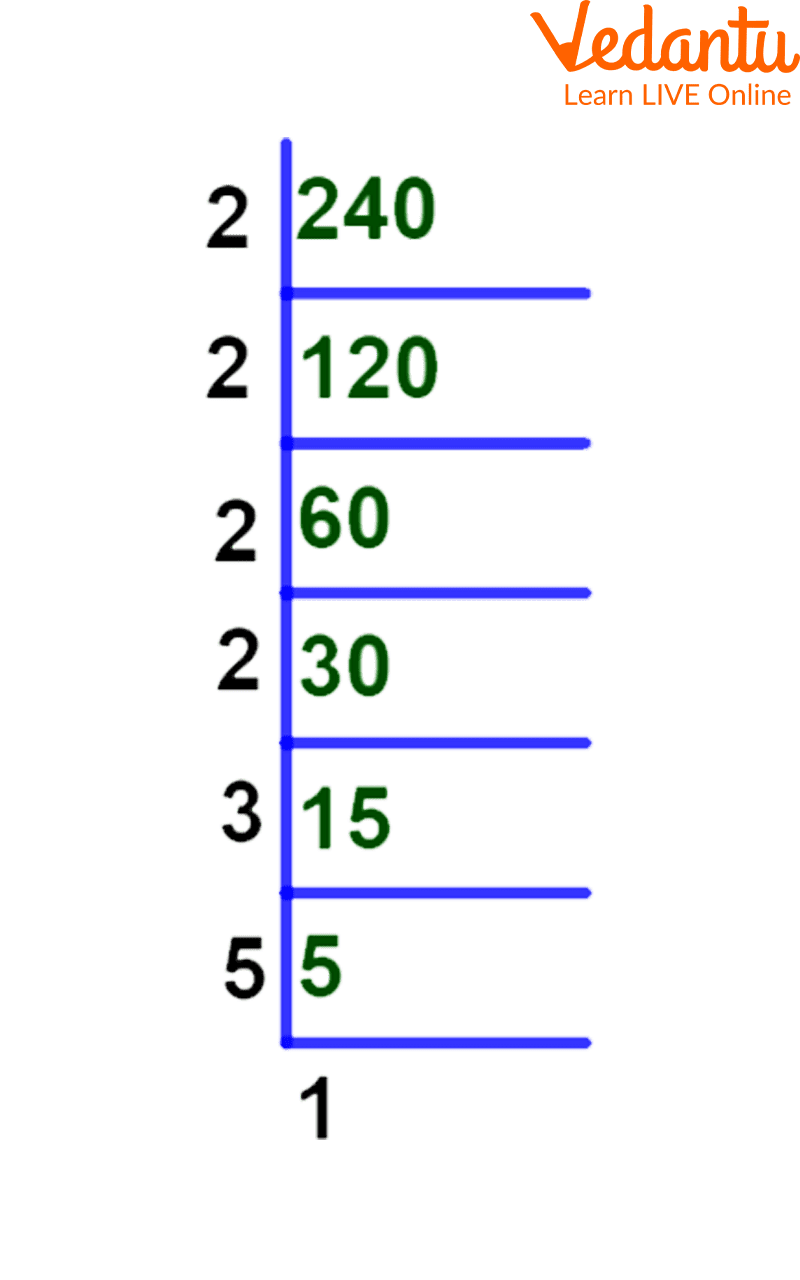
Factorization

Therefore, the prime factorization of 240 yields the prime factors 1, 2, 2, 2, 2, 3, and 5.

We can express the prime factorization of 240 in terms of its prime factors in the following way.

$240 = 2 \times 2 \times 2 \times 2 \times 3 \times 5 $

$200 = 2^{4} \times 3 \times 5 $

Factor Tree Method to Identify the Prime Factors of 240

Look at the illustration provided below to comprehend the idea of identifying the prime factors by the factor tree method.

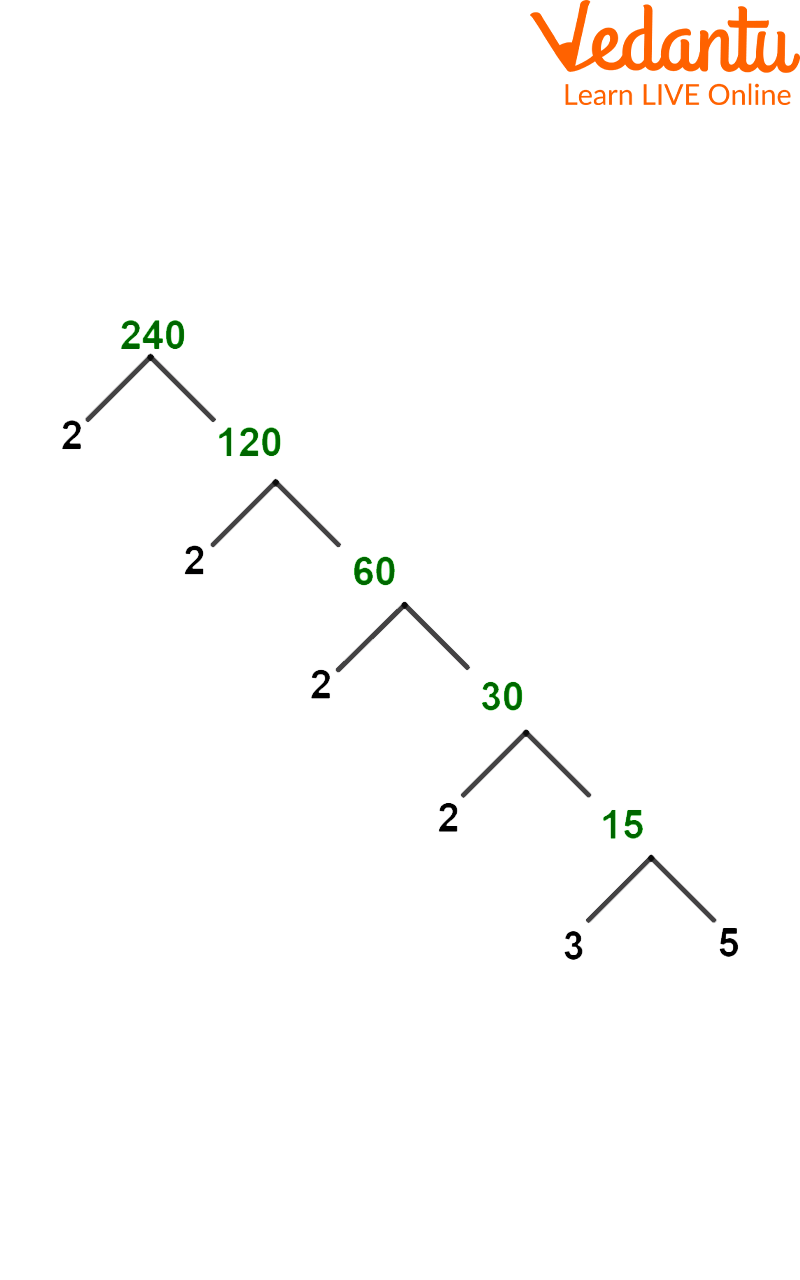
Prime Factorization Using Factor Tree Method

What are the Factors of 240?

The factors, when multiplied together, yield the original number. For example, the number 240 is equivalent to 3 times 80 or 2 times 120. Here, the numbers 2, 3, 80, and 120 are some of the factors of 12. As such, the total count for the 240 factors is twenty.

The twenty factors of 240 can be obtained in any of the two ways.

The Method of Factorization

This method shows the following mathematical calculations.

$\begin{align}240=1\times 240\end{align}$

$\begin{align}240=2\times 120\end{align}$

$\begin{align}240=3\times 80\end{align}$

$\begin{align}240=4\times 60\end{align}$

$\begin{align}240=5\times 48\end{align}$

$\begin{align}240=6\times 40\end{align}$

$\begin{align}240=8\times 30\end{align}$

$\begin{align}240=10\times 24\end{align}$

$\begin{align}240=12\times 20\end{align}$

$\begin{align}240=15\times 16\end{align}$

Thus, the 240 factors are 1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 16, 20, 24, 30, 40, 48, 60, 80, 120, and 240. The factors of 240 in pairs can be grouped as (1, 240), (2, 120), (3, 80), (4, 60), (5, 48), (6, 40), (8, 30), (10, 24), (12, 20) and (15, 16).

Using the Prime Factorization

The prime factors of 240, found out by the factor tree method or the division method of the prime factorisation, are 1, 2, 2, 2, 2, 3, and 5.

On writing all the possible combinations of multiplications among the above prime factors, irrespective of the method employed, we get that the factors of 240 are 1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 16, 20, 24, 30, 40, 48, 60, 80, 120, and 240. Therefore, we have correctly identified the twenty factors of 240.

Interesting Facts

• The factorisation of any composite number yields more than two factors of the composite number.

• The factorisation of any composite number reveals only two factors of the prime number, in which one factor is always 1, and the other factor is the number itself.

• The factors and the multiples of the numbers are well-defined in the multiplication tables.

• The HCF of any given set of numbers is the highest common factor among all the factors of the numbers.

• The LCM of a set of numbers is the least common multiple among all the multiples of the numbers.

• The common factors of 240 and 2 are 1 and 2.

• The common factors of 240 and 3 are 1 and 3.

• The common factors of 240 and 5 are 1 and 5.

Do You Know?

• The factors are those integers which, when divided by the concerned number, yield no remainder in the division.

• The factors are multiplied together to obtain the respective multiples.

• The prime factors are multiplied together to obtain the original number.

• The factors of a prime number are equal to its prime factors.

• The number of factors of a composite number is greater than the number of its prime factors.

Solved Examples

1. Find the prime factors of 999.

Refer to the following steps for the mathematical calculation to find the prime factors of 999.

• Divide 999 by 3 to get 333.

$999 \div 3 = 333$

• Divide 333 by 3 to get 111.

$333 \div 3 = 111$

• Divide 111 by 3 to get 37.

$111 \div 3 = 37$

• Divide 37 by 37 to get 1.

$37 \div 37 = 1$

Therefore, the prime factors of 999 are 1, 3, 3, 3, and 37.

2. Find the factors of 7.

Since the number 7 is a prime factor, its factors are two in number, and they are 1 and 7.

3. Is the number 1 a prime or a composite?

The number 1 is neither a composite number nor a prime number.

4. Which of the factor of 240 is even a prime number?

The factors of 240 are 1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 16, 20, 24, 30, 40, 48, 60, 80, 120, and 240. Here, factor 2 is revealed as the only even prime number.

5. Which of the factor of 240 is the smallest even cube?

The factors of 240 are 1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 16, 20, 24, 30, 40, 48, 60, 80, 120, and 240. Here, factor 8 is the smallest even cube.

Summary

• There are twenty distinct factors of 240.

• The prime factorization of 240 reveals the prime factors of 1, 2, 2, 2, 2, 3, and 5.

• The factors of 240 are 1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 16, 20, 24, 30, 40, 48, 60, 80, 120, and 240.

• The factors of 240 in pairs are (1, 240), (2, 120), (3, 80), (4, 60), (5, 48), (6, 40), (8, 30), (10, 24), (12, 20) and (15, 16)

• Prime factorization is of two types, namely, the factor tree method and the division method.

• The factorization method splits the referred number into all the possible operations of multiplication, each involving the factor pair of any two integers, such that the obtained product is always the original number (whose factors are sought).