Understanding Equivalent Ratio with Solved Examples

Equivalent ratios are the kind of ratios that remain the same when we compare them. We compare multiple ratios alongside each other to check whether they are equivalent or not. It can be shown easily by an example, i.e. $1:2$ and $2:4$ are equivalent ratios. We can find the two equivalent ratios by using multiplication and division as tools.

If we want to get a ratio that is equivalent to an already given ratio, we need to multiply or divide both of the terms of the given ratio by the same non-zero number.

Ratios

Equivalent Ratios and Equivalent Fractions

In order to find the equivalent ratios of a given ratio, we write the ratio as a fraction and then multiply and divide for them to be compared. The ratio can also be expressed as a fraction. Let a:b, be a ratio, then a/b can be the fraction form. It can also be compared to two or more equivalent ratios in the form of equivalent fractions.

How Do We Find the Equivalent Ratios of a Given Ratio?

The step-by-step process to find the equivalent ratios of a given ratio is given below:

• We can find the two equivalent ratios by using multiplication and division as tools

• If we want to get a ratio that is equivalent to an already given ratio, we need to multiply or divide both of the terms of the given ratio by the same non-zero number.

• In order to find the equivalent ratios of a given ratio, we write the ratio as a fraction and then multiply and divide for them to be compared.

Ratio Multiplication

Ratio multiplication is the mathematical operation of multiplying two ratios or more by one another. Let’s understand it by examples.

Solved Examples

Example 1. Give two equivalent ratios of $6:16$

Ans: It begins with finding the equivalent ratio of $6:16$ by using multiplication.

The first step is to represent the ratio as a fraction, = $6/16$

Now we multiply it by the same number.

$=\dfrac{6 \times 2}{16 \times 2}=\dfrac{12}{32}=12: 32$

(one equivalent ratio),

So, $12:32$ is an equivalent ratio of $6:16$.

We can also find the equivalent ratio of $6:16$ by using division.

Here also, the first step is to represent the ratio as a fraction,

$=\dfrac{6}{165}=\dfrac{6 \div 2}{16 \div 2}=\dfrac{3}{8}=3: 8$

(another equivalent ratio)

So, 6: 165 is an equivalent ratio of $3:8$.

We can see that the equivalent ratios of $6:16$ are $12:32$ and $3:8$.

Example 2. Find the two equivalent ratios of $4:5$

Ans: It begins with finding the equivalent ratio of $4:5$ by using multiplication.

The first step is to represent the ratio as a fraction.

$=\dfrac{4}{5}$

Now, we multiply it by the same number.

$=\dfrac{4 \times 2}{5 \times 2}=\dfrac{8}{10}=8: 10$ is one equivalent ratio.

In order to find another equivalent ratio, we multiply again with another number.

The first step is to represent the ratio as a fraction.

$=\dfrac{4}{5}$

Now, we multiply it by the same number.

$\dfrac{4 \times 3}{5 \times 3}=\dfrac{12}{15}$ is another equivalent ratio

We can see that the equivalent ratios are $4:5$, $8:10$, and $12:15$.

Note: We can see that the division method was not applied in this case to get the answer in integer form, which is due to the G.C.F. of 4, and 5 is 1. Hence, 4 and 5 is not divisible by any other number other than 1.

Example 3. If the ratio is $11:13$ find its equivalent ratios.

Ans: It begins with finding the equivalent ratio of $11:13$ by using multiplication.

The first step is to represent the ratio as a fraction.

$=\dfrac{11}{13}$

Now we multiply it by the same number.

$=\dfrac{11 \times 2}{13 \times 2}=\dfrac{22}{26}=22: 26$ is the equivalent ratio.

Equivalent Ratio of 8:15

Now, let’s see the equivalent ratio of 8:15. Below are the step to find out the ratio:

In order to find the equivalent ratios of 8:15 by multiplication, we must multiply the numbers by 2, i.e. 8x2 : 15x2

Therefore, the equivalent ratio now is 16:30.

Practice Questions

Q1. Write the equivalent ratio of 3:9

Ans: 6:18

Q2. Write the equivalent ratio of 7:8

Ans: 14:16

Q3. Write two equivalent ratios for 5:7

Ans: 10:14 and 15:21

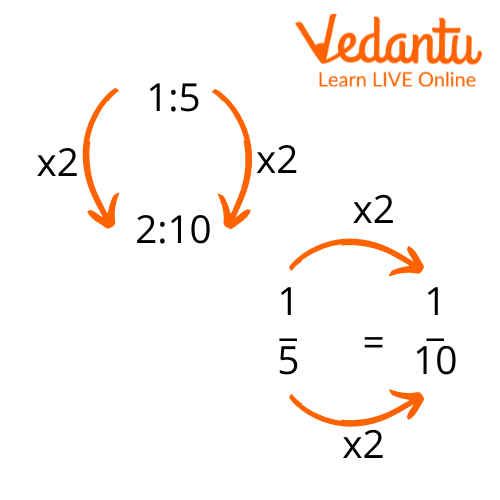
Finding an Equivalent Ratio

Summary

Ratios that are identical when compared are referred to as equivalent ratios. To determine whether two or more ratios are equivalent, they can be put side by side. An equivalent ratio is, for instance, 1:2 and 2:4. These ratios remain the same even after being changed via mathematical tools. The ratios can be represented using a fraction and thus modified by these tools. There can be multiple equivalent ratios based on the change in values and the tool used.