Application of Pythagorean Theorem in Daily Life

The Pythagorean theorem also known as the Pythagoras theorem explains “the relationship between the three sides of a right-angled triangle which are also referred to as the Pythagorean Triplet”.

Right-Angled Triangle

In the figure shown above, $ABC$ is a right-angle triangle with right angled at $B$ and $AC$ in the hypotenuse, $BC$ is the base for angle $C$ and $AB$ is perpendicular. $\underline{\underline{\text { So }}}$ in this Triangle according to Pythagoras' Theorem:

$(A C)^{2}=(A B)^{2}+(BC)^{2}$

In this article, we will be discussing the real-life application of the Pythagoras theorem, i.e., the application of the theorem in our daily life.

History of Mathematician

The Pythagorean theorem takes its name from the ancient Greek mathematician Pythagoras.

Scientist Pythagoras

• Name: Pythagoras

• Born: About 570 BC

• Died: About 490 BC

• Field: Mathematics and Philosopher

• Nationality: Greek

Statement of Pythagoras Theorem

Pythagoras theorem states that “In a right-angled triangle, the square of the hypotenuse side is equal to the sum of squares of the perpendicular and the base, i.e., the other sides of the triangle.”

Statement of Pythagoras Theorem

In the above triangle, for angle $B, B C$ is the hypotenuse, $A B$ is the base, and $A C$ is the perpendicular. So,

$(B C)^{2}=(A B)^{2}+(AC)^{2}$

Note: Hypotenuse is the longest side of the right-angle triangle.

The Formula of Pythagoras Theorem

$(\text { Hypotenuse })^{2}=(\text { Base })^{2}+(\text { Perpendicular })^{2} \\$

$(B C)^{2}=(A B)^{2}+(AC)^{2}$

where BC is hypotenuse, AB is base, and AC is perpendicular for right-angled triangle ABC.

Proof of Pythagoras Theorem

• Given: A right-angled triangle $\mathrm{ABC}$, right-angled at $\mathrm{B}$.

• To Prove: $A C^{2}=A B^{2}+B C^{2}$

• Construction: Draw a perpendicular BD meeting $A C$ at $D$.

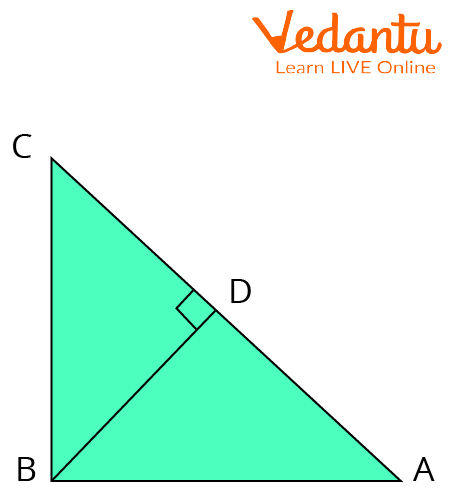
Construction to Prove Pythagoras Theorem

We know $\triangle A D B \sim \triangle A B C$

Therefore,

$\dfrac{A D}{A B}=\dfrac{A B}{A C}$

(Corresponding sides of similar triangles)

Or, $A B^{2}=A D \times A C$

Also, $\triangle B D C \sim \triangle A B C$

Therefore,

$\dfrac{C D}{B C}=\dfrac{B C}{A C}$

(Corresponding sides of similar triangles)

or, $B C^{2}=C D \times A C$

Adding the equations (1) and (2), we get,

$A B^{2}+B C^{2}=A D \times A C+C D \times A C$

$\Rightarrow A B^{2}+B C^{2}=A C(A D+C D)$

Since $A D+C D=A C$

Therefore, $A C^{2}=A B^{2}+B C^{2}$

Hence, we proved Pythagoras theorem.

Now, Let us discuss the converse of Pythagoras Theorem with detailed proof.

Converse of Pythagoras Theorem and Its Proof

Two Right-Angled Similar Triangles

• In a triangle, if the square of one side is equal to the sum of the other two sides, then the angle opposite the first side is a right angle.

• Given: $\ln \Delta X Y Z, X Y^{2}+Y Z^{2}=X Z^{2}$

• To prove: $\angle X Y Z=90^{\circ}$

• Construction: A triangle PQR is constructed such that a triangle $P Q R$ is constructed such that

$P Q=X Y, Q R=Y Z \angle P Q R=90^{\circ}$

Proof: $\ln \triangle P Q R, \angle Q=90^{\circ}$

$P R^{2}=P Q^{2}+Q R^{2}$ {Pythagoras theorem}

or $P R^{2}=X Y^{2}+Y Z^{2} \ldots$ (i) $[P Q=X Y, Q R=Y Z]$

But we know $X Z^{2}=X Y^{2}+Y Z^{2} \ldots \ldots$ (ii) (given)

Therefore, $X Z^{2}=P R^{2}$ {From equation (i) and (ii)}

or $X Z=P R$

or $\triangle X Y Z \cong \triangle P Q R$ {SSS congruence rule}

Therefore, $\angle Y=\angle Q=90^{\circ}$ {CPCT}

Hence, $\angle X Y Z=90^{\circ}$

The converse of Pythagoras theorem is proved.

Application of Pythagoras Theorem

• Pythagoras Theorem is used to find the steepness of hills.

• In Artificial intelligence: face recognition features in security cameras use the Pythagorean theorem. The distance between the camera and the person is recorded.

• Pythagoras Theorem is used to find the shortest distance in Navigation.

• The concept of the Pythagoras Theorem is also used in Interior Designing.

• Pythagoras theorem is used to find the third side of a right-angled triangle when 2 sides are given.

• In Engineering, the diameter can be easily calculated when length and breadth are known using Pythagoras Theorem.

Limitations

• Pythagoras Theorem is only applicable in the case of the Right-Angled Triangle. If one of the angles is not 90 degrees, then we cannot use Pythagoras Theorem.

• Pythagoras Theorem is only useful in the case of 2-dimensional figures. It cannot be applied in the case of 3-dimensional figures or objects.

Solved Examples

1. The perpendicular of a right-angled triangle is given as 12cm and the hypotenuse is given as 13cm. Find the base of the given triangle.

Solution:

Perpendicular $=12 \mathrm{~cm}$

Base $=b \mathrm{~cm}$

Hypotenuse $=13 \mathrm{~cm}$

As per the Pythagorean Theorem, we have

$Perpendicular^{2}+ Base^{2}= Hypotenuse^{2}$

$\Rightarrow 12^{2}+b^{2}=13^{2}$

$\Rightarrow 144+b^{2}=169$

$\Rightarrow b^{2}=169-144$

$\Rightarrow b^{2}=25$

$\Rightarrow b=\sqrt{25}$

Therefore, $b=5 \mathrm{~cm}$

2. The sides of a triangle are 15, 17, and 8 units. Check if it has a right angle or not.

Solution: Clearly, 17 is the longest side.

It also satisfies the condition $15+8>17$

We know

$c^{2}=a^{2}+b^{2}$

So, let $a=15, b=8$, and $c=17$

First, we will solve R.H.S. of Equation (1).

$a^{2}+b^{2}=15^{2}+8^{2}=225+64=289$

Now, taking L.H.S, we get

$c^{2}=17^{2}=289$

We can see LHS=RHS.

Therefore, the given triangle is a right triangle, as it satisfies the Pythagoras theorem.

To Check Angle of Triangle

Important Formulas

For any Right-Angled Triangle,

$(\text { Hypotenuse })^{2}=(\text { Base })^{2}+(\text { Perpendicular })^{2}$

Important Points to Remember

• Pythagoras theorem is applicable only in case of a right-angled triangle.

• Trigonometry is based on the Pythagoras Theorem.

Conclusion

In this article, we discussed the Pythagoras Theorem in depth. The proof, statement, applications, and examples are thoroughly explained above. From the discussion above about the Pythagoras theorem, we can conclude that it is a very useful theorem to be used in solving questions of a right-angle triangle and it helps us in real life a lot.