




How to Apply 3D Maths Formulas in Exams and Real Life
A 3D shape is a solid shape or object with three dimensions (length, width, and height) instead of a 2D object with only length and width. Other essential terms related to 3D geometric shapes are faces, edges, and vertices, for example, spheres, cubes and many more.
In mathematics, the concept of three-dimensional objects is studied and applied to real life. These 3D objects are those figures which occupy space and have volume area due to their length, width, and height. To calculate their volume or area, we can use the formula of 3D shapes.
Real-life Examples of 3D Shapes
Here are some real-world examples of 3D shapes like soccer balls, cubes, books and other objects you can touch and feel.

Example of 3D shapes
Types of 3D Shapes
Many 3D shapes (3D shapes) have different bases, volumes, and surface areas. Let's discuss each of them.
1. Sphere
The sphere is rounded in shape. This is a three-dimensional geometry in which all points on the surface are equidistant from the centre. It has a radius, diameter, circumference, volume, and surface area.

3D Representation of Sphere
2. Cube and Cuboid
Cubes and cuboids are three-dimensional shapes (three-dimensional shapes) with the same number of faces, vertices, and edges.
The main difference between a cube and a cuboid is that a cube has all six faces square and a cuboid has all six faces as a rectangle. Cubes and cuboids have different volumes and different surface areas. The length, width, and height of a cube are the same, but the length, height, and width of a cube are different.
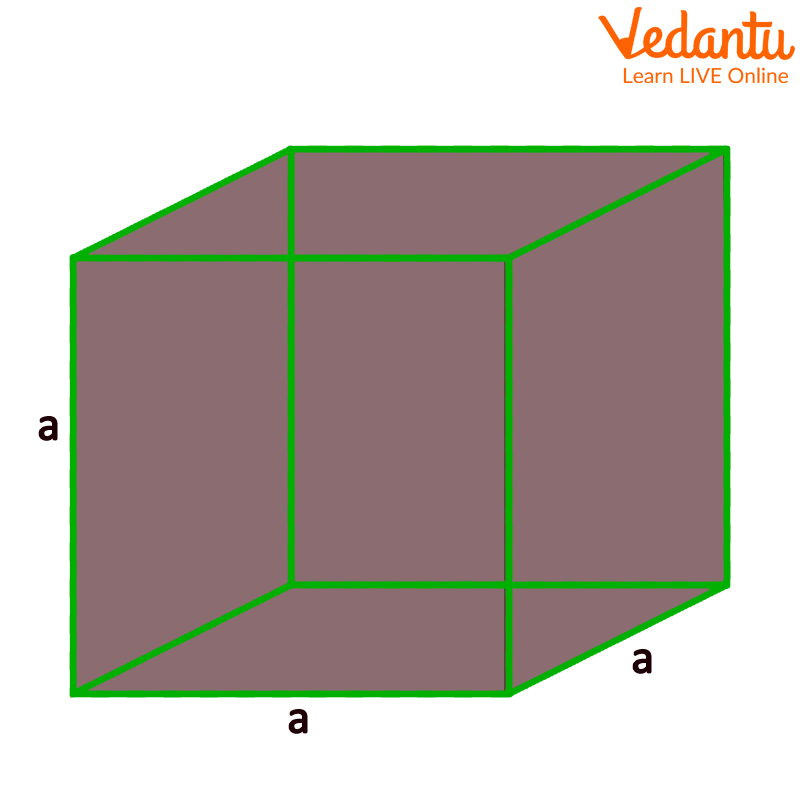
3D Representation Of Cube
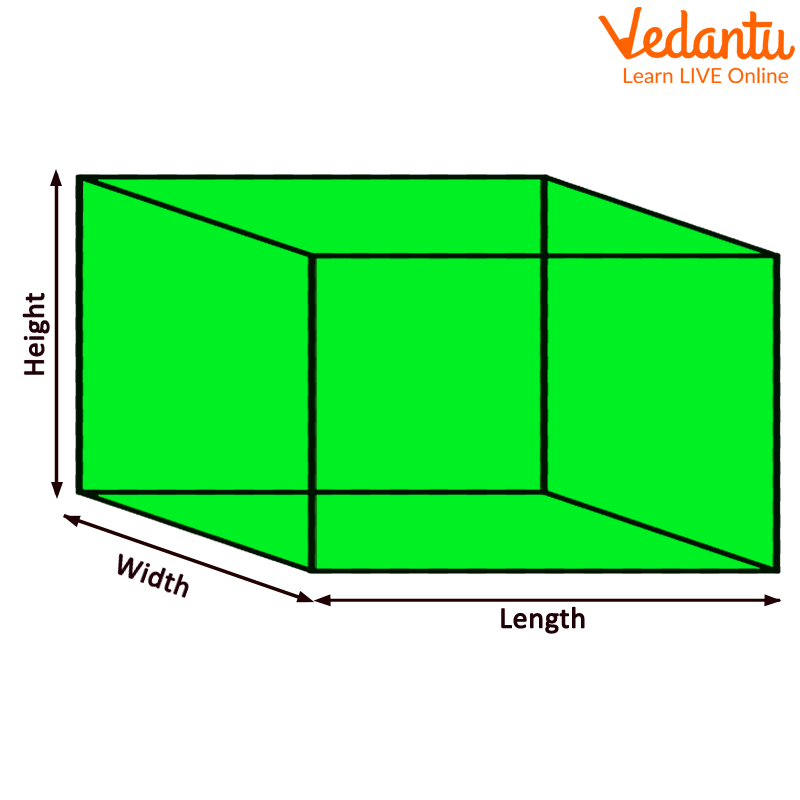
3D Representation of Cuboid
3. Cylinder
A cylinder is a three-dimensional shape with two round faces (one at the top and one at the bottom) and one curved surface. A cylinder has a height and a radius. The height of a cylinder is the vertical distance between its top and bottom faces. It has one curved edge. The shape remains the same from bottom to top.
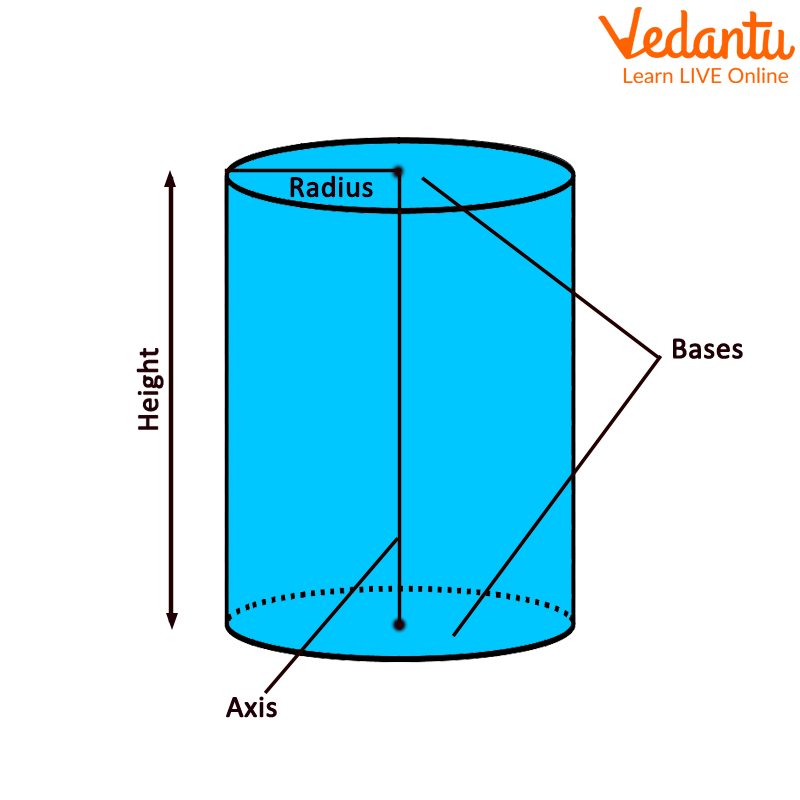
3D Representation of Cylinder
4. Cone
A cone is another three-dimensional shape (3D shape) with a flat bottom (round shape) and a pointed tip on the top. The sharp end of the top of the cone is called the "top". A cone also has a curved surface. A cone has a height and a radius. In addition to height, cones have an oblique height, which is the distance between a vertex and a point on the perimeter of the cone's circular base.
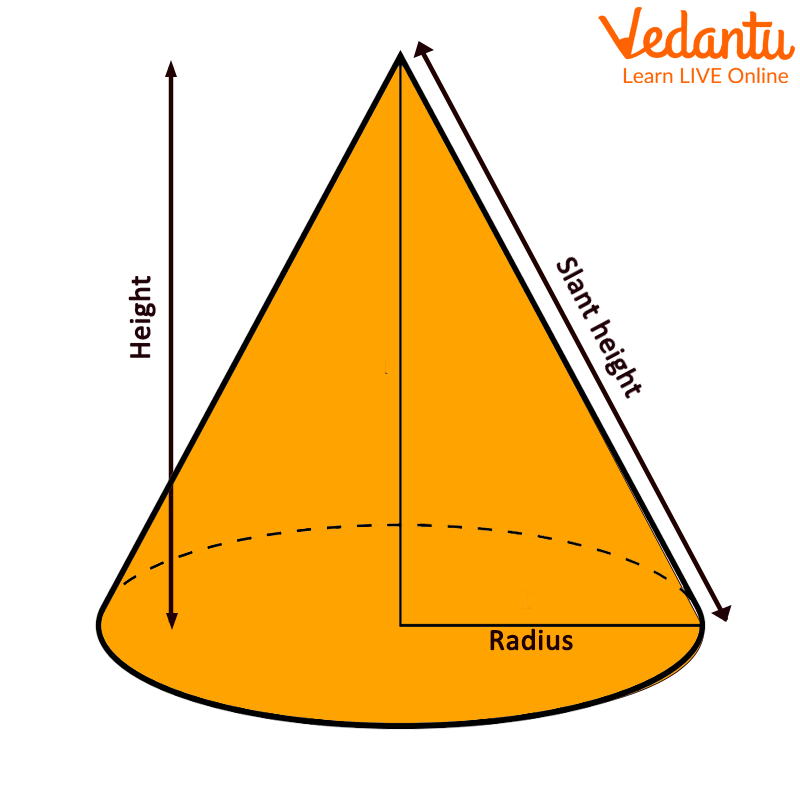
3D Representation of Cone
3D Geometry Formulas
In this, you will see the 3D figure formulas, which include the lateral surface area, total surface area, and volume of each 3D figure discussed above. Let’s discuss these terms first:
Lateral Surface Area: The size of the lateral surface is referred to as its area. This must be distinguished from the total surface area, consisting of the base and top areas and the lateral surface area. The four sides' surface area would be a cube's lateral surface area.
Total Surface Area: The area of all the surfaces or the total area of the whole figure. It is measured in square units.
Volume: Volume is defined as the space occupied by the 3D object. Volume is measured in cubic units.
1. Sphere
Curved surface area = Total surface area = \[4\pi {r^2}\]
Volume = \[\dfrac{4}{3}\pi {r^3}\]
Where r is the radius of the sphere.
2. Cube
Lateral surface area=\[4{a^2}\]
Total surface area= \[6{a^2}\]
Volume= \[{a^3}\]
Where a is the side of the cube.
3. Cuboid
Lateral surface area= \[2h(l + w)\]
Total surface area=\[2(lw + wh + lh)\]
Volume=\[l \times w \times h\]
Where l, w, and h are the cuboid's length, width and height, respectively.
4. Cylinder
Curved surface area = \[2π rh\]
Total surface area = \[2π r(h + r)\]
Volume = \[π {r^2}h\]
Where r is the radius and h is the height of the cylinder.
5. Cone
Curved surface area = \[π rl\]
Total surface area = \[π r(l + r)\]
Volume = \[\dfrac{1}{3}π {r^2}h\]
Where r is the radius, l is the slant height and l = \[\sqrt {({h^2} + {r^2})} \]
Conclusion
Mensuration is the study of measuring geometric forms and their properties such as length, volume, shape, surface area, lateral surface area, and so on. A 3D form is surrounded by several surfaces or planes. These are also solid forms; unlike 2D shapes, they include height and depth.
Solved Examples
1. Izak has a cylindrical shaped glass for drinking milk. The height of the glass is 15 units, and the radius of the base is 3 units. How much volume of milk does she need to fill her glass?
a. 421.5 cubic units
b. 451.8 cubic units
c. 423.9 cubic units
d. 400.6 cubic units
Ans: 423.9 cubic units
Explanation: In this case, the height of the glass is 15 units, and the radius of the base is 3 units. To find the volume of the glass, she must use the formula for the volume of a cylinder, which is \[\pi {r^2}h\]
\[\begin{array}{l}V = \pi {r^2}h\\V = 3.14 \times {(3)^2} \times 15\\V = 423.9\end{array}\]
So, she needs about 424 cubic units of milk to fill a glass.
2. Find the surface area of a cuboid 3 units long, 4 units wide, and 5 units high.
a. 97 square units
b. 87 square units
c. 94 square units
d. 189 square units
Ans: 94 square units
Explanation: Given the length of the cuboid= 3 units
The width of the box = 4 units
And the height of the box = 5 units.
Total surface area= \[2(lw + wh + lh)\]
\[\begin{array}{l}area = 2(3 \times 4 + 4 \times 5 + 5 \times 3)\\area = 2(12 + 20 + 15) = 2 \times 47\end{array}\]
Area = 94 square units
Therefore, the surface area of a cuboid is 94 square units.
FAQs on 3D Formulas Made Easy: Definitions, Examples & Tricks
1. Do 3D geometric shapes only have flat surfaces?
No, 3D shapes can have flat surfaces as well as curved ones. For example, cones and cylinders have flat circular surfaces and curved surfaces.
2. How do 2D and 3D shapes differ from each other?
A 2D shape has an area and does not occupy a volume, whereas a 3D shape has a surface area and a volume.
3. Define the surface area and volume of a 3D shape?
The surface area represents the area of every individual face of a 3D shape. All 3D shapes have some depth. The space inside a three-dimensional figure is the object's volume.
4. What exactly are the differences between mensuration and geometry?
Mensuration is the determination of numerous characteristics of forms, such as perimeter, area, volume, and so on, while geometry analyses the properties and connections of points and lines of diverse shapes.
5. What is the difference between the side area and the surface area of a 3D shape?
The lateral area refers to the area of all surfaces except the top and bottom surfaces of the 3D shape. The area of the curved surface includes only the area of the three-dimensional curved surface.























