Concise Mathematics Class 10 ICSE Solutions for Chapter 25 - Probability

Exercise 25 (A)

1. A coin is tossed once. Find the probability of:

(i) getting a tail

(ii) not getting a tail

Ans: 

From the question, we know that when the coin is tossed, the sample space would be = {H, T}, hence n(S) = 2.

Now, 

(i) If A = Event of getting a tail = {T}

Then, n(A)= 1

Hence, now the probability of getting a tail = $\frac{{{\text{n}}\left( {\text{A}} \right)}}{{{\text{n}}\left( {\text{S}} \right)}} = \frac{1}{2}$ 

(ii) Not getting a tail

We know that the P(getting a tail) + P(not getting a tail) = 1

So, P(not getting a tail) = 1 – (1/2) = $\frac{1}{2}$

2. A bag contains 3 white, 5 black, and 2 red balls, all of the same shape and size. A ball is drawn from the bag without looking into it, find the probability that the ball drawn is:

(i) A black ball.

(ii) A red ball.

(iii) A white ball.

(iv) Not a red ball.

(v) Not a black ball.

Ans: 

From the question, it is given that, 

The total number of balls= 3 + 5 + 2 = 10 

Now the total number of possible outcomes = 10 

(i) To find the probability black ball 

Now there are 5 black balls.

So the number of favourable outcomes = 5 

Thus the probability of getting a black ball = $\frac{5}{{10}} = \frac{1}{2}$ 

(ii) The probability of the ball to be red,

There are 2 red balls 

So now the number of favourable outcomes = 2 

Thus now the probability of getting a red ball = $\frac{{\text{2}}}{{{\text{10}}}}{\text{ = }}\frac{{\text{1}}}{{\text{5}}}$

(iii) The probability of a white ball draw? 

There are 3 white balls.

So now the number of favourable outcomes = 3 

Thus now the probability of getting a white ball = $\frac{3}{{10}}$

(iv) The probability of not getting a red ball 

There are 8 balls that are not red, 

Thus the number of favourable outcomes = 8 

Thus the probability of getting a white ball = $\frac{8}{{10}}$ = $\frac{4}{5}$

(v) The probability of not getting a black ball 

Now there are 3+ 2 = 5 ball which aren't black 

So now the number of favourable outcomes = 5 

Thus the probability of not getting a black ball = $\frac{5}{{10}} = \frac{1}{2}$ 

3. In a single throw of a die, find the probability of getting a number:

(i) greater than 4.

(ii) less than or equal to 4.

(iii) not greater than 4.

Ans: 

From the question, the sample space we get when we throw a die= {1, 2, 3, 4, 5, 6}

So now, n(s)= 6 

(i) The probability of getting a number greater than 4 

If E = event of getting a number greater than 4 = {5, 6}

So, n (E) = 2

Hence the probability of getting a number greater than 4 = $\frac{{{\text{n}}\left( {\text{E}} \right)}}{{{\text{n}}\left( {\text{S}} \right)}}$= $\frac{2}{6}$= $\frac{1}{3}$

(ii) The probability of getting a number less than or equal to 4.

Let E = event of getting a number less than or equal to 4 = {1, 2, 3, 4}

Hence, n (E) = 4

Now the probability of getting a number less than or equal to 4 = $\frac{{{\text{n}}\left( {\text{E}} \right)}}{{{\text{n}}\left( {\text{S}} \right)}}$= $\frac{4}{6}$= $\frac{2}{3}$

(iii) The probability of getting a number not greater than 4?

Let E = event of getting a number not greater than 4 = {1, 2, 3, 4}

So now n(E) = 4

Then now the probability of getting a number not greater than 4 = $\frac{{{\text{n}}\left( {\text{E}} \right)}}{{{\text{n}}\left( {\text{S}} \right)}} = \frac{2}{3}$ 

4. In a single throw of a die, find the probability that the number:

(i) Will be an even number.

(ii) Will not be an even number.

(iii) Will be an odd number.

Ans: 

Here from the question we know that the sample space when the die is thrown = {1, 2, 3, 4, 5, 6}

n(E)=3

(i) To find the probability of getting an even number when the die is thrown.

If we consider E = event of getting an even number = {2, 4, 6}

n(E)=3

Then now the probability of a getting an even number = $\frac{{{\text{n}}\left( {\text{E}} \right)}}{{{\text{n}}\left( {\text{S}} \right)}} = \frac{3}{6} = \frac{1}{2}$

(ii) The probability of not getting an even number 

If we consider E= event of not getting an even number = {1, 3, 5}

n(E)=3

Then now the probability of not getting an even number = $\frac{{{\text{n}}\left( {\text{E}} \right)}}{{{\text{n}}\left( {\text{S}} \right)}} = \frac{3}{6} = \frac{1}{2}$

(iii) The probability of getting an odd number. 

If we consider E= event of not getting an even number = {1, 3, 5}

n(E)=3

Then the probability of getting an odd number =  $\frac{{{\text{n}}\left( {\text{E}} \right)}}{{{\text{n}}\left( {\text{S}} \right)}} = \frac{3}{6} = \frac{1}{2}$

5. From a well-shuffled deck of 52 cards, one card is drawn. Find the probability that the card is drawn will:

(i) be a black card.

(ii) not be a red card.

(iii) be a red card.

(iv) be a face card.

(v) be a face card of red color.

Ans: 

From the question we know that, 

The total number of cards = 52 

So now the total number of outcomes = 52

In a deck of cards there are 13 cards of each type and the cards of heart and diamonds are red in colour, the cards of spade and diamond are black. Hence we could say that there are 26 red cards and 26 black cards. 

(i)  To find the probability that the card drawn is a black card. 

Number of black cards in a single deck = 26 

Now the number of favourable outcomes for the event of drawing a black card = 26

Then now the probability of drawing a black card = $\frac{{26}}{{52}} = \frac{1}{2}$

(ii) To find the probability that the card drawn is not a red card. 

Number of red cards in a deck = 26 

Therefore we can say that the number of non-red or the black cards = 52 - 26 = 26 

Now the number of favourable outcomes for the event of not drawing a red card = 26. 

Therefore the probability of not drawing a red card = \[\frac{{26}}{{52}} = \frac{1}{2}\] 

(iii) To find the probability that the card drawn is a red card

The number of red cards in a deck = 26

The total number of favourable outcomes for an event of drawing a red card = 26 

Then now the probability of drawing a red card = $\frac{{26}}{{52}} = \frac{1}{2}$

(iv) The probability that the card drawn will be a face card of red colour. 

Now there are 52 cards in a deck of cards, and 12 of these cards are face cards (4 kings, 4 queens and 4 jacks).

Now the number of favourable outcomes for the event of drawing a face card = 12 

Then the probability of drawing a face card = $\frac{{12}}{{52}} = \frac{3}{{13}}$

(v) The probability that the card drawn is a face card of red colour. 

There are 26 red cards in a deck and 6 of these cards are face cards (2 kings, 2 jacks and 2 queens)

Then the number of favourable outcomes for the event of drawing a face card of red colour = 6 

Then the probability of drawing a red face card = $\frac{6}{{52}} = \frac{3}{{26}}$

6. 

(i) If A and B are two complementary events then what is the relation between P(A) and P(B)?

(ii) If the probability of happening an event A is 0.46. What will be the probability of not happening of event A?

Ans: 

(i) It is given that the A and B are the two complementary events then what is the relation between P(A) and P(B)?

The two complementary events, taken together include all the outcomes for an experiment and the sum of the probability of all the outcomes is 1. 

P(A) + P(B) = 1

(ii) What will be the probability of not happening of event A if the probability of happening an event A is 0.46. 

P(A)= 0.46 

Let us consider that P(B) is the probability of not happening of event A. 

Now we know that, 

P(A) + P(B) = 1

P(B) = 1 – P(A)

P(B) = 1 – 0.46

P(B) = 0.54

Thus now the probability of not happening of an event A is 0.54. 

7. In a T.T. match between Geeta and Ritu, the probability of the winning of Ritu is 0.73. Find the probability of:

(i) winning of Geeta

(ii) not winning of Ritu

Ans: 

Now it is given that in a T.T match between Geeta and Ritu, the probability of the winning of Ritu is 0.73. 

(i) Winning of Geeta? 

In any match between two players, if one wants to win, the other has to lose the match. 

Thus, 

The probability of winning of Ritu Probability of winning of Geeta = 1 

Probability of winning Geeta = 1 - Probability that Ritu will win. 

Probability that Geeta will win = 1 – 0.73 = 0.27

(ii) The probability that Ritu will win the game?

Thus now, Let P be the probability

P (Ritu won)+ P (Ritu not winning) = 1 

P (Ritu not winning) = 1 - P (Ritu won)

P (Ritu not winning)  =  1-0.73

P (Ritu not winning)  =  0.27 

8. In a race between Mahesh and John, the probability that John will lose the race is 0.54. Find the probability of:

(i) winning of Mahesh

(ii) winning of John

Ans: 

It is given that in a race between Mahesh and John, the probability that John will lose the race is 0.54.

(i) The probability that Mahesh wins the race? 

If only John loses then Mahesh wins. 

Hence the probability of John losing the race = Probability of Mahesh winning the race since it is a race between these two only 

Therefore the probability of Mahesh winning the race = 0.54. 

(ii) The probability of John winning the race.

Let P be the probability of winning the race and now

P of John winning + P of Mahesh winning = 1 

0.54 + P of John winning=1 

P of John winning = 1 - 0.54 

P of John winning the game = 0.46 

9. 

(i) Write the probability of a sure event

(ii) Write the probability of an event when impossible

(iii) For an event E, write a relation representing the range of values of P(E)

Ans: 

(i) To find the probability of sure events 

We know that if the probability of an event is 1 then the probability is called a certain event or a sure event. 

Hence, the probability of sure event = 1 

(ii) The probability of an event which is impossible = 0 

(iii)For an event E, write a relation representing the range of values of P(E)

The probability of no event can be less than 0 and more than 1 and E be any event then, 0 ≤ P(E) ≤ 1

10. In a single throw of a die, find the probability of getting:

(i) 5

(ii) 8

(iii) a number less than 8

(iv) a prime number

Ans: 

The numbers on the die are 1, 2, 3, 4, 5 and 6 and so 

The number of possible outcomes = 6 

(i) The number of favourable outcomes = 1 which is 5 

Therefore P(E) = $\frac{{{\text{Number of favourable outcomes}}}}{{{\text{Number of all possible outcomes}}}}$ = $\frac{1}{6}$

(ii) The number of favourable outcomes = 0 (As 8 is not possible)

Therefore P(E) = $\frac{{{\text{Number of favourable outcomes}}}}{{{\text{Number of all possible outcomes}}}}$ = $\frac{0}{6}$ = 0

(iii) A number less than 8

The number less than 8 will be 1, 2, 3, 4, 5, 6 

Therefore P(E) = $\frac{{{\text{Number of favourable outcomes}}}}{{{\text{Number of all possible outcomes}}}}$  = $\frac{6}{6}$ = 1

(iv) A prime number

The prime numbers will be = 2, 3, 5 

Therefore P(E)= $\frac{{{\text{Number of favourable outcomes}}}}{{{\text{Number of all possible outcomes}}}}$ $ = \frac{3}{6} = \frac{1}{2}$

11. A die is thrown once. Find the probability of getting:

(i) an even number

(ii) a number between 3 and 8

(iii) an even number or a multiple of 3

Ans: 

The numbers on the die are 1, 2, 3, 4, 5 and 6 and so 

The number of possible outcomes = 6 

(i) The probability of getting an even number 

Number of the even numbers on the die = 2, 4, 6 = 3

Therefore P(E ) = $\frac{{{\text{Number of favourable outcomes}}}}{{{\text{Number of all possible outcomes}}}}$ $ = \frac{3}{6} = \frac{1}{2}$ 

(ii) The number between 3 and 8 on the die = 3, 4, 5, 6 = 4 

Therefore P(E) = $\frac{{{\text{Number of favourable outcomes}}}}{{{\text{Number of all possible outcomes}}}}$  $ = \frac{4}{6} = \frac{2}{3}$ 

(iii) An even number or a multiple of 3 = 2,3,4, 6= 4

Therefore P(E) = $\frac{{{\text{Number of favourable outcomes}}}}{{{\text{Number of all possible outcomes}}}}$  $ = \frac{4}{6} = \frac{2}{3}$  

12. Which of the following cannot be the probability of an event?

(i) 3/5

(ii) 2.7

(iii) 43%

(iv) – 0.6

(v) – 3.2

(vi) 0.35

Ans: 

We know that the probability of no event can be more than 1 or less than 0. 

Therefore the probability of any event can be less than 0 or more than 1 and now 

(i) $\frac{3}{5}$, is between 0 and 1 and therefore it is the probability of an event. 

(ii) 2.7 is greater than 1 and therefore it is not the probability of an event.

(iii) 43% = $\frac{{43}}{{100}}$ , it is in between 0 and 1

Therefore it is the probability of an event.

(iv) -0.6 is less than 0 and therefore it is not the probability of an event. 

(v) -3.2, is less than 0 

Therefore it is not the probability of an event. 

(vi) 0.35 = $\frac{{35}}{{100}}$ which is in between 0 and 1.

Therefore the probability of an event. 

13. A bag contains six identical black balls. A child withdraws one ball from the bag without looking into it. What is the probability that he takes out:

(i) a white ball

(ii) a black ball

Ans: 

Since there are 6 black balls in a bag

Therefore number of possible outcome= 6 

(i) A White ball

As there is no white ball in the bag 

Therefore its probability is 0 = or P(E) = 0

(ii) A Black ball

Therefore the number of favourable outcomes= 1. 

14. A single letter is selected at random from the word ‘Probability’. Find the probability that it is a vowel.

Ans: 

In the word, the Probability, the number of letters are 

i.e. P, R, O, B, A, I, L, T, Y and the number of favourable outcomes = o.a.i = 3

Therefore, P(E) = $\frac{{{\text{Number of favourable outcomes}}}}{{{\text{Number of all possible outcomes}}}}$  $ = \frac{3}{9} = \frac{1}{3}$ 

15. Ramesh chooses a date at random in January for a party (see the following figure).

Find the probability that he chooses:

(i) a Wednesday 

(ii) A friday 

(iii) a Tuesday or a Saturday 

Ans: 

It is given that the days of the month of January which has 31 days 

Therefore the number of possible outcomes = 31 

(i) The number of Wednesday in the month = 5 

Therefore, P(E) = $\frac{{{\text{Number of favourable outcomes}}}}{{{\text{Number of all possible outcomes}}}}$  = $\frac{5}{{31}}$

(ii) The number of Friday in the month = 5 

Therefore, P(E) = $\frac{{{\text{Number of favourable outcomes}}}}{{{\text{Number of all possible outcomes}}}}$  = $\frac{5}{{31}}$

(iii) The Number of Tuesdays = 4 

The number of Saturday = 4 

Therefore the total number of Tuesday and Saturday = 4 + 4 = 8

Therefore, P(E) = $\frac{{{\text{Number of favourable outcomes}}}}{{{\text{Number of all possible outcomes}}}}$  = $\frac{8}{{31}}$

Exercise 25 (B)

1. Nine cards (identical in all respects) are numbered 2 to 10. A card is selected from them at random. Find the probability that the card selected will be:

(i) an even number

(ii) a multiple of 3

(iii) an even number and a multiple of 3

(iv) an even number or a multiple of 3

Ans:

It is given that there are totally 9 cards from which one card is drawn. 

Total number of elementary events = n(S)= 9 

(i) To find the probability that the card selected is an even number

From numbers 2 to 10, there are 5 even numbers that is 2, 4, 6, 8, 10

So now the favourable number of events = n(E) = 5

Hence, the probability of selecting a card with an even number = $\frac{{{\text{n}}\left( {\text{E}} \right)}}{{{\text{n}}\left( {\text{S}} \right)}}$= $\frac{5}{9}$

(ii) To find the probability that the card selected will be a multiple of 3 

From the numbers 2 to 10, there are 3 numbers which are the multiples of 3 i.e. 3, 6, 9

So now the favourable number of events = n(E) = 3

Hence the probability of selecting a card with a multiple of 3 = $\frac{{{\text{n}}\left( {\text{E}} \right)}}{{{\text{n}}\left( {\text{S}} \right)}}$= $\frac{3}{9} = \frac{1}{3}$

(iii)To find the probability that the card selected will be an even number and a multiple of 3. 

From numbers 2 to 10, there is only one number which is an even number as well as a multiple of 3 that is 6 

So, favourable number of events = n(E) = 1

Hence the probability of selecting a card with a number that is an even number as well as a multiple of 3 = $\frac{{{\text{n}}\left( {\text{E}} \right)}}{{{\text{n}}\left( {\text{S}} \right)}}$= $\frac{1}{9}$

(iv) To find the probability that the card selected will be an even number or  a multiple of 3.

From the numbers 2 to 10, there are 7 numbers which are even numbers or a multiple of 3 that is 2, 3, 4, 6, 8, 9, 10.

So now the favorable number of events = n(E) = 7

Hence, the probability of selecting a card with a number that is an even number or a multiple of 3 = $\frac{{{\text{n}}\left( {\text{E}} \right)}}{{{\text{n}}\left( {\text{S}} \right)}}$ = $\frac{7}{9}$

2. Hundred identical cards are numbered from 1 to 100. The cards are well shuffled and then a card is drawn. Find the probability that the number on the card drawn is:

(i) a multiple of 5

(ii) a multiple of 6

(iii) between 40 and 60

(iv) greater than 85

(v) less than 48

Ans:

It is given that there are 100 cards from which only one card is drawn. 

The total number of elementary events = n(S) = 100

(i) To find the probability that the number on the card drawn is a multiple of 5. 

From the numbers 1 to 100, there are 20 numbers which are the multiple of 5 which are 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, 65, 70, 75, 80, 85, 90, 95, 100. 

So now the favourable number of events = n(E) = 20

Hence the probability of selecting a card with the multiple of 5 = $\frac{{{\text{n}}\left( {\text{E}} \right)}}{{{\text{n}}\left( {\text{S}} \right){\text{}}}}$= $\frac{{20}}{{100}} = \frac{1}{5}$

(ii) To find the probability that the number on the card drawn is a multiple of 6. 

From the numbers 1 to 100, there are only 16 numbers which are the multiple of 6 which are 6, 12, 18, 24, 30, 36, 42, 48, 54, 60, 66, 72, 78, 84, 90, 96.

So now the favorable number of events =  n(E) = 16

Hence the probability of selecting a card with the multiple of 5 = $\frac{{{\text{n}}\left( {\text{E}} \right)}}{{{\text{n}}\left( {\text{S}} \right){\text{}}}}$ = $\frac{{16}}{{100}} = \frac{4}{{25}}$

(iii) To find the probability that the number on the card drawn is between 40 and 60.

From the numbers 1 to 100, there are around 19 numbers which are between 40 and 60 which are actually 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59.

So, now the favourable number of events = n(E) = 19

Hence the probability of selecting a card with the multiple of 5 = $\frac{{{\text{n}}\left( {\text{E}} \right)}}{{{\text{n}}\left( {\text{S}} \right){\text{}}}}$ = $\frac{{19}}{{100}}$

(iv) To find the probability that the number on the card drawn is greater than 85. 

From the numbers 1 to 100, there are around 15 numbers that are greater than 85 that is 86, 87, 88, 89, 90, 91, 92, 92, .…. , 98, 99, 100

So now the favourable number of events = n(E) = 15

Hence the probability of selecting a card with the multiple of 5 = $\frac{{{\text{n}}\left( {\text{E}} \right)}}{{{\text{n}}\left( {\text{S}} \right){\text{}}}}$= $\frac{{15}}{{100}}$= $\frac{3}{{20\;}}$

(v) Find the probability that the number on the card drawn is less than 48. 

From the numbers 1 to 100, there are 47 numbers which are less than 48, that is 1, 2, 3, 4, 5, 6, ….. , 46, 47. 

So now the favourable number of events = n(E) = 47 

Hence the probability of selecting a card with number less than 48 = $\frac{{{\text{n}}\left( {\text{E}} \right)}}{{{\text{n}}\left( {\text{S}} \right){\text{}}}}$= $\frac{{47}}{{100}}$

3. From 25 identical cards, numbered 1, 2, 3, 4, 5, ……, 24, 25: one card is drawn at random. Find the probability that the number on the card drawn is a multiple of:

(i) 3

(ii) 5

(iii) 3 and 5

(iv) 3 or 5

Ans:

From the question we know that there are 25 cards from which one card is drawn. 

So now the total number of elementary events or the sample space =  n(S) = 25

(i) To find the probability that the number on the card drawn is a multiple of 3 .

From the numbers 1 to 25 there are 8 numbers which are the multiple of 3 that is 3, 6, 9, 12, 15, 18, 21, 24. 

So now the favourable number of events =  n(E) = 8

Hence the probability of selecting a card with a multiple of 3 = $\frac{{{\text{n}}\left( {\text{E}} \right)}}{{{\text{n}}\left( {\text{S}} \right){\text{}}}}$ = $\frac{{8}}{{25}}$

(ii) To find the probability that the number on the card drawn is a multiple of 5.

From the numbers 1 to 25 there are 5 numbers which are the multiple of 5 that is 5, 10, 15, 20, 25. 

So now the favourable number of events = n(E) = 5

Hence the probability of selecting a card with a multiple of 3 = $\frac{{{\text{n}}\left( {\text{E}} \right)}}{{{\text{n}}\left( {\text{S}} \right){\text{}}}}$ = $\frac{{5}}{{25}}$ = $\frac{1}{5}$

(iii) To find the probability that the number on the card drawn is a multiple of 3 and 5. 

From the numbers 1 to 25 there is only one number which is the multiple of 3 and 5 that is 15

So now the favourable number of events = n(E) = 1

Hence the probability of selecting a card with a multiple of 3 and 5 = $\frac{{{\text{n}}\left( {\text{E}} \right)}}{{{\text{n}}\left( {\text{S}} \right){\text{}}}}$= $\frac{{1}}{{25}}$

(iv) To find the probability that the number on the card drawn is a multiple of 3 or 5. 

From the numbers 1 to 25 there is 12 numbers which is the multiple of 3 or 5 that are 3, 5, 6, 9, 10, 12, 15, 18, 20, 21, 24, 25

So now the favourable number of events = n(E) = 12

Hence the probability of selecting a card with a multiple of 3 or 5 = $\frac{{{\text{n}}\left( {\text{E}} \right)}}{{{\text{n}}\left( {\text{S}} \right){\text{}}}}$ = $\frac{{12}}{{25}}$

4. A die is thrown once. Find the probability of getting a number:

(i) less than 3

(ii) greater than or equal to 4

(iii) less than 8

(iv) greater than 6

Ans:

It is given that the die is thrown once, then the total possible outcomes = {1, 2, 3, 4, 5, 6}

So now n(S) = 6 

(i) To find the probability of getting a number less than 3

On the dice, numbers less than 3 = {1.2}

So now n(E) = 2

Hence the probability of getting a number less than 3 = $\frac{{{\text{n}}\left( {\text{E}} \right)}}{{{\text{n}}\left( {\text{S}} \right){\text{}}}}$= $\frac{2}{6} = \frac{1}{3}$

(ii) To find the probability of getting a number greater than or equal to 4 

On the dice the numbers which are greater than or equal to 4 = {4, 5, 6}

So now, n(E) = 3

Therefore the probability of getting a number greater than or equal to 4 = $\frac{{{\text{n}}\left( {\text{E}} \right)}}{{{\text{n}}\left( {\text{S}} \right){\text{}}}}$= $\frac{3}{6} = \frac{1}{2}$

(iii) To find the probability of getting a number less than 8. 

On the dice, the numbers less than 8 = {1, 2, 3, 4, 5, 6}

So, n(E) = 6

Therefore the probability of getting the number less than 8 = $\frac{{{\text{n}}\left( {\text{E}} \right)}}{{{\text{n}}\left( {\text{S}} \right){\text{}}}}$ = $\frac{6}{6} = 1$

(iv) To find the probability of getting a number greater than 6

On the dice the number greater than 6 = 0 

So now n(E)= 0 

Therefore, the probability of getting the number less than 8 = $\frac{{{\text{n}}\left( {\text{E}} \right)}}{{{\text{n}}\left( {\text{S}} \right){\text{}}}}$ = $\frac{0}{6} = 0$

5. A book contains 85 pages. A page is chosen at random. What is the probability that the sum of the digits on the page is 8?

Ans:

From the question we know that the number of pages in the book = 85 

Therefore the number of possible outcomes or the sample space = n(S) = 85 

Out of 85 pages, the pages that sum up to 8 = {8, 17, 26, 35, 44, 53, 62, 71, 80}

So the pages that sum up to 8 = n(E) = 9 

Therefore the probability of choosing a page with the sum of digits on the page equals 8 = $\frac{{{\text{n}}\left( {\text{E}} \right)}}{{{\text{n}}\left( {\text{S}} \right){\text{}}}}$= $\frac{9}{{85}}$

6. A pair of dice is thrown. Find the probability of getting a sum of 10 or more, if 5 appears on the first die.

Ans:

When the dice is thrown, the total possible outcomes = {1, 2, 3, 4, 5, 6}

So now the sample space, n(S) = 6 

As its given that a pair of dice is thrown, then n(S) = 6 x 6 = 36

The favourable cases where the sum is 10 or more with 5 on the 1st die = {(5, 5), (5, 6)}

Event of getting the sum is 10 or more with 5 on the 1st die = {(5, 5), (5, 6)}

Event of getting the sum is 10 or more with 5 on the 1st die = n(E) = 2

Therefore the probability of getting a sum of 10 or more, if 5 appears on the first die= $\frac{{{\text{n}}\left( {\text{E}} \right)}}{{{\text{n}}\left( {\text{S}} \right){\text{}}}}$= $\frac{2}{{36}} = \frac{1}{{18}}$

7. If two coins are tossed once, what is the probability of getting:

(i) Both heads.

(ii) At least one head.

(iii) Both heads or both tails.

Ans:

When two coins are tossed together, the possible number of outcomes = {HH, HT, TH, TT}

Therefore the sample space, n(S) = 4

(i) The probability of getting heads. 

Let E be the event of getting both heads = {HH}

n(E)=1 

The probability of getting both heads = $\frac{{{\text{n}}\left( {\text{E}} \right)}}{{{\text{n}}\left( {\text{S}} \right){\text{}}}}$= $\frac{1}{4}$

(ii) The probability of getting at least one head. 

Let E be the event of getting at least one head = {HH, TH, HT}

n(E)=3

The probability of getting both heads = $\frac{{{\text{n}}\left( {\text{E}} \right)}}{{{\text{n}}\left( {\text{S}} \right){\text{}}}}$= $\frac{3}{4}$

(iii) The probability of getting both heads and both tails 

Let E be the event of getting at least one head = {HH, TT}

n(E)=2

The probability of getting both heads = $\frac{{{\text{n}}\left( {\text{E}} \right)}}{{{\text{n}}\left( {\text{S}} \right){\text{}}}}$ = $\frac{2}{4}$ = $\frac{1}{2}$.

8. Two dice are rolled together. Find the probability of getting:

(i) A Total of at least 10.

(ii) A Multiple of 2 on one die and an odd number on the other die.

Ans:

A dice as we know has 6 faces which are 1, 2, 3, 4, 5, 6. 

Therefore on rolling two dice at a time, the number of outcomes = 6 x 6 = 36

Therefore the total number of possible outcomes = 36.

(i) To find the probability of getting a total of at least 10.

Let E be the event of getting a total of at least 10 = (4, 6), (5, 5), (5, 6), (6, 4), (6, 5), (6, 6).

n(E) = 6 

Therefore the probability of getting a total of at least 10, 

P(E) = $\frac{{{\text{n}}\left( {\text{E}} \right)}}{{{\text{n}}\left( {\text{S}} \right)}}$ = $\frac{6}{{36}}$ = $\frac{1}{6}$

(ii) To find the probability of getting a multiple of 2 on one die and an odd number on the other die.

Let E be the event of getting a multiple of 2 on one die and an odd number on the other 

The outcomes can be (2, 1), (2, 3), (g, 5), (4, 1), (4,3) , (4, 5), (6, 1), (6, 3), (6, 5), (1, 2), (3, 2), (5, 2), (1, 4), (3, 4), (5, 4), (1, 6), (3, 6), 5, 6)

n(E) = 18

The probability of getting a multiple of 2 on one die and an odd number on the other die, 

P(E) = $\frac{{{\text{n}}\left( {\text{E}} \right)}}{{{\text{n}}\left( {\text{S}} \right)}}$= $\frac{{18}}{{36}}$= ½ 

9. A card is drawn from a well-shuffled pack of 52 cards. Find the probability that the card drawn is:

(i) A Spade.

(ii) A Red Card.

(iii) A Face Card.

(iv) 5 of Heart or Diamond.

(v) Jack or Queen.

(vi) Ace and King.

(vii) A Red and a King.

(viii) A Red or a King.

Ans:

The number of possible outcomes when the card is drawn from a pack of 52 cards = 52. 

n(S) = 52 

(i) To find the probability that the card drawn is a spade. 

The number of spade cards = 13 and let that be E, which is the event of drawing a spade.

n(E)= 13

The probability of drawing a spade, P(E) = $\frac{{{\text{n}}\left( {\text{E}} \right)}}{{{\text{n}}\left( {\text{S}} \right)}}$=  $\frac{{13}}{{52}}$= ¼ 

(ii) To find the probability that the card drawn is a red card. 

Number of red cards = 26 and let let that be equal to E which is the event of drawing the red cards 

n(E)=26  

The probability of drawing red card, P(E) = $\frac{{{\text{n}}\left( {\text{E}} \right)}}{{{\text{n}}\left( {\text{S}} \right)}}$=  $\frac{{26}}{{52}}$= ½ 

(iii) The number of face cards = 12 which is also the event E of drawing the face cards

n(E) = 12 

The probability of drawing a face card, P(E) = $\frac{{{\text{n}}\left( {\text{E}} \right)}}{{{\text{n}}\left( {\text{S}} \right)}}$ =  $\frac{{12}}{{52}}$= $\frac{3}{{13}}$

(iv) The probability that the card drawn is 5 of heart or diamond.

Let E be the event of drawing a 5 of heart or of diamond = (5H, 5D)

n(E) = 2

Therefore the probability of drawing a 5 of heart or a diamond, 

P(E) = $\frac{{{\text{n}}\left( {\text{E}} \right)}}{{{\text{n}}\left( {\text{S}} \right)}}$ = $\frac{2}{{52}}$ = $\frac{1}{{26}}$

(v) The probability that the card drawn is Jack or queen. 

Let E be the event of drawing a jack or a queen, (JH, JS, JD, JC, QH, QS, QD, QC)

n(E) = 8 

Therefore the probability of drawing a Jack or a queen

P(E) = $\frac{{{\text{n}}\left( {\text{E}} \right)}}{{{\text{n}}\left( {\text{S}} \right)}}$ = $\frac{8}{{52}}$ = $\frac{2}{{13}}$

(vi) The probability that the card drawn is ace and a king 

There is no such possibility that the card drawn could be both an ace and a king.

P(E) = 0  

(vii) The probability that the card drawn is red and a king 

There are only two such cards which are red kings 

Therefore P(E) = $\frac{{{\text{Number of favourable outcomes}}}}{{{\text{Number of all possible outcomes}}}}$  = $\frac{8}{{52}} = \frac{2}{{13}}$

(viii) The probability that the card drawn is red or a king 

There are 26 cards which are red in color in which 2 kings are red and 2 more kings which are balck = 26+2 = 28

Therefore P(E) = $\frac{{{\text{Number of favourable outcomes}}}}{{{\text{Number of all possible outcomes}}}}$  = $\frac{{28}}{{52}} = \frac{7}{{13}}$

10. A bag contains 16 colored balls. Six are green, 7 are red and 3 are white. A ball is chosen, without looking into the bag. Find the probability that the ball chosen is:

(i) Red

(ii) Not Red

(iii) White

(iv) Not White

(v) Green or Red

(vi) White or Green

(vii) Green or Red or White.

Ans:

It is given that there are 16 balls in the bag and let that be equal to the number of balls that could be drawn. So now the sample space, 

n(S) = 16 

(i) To find the probability that the ball drawn is red

Let E be the event of drawing a red ball which will be equal to the number of red balls = 7 

So now n(E) = 7 

Now, P(E) = $\frac{{{\text{n}}\left( {\text{E}} \right)}}{{{\text{n}}\left( {\text{S}} \right)}}$ = $\frac{7}{{16}}$

(ii) To find the probability that the ball drawn is not red

Now, The ball drawn is not red = 16 - number of red balls 

= 16 - 7 = 9

n(E) =  9 

Now P(E), not a red ball = $\frac{{{\text{n}}\left( {\text{E}} \right)}}{{{\text{n}}\left( {\text{S}} \right)}}$ = $\frac{{9}}{{16}}$

(iii) To find the probability that the ball drawn is white in color 

Let E be the event of drawing a white ball which will be equal to white balls = 3 

Therefore n(E) = 3

The probability of drawing a white ball, P(E) = $\frac{{{\text{n}}\left( {\text{E}} \right)}}{{{\text{n}}\left( {\text{S}} \right)}}$ = $\frac{3}{{16}}$

(iv) To find the probability that the ball drawn is not white ball 

Now, The ball drawn is not red = 16 - number of red balls 

= 16 - 3 = 13

n(E) =  13 

Now P(E), not a red ball = $\frac{{{\text{n}}\left( {\text{E}} \right)}}{{{\text{n}}\left( {\text{S}} \right)}}$ = $\frac{{13\;}}{{16}}$

(v) To find the probability that the ball drawn is green or red

Let E be the event of drawing a green or a red ball = number of green balls red balls = 6+7 =13 

n(E) =13

The probability of drawing a red or a green ball = $\frac{{{\text{n}}\left( {\text{E}} \right)}}{{{\text{n}}\left( {\text{S}} \right)}}$ = $\frac{{13}}{{16}}$

(vi) The probability of drawing a white or green ball.

Let E be the event of drawing a green or a white ball = Number of green + white balls = 6+3 =9 

n(E) = 9 

The probability of drawing a white or green ball = $\frac{{{\text{n}}\left( {\text{E}} \right)}}{{{\text{n}}\left( {\text{S}} \right)}}$= $\frac{9}{{16}}$

(vii) The probability of drawing a green or red or whote ball 

Let E be the event of drawing a green or red or a white ball = Number of green + white ball red ball = 6 + 3 + 7 = 16 

The probability of drawing a white or red or green ball = $\frac{{{\text{n}}\left( {\text{E}} \right)}}{{{\text{n}}\left( {\text{S}} \right)}}$ = $\frac{{16}}{{16}}$ = 1

11. A ball is drawn at random from a box onramp 12 white. 16 red and 20 green balls. Determine the probability that the ball drawn is:

(i) White

(ii) Red

(iii) Not Green

(iv) Red or White.

Ans:

The total number of balls in the box = 48 

The total possible outcomes when a ball is drawn = 48, 

n(S) = 48 

(i) The probability that the ball drawn is white. 

Event of drawing a white ball = E= 12 

n(E)= 12 

The probability of drawing a white ball = $\frac{{{\text{n}}\left( {\text{E}} \right)}}{{{\text{n}}\left( {\text{S}} \right)}}$ = $\frac{{12}}{{48}}$ = $\frac{1}{4}$

(ii) The probability that the ball drawn is red. 

Event of drawing a red ball = E= 16 

n(E)= 16

The probability of drawing a red ball = $\frac{{{\text{n}}\left( {\text{E}} \right)}}{{{\text{n}}\left( {\text{S}} \right)}}$ = $\frac{{16}}{{48}}$ = ⅓ 

(iii) The probability that the ball drawn is not green

The number of balls = 12+16 = 28 

Therefore the total number of favourable outcomes = 28

Let the probability that the ball drawn is not green be P(E), 

P(E) = $\frac{{{\text{n}}\left( {\text{E}} \right)}}{{{\text{n}}\left( {\text{S}} \right)}}$ = $\frac{{28}}{{48}}$= $\frac{7}{{12}}$

(iv) The probability that the ball drawn is red or white.

Total red or the white balls = 12+16 = 28 balls 

Event of drawing a red or the white ball = E = 28 

n(E) = 28 

P(E) = $\frac{{{\text{n}}\left( {\text{E}} \right)}}{{{\text{n}}\left( {\text{S}} \right)}}$ = $\frac{{28}}{{48}}$ = $\frac{7}{{12}}$

12. A card is drawn from a pack of 52 cards. Find the probability that the card drawn is:

(i) A Red Card

(ii) A Black Card

(iii) A Spade

(iv) An Ace

(v) A Black Ace

(vi) Ace of Diamonds

(vii) Not a Club

(viii) A Queen or a Jack

Ans:

The total number of cards in the deck = 52 

Therefore the total number of possible outcomes = 52 

(i) The probability that the card drawn is red card

There are a total of 26 red cards in the deck.

Therefore the number of favourable outcome= 26 

P(E) = $\frac{{{\text{Number of favourable outcomes}}}}{{{\text{Number of total outcomes}}}}$ = $\frac{{26}}{{52}}$ = $\frac{{1}}{{2}}$ 

(ii) The probability that the card drawn is a black card

There are a total of 26 black cards in the deck.

Therefore the number of favourable outcome= 26 

P(E) = $\frac{{{\text{Number of favourable outcomes}}}}{{{\text{Number of total outcomes}}}}$  = $\frac{{26}}{{52}}$= $\frac{{1}}{{2}}$

(iii) The probability that the card drawn is a spade card 

There are a total of 13 spade cards in the deck.

Therefore the number of favorable outcome= 13 

P(E) =  $\frac{{{\text{Number of favourable outcomes}}}}{{{\text{Number of total outcomes}}}}$ = $\frac{{13}}{{52}}$= $\frac{{1}}{{4}}$

(iv) The probability that the card drawn is an ace

There are a total of 4 aces in the deck 

The number of favourable outcomes = 4 

P(E) =  $\frac{{{\text{Number of favourable outcomes}}}}{{{\text{Number of total outcomes}}}}$ = $\frac{4}{{52}}$= $\frac{1}{{13}}$  

(v) The probability that the card drawn is a black ace

There are only 2 black ace in the deck 

The number of favourable outcomes = 2 

P(E) =  $\frac{{{\text{Number of favourable outcomes}}}}{{{\text{Number of total outcomes}}}}$ = $\frac{2}{{52}}$= $\frac{1}{{26}}$  

(vi)The probability that the card drawn is a ace of diamonds

There is only one card which is a ace of diamonds and now, 

The number of favourable outcomes = 1

P(E) =  $\frac{{{\text{Number of favourable outcomes}}}}{{{\text{Number of total outcomes}}}}$ = $\frac{1}{{52}}$

(vii) The probability that the card drawn is a not a club

There are 39 cards in total which are not a club.

Therefore the number of favourable outcomes = 39 

P(E) = $\frac{{{\text{Number of favourable outcomes}}}}{{{\text{Number of total outcomes}}}}$= $\frac{{39}}{{52}}$=$\frac{3}{4}$

(viii)The probability that the card drawn is a queen or a jack. 

There are only 4 queens and Jack cards in the deck of cards. 

Therefore the number of favourable outcomes = 4+4 = 8 

P(E) =  $\frac{{{\text{Number of favourable outcomes}}}}{{{\text{Number of total outcomes}}}}$ = $\frac{8}{{52}}$=$\frac{2}{{13}}$

13. Thirty identical cards are marked with numbers 1 to 30. If one card is drawn at random, find the probability that it is:

(i) A Multiple of 4 or 6.

(ii) A Multiple of 3 and 5

(iii) A Multiple of 3 or 5

Ans:

It is given that there are 30 cards which are marked with the numbers 1 to 30 and only one card is drawn. 

(i) To find the probability that the card drawn is a multiple of 4 or 6 

There are 10 numbers which are the multiple of 4 or 6 and the multiples are 4, 6, 8, 12, 16, 18, 20, 24, 28, 30. 

Therefore the total number of favourable outcomes = 10 

Therefore, P(E) = $\frac{{{\text{Number of favourable outcomes}}}}{{{\text{Number of total outcomes}}}}$ = $\frac{{10}}{{30}}$= $\frac{{1}}{{3}}$ 

(ii) To find the probability that the card drawn is a multiple of 3 and 5 

The multiples of 3 and 5 are 15, 30 which is only 2. 

Therefore the total number of favourable outcomes = 2

Therefore,  P(E) =  $\frac{{{\text{Number of favourable outcomes}}}}{{{\text{Number of total outcomes}}}}$  = $\frac{2}{{30}}$= $\frac{1}{{15}}$

(iii) To find the probability that the card drawn is a multiple of 3 or 5 

There are 14 numbers  which are the multiples of 3 or 5 and the multiples are 3, 5, 6, 9, 10, 12, 15, 18, 20, 21, 24, 25, 27, 30. 

Therefore the total number of favourable outcomes = 14 

Therefore, P(E) =  $\frac{{{\text{Number of favourable outcomes}}}}{{{\text{Number of total outcomes}}}}$ = $\frac{{14}}{{30\;}}$= $\frac{7}{{15}}$ 

14. In a single throw of two dice, find the probability of :

(i) A Doublet

(ii) A Number Less than 3 on Each Dice.

(iii) An Odd Number as a Sum.

(iv) A Total of at Most 10.

(v) An Odd Number on one dice and a number less than or equal to 4 on the other dice.

Ans:

It is given that two dice are thrown at once. Each dice has 1 to 6 numbers on its faces and therefore the number of possible outcomes = 36.

(i) To find the probability of a doublet. 

A doublet can be (1, 1), (2, 2),(3, 3), (4, 4), (5, 5) and (6, 6) which are 6

Therefore the number of favourable outcomes = 6 

P(E) =  $\frac{{{\text{Number of favourable outcomes}}}}{{{\text{Number of total outcomes}}}}$ = $\frac{6}{{36}}$= $\frac{1}{{6}}$ 

(ii) a number less than 3 on each dice.

The number which is less than 3 on each dice can be (1, 1), (1, 2), (2, 1), (2, 2) which are 4 in numbers. 

Therefore the total number of favourable outcomes= 4

P(E) =  $\frac{{{\text{Number of favourable outcomes}}}}{{{\text{Number of total outcomes}}}}$ = $\frac{4}{{36}}$=$\frac{1}{9}$

(iii) an odd number as a sum.

An odd number as a sum which can be (1, 1), (1,3), (1,5), (2, 1), (2,3), (2,5), (3, 1), (3,3), (3,5), (4, 1), (4,3), (4, 5), (5,1),(5,3), (5,5), (6, 1), (6, 3), (6, 5) which are 18 in numbers. 

Number of favourable outcomes= 18 

P(E) =  $\frac{{{\text{Number of favourable outcomes}}}}{{{\text{Number of total outcomes}}}}$ = $\frac{{18}}{{36}}$= ½  

(iv) A total of at most 10.

An utmost of 10 can be = 36-3 (which can be(5, 6), (6, 6), (6, 5) = 33)

Therefore the number of favourable outcomes = 33 

P(E) = $\frac{{{\text{Number of favourable outcomes}}}}{{{\text{Number of total outcomes}}}}$ = $\frac{{33}}{{36}}$= $\frac{{11}}{{12}}$

(v) An odd number on one dice and a number less than or equal to 4 on the other dice.

All the possible combinations are (1, 1), (1,2), (1,3), (1,4), (3,1), (3,2), (3, 3), (3,4) , (5, 1), (5, 2), (5, 3), (5, 4), (2, 1), (3, 1), (4, 1),(1, 3), (2, 3), (2, 5), (3, 1), (3, 5), (4, 1), (4, 3), (4,5) which are 23 in total. 

Therefore the number of favourable outcomes = 23 

Therefore P(E) =  $\frac{{{\text{Number of favourable outcomes}}}}{{{\text{Number of total outcomes}}}}$ = $\frac{{23}}{{36}}$

Exercise 25 (C)

1. A bag contains 3 red balls, 4 blue balls and 1 yellow ball, all the balls being identical in shape and size. If a ball is taken out of the bag without looking into it; find the probability that the ball is:

(i) Yellow

(ii) Red

(iii) Not Yellow

(iv) Neither Yellow Nor Red

Ans: 

It is given that in a bag there are a total of 8 balls of which 3 are red, 4 or blue and 1 is a yellow ball.

The total possible outcome = 8 

(i) To find the probability that the ball is yellow. 

Yellow balls =1 

Therefore the number of favourable outcomes =1 

P(E) =  $\frac{{{\text{Number of favourable outcomes}}}}{{{\text{Number of total outcomes}}}}$  = $\frac{1}{8}$

(ii)To find the probability that the ball is red

Red balls = 4 

Therefore the number of favourable outcomes =4 

P(E) =  $\frac{{{\text{Number of favourable outcomes}}}}{{{\text{Number of total outcomes}}}}$ = $\frac{4}{8}$= ½ 

(iii) To find the probability that the ball is not yellow

Not yellow ball = red +blue balls = 3+4 = 7

Therefore the number of favourable outcomes =7

P(E) =  $\frac{{{\text{Number of favourable outcomes}}}}{{{\text{Number of total outcomes}}}}$ = $\frac{7}{8}$

(iv) To find the probability that the ball is neither yellow nor red

 Neither yellow nor red ball means its blue balls only 

Blue balls = 4

P(E) =  $\frac{{{\text{Number of favourable outcomes}}}}{{{\text{Number of total outcomes}}}}$ = $\frac{4}{8}$= ½ 

2. A dice is thrown once. What is the probability of getting a number?

(i) Greater than 2?

(ii) Less than or Equal to 2?

Ans: 

It is given that the dice is thrown once. 

The numbers which are marked on the faces of a die are 1, 2, 3, 4, 5 and 6.

Therefore the total number of possible outcomes = 6 

(i) The probability of getting a number greater than 2

Numbers greater than 2 = 3, 4, 5 and 6 = 4 numbers. 

P(E) =  $\frac{{{\text{Number of favourable outcomes}}}}{{{\text{Number of total outcomes}}}}$ = $\frac{4}{6}$= ⅔ 

(ii) The probability of getting a number less than or equal to 2 

The numbers less than or equal to 2 are 1 and 2 = 2 numbers. 

P(E) =  $\frac{{{\text{Number of favourable outcomes}}}}{{{\text{Number of total outcomes}}}}$ = $\frac{2}{6}$= ⅓ 

3. From a well shuffled deck of 52 cards, one card is drawn. Find the probability that the card drawn is:

(i) A Face Card

(ii) Not a Face Card

(iii) A Queen of Black Card

(iv) A Card with Number 5 or 6

(v) A Card with Number Less than 8

(vi) A Card with Number Between 2 and 9

Ans: 

A deck of cards have 52 cards in total 

Therefore the number of possible outcome = 52 

(i) The probability that the card drawn is a face card.

The face cards in a deck are = 3 x 4 = 12

Therefore the number of favourable outcome =12

P(E) =  $\frac{{{\text{Number of favourable outcomes}}}}{{{\text{Number of total outcomes}}}}$ =$\frac{{12}}{{52}}$= $\frac{3}{{13}}$

(ii)  The probability that the card drawn is not a face card

Not a face card = 52 -12 = 40 

Therefore the number of favourable outcome = 40 

P(E) =  $\frac{{{\text{Number of favourable outcomes}}}}{{{\text{Number of total outcomes}}}}$ =$\frac{{40}}{{52}}$= $\frac{{10}}{{13}}$

(iii) The probability that the card drawn is a queen of black card

A queen of black colour which is 2 in numbers in the deck.

Therefore the number of favourable outcome = 2

P(E) =  $\frac{{{\text{Number of favourable outcomes}}}}{{{\text{Number of total outcomes}}}}$ =$\frac{2}{{52}}$= $\frac{1}{{26}}$

(iv) The probability that the card drawn is a card with number 5 or 6

Number of favourable outcomes = 8 

P(E) =  $\frac{{{\text{Number of favourable outcomes}}}}{{{\text{Number of total outcomes}}}}$ =$\frac{8}{{52}}$= $\frac{2}{{13}}$

(v) The probability that the card drawn is a card with number less than 8

A card with numbers less than 8 are 2, 3,4 ,5 ,6 and 7 which are 6 in total. 

P(E) =  $\frac{{{\text{Number of favourable outcomes}}}}{{{\text{Number of total outcomes}}}}$ =$\frac{6}{{52}}$= $\frac{2}{{26}}$

(vi)The probability that the card drawn is a card with number between 2 and 9

A card with numbers less than 8 which can be 2,3, 4,5,6,7 = 6 

P(E) =  $\frac{{{\text{Number of favourable outcomes}}}}{{{\text{Number of total outcomes}}}}$ =$\frac{6}{{52}}$= $\frac{2}{{26}}$

4. In a match between A and B:

(i) the probability of winning of A is 0.83. What is the probability of winning of B?

(ii) the probability of losing the match is 0.49 for B. What is the probability of winning of A?

Ans: 

A match is played between two persons, A and B 

Therefore the number of possible outcomes = 1 

(i) The probability of winning of A is 0.83. What is the probability of winning of B?

The probability that A wins is 0.83

Therefore the probability that B wins = 1- 0.83 = 0.17 (As P(E) + P($\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{E} $) =  1)

(ii) The probability of losing the match is 0.49 for B. What is the probability of winning of A?

It is given that the probability of losing the match is 0.49 by B.

Therefore the probability of losing of B or winning of A = 0.49 

5. A and B are friends. Ignoring the leap year, find the probability that both friends will have:

(i) different birthdays?

(ii) the same birthday?

Ans: 

There are a total of 365 days in a year and a person can only have only one day which is celebrated as his or her birthday. 

(i) Different Birthdays

Different birthdays can be celebrated only is 365 - 1 = 364 ways 

P(E) =  $\frac{{{\text{Number of favourable outcomes}}}}{{{\text{Number of total outcomes}}}}$ = $\frac{{364}}{{365}}$

(ii) the Same Birthday. 

If two person have same day as birthday = 1 way 

P(E) =  $\frac{{{\text{Number of favourable outcomes}}}}{{{\text{Number of total outcomes}}}}$ = $\frac{1}{{365}}$ 

6. A man tosses two different coins (one of Rs 2 and another of Rs 5) simultaneously. What is the probability that he gets:

(i) At least one head?

(ii) At most one head?

Ans: 

It is given that there are two coins in which one is of 2 rupees and the other is of 5 rupees. 

Therefore the number of heads = 1+1=2 

The number of tails are 2 in number which are 2 and 5 

Therefore the number of possible outcomes = 2 x 2 = 4

(i) The probability that he gets at least one head. 

Number of favourable outcomes = 3 

P(E) =  $\frac{{{\text{Number of favourable outcomes}}}}{{{\text{Number of total outcomes}}}}$ = $\frac{3}{4}$

(ii) The probability that he gets at most one head?

Utmost one head = 3 

P(E) =  $\frac{{{\text{Number of favourable outcomes}}}}{{{\text{Number of total outcomes}}}}$ = $\frac{3}{4}$

7. A box contains 7 red balls, 8 green balls and 5 white balls. A ball is drawn at random from the box. Find the probability that the ball is:

(i) White

(ii) Neither red nor white.

Ans: 

The number of balls in the box are 20 in which 7 are red, 8 are green and 5 are white in colour 

Therefore the number of possible outcomes = 20.

(i)The probability that the ball is white in colour. 

Total white balls= 5 

Therefore the number of favourable outcomes = 5 

P(E) =  $\frac{{{\text{Number of favourable outcomes}}}}{{{\text{Number of total outcomes}}}}$ = $\frac{5}{{20}} = \frac{1}{4}$

(ii) The probability that the ball is neither red nor white 

If the ball is not green or white then it's probably a green ball. 

All the green balls = 8 

P(E) =  $\frac{{{\text{Number of favourable outcomes}}}}{{{\text{Number of total outcomes}}}}$ = $\frac{8}{{20}} = \frac{2}{5}$

8. All the three face cards of spades are removed from a well shuffled pack of 52 cards. A card is then drawn at random from the remaining pack. Find the probability of getting:

(i) A Black face card

(ii) A Queen

(iii) A Black card

Ans: 

In a deck of playing cards there are 52 cards in total. 

Cards which are removed = 3 (3 face cards of spades)

Balance cards in the deck = 52 -3 = 49 

(i) The probability of getting a black face card.

A black face cards are 3 in numbers. 

Therefore the number of favourable outcomes = 3 

 P(E) =  $\frac{{{\text{Number of favourable outcomes}}}}{{{\text{Number of total outcomes}}}}$ = $\frac{3}{{49}}$

(ii) The probability of getting a queen 

In a deck of cards there are 3 queen cards (4-1)

P(E) =  $\frac{{{\text{Number of favourable outcomes}}}}{{{\text{Number of total outcomes}}}}$ = $\frac{3}{{49}}$

(iii)  The probability of getting a black card

The black cards = 26 -3= 23 cards in number. 

P(E) =  $\frac{{{\text{Number of favourable outcomes}}}}{{{\text{Number of total outcomes}}}}$ = $\frac{{23}}{{49}}$

9. In a musical chairs game, a person has been advised to stop playing the music at any time within 40 seconds after its start. What is the probability that the music will stop within the first 15 seconds?

Ans: 

Total time required for the musical race = 0 to 40 seconds = 40 seconds. 

The time taken by a player = 15 seconds.(0 to 15 seconds)

P(E) =  $\frac{{{\text{Number of favourable outcomes}}}}{{{\text{Number of total outcomes}}}}$ = $\frac{{15}}{{40}}$= $\frac{3}{8}$

10. In a bundle of 50 shirts, 44 are good, 4 have minor defects and 2 have major defects. What is the probability that:

(i) is it acceptable to a trader who accepts only a good shirt?

(ii) is it acceptable to a trader who rejects only a shirt with major defects?

Ans: It is given that, 

The total number of shirts in a bundle = 50 

Number of good shirts = 44 

Minor defected shirts = 4 

Major defected shirts = 2

Therefore the number of possible outcome = 50 

(i) Is it Acceptable to a Trader who Accepts only a Good Shirt?

Acceptance of only for a good shirt = 44

P(E) =  $\frac{{{\text{Number of favourable outcomes}}}}{{{\text{Number of total outcomes}}}}$ = $\frac{{44}}{{50}} = \frac{{22}}{{25}}$

(ii) Is it Acceptable to a Trader who Rejects Only a Shirt with Major Defects?

Good shorts + major defect shirts = 44 + 4 = 48

P(E) =  $\frac{{{\text{Number of favourable outcomes}}}}{{{\text{Number of total outcomes}}}}$ = $\frac{{48}}{{50}} = \frac{{24}}{{25}}$

11. Two dice are thrown at the same time. Find the probability that the sum of the two numbers appearing on the top of the dice is:

(i) 8

(ii) 13

(iii) less than or equal to 12

Ans: 

It is given that two dice are thrown at the same time and each dice has 6 numbers on its faces which are 1, 2, 3, 4, 5 and 6.

Therefore the possible number of outcomes = 36. 

(i) The probability that the sum of the two numbers appearing on the top of the dice is 8.

The sum of two numbers on the top is 8 that is (2, 6), (3, 5), (4, 4), (5, 3), (6, 2)

Therefore the number of favourable outcomes = 5. 

P(E) =  $\frac{{{\text{Number of favourable outcomes}}}}{{{\text{Number of total outcomes}}}}$ = $\frac{5}{{36}}$

(ii) The probability that the sum of the two numbers appearing on the top of the dice is 13

Sum of two numbers on the top is 13 

At the most then the sum can be (6, 6) = 12 

Therefore the number of favourable outcomes = 0

P(E) = 0

(iii) The probability that the sum of the two numbers appearing on the top of the dice is less than or equal to 12.

The sum if less than or equal to 12, that is (1, 1), (1,2), (1,3), (1,4), (1,5), (1,6), (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6), (3, 1), (3, 2), (3, 3). (3, 4), (3. 5), (3, 6), (4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6), (5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5,6) , (6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6) = 36

Therefore the number of favourable outcomes = 36

P(E) =  $\frac{{{\text{Number of favourable outcomes}}}}{{{\text{Number of total outcomes}}}}$ = $\frac{{36}}{{36}}$= 1

12. Which of the following cannot be the probability of an event?

(i) 3/7

(ii) 0.82

(iii) 37%

(iv) -2.4

Ans: 

We all know that the probability of an event E is 0 ≤ P(E) ≤ 1

(i) 3/7

As 0 ≤ 3/7 ≤ 1 

Thus $\frac{3}{7}$ can be a probability of an event.

(ii) 0.82

As 0 ≤ 0.82 ≤ 1

Hence 0.82 can be the probability of an event.

(iii) 37%

As 0 ≤ 37 % = (37/100) ≤ 1 

Hence 37% can be the probability of an event. 

(iv) -2.4

As -2.4 < 0

Thus, -2.4 cannot be a probability of an event. 

13. If P(E) = 0.59; find P(not E)

Ans: 

From the formula we know that 

P(E) + P(not E) = 1

So, 0.59 + P(not E) = 1

Hence now, P(not E) = 1 – 0.59 = 0.41

14. A bag contains a certain number of red balls. A ball is drawn. Find the probability that the ball drawn is:

(i) Black

(ii) Red

Ans: 

It is given that a bag contains a certain number of red balls, now let us assume it to be x balls. 

If one ball is drawn out then 

(i) The probability that the ball drawn is black

As there is no balck ball in the bag

The probability that a black ball is drawn = 0 

(ii) The probability that the ball drawn is red

We have assumed the red balls drawn as x so now the probability would be 

P(E) =  $\frac{{{\text{Number of favourable outcomes}}}}{{{\text{Number of total outcomes}}}}$ = $\frac{{\text{x}}}{{\text{x}}}$ = 1

15. The probability that two boys do not have the same birthday is 0.897. What is the probability that the two boys have the same birthday?

Ans: 

In the question it is given that the probability that the two boys do not have the same birthday is 0.897, then now 

Let P be the probability

P(do not have the same birthday) + P(have same birthday) = 1

0.897+ P(have same birthday) = 1

Thus we have, 

P(have same birthday) = 1 – 0.897

P(have same birthday) = 0.103

16. A bag contains 10 red balls, 16 white balls and 8 green balls. A ball is drawn out of the bag at random. What is the probability that the ball drawn will be:

(i) Not Red?

(ii) Neither Red nor Green?

(iii) White or Green?

Ans: 

From the question, 

The total number of possible outcomes = 10 + 16 + 8 = 34 balls

So, n(S) = 34

(i) The Probability that the Ball Drawn will not be Red?

The Favourable outcomes for not a red ball = favourable outcomes for white or green ball

So 

(ii) The Probability that the Ball Drawn will be Neither Red nor Green?

As a result, the number of successful outcomes for either the white or green ball is 16 + 8 = 24 = n. (E)

As a result, the probability of not drawing a red ball is equal to $\frac{{{\text{n}}\left( {\text{E}} \right)}}{{{\text{n}}\left( {\text{S}} \right)}}$=$\frac{{24}}{{34}}$ = $\frac{{12}}{{17}}$ .

As a result, the probability of not drawing a red ball is equal to $\frac{{{\text{n}}\left( {\text{E}} \right)}}{{{\text{n}}\left( {\text{S}} \right)}}$ = $\frac{{24}}{{34}}$ = $\frac{{12}}{{17}}$ . When neither a red nor a green ball has a favourable outcome, the white ball has a favourable outcome.

As a result, the number of good outcomes for the white ball = 16 = n. (E)

As a result, the probability of not drawing a red or green ball is equal to 

$\frac{{{\text{n}}\left( {\text{E}} \right)}}{{{\text{n}}\left( {\text{S}} \right)}}$=$\frac{{16}}{{34}}$ = $\frac{8}{{17}}$ .

(iii) The Probability that the Ball Drawn will be White or Green?

The total number of positive outcomes for white or the green ball = 16 + 8 = 24 = n(E)

Hence now P(E)= $\frac{{{\text{n}}\left( {\text{E}} \right)}}{{{\text{n}}\left( {\text{S}} \right)}}$=$\frac{{24}}{{34}}$ =$\frac{{12}}{{17}}$

17. A bag contains twenty Rs 5 coins, fifty Rs 2 coins and thirty Re 1 coins. If it is equally likely that one of the coins will fall down when the bag is turned upside down, what is the probability that the coin:

(i) Will it be a Rupees 1 coin?

(ii) Will it not be a Rs 2 coin?

(iii) Will neither be a Rs 5 coin nor be a Re 1 coin?

Ans: 

From the question we have, 

The total number of coins = 20 + 50 + 30 = 100

Therefore the total possible outcomes = 100 = n(S)

(i)The Probability that the Coin will be a Rupees 1 Coin?

Number of favourable outcomes for rupees 1 coins = 30 = n(E)

Probability (Re 1 coin) = $\frac{{{\text{n}}\left( {\text{E}} \right)}}{{{\text{n}}\left( {\text{S}} \right)}}$ = $\frac{{30}}{{100}}$ = $\frac{3}{{10}}$

(ii) The Probability that the Coin will Not be a Rs 2 Coin?

The total number of favourable outcomes for not a rupees 2 coins = number of favourable outcomes for rupees 1 or rupees 5 coins = 30+20 = 50 =n(E)

Hence, probability (not Rs 2 coin) = $\frac{{{\text{n}}\left( {\text{E}} \right)}}{{{\text{n}}\left( {\text{S}} \right)}}$ = ½ 

(iii) The Probability that the Coin   will Neither be a Rs 5 Coin Nor be a Re 1 Coin?

The number of favourable outcomes for neither rupees 1 nor rupees 5 coins = number of favourable outcomes for rupees 2 coins = 50 = n(E).

Hence the probability (neither Re 1 nor Rs 5 coin) =$\frac{{{\text{n}}\left( {\text{E}} \right)}}{{{\text{n}}\left( {\text{S}} \right)}} = {\text{}}\frac{{50}}{{100}} = $½ 

18. A game consists of a spinning arrow which comes to rest pointing at one of the numbers 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12; as shown below.

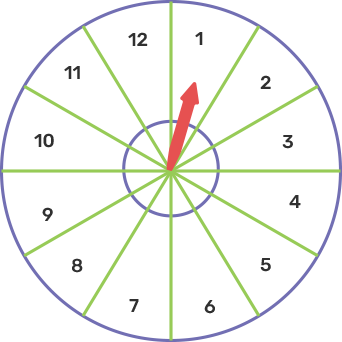
If the outcomes are equally likely, find the probability that the pointer will point at:

(i) 6                                            

(ii) an even number                  

(iii) a prime number 

(iv) a number greater than 8 

(v) a number less than or equal to 9

(vi) a number between 3 and 11

Ans: 

Now from the question we have, 

The total number of possible outcomes = 12 

(i)The total number of favourable outcomes for 6 = 1

Hence probability that he pointer will point at 6 = $\frac{1}{{12}}$

(ii) The favorable outcomes for an even number are 2, 4, 6, 8, 10, 12.

So the number of favourable outcomes = 6

Hence now the probability that the pointer will be at an even number = $\frac{6}{{12}} = $½ 

(iii) The favorable outcomes for a prime number are 2, 3, 5, 7, 11

 So now the number of favorable outcomes = 5 

Hence now the probability that the pointer will be at a prime number = $\frac{5}{{12}}$

(iv) For a number greater than 8, the best outcomes are 9, 10, 11, and 12.

As a result, the number of favourable outcomes is equal to 4.

As a result, P(the pointer will be greater than 8) = $\frac{4}{{12}}$ = ⅓ 

(v) For a number less than or equal to 9, the best outcomes are 1, 2, 3, 4, 5, 6, 7, 8, 9.

So, P(the pointer will be at a number less than or equal to 9) = $\frac{9}{{12}}$ = ¾ because the number of favourable outcomes = 9. 

(vi) For a number between 3 and 11, the best outcomes are 4, 5, 6, 7, 8, 9, 10.

As a result, the number of favourable outcomes equals 7.

As a result, P(the pointer will be between 3 and 11) = $\frac{7}{{12}}$. 

19. One card is drawn from a well shuffled deck of 52 cards. Find the probability of getting:

(i) a queen of red color

(ii) a black face card

(iii) the jack or the queen of the hearts

(iv) a diamond

(v) a diamond or a spade

Ans: 

From the question we have, 

The total possible outcomes = 52 

(i) A Queen of Red Color

The number of queens of red colour= 2

The number of favourable outcomes=2 

Hence now the probability of getting queens of red color = $\frac{2}{{52}}$

(ii) A Black Face Card

The number of black cards = 26 

The number of black face cards = 6 

So therefore the number of favourable outcomes = 6 

Hence the probability of black face cards = $\frac{6}{{52}}$= $\frac{3}{{26}}$

(iii) The Jack Or the Queen of the Hearts

The favourable outcomes for jack or a queen of hearts = 1 jack + 1 queen

So now the number of favourable outcomes = 2 

Hence, the probability of having jack or a queen of hearts = $\frac{2}{{52}}$= $\frac{1}{{26}}$

(iv) A Diamond

The number of favourable outcomes = 13 

Hence the probability of getting a diamond = $\frac{{13}}{{52}}$= ¼ 

(v) A Diamond or a Spade

The number of favorable outcomes for a diamond or spade = 13+ 13 = 26 

Therefore the number of favorable outcomes = 26

20. From a deck of 52 cards, all the face cards are removed and then the remaining cards are shuffled. Now one card is drawn from the remaining deck. Find the probability that the card drawn is:

(i) a black card.

(ii) 8 of red color.

(iii) a king of black color.

Ans: 

There are a total of 12 face cards in a deck. 

Therefore the possible number of outcomes = 52 -12 = 40 

(i) The probability that the card drawn is a black card.

The total number of favourable outcomes for the black cards = 26 cards - 6 face cards = 20 

The probability of black cards = $\frac{{20}}{{40}}$= ½ 

(ii) The probability that the card drawn is 8 of red color.

The number of favourable outcomes for 8 of the red colour = 2 

The probability the getting a card with 8 of red colour = $\frac{{20}}{{40}}$ = $\frac{1}{{20}}$

(iii) The probability that the card drawn is a king of black color.

Since all the face cards are removed.

The number of favourable outcomes for a king of black colour = 0 

The probability of getting a king of black colour = $\frac{0}{{40}} = 0$

21. Seven cards:- the eight, the nine, the ten, jack, queen, king and ace of diamonds are well shuffled. One card is then picked up at random.

(i) What is the probability that the card drawn is the eight or the king?

(ii) If the king is drawn and put aside, what is the probability that the second card picked up is

1. An ace?

2. A king?

Ans: 

It is given that there are 7 cards which are the eight, the nine, the ten, the jack, the’ queen, the king and the ace of diamond.

Therefore the number of possible outcome = 7 

(i) card having the eight or a king which are 2.

Let P(E) be the probability,

P(E) = $\frac{{{\text{Number of favourable outcomes}}}}{{{\text{Number of all possible outcomes}}}}$ = $\frac{2}{7}$

(ii) If the king is drawn and put aside, what is the probability that the second card picked up is

1. An ace ?

If a king is drawn, then the number of remaining playing cards = 7-1 = 6 

P(E) = $\frac{{{\text{Number of favourable outcomes}}}}{{{\text{Number of all possible outcomes}}}}$  = $\frac{1}{6}$

2. A king ?

As there are no card of king hence, 

The probability P(E) = 0. 

22. A box contains 150 bulbs out of which 15 are defective. It is not possible to just look at a bulb and tell whether or not it is defective. One bulb is taken out at random from this box. Calculate the probability that the bulb taken out is :

(i) A Good one

(ii) A Defective one.

Ans: 

In a box, there are 150 bulbs.

The number of defective bulbs is 15

The number of good bulbs is 150 – 15 = 135

The number of possible outcomes = 150

(i)  The probability that the bulb taken out is a good one

P(E) = $\frac{{{\text{Number of favourable outcomes}}}}{{{\text{Number of all possible outcomes}}}}$  = $\frac{{135}}{{150}}$=$\frac{9}{{10}}$

(ii) The probability that the bulb taken out is a defective one.

The number of defective bulb = 15 

P(E) = $\frac{{{\text{Number of favourable outcomes}}}}{{{\text{Number of all possible outcomes}}}}$  = $\frac{{15}}{{150}}$= $\frac{1}{{10}}$

23. (i) 4 defective pens are accidentally mixed with 16 good ones. It is not possible to just look at a pen and tell whether or not it is defective. One pen is drawn at random from the lot. What is the probability that the pen is defective? (ii) Suppose the pen drawn in (i) is defective and is not replaced. Now one more pen is drawn at random from the rest. What is the probability that this pen is:

1. Defective

2. Not defective?

Ans: 

(i) The total number of pens = 4 + 16 = 20 

The total possible outcomes = 20 

The number of defective pens = 4 

The probability of having a defective pen = $\frac{4}{{20}}$= ⅕ 

(ii) If we take into consideration that the defective pen is first drawn is not eventually replaced, then the total possible outcomes = 20-1 = 19 

1. The number of defective pens = 3 

The probability of defective pens = $\frac{3}{9}$

2. The number of not the defective pens = 16 

The probability of not defective pens = $\frac{{16}}{{19}}$

24. A bag contains 100 identical marble stones which are numbered from 1 to 100. If one stone is drawn at random from the bag, find the probability that it bears:

(i) A Perfect Square Number.

(ii) A Number Divisible by 4.

(iii) A Number Divisible by 5.

(iv) A Number Divisible by 4 or 5.

(v) A Number Divisible by 4 and 5.

Ans: 

The total number of stones = 100 

On which numbers 1 to 100 are marked.

Therefore the number of possible outcomes = 100

(i) A Perfect Square Number.

From 1 to 100, the perfect squares are 1, 4, 9, 16, 25, 36, 49, 64, 81, 100 which are 10 in numbers. 

P(E) = $\frac{{{\text{Number of favourable outcomes}}}}{{{\text{Number of all possible outcomes}}}}$  = $\frac{{10}}{{100}}$= $\frac{1}{{10{\text{}}}}$

(ii) A Number Divisible By 4.

The number of divisible by 4 are 4, 8, 12, 16, …, 96, 100 which are 25 in numbers 

P(E) = $\frac{{{\text{Number of favourable outcomes}}}}{{{\text{Number of all possible outcomes}}}}$  = $\frac{{25}}{{100}}$= ¼ 

(iii) A Number Divisible By 5.

The number divisible by 5 are 5, 10, 15, 20, ….., 95, 100 which are 20 in numbers,

P(E) = $\frac{{{\text{Number of favourable outcomes}}}}{{{\text{Number of all possible outcomes}}}}$  = $\frac{{20}}{{100}}$=⅕ 

(iv) A Number Divisible By 4 or 5.

The number divisible by 5 or 5 are 4, 5, 8, 10,12, 15, 16, 20, 24, 25, 28, 30, 32, 35, 36, 40, 96,95, 100 which are 40 in numbers

P(E) = $\frac{{{\text{Number of favourable outcomes}}}}{{{\text{Number of all possible outcomes}}}}$  = $\frac{{40}}{{100}}$= ⅖ 

(v) A Number Divisible By 4 and 5.

The numbers divisible by 4 and 5 are 20, 40, 60, 80 and 100 which are 5 in numbers.

P(E) = $\frac{{{\text{Number of favourable outcomes}}}}{{{\text{Number of all possible outcomes}}}}$  = $\frac{5}{{100}}$= $\frac{1}{{20{\text{}}}}$

25. A circle with diameter 20 cm is drawn somewhere on a rectangular piece of paper with length 40 cm and width 30 cm. This paper is kept horizontal on the table top and a die, very small in size, is dropped on the rectangular paper without looking towards it. If the die falls and lands on the paper only, find the probability that it will fall and land:

(i) inside the circle.

(ii) outside the circle.

Ans:

It is given that the diameter of the circle = 20 

Radius = 10 cm 

Area of the circle = ${{\Pi }}{{\text{r}}^2} = \frac{{2200}}{7}{\text{c}}{{\text{m}}^2}$

The length of the paper = 40 cm 

Width of the apper = 30 cm 

Area of the paper = 1200 ${\text{c}}{{\text{m}}^2}$

The total possible outcomes = Area of the rectangular paper. 

(i) Inside the circle.

As the paper is kept on the table top and die falls and lands on the paper. 

The number of favourable outcomes = Area of the circle 

Let P be the probability, 

P(Inside the circle) = $\frac{{{\text{Area of the circle}}}}{{{\text{Area of the rectangular paper}}}}$= $\frac{{2200/7}}{{1200}} = {\text{}}\frac{{11}}{{42}}$

(ii) Outside the circle.

The P(outside the circle) = 1 - P(Inside the circle )

  = 1 - $\frac{{11}}{{42}}$= $\frac{{31}}{{42}}$

26. Two dice (each bearing numbers 1 to 6) are rolled together. Find the probability that the sum of the numbers on the upper-most faces of two dice is:

(i) 4 or 5

(ii) 7, 8 or 9.

(iii) between 5 and 8

(iv) more than 10

(v) less than 6

Ans: 

It is given that the two dice having numbers 1 to 6 are rolled together.

Therefore the number of possible outcomes = 6 x 6 = 36

(i) The probability that the sum of the numbers on the upper-most faces of two dice is 4 or 5

If the sum is 4 or 5 of the numbers on the uppermost face, 

The total number of favourable outcomes = (1,3), (2, 2), (3, 1), (1, 4), (2, 3), (3, 2), (4, 1) which are 7 in numbers

P(E) = $\frac{{{\text{Number of favourable outcomes}}}}{{{\text{Number of all possible outcomes}}}}$ = $\frac{7}{{36}}$

(ii) The probability that the sum of the numbers on the upper-most faces of two dice is 7, 8 or 9.

If the sum of numbers on the upper faces is 7, 8 or 9, then these can be (1, 6), (2, 6), (3, 6), (4, 3), (5. 2). (6, 1). (4, 3), (2, 5), (3, 4), (4, 4), (5, 3), (5, 4), (6, 2), (6, 3), (4, 5) which are a total of 15 in numbers. 

P(E) = $\frac{{{\text{Number of favourable outcomes}}}}{{{\text{Number of all possible outcomes}}}}$= $\frac{{15}}{{36}}$ = $\frac{5}{{12}}$

(iii) The probability that the sum of the numbers on the upper-most faces of two dice is between 5 and 8.

The sum is between 5 and 8 which is sum is 6 0r 7 

These can be, (1, 5), (2, 5), (1, 6), (5, 1), (5, 2), (6, 1), (3, 3), (3, 4), (4, 3), (2, 4), (4, 2) which are 11 in number.

Therefore the number of favourable outcomes = 11 

P(E) = $\frac{{{\text{Number of favourable outcomes}}}}{{{\text{Number of all possible outcomes}}}}$ = $\frac{{11}}{{36}}$

(iv) The probability that the sum of the numbers on the upper-most faces of two dice is more than 10

If the sum is more than 10, then these can be (5,  6), (6, 5), (6, 6) which are a total of 3 in number. 

P(E) = $\frac{{{\text{Number of favourable outcomes}}}}{{{\text{Number of all possible outcomes}}}}$ = $\frac{3}{{36}}$= $\frac{1}{{12}}$

(v) The probability that the sum of the numbers on the upper-most faces of two dice is less than 6

If the sum is less than 6 then the possible combinations are (1, 2), (2, 1), (1, 3), (3, 1), (4, 1), (1, 4), (2, 3), (3, 2), (2, 4), (4, 2)

P(E) = $\frac{{{\text{Number of favourable outcomes}}}}{{{\text{Number of all possible outcomes}}}}$= $\frac{{10}}{{36}}$= $\frac{5}{{18}}$

27. Three coins are tossed together. Write all the possible outcomes. Now, find the probability of getting?

(i) Exactly two heads.

(ii) At least two heads.

(iii) At most two heads.

(iv) All tails.

(v) At least one tail.

Ans: 

It is given that 3 coins are tossed together. 

Therefore the number of possible outcome = 23 = 2 x 2 x 2 = 8

Which is, HHH, HHT, HTH, HTT, TTT, THH, THT, TTH

(i) The probability of getting exactly two heads.

The probability of getting exactly 3 heads when 3 coins are tossed is 3 in numbers ,HHT, THH, HTH.

 P(E) = $\frac{{{\text{Number of favourable outcomes}}}}{{{\text{Number of all possible outcomes}}}}$= = $\frac{3}{8}$

(ii)  The probability of getting at least two heads.

For at least 2 heads it can be HHH, HHT, HTH, THH, 4 in numbers. 

 P(E) = $\frac{{{\text{Number of favourable outcomes}}}}{{{\text{Number of all possible outcomes}}}}$= = $\frac{4}{8}$ = ½ 

(iii) The probability of getting at most two heads.

When 3 coins are coins for utmost 2 heads we get THH, HHT, HTH, HTT, THT, TTH, TTT which are 8 in numbers. 

P(E) = $\frac{{{\text{Number of favourable outcomes}}}}{{{\text{Number of all possible outcomes}}}}$= =$\frac{7}{8}$

(iv)  The probability of getting all tails.

For all tails there can be only one outcome which is TTT. 

P(E) = $\frac{{{\text{Number of favourable outcomes}}}}{{{\text{Number of all possible outcomes}}}}$ = $\frac{1}{8}$

(v)  The probability of getting at least one tail.

For at least one tail , there can be HHT, HTH, HTT, TTT, THH, THT, TTH which is 7 in numbers. 

P(E) = $\frac{{{\text{Number of favourable outcomes}}}}{{{\text{Number of all possible outcomes}}}}$= $\frac{7}{8}$

28. Two dice are thrown simultaneously. What is the probability that?

(i) 4 will not come up either time?

(ii) 4 will come up at least once?

Ans: 

It is given that two dice are thrown simultaneously and each dice has 1-6 numbers on its faces. 

Now the number of possible outcomes = 6 x 6 = 36

(i) 4 will not come up either time?

The number of favourable outcomes = (6 – 1)² = (5)² = 25

P(E) = $\frac{{{\text{Number of favourable outcomes}}}}{{{\text{Number of all possible outcomes}}}}$ = $\frac{{25}}{{36}}$

(ii) 4 will come up at least once?

For this, the combinations are (1, 4), (2, 4), (3, 4), (4, 4), (4, 5),(4, 6), (4, 1), (4, 2), (4, 3), (4, 5), (4, 6)

∴ Number of favourable outcome =11

P(E) = $\frac{{{\text{Number of favourable outcomes}}}}{{{\text{Number of all possible outcomes}}}}$  = $\frac{{11}}{{36}}$

29. Cards marked with numbers 1, 2, 3, 4, …, 20 are well shuffled and a card is drawn at random. What is the probability that the number on the card is

(i) A Prime number

(ii) Divisible by 3

(iii) A Perfect square ?

Ans: 

The total possible outcomes = 20 

(i) A prime number

The favourable outcomes for a prime number = 2, 3, 5, 7, 11, 13, 17, 19.

The number of favourable outcomes = 8 

The probability that the number on the card is a prime number = $\frac{8}{{20}}$= ⅖ 

(ii) Divisible by 3

The favourable outcomes for a number divisible by 3 = 3,6,9,12,15, 18. 

The number of favourable outcomes= 6 

P(E) = $\frac{6}{{20}} = \frac{3}{{10}}$

(iii) A perfect square 

All the favourable outcomes for a perfect square = 1, 4, 9, 16 

The number of favourable outcomes = 4 

The probability of having a perfect square = $\frac{4}{{20}} = 1/5{\text{}}$

30. Offices in Delhi are open for five days in a week (Monday to Friday). Two employees of an office remain absent for one day in the same particular week. Find the probability that they remain absent on:

(i) The same day

(ii) Consecutive day

(iii) Different days.

Ans: 

It is given that the office is open for 5 days a week.

Therefore the number of possible outcomes for 2 employees = 5 x 5 = 25

Let us just denote the 5 working days by M, T, W, Th, F for Mondays, Tuesday, Wednesday Thursday and Friday respectively

The total number of possible outcomes = 5$ \times 5 = 25{\text{}}$

(i) The probability that they remain absent on the same day

The favorable outcomes for two employees remaining absent on the same day: MM, TT, WW, ThTh, FF 

Therefore the number of favourable outcomes = 5 

The probability of been absent on the same day = $\frac{5}{{25}}$= ⅕ 

(ii) The probability that they remain absent on consecutive days.

The favourable outcomes for two employees remaining absent on the consecutive days: MT, TM, TW, WT, WTh, ThW, ThF, FTh. 

The number of favourable outcomes = 8 

The probability of been absent in consecutive days = $\frac{8}{{25}}$

(iii) The probability that they remain absent on the different days.

Let P be the probability of events and now, 

P(absent on different days) = 1 -  P(absent on same days)

                                           =  1 - ⅕ = ⅘ 

31. A box contains some black balls and 30 white balls. If the probability of drawing a black ball is two-fifths of white ball; find the number of black balls in the box.

Ans: 

Let us assume that the number of black balls in the box be x 

The total number of balls in the box = x + 30

Let P be the probability and now 

P(drawing a black ball) = $\frac{{\text{x}}}{{{\text{x}} + 30}}$

P(drawing a white  ball) = $\frac{{30}}{{{\text{x}} + 30}}$

But now the P(drawing a black ball) = $\frac{2}{5} \times $P(drawing a white  ball)

 $\frac{{\text{x}}}{{{\text{x}} + 30}}$= $\frac{2}{5} \times \frac{{30}}{{{\text{x}} + 30}}$

x = 12 

The number of black balls in the box = 12

32. From a pack of 52 playing cards all cards whose numbers are multiples of 3 are removed. A card is now drawn at random.

What is the probability that the card drawn is

(i) A Face card (King, Jack or Queen)

(ii) An Even numbered red card ?

Ans: 

From the question the number of total cards = 52 cards removed of 4 colours = 3, 6, 9, 12 = 4 x 4 = 16

Remaining cards to be used = 52 – 16 = 36

(i) The probability that the card drawn is a face card.

Number of faces cards = 2 x 4 = 8 cards (Excluding queen)

Therefore the probability P(E) = $\frac{8}{{36}}$= $\frac{2}{9}$

(ii)The probability that the card drawn is an even numbered red card?

An even number red cards = 2, 4, 8, 10 = 4 × 2 = 8 cards

Therefore the probability P(E) = $\frac{{{\text{n}}\left( {\text{E}} \right)}}{{{\text{n}}\left( {\text{S}} \right)}}$ = $\frac{8}{{36}}$ = $\frac{2}{9}$

33. A die has 6 faces marked by the given numbers as shown below:

The die is thrown once. What is the probability of getting

(i) A Positive integer.

(ii) An Integer greater than -3.

(iii) The Smallest integer.

Ans: 

It is given that the die has 6 faces, and the die is thrown once. 

Total outcomes n(S) = 6 

(i) The probability of a positive integer.

The positive integer = (1, 2, 3)

Number of favourable outcomes n(E) = 3

P(E) = $\frac{{{\text{n}}\left( {\text{E}} \right)}}{{{\text{n}}\left( {\text{S}} \right)}}$= $\frac{3}{6}$= ½ 

(ii) The probability of an integer greater than -3.

The integer greater than -3 = 1, 2, 3, -1, -2

Number of favourable outcomes = n(E) = 5

P(E) = $\frac{{{\text{n}}\left( {\text{E}} \right)}}{{{\text{n}}\left( {\text{S}} \right)}}$= $\frac{5}{6}$

(iii) The probability of the smallest integer.

The smallest integer = -3

Number of favourable outcomes n(E) = 1

P(E) = $\frac{{{\text{n}}\left( {\text{E}} \right)}}{{{\text{n}}\left( {\text{S}} \right)}}$= $\frac{1}{6}$.

34. A bag contains 5 white balls, 6 red balls and 9 green balls. A ball is drawn at random from the bag. Find the probability that the ball drawn is:

(i) A Green Ball.

(ii) A White or A Red Ball.

(iii) Neither a Green Ball Nor a White Ball.

Ans: 

It is given that the bag contains 5 white balls, 6 red balls and 9 green balls. 

Therefore the total number of balls = 5 + 6 + 9 = 20 balls

It is given that one ball is drawn at random. 

(i) The probability that the ball drawn is a green ball.

Let the probability that the ball drawn is a green ball be P(E)

P(E)= $\frac{{{\text{Number ofpossible outcomes}}}}{{{\text{Total number of outcomes}}}}$= $\frac{9}{{20}}$

(ii) The probability that the ball drawn is a white or a red ball.

The probability of a white or a red ball, P(E)= $\frac{{5 + 6}}{{20}} = \frac{{11}}{{20}}$

(iii) The probability that the ball drawn is neither a green ball nor a white ball.

The probability of neither a green ball nor a white ball, P(E) = $\frac{6}{{20}}$= $\frac{3}{{10}}$

35. A game of numbers has cards marked with 11, 12, 13, ….. 40. A card is drawn at random. Find the probability that the number on the card drawn is:

(i) A perfect square

(ii) Divisible by 7

Ans: 

(i) To find the probability that the number on the card is a perfect square. 

The perfect square squares which are between 11 and 40 and 16, 25 and 36.

So therefore the number of possible outcomes = 3 

The total number of cards from 11 to 40 = 30 (40-11+1)

Let the probability that the number on the card is a perfect square, P(E)

P(E) = $\frac{{{\text{Number of possible outcomes}}}}{{{\text{Total number of outcomes}}}}$ = $\frac{3}{{30}}$=$\frac{1}{{10}}$

(ii)To find the probability that the number on the card is divisible by 7

The numbers from 11 to 40 which are divisible by 7 are 14, 21, 28 and 35. 

So the number of possible outcomes is 4. The total number of cards from 11 to 40 is 30.

Let the probability that the number on the card drawn is divisible by 7 is P(E)

P(E)= $\frac{{{\text{Number of possible outcomes}}}}{{{\text{Total number of outcomes}}}}$ = $\frac{4}{{30}}$=$\frac{2}{{15}}$

36. Sixteen cards are labelled as a, b, c, … , m, n, o, p. They are put in a box and shuffled. A boy is asked to draw a card from the box. What is the probability that the card drawn is:

i. A vowel

ii. A consonant

iii. None of the letters of the word median?

Ans: 

i. From the question the total number of all possible outcomes = 16 

As a, e, i, o are the vowels. 

The number of favourable outcomes = 4 

Required probability, P(E) = $\frac{{{\text{Number of possible outcomes}}}}{{{\text{Total number of outcomes}}}}$ = $\frac{4}{{16}}$= \[\frac{1}{4}\] 

ii. A consonant

The number of consonants = 16 - 4 (Vowels) = 12 

Therefore the number of favourable outcomes = 12 

Required probability, P(E) = $\frac{{{\text{Number of possible outcomes}}}}{{{\text{Total number of outcomes}}}}$ = $\frac{{12}}{{16}}$= \[\frac{3}{4}\] 

iii. None of the letters of the word median?

A median contains 6 letters.

Therefore the number of favourable outcomes = 16-6 = 10

Required probability, P(E) = $\frac{{{\text{Number of possible outcomes}}}}{{{\text{Total number of outcomes}}}}$ = $\frac{{10}}{{16}}$= \[\frac{5}{8}\] 

37. A box contains a certain number of balls. On each of 60% balls, letter A is marked. On each of 30% balls, letter B is marked and on each of the remaining balls, letter C is marked. A ball is drawn from the box at random. Find the probability that the ball drawn is:

i. Marked C

ii. A or B

iii. Neither B nor C

Ans: 

It is given that the box contains, 

60% balls, letter A is marked.

30% balls, letter B is marked.

10% balls, letter C is marked.

i. Marked C

The total number of all possible outcomes = 100

The number of favourable outcomes= 10 

The required probability = $\frac{{{\text{Number of possible outcomes}}}}{{{\text{Total number of outcomes}}}}$ = $\frac{{10}}{{100}}$= $\frac{1}{{10}}$

ii. A or B

The probability that the ball is marked A = $\frac{{{\text{Number of possible outcomes}}}}{{{\text{Total number of outcomes}}}}$ = $\frac{{60}}{{100}}$= $\frac{6}{{10}}$..(1)

The probability that the ball is marked B = $\frac{{{\text{Number of possible outcomes}}}}{{{\text{Total number of outcomes}}}}$ = $\frac{{30}}{{100}}$= $\frac{3}{{10}}$..(2) 

Now add (1) and (2)

$\frac{6}{{10}}$+ $\frac{3}{{10}}$= $\frac{9}{{10}}$

iii. The probability that the ball drawn is neither B nor C

= 1- [P(B)+P(C)]

= 1-$[\frac{3}{{10}}$+$\frac{1}{{10}}]$

= 1- $\frac{4}{{10}}$

= $\frac{3}{5}$

38. A box contains a certain number of balls. Some of these balls are marked A, some are marked B and the remaining are marked C. When a ball is drawn at random from the box P(A) = 1/3 and P(B) = 1/4. If there are 40 balls in the box which are marked C, find the number of balls in the box.

Ans: 

Now from the question we can say that, 

P(C) = 1-[P(A)+P(B)] =  1 - $\left[ {\frac{1}{3} + \frac{1}{4}} \right]$

P(C) = $\frac{5}{{12}}$.

It is given that there are 40 balls in the box are marked as C 

The probability is given by, 

P(E) = $\frac{{{\text{Number of possible outcomes}}}}{{{\text{Total number of outcomes}}}}$

$\frac{5}{{12}}$ = $\frac{{40{\text{}}}}{{{\text{Total number of outcomes}}}}$

The total number of all the possible outcomes = $\frac{{40 \times 12}}{5}$= 96.

Importance of ICSE Class 10 Selina Concise Solutions for Chapter 25 - Probability provided by Vedantu

ICSE Class 10 Maths solutions for Probability chapter is one of the crucial and most scoring subjects in ICSE Class 10. Vedantu presents solutions for ICSE Class 10 Mathematics which will enable students to score well in the ICSE board examination.

The Vedantu Selina ICSE solutions work as a step-by-step guide and are essential when preparing for the examination. Selina solutions for ICSE Class 10 Chapter 25 - Probability help students to understand and learn the concepts better so that they can study anytime, anywhere from the comfort of their homes. To help most students prepare for this subject and score good marks in the Class 10 ICSE board examinations, the Vedantu Selina solutions for Class 10 chapter Probability can be downloaded free of cost from our website. The PDF is also available for all the chapters.

Introduction of the Chapter Probability

Probability is the measure of the likelihood that an event will occur. The probability of an event may be described as a fraction or occasionally as a percentage. The concept of probability has been extended over the centuries from purely theological roots, first to encompass Actor-Observer Dualism in the 17th century, and then again to include more abstract ideas in the 19th century. In mathematical terms, a probability distribution is a way of assigning probabilities to events or outcomes which can be thought of as results of an experiment. It is a notion employed in statistics and also in many other fields, such as physics and economics.

How to Solve Problems Based on Probability?

In this chapter, you will learn how to solve problems based on probability. We will start with the definition of probability and then see different types of probabilities. You will also be shown a few examples along with their solutions to get a clear idea about how to solve problems involving the concept of probability. With the practice of these problems, you will be able to solve probability-based questions in your board examinations.

1. What are the five rules of probability?

Ans: The five rules of probability are as follows:

1. Two events A and B occur together, then the probability that either of them occurs is the sum of their separate probabilities. For e.g., if A = {getting a face on first throw} and B = {getting an odd number on first throw}. Then P(A or B) = P(A) + P(B).

2. The events A and B occur together, then the probability that both of them occur is the product of their separate probabilities. For e.g., if A = {getting a face on first throw} and B = {getting an odd number on first throw}. Then P(A and B) = P(A) × P(B).

3. Three events A, B and C occur together, then the probability that exactly two of them out of the three occur is given by:

P(A and B) + P(A and C) + P(B and C)= 3 P (A or B or C)

4. If an event A is certain to occur, then the probability that it occurs is 1. For e.g., if A = {It will rain tomorrow}. Then P(A) =1.

5. The sum of probabilities of all possible outcomes of an experiment is equal to 1 or 100%. This rule essentially states that the probability of an event is never zero. For e.g., if A = {Getting a face on the first throw}. Then P(A) ≠ 0.

Basic Concepts of Probability

Probability is the chapter in Class 10 Maths that contains the concepts that are most likely to be used in daily life. The chapter deals with different topics related to the probability that includes:

1. The difference between experimental probability and theoretical probability

2. The probability of a sure event (or certain event) is 1.

3. The probability of an impossible event is 0?

4. Elementary events.

5. Complementary events.

6. Finding the probability of different events.

Probability Formula

The formula for probability can tell us how many choices we have over the total number of possible combinations. Therefore, the formula can be written as:

Probability = possible choices

Total number of options

Probability = possible choices total number of options

Key Features of Vedantu Solutions

The key features of Vedantu solutions are as follows:

• Easy & reliable solutions.

• Available free of cost.

• Highlight important examination questions.

• Step-by-step solutions for all questions.

• Prepared by subject experts.

• Designed according to the latest ICSE syllabus pattern.

• Available online 24/7.

• In-depth knowledge of the chapter is provided in easy language.

• Is based on the latest ICSE syllabus.

• Best study material to prepare for the Class 10 ICSE board exam.

• All the doubts that might arise while solving the exercise questions will vanish by going through these Vedantu Selina solutions.