Concise Mathematics Class 10 ICSE Solutions for Chapter 16 - Loci (Locus and Its Constructions)

Exercise 16(A)

1. Given: PQ is a perpendicular bisector of side AB of the triangle ABC.

Prove: Q is equidistant from A and B.

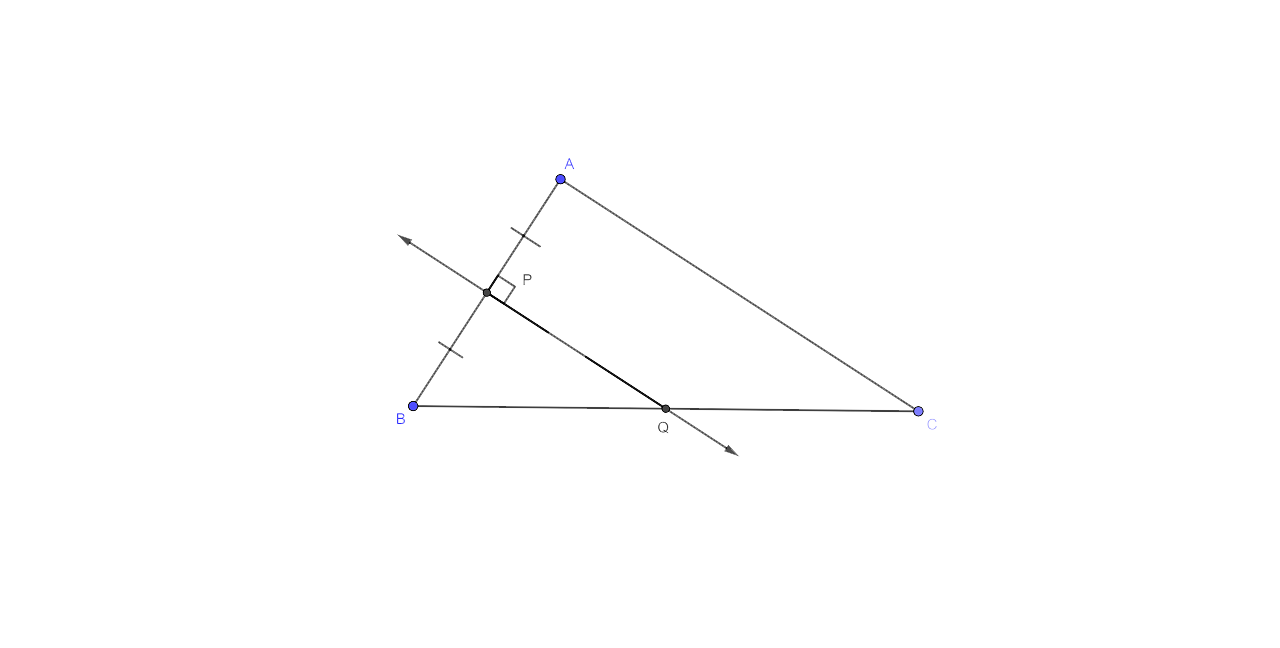
Ans:

It is given that PQ is a perpendicular bisector of side AB of the triangle ABC.

Now in the triangle ABC joins AQ.

Proof: 

Let us consider ∆AQP and ∆BQP,

AP = BP (Given information)

∠QPA = ∠QPB (Each angle is equal to ${{90}^{\circ }}$)

PQ = PQ (Common)

Hence by considering the SAS criterion of congruence we can  say that,

∆AQP ≅ ∆BQP

Now by considering the Corresponding Parts of Congruent Triangle (CPCT) we can say that, AQ = BQ

Therefore, Q is equidistant from A and B

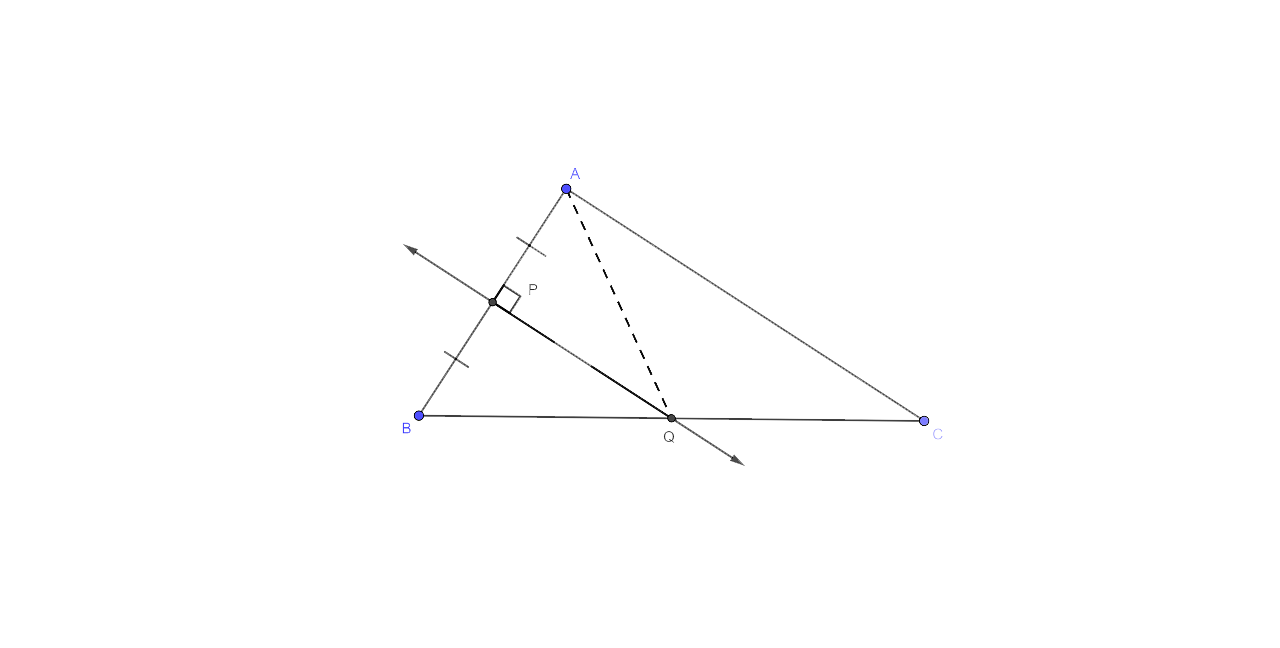
2. Given: CP is the bisector of angle C of ∆ABC

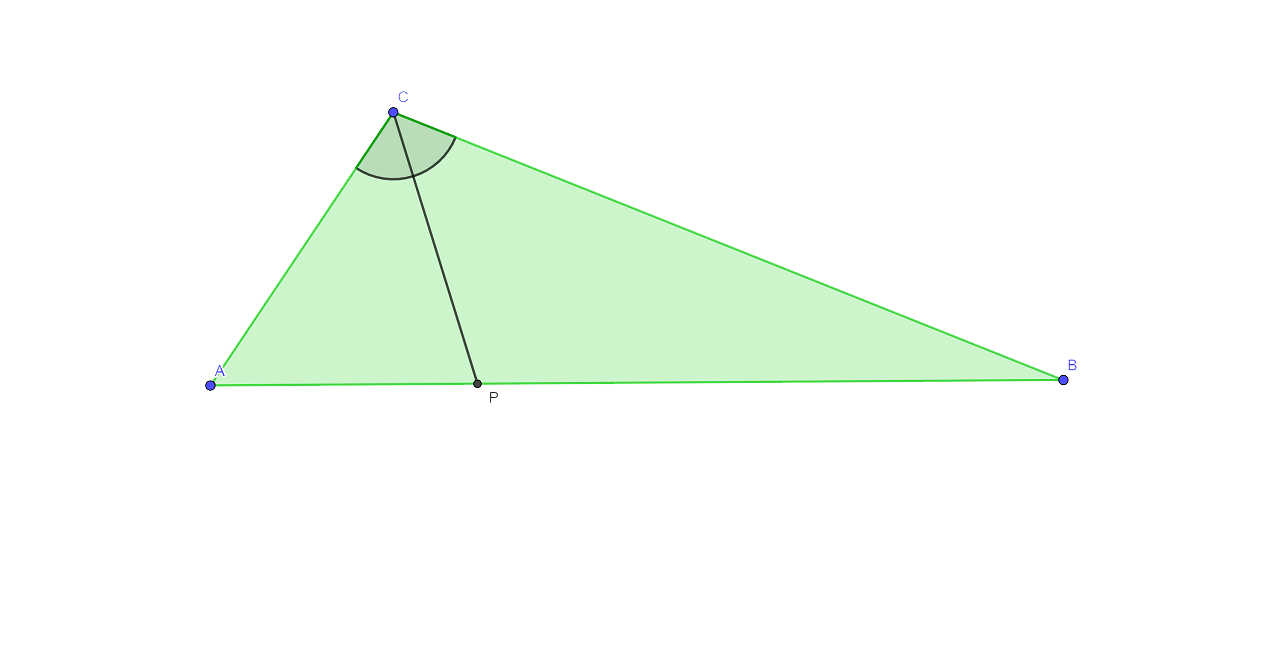
Prove: p is equidistant from AC and BC

Ans: 

It is given that CP is the bisector of angle C of ∆ABC. 

Now in the given ∆ABC from P, draw PL ⊥ AC and PM ⊥ CB

Proof:

Let us consider ∆LPC and ∆MPC,

∠PLC = ∠PMC (Each angle is equal to ${{90}^{\circ }}$)

∠PCL = ∠MCP (Given information)

PC = PC (Common)

Hence by AAS criterion of congruence we can say that  ∆LPC ≅ ∆MPC

Now by considering the Corresponding Parts of Congruent Triangle (CPCT) we can say that, PL = PM.

Therefore we can say that P is equidistant from AC and BC. 

3. Given - AX bisects angle BAG and PQ is the perpendicular bisector of AC which meets AX at point Y.

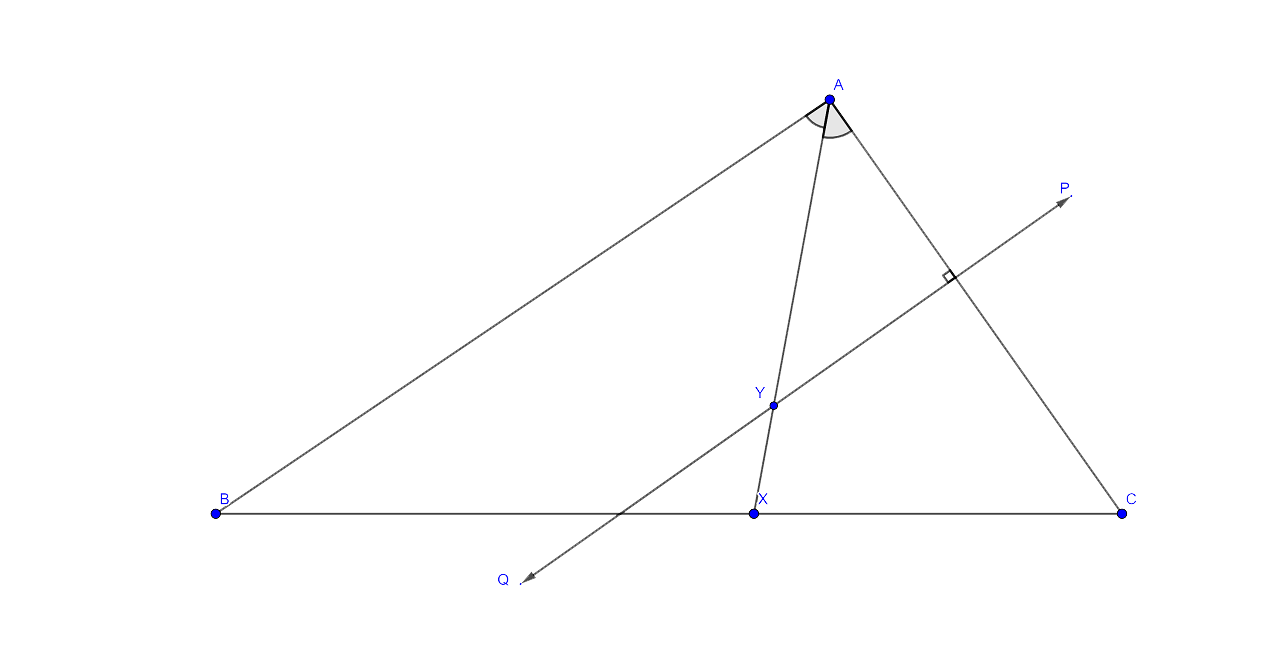
Prove:

(i) X is equidistant from AB and AC.

(ii) Y is equidistant from A and C.

Ans: 

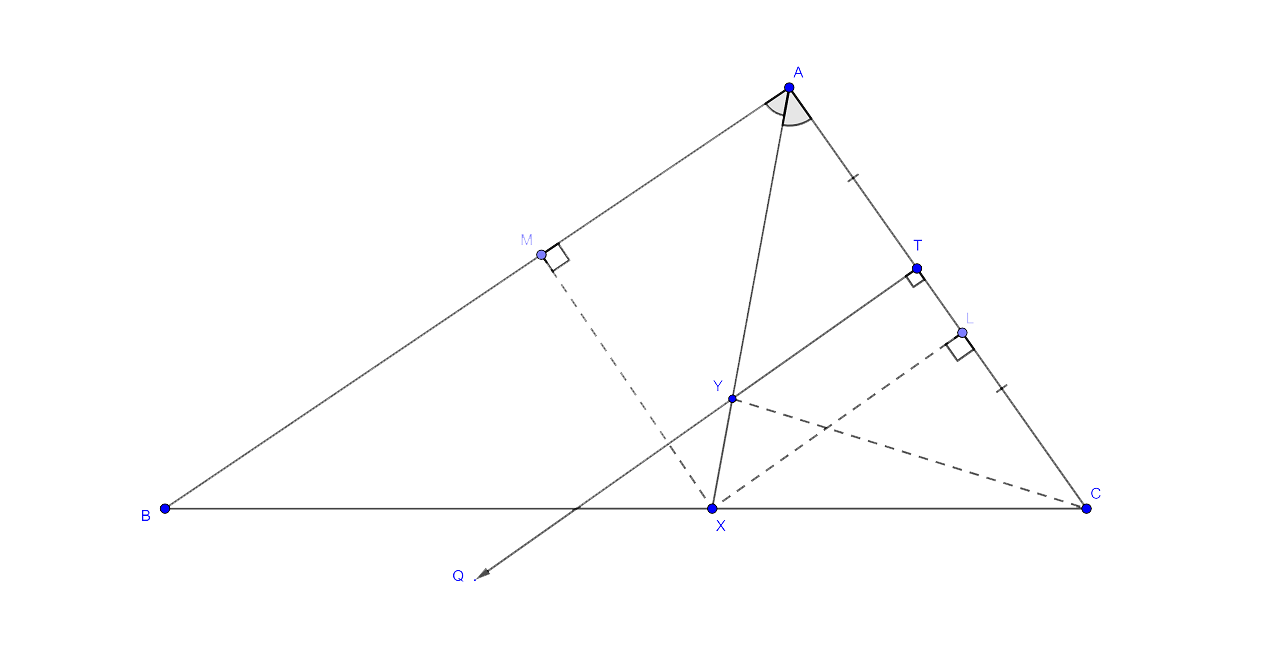
It is given that AX bisects angle BAG and PQ is the perpendicular bisector of AC which meets AX at point Y.

In the given triangle from X draw XL ⊥ AC and XM ⊥ AB. Now join YC.

Proof 

(i) Now let us consider ∆AXL and ∆AXM,

∠XAL = ∠XAM (Given information )

AX = AX (Common angle)

∠XLA = ∠XMA (Each angle is equal to ${{90}^{\circ }}$)

Hence by the ASA criterion of congruence, we can say that ∆AXL ≅ ∆AXM

Now by considering the Corresponding Parts of Congruent Triangle (CPCT) we can say that, XL = XM

Hence we can say that X is equidistant from AC and AB.

(ii) Let us consider ∆YTA and ∆YTC,

AT = CT (As  PQ is perpendicular bisector of AC)

∠YTA = ∠YTC (Each angle is equal to ${{90}^{\circ }}$)

YT = YT (Common angle)

Hence by the ASA criterion of congruence, we can say that ∆YTA ≅ ∆YTC

Now by considering the Corresponding Parts of Congruent Triangle (CPCT) we can say that, YA = YC

Hence we can say that Y is equidistant from A and C. 

4. Construct a triangle ABC, in which AB = 4.2 cm, BC = 6.3 cm and AC = 5 cm. Draw a perpendicular bisector of BC that meets AC at point D. Prove that D is equidistant from B and C.

Ans: 

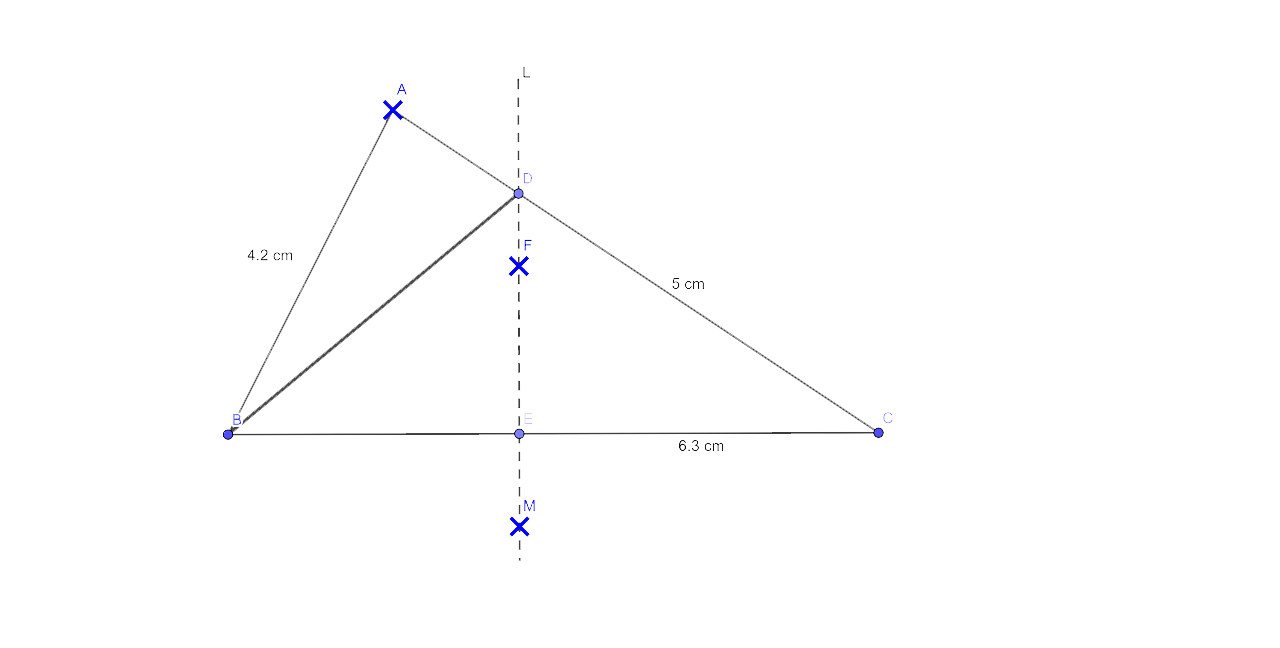
It is given that in the triangle ABC, AB = 4.2 cm, BC = 6.3 cm and AC = 5 cm

Steps to construct triangle ABC 

1. A line segment BC = 6.3 cm should be drawn.

2. Draw an arc with centre B and radius 4.2 cm 

3. Draw another arc with the centre C and radius 5 cm which intersects the first arc at A. 

4. Join AC and AB. Then, ∆ABC is the required triangle.

5. Again with centre B and C and radius greater than ½ BC, draw arcs which intersect each other at L and M.

6. Join LM intersecting AC at D and BC at E.

7. Finally join DB. 

Proof: 

Let us consider ∆DBE and ∆DCE,

BE = EC (As LM is the bisector of BC)

∠DEB = ∠DEC (Each angle is equal to ${{90}^{\circ }}$)

DE = DE (Common)

Hence by the ASA criterion of congruence, we can say that ∆DBE ≅ ∆DCE

Now by considering the Corresponding Parts of Congruent Triangle (CPCT) we can say that, DB = DC

Hence, D is equidistant from B and C. 

5. In each of the given figures: PA = PH and QA = QB. 

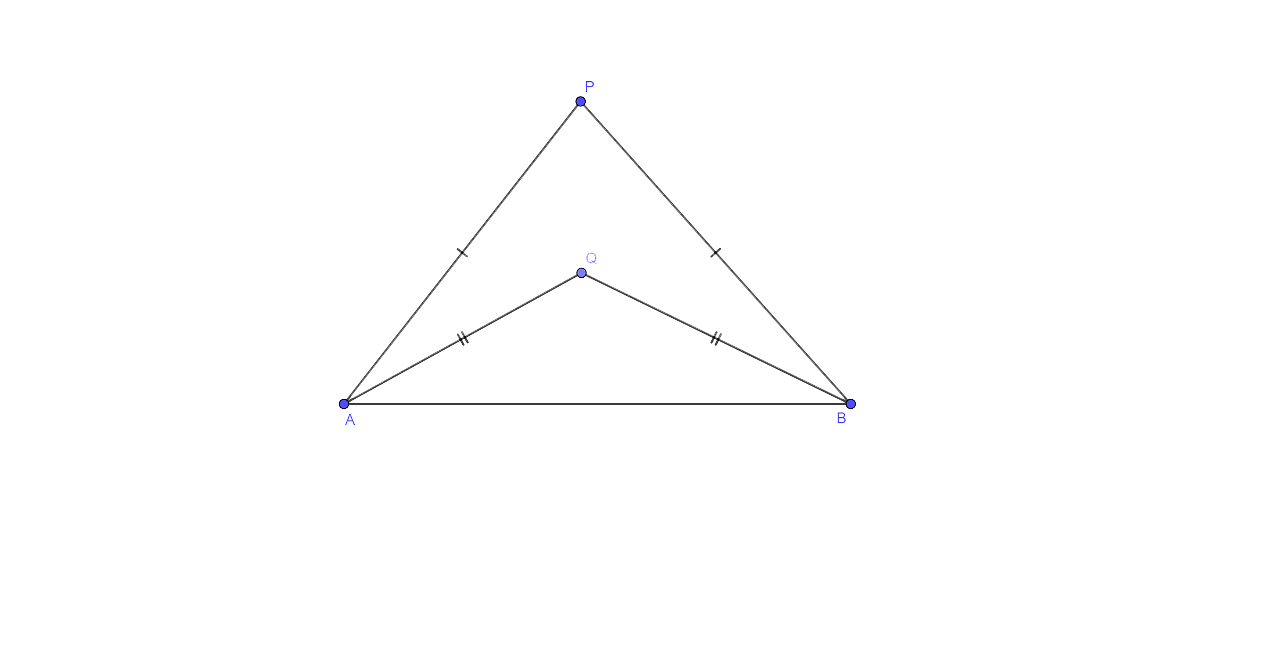
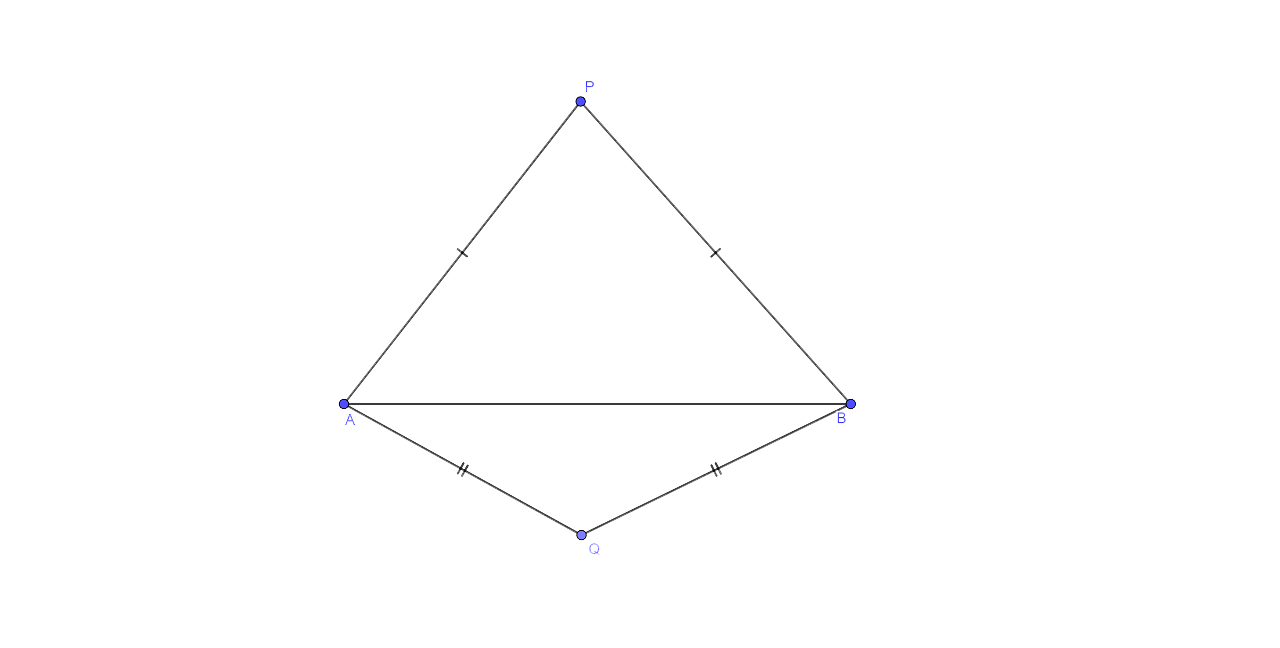
Prove, in each case, that PQ (produce, if required) is perpendicular bisector of AB. Hence, state the locus of points equidistant from two given fixed points.

Ans: 

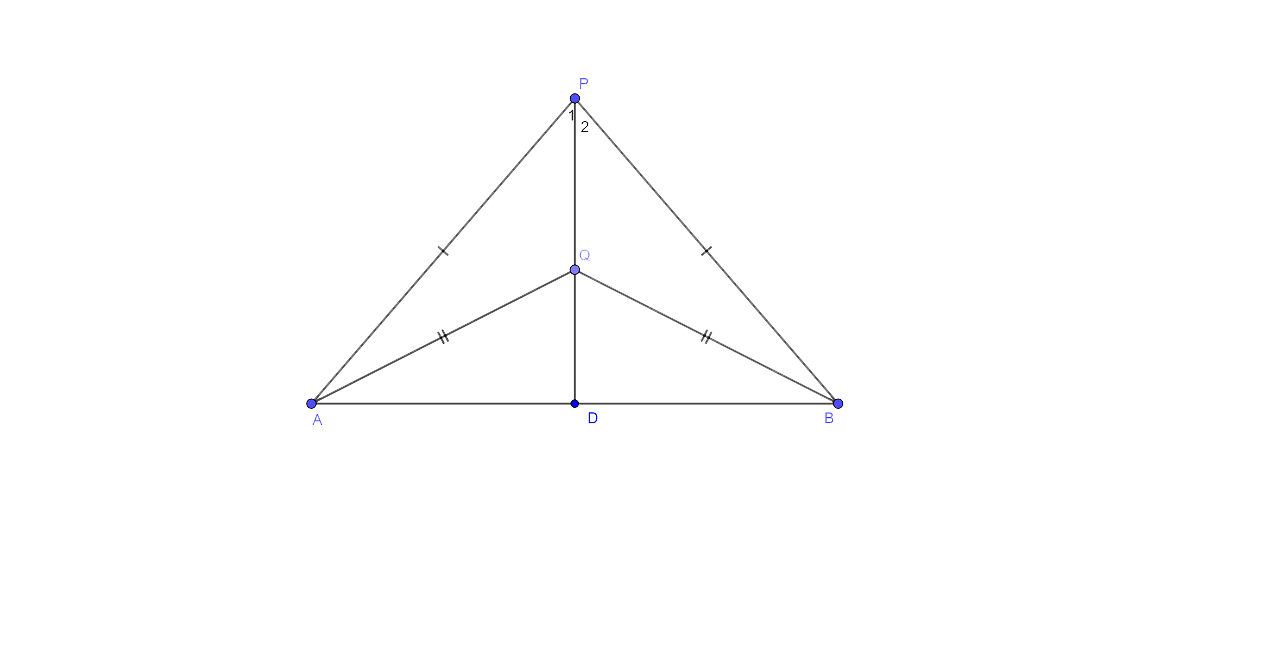
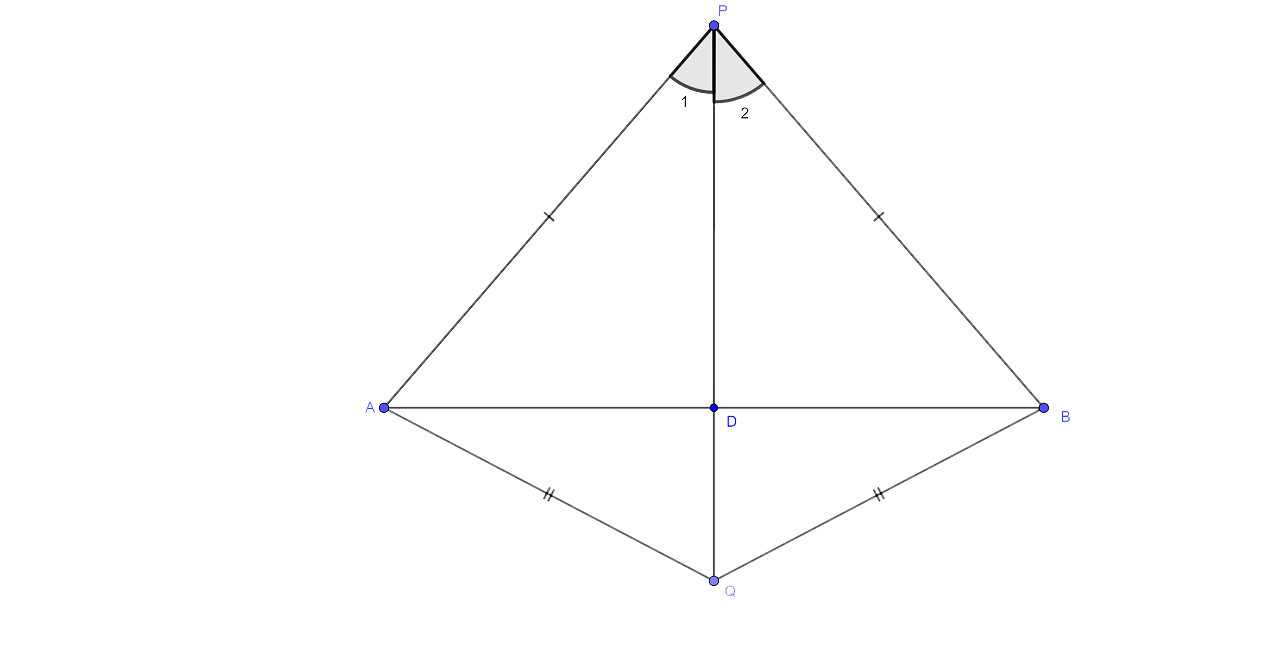
Construction: In the given figures join PQ which then meets AB in D.

Proof: As it is given that P is equidistant from A and B. 

Thus we could say that P lies on the perpendicular bisector of AB. 

Similarly, Q is also equidistant from A and B.

Q lies on the perpendicular bisector of AB. 

As P and Q lie on the perpendicular bisector of AB.

∴, PQ is the perpendicular bisector of AB. 

Hence now we can say that the locus of the points which are equidistant from two fixed points, is a perpendicular bisector of the line joining the fixed points.

6. Construct a right angled triangle PQR, in which ∠Q = 90°, hypotenuse PR = 8 cm and QR = 4.5 cm. Draw a bisector of angle PQR and let it meet PR at point T. Prove that T is equidistant from PQ and QR.

Ans:

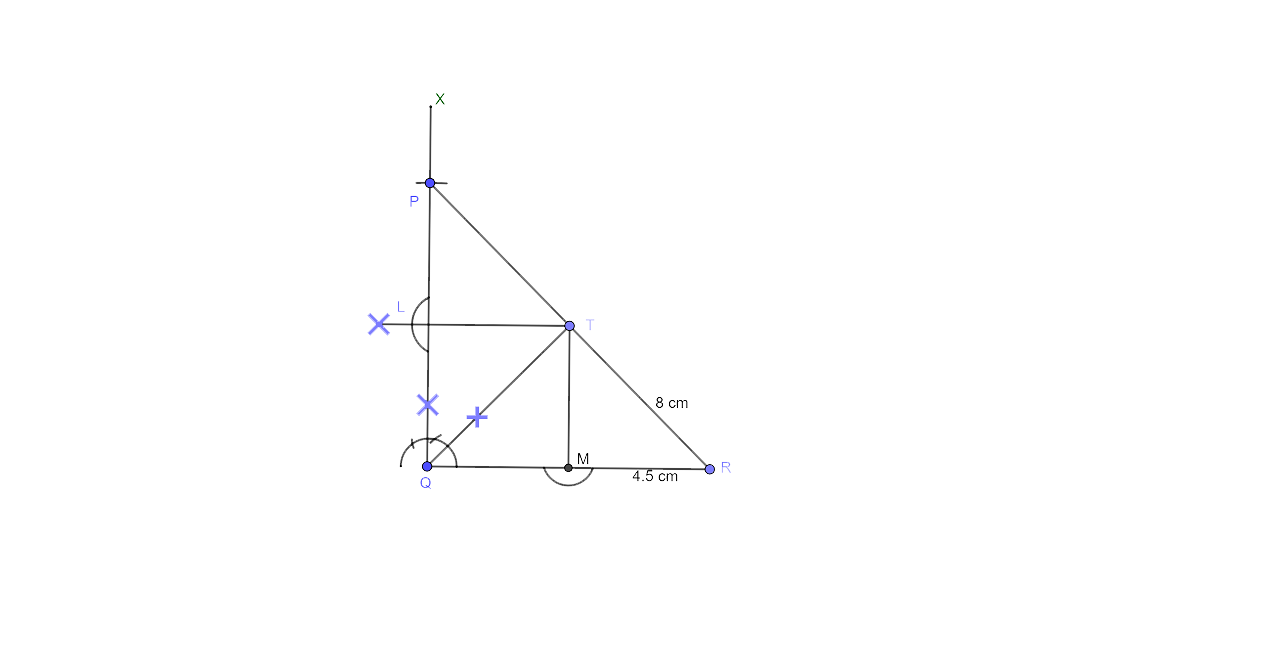
Steps to construct a right-angled triangle PQR

1. Now draw a line segment QR = 4.5 cm

2. At the point, Q, draw a ray QX which makes an angle ${{90}^{\circ }}$

3. Now with center R and radius 8 cm, draw an arc that intersects QX at P.

4. Join RP. Now ∆PQR is the required triangle.

5. Draw the bisector of ∠PQR which meets PR at T.

6. From T, draw perpendicular TL and TM respectively on PQ and QR.

Required Proof 

Let us consider ∆LTQ and ∆MTQ

∠TLQ = ∠TMQ (Each angle is equal to ${{90}^{\circ }}$)

∠LQT = ∠TQM ( As QT is angle bisector) 

QT = QT (Common angle)

Hence by the ASA criterion of congruence, we can say that ∆LTQ ≅ ∆MTQ

Now by considering the Corresponding Parts of Congruent Triangle (CPCT), we can say that, TL = TM

Hence, T is equidistant from PQ and QR.

7. Construct a triangle ABC in which angle ABC = 75°. AB = 5 cm and BC = 6.4 cm.

Draw a perpendicular bisector of side BC and also the bisector of angle ACB. If these bisectors intersect each other at point P, prove that P is equidistant from B and C ; and also from AC and BC.

Ans: 

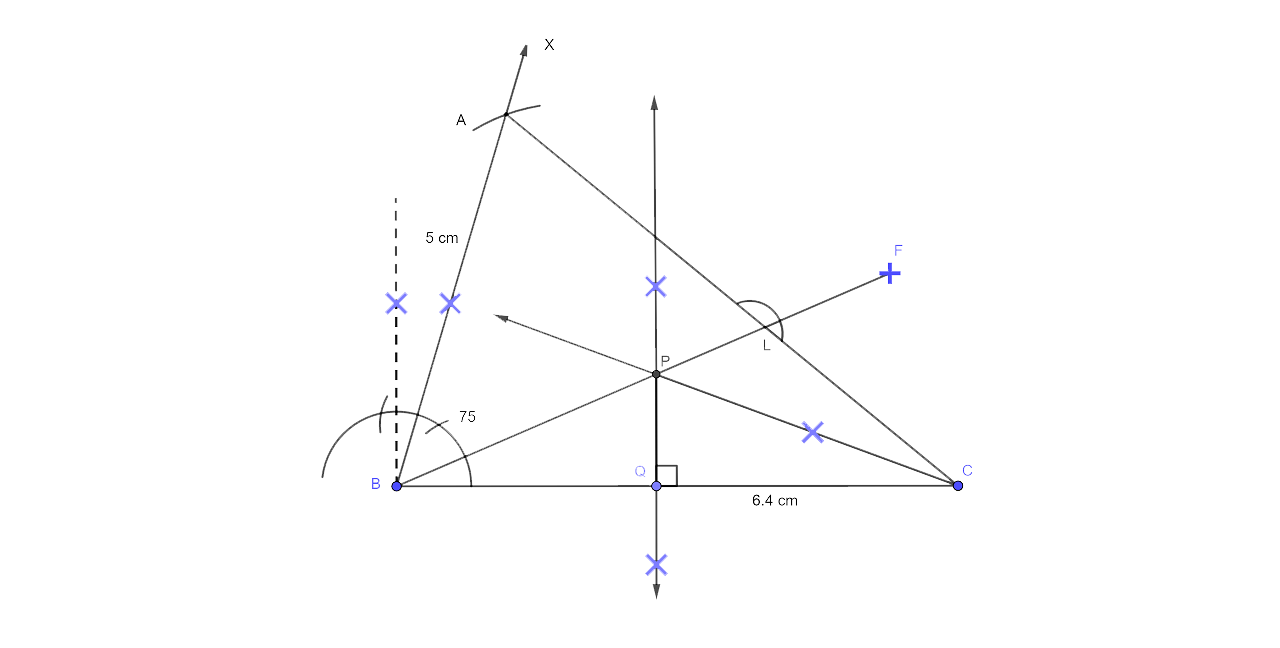
Steps of Constructing 

1. Draw a line segment BC which is 6.4 cm. 

2. Draw a ray BX at B which makes an angle ${{75}^{\circ }}$with BC and cut off BA = 5 cm. 

3. Now joining AC we have ∆ABC which is the required triangle. 

4. Draw the perpendicular bisector of BC.

5. Draw the angle bisector of angle ACB which intersects the perpendicular bisector of BC at P.

6. Now join PB and draw PL ⊥ AC.

Required Proof

Let us consider ∆PBQ and ∆PCQ.

PQ = PQ(Common angle)

∠PQB = ∠PQC (Each angle is equal to ${{90}^{\circ }}$)

BQ = QC (As PQ is the perpendicular bisector of BC)

Hence by ASA criterion of congruence, we can say that ∆PBQ ≅ ∆PCQ

Now by considering the Corresponding Parts of Congruent Triangle (CPCT) we can say that, PB = PC

Therefore, P is equidistant from B and C.

Alos now let us consider ∆PQC and ∆PLC,

∠PQC = ∠PLC (Each angle is equal to ${{90}^{\circ }}$)

∠PCQ = ∠PCL (Given information)

PC = PC (Common)

Hence by AAS criterion of congruence, we can say that ∆PQC ≅ ∆PLC

Now by considering the Corresponding Parts of Congruent Triangle (CPCT) we can say that, PQ = PL

Therefore now we could say that P is equidistant from AC and BC.

8. In parallelogram ABCD, side AB is greater than side BC and P is a point in AC such that PB bisects angle B.

Prove that P is equidistant from AB and BC.

Ans: 

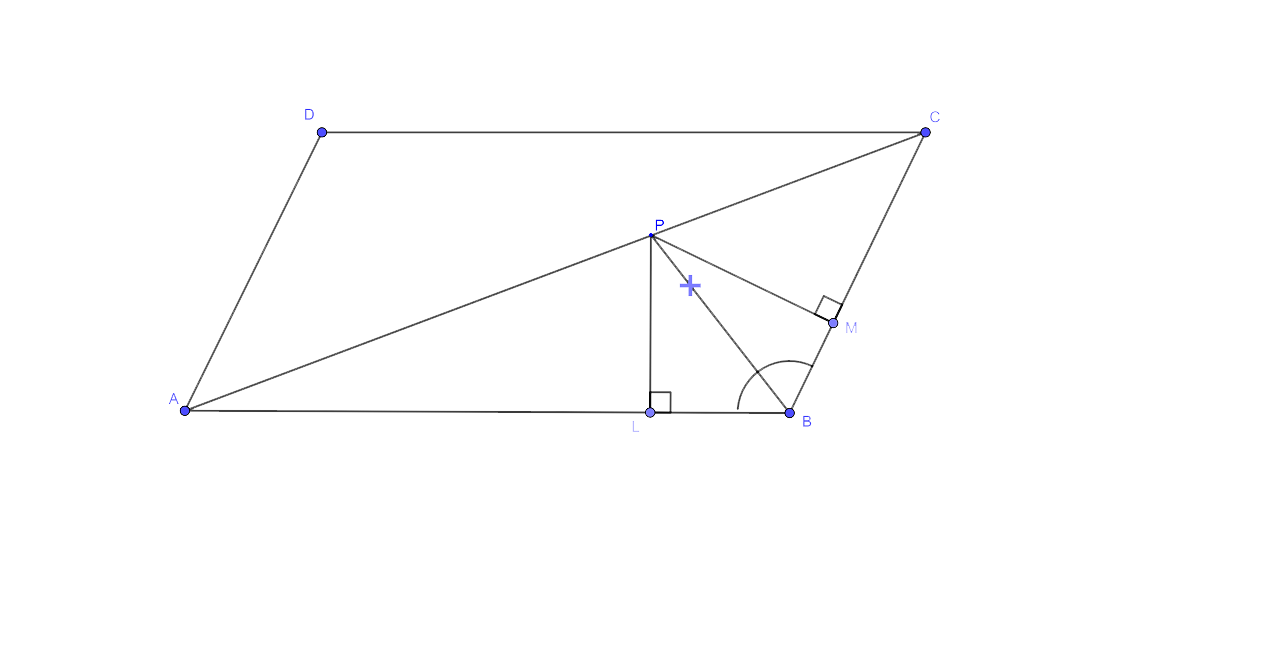
Construction: From P, let us draw PL ⊥ AB and PM ⊥ BC

Required Proof 

Let us consider ∆PLB and ∆PMB,

∠PLB = ∠PMB (Each angle is equal to ${{90}^{\circ }}$)

∠PBL = ∠PBM (Given information)

PB = PB (Common angle)

Hence by AAS criterion of congruence we can say that ∆PLB ≅ ∆PMB

Now by consider the Corresponding Parts of Congruent Triangle (CPCT) we can say that, PL = PM

Therefore, P is equidistant from AB and BC.

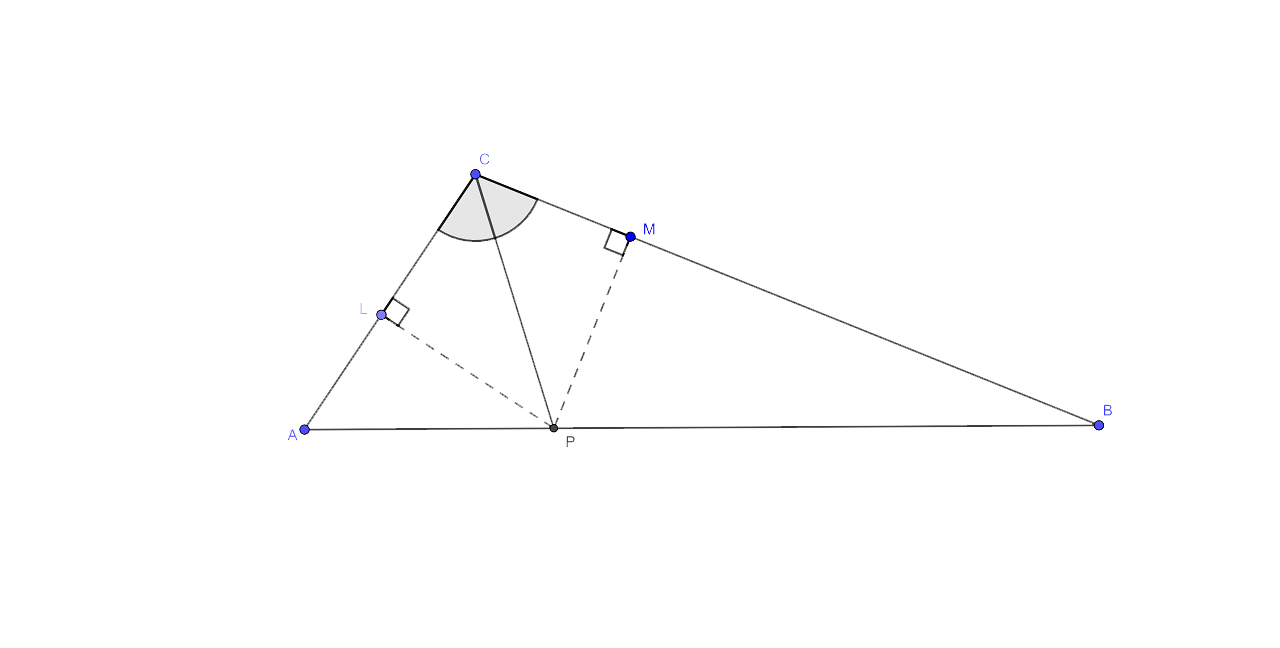
9. In triangle LMN, bisectors of interior angles at L and N intersect each other at point A.

Prove that:

(i) point A is equidistant from all three sides of the triangle.

(ii) AM bisects angle LMN.

Ans: 

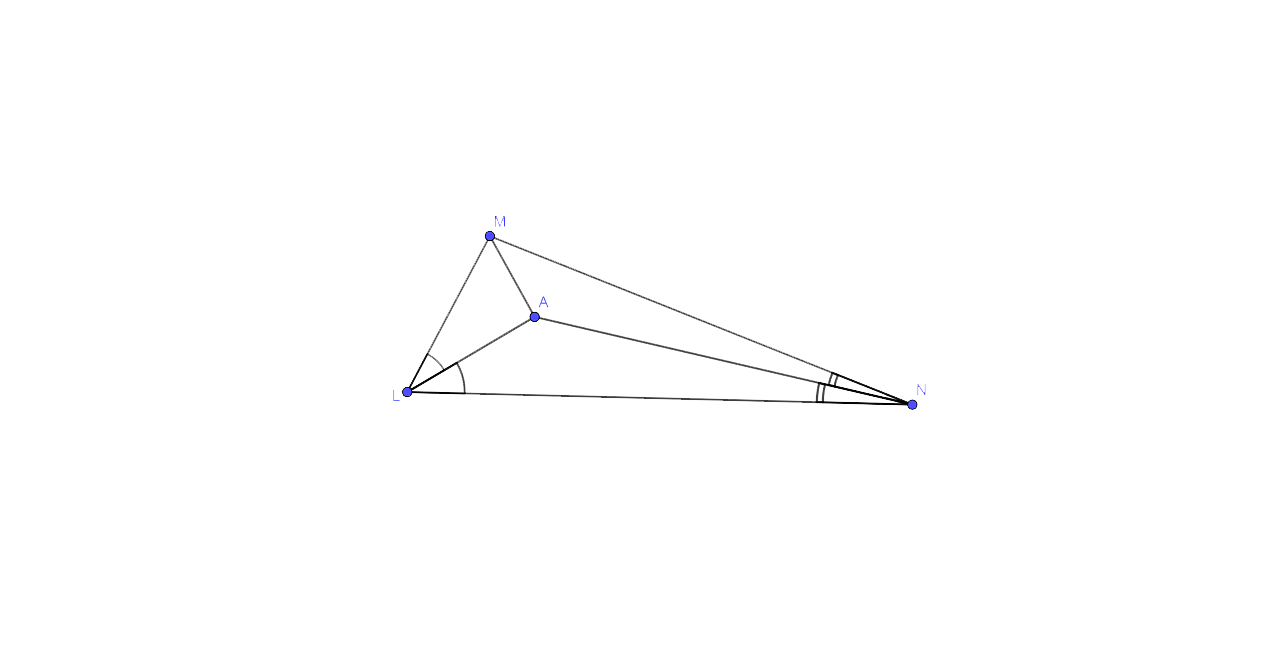
Construction: Join AM in triangle LMN 

Required Proof 

(i) As A lies on bisector of ∠N

So now we can say that A is equidistant from LN and LM.

As A lies on the bisector of ∠L

Therefore A is equidistant from all the three slides of the triangle LMN. 

Similarly, 

(ii) As A lies on the bisector of ∠M.

We can say that AM bisects ∠LMN

10. Use ruler and compasses only for this question:

(i) construct ΔABC, where AB = 3.5 cm, BC = 6 cm and ∠ABC = 60°.

(ii) Construct the locus of points inside the triangle which are equidistant from BA and BC.

(iii) Construct the locus of points inside the triangle which are equidistant from B and C.

(iv) Mark the point P which is equidistant from AB, BC and also equidistant from B and C. Measure and record the length of PB.

Ans: 

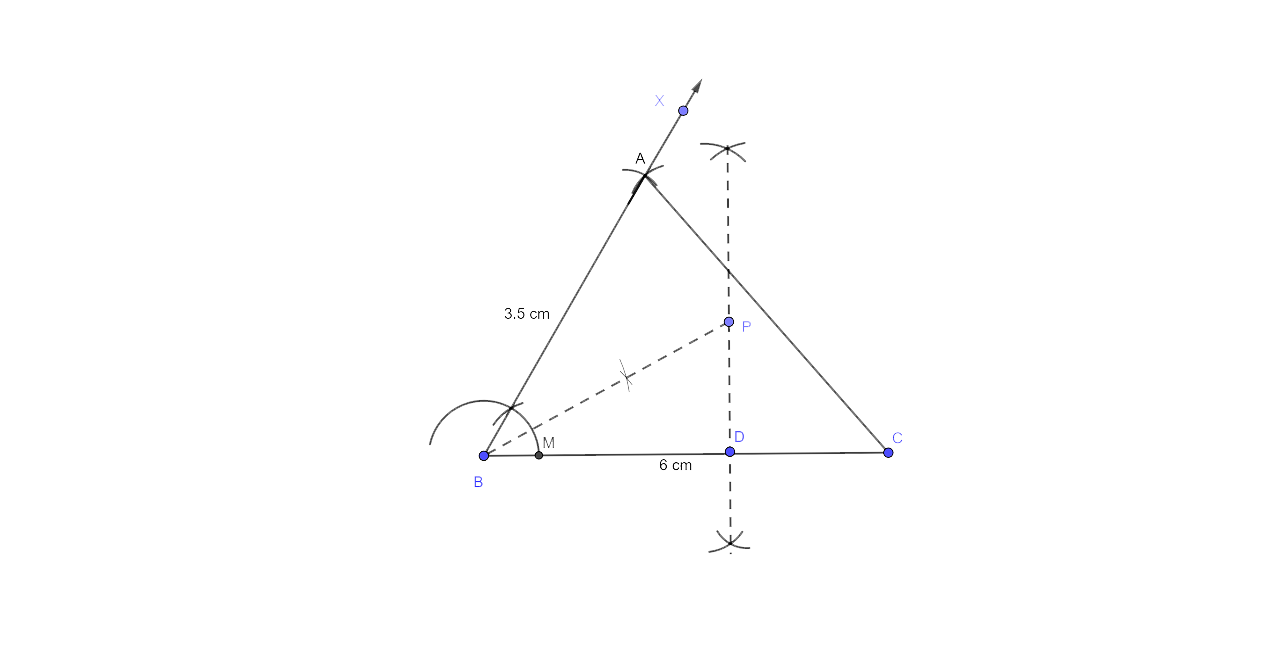
Step by step Procedure for Construction

1. Draw line BC = 6cm and then construct an angle CBX = ${{60}^{\circ }}$. Cut off AB = 3.5.Now join AC and thus ABC is the required triangle. 

2. Now draw the perpendicular bisector of BC and bisector of angle B. 

3. Now the bisector of angle B meets the bisector of BC at P. Thus BP is the required length where PB = 3.5 cm.

4. Here we can say that P is the point that is equidistant from BA and BC which is also a point that is equidistant from B and C. 

PB = 3.5 cm

11. The given figure shows a triangle ABC in which AD bisects angle BAC. EG is the perpendicular bisector of side AB which intersects AD at point E Prove that:

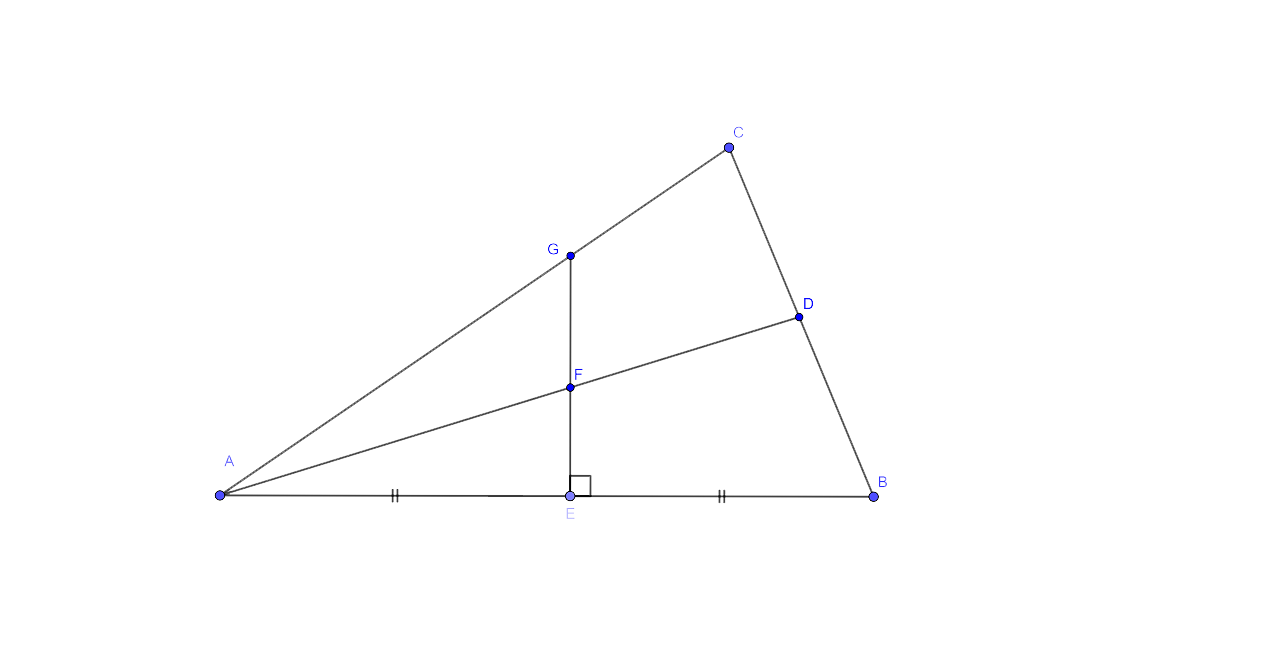
(i) F is equidistant from A and B.

(ii) F is equidistant from AB and AC.

Ans: 

It is given in the figure that in 

Given : In the figure, ΔABC, AD is the bisector of ∠BAC Which meets BC at D EG is the perpendicular bisector of AB which intersects AD at F

We have to prove that:

(i) F is equidistant from A and B.

(ii) F is equidistant from AB and AC.

Required Proof

(i) As F lies on the perpendicular bisector of AB, therefore we could say that F is equidistant from A and B.

(ii) Similarly from (i) we can say that F lies on the bisector of ∠BAC, 

∴ F is equidistant from AB and AC.

Hence it is proved. 

12. The bisectors of ∠B and ∠C of a quadrilateral ABCD intersect each other at point P. Show that P is equidistant from the opposite sides AB and CD.

Ans: 

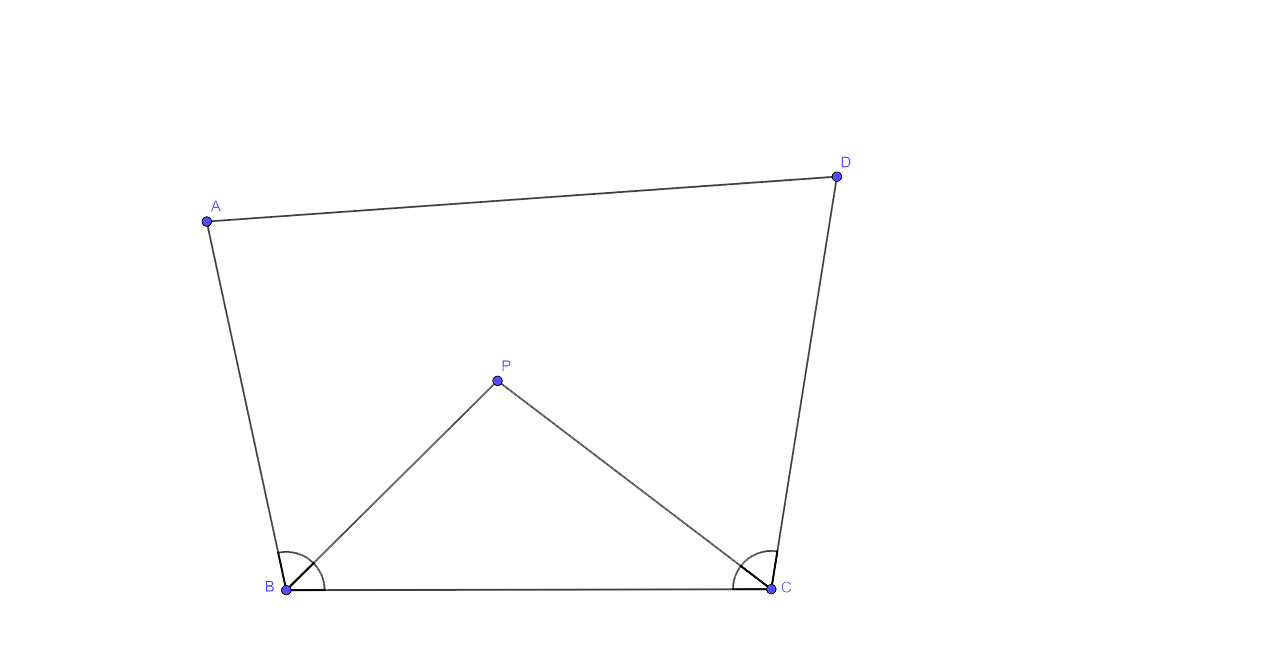
Let us consider the quadrilateral ABCD in which the bisectors of ∠B and ∠C meet each other at P. 

We have to prove that D is equidistant from the sides AB and CD.

The required proof: 

As P lies on the bisector of ∠B, P is equidistant from AB and BC …. (1)

Similarly, we could say that P lies on the bisector of ∠C, P is equidistant from BC and CD …. (2)

From (1) and (2) we can say that  P is equidistant from AB and CD

Hence it is proved. 

13. Draw a line AB = 6 cm. Draw the locus of all the points which are equidistant from A and B.

Ans: 

Steps of Construction:

(i) The first step is to draw a line segment AB = 6 cm

(ii) Now draw the perpendicular bisector LM of AB. LM is the required locus.

(iii) Take any point on LM, let just take P 

(iv) Join PA and PB

∵ P lies on the right bisector of line AB

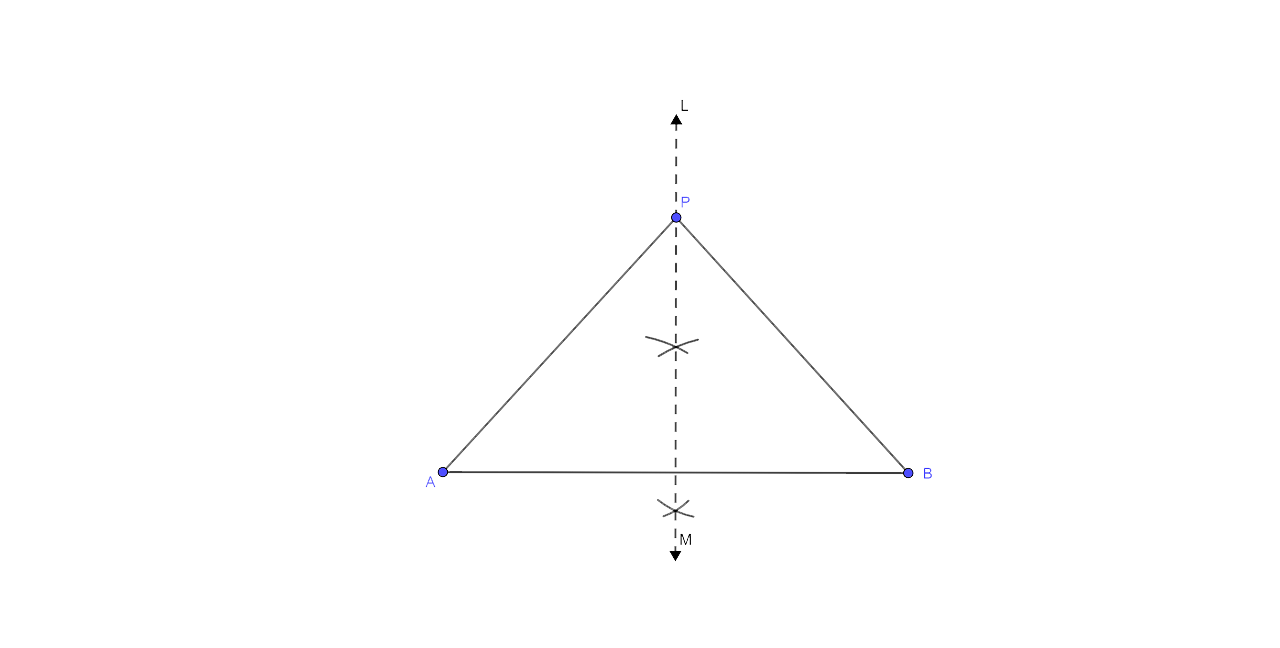
From the figure we could say that  P is equidistant from A and B.

∴ PA = PB

∴ The perpendicular bisector of AB is the locus of all points which are equidistant from A and B.

14. Draw an angle ABC = 75°. Draw the locus of all the points equidistant from AB and BC.

Ans: 

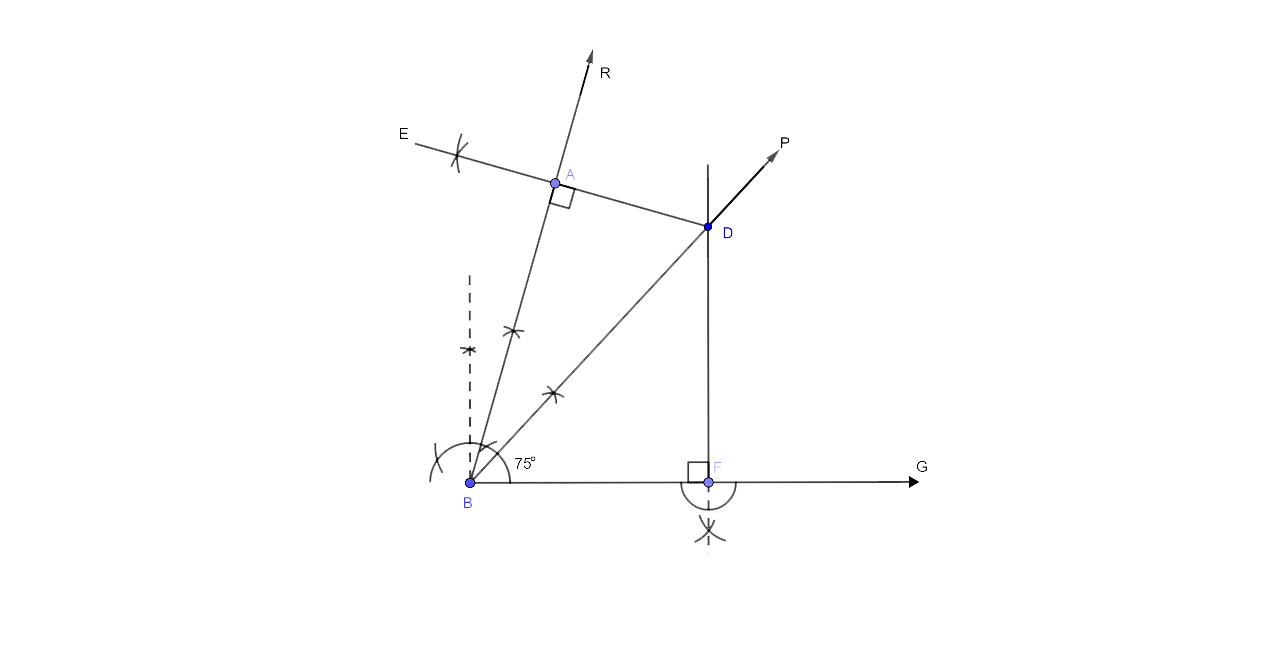
Step by step Procedure for the Construction

(i) The first step is to draw a ray BC.

(ii) After drawing a ray BC now again constructs a ray RA which makes an angle of ${{75}^{\circ }}$with BC. 

(iii) ∴ we could say that  ∠ABC = 75°

(iv) Now draw the angle bisector BP of ∠ABC. Hence BP is the required locus.

(v) Take any point D on BP.

(vi) From D, draw DE ⊥ AB and DF ⊥ BC.

As D lies on the angle bisector ∠ABC.

∴ We can say that  D is equidistant from AB and BC.

∴ DE = DF

Similarly, any point on BP, is equidistant from AB and BC.

∴BP is the locus of all points which are equidistant from AB and BC.

15. Draw an angle ABC = 60°, having AB = 4.6 cm and BC = 5 cm. Find a point P equidistant from AB and BC ; and also equidistant from A and B

Ans: 

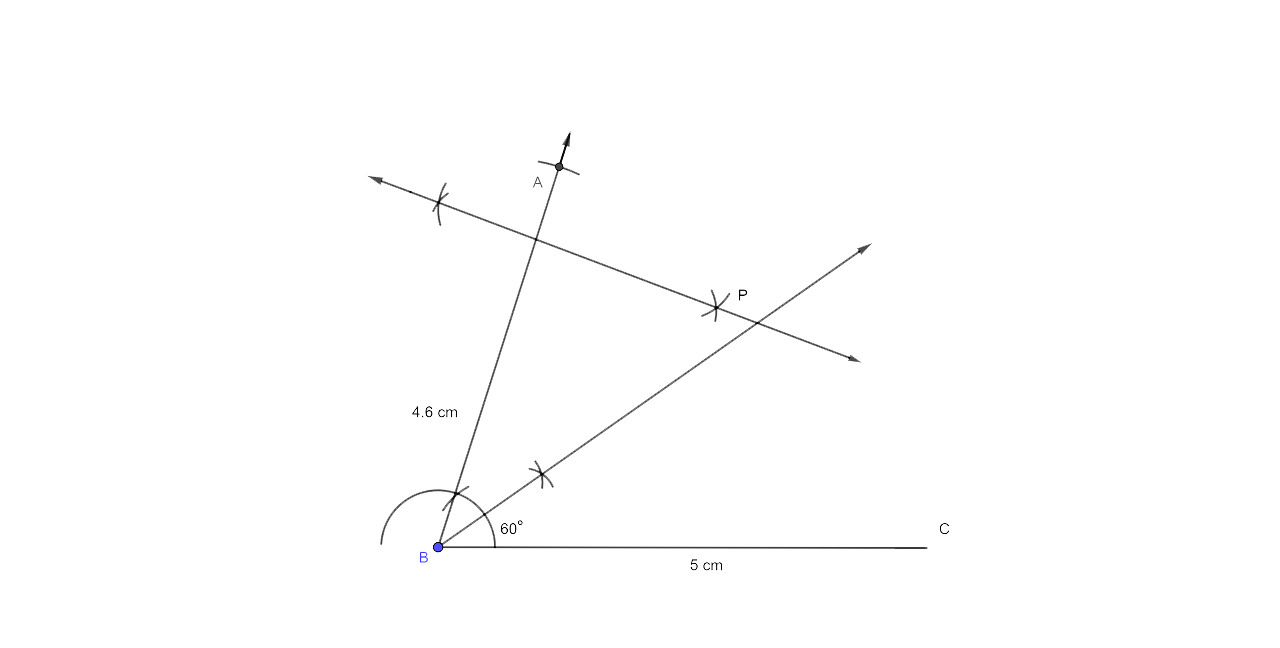
Step by step Procedure for the Construction

(i)  The first step is to construct a line segment BC of 5cm. 

(ii) Now at B draw a ray BX which makes an angle of 60° and then cut off BA= 4.6 cm.

(iii) Now draw an angle bisector of ∠ABC.

(iv) The final step is to draw the perpendicular bisector of AB which intersects the angle bisector at P.

Now from this we could say that P is the required point which is equidistant from AB and BC as well as from points A and B.

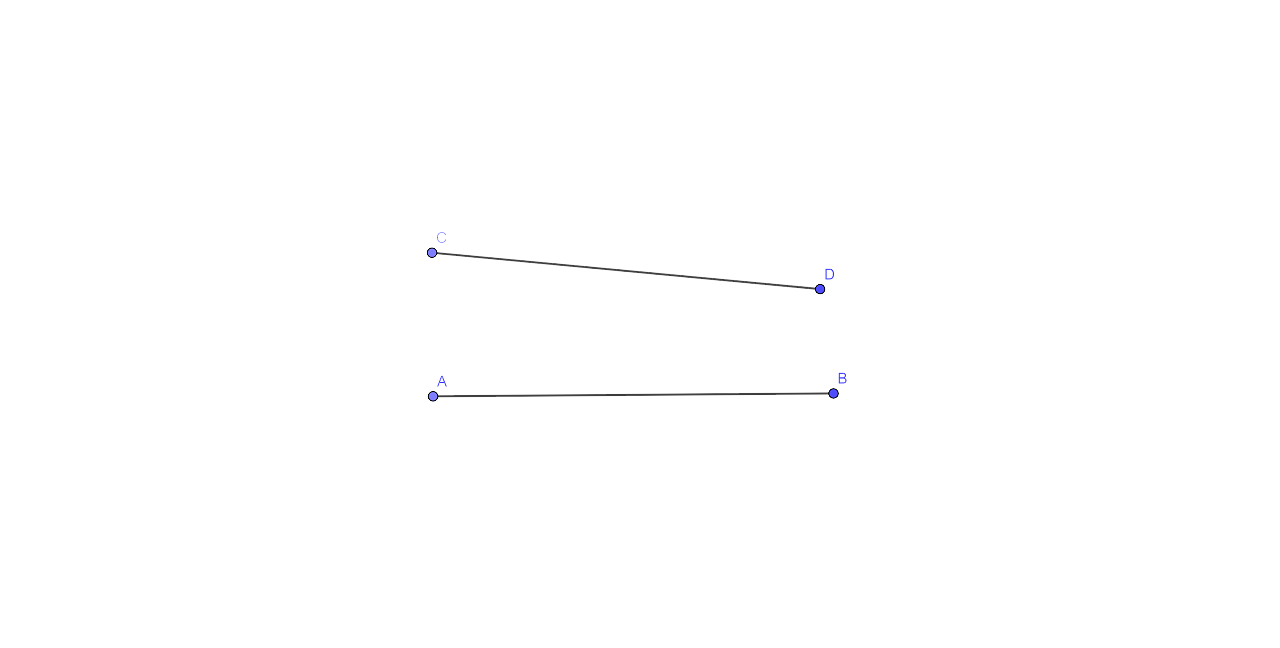
16. In the figure given below, find a point P on CD equidistant from points A and B.

Ans: 

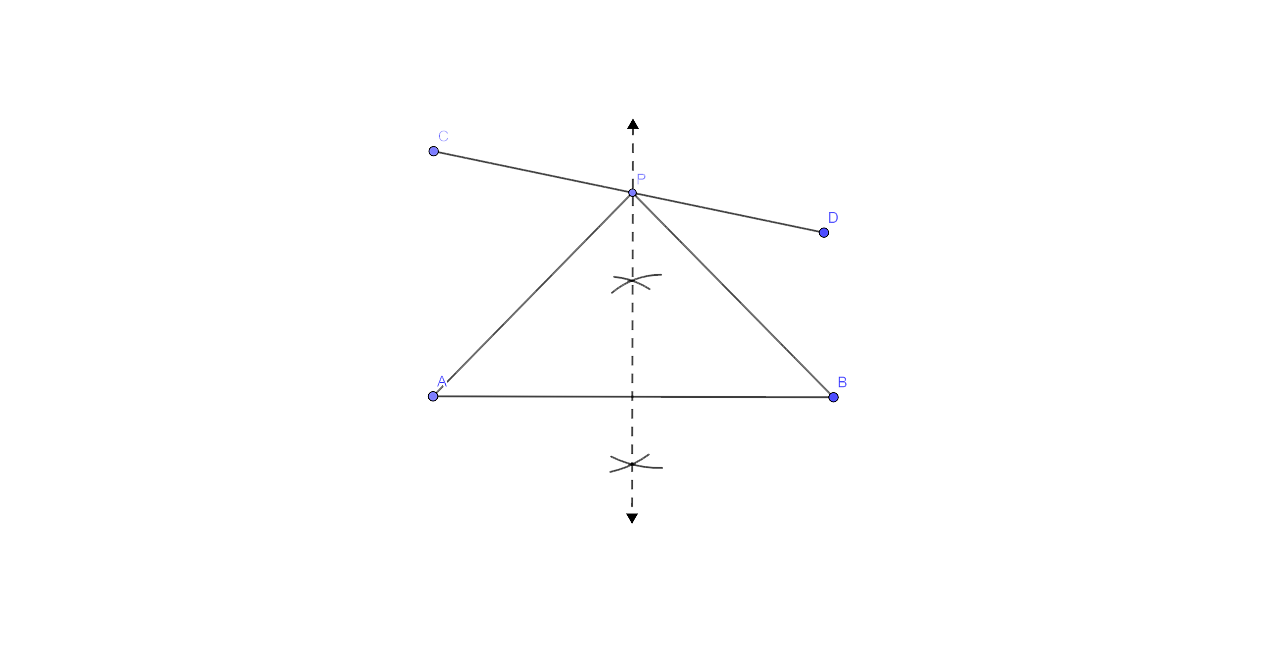
Step by step Procedure for the Construction

(i) The figures which have been provided, we can say that AB and CD are two line segments. 

(ii) Now a perpendicular bisector  of AB should be drawn which then intersects CD in P. 

From here we could say that P is the required point which is equidistant from A and B. 

As P lies on the perpendicular bisector of AB. 

(i) In the figure AB and CD are two line segments.

(ii) Draw the perpendicular bisector of AB which intersects CD in P.

P is the required point which is equidistant from A and B

∴ PA = PB.

17. In the given triangle ABC, find a point P equidistant from AB and AC; and also equidistant from B and C

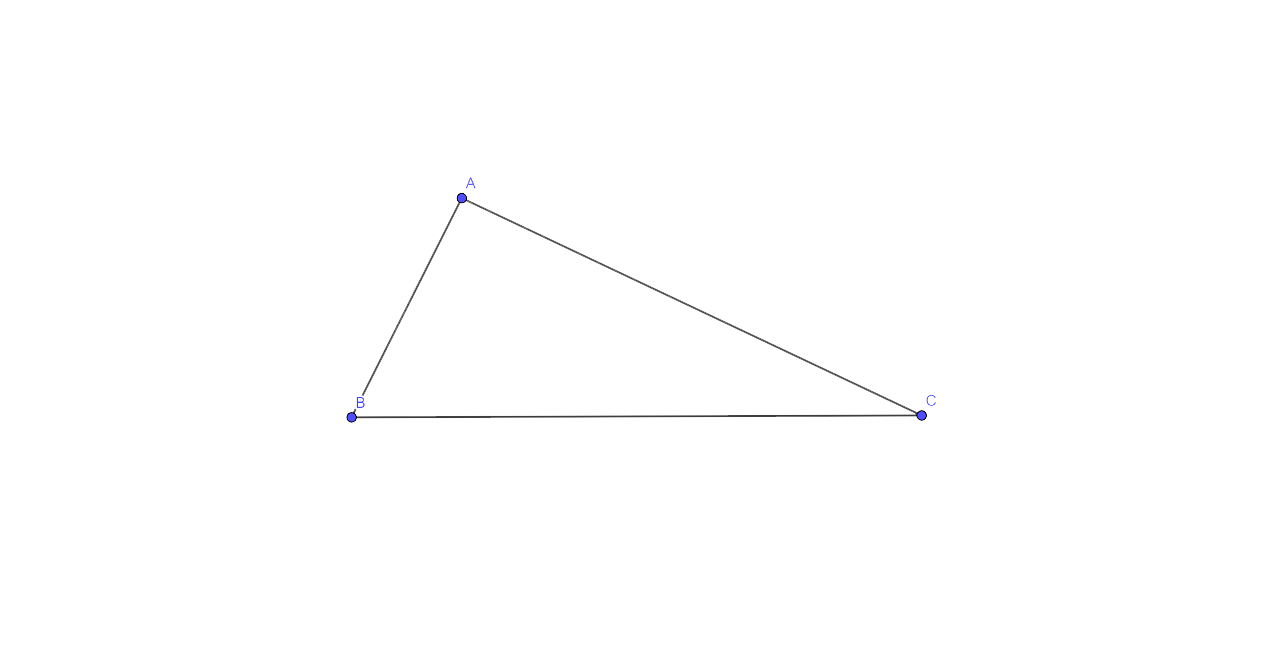
Ans: 

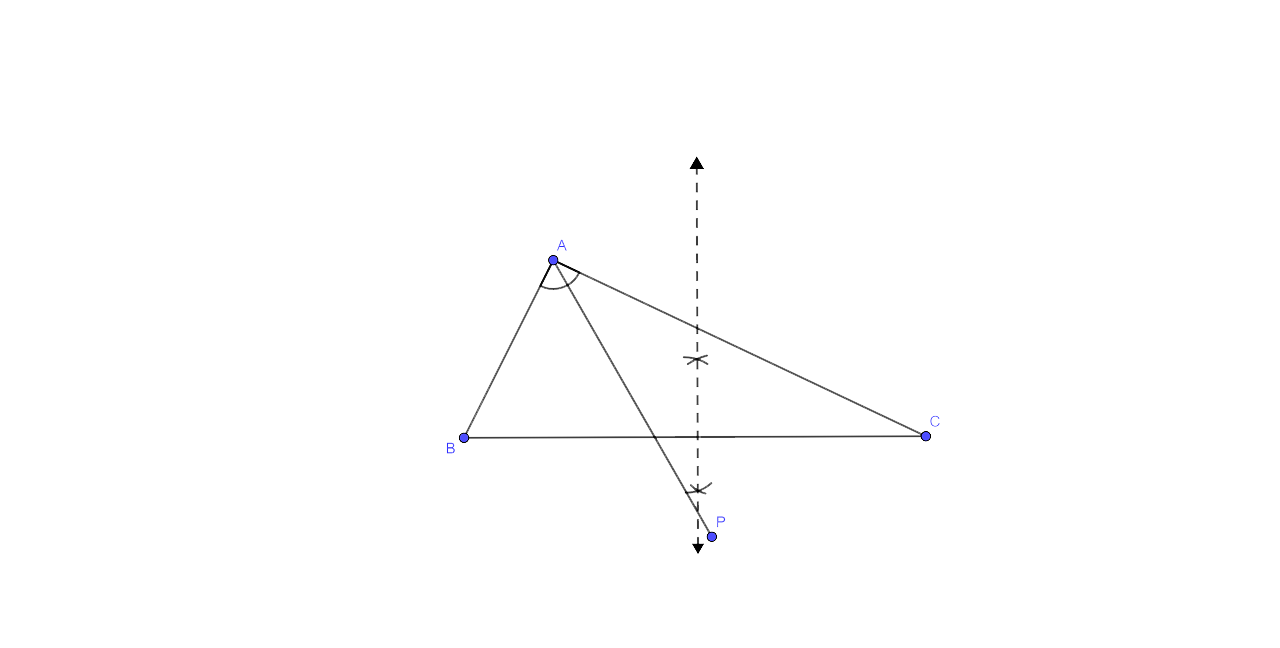
Step by step Procedure for the Construction

(i) In the triangle which is given, let us first draw the angle bisector of ∠BAC.

(ii) Now draw the perpendicular bisector of BC which then intersects the angle bisector of ∠A at P.

Now from here we could say that P is the required point which is equidistant from AB and AC as well as from C and B. 

As P lies on the angle bisector of ∠BAC.∴ It is equidistant from AB and AC.

Similarly P lies on the perpendicular bisector of BC from which again we can say that P is equidistant from B and C.

18. Construct a triangle ABC, with AB = 7 cm, BC = 8 cm and ∠ABC = 60°. Locate by construction the point P such that :

(i) P is equidistant from B and C.

(ii) P is equidistant from AB and BC.

(iii) Measure and record the length of PB.

Ans: 

Step by step Procedure for the Construction

1. The first step is to draw a line segment AB = 7cm

2.  Now draw angle ∠ABC = 60° with the help of a compass.

3. Cut off BC = 8 cm.

4. Join A and C.

5. The triangle ABC so formed is a required triangle.

(i) Now draw a perpendicular bisector of line BC. The point situated on this line will be exactly equidistant from B and C.

(ii) Now draw an angular bisector of ∠ABC. Any point which is situated on this angular bisector is equidistant from lines AB and BC. 

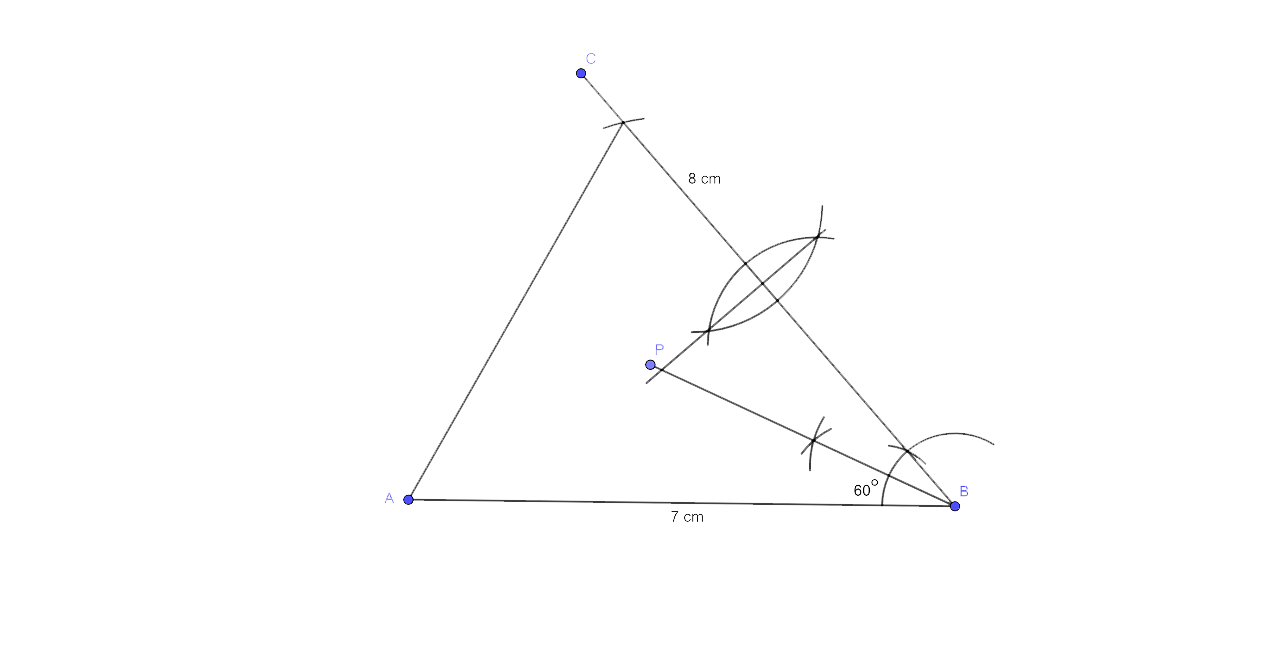
The point which completely fulfills the condition required in (i) and (ii) is the intersection point of bisector of line BC and angular bisector of ∠ABC.

(iii) Length of PB is 4.5 cm.

19. On a graph paper, draw the lines x = 3 and y = -5. Now, on the same graph paper, draw the locus of the point which is equidistant from the given lines.

Ans: 

Now on the graph paper, draw axis XOX’ and YOY’. Draw a line 1, at x = 3 which is parallel to y-axis and another line m, y = -5, which is parallel to the x-axis

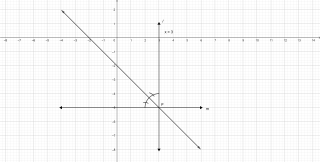
Now from the graph, we can see that the two lines intersect each other at P.

Now the next step is to draw the angle bisector p of ∠P

As p is the bisector of ∠P

Therefore any point on P, is equidistant from l and m

Therefore the line p is equidistant from 1 and m.

20. On graph paper, draw the line x = 6. Now, on the same graph paper, draw the locus of the point which moves in such a way that its distance from the given line is always equal to 3 units.

Ans: 

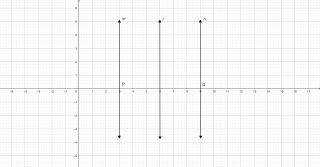
Now on the graph, draw axis XOX’ and YOY’

Let us draw a line 1, x= 6 which is parallel to -axis

Take the point P and Q which are at a distance of 3 units from the line 1 

Let us now draw a line rn and n from P and Q parallel to P respectively 

The required locus of the points P and Q are the line m and n. 

This arc is always 3 units from line 1. Hence it is proved. 

Exercise 16(B)

1. Describe the locus for questions 1 to 13 given below:

1. The locus of a point at a distance of 3 cm from a fixed point.

Ans:

The locus of the point which is at a distance of 3 cm away from the fixed point is the circumference of a circle in which its radius is 3 cm and the fixed point is the centre of the circle. 

2. The locus of a point at a distance of 2 cm from a fixed-line.

Ans:

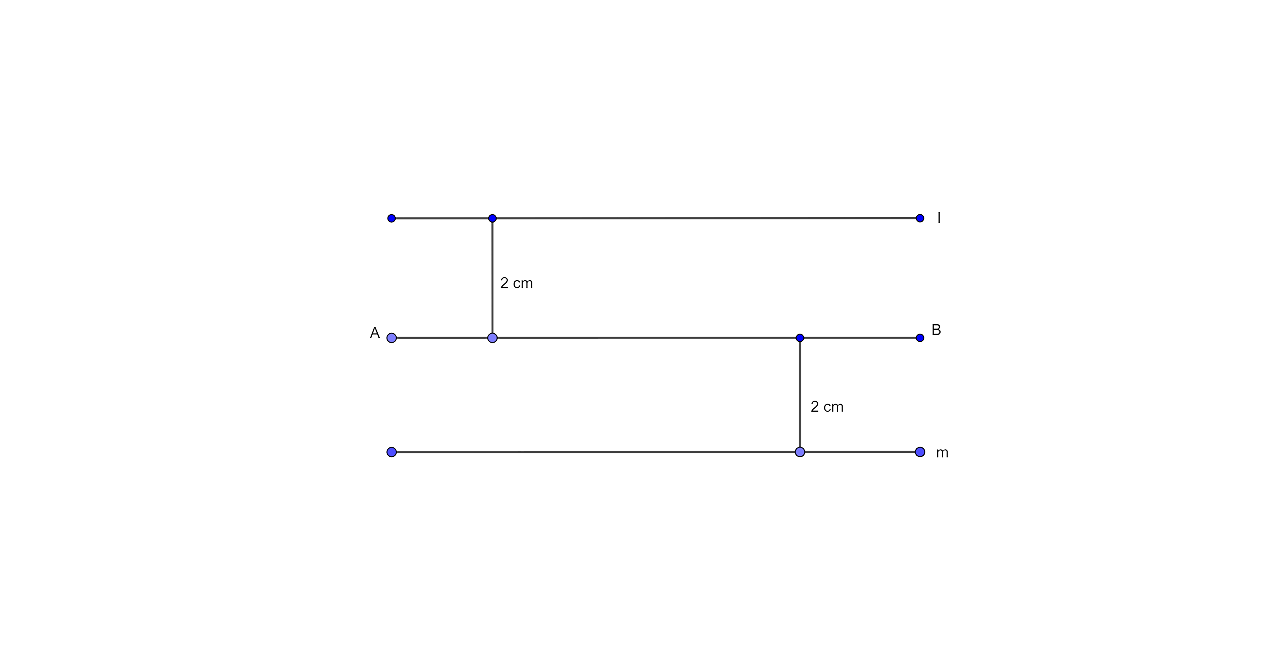
The locus of the points which are at the distance of 2 cm from the fixed line AB are nothing but a pair of straight lines l and m which are parallel to the given line at the distance of 2 cm.  

3. The locus of the centre of a wheel of a bicycle going straight along a level road.

Ans:  

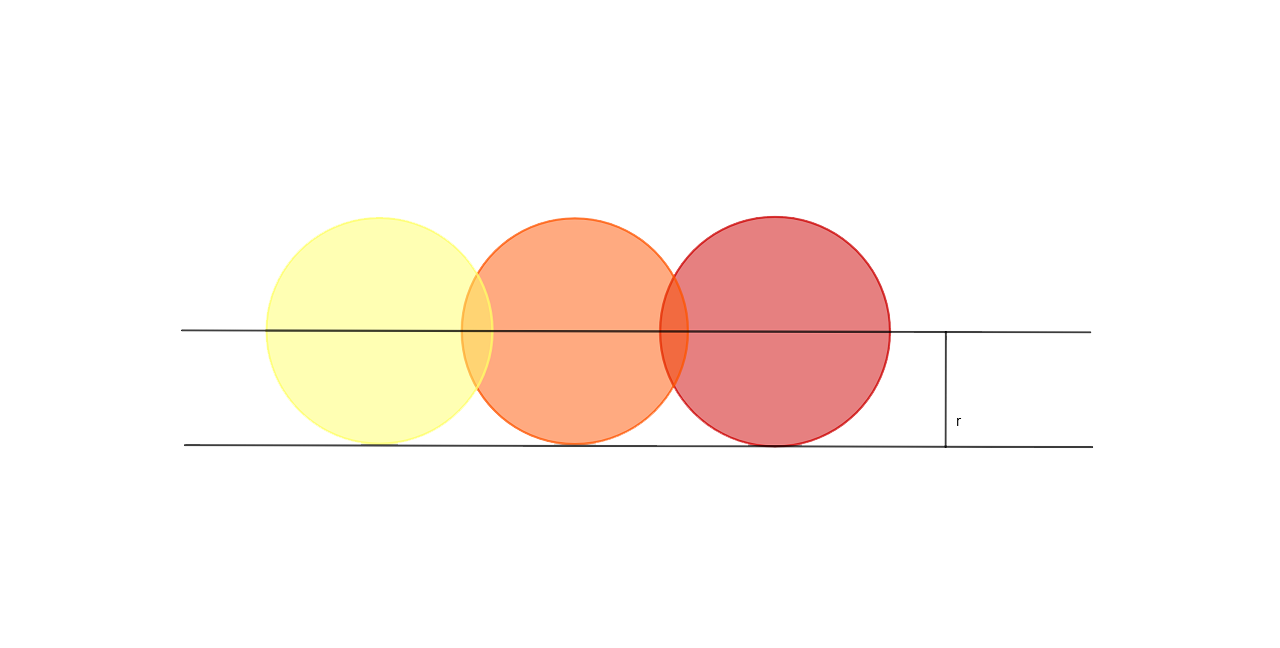
Now the locus of the centre of the wheel, that is going straight along the level road will be the straight line which is parallel to the road at a distance equal to the radius of the wheel. 

4. The locus of the moving end of the minute hand of a clock.

Ans: 

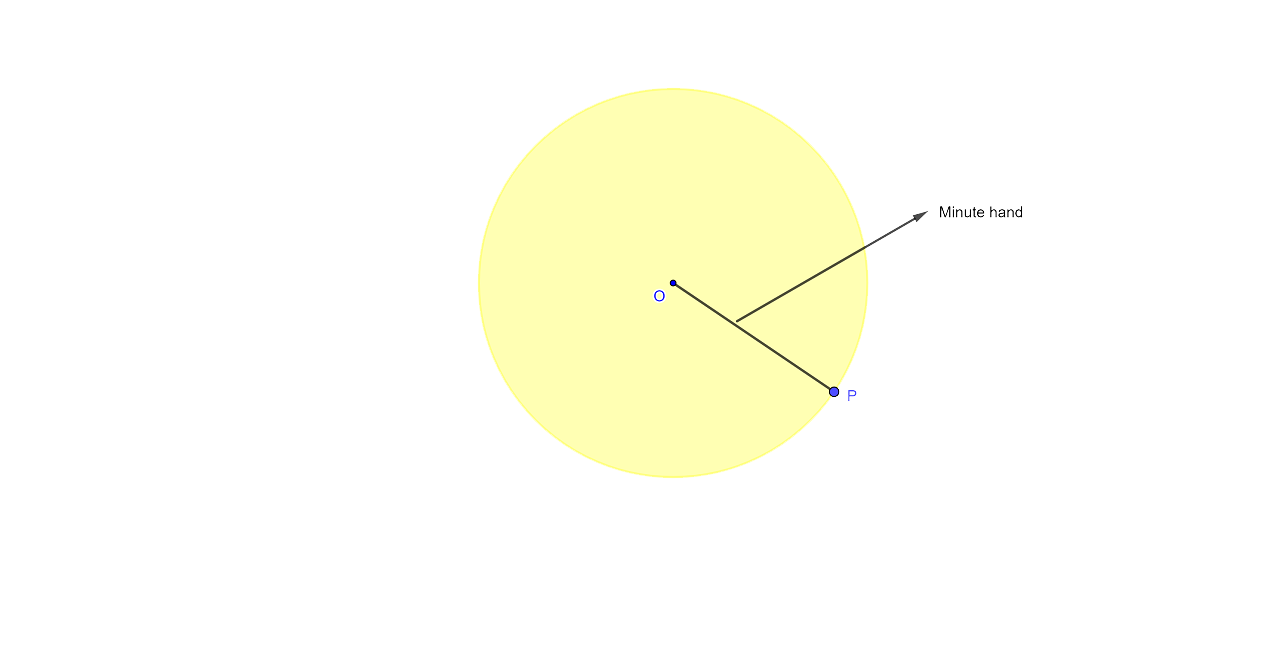
The locus of the moving end of the minute hand of the clock would be a circle in which its radius will be the length of the minute hand. 

5. The locus of a stone dropped from the top of a tower.

Ans:

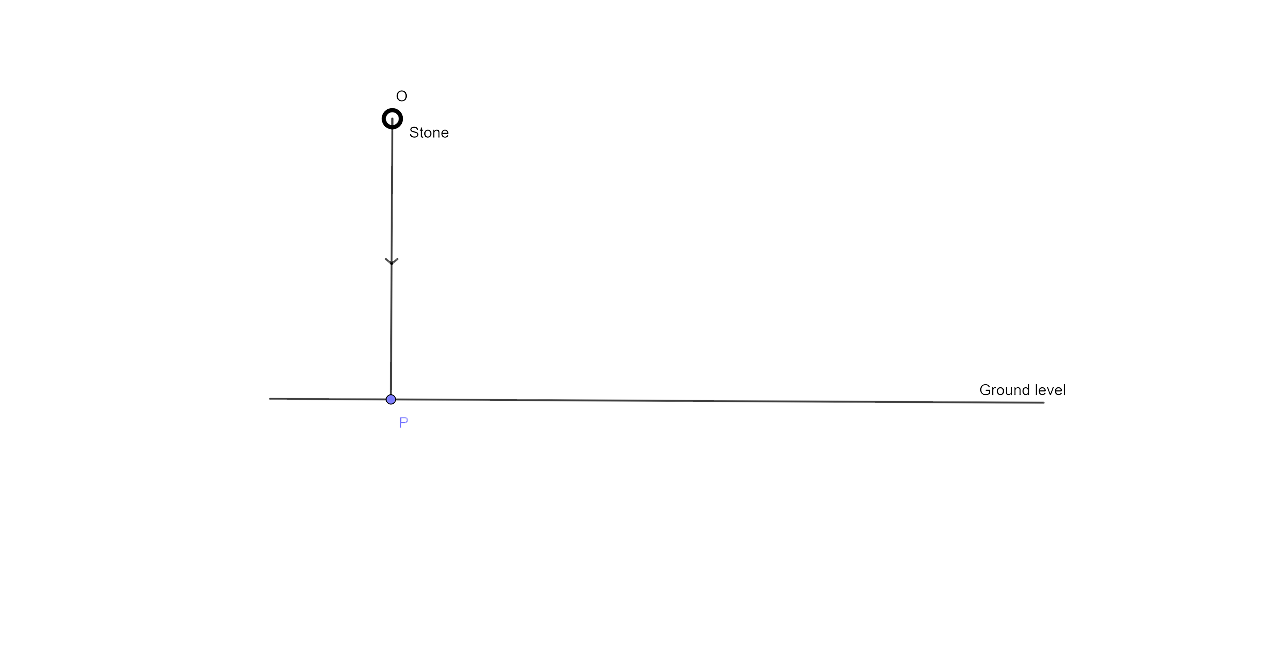
The locus of the stone that is dropped from the top of the tower would be a vertical line from the point from which the stone is dropped. 

6. The locus of a runner, running around a circular track and always keeping a distance of 1.5 m from the inner edge.

Ans:

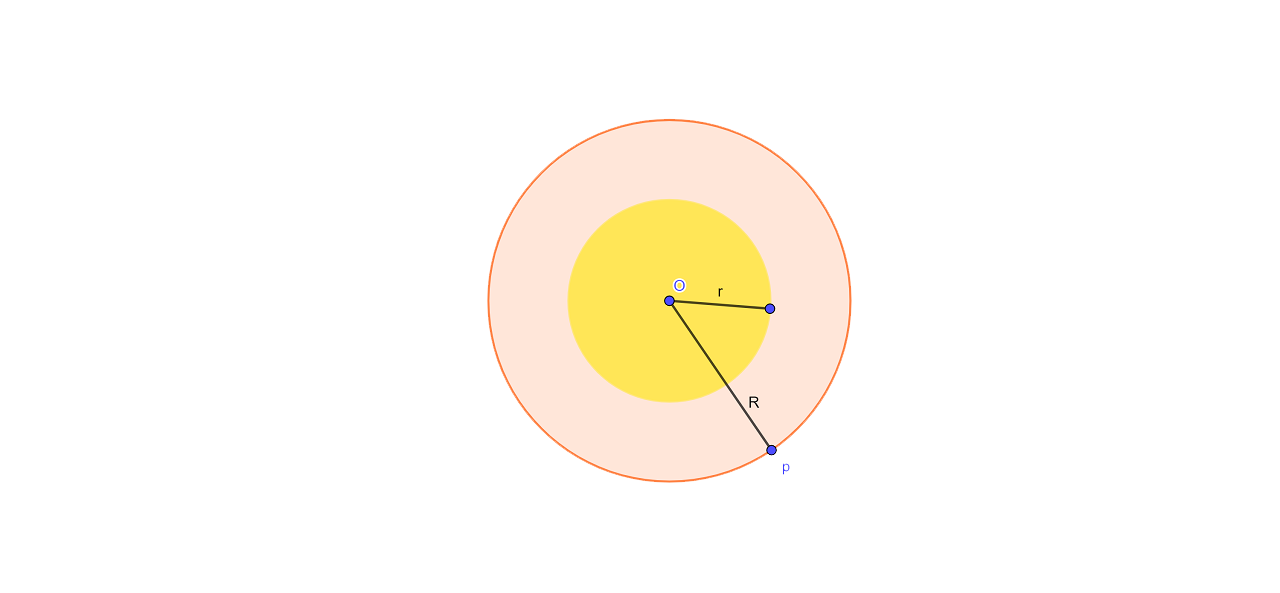
The locus of the runner who is running around the circular track and who is always keeping a distance of 1.5 m from the inner edge would be the circumference of a circle in which the radius is equal to the radius of the inner circular track and exceeds 1.5 m. 

7. The locus of the door-handle, as the door opens.

Ans:

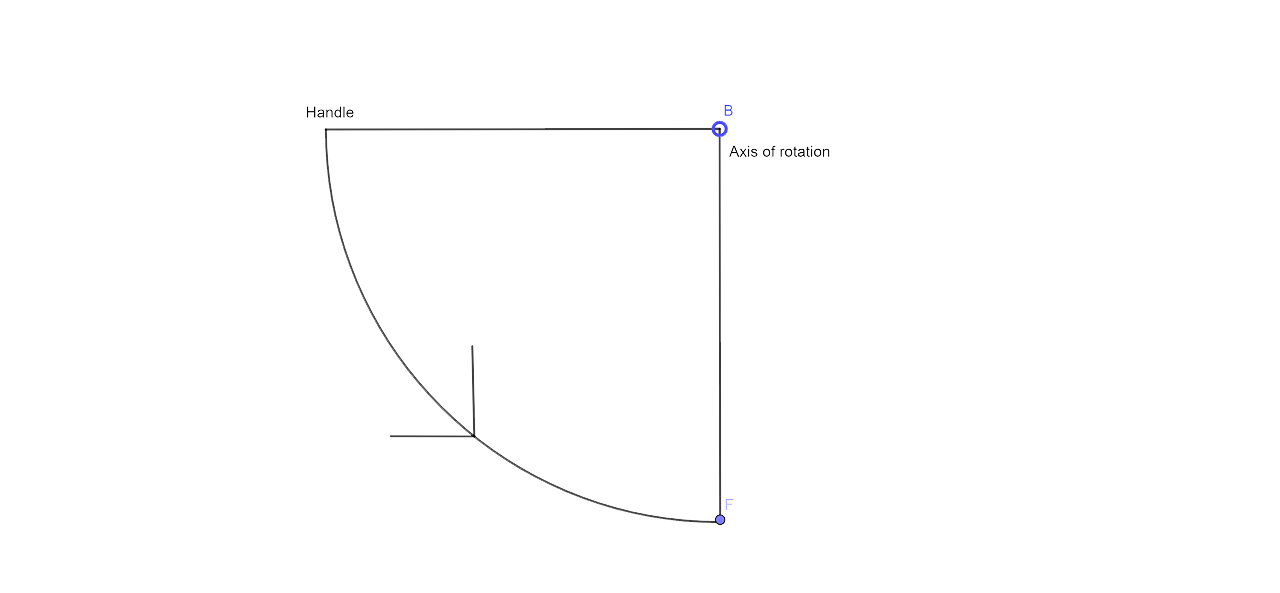
We have to find the locus of the door handle. Now the locus of the door handle would be the circumference of a circle with the center at the axis of the rotation of the door and the radius which is equal to the distance between the door handle and the axis of the rotation of the door. 

8. The locus of a point inside a circle and equidistant from two fixed points on the circumference of the circle.

Ans:

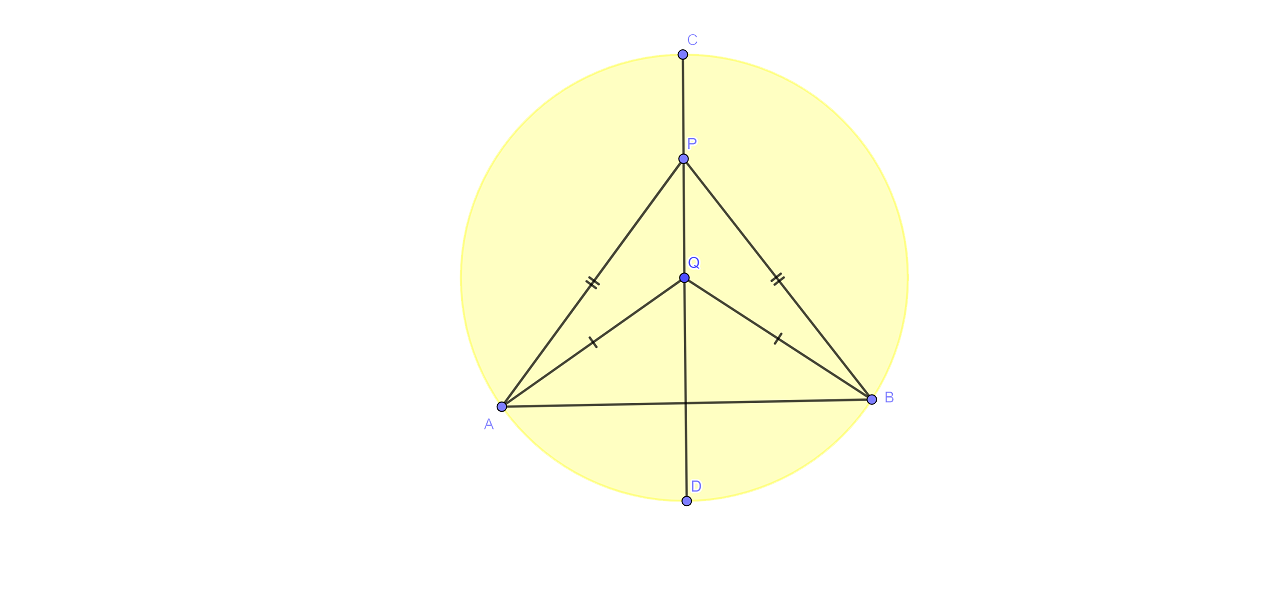
We have to find the locus of a point inside a circle and equidistant from two fixed points on the circumference of the circle.

A diameter equal to the perpendicular bisector of the line uniting the two fixed points on the circumference of a circle will be the locus of the points inside the circle that are equidistant from the fixed points on the circumference of a circle.

9. The locus of the centers of all circles passes through two fixed points.

Ans:

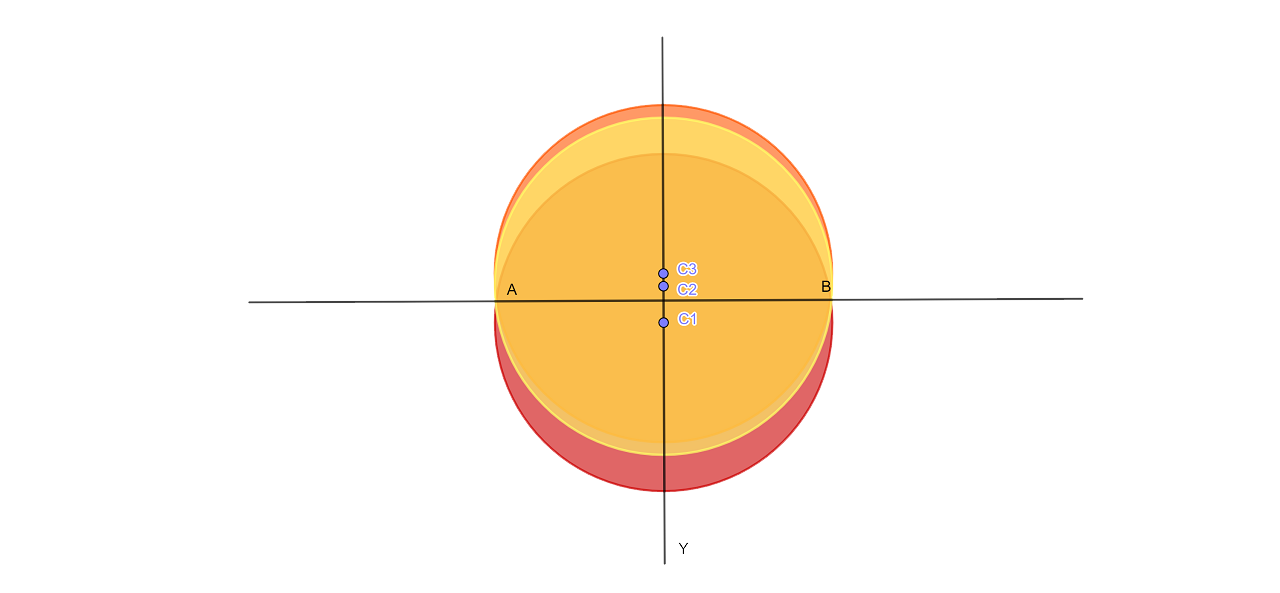
The perpendicular bisector of the line segment connecting the two supplied fixed points will be the locus of the centers of all the circles going through two fixed points.

10. The locus of vertices of all isosceles triangles having a common base.

Ans:

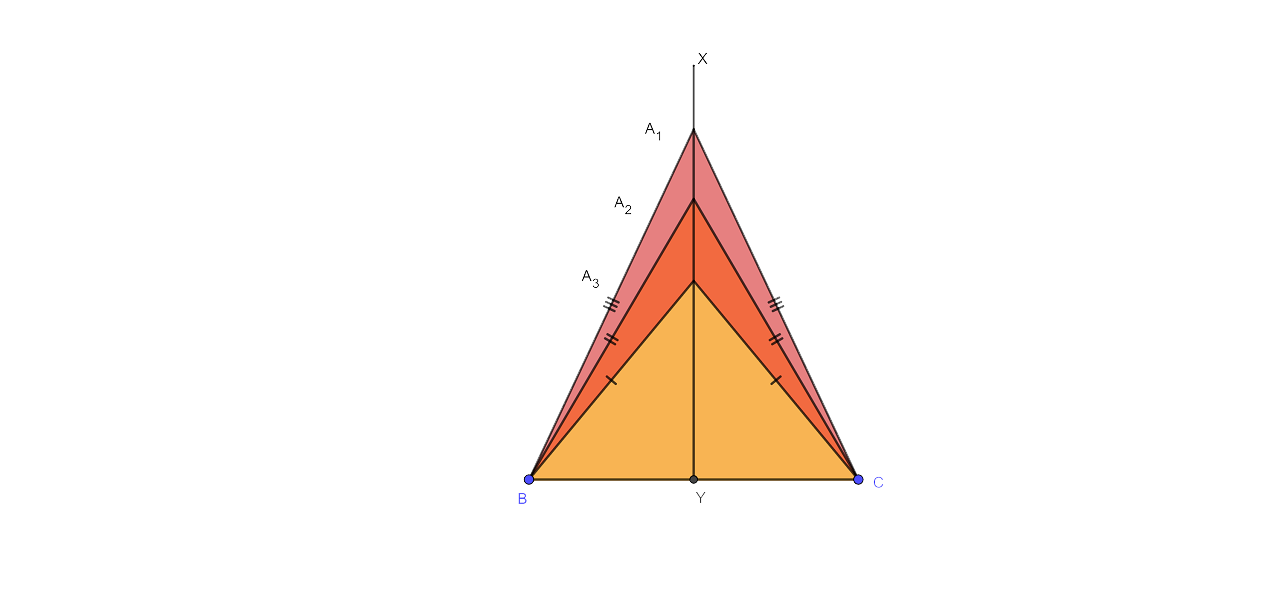
The perpendicular bisector of all isosceles triangles with a common base will be the locus of vertices of all isosceles triangles with a common base.

11. The locus of a point in space is always at a distance of 4 cm from a fixed point.

Ans: The surface of the sphere with the fixed point at its center and a radius of 4 cm is the locus of a point in space.

12. The locus of a point P, so that:

$A{{B}^{2}}$ = $A{{P}^{2}}$+$B{{P}^{2}}$, where A and B are two fixed points.

Ans:

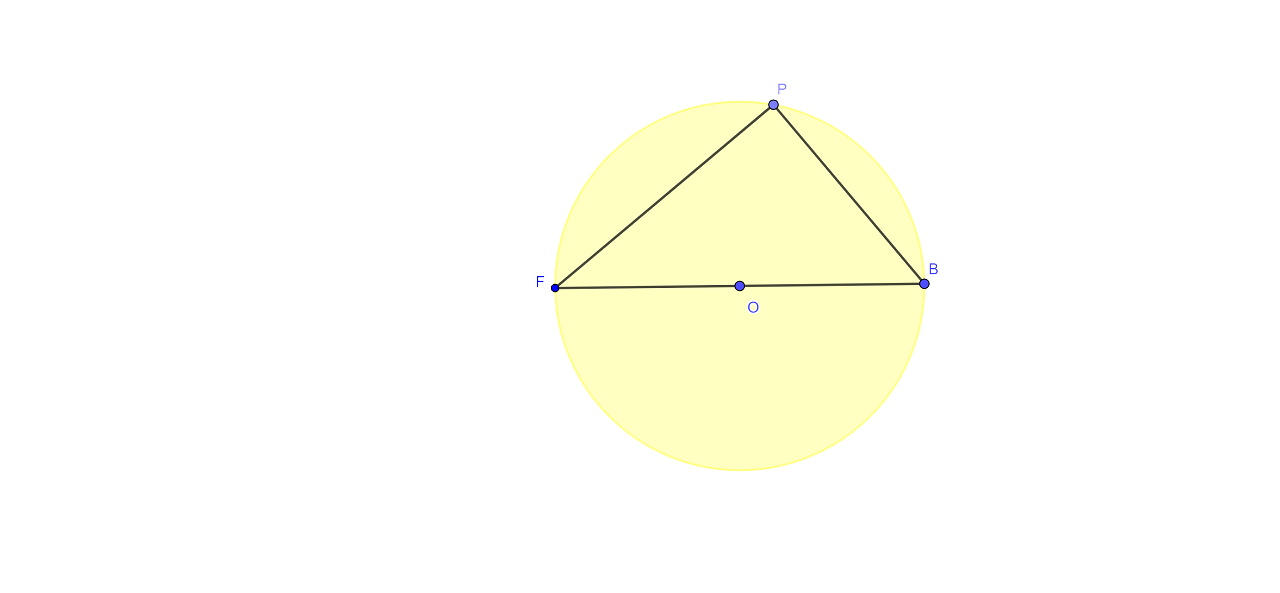
The circumference of a circle with a diameter of AB is the locus of the point P, and it meets the equation $A{{B}^{2}}$ = $A{{P}^{2}}$+$B{{P}^{2}}$.

13. The locus of a point in rhombus ABCD, so that it is equidistant from

i) AB and BC

ii) B and D.

Ans:

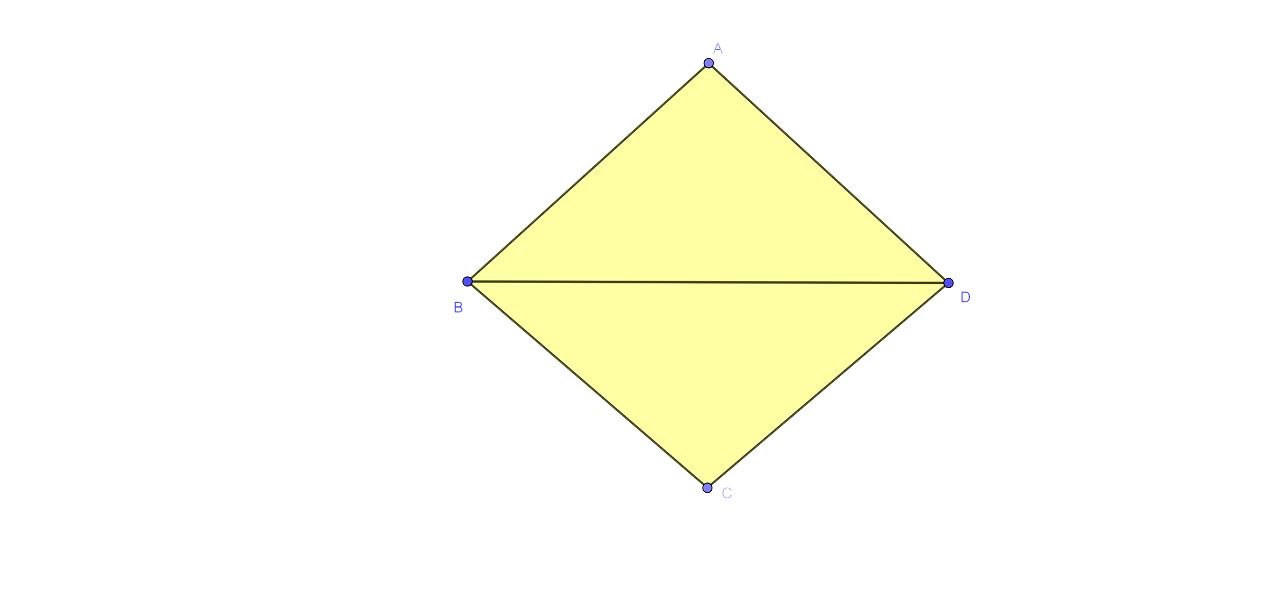
The diagonal BD of the rhombus will be the locus of the point in a rhombus ABCD that is equidistant from AB and BC.

ii)

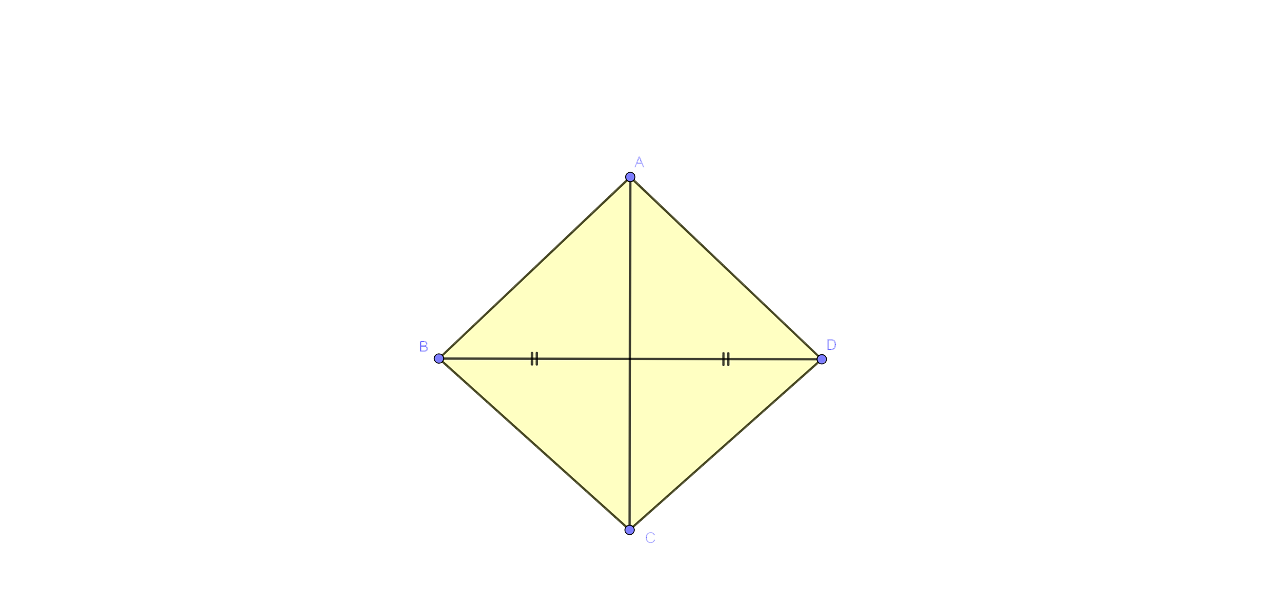
The diagonal AC is the locus of the point in a rhombus ABCD that is equidistant from B and D.

14. The speed of sound is 332 meters per second. A gun is fired. Describe the locus of all the people on the Earth’s surface, who hear the sound exactly one second later.

Ans: The circumference of a circle with a radius of 332 meters is the locus of all individuals on Earth's surface, and the center is the point where the gun is launched.

15. Describe:

i) The locus of points at distances less than 3 cm from a given point.

ii) The locus of points at distances greater than 4 cm from a given point.

iii) The locus of points at distances less than or equal to 2.5 cm from a given point.

iv) The locus of points at distances greater than or equal to 35 mm from a given point.

v) The locus of the centre of a given circle which rolls around the outside of a second circle and is always touching it.

vi) The locus of the centres of all circles that are tangent to both the arms of a given angle.

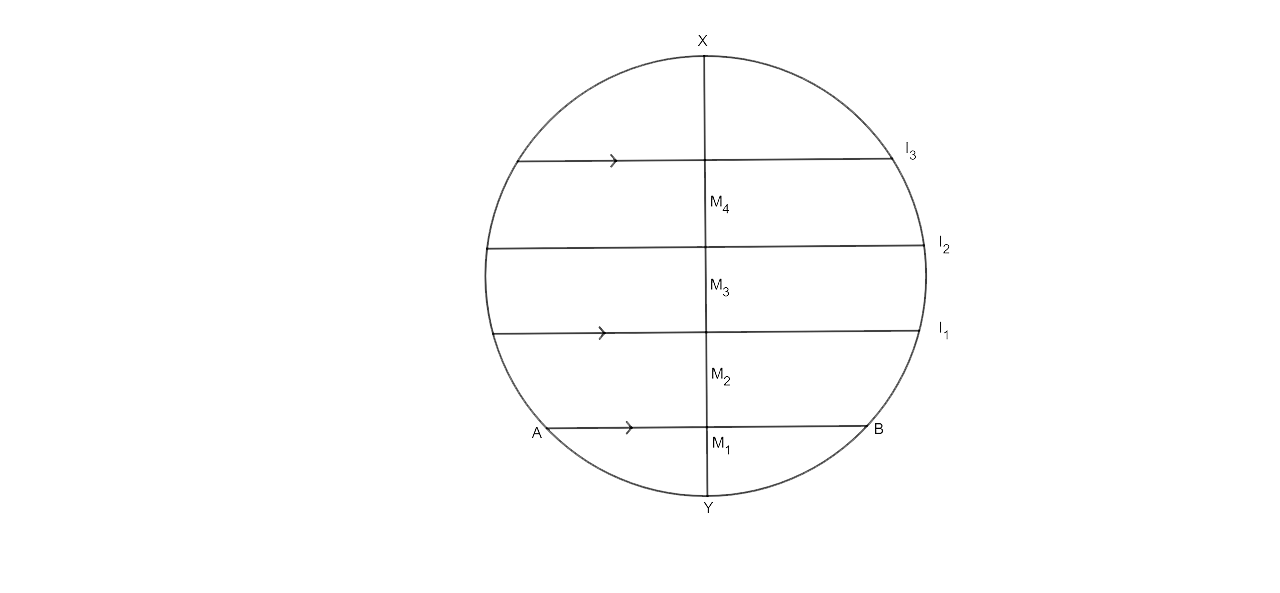
vii) The locus of the mid-points of all chords parallel to a given chord of a circle.

viii) The locus of points within a circle that are equidistant from the endpoints of a given chord.

Ans:

(i) The interior space of a circle with a radius of 3 cm and a fixed point that is given.

(ii) The area outside of a circle with a radius of 4 cm and a fixed point that is given.

(iii) The specified fixed point is the space within and circumference of a circle with a radius of 2.5 cm.

(iv) The supplied fixed point is the space outside and the circumference of a circle with a radius of 35 mm.

(v) The circumference of the circle that is concentric with the second circle and whose radius equals the total of the radii of the two circles.

vi)The bisector of a given angle is the locus of the centre of all circles whose tangents are the arms of that angle.

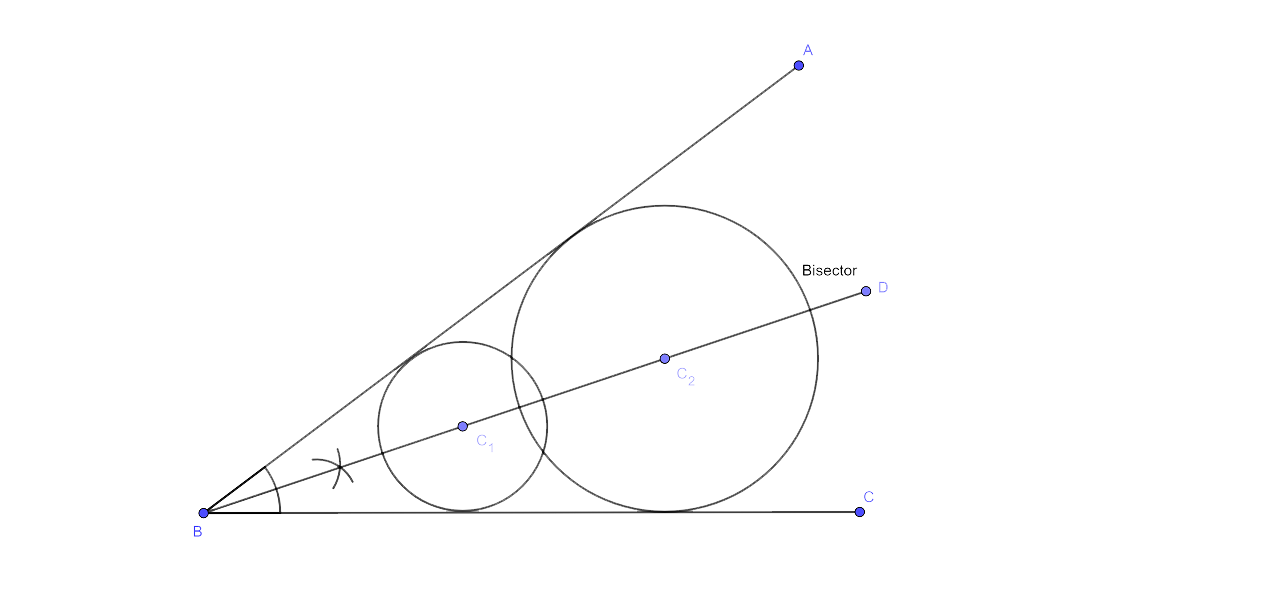
vii) The diameter perpendicular to the given chords is the locus of the mid-points of the chords that are parallel to the given chords.

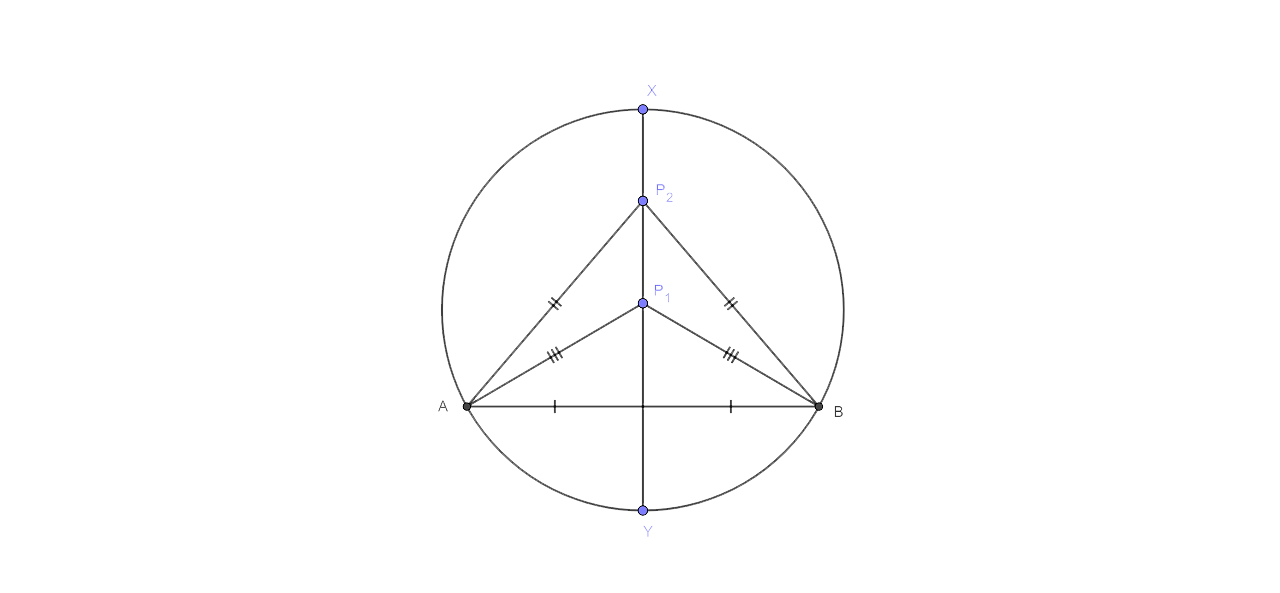
viii) The diameter of the perpendicular bisector of a certain chord is the locus of the points within a circle that is equidistant from the endpoints of the chord.

16. Sketch and describe the locus of the vertices of all triangles with a given base and a given altitude.

Ans: Steps for construction: 

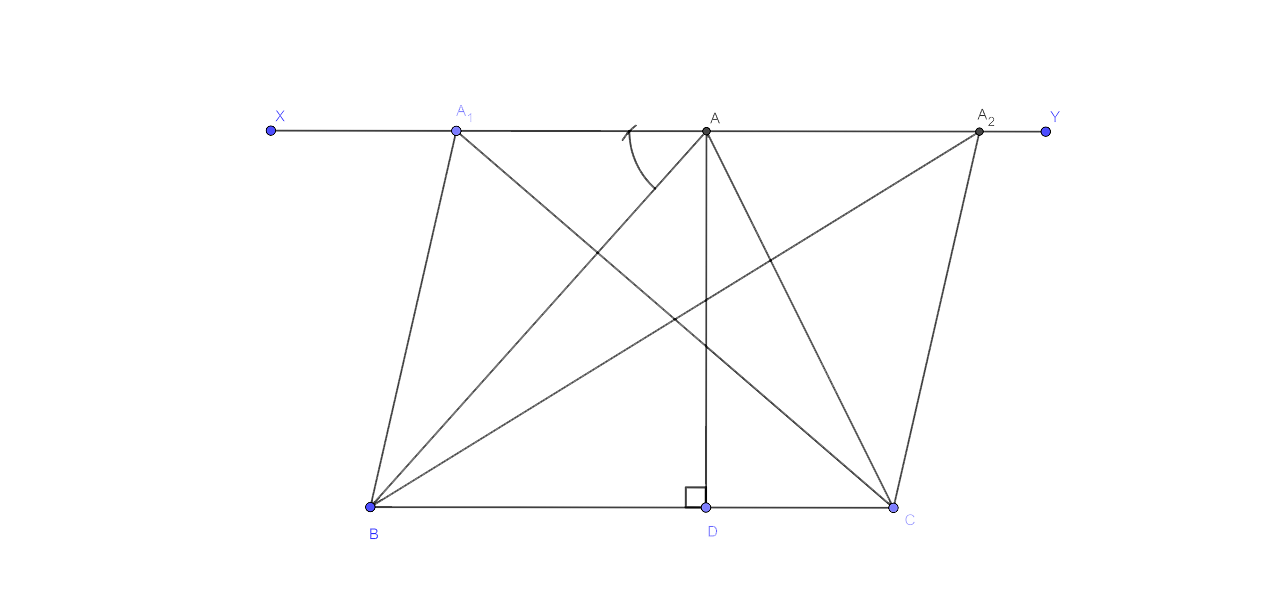
Draw a line XY which is parallel to the base BC from the vertex A. 

This line is the locus of vertex A. All the triangles have the base and the length equal to AD. 

17. In the given figure, obtain all the points equidistant from lines m and n ; and 2.5 cm from O.

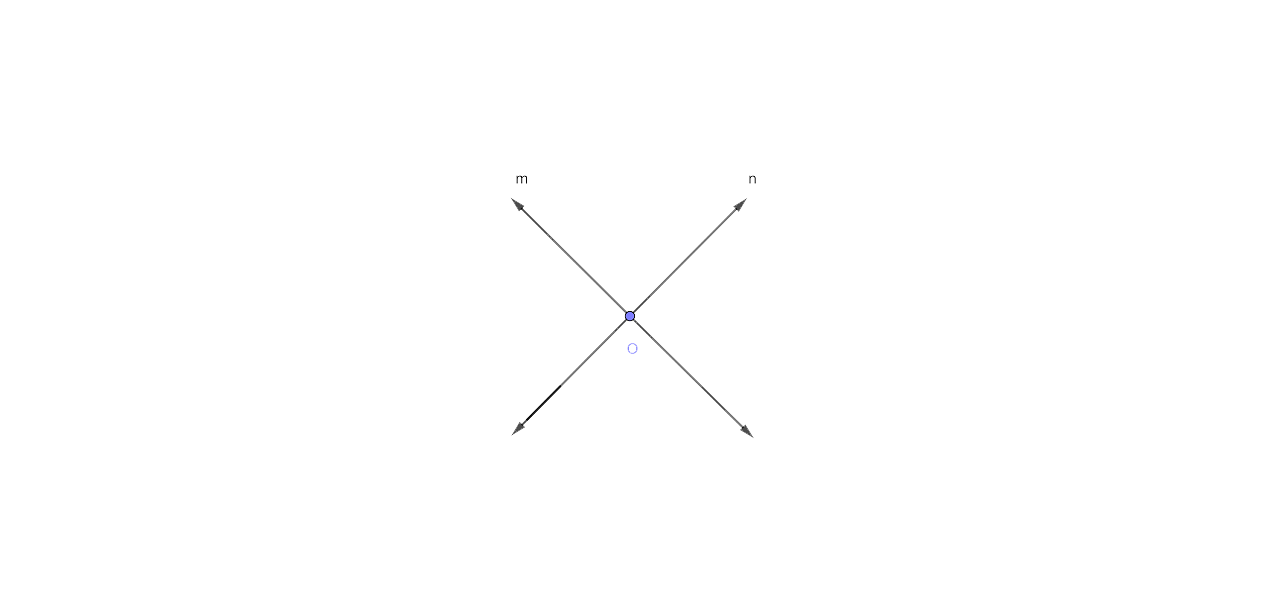
Ans:

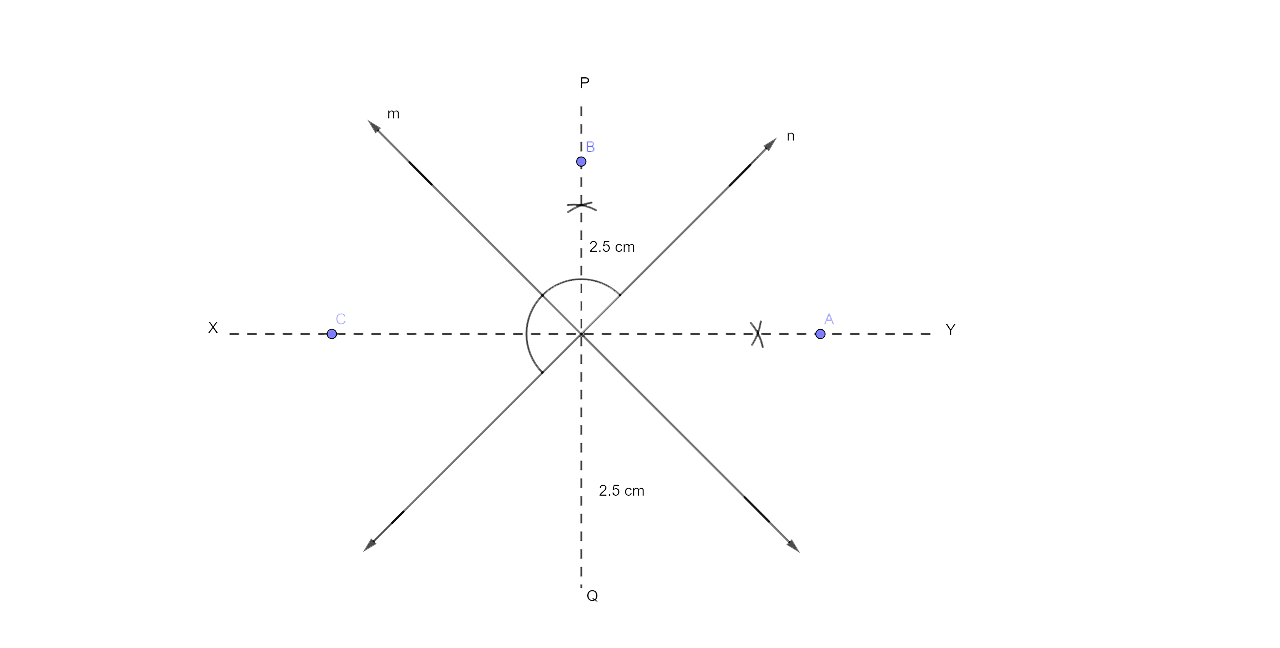
Draw the PQ and XY angle bisectors of the angles generated by the lines m and n. Now draw arcs with a radius of 2.5 cm from O, intersecting the angle bisectors at A, B, C, and D.

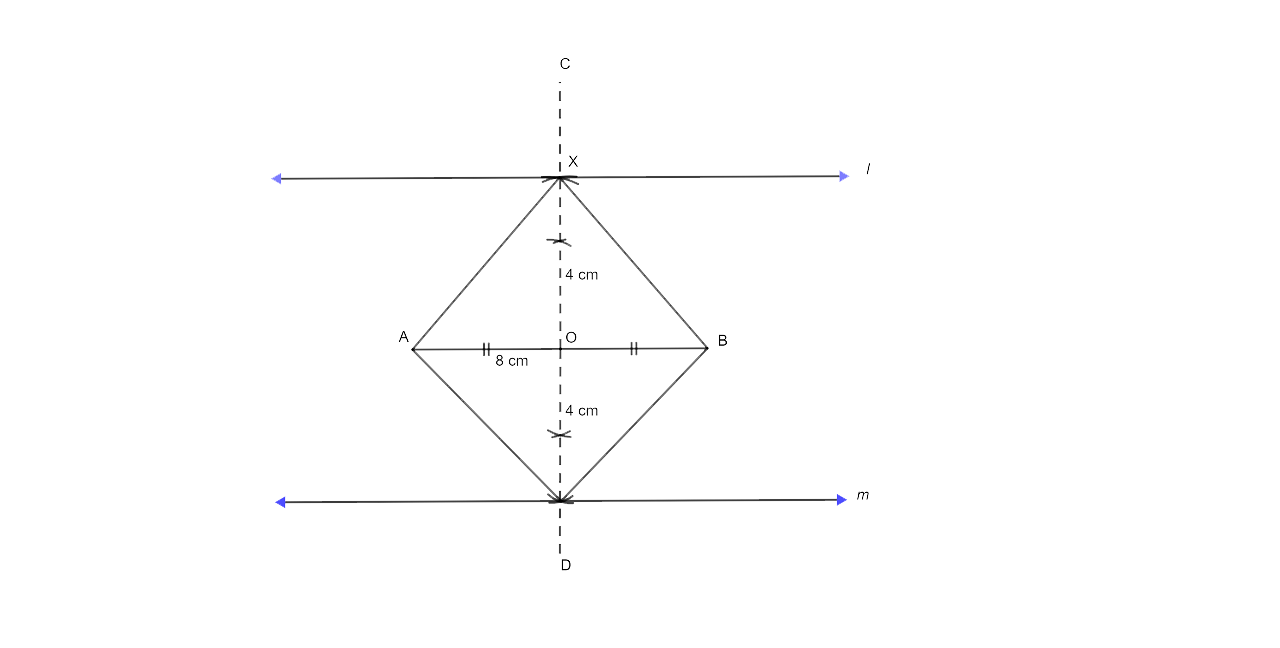
18. A straight line AB is 8 cm long. Draw and describe the locus of a point which is :

(i) always 4 cm from the line AB.

(ii) equidistant from A and B.

Mark the two points X and Y, which are 4 cm from AB and equidistant from A and B. Describe the figure AXBY.

Ans:

Steps for construction:

(i) Now the first step is to draw a line segment AB which is equal to 8 cm. 

(ii) Now draw two parallel lines l and m to AB at a distance of 4 cm. 

(iii) The third step is to draw a perpendicular bisector of AB which then intersects the parallel lines l and m at X and Y respectively then X and Y are the required points. 

(iv) The last step is to join AX.AY, BX and BY. The figure which is formed is a square as its diagonals are equal and intersect at 90°.

19. Angle ABC = 60° and BA = BC = 8 cm. The mid-points of BA and BC are M and N respectively. Draw and describe the locus of a point which is :

(i) equidistant from BA and BC.

(ii) 4 cm from M.

(iii) 4 cm from N.

Mark the point P, which is 4 cm from both M and N, and equidistant from BA and BC. Join MP and NP, and describe the figure BMPN.

Ans:

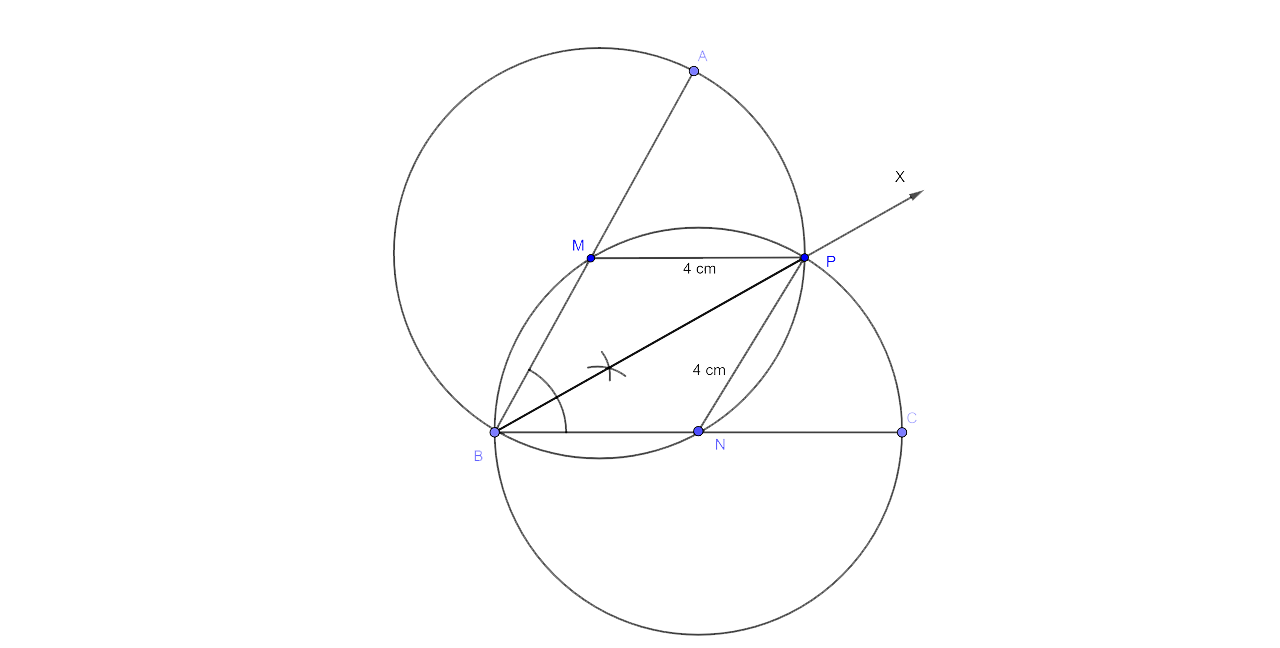
Steps for Construction

(i) The first step is to draw an angle of  60° with AB = BC = 8 cm.

(ii) Now draw the angle bisector BX of ∠ABC.

(iii) Draw four-centimeter-radius circles with the centres M and N intersecting at P. The necessary point is P.

(iv) The last step is to join MP, NP.

Therefore BMPN is a rhombus.

As MP = PM = BN = PN = 4 cm.

20. Draw a triangle ABC in which AB = 6 cm, BC = 4.5 cm and AC = 5 cm. Draw and label:

(i) the locus of the centers of all circles which touch AB and AC ;

(ii) the locus of the centers of all the circles of radius 2 cm which touch AB.

Hence, construct the circle of radius 2 cm which touches AB and AC.

Ans:

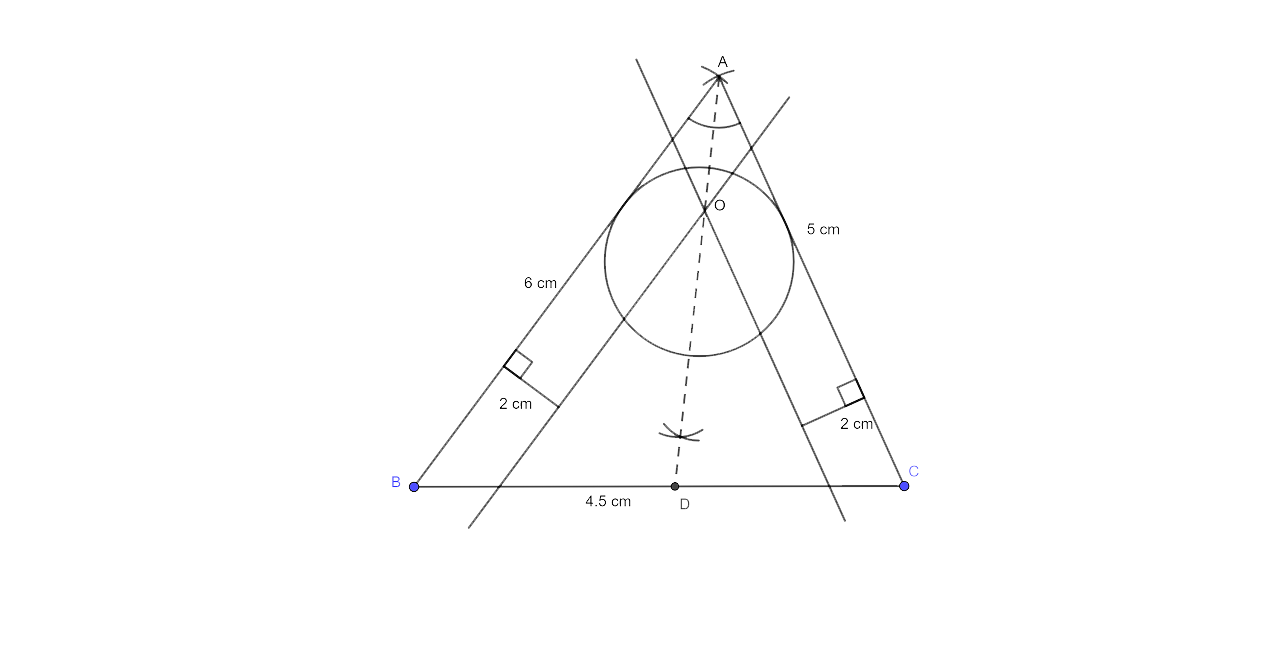
Step for Construction

(i) Now the first step is to draw a line segment BC = 4.5 cm

(ii) Draw two arcs intersecting at point A, one with a radius of 6 cm and the other with a radius of 5 cm.

(iii) Now the next step is to join AB and AC. Hence ABC is the required triangle. 

(iv) An angle bisector of ∠BAC should be drawn next. 

(v) At a distance of 2 cm, draw a line parallel to AC and AB that intersects AD at O.

(vi) The last step is to draw a circle of radius 2 cm with centre which touches AB and AC. 

21. Construct a triangle ABC, having given AB = 4.8 cm. AC = 4 cm and ∠A = 75°. Find a point P.

(i) inside the triangle ABC.

(ii) outside the triangle ABC.

equidistant from B and C; and at a distance of 1.2 cm from BC.

Ans:

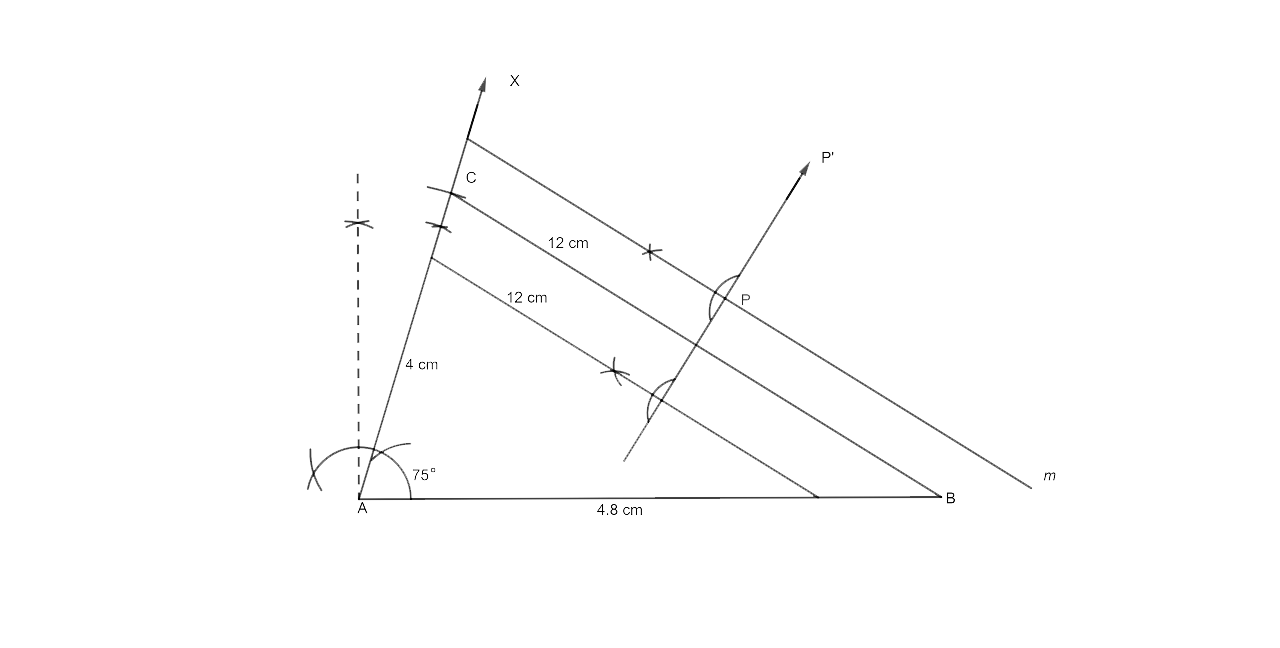
Steps for Construction

(i) Now the first step is to draw a line segment AB which is equal to 4.8 cm. 

(ii) The second step is at A draw a ray AX which will make an angle of 75°.

(iii) Now from AC cut off AC = 4cm. 

(iv) Now join BC. 

(v) Now we have to draw two lines l and m which are parallel to BC at a distance of 1.2 cm. 

(vi) Draw the perpendicular bisector of BC that passes through P and P and intersects l and m.

P and P1 are the needed points on the inside and outside of the triangle ABC, respectively.

22. Draw an angle ABC = 75°. Find a point P such that P is at a distance of 2 cm from AB and 1.5 cm from BC.

Ans:

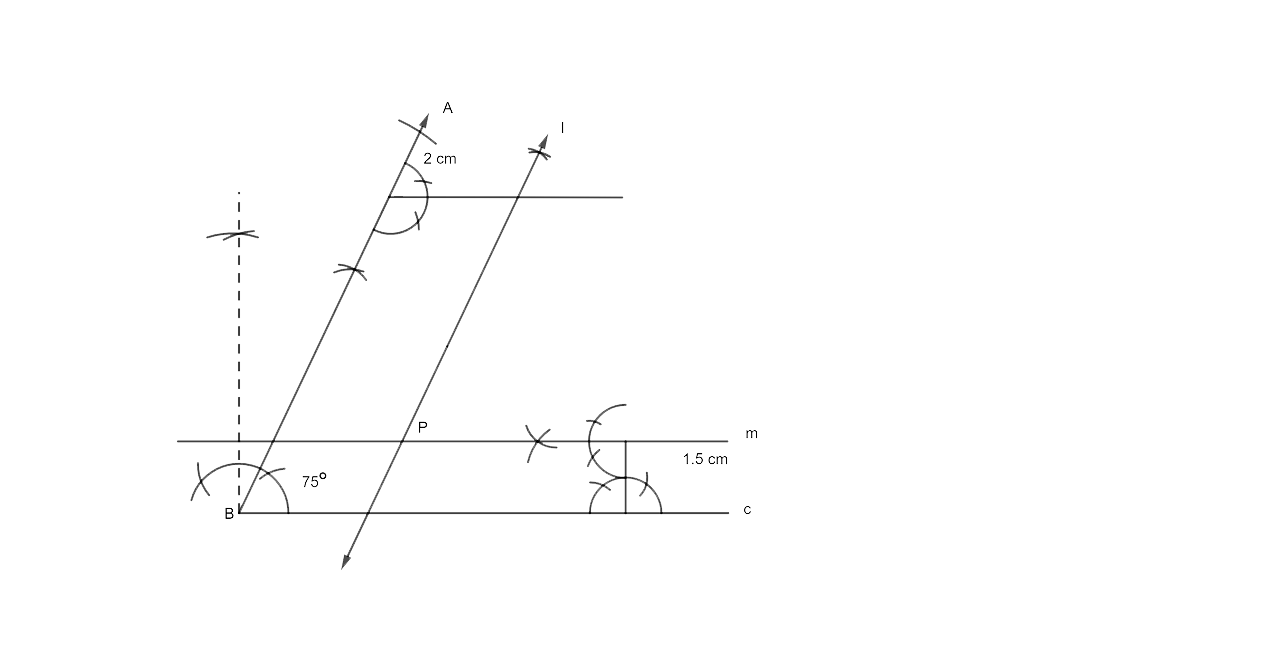
Steps for Reconstruction:

(i) Now the first step is to draw a ray BC.

(ii) At B we have to draw a ray BA which makes an angle of 75° with BC.

(iii) We have to then draw a line l parallel to AB at a distance of 2 cm. 

(iv) Draw another line m parallel to BC at a 1.5 cm distance, intersecting m at P, which is the needed point.

23. Construct a triangle ABC, with AB = 5.6 cm, AC = BC = 9.2 cm. Find the points equidistant from AB and AC; and also 2 cm from BC. Measure the distance between the two points obtained

Ans:

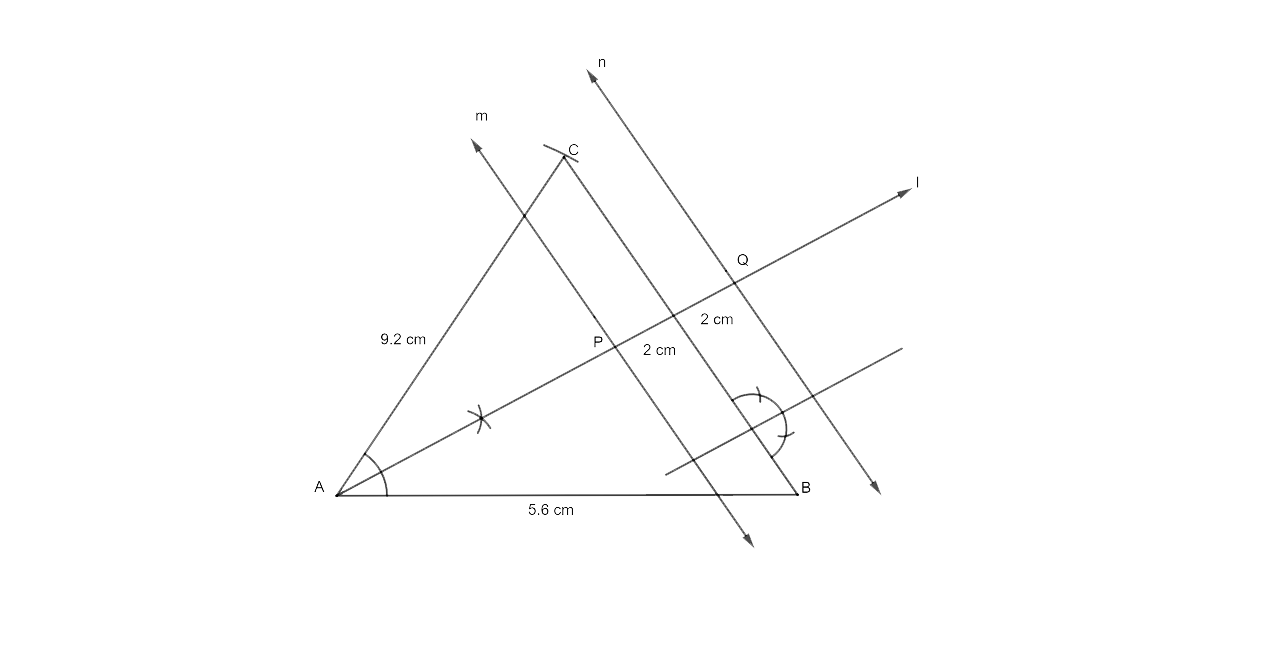
Steps for Construction

1. The first step is to draw a line segment AB = 5.6 cm.

2. Draw the arcs that meet at C using A and B as centers and a radius of 9.2 cm.

3. Now let us join CA and CB. 

4. The next step is to draw two lines m and n which are parallel to BC at a distance of 2cm each. 

5. Draw the  ∠CAB  angle bisector that crosses the parallel lines m and n at P and Q, respectively.

The required points are P and Q, which are equidistant from AB and AC.

The distance between P and Q is 4.3 cm when measured.

24. Construct a triangle ABC, with AB = 6 cm, AC = BC = 9 cm. Find a point 4 cm from A and equidistant from B and C.

Ans:

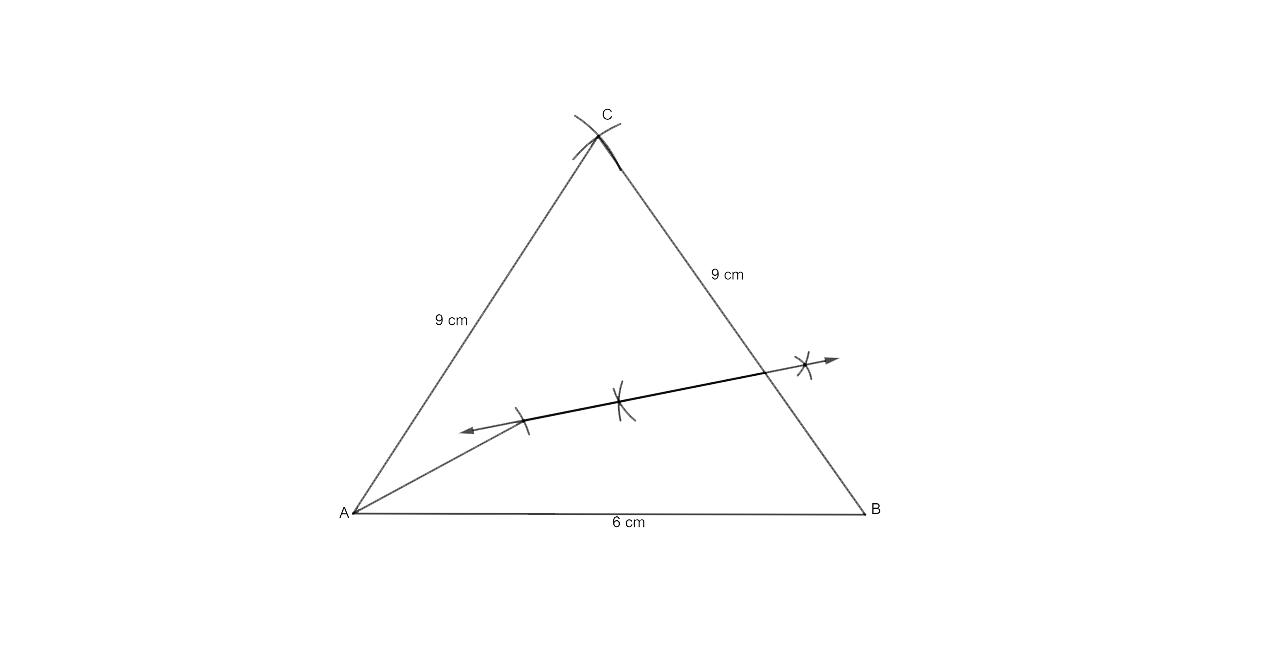
Steps for Construction

(i)Draw a line segment with the length AB = 6 cm.

ii) Draw two arcs that intersect at C, with A and B as centers and a radius of 9 cm.

iii)Now join AC and BC.

iv) Construct BC's perpendicular bisector.

v) Draw an arc with A as the center and a radius of 4 cm that intersects the perpendicular bisector of BC at P.

P is the essential point, which is 4 cm away from A and equidistant from B and C.

25. Ruler and compasses may be used in this question. All construction lines and arcs must be clearly shown and be of sufficient length and clarity to permit assessment.

(i) Construct a triangle ABC, in which BC = 6 cm, AB = 9 cm and angle ABC = 60°.

(ii) Construct the locus of all points inside triangle ABC, which are equidistant from B and C.

(iii) Construct the locus of the vertices of the triangles with BC as base and which are equal in area to triangle ABC.

(iv) Mark the point Q, in your construction, which would make A QBC equal in area to A ABC, and isosceles.

(v) Measure and record the length of CQ.

Ans:

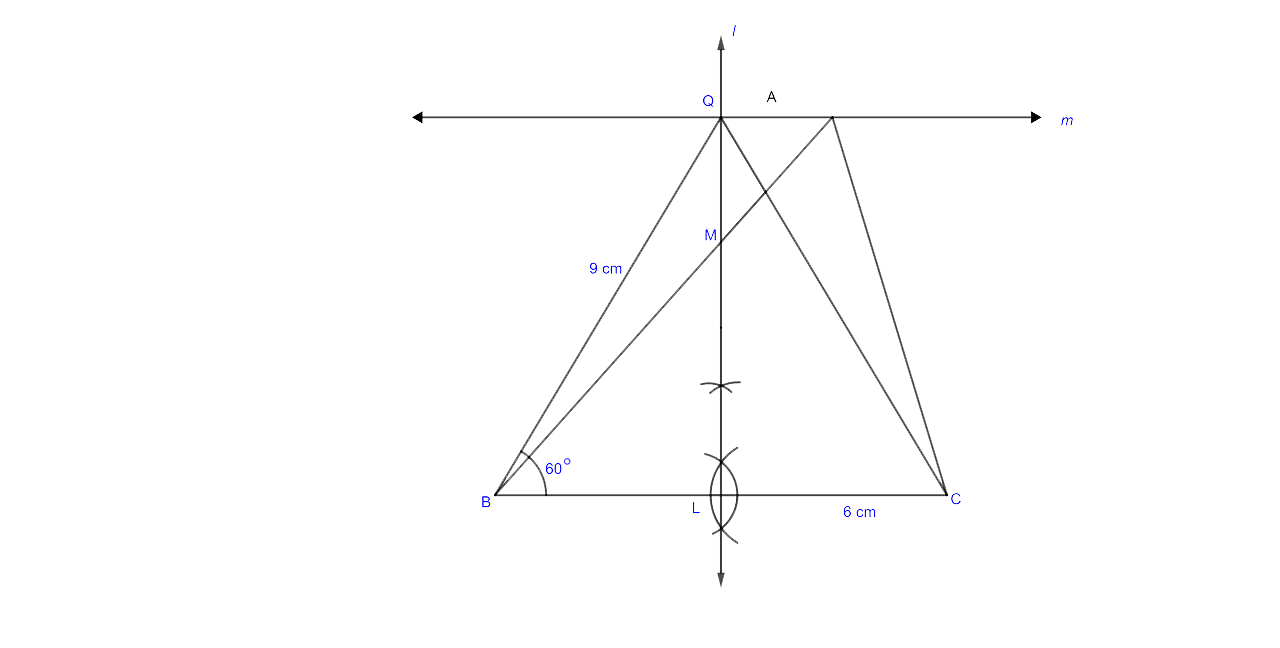
Steps for Construction

(i) The first step is to draw a line segment BC = 6 cm.

(ii) Now at B, let us draw a ray BX which makes an angle 60 degrees and cuts off BA=9 cm.

(iii) Now join AC and thus ABC is the required triangle. 

(iv) If you draw a perpendicular bisector from BC to BA in M, then any point on LM is equidistant from B and C.

(v) Draw a line m || BC through A.

(vi) At Q, the perpendicular bisector of BC intersects the parallel line m.

(vii) Then triangle QBC and triangle ABC have the same area. m is the point through which any triangle with base BC will have the same area as triangle ABC.

The length of CQ on measuring is 8.4 cm.

26. State the locus of a point in a rhombus ABCD, wi.rich is equidistant (i) from AB and AD; (ii) from the vertices A and C.

Ans:

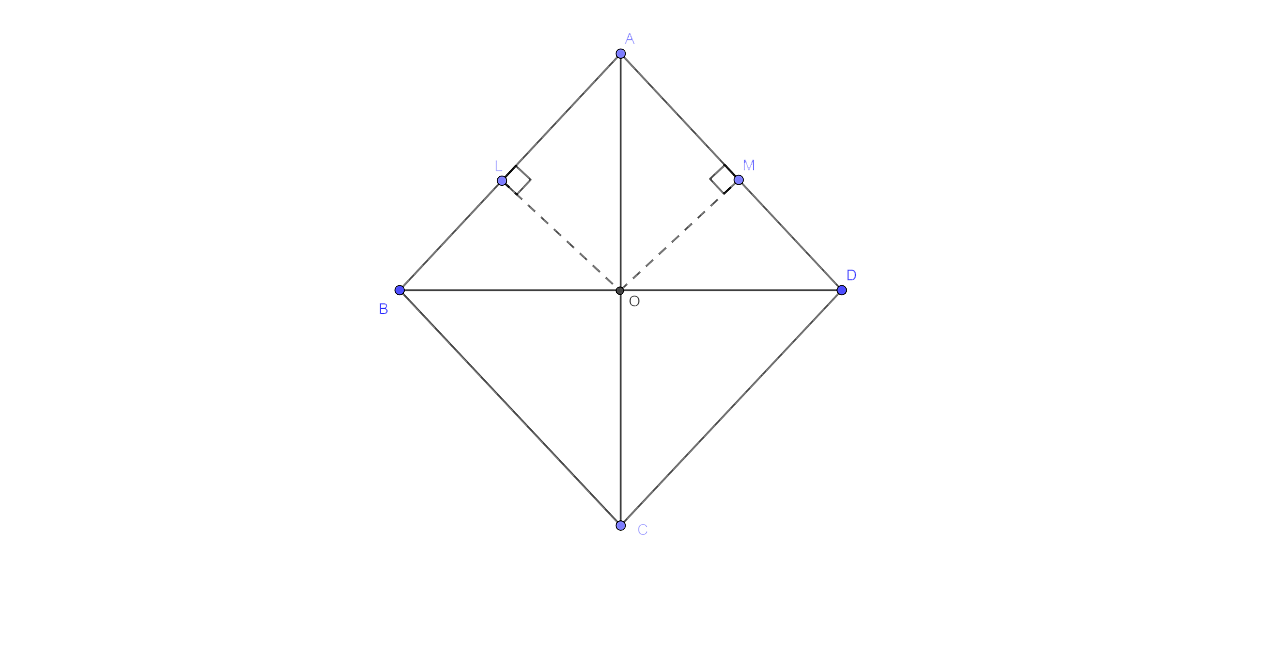
Now in the rhombus ABCD, let us draw the angle bisector of ∠A which meets in C

Now join BD, which intersects AC at O.The required locus is O.

Now from O, draw OL ⊥ AB and OM ⊥ AD.

Let us consider Δ AOL and Δ AOM

∠OLA = ∠OAM (As AC is the bisector of ∠A)

∠OLA = ∠ OMA (As each angle is equal to 90 degrees)

AO= AO (Common)

Hence by AAS Postulates, we can say that Δ AOL is similar to  Δ AOM. 

∴ Now O is equidistant from AB and AD.

Since diagonal AC and BD bisect each other at O at right angles.

∴ AO = OC

O is equidistant from A and C.

27. Use graph paper for this question. Take 2 cm = 1 unit on both the axes.

(i) Plot the points A (1,1), B (5,3), and C (2.7).

(ii) Construct the locus of points equidistant from A and B.

(iii) Construct the locus of points equidistant from ABandAC.

(iv) Locate the point P such that PA = PB and P is equidistant from AB and AC.

(v) Measure and record the length PA in cm.

Ans:

On the graph, connect the points A (1, 1), B (5, 3) and C (2, 7) to get AB, BC, and CA.

Draw the angle bisector of A and the perpendicular bisector of AB intersecting at P. P is the needed point, and it is located on AB's perpendicular bisector.

P is in the same plane as A and B.

P is equidistant from AB and AC because it is on the angle bisector of A.

Now when we measure the length of PA it is equal to 5.2 cm. 

28. Construct an isosceles triangle ABC such that AB = 6 cm, BC = AC = 4 cm. Biscet ∠C internally and mark a point P on this bisector such that CP = 5 cm. Find the points Q and R which are 5 cm from P and also 5 cm from the line AB.

Ans:

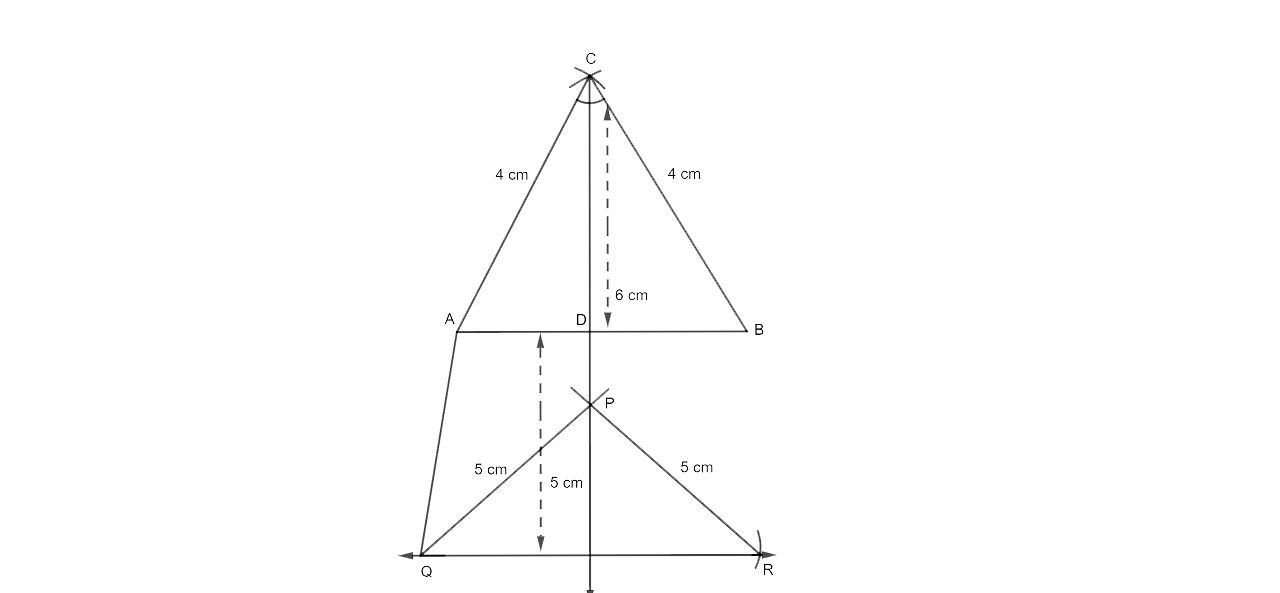
(i) Draw a line segment with the length AB = 6 cm.

ii) Draw two arcs with centres A and B and a radius of 4 cm, intersecting at C.

iii) Now join CA and CB.

iv) Cut off CP = 5 cm by drawing the angle bisector of angle C.

v) At a distance of 5 cm, a line m is drawn parallel to AB.

Draw arcs that meet the line m at Q and R, using P as the center and a radius of 5 cm.

vii) Now join PQ, PR, and AQ.

The essential points are Q and R.

29. Plot the points A (2,9), B (-1,3) and C (6,3) on a graph paper. On the same graph paper, draw the locus of point A so that the area of ΔABC remains the same as A moves.

Ans:

Let us first draw axis XOX’ and YOY’ on the graph paper. We have to then plot the points s A (2, 9), B (-1,3), and C (6, 3). Let us then join AB, BC, and CA which form a ΔABC.

From point A let us draw a line 1 which is parallel to BC on the x-axis. Thus the locus of point A is line 1. 

As l || BC and triangles on the same base BC and between the same parallel are equal in area.

Therefore we could say that l is the required locus of point A.

30.Construct a triangle BCP given BC = 5 cm, BP = 4 cm and ∠PBC = 45°.

(i) Complete the rectangle ABCD such that:

(a) P is equidistant from A B and BC.

(b) P is equidistant from C and D.

(ii) Measure and record the length of AB.

Ans:

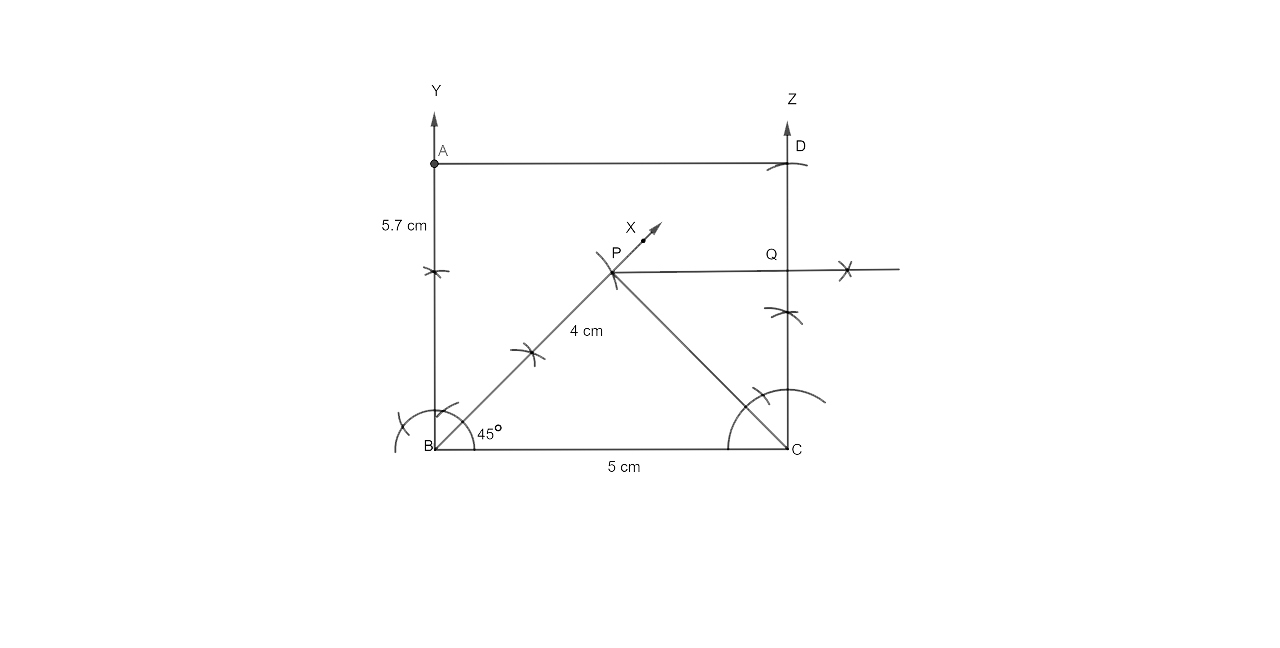
Step by step Procedure for Construction

(i) The first step is to draw a line segment BC = 5cm 

(ii) Now at B draw a ray making an angle of 45° and cut off BP = 4 cm.

(iii) Now Join PC.

(iv) v P is equidistant from AB and BC.

Therefore we could say that  P lies on the bisector of ∠ABC.

Now the next step is to draw a ray BY making an angle of 90°.

C and D are equidistant from P. P is located on CD's perpendicular bisector.

(v) Draw CZ BC from C, crossing the perpendicular bisector at Q.

(vi) Cut off QD = CQ, and cut off BA = CD from BP.

(vii) Now join AD.

The required rectangle is then ABCD. AB is approximately 5.7 cm in length when measured.

31. Use rulers and compasses only for the following questions. All construction lines and arcs must be clearly shown.

(i) Construct a ΔABC in which BC = 6.5 cm, ∠ABC = 60°, AB = 5 cm.

(ii) Construct the locus of points at a distance of 3.5 cm from A.

(iii) Construct the locus of points equidistant from AC and BC.

(iv) Mark 2 points X and Y which are at

A distance of 3.5 cm from A and also equidistant from AC and BC. Measure XY.

Ans:

(i) Steps by step procedure for reconstruction 

(1) Using a ruler, draw BC = 6.5 cm.

(2) Cut off BA = 5 cm at B by drawing CBP = 60° from BP.

(3) Join AC to complete the triangle.

(4) Draw a circle with A as the centre and a radius of 3.5 cm. At a distance of 3.5 cm from A, this circle is the needed locus of points.

(5) Draw the ACB bisector. The locus of points equidistant from AC and BC is this bisector.

(6) The circle is sliced at X and Y by the angle bisector shown above. These are the spots that are 3.5 cm apart from A, as well as equidistant from AC and BC. XY is 5.2 centimeters long, according to the measurements.

About the Syllabus

The syllabus of the ICSE Class 10 helps the students to know about the topics and the concepts and learn regularly. Along with the syllabus, they should know the marking scheme and the time they take to solve the problem.

To get a proper grip of the subject, students should solve the previous year papers which will help them to know if they are well prepared enough to complete it in the given time or not. Further, this will help in the enhancement of speed and rectify the mistakes. By solving the paper students will be aware of the pattern, weightage of marks, important topics and time duration.

Students should solve at least the previous 5-year question paper to improve the overall performance.

Practising the answers from Vedantu’s solutions will help the students to be familiar with all the variety of problems from the topic. Practising more and more of the problems helps to have a strong foundation and lead the students to score well in the exam.

The exercise and the practice questions will help the students to think and solve any type of problem in the exam. Practice is the key to success especially if it is Maths. More practising will enhance speed and accuracy.

A proper schedule and practice are all that is required to excel in the subject. Practice as much as possible with different problems. Remember the formulas and theorems well. Be positive and learn with focus and dedication.

Practice and only practice is the solution to ace the Maths exams.