Concise Mathematics Class 10 ICSE Solutions for Chapter 13 - Section and Mid-Point Formula

1. Calculate the coordinates of the point P which divides the line segment joining:

(i) A(1, 3) and B(5, 9) in the ratio 1 : 2

Ans: The given points are A = (1, 3), B = (5, 9) and the ratio m : n = 1 : 2

Let us consider the coordinates of the point P be (x, y)

Then, using section formula we have,

P(x, y) = $\left( \dfrac{m{{x}_{2}} + n{{x}_{1}}}{m + n},\dfrac{m{{y}_{2}} + n{{y}_{1}}}{m + n} \right) $

$x=\dfrac{m{{x}_{2}} + n{{x}_{1}}}{m + n}$ and $y=\dfrac{m{{y}_{2}} + n{{y}_{1}}}{m + n}$

$x=\dfrac{1 \times  5 + 2 \times  1}{1 + 2}$ and $y=\dfrac{1 \times  9 + 2 \times  3}{1 + 2}$

$x=\dfrac{5 + 2}{3}$ and $y=\dfrac{9 + 6}{3}$

$x=\dfrac{7}{3}$ and $y=\dfrac{15}{3}$

$x=\dfrac{7}{3}$ and $y=5$

Hence the coordinates of the point P is $\left( \dfrac{7}{3}, 5 \right)$

(ii) A(-4, 6) and B(3, -5) in the ratio 3 : 2

Ans: The given points are A = (-4, 6), B = (3, -5) and the ratio m : n = 3 : 2

Let us consider the coordinates of the point P be (x, y)

Then, using section formula we have

P(x, y) = $\left( \dfrac{m{{x}_{2}} + n{{x}_{1}}}{m + n},\dfrac{m{{y}_{2}} + n{{y}_{1}}}{m + n} \right) $

$x=\dfrac{m{{x}_{2}} + n{{x}_{1}}}{m + n}$ and $y=\dfrac{m{{y}_{2}} + n{{y}_{1}}}{m + n}$

$x=\dfrac{3 \times  3 + 2 \times  \left( -4 \right)}{3 + 2}$ and $y=\dfrac{3 \times  \left( -5 \right) + 2 \times  6}{3 + 2}$

$x=\dfrac{9 - 8}{5}$ and $y=\dfrac{-15 + 12}{5}$

$x=\dfrac{1}{5}$  and $y=\dfrac{-3}{5}$

Hence the coordinates of the point P is $\left( \dfrac{1}{5}, -\dfrac{3}{5} \right)$

2. In what ratio is the line joining (2. -3) and (5, 6) divided by the x-axis?

Ans: Let us consider the line joining the points are A(2, -3) and B(5, 6) which is dividing by the x-axis at point P(x, 0) in the ratio k : 1

Using section formula, we have

P(x, y) = $\left( \dfrac{m{{x}_{2}} + n{{x}_{1}}}{m + n},\dfrac{m{{y}_{2}} + n{{y}_{1}}}{m + n} \right) $

For x-coordinate,

 $y=\dfrac{m{{y}_{2}} + n{{y}_{1}}}{m + n}$

 $y=\dfrac{k \times  6 + 1 \times  \left( -3 \right)}{k + 1}$

 $0=\dfrac{6 k - 3}{k + 1}$

 $6k-3=0$

 $6k=3$

 $k=\dfrac{3}{6}$

 $k=\dfrac{1}{2}$

Thus the ratio will be 1 : 2

3. In what ratio is the line joining (2, -4) and (-3, 6) divided by the y-axis?

Ans: Let us consider the line joining the points are A(2, -4) and B(-3, 6) which is dividing by the y-axis at point P(0, y) in the ratio k : 1

Using section formula, we have

P(x, y) = $\left( \dfrac{m{{x}_{2}} + n{{x}_{1}}}{m + n},\dfrac{m{{y}_{2}} + n{{y}_{1}}}{m + n} \right) $

For y-coordinate,

 $x=\dfrac{m{{x}_{2}} + n{{x}_{1}}}{m + n}$

 $x=\dfrac{k \times  \left( -3 \right) + 1 \times  2}{k + 1}$

 $0=\dfrac{-3 k + 2}{k + 1}$

 $-3k+2=0$

 $-3k=-2$

 $k=\dfrac{2}{3}$

Thus the ratio will be 2 : 3

4. In what ratio does the point (1, a) divide the join of (-1, 4) and (4, -1)?

Also find the value of ‘a’.

Ans: Let the point (1, a) divides the given points (−1, 4) and (4, -1) in the ratio of k :1. Thus,

$x=\dfrac{m{{x}_{2}} + n{{x}_{1}}}{m + n}$

$1=\dfrac{4 \times  k + 1 \times  \left( -1 \right)}{k + 1}$  

$1=\dfrac{4 k - 1}{k + 1}$  

$k+1=4k-1$  

$4k-k=1+1$  

$3k=2$  

$k=\dfrac{2}{3}$  

Thus the ratio will be 2 : 3

Now let us consider the ratio m : n = 2 : 3 to find the value of ‘a’

 $y=\dfrac{m{{y}_{2}} + n{{y}_{1}}}{m + n}$

 $a=\dfrac{2 \times  \left( -1 \right) + 3 \times  4}{2 + 3}$

 $a=\dfrac{-2 + 12}{5}$

 $a=\dfrac{10}{5}$

 $a=2$

Hence the value of ‘a’ is 2

5. In what ratio does the point (a, 6) divide the join of (-4, 3) and (2, 8)? Also find the value of ‘a’.

Ans: Let the point (a, 6) divides the given points (−4, 3) and (2, 8) in the ratio of k :1.

 $y=\dfrac{m{{y}_{2}} + n{{y}_{1}}}{m + n}$

$6=\dfrac{k \times  8 + 1 \times  3}{k + 1}$  

$6=\dfrac{8 k + 3}{k + 1}$  

$6k+6=8k+3$  

$8k-6k=6-3$  

$2k=3$  

$k=\dfrac{3}{2}$  

Thus the ratio will be 3 : 2

Now let us consider the ratio m : n = 3 : 2 to find the value of ‘a’

 $x=\dfrac{m{{x}_{2}} + n{{x}_{1}}}{m + n}$

 $a=\dfrac{3 \times  2 + 2 \times  \left( -4 \right)}{3 + 2}$

 $a=\dfrac{6 - 8}{5}$

 $a=\dfrac{-2}{5}$

Hence the value of ‘a’ is $\dfrac{-2}{5}$

6. In what ratio is the join of (4, 3) and (2, -6) divided by the x-axis? Also find the coordinates of the point of intersection?

Ans: Let the ratio is k : 1 and the coordinate of the intersection with the x−axis is (x, 0). 

For y−coordinate.

 $y=\dfrac{m{{y}_{2}} + n{{y}_{1}}}{m + n}$

$0=\dfrac{k \times  \left( -6 \right) + 1 \times  3}{k + 1}$  

$0=\dfrac{-6 k + 3}{k + 1}$  

$0=-6k+3$  

$6k=3$  

 $k=\dfrac{3}{6}$

$k=\dfrac{1}{2}$  

Thus the ratio will be 1 : 2

Now let us consider the ratio m : n = 1 : 2

 $x=\dfrac{m{{x}_{2}} + n{{x}_{1}}}{m + n}$

 $x=\dfrac{1 \times  2 + 2 \times  4}{1 + 2}$

 $x=\dfrac{2 + 8}{3}$

 $x=\dfrac{10}{5}$

Hence the coordinate of intersection with x-axis is $\left( \dfrac{10}{5}, 0 \right)$

7. Find the ratio in which the join of (-4, 7) and (3, 0) is divided by the y-axis, Also find the coordinates of the point of intersection

Ans: Let the ratio is k :1 and the coordinate of the intersection with the y-axis is (0, y).

For x-coordinate.

 $x=\dfrac{m{{x}_{2}} + n{{x}_{1}}}{m + n}$

$0=\dfrac{k \times  3 + 1 \times  \left( -4 \right)}{k + 1}$  

$0=\dfrac{3 k - 4}{k + 1}$  

3$k-4=0$  

$3k=4$  

$k=\dfrac{4}{3}$  

Thus the ratio will be 4 : 3

Now let us consider the ratio m : n = 4 : 3

 $y=\dfrac{m{{y}_{2}} + n{{y}_{1}}}{m + n}$

 $y=\dfrac{4 \times  0 + 3 \times  7}{4 + 3}$

 $y=\dfrac{21}{7}$

 $y=3$

Hence, the coordinate of intersection with x-axis is (0, 3)

8. Point A, B, C and D divide the line segment joining the point (5, -10) and the origin in five equal parts. Find the coordinates of B and D.

Ans: Let the segment as shown below,

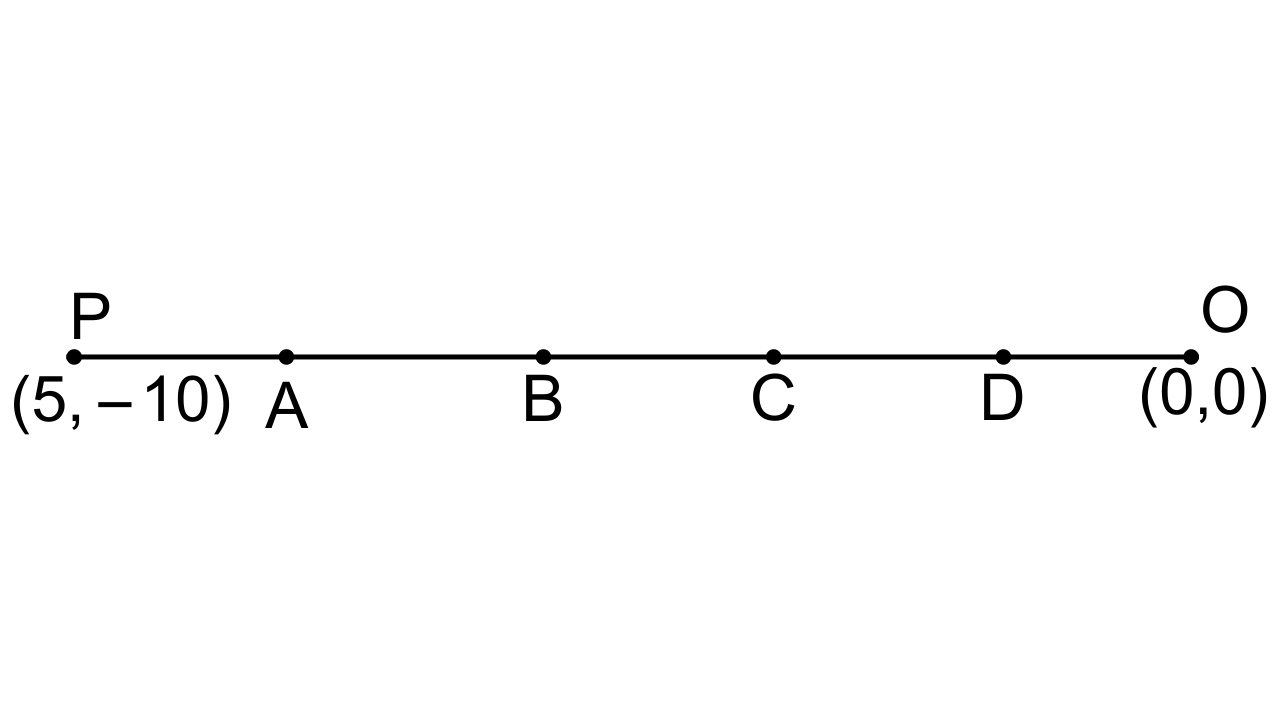
Here, points ABCD divides the segment in equal parts. 

The point B and point D will divide the line segment PQ in a ratio of 2 : 3 and 4 : 1.

Therefore,

 $B=\left( \dfrac{m{{x}_{2}} + n{{x}_{1}}}{m + n}, \dfrac{m{{y}_{2}} + n{{y}_{1}}}{m + n} \right)$

 $B=\left( \dfrac{2 \times  0 + 3 \times  5}{2 + 3}, \dfrac{2 \times  0 + 3 \times  \left( -10 \right)}{2 + 3} \right)$

 $B=\left( \dfrac{15}{5}, \dfrac{-30}{5} \right)$

 $B=\left( 3,-6 \right)$

And 

 $D=\left( \dfrac{m{{x}_{2}} + n{{x}_{1}}}{m + n}, \dfrac{m{{y}_{2}} + n{{y}_{1}}}{m + n} \right)$

 $D=\left( \dfrac{4 \times  0 + 1 \times  5}{4 + 1}, \dfrac{4 \times  0 + 1 \times  \left( -10 \right)}{4 + 1} \right)$

 $D=\left( \dfrac{4 \times  0 + 1 \times  5}{4 + 1}, \dfrac{4 \times  0 + 1 \times  \left( -10 \right)}{4 + 1} \right)$

 $D=\left( \dfrac{5}{5}, \dfrac{-10}{5} \right)$

 $D=\left( 1,-2 \right)$

9. The line joining the points (-3, -10) and B(-2, 6) is divided by the point P such that $\dfrac{PB}{AB}=\dfrac{1}{5}$. Find the coordinates of P.

Ans: The given points are A = (-3, -10) and B = (-2, 6)

Let the coordinates of the point P be (x, y)

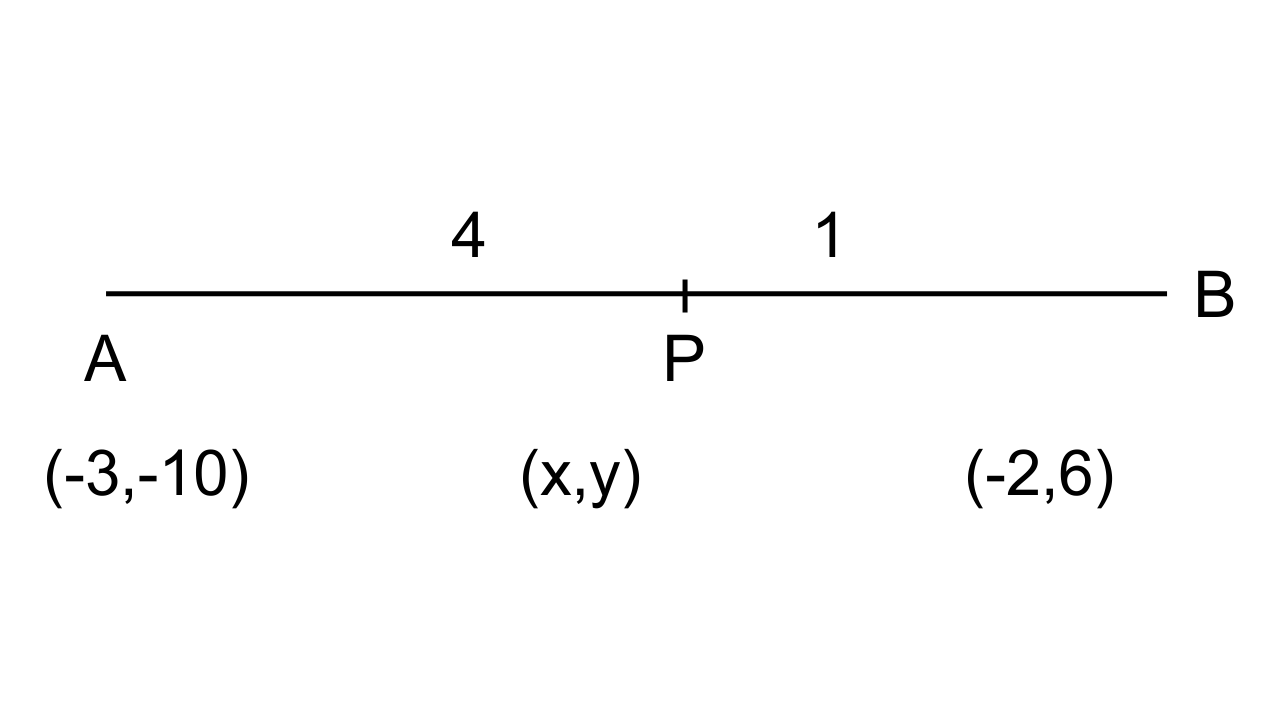
Given, PB : AB = 1 : 5

Therefore, PB : PA = 4 : 1

Thus Point P divides AB in a ratio 4 : 1.

Therefore the coordinate of point P will be,

 $P=\left( \dfrac{m{{x}_{2}} + n{{x}_{1}}}{m + n}, \dfrac{m{{y}_{2}} + n{{y}_{1}}}{m + n} \right)$

 $P=\left( \dfrac{4 \times  \left( -2 \right) + 1 \times  \left( -3 \right)}{4 + 1}, \dfrac{4 \times  6 + 1 \times  \left( -10 \right)}{4 + 1} \right)$

 $P=\left( \dfrac{-8 - 3}{5}, \dfrac{24 -10}{5} \right)$

 $P=\left( \dfrac{-11}{5}, \dfrac{14}{5} \right)$

10. P is a point on the line joining A(4, 3) and B(-2, 6) such that 5AP = 2BP. Find the coordinates of the point P.

Ans: The given points are A = (4, 3) and B = (-2, 6).

And, 5AP = 2BP

Thus $\dfrac{AP}{BP}=\dfrac{5}{2}$

Therefore, Point P divides AB in a ratio of 2 : 5.

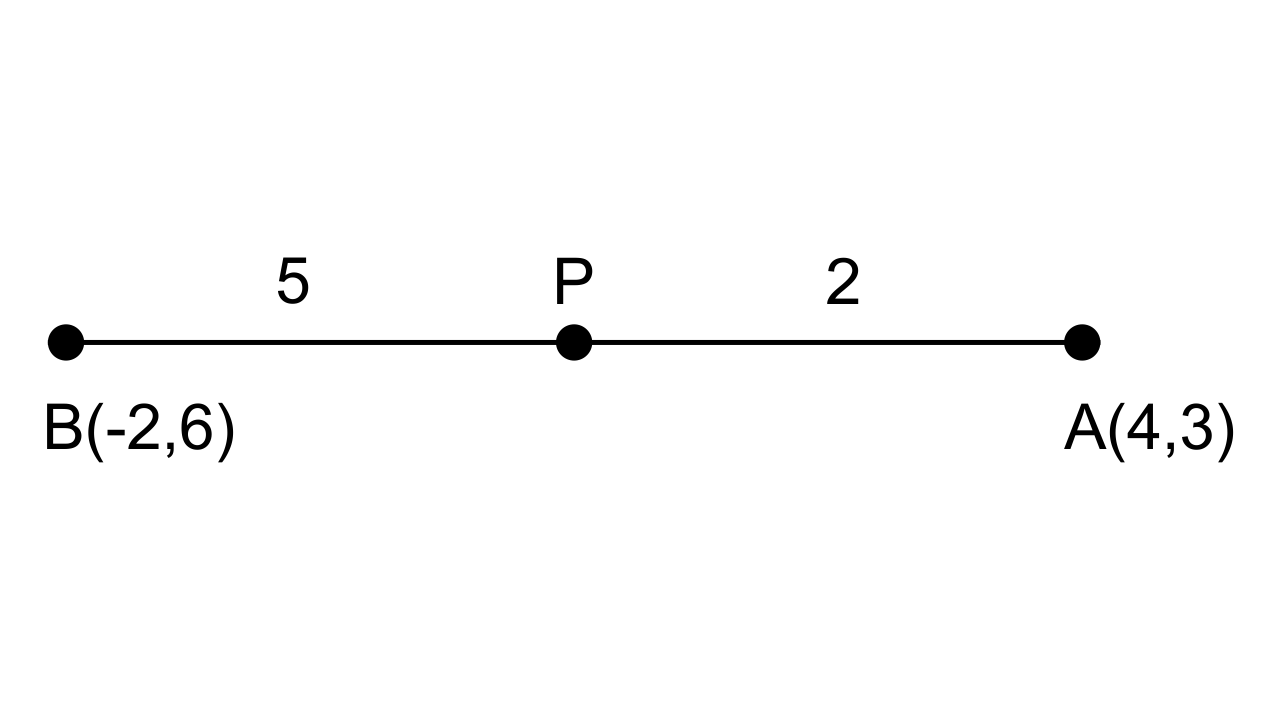
Therefore the coordinate of point P will be,

 $P=\left( \dfrac{m{{x}_{2}} + n{{x}_{1}}}{m + n}, \dfrac{m{{y}_{2}} + n{{y}_{1}}}{m + n} \right)$

 $P=\left( \dfrac{2 \times  \left( -2 \right) + 5 \times  4}{2 + 5}, \dfrac{2 \times  6 + 5 \times  3}{2 + 5} \right)$

 $P=\left( \dfrac{-4 + 20}{7}, \dfrac{12 + 15}{7} \right)$

 $P=\left( \dfrac{16}{7}, \dfrac{27}{7} \right)$

11. Calculate the ratio in which the line joining the points (-3, -1) and (5, 7) is divided by the line x = 2. Also, find the coordinates of the point of intersection.

Ans: Let the given points be A = (-3, -1) and B = (5, 7), and the ratio of the intersection is k : 1.

Thus, $x=\dfrac{m{{x}_{2}} + n{{x}_{1}}}{m + n}$

 $x=\dfrac{k \times  5 + 1 \times  \left( -3 \right)}{k + 1}$

 $2=\dfrac{5 k - 3}{k + 1}$

 $2k+2=5k-3$

 $5k-2k=2+3$

 $3k=5$

 $k=\dfrac{5}{3}$

Thus, the Point of intersection divides AB in a ratio of 5 : 3.

Now,

 $y=\dfrac{m{{y}_{2}} + n{{y}_{1}}}{m + n}$

 $y=\dfrac{5 \times  7 + 3 \times  \left( -1 \right)}{5 + 3}$

 $y=\dfrac{35 - 3}{8}$

 $y=\dfrac{32}{8}$

 $k=4$

Thus, the coordinate of the intersection is (2, 4).

12. Calculate the ratio in which the line joining A(6, 5) and B(4, -3) is divided by the line y = 2

Ans: The given points are A = (6, 5) and B = (4, -3)

Let the ratio of the intersection is k : 1. So,

 $y=\dfrac{m{{y}_{2}} + n{{y}_{1}}}{m + n}$

 $2=\dfrac{k \times  \left( -3 \right) + 1 \times  5}{k + 1}$

 $2=\dfrac{-3 k + 5}{k + 1}$

 $2k + 2= -3k+5$

 $2k+3k=5-2$

 $5k=3$

 $k=\dfrac{3}{5}$

Thus, the Point of intersection divides AB in a ratio of 3 : 5.

13. The point P(5, -4) divides the line segment AB, as shown in the figure, in the ratio 2 : 5. Find the coordinates of points A and B. Given AP is smaller than BP

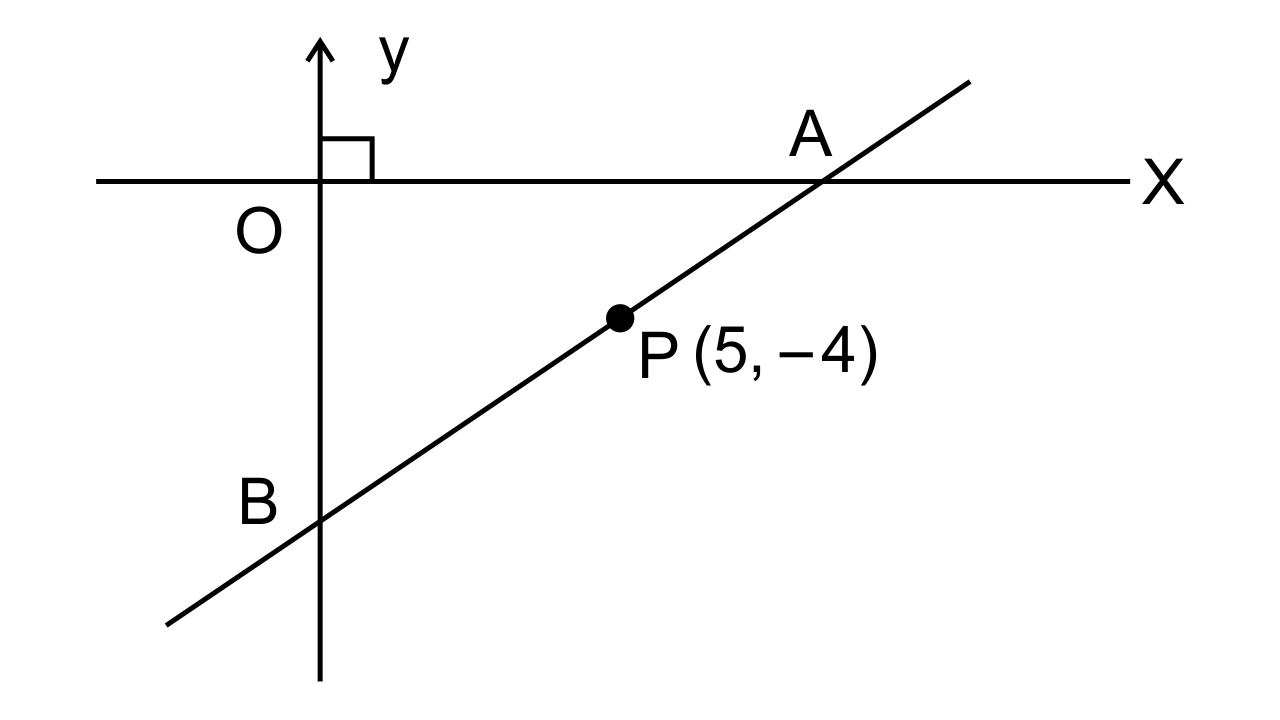
Ans: Let the coordinate of points A and B be (a, 0) and (0, b) respectively. Point P divides AB in the ratio of 2 : 5.

Therefore,

 $P=\left( \dfrac{m{{x}_{2}} + n{{x}_{1}}}{m + n}, \dfrac{m{{y}_{2}} + n{{y}_{1}}}{m + n} \right)$

 $\left( 5, -4 \right)=\left( \dfrac{2 \times  0 + 5 \times  a}{ 2 + 5}, \dfrac{2 \times  b + 5 \times  0}{2 + 5} \right)$

 $\left( 5, -4 \right)=\left( \dfrac{5 a}{7}, \dfrac{2 b}{7} \right)$

On comparing the sides, we get,

$\dfrac{5 a}{7}=5$  and  $\dfrac{2 b}{7}= -4$

$5a=35$  and  $2b= -28$

$a=\dfrac{35}{5}$  and  $b=\dfrac{-28}{2}$

Therefore, a = 7 and b = -14

Thus, the coordinates of A and B are (7, 0) and (0, -14) respectively.

14. Find the coordinates of the points of trisection of the line joining the points (-3, 0) and (6, 6)

Ans: Let the joining points be A = (-3, 0) and Q = (6, 6).

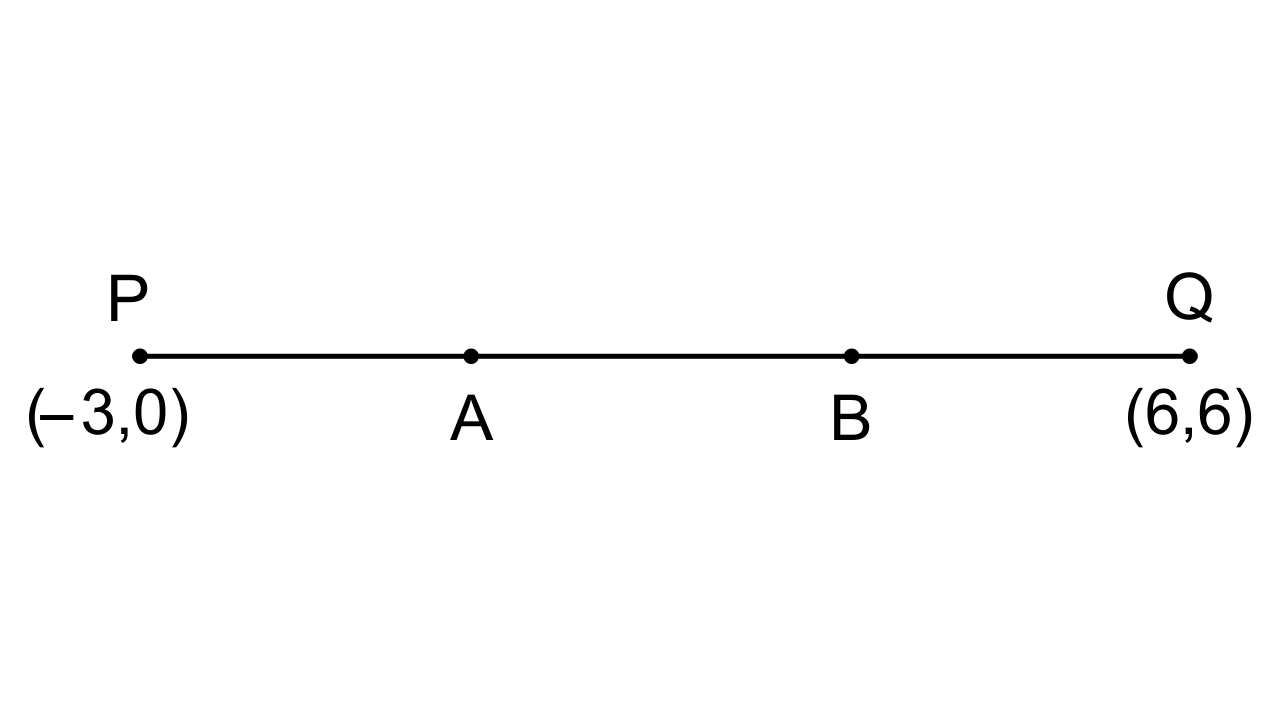
Here, points A and B trisect PQ.

Thus, PA : AQ = 1 : 2 and PB : BQ = 2 : 1.

Therefore, the coordinate of point A will be,

 $A=\left( \dfrac{m{{x}_{2}} + n{{x}_{1}}}{m + n}, \dfrac{m{{y}_{2}} + n{{y}_{1}}}{m + n} \right)$

 $A=\left( \dfrac{1 \times  6 + 2 \times  \left( -3 \right)}{1 + 2}, \dfrac{1 \times  6 + 2 \times  0}{1 + 2} \right)$

 $A=\left( \dfrac{6 - 6}{3}, \dfrac{6}{3} \right)$

 $A=\left( 0, 2 \right)$

And, the coordinate of point B will be,

 $B=\left( \dfrac{m{{x}_{2}} + n{{x}_{1}}}{m + n}, \dfrac{m{{y}_{2}} + n{{y}_{1}}}{m + n} \right)$

 $B=\left( \dfrac{2 \times  6 + 1 \times  \left( -3 \right)}{2 + 1}, \dfrac{2 \times  6 + 1 \times  0}{2 + 1} \right)$

 $B=\left( \dfrac{12 - 3}{3}, \dfrac{12}{3} \right)$

 $B=\left( \dfrac{9}{3}, 4 \right)$

 $A=\left( 3, 4 \right)$

15. Show that the line segment joining the points (-5, 8) and (10, -4) is trisected by the coordinate axis.

Ans: Let P = (-5, 8) and Q = (10, -4)

Let points A and B trisect PQ.

Therefore, PA : AQ = 1 : 2 and PB : BQ = 2 : 1

Thus, the coordinate of point A will be,

 $A=\left( \dfrac{m{{x}_{2}} + n{{x}_{1}}}{m + n}, \dfrac{m{{y}_{2}} + n{{y}_{1}}}{m + n} \right)$

 $A=\left( \dfrac{1 \times  10 + 2 \times  \left( -5 \right)}{1 + 2}, \dfrac{1 \times  \left( -4 \right) + 2 \times  8}{1 + 2} \right)$

 $A=\left( \dfrac{10 - 10}{3}, \dfrac{-4 + 16}{3} \right)$

 $A=\left( 0, \dfrac{12}{3} \right)$

 $A=\left( 0, 4 \right)$

And, the coordinate of point B will be,

 $B=\left( \dfrac{m{{x}_{2}} + n{{x}_{1}}}{m + n}, \dfrac{m{{y}_{2}} + n{{y}_{1}}}{m + n} \right)$

 $B=\left( \dfrac{2 \times  10 + 1 \times  \left( -5 \right)}{2 + 1}, \dfrac{2 \times  \left( -4 \right) + 1 \times  8}{2 + 1} \right)$

 $B=\left( \dfrac{20 - 5}{3}, \dfrac{-8 + 8}{3} \right)$

 $B=\left( \dfrac{15}{3}, 0 \right)$

 $B=\left( \dfrac{15}{3}, 0 \right)$

 $B=\left( 5, 0 \right)$

Here, points A and B are on the y and x axis. Thus, the coordinate axes trisect PQ.

Hence proved.

16. Show that A(3, -2) is a point of trisection of the line segment joining the points (2, 1) and (5, -8). Also, find the coordinates of the other points of trisection.

Ans: Let points A and B be the point of trisection of the line segment, say PQ.

Where P = (2, 1) and Q = (5, -8).

Therefore, PA : AQ = 1 : 2 and PB : BQ = 2 : 1

Thus, the coordinate of point A will be

 $A=\left( \dfrac{m{{x}_{2}} + n{{x}_{1}}}{m + n}, \dfrac{m{{y}_{2}} + n{{y}_{1}}}{m + n} \right)$

 $A=\left( \dfrac{1 \times  5 + 2 \times  2}{1 + 2}, \dfrac{1 \times  \left( -8 \right) + 2 \times  1}{1 + 2} \right)$

 $A=\left( \dfrac{5 + 4}{3}, \dfrac{-8 + 2}{3} \right)$

 $A=\left( \dfrac{9}{3}, \dfrac{-6}{3} \right)$

 $A=\left( 3, -2 \right)$

Hence proved that A(3, -2) is a point of trisection of PQ

And, the coordinate of point B will be,

 $B=\left( \dfrac{m{{x}_{2}} + n{{x}_{1}}}{m + n}, \dfrac{m{{y}_{2}} + n{{y}_{1}}}{m + n} \right)$

 $B=\left( \dfrac{2 \times  5 + 1 \times  2}{2 + 1}, \dfrac{2 \times  \left( -8 \right) + 1 \times  1}{2 + 1} \right)$

 $B=\left( \dfrac{10 + 2}{3}, \dfrac{-16 + 1}{3} \right)$

 $B=\left( \dfrac{12}{3}, \dfrac{-15}{3} \right)$

 $B=\left( 4, -5 \right)$

17. If A = (-4, 3) and B = (8, -6)

(i) Find the length of AB.

(ii) In what ratio is the line joining A and B divided by the x-axis?

Ans: Given that A = (-4, 3) and B = (8, -6)

(i) Using distance formula we can find length of AB, So

 $AB=\sqrt{{{({{x}_{2}}-{{x}_{1}})}^{2}}+{{({{y}_{2}}-{{y}_{1}})}^{2}}}$

 $AB=\sqrt{{{(8-\left( -4 \right))}^{2}}+{{(\left( -6 \right)-3)}^{2}}}$

 $AB=\sqrt{{{(12)}^{2}}+{{(9)}^{2}}}$

 $AB=\sqrt{144+81}$

 $AB=\sqrt{225}$

 $AB=15 units$

(ii) Let (x, 0) be the point of intersection with the x-axis, and k : 1 be the ratio in which the point of intersection divides the line joining points A and B.

Therefore,

 $y=\dfrac{m{{y}_{2}} + n{{y}_{1}}}{m + n}$

 $0=\dfrac{k \times  \left( -6 \right) + 1 \times  3}{k + 1}$

 $0=\dfrac{-6 k + 3}{k + 1}$

 $-6 k + 3=0$

 $-6 k= -3$

 $k=\dfrac{-3}{-6}$

 $k=\dfrac{1}{2}$

18. The line segment joining the points M(5, 7) and N(-3, 2) is intersected by the y-axis at point L. Write down the abscissa of L. Hence, find the ratio in which L divides MN. Also find the coordinates of L.

Ans: Given M = (5, 7) and N = (-3, 2)

The line segment MN intersects the y-axis at point L. Hence, the abscissa of L will be zero.

Let point L divides MN in k : 1.

Therefore,

 $x=\dfrac{m{{x}_{2}} + n{{x}_{1}}}{m + n}$

$0=\dfrac{k \times  \left( -3 \right) + 1 \times  5}{k + 1}$  

$0=\dfrac{-3 k + 5}{k + 1}$  

$-3k+5=0$  

$-3k= -5$  

$k=\dfrac{-5}{-3}=\dfrac{5}{3}$  

Thus the ratio is 5 : 3

Now let us consider the ratio m : n = 4 : 3, So

 $y=\dfrac{m{{y}_{2}} + n{{y}_{1}}}{m + n}$

 $y=\dfrac{5 \times  2 + 3 \times  7}{5 + 3}$

 $y=\dfrac{10 + 21}{8}$

 $y=\dfrac{31}{8}$

Thus the coordinates of L is $\left( 0, \dfrac{31}{8} \right)$

19. A (2, 5), B (-1, 2) and C (5, 8) are the coordinates of the vertices of the triangle ABC. Points P and Q lie on AB and AC respectively, such that: 

AP : PB = AQ : QC = 1 : 2. 

(i) Calculate the coordinates of P and Q. 

(ii) Show that : PQ = $\dfrac{1}{3}$ BC. 

Ans: The given vertices of triangle are A = (2, 5), B = (-1, 2) and C = (5, 8)

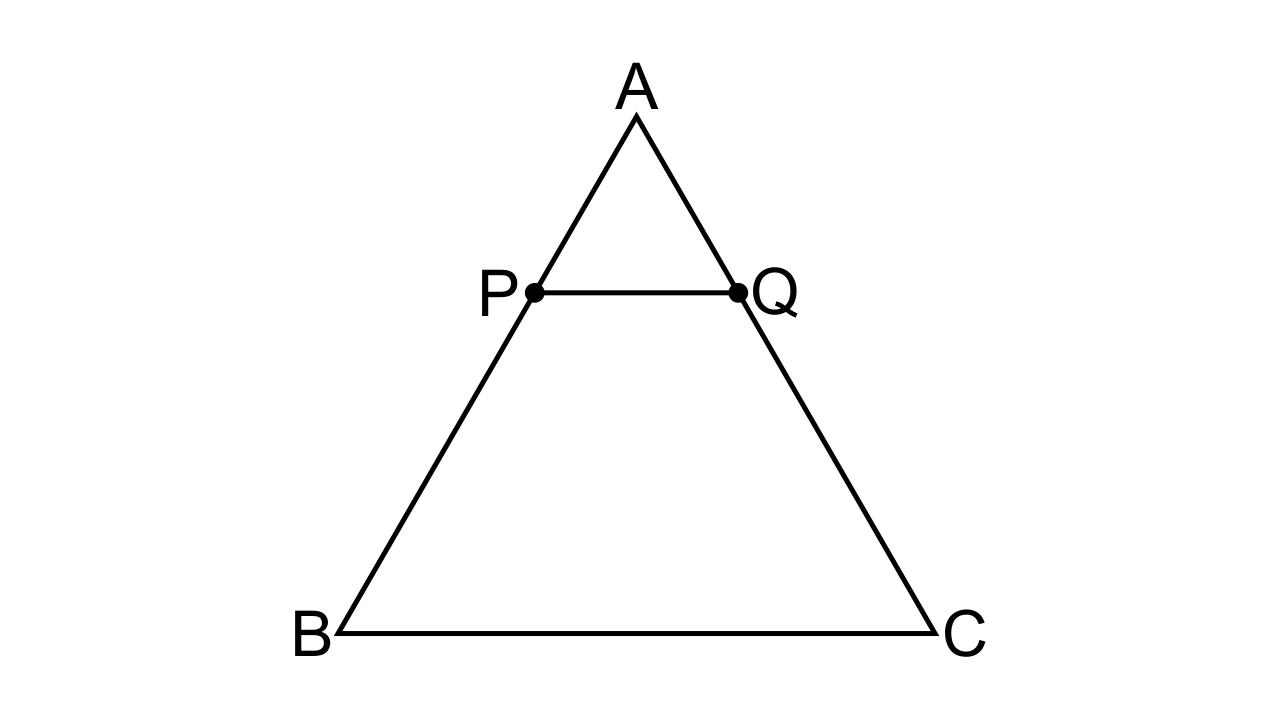
(i) Here, AP : PB = AQ : QC = 1 : 2.

So, The coordinate of P will be,

 $P=\left( \dfrac{m{{x}_{2}} + n{{x}_{1}}}{m + n}, \dfrac{m{{y}_{2}} + n{{y}_{1}}}{m + n} \right)$

 $P=\left( \dfrac{1 \times  \left( -1 \right) + 2 \times  2}{1 + 2}, \dfrac{1 \times  2 + 2 \times  5}{1 + 2} \right)$

 $P=\left( \dfrac{-1 + 4}{3}, \dfrac{2 + 10}{3} \right)$

 $P=\left( \dfrac{3}{3}, \dfrac{12}{3} \right)$

 $P=\left( 1, 4 \right)$

And, the coordinate of Q will be

 $Q=\left( \dfrac{m{{x}_{2}} + n{{x}_{1}}}{m + n}, \dfrac{m{{y}_{2}} + n{{y}_{1}}}{m + n} \right)$

 $Q=\left( \dfrac{1 \times  5 + 2 \times  2}{1 + 2}, \dfrac{1 \times  8 + 2 \times  5}{1 + 2} \right)$

 $Q=\left( \dfrac{5 + 4}{3}, \dfrac{8 + 10}{3} \right)$

 $Q=\left( \dfrac{9}{3}, \dfrac{18}{3} \right)$

 $Q=\left( 3, 6 \right)$

(ii) We have to show that PQ = $\dfrac{1}{3}$ BC.

Coordinates of P and Q are (1, 4) and (3, 6)

Using distance formula,

 $PQ=\sqrt{{{({{x}_{2}}-{{x}_{1}})}^{2}}+{{({{y}_{2}}-{{y}_{1}})}^{2}}}$

 $PQ=\sqrt{{{(3-1)}^{2}}+{{(6-4)}^{2}}}$

 $PQ=\sqrt{{{2}^{2}}+{{2}^{2}}}$

 $PQ=2\sqrt{2}$

And,

 $BC=\sqrt{{{({{x}_{2}}-{{x}_{1}})}^{2}}+{{({{y}_{2}}-{{y}_{1}})}^{2}}}$

 $BC=\sqrt{{{(5-\left( -1 \right))}^{2}}+{{(8-2)}^{2}}}$

 $BC=\sqrt{{{6}^{2}}+{{6}^{2}}}$

 $BC=6\sqrt{2}$

Hence,

 $\dfrac{PQ}{BC}=\dfrac{2\sqrt{2}}{6\sqrt{2}}$

 $\dfrac{PQ}{BC}=\dfrac{2}{6}$

 $\dfrac{PQ}{BC}=\dfrac{1}{3}$

Therefore PQ = $\dfrac{1}{3}$BC

Hence Proved

20. If A (-3, 4), B (3, -1) and C (-2, 4) are the vertices of a triangle ABC. Find the length of line segment AP, where point P lies inside BC, such that BP : PC = 2 : 3. 

Ans: Given A = (-3, 4), B = (3, -1) and C = (-2, 4)

We have to find the coordinates of P, Also we know that P is a point which lies inside BC which divides BC in the ratio 2 : 3

B(3, -1) and C(-2, 4) are given now using section formula we can find P(x, y)

 $P\left( x, y \right)=\left( \dfrac{m{{x}_{2}} + n{{x}_{1}}}{m + n}, \dfrac{m{{y}_{2}} + n{{y}_{1}}}{m + n} \right)$

 $P\left( x, y \right)=\left( \dfrac{2 \times  \left( -2 \right) + 3 \times  3}{2 + 3}, \dfrac{2 \times  4 + 3 \times  \left( -1 \right)}{2 + 3} \right)$

 $P\left( x, y \right)=\left( \dfrac{-4 + 9}{5}, \dfrac{8 - 3}{5} \right)$

 $P\left( x, y \right)=\left( \dfrac{5}{5}, \dfrac{5}{5} \right)$

 $P\left( x, y \right)=\left( 1, 1 \right)$

Now that we have A(- 3, 4) and P(1,1), we can use these to find the length of AP using distance formula,

 $AP=\sqrt{{{({{x}_{2}}-{{x}_{1}})}^{2}}+{{({{y}_{2}}-{{y}_{1}})}^{2}}}$

 $AP=\sqrt{{{(1-\left( -3 \right))}^{2}}+{{(1-4)}^{2}}}$

 $AP=\sqrt{{{4}^{2}}+{{(-3)}^{2}}}$

 $AP=\sqrt{16+9}$

 $AP=\sqrt{25}$

 $AP=5 units$

21. The line segment joining A(2, 3) and B(6, -5) is intercepted by x-axis at the point K. Write down the ordinate of the point K. Hence, find the ratio in which K divides AB. Also, find the coordinates of the point K. 

Ans: Given that A = (2, 3) and B = (6, -5)

The line segment AB intersects the x-axis at point K.

Hence, the ordinate of K will be zero.

Now, let point K divides AB in the ratio k : 1.

Therefore,

 $y=\dfrac{m{{y}_{2}} + n{{y}_{1}}}{m + n}$

 $0=\dfrac{k \times  \left( -5 \right) + 1 \times  3}{k + 1}$

 $0=\dfrac{-5 k + 3}{k + 1}$

 $-5k+3=0$

 $-5k= -3$

 $k=\dfrac{3}{5}$

Thus the ratio is 3 : 5. Now,

 $x=\dfrac{m{{x}_{2}} + n{{x}_{1}}}{m + n}$

 $x=\dfrac{3 \times  6 + 5 \times  2}{3 + 5}$

 $x=\dfrac{18 + 10}{8}$

 $x=\dfrac{28}{8}$

 $x=\dfrac{7}{2}$

Thus the coordinates of L is $\left( \dfrac{7}{2}, 0 \right)$.

22. The line segment joining A(4, 7) and B(-6, -2) is intercepted by the y-axis at the point K. Write down the abscissa of the point K. Hence, find the ratio in which K divides AB. Also, find the coordinates of the point K. 

Ans: Given that A = (4, 7) and B = (-6, -2)

The line segment AB intersects the y-axis at point K.

Hence, the abscissa of K will be zero.

Now, let point K divides AB in k : 1.

Therefore,

 $x=\dfrac{m{{x}_{2}} + n{{x}_{1}}}{m + n}$

 $0=\dfrac{k \times  \left( -6 \right) + 1 \times  4}{k + 1}$

 $0=\dfrac{-6 k + 4}{k + 1}$

 $-6k+4=0$

 $-6k= -4$

 $k=\dfrac{4}{6}$

 $k=\dfrac{2}{3}$

Thus the ratio is 2 : 3. Now,

 $y=\dfrac{m{{y}_{2}} + n{{y}_{1}}}{m + n}$

 $y=\dfrac{2 \times  \left( -2 \right) + 3 \times  7}{2 + 3}$

 $y=\dfrac{-4 + 21}{5}$

 $y=\dfrac{17}{5}$

Thus the coordinates of L is $\left( 0, \dfrac{17}{5} \right)$.

23. The line joining P(-4, 5) and Q(3. 2) intersect the y-axis at point R. PM and QN are perpendiculars from P and Q on the x-axis. Find

(i) the ratio PR : RQ. 

(ii) the coordinates of R. 

(iii) the area of the quadrilateral PMNQ

Ans: (i) Given that P = (-4, 5) and Q = (3. 2), where PQ intersects the y-axis at point R.

So let us consider the point R = (0, y) and R divides PQ in the ratio k :1.

 $x=\dfrac{m{{x}_{2}} + n{{x}_{1}}}{m + n}$

 $0=\dfrac{k \times  3 + 1 \times  \left( -4 \right)}{k + 1}$

 $3k-4=0$

 $3k= 4$

 $k=\dfrac{4}{3}$

Thus the ratio is PQ : RQ = 4 : 3. 

(ii) Now, the y-coordinate of the point R will be

 $y=\dfrac{m{{y}_{2}} + n{{y}_{1}}}{m + n}$

 $y=\dfrac{4 \times  2 + 3 \times  5}{4 + 3}$

 $y=\dfrac{8 + 15}{7}$

 $y=\dfrac{23}{7}$

Thus the coordinates of R is $\left( 0, \dfrac{23}{7} \right)$.

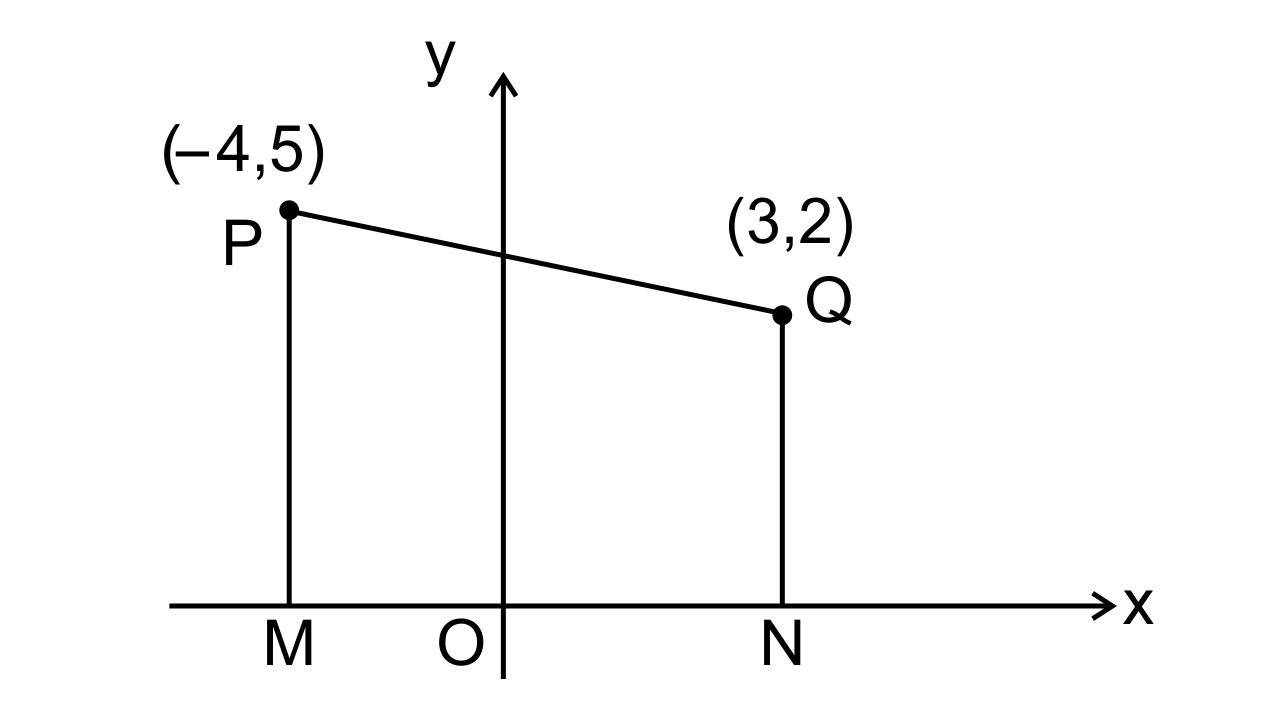
(iii) Here, PM = 5, QN = 2, MN = 7. So

Area of the quadrilateral PMNQ

 $=\dfrac{1}{2}\times \left( PM+QN \right)\times MN$

 $=\dfrac{1}{2}\times \left( 5+2 \right)\times 7$

 $=\dfrac{1}{2}\times \left( 7 \right)\times 7$

 $=\dfrac{1}{2}\times 49$

$=24.5$square units

24. In the given figure, line APB meets the x-axis at point A and y-axis at point B. P is the point (-4, 2) and AP : PB = 1 : 2. Find the coordinates of A and B. 

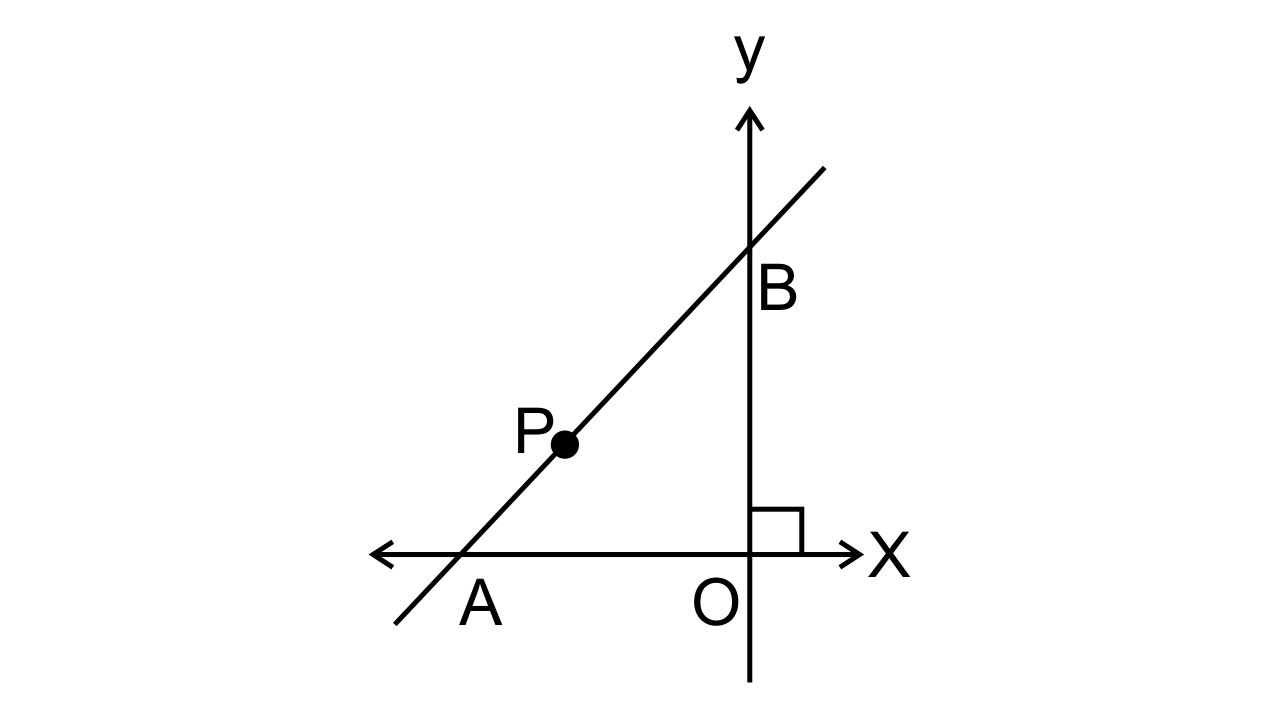
Ans: Let the coordinate of points A and B be (a, 0) and (0, b) respectively.

Given, P = (−4, 2) and AP : PB = 1 : 2

Therefore,

 $P=\left( \dfrac{m{{x}_{2}} + n{{x}_{1}}}{m + n}, \dfrac{m{{y}_{2}} + n{{y}_{1}}}{m + n} \right)$

 $\left( -4, 2 \right)=\left( \dfrac{1 \times  0 + 2 \times  a}{1 + 2}, \dfrac{1 \times  b + 2 \times  0}{1 + 2} \right)$

 $\left( -4, 2 \right)=\left( \dfrac{2 a}{3}, \dfrac{b}{3} \right)$

On comparing both the sides and equating we get,

$-4=\dfrac{2 a}{3}$  and  $2=\dfrac{b}{3}$

$2a= -12$  and  $b=6$

$a=\dfrac{-12}{2}$  and  $b=6$

$a= -6$  and  $b=6$

Thus, the coordinates of points A and B are (-6, 0) and (0, 6) respectively.

25. Given a line segment AB joining the point, A(-4, 6) and B(8, -3). Find: 

(i) the ratio in which AB is divided by the y-axis. 

(ii) find the coordinates of the point of intersection. 

(iii) the length of AB

Ans: 

(i) Given that A = (-4, 6) and B = (8, -3)

The line segment AB intersects the y-axis at point R. Hence, the abscissa of R will be zero.

Let point R divides AB in the ratio k : 1.

 $x=\dfrac{m{{x}_{2}} + n{{x}_{1}}}{m + n}$

 $0=\dfrac{k \times  8 + 1 \times  \left( -4 \right)}{k + 1}$

 $8k-4=0$

 $8k= 4$

 $k=\dfrac{4}{8}$

 $k=\dfrac{1}{2}$

Thus, the ratio in which AB is divided by the y-axis is 1 : 2.

(ii) Now, the y-coordinate of point R will be

 $y=\dfrac{m{{y}_{2}} + n{{y}_{1}}}{m + n}$

 $y=\dfrac{1 \times  \left( -3 \right) + 2 \times  6}{1 + 2}$

 $y=\dfrac{-3 + 12}{3}$

 $y=\dfrac{9}{3}$

 $y=3$

Thus the coordinates of R is $\left( 0, 3 \right)$.

(iii) To find the length of AB using distance formula,

 $AB=\sqrt{{{({{x}_{2}}-{{x}_{1}})}^{2}}+{{({{y}_{2}}-{{y}_{1}})}^{2}}}$

 $AB=\sqrt{{{(8-\left( -4 \right))}^{2}}+{{(-3-6)}^{2}}}$

 $AB=\sqrt{{{12}^{2}}+{{(-9)}^{2}}}$

 $AB=\sqrt{144+81}$

 $AB=\sqrt{225}$

 $AB=15 units$

26. If P(-b, 9a - 2) divides the line segment joining the points A(-3, 3a + 1) and B(5, 8a) in the ratio 3 : I, find the values of a and b. 

Ans: The given points are A = (-3, 3a + 1) and B = (5, 8a), point P divides the line segment AB in a ratio of 3 : 1.

Therefore

 $P=\left( \dfrac{m{{x}_{2}} + n{{x}_{1}}}{m + n}, \dfrac{m{{y}_{2}} + n{{y}_{1}}}{m + n} \right)$

 $\left( -b, 9a - 2 \right)=\left( \dfrac{3 \times  5 + 1 \times  \left( -3 \right)}{3 + 1}, \dfrac{3 \times  8 a + 1 \times  \left( 3 a + 1 \right)}{3 + 1} \right)$

 $\left( -b, 9a - 2 \right)=\left( \dfrac{15 - 3}{4}, \dfrac{24 a + 3 a + 1}{4} \right)$

 $\left( -b, 9a - 2 \right)=\left( \dfrac{12}{4}, \dfrac{27 a  + 1}{4} \right)$

On comparing both the sides o the equation, we get

$-b=\dfrac{12}{4}$  and  $9a-2=\dfrac{27 a + 1}{4}$

$b= -3$  and  $36a-8=27a+1$

$b= -3$  and  $36a-8=27a+1$

$b= -3$  and  $36a-27a=1+8$

$b= -3$  and  $9a=9$

$b= -3$  and  $a=1$

Hence the values of a and b are -3 and 1

EXERCISE 13(B)

1. Find the midpoint of the line segment joining the points:

(i) (-6, 7) and (3, 5)

Ans: 

Given points are $\left( {{x}_{1}}, {{y}_{1}} \right)=\left( -6, 7 \right)$ and $\left( {{x}_{2}}, {{y}_{2}} \right)=\left( 3, 5 \right)$.

Thus the midpoint will be,

 $P=\left( \dfrac{{{x}_{1}} + {{x}_{2}}}{2}, \dfrac{{{y}_{1}} + {{y}_{2}}}{2} \right)$

 $P=\left( \dfrac{-6 + 3}{2}, \dfrac{7 + 5}{2} \right)$

 $P=\left( \dfrac{-3}{2}, \dfrac{12}{2} \right)$

 $P=\left( \dfrac{-3}{2}, 6 \right)$

(ii) (5, -3) and (-1, 7)

Ans: Given points are $\left( {{x}_{1}}, {{y}_{1}} \right)=\left( 5, -3 \right)$ and $\left( {{x}_{2}}, {{y}_{2}} \right)=\left( -1, 7 \right)$.

Thus the midpoint will be,

 $P=\left( \dfrac{{{x}_{1}} + {{x}_{2}}}{2}, \dfrac{{{y}_{1}} + {{y}_{2}}}{2} \right)$

 $P=\left( \dfrac{5 + \left( -1 \right)}{2}, \dfrac{\left( -3 \right) + 7}{2} \right)$

 $P=\left( \dfrac{4}{2}, \dfrac{4}{2} \right)$

 $P=\left( 2, 2 \right)$

2. Point A and B have coordinates (3, 5) and (x, y) respectively. The midpoint of AB is (2, 3). Find the value of x and y.

Ans: Given points are A = (3, 5), B = (x, y), and the midpoint is C = (2, 3).

Therefore, 

 $P=\left( \dfrac{{{x}_{1}} + {{x}_{2}}}{2}, \dfrac{{{y}_{1}} + {{y}_{2}}}{2} \right)$

 $\left( 2, 3 \right)=\left( \dfrac{3 + x}{2}, \dfrac{5 + y}{2} \right)$

On comparing both the sides, we get

$2=\dfrac{3 + x}{2}$  and  $3=\dfrac{5 + y}{2}$

$4=3+x$  and  $6=5+y$

$x=4-3$  and  $y=6-5$

$x=1$  and  $y=1$

Hence the value of (x, y) is (1 , 1)

3. A (5, 3), B (-1, 1) and C (7, -3) are the vertices of triangle ABC. If L is the midpoint of AB and M is the midpoint of AC, show that : LM = $\dfrac{1}{2}$BC. 

Ans: The given vertices of the triangle are A (5, 3), B (-1, 1) and C (7, -3). L is mid-point on AB.

Therefore the coordinate of point L will be,

 $L=\left( \dfrac{{{x}_{1}} + {{x}_{2}}}{2}, \dfrac{{{y}_{1}} + {{y}_{2}}}{2} \right)$

 $L=\left( \dfrac{5 + \left( -1 \right)}{2}, \dfrac{3 + 1}{2} \right)$

 $L=\left( \dfrac{4}{2}, \dfrac{4}{2} \right)$

 $L=\left( 2, 2 \right)$

And, the coordinate of point M will be,

 $M=\left( \dfrac{{{x}_{1}} + {{x}_{2}}}{2}, \dfrac{{{y}_{1}} + {{y}_{2}}}{2} \right)$

 $L=\left( \dfrac{5 + 7}{2}, \dfrac{3 + \left( -3 \right)}{2} \right)$

 $L=\left( \dfrac{12}{2}, 0 \right)$

 $L=\left( 6, 0 \right)$

By using distance formula, let's show that LM = $\dfrac{1}{2}$BC

 $LM=\sqrt{{{({{x}_{2}}-{{x}_{1}})}^{2}}+{{({{y}_{2}}-{{y}_{1}})}^{2}}}$

 $LM=\sqrt{{{(6-2)}^{2}}+{{(0-2)}^{2}}}$

 $LM=\sqrt{{{(4)}^{2}}+{{(-2)}^{2}}}$

 $LM=\sqrt{16+4}$

 $LM=\sqrt{20}$

 $LM=2\sqrt{5} unit$

And,

 $BC=\sqrt{{{({{x}_{2}}-{{x}_{1}})}^{2}}+{{({{y}_{2}}-{{y}_{1}})}^{2}}}$

 $BC=\sqrt{{{(-1-7)}^{2}}+{{(1-\left( -3 \right))}^{2}}}$

 $BC=\sqrt{{{(-8)}^{2}}+{{(4)}^{2}}}$

 $BC=\sqrt{64+16}$

 $BC=\sqrt{80}$

 $BC=4\sqrt{5} unit$

Now that we know the value of LM and BC,

 $\dfrac{LM}{BC}=\dfrac{2\sqrt{5}}{4\sqrt{5}}$

 $\dfrac{LM}{BC}=\dfrac{1}{2}$

 $LM=\dfrac{1}{2} BC$

Hence proved

4. Given M is the midpoint of AB, find the coordinates of: 

(i) A; if M = (1, 7) and B = (-5, 10), 

Ans: Let the given points are A = (x, y) and B = (5, 10). The mid-point is M = (1, 7).

 $M=\left( \dfrac{{{x}_{1}} + {{x}_{2}}}{2}, \dfrac{{{y}_{1}} + {{y}_{2}}}{2} \right)$

 $\left( 1,7 \right)=\left( \dfrac{x + \left( -5 \right)}{2}, \dfrac{y + 10}{2} \right)$

Compare both the sides, we get

$1=\dfrac{x - 5}{2}$  and  $7=\dfrac{y + 10}{2}$

$2=x - 5$  and  $14=y + 10$

$x=2 + 5$  and  $y=14 - 10$

$x=7$  and  $y=4$

Thus, the coordinate of point A is (7, 4).

(ii) B; if A = (3, -1) and M = (-1, 3). 

Ans: Let the given points are A = (3, -1) and B = (x, y), the mid-point is M = (-1, 3)

 $M=\left( \dfrac{{{x}_{1}} + {{x}_{2}}}{2}, \dfrac{{{y}_{1}} + {{y}_{2}}}{2} \right)$

 $\left( -1,3 \right)=\left( \dfrac{3 + x}{2}, \dfrac{-1 + y}{2} \right)$

Compare both the sides, we get

$-1=\dfrac{3 + x}{2}$  and  $3=\dfrac{-1 + y}{2}$

$-2=3 + x$  and  $6=y - 1$

$x= -2-3$  and  $y= 6+1$

$x= -5$  and  $y=7$

Thus, the coordinate of point A is (-5, 7).

5. If P (-3, 2) is the midpoint of line segment AB as shown in the given figure. Find the coordinates of points A and B. 

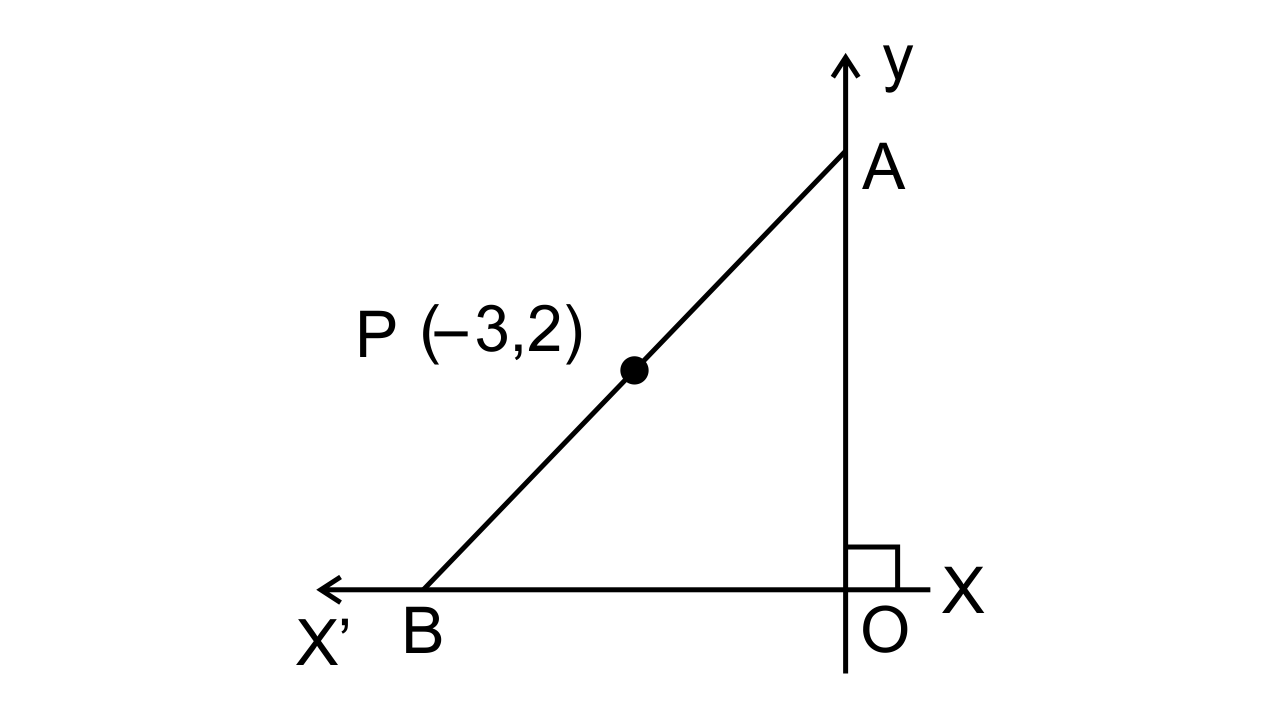
Ans: Let the coordinate of points A and B are (0, a) and (b, 0) respectively. Mid-point is P = (-3, 2).

 $P=\left( \dfrac{{{x}_{1}} + {{x}_{2}}}{2}, \dfrac{{{y}_{1}} + {{y}_{2}}}{2} \right)$

 $\left( -3,2 \right)=\left( \dfrac{0 + b}{2}, \dfrac{a + 0}{2} \right)$

Compare both the sides, we get

$-3=\dfrac{b}{2}$  and  $2=\dfrac{a}{2}$

$b= -6$  and  $a=4$

Hence, the coordinates of points A and B are (0, 4) and (−6, 0) respectively.

6. In the given figure, P (4, 2) is the midpoint of line segment AB. Find the coordinates of A and B. 

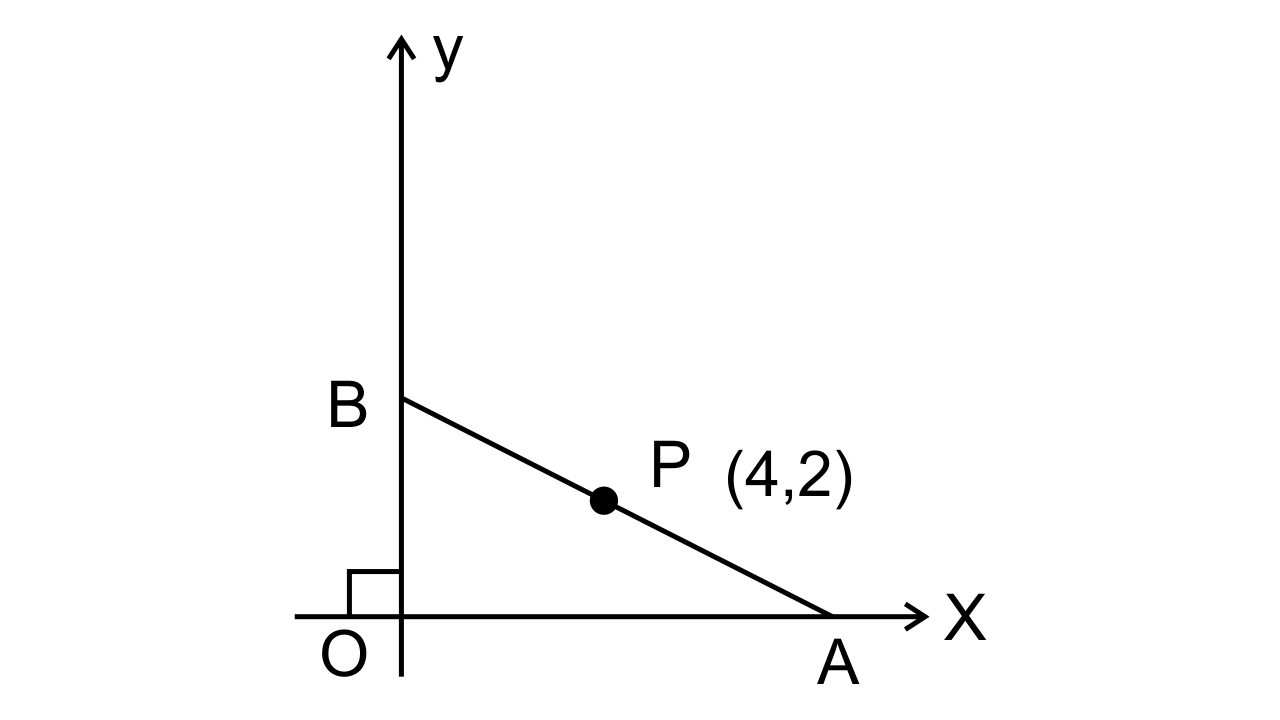
Ans: Let the coordinates of points A and B are (a, 0) and (0, b) respectively, the mid-point is P = (4, 2).

 $P=\left( \dfrac{{{x}_{1}} + {{x}_{2}}}{2}, \dfrac{{{y}_{1}} + {{y}_{2}}}{2} \right)$

 $\left( 4,2 \right)=\left( \dfrac{a + 0}{2}, \dfrac{0 + b}{2} \right)$

Compare both the sides, we get

$4=\dfrac{a}{2}$  and  $2=\dfrac{b}{2}$

$a=8$  and  $b=4$

Hence, the coordinates of points A and B are (8, 0) and (0, 4) respectively.

7. (-5, 2) (3, -6) and (7, 4) are the vertices of a triangle. Find the length of its median through the vertex (3, -6).

Ans: Let the given vertices of the triangle be A = (-5, 2), B = (3, -6) and C = (7, 4).

So, the mid-point on AC will be,

$P=\left( \dfrac{{{x}_{1}} + {{x}_{2}}}{2}, \dfrac{{{y}_{1}} + {{y}_{2}}}{2} \right)$

$P=\left( \dfrac{-5 + 7}{2}, \dfrac{2 + 4}{2} \right)$

$P=\left( \dfrac{2}{2}, \dfrac{6}{2} \right)$

$P=\left( 1, 3 \right)$

Now, the length of median AP can be found using distance formula,

$AP=\sqrt{{{({{x}_{2}}-{{x}_{1}})}^{2}}+{{({{y}_{2}}-{{y}_{1}})}^{2}}}$

$AP=\sqrt{{{(1-3)}^{2}}+{{(3-\left( -6 \right))}^{2}}}$

$AP=\sqrt{{{(-2)}^{2}}+{{(9)}^{2}}}$

$AP=\sqrt{4+81}$

$AP=\sqrt{85}$

$AP=9.22 units$

8. Given a line ABCD in which AB = BC = CD, B= (0, 3) and C= (1, 8). Find the coordinates of A and D. 

Ans: Given that AB = BC and BC = CD, Here B= (0, 3) and C= (1, 8)

Therefore the points B and C are the midpoint of AC and BD.

Thus, to find the coordinates of A,

$B=\left( \dfrac{{{x}_{1}} + {{x}_{2}}}{2}, \dfrac{{{y}_{1}} + {{y}_{2}}}{2} \right)$

$\left( 0, 3 \right)=\left( \dfrac{{{x}_{1}} + 1}{2}, \dfrac{{{y}_{1 }}+ 8}{2} \right)$

On compare both the sides, we get

$0=\dfrac{{{x}_{1}} + 1}{2}$  and  $3= \dfrac{{{y}_{1 }}+ 8}{2}$

${{x}_{1}} + 1=0$  and  ${{y}_{1 }}+ 8=6$

${{x}_{1}}= -1$  and  ${{y}_{1 }}=6-8$

${{x}_{1}}= -1$  and  ${{y}_{1 }}= -2$

Hence, the coordinate of point A is (-1, -2).

Now to find the coordinates of D,

 $C=\left( \dfrac{{{x}_{1}} + {{x}_{2}}}{2}, \dfrac{{{y}_{1}} + {{y}_{2}}}{2} \right)$

 $\left( 1, 8 \right)=\left( \dfrac{{{x}_{2}} + 0}{2}, \dfrac{{{y}_{2 }}+ 3}{2} \right)$

On compare both the sides, we get

$1=\dfrac{{{x}_{2}} + 0}{2}$  and  $8= \dfrac{{{y}_{2 }}+ 3}{2}$

${{x}_{2}} + 0=2$  and  ${{y}_{2 }}+ 3=16$

${{x}_{2}}=2$  and  ${{y}_{2}}=16-3$

${{x}_{2}}=2$  and  ${{y}_{2 }}=13$

Hence, the coordinate of point D is (2, 13)

9. One end of the diameter of a circle is (-2, 5). Find the coordinates of the other end of it, if the centre of the circle is (2, -1). 

Ans: Let A = (x, y), B = (-2, 5) and C = (2, -1). Here, A and B are the endpoints of diameter. As we know that the center of the circle is the midpoint of its diameter.

So to find the coordinates of A, we have

 $C=\left( \dfrac{{{x}_{1}} + {{x}_{2}}}{2}, \dfrac{{{y}_{1}} + {{y}_{2}}}{2} \right)$

 $\left( 2, -1 \right)=\left( \dfrac{x + \left( -2 \right)}{2}, \dfrac{y + 5}{2} \right)$

On comparing both the sides,

$2=\dfrac{x -2}{2}$  and  $-1= \dfrac{y + 5}{2}$

$4=x-2$  and  $-2= y + 5$

$x=4+2$  and  $y= -2- 5$

$x=6$  and  $y= -7$

Hence, the coordinate of point A is (6, -7).

10. A (2, 5), B (1, 0), C (-4, 3) and D (-3, 8) are the vertices of quadrilateral ABCD. Find the coordinates of the midpoints of AC and BD. Give a special name to the quadrilateral.

Ans: Given vertices of quadrilateral ABCD are A = (2, 5), B = (1, 0), C = (-4, 3) and D = (-3, 8)

Let us consider the midpoints of AC and BD as M and N

So, the midpoint of AC will be,

 $M=\left( \dfrac{{{x}_{1}} + {{x}_{2}}}{2}, \dfrac{{{y}_{1}} + {{y}_{2}}}{2} \right)$

 $M=\left( \dfrac{2 + \left( -4 \right)}{2}, \dfrac{5 + 3}{2} \right)$

 $M=\left( \dfrac{-2}{2}, \dfrac{8}{2} \right)$

 $M=\left( -1, 4 \right)$

And, midpoint of BD will be,

 $N=\left( \dfrac{{{x}_{1}} + {{x}_{2}}}{2}, \dfrac{{{y}_{1}} + {{y}_{2}}}{2} \right)$

 $N=\left( \dfrac{1 + \left( -3 \right)}{2}, \dfrac{0 + 8}{2} \right)$

 $N=\left( \dfrac{-2}{2}, \dfrac{8}{2} \right)$

 $N=\left( -1, 4 \right)$

As a result, points M and N are the same, and the diagonal will bisect each other. 

Hence, the ABCD quadrilateral is a parallelogram.

11. P (4, 2) and Q (-1, 5) are the vertices of parallelogram PQRS and (-3, 2) are the coordinates of the point of intersection of its diagonals. Find coordinates of R and S. 

Ans: Given vertices of parallelogram are P = (4, 2), Q = (-1, 5) and the point of intersection of the diagonals is (-3, 2).

In diagonal PR its midpoint is O,

Let coordinate of point R be $\left( {{x}_{1}}, {{y}_{1}} \right)$

 $O=\left( \dfrac{{{x}_{1}} + {{x}_{2}}}{2}, \dfrac{{{y}_{1}} + {{y}_{2}}}{2} \right)$

 $\left( -3,2 \right)=\left( \dfrac{4 + {{x}_{1}}}{2}, \dfrac{2 + {{y}_{1}}}{2} \right)$

On comparing both the sides,

$-3=\dfrac{4 + {{x}_{1}}}{2}$  and  $2=\dfrac{2 + {{y}_{1}}}{2}$

$-6=4 + {{x}_{1}}$  and  $4=2+{{y}_{1}}$

${{x}_{1}}= -6-4$  and  ${{y}_{1}}=4-2$

${{x}_{1}}= -10$  and  ${{y}_{1}}=2$

Hence, the coordinate of point R is (−10, 2).

Now, let us consider the coordinate of point S be $\left( {{x}_{2}}, {{y}_{2}} \right)$

 $\text{O}=\left( \dfrac{{{x}_{1}} + {{x}_{2}}}{2}, \dfrac{{{y}_{1}} + {{y}_{2}}}{2} \right)$

 $\left( -3, 2 \right)=\left( \dfrac{{{x}_{2}} + \left( -1 \right)}{2}, \dfrac{{{y}_{2}} + 5}{2} \right)$

On comparing both the sides,

$-3=\dfrac{{{x}_{2}} - 1}{2}$  and  $2= \dfrac{{{y}_{2}} + 5}{2}$

$-6={{x}_{2}}-1$  and  $4={{y}_{2}}+5$

${{x}_{2}}= -6+1$  and  ${{y}_{2}}=4-5$

${{x}_{2}}= -5$  and  ${{y}_{2}}= -1$

Hence, the coordinate of point S is (-5, -1).

12. A (-1, 0), B (1, 3) and D (3, 5) are the vertices of a parallelogram ABCD. Find the coordinates of vertex C. 

Ans: Let the coordinate of point C be (x, y). In parallelogram 

Midpoint of AC = Midpoint of BD.

 $\left( \dfrac{{{x}_{1}} + {{x}_{2}}}{2}, \dfrac{{{y}_{1}} + {{y}_{2}}}{2} \right)=\left( \dfrac{{{x}_{1}} + {{x}_{2}}}{2}, \dfrac{{{y}_{1}} + {{y}_{2}}}{2} \right)$

 $\left( \dfrac{-1 + x}{2}, \dfrac{0 + y}{2} \right)= \left( \dfrac{1 + 3}{2}, \dfrac{3 + 5}{2} \right)$

 $\left( \dfrac{-1 + x}{2}, \dfrac{y}{2} \right)= \left( \dfrac{4}{2}, \dfrac{8}{2} \right)$

On comparing both the sides, we get

$\dfrac{-1 + x}{2}=\dfrac{4}{2}$  and  $\dfrac{y}{2}=\dfrac{8}{2}$

$2\left( -1+x \right)=4\times 2$  and  $2y=8\times 2$

$-2+2x=8$  and  $2y=16$

$2x=10$  and  $2y=16$

$x=\dfrac{10}{2}$  and  $y=\dfrac{16}{2}$

$x=5$  and  $y=8$

Hence, the coordinate of point C is (5,8).

13. The points (2, -1), (-1, 4) and (-2, 2) are midpoints of the sides of a triangle. Find its vertices.

Ans: Let the coordinate of the triangles be A = $\left( {{x}_{1}}, {{y}_{1}} \right)$, B = $\left( {{x}_{2}}, {{y}_{2}} \right)$ and C = $\left( {{x}_{3}}, {{y}_{3}} \right)$

The midpoint of AB, AC and BC are (2, -1), (-1, 4) and (-2, 2) respectively.

So for AB,

 $\left( 2, -1 \right)= \left( \dfrac{{{x}_{1}} + {{x}_{2}}}{2}, \dfrac{{{y}_{1}} + {{y}_{2}}}{2} \right)$

On comparing both the sides, we get

$2=\dfrac{{{x}_{1}} + {{x}_{2}}}{2}$  and  $-1=\dfrac{{{y}_{1}} + {{y}_{2}}}{2}$

$4={{x}_{1}} + {{x}_{2}}$  and  $-2={{y}_{1}} + {{y}_{2}}$

Hence,

${{x}_{1}} + {{x}_{2}}=4$ $\to $(1)

${{y}_{1}} + {{y}_{2}}= -2$ $\to $(2)

For AC,

 $\left( -1, 4 \right)= \left( \dfrac{{{x}_{1}} + {{x}_{3}}}{2}, \dfrac{{{y}_{1}} + {{y}_{3}}}{2} \right)$

On comparing both the sides, we get

$-1=\dfrac{{{x}_{1}} + {{x}_{3}}}{2}$  and  $4=\dfrac{{{y}_{1}} + {{y}_{3}}}{2}$

$-2={{x}_{1}} + {{x}_{3}}$  and  $8={{y}_{1}} + {{y}_{3}}$

Hence,

${{x}_{1}} + {{x}_{3}}= -2$ $\to $(3)

${{y}_{1}} + {{y}_{3}}=8$ $\to $(4)

For BC,

 $\left( -2, 2 \right)= \left( \dfrac{{{x}_{2}} + {{x}_{3}}}{2}, \dfrac{{{y}_{2}} + {{y}_{3}}}{2} \right)$

On comparing both the sides, we get

$-2=\dfrac{{{x}_{2}} + {{x}_{3}}}{2}$  and  $2=\dfrac{{{y}_{2}} + {{y}_{3}}}{2}$

$-4={{x}_{2}} + {{x}_{3}}$  and  $4={{y}_{2}} + {{y}_{3}}$

Hence,

${{x}_{2}} + {{x}_{3}}= -4$ $\to $(5)

${{y}_{2}} + {{y}_{3}}=4$ $\to $(6)

Adding equations (1), (3) and (5) we get,

 $2\left( {{x}_{1}}+{{x}_{2}}+{{x}_{3}} \right)= -2$

${{x}_{1}}+{{x}_{2}}+{{x}_{3}}= -1$ $\to $ (7)

Substitute value of equation (5) in above equation,

 ${{x}_{1}}+{{x}_{2}}+{{x}_{3}}= -1$

 ${{x}_{1}}+\left( -4 \right)= -1$

 ${{x}_{1}}=3$

Substitute value of equation (3) in equation (7),

 ${{x}_{1}}+{{x}_{2}}+{{x}_{3}}= -1$

 ${{x}_{2}}+{{x}_{1}}+{{x}_{3}}= -1$

 ${{x}_{2}}+\left( -2 \right)= -1$

 ${{x}_{2}}=1$

Substitute value of equation (1) in equation (7),

 ${{x}_{1}}+{{x}_{2}}+{{x}_{3}}= -1$

 $3+1+{{x}_{3}}= -1$

 $4+{{x}_{3}}= -1$

 ${{x}_{3}}= -5$

Adding equations (2), (4) and (6),

 $2\left( {{y}_{1}}+{{y}_{2}}+{{y}_{3}} \right)=10$

${{y}_{1}}+{{y}_{2}}+{{y}_{3}}=5$ $\to $ (8)

Substitute value of equation (6) in above equation,

 ${{y}_{1}}+{{y}_{2}}+{{y}_{3}}=5$

 ${{y}_{1}}+4=5$

 ${{y}_{1}}=1$

Substitute value of equation (4) in equation (8),

 ${{y}_{1}}+{{y}_{2}}+{{y}_{3}}=5$

 ${{y}_{2}}+{{y}_{1}}+{{y}_{3}}=5$

 ${{y}_{2}}+8=5$

 ${{y}_{2}}= -3$

Substitute value of equation (2) in equation (8),

 ${{y}_{1}}+{{y}_{2}}+{{y}_{3}}=5$

 $-2+{{y}_{3}}=5$

 ${{y}_{3}}=7$

Hence, the coordinates of vertices are (3, 1), (1, -3 ) and (-5, 7).

14. Points A (-5, x), B (y, 7) and C (1, -3) are collinear (i.e. lie on the same straight line) such that AB = BC. Calculate the values of x and y.

Ans: Given points A, B and C are collinear and AB = BC. Therefore, B is the midpoint of AC.

 $\left( y,7 \right)= \left( \dfrac{-5 + 1}{2},\dfrac{x + \left( -3 \right)}{2} \right)$

 $\left( y,7 \right)= \left( \dfrac{-4}{2},\dfrac{x - 3}{2} \right)$

On comparing both the sides, we get

$y=\dfrac{-4}{2}$  and  $7=\dfrac{x - 3}{2}$

$2y= -4$  and  $14=x-3$

$y=\dfrac{-4}{2}$  and  $x=14+3$

$y= -2$  and  $x=17$

Hence the values of x and y are -2 and 17.

15. Points P(a, -4), Q(-2, b) and R(0, 2) are collinear. If Q lies between P and R, such that PR = 2QR, calculate the values of a and b.

Ans: Given that the points P, Q and R are collinear and PR = 2QR.

Thus,

PR = 2QR

PQ + QR = 2QR

PQ = QR

Hence, we can say that point Q is the midpoint.

 $\left( -2,b \right)= \left( \dfrac{a + 0}{2},\dfrac{-4 + 2}{2} \right)$

 $\left( -2,b \right)=\left( \dfrac{a}{2},-1 \right)$

On comparing both the sides, we get

$-2=\dfrac{a}{2}$ and $b= -1$

Therefore a = -4 and b = -1

16. Calculate the coordinates of the centroid of the triangle ABC, if A = (7, -2), B = (0. l) and C = (-1, 4).

Ans: The coordinate of the centroid of triangle will be,

 $\left( x,y \right)=\left( \dfrac{{{x}_{1}} + {{x}_{2}} + {{x}_{3}}}{3},\dfrac{{{y}_{1}} + {{y}_{2}} + {{y}_{3}}}{3} \right)$

 $\left( x,y \right)=\left( \dfrac{7 + 0 + \left( -1 \right)}{3},\dfrac{-2 + 1 + 4}{3} \right)$

 $\left( x,y \right)=\left( \dfrac{6}{3}, \dfrac{3}{3} \right)$

 $\left( x,y \right)=\left( 2,1 \right)$

17. The coordinates of the centroid of a triangle PQR are (2, -5). If Q = (-6, 5) and R = (11, 8); calculate the coordinates of vertex P.

Ans: The coordinate of centroid of a triangle PQR is,

 $\left( x,y \right)= \left( \dfrac{{{x}_{1}} + {{x}_{2}} + {{x}_{3}}}{3},\dfrac{{{y}_{1}} + {{y}_{2}} + {{y}_{3}}}{3} \right)$

 $\left( 2, -5 \right)=\left( \dfrac{x + \left( -6 \right) + 11}{3},\dfrac{y + 5 + 8}{3} \right)$

 $\left( 2, -5 \right)=\left( \dfrac{x + 5}{3},\dfrac{y + 13}{3} \right)$

On comparing both the sides, we get

$2=\dfrac{x + 5}{3}$  and  $-5=\dfrac{y + 13}{3}$

$6=x+5$  and  $-15=y+13$

$x=1$  and  $y= -28$

Thus, the vertex P is (1, -28).

18. A(5, x), B(-4, 3) and C(y, -2) are the vertices of the triangle ABC whose centroid is the origin. Calculate the values of x and y. 

Ans: The coordinate of centroid is,

 $\left( 0,0 \right)= \left( \dfrac{{{x}_{1}} + {{x}_{2}} + {{x}_{3}}}{3},\dfrac{{{y}_{1}} + {{y}_{2}} + {{y}_{3}}}{3} \right)$

 $\left( 0,0 \right)=\left( \dfrac{5 + \left( -4 \right) + y}{3},\dfrac{x + 3 + \left( -2 \right)}{3} \right)$

 $\left( 0,0 \right)=\left( \dfrac{1 + y}{3},\dfrac{x + 1}{3} \right)$

On comparing both the sides,

$0=\dfrac{1 + y}{3}$  and  $0=\dfrac{x + 1}{3}$

$1+y=0$  and  $x+1=0$

$y= -1$  and  $x= -1$

EXERCISE 13(C)

1. Given a triangle ABC in which A = (4, -4), B = (0, 5) and C = (5, 10). A point P lies on BC such that BP : PC = 3 : 2. Find the length of line segment AP. 

Ans: Given vertices of triangle are A = (4, -4), B = (0, 5) and C = (5, 10), BP : PC = 3: 2.

 $\text{P}=\left( \dfrac{m{{x}_{2}} + n{{x}_{1}}}{m + n}, \dfrac{m{{y}_{2}} + n{{y}_{1}}}{m + n} \right)$

 $P=\left( \dfrac{3 \times  5 + 2 \times  0}{3 + 2}, \dfrac{3 \times  10 + 2 \times  5}{3 + 2} \right)$

 $P=\left( \dfrac{15}{5}, \dfrac{40}{5} \right)$

 $P=\left( 3, 8 \right)$

Now by using distance formula find the length of the line segment AP,

 $AP=\sqrt{{{({{x}_{2}}-{{x}_{1}})}^{2}}+{{({{y}_{2}}-{{y}_{1}})}^{2}}}$

 $AP=\sqrt{{{(3-4)}^{2}}+{{(8-\left( -4 \right))}^{2}}}$

 $AP=\sqrt{{{(-1)}^{2}}+{{(12)}^{2}}}$

 $AP=\sqrt{1+144}$

 $AP=\sqrt{145}$

 $AP=12.04 units$

2. A(20, 0) and B(10, -20) are two fixed points. Find the coordinates of the point P in AB such that : 3PB = AB. Also, find the coordinates of some other point Q in AB such that : AB = 6AQ.

Ans: The given points are A = (20, 0), B = (10, -20) and 3PB = AB, Thus

3PB = AP + PB

2PB = AP

 $\dfrac{AP}{PB}=\dfrac{2}{1}$

Hence, AP : PB = 2 : 1

Now, to find the coordinate of point P,

 $P=\left( \dfrac{m{{x}_{2}} + n{{x}_{1}}}{m + n}, \dfrac{m{{y}_{2}} + n{{y}_{1}}}{m + n} \right)$

 $P=\left( \dfrac{2 \times  10 + 1 \times  20}{2 + 1}, \dfrac{2 \times  \left( -20 \right) + 1 \times  0}{2 + 1} \right)$

 $P=\left( \dfrac{20 + 20}{3}, \dfrac{-40}{3} \right)$

 $P=\left( \dfrac{40}{3}, \dfrac{-40}{3} \right)$

And also given AB = 6AQ

AQ + QB = 6AQ

QB = 5AQ

 $\dfrac{AQ}{QB}=\dfrac{1}{5}$

Now, the coordinate of point Q will be,

 $\text{Q}=\left( \dfrac{m{{x}_{2}} + n{{x}_{1}}}{m + n}, \dfrac{m{{y}_{2}} + n{{y}_{1}}}{m + n} \right)$

 $\text{Q}=\left( \dfrac{1 \times  10 + 5 \times  20}{1 + 5}, \dfrac{1 \times  \left( -20 \right) + 5 \times  0}{1 + 5} \right)$

 $\text{Q}=\left( \dfrac{10 + 100}{6}, \dfrac{-20}{6} \right)$

 $\text{Q}=\left( \dfrac{110}{6}, \dfrac{-20}{6} \right)$

 $\text{Q}=\left( \dfrac{55}{3}, \dfrac{-10}{3} \right)$

3. A(-8, 0), B(0, 16) and C(0, 0) are the vertices of a triangle ABC. Point P lies on AB and Q lies on AC such that AP : PB = 3 : 5 and AQ : QC = 3 : 5.

Show that PQ = $\dfrac{3}{8}$ BC

Ans: Given vertices of triangle are A = (-8, 0), B = (0, 16) and C = (0, 0)

Point P lies on AB such that AP : PB = 3 : 5.

Therefore, the coordinate of point P will be,

 $\text{P}=\left( \dfrac{m{{x}_{2}} + n{{x}_{1}}}{m + n}, \dfrac{m{{y}_{2}} + n{{y}_{1}}}{m + n} \right)$

 $P=\left( \dfrac{3 \times  0 + 5 \times  \left( -8 \right)}{3 + 5}, \dfrac{3 \times  16 + 5 \times  0}{3 + 5} \right)$

 $P=\left( \dfrac{-40}{8}, \dfrac{48}{8} \right)$

 $P=\left( -5, 6 \right)$

Point Q lies on AC such that AQ : QB = 3 : 5

Therefore, the coordinate of point Q will be,

 $Q=\left( \dfrac{m{{x}_{2}} + n{{x}_{1}}}{m + n}, \dfrac{m{{y}_{2}} + n{{y}_{1}}}{m + n} \right)$

 $Q=\left( \dfrac{3 \times  0 + 5 \times  \left( -8 \right)}{3 + 5}, \dfrac{3 \times  0 + 5 \times  0}{3 + 5} \right)$

 $Q=\left( \dfrac{-40}{8}, \dfrac{0}{8} \right)$

 $Q=\left( -5, 0 \right)$

Now by using distance formula find PQ and BC,

 $PQ=\sqrt{{{({{x}_{2}}-{{x}_{1}})}^{2}}+{{({{y}_{2}}-{{y}_{1}})}^{2}}}$

 $PQ=\sqrt{{{(-5-\left( -5 \right))}^{2}}+{{(0-6)}^{2}}}$

 $PQ=\sqrt{{{(-5+5)}^{2}}+{{(-6)}^{2}}}$

 $PQ=\sqrt{0+36}$

 $PQ=6$

And, $BC=\sqrt{{{({{x}_{2}}-{{x}_{1}})}^{2}}+{{({{y}_{2}}-{{y}_{1}})}^{2}}}$

 $BC=\sqrt{{{(0-0)}^{2}}+{{(0-16)}^{2}}}$

 $BC=\sqrt{0+{{(-16)}^{2}}}$

 $BC=16$

Now to show that PQ = $\dfrac{3}{8}$BC

 $\dfrac{PQ}{BC}=\dfrac{6}{16}$

 $\dfrac{PQ}{BC}=\dfrac{3}{8}$

Therefore PQ = $\dfrac{3}{8}$BC

Hence proved

4. Find the coordinates of points of trisection of the line segment joining the point (6, -9) and the origin.

Ans: Let the given points are P = (6, -9) and Q = (0, 0).

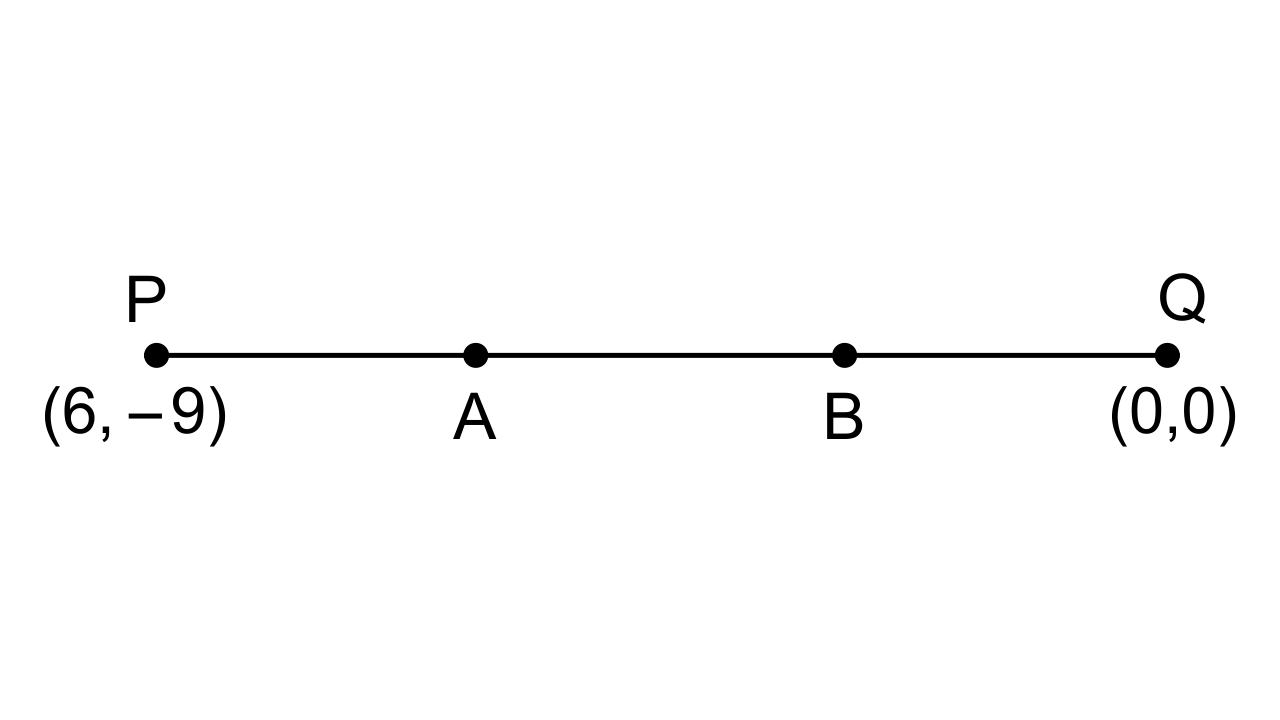
Let the points A and B trisect the line segment PQ.

Thus, we can say that PA : AQ = 1 : 2 and PB : BQ = 2 :1.

The coordinate of point A will be,

 $A=\left( \dfrac{m{{x}_{2}} + n{{x}_{1}}}{m + n}, \dfrac{m{{y}_{2}} + n{{y}_{1}}}{m + n} \right)$

 $A=\left( \dfrac{1 \times  0 + 2 \times  6}{1 + 2}, \dfrac{1 \times  0 + 2 \times  \left( -9 \right)}{1 + 2} \right)$

 $A=\left( \dfrac{12}{3}, \dfrac{-18}{3} \right)$

 $A=\left( 4, -6 \right)$

The coordinate of point B will be,

 $B=\left( \dfrac{m{{x}_{2}} + n{{x}_{1}}}{m + n}, \dfrac{m{{y}_{2}} + n{{y}_{1}}}{m + n} \right)$

 $B=\left( \dfrac{2 \times  0 + 1 \times  6}{2 + 1}, \dfrac{2 \times  0 + 1 \times  \left( -9 \right)}{2 + 1} \right)$

 $B=\left( \dfrac{6}{3}, \dfrac{-9}{3} \right)$

 $B=\left( 2, -3 \right)$

Thus the required points are (4, -6) and (2, -3)

5. A line segment joining A(-1, $\dfrac{5}{3}$) and B(a, 5) is divided in the ratio 1 : 3 at P, the point where the line segment AB intersects the y-axis. 

(i) Calculate the value of 'a'. 

(ii) Calculate the coordinates of 'P'. 

Ans: (i) The given points are A = $\left( -1,\text{ }\!\! \!\!\text{ }\dfrac{5}{3} \right)$ and B = (a, 5). Here the segment AB intersects y − axis at point P such that AP : PB = 1 : 3.

Therefore the coordinate of point P will be (0, y).

 $x=\dfrac{m{{x}_{2}} + n{{x}_{1}}}{m + n}$

 $0=\dfrac{1 \times  a + 3 \times  \left( -1 \right)}{1 + 3}$

 $0=\dfrac{a - 3}{1 + 3}$

Therefore, the value of a = 3.

(ii) The y-coordinate of point P will be,

 $y=\dfrac{m{{y}_{2}} + n{{y}_{1}}}{m + n}$

 $y=\dfrac{1 \times  5 + 3 \times  \dfrac{5}{3}}{1 + 3}$

 $y=\dfrac{5 + 5}{4}$

 $y=\dfrac{5}{2}$

Thus, y-coordinate of point P will be $\left( 0, \dfrac{5}{2}  \right)$

6. In what ratio is the line joining A(0, 3) and B(4, -1) divided by the x-axis ? Write the coordinates of the point where AB intersects the x-axis. 

Ans: The given points are A = (0, 3) and B = (4, -1)

Let the segment AB intersects the y−axis at point P in the ratio of k : 1.

Therefore the coordinate of point P will be (x, 0).

 $y=\dfrac{m{{y}_{2}} + n{{y}_{1}}}{m + n}$

 $0=\dfrac{k \times  \left( -1 \right) + 1 \times  3}{k + 1}$

 $0=\dfrac{-k + 3}{k + 1}$

 $-k+3=0$

 $k=3$

Thus the ratio 3 : 1

The coordinate of point P will be,

 $x=\dfrac{m{{x}_{2}} + n{{x}_{1}}}{m + n}$

 $x=\dfrac{3 \times  4 + 1 \times  0}{3 + 1}$

 $x=\dfrac{12}{4}$

 $x=3$

Thus, the coordinates of point P are (3, 0).

7. The mid-point of the segment AB, as shown in the diagram, is C(4, -3). Write down the coordinates of A and B.

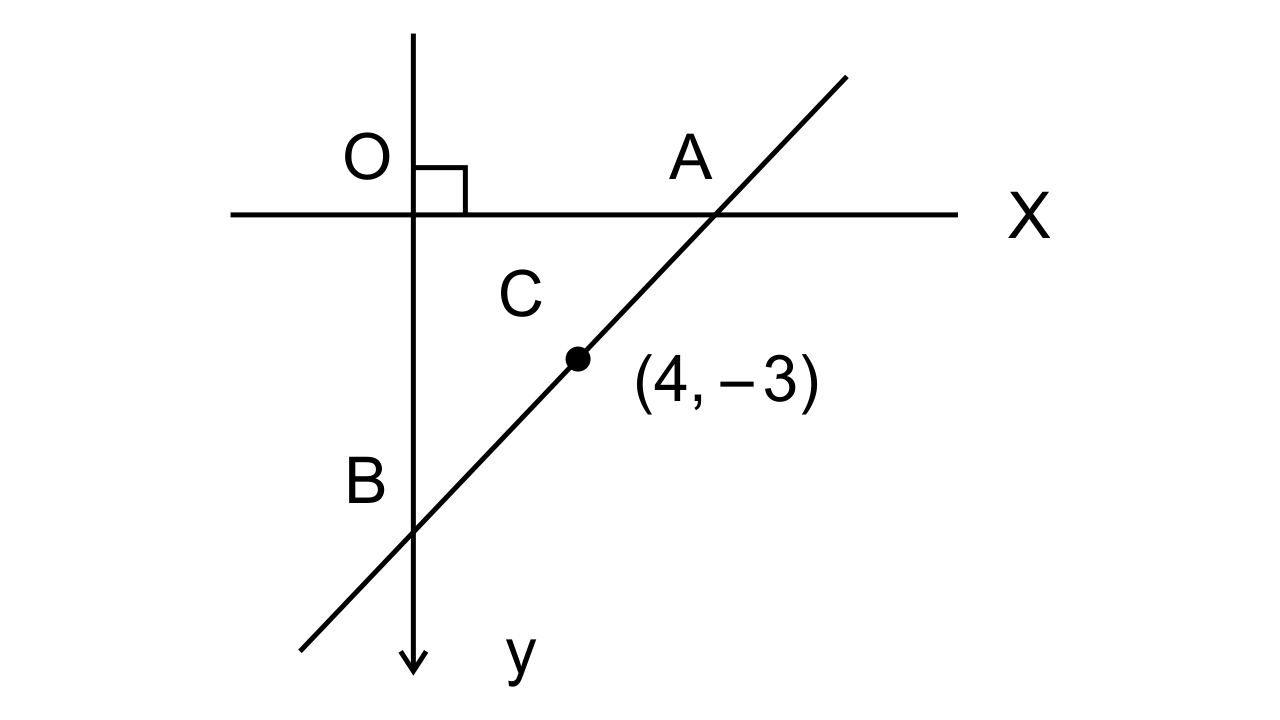
Ans: Let the coordinates of point A and B be (a, 0) and (0, b) respectively. Here point C is the midpoint of AB.

Therefore,

 $\text{C}=\left( \dfrac{{{x}_{2}} + {{x}_{1}}}{2}, \dfrac{{{y}_{2}} + {{y}_{1}}}{2} \right)$

 $\text{C}=\left( \dfrac{a + 0}{2},\dfrac{0 + b}{2} \right)$

 $\left( 4, -3 \right)=\left( \dfrac{a}{2},\dfrac{b}{2} \right)$

On comparing both the sides,

$4=\dfrac{a}{2}$  and  $-3=\dfrac{b}{2}$

$a=8$  and  $b= -6$

Thus, the coordinates of A and B are (8, 0) and (0, -6) respectively.

8. AB is a diameter of a circle with centre C = (-2, 5). If A = (3, -7), find 

(i) the length of radius AC. 

(ii) the coordinates of B.

Ans: 

(i) The given points are A = (3, -7) and C = (-2, 5).

By using distance formula,

 $AC=\sqrt{{{({{x}_{2}}-{{x}_{1}})}^{2}}+{{({{y}_{2}}-{{y}_{1}})}^{2}}}$

 $AC=\sqrt{{{(-2-3)}^{2}}+{{(5-\left( -7 \right))}^{2}}}$

 $AC=\sqrt{{{(-5)}^{2}}+{{(12)}^{2}}}$

 $AC=\sqrt{25+144}$

 $AC=\sqrt{25+144}$

 $AC=\sqrt{169}$

 $AC=13 units$

(ii) Now that we know that AB is a diameter, we can find B's coordinates.

Hence C will be the midpoint of AB

 $C=\left( \dfrac{{{x}_{2}} + {{x}_{1}}}{2}, \dfrac{{{y}_{2}} + {{y}_{1}}}{2} \right)$

 $\left( -2,5 \right)=\left( \dfrac{3 + x}{2},\dfrac{-7 + y}{2} \right)$

On comparing both the sides,

$-2=\dfrac{3 + x}{2}$  and  $5=\dfrac{-7 + y}{2}$

$3+x= -4$  and  $-7+y=10$

$x= -7$  and  $y=17$

Thus, the coordinate of B is (-7, 17).

9. Find the coordinates of the centroid of a triangle ABC whose vertices are: 

A(-1, 3), B(1, -1) and C(5, 1).

Ans: The coordinate of the centroid of triangle ABC will be,

 $P=\left( \dfrac{{{x}_{1}} + {{x}_{2}} + {{x}_{3}}}{3},\dfrac{{{y}_{1}} + {{y}_{2}} + {{y}_{3}}}{3} \right)$

 $P=\left( \dfrac{-1 + 1 + 5}{3},\dfrac{3 + \left( -1 \right) + 1}{3} \right)$

 $P=\left( \dfrac{5}{3},\dfrac{3}{3} \right)$

 $P=\left( \dfrac{5}{3},1 \right)$

10. The midpoint of the line segment joining (4a, 2b - 3) and (-4, 3b) is (2, -2a). Find the values of a and b. 

Ans: Given points are A = (4a, 2b - 3), B = (-4, 3b) and C = (2, -2a).

Here, C is the midpoint of AB.

 $\text{C}=\left( \dfrac{{{x}_{2}} + {{x}_{1}}}{2}, \dfrac{{{y}_{2}} + {{y}_{1}}}{2} \right)$

 $\left( 2, -2a \right)=\dfrac{-4 + 4a}{2}, \dfrac{3b + 2b - 3}{2}$

Comparing both the sides of the equation, we get

$2=\dfrac{-4 + 4a}{2}$  

$-4 + 4a =4$-----$\left( \div 4 \right)$

 $-1+a=1$

Therefore $a=1$

Now that we have got the value of ‘a’ substitute the given value and find ‘b’

 $-2a=\dfrac{3b + 2b - 3}{2}$

$5b- 3= -4\left( 2 \right)$  (Because a = 1)

 $5b= -8+3$

 $5b= -5$

 $b=\dfrac{-5}{5}$

 $b= -1$

Hence the value of a = 1 and b = -1

11. The midpoint of the line segment joining (2a, 4) and (-2, 2b) is (1, 2a+1). Find the values of a and b.

Ans: Let the given points are A = (2a, 4), B = (-2, 2b) and C = (1, 2a + 1). C is the midpoint of AB.

 $C=\left( \dfrac{{{x}_{2}} + {{x}_{1}}}{2}, \dfrac{{{y}_{2}} + {{y}_{1}}}{2} \right)$

 $\left( 1, 2a+1 \right)=\left( \dfrac{2a + \left( -2 \right)}{2}, \dfrac{4 + 2b}{2} \right)$

On comparing both the sides of the equation, we get,

 $1=\dfrac{2a - 2}{2}$

 $2a - 2=2$

 $2a=4$

 $a=\dfrac{4}{2}$

 $a=2$

Now that we know the value of ‘a’ substitute the given value and find ‘b’

 $2a+1=\dfrac{4 + 2b}{2}$

$4\left( 2 \right)+2=4 + 2b$ ------$\left( \div 2 \right)$

 $4+1=2 + b$

 $b=4+1-2$

 $b=3$

Hence the value of a = 2 and b = 3.

12. (i) Write down the coordinates of the point P that divides the line joining A(-4, 1) and B(17, 10) in the ratio 1 : 2. 

(ii) Calculate the distance OP, where O is the origin. 

(iii) In what ratio does the y-axis divide the line AB.

Ans: (i) The given points are A = (-4, 1) and B = (17, 10). Then the coordinate of point P is,

 $P=\left( \dfrac{m{{x}_{2}} + n{{x}_{1}}}{m + n}, \dfrac{m{{y}_{2}} + n{{y}_{1}}}{m + n} \right)$

 $P=\left( \dfrac{1 \times  17 + 2 \times  \left( -4 \right)}{1 + 2}, \dfrac{1 \times  10 + 2 \times  1}{1 + 2} \right)$

 $P=\left( \dfrac{17 - 8}{3}, \dfrac{10 + 2}{3} \right)$

 $P=\left( \dfrac{9}{3}, \dfrac{12}{3} \right)$

 $P=\left( 3, 4 \right)$

(ii) The distance of OP can be calculated using the distance formula.

 $OP=\sqrt{{{({{x}_{2}}-{{x}_{1}})}^{2}}+{{({{y}_{2}}-{{y}_{1}})}^{2}}}$

 $OP=\sqrt{{{(3-0)}^{2}}+{{(4-0)}^{2}}}$

 $OP=\sqrt{9+16}$

 $OP=\sqrt{25}$

 $OP=5 units$

(iii) Let the y-axis divides AB in a ratio of k : 1. So, the coordinate of the point will be (0, y).

 $x=\dfrac{m{{x}_{2}} + n{{x}_{1}}}{m + n}$

 $0=\dfrac{k \times  17 + 1 \times  \left( -4 \right)}{k + 1}$

 $0=\dfrac{17 k - 4}{k + 1}$

 $17 k - 4=0$

 $k=\dfrac{4}{17}$

Thus, the ratio in which the y-axis divides line AB is 4 : 17.

13. Prove that the points A(-5, 4), B(-1, -2) and C(5, 2) are the vertices of an isosceles right-angled triangle. Find the coordinates of D so that ABCD is a square. 

Ans: The given points are A = (-5, 4), B = (-1, -2) and C = (5, 2).

By using distance formula,

 $P=\sqrt{{{({{x}_{2}}-{{x}_{1}})}^{2}}+{{({{y}_{2}}-{{y}_{1}})}^{2}}}$

To find AB,

 $AB=\sqrt{{{(-1-\left( -5 \right))}^{2}}+{{(-2-4)}^{2}}}$

 $AB=\sqrt{{{(4)}^{2}}+{{(-6)}^{2}}}$

 $AB=\sqrt{16+36}$

 $AB=\sqrt{52}$

To find BC,

 $BC=\sqrt{{{(5-\left( -1 \right))}^{2}}+{{(2-\left( -2 \right))}^{2}}}$

 $BC=\sqrt{{{(6)}^{2}}+{{(4)}^{2}}}$

 $BC=\sqrt{36+16}$

 $BC=\sqrt{52}$

To find AC,

 $AC=\sqrt{{{(5-\left( -5 \right))}^{2}}+{{(2-4)}^{2}}}$

 $AC=\sqrt{{{(10)}^{2}}+{{(-2)}^{2}}}$

 $AC=\sqrt{100+4}$

 $AC=\sqrt{104}$

Here, AB = AC and $A{{B}^{2}}+B{{C}^{2}}=A{{C}^{2}}$

Hence, ABC is an isosceles right angled triangle.

Now let the coordinates of point D is (x, y).

If ABCD is a square, then

Midpoint of diagonal BD = Midpoint of diagonal AC.

 $\left( \dfrac{-1 + x}{2}, \dfrac{-2 + y}{2} \right) = \left( \dfrac{-5 + 5}{2}, \dfrac{4 + 2}{2} \right)$

 $\left( \dfrac{x - 1}{2}, \dfrac{y - 2}{2} \right) = \left( 0, 3 \right)$

On comparing both the sides of the equation,

$0=\dfrac{x - 1}{2}$  and  $3= \dfrac{y - 2}{2}$

$x-1=0$  and  $y-2=6$

$x=1$  and  $y=8$

Hence, the coordinates of point D is (1, 8)

14. M is the midpoint of the line segment joining the points A(-3, 7) and B(9, -1). Find the coordinates of point M. Further, if R(2, 2) divides the line segment joining M and the origin in the ratio p : q, find the ratio p : q.

Ans: The given points are A = (-3, 7) and B = (9, -1).

Here M is the midpoint of AB,

 $M=\left( \dfrac{{{x}_{2}} + {{x}_{1}}}{2}, \dfrac{{{y}_{2}} + {{y}_{1}}}{2} \right)$

 $M=\left( \dfrac{-3 + 9}{2}, \dfrac{7 + \left( -1 \right)}{2} \right)$

 $M=\left( \dfrac{6}{2}, \dfrac{6 }{2} \right)$

 $M=\left( 3, 3 \right)$

Point R divides the line segment OM in the ratio of p : q where O is the origin.

Therefore,

 $R=\left( \dfrac{m{{x}_{2}} + n{{x}_{1}}}{m + n}, \dfrac{m{{y}_{2}} + n{{y}_{1}}}{m + n} \right)$

 $\left( 2,2 \right)=\left( \dfrac{p \times  0 + q \times  3}{p + q}, \dfrac{p \times  0 + q \times  3}{p + q} \right)$

 $\left( 2,2 \right)=\left( \dfrac{3q}{p + q}, \dfrac{3q}{p + q} \right)$

Compare both the sides of the equation,

$2=\dfrac{3q}{p + q}$ and $2=\dfrac{3q}{p + q}$

 $2p+2q=3q$

 $2p=q$

 $\dfrac{p}{q}=\dfrac{1}{2}$

Hence, p : q = 1 : 2.

15. Calculate the ratio in which the line joining A(-4, 2) and B(3, 6) is divided by point P(x, 3). Also, find 

(i) x 

(ii) length of AP.

Ans: (i) The given points are A = (-4, 2) and B = (3, 6)

Let P divides AB in the ratio k : 1,

 $P=\left( \dfrac{m{{x}_{2}} + n{{x}_{1}}}{m + n}, \dfrac{m{{y}_{2}} + n{{y}_{1}}}{m + n} \right)$

 $\left( x, 3 \right)=\left( \dfrac{k \times  3 + 1\times  \left( -4 \right)}{k + 1},\dfrac{k \times  6 + 1 \times  2}{k + 1} \right)$

 $\left( x, 3 \right)=\left( \dfrac{3 k - 4}{k + 1},\dfrac{6 k + 2}{k + 1} \right)$

On comparing both the sides, we get

$x=\dfrac{3 k - 4}{k + 1}$  and  $3=\dfrac{6 k + 2}{k + 1}$

For, $3=\dfrac{6 k + 2}{k + 1}$

 $3k+1=6k+2$

 $3k=1$

 $k=\dfrac{1}{3}$

Now as we know the value of k substitute in the other equation and find the value of x,

 $x=\dfrac{3 k - 4}{k + 1}$

 $\dfrac{1}{3}x+x=3\dfrac{1}{3}-4$

 $\dfrac{x}{3}+x=1-4$

 $\dfrac{x + 3x}{3}= -3$

 $x+3x= -9$

 $4x= -9$

 $x=\dfrac{-9}{4}$

(ii) Length of AP,

As P = (x, 3) then P = $\left( \dfrac{-9}{4},3 \right)$  [As we have already found, x = $\dfrac{-9}{4}$]

Using distance formula,

 $AP=\sqrt{{{({{x}_{2}}-{{x}_{1}})}^{2}}+{{({{y}_{2}}-{{y}_{1}})}^{2}}}$

 $AP=\sqrt{{{(-\dfrac{9}{4}-\left( -4 \right))}^{2}}+{{(3-2)}^{2}}}$

 $AP=\sqrt{{{(\dfrac{-9 + 16}{4})}^{2}}+{{(1)}^{2}}}$

 $AP=\sqrt{{{(\dfrac{7}{4})}^{2}}+1}$

 $AP=\sqrt{\dfrac{49}{16}+1}$

 $AP=\sqrt{\dfrac{49+16}{16}}$

 $AP=\sqrt{\dfrac{49+16}{16}}$

 $AP=\sqrt{\dfrac{65}{16}}$

 $AP=\dfrac{\sqrt{65}}{4} units$

16. Find the ratio in which the line 2x + y = 4 divides the line segment joining the points P(2, -2) and Q(3, 7).

Ans: Let the given line divides the line segment PQ in the ratio of k :1.

Then, 

 $\left( x,y \right)=\left( \dfrac{k \times  3 + 1 \times  2}{k + 1},\dfrac{k \times  7 + 1 \times  \left( -2 \right)}{k + 1} \right)$

 $\left( x,y \right)=\left( \dfrac{3 k + 2}{k + 1},\dfrac{7 k - 2}{k + 1} \right)$

Comparing both the sides, we get

$x=\dfrac{3 k + 2}{k + 1}$  and  $y=\dfrac{7 k - 2}{k + 1}$

Now that we have the value of x and y substitute this in the equation of the line 2x + y = 4

 $2\left( \dfrac{3 k + 2}{k + 1} \right)+\dfrac{7 k - 2}{k + 1}=4$

 $\dfrac{6 k + 4 + 7 k - 2}{k + 1}=4$

 $13 k + 2=4k+4$

 $9 k = 2$

 $k=\dfrac{2}{9}$

Thus, the ratio is 2 : 9.

17. If the abscissa of a point P is 2, find the ratio in which this point divides the line segment joining the points (-4, 3) and (6, 3). Also, find the coordinates of point P. 

Ans: Let the given points be A = (-4, 3) and B = (6, 3)

The abscissa of the point P is 2. Point P divides the line segment AB in a ratio of k : 1.

 $x=\dfrac{m{{x}_{1}} + n{{x}_{2}}}{m + n}$

 $2=\dfrac{k \times  6 + 1 \times  \left( -4 \right)}{k + 1}$

 $2k+2=6k - 4$

 $4k=6$

 $k=\dfrac{6}{4}$

 $k=\dfrac{3}{2}$

Thus, the ratio is 3 : 2.

So, the ordinate of point P will be,

 $y=\dfrac{m{{y}_{1}} + n{{y}_{2}}}{m + n}$

 $y=\dfrac{3 \times  3 + 2 \times  3}{3 + 2}$

 $y=\dfrac{9 + 6}{5}$

 $y=\dfrac{15}{5}$

 $y=3$

Thus, the coordinate of point P is (2, 3).

18. The line joining the points (2, 1) and (5, -8) is trisected at the points P and Q. If point P lies on the line 2x - y + k = 0, find the value of k. Also, find the coordinates of point Q.

Ans: 

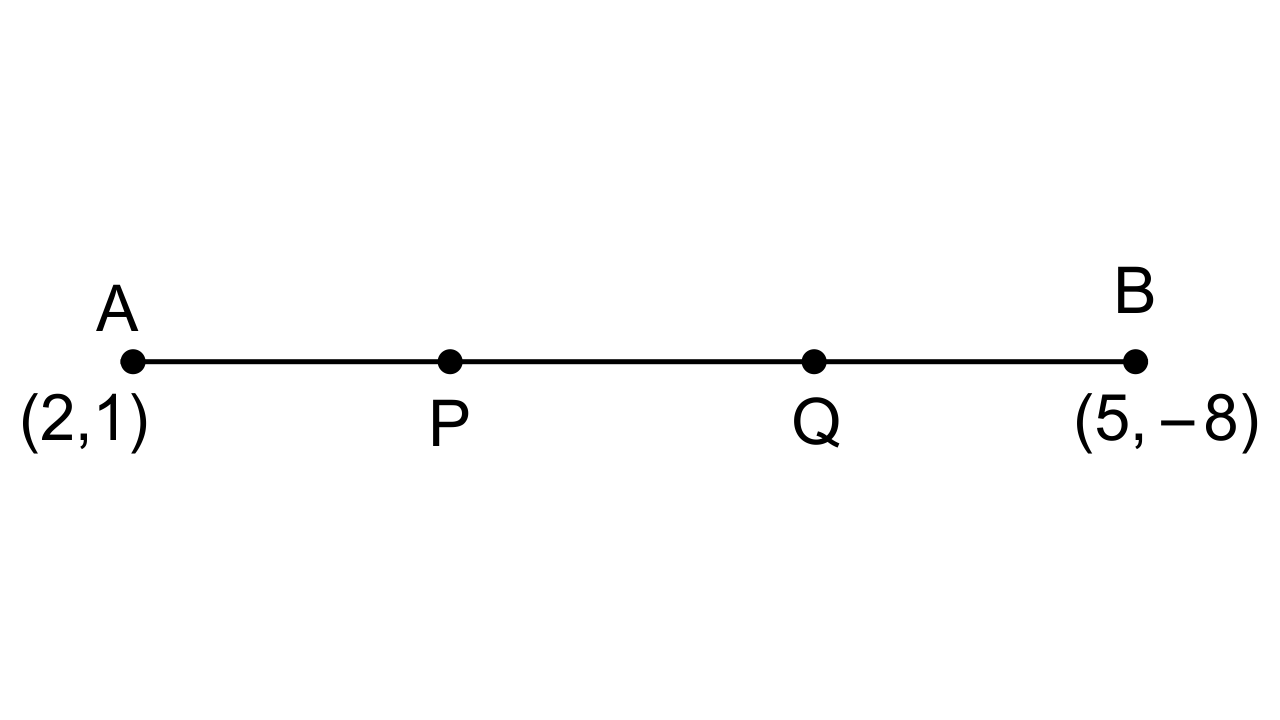
Here, points P and Q trisects AB.

Therefore, AP : PB = 1 : 2 and AQ : QB = 2 : 1.

Thus, $P=\left( \dfrac{m{{x}_{2}} + n{{x}_{1}}}{m + n}, \dfrac{m{{y}_{2}} + n{{y}_{1}}}{m + n} \right)$

 $\text{P}=\left( \dfrac{1 \times  5 + 2 \times  2}{1 + 2},\dfrac{1 \times  \left( -8 \right) + 2 \times  1}{1 + 2} \right)$

 $\text{P}=\left( \dfrac{5 + 4}{3},\dfrac{-8 + 2}{3} \right)$

 $\text{P}=\left( \dfrac{9}{3},\dfrac{-6}{3} \right)$

 $P=\left( 3, -2 \right)$

Given point P lies on the line 2x - y + k = 0

2(3) - (-2) + k = 0

6 + 2 + k = 0

k = -8

Hence the coordinate of point Q will be,

 $\text{Q}=\left( \dfrac{m{{x}_{2}} + n{{x}_{1}}}{m + n}, \dfrac{m{{y}_{2}} + n{{y}_{1}}}{m + n} \right)$

 $\text{Q}=\left( \dfrac{2 \times  5 + 1 \times  2}{2 + 1},\dfrac{2 \times  \left( -8 \right) + 1 \times  1}{2 + 1} \right)$

 $\text{Q}=\left( \dfrac{10 + 2}{3},\dfrac{-16 + 1}{3} \right)$

 $\text{Q}=\left( \dfrac{12}{3},\dfrac{-15}{3} \right)$

 $Q=\left( 4,-5 \right)$

19. Find the image of the point A(5, -3) under reflection in the point P(-1, 3). 

Ans: The point P is a midpoint in between point A and its image.

So, let the coordinate of the image be (x, y).

Therefore,

 $\text{P}=\left( \dfrac{{{x}_{2}} + {{x}_{1}}}{2},\dfrac{{{y}_{2}} + {{y}_{1}}}{2} \right)$

 $\left( -1, 3 \right)=\left( \dfrac{5 + x}{2},\dfrac{-3 + y}{2} \right)$

Comparing both the sides of the equation,

$-1=\dfrac{5 + x}{2}$  and  $3=\dfrac{-3 + y}{2}$

$x+5= -2$  and  $-3+y=6$

$x= -7$  and  $y=9$

Thus, the coordinate of the image is (−7, 9).

20. M is the mid-point of the line segment joining the points A(0, 4) and B(6, 0). M also divides the line segment OP in the ratio 1 : 3. Find: 

(i) coordinates of M 

(ii) coordinates of P 

(iii) length of BP 

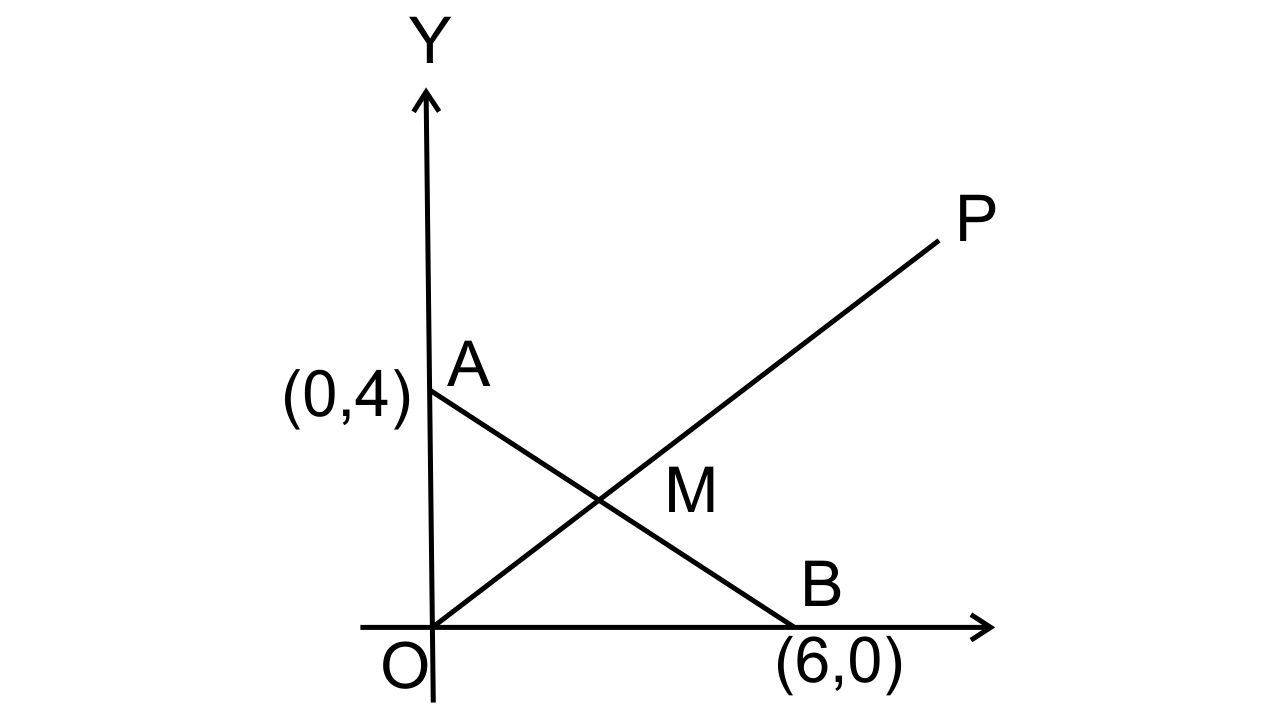
Ans: (i) Given that M is the midpoint of AB.

 $M=\left( \dfrac{{{x}_{2}} + {{x}_{1}}}{2},\dfrac{{{y}_{2}} + {{y}_{1}}}{2} \right)$

 $M=\left( \dfrac{0 + 6}{2},\dfrac{4 + 0}{2} \right)$

 $M=\left( 3, 2 \right)$

(ii) Now, Let the coordinate of point P be (x, y) where point P divides OP in a ratio of 1 : 3.

 $M=\left( \dfrac{m{{x}_{2}} + n{{x}_{1}}}{m + n}, \dfrac{m{{y}_{2}} + n{{y}_{1}}}{m + n} \right)$

 $\left( 3, 2 \right)=\left( \dfrac{1 \times  x + 3 \times  0}{1 + 3},\dfrac{1 \times  y + 3 \times  0}{1 + 3} \right)$

 $\left( 3,2 \right)=\left( \dfrac{x}{4},\dfrac{y}{4} \right)$

On comparing both the sides of the equation,

$\dfrac{x}{4}=3$  and  $\dfrac{y}{4}=2$

$x=12$  and  $y=8$

Thus, coordinates of point P are (12, 8).

(iii) Using distance formula length of BP can be calculated,

 $BP=\sqrt{{{({{x}_{2}}-{{x}_{1}})}^{2}}+{{({{y}_{2}}-{{y}_{1}})}^{2}}}$

 $BP=\sqrt{{{(12-6)}^{2}}+{{(8-0)}^{2}}}$

 $BP=\sqrt{{{(6)}^{2}}+{{(8)}^{2}}}$

 $BP=\sqrt{36+64}$

 $BP=\sqrt{100}$

 $BP=10 units$

21. A(-4, 2), B(0, 2) and C(-2. -4) are vertices of a triangle ABC. P, Q and R are midpoints of sides BC, CA and AB respectively. Show that the centroid of $\Delta $PQR is the same as the centroid of $\Delta $ABC.

Ans: Given vertices of triangle ABC are A = (-4, 2), B = (0, 2) and C = (-2. -4)

So the centroid of triangle ABC will be,

 $\text{L}=\left( \dfrac{{{x}_{1}} + {{x}_{2}} + {{x}_{3}}}{3},\dfrac{{{y}_{1}} + {{y}_{2}} + {{y}_{3}}}{3} \right)$

 $\text{L}=\left( \dfrac{-4 + 0 + \left( -2 \right)}{3},\dfrac{2 + 2 + \left( -4 \right)}{3} \right)$

 $L=\left( \dfrac{-6}{3},\dfrac{0}{3} \right)$

 $L= \left( -2, 0 \right)$

Points P, Q and R are the midpoints of sides BC, CA and AB respectively.

So, the coordinates of P will be,

 $\text{P}=\left( \dfrac{{{x}_{1}} + {{x}_{2}}}{2},\dfrac{{{y}_{1}} + {{y}_{2}}}{2} \right)$

 $\text{P}=\left( \dfrac{0 + \left( -2 \right)}{2},\dfrac{2 + \left( -4 \right)}{2} \right)$

 $\text{P}=\left( \dfrac{-2}{2},\dfrac{-2}{2} \right)$

 $P=\left( -1, -1 \right)$

Coordinate of Q will be,

 $\text{Q}=\left( \dfrac{{{x}_{1}} + {{x}_{2}}}{2},\dfrac{{{y}_{1}} + {{y}_{2}}}{2} \right)$

 $\text{Q}=\left( \dfrac{-4 + \left( -2 \right)}{2},\dfrac{2 + \left( -4 \right)}{2} \right)$

 $\text{Q}=\left( \dfrac{-6}{2},\dfrac{-2}{2} \right)$

 $Q=\left( -3,-1 \right)$

Coordinate of R will be,

 $\text{R}=\left( \dfrac{{{x}_{1}} + {{x}_{2}}}{2},\dfrac{{{y}_{1}} + {{y}_{2}}}{2} \right)$

 $\text{R}=\left( \dfrac{-4 + 0}{2},\dfrac{2 + 2}{2} \right)$

 $\text{R}=\left( \dfrac{-4}{2},\dfrac{4}{2} \right)$

 $R=\left( -2, 2 \right)$

Thus the centroid of triangle PQR will be,

 $M=\left( \dfrac{{{x}_{1}} + {{x}_{2}} + {{x}_{3}}}{3},\dfrac{{{y}_{1}} + {{y}_{2}} + {{y}_{3}}}{3} \right)$

 $M=\left( \dfrac{-1 + \left( -3 \right) + \left( -2 \right)}{3},\dfrac{\left( -1 \right) + \left( -1 \right) + 2}{3} \right)$

 $M=\left( \dfrac{-6}{3},\dfrac{0}{3} \right)$

 $M=\left( -2, 0 \right)$

In this case points L and M are at the same point.

Thus, the centroid of ∆ABC is the same as the centroid of ∆PQR.

22. A(3, 1), B(y, 4) and C(l, x) are vertices of triangle ABC and G(3, 4) is its centroid. Find the values of x and y. Also, find the length of side BC. 

Ans: Given vertices of triangle ABC are A = (3, 1), B = (y, 4) and C = (l, x)

Thus the centroid of triangle ABC will be,

 $\text{G}= \left( \dfrac{{{x}_{1}} + {{x}_{2}} + {{x}_{3}}}{3},\dfrac{{{y}_{1}} + {{y}_{2}} + {{y}_{3}}}{3} \right)$

 $\left( 3, 4 \right)=\left( \dfrac{3 + y + 1}{3},\dfrac{1 + 4 + x}{3} \right)$

 $\left( 3, 4 \right)=\left( \dfrac{4 + y}{3},\dfrac{5 + x}{3} \right)$

On comparing both the sides of the equation

$3=\dfrac{y + 4}{3}$  and  $4=\dfrac{x + 5}{3}$

$y+4=9$  and  $x+5=12$

$y=5$  and  $x=7$

So, the coordinate of points B = (5, 4) and C = (1, 7).

Thus the length of side BC can be calculated using distance formula,

 $BC=\sqrt{{{({{x}_{2}}-{{x}_{1}})}^{2}}+{{({{y}_{2}}-{{y}_{1}})}^{2}}}$

 $BC=\sqrt{{{(1-5)}^{2}}+{{(7-4)}^{2}}}$

 $BC=\sqrt{{{(-4)}^{2}}+{{(3)}^{2}}}$

 $BC=\sqrt{16+9}$

 $BC=\sqrt{25}$

 $BC=5 units$.

Selina Concise Mathematics Class 10 ICSE Solutions for Chapter 13 Section and MidPoint Formula Part-1

Vedantu offers ICSE Class 10 Chapter 13 Maths Solutions for free to benefit the students preparing for the examinations. As discussed earlier, this chapter is extremely important in dealing with the majority of problems in coordinate geometry. This PDF of ICSE Class 10 Chapter 13 Maths Solution has detailed explanations of both Mid-point and Section formulas. Also, this chapter discusses many practical applications in finding the coordinates of major points in triangles such as centroid, incenter, circumcenter, and so on under applications of section formula. Now let us look at important topics that are covered in ICSE Mathematics Class 10 Solutions Chapter 13:

• Section formula

• Finding points of trisection

• Midpoint formula

• Calculating the centroid of a triangle

• Section Formula

How to solve the Questions Given in Chapter 13 - Section and Midpoint Formula?

A point on the line segment splits it into two sections that may or may not be equal. If we know the coordinates of the point, we can calculate the ratio by which it divides the given line segment. Also, if we know the ratio of the line segment joining two points, we can find the point of division. These two objectives can be achieved with the help of a section formula in coordinate geometry.

The section formula is used to calculate the coordinate of a point that divides a line segment separating two points into two sections with a length ratio of m:n.

Let P and Q denote the given two points (x1,y1) and (x2,y2), respectively, and M represents the point dividing the line segment PQ internally in the ratio m:n, then the Section Formula for determining the coordinate of a point M is defined by:

M(x,y)=\[\left (\frac{mx_{2}+nx_{1}}{m+n} , \frac{my_{2}+ny_{1}}{m+n}\right )\]

Sectional Formula when the Line-Segment Divides Externally

The Sectional Formula can also be used to find the coordinates of a point that lies outside the line when the length of a point from both lines segments is in the ratio m:n. Section Formula for determining the coordinate, in this case, is defined by:

\[\left (\frac{mx_{2}-nx_{1}}{m-n} , \frac{my_{2}-ny_{1}}{m-n}\right )\]

Mid-Point

The Midpoint formula is used to calculate the center of a straight line. You may sometimes need to find the number that is half of two specific numbers. You have to find the average of the two numbers for this. Similarly, in coordinate geometry, we use the midpoint formula to find the Midpoint between two coordinates.

1. Formula to the Midpoint

To find the midpoint of a straight line in the graph, we can use this Midpoint formula that will help us to find the coordinates of the midpoint of that given line. Let the endpoints of the line be A (x1, y1) and B (x2, y2) then the midpoint is calculated using the formula given below.

\[(x,y)  = \left [ \frac{x_{1}+x_{2}}{2}, \frac{y_{1}+y_{2}}{2}\right ]\]

The section formula not only gives us the coordinates of the point which divides the given line segment or line segment joining two points into two parts such that their lengths are in the ratio m: n internally or externally but also have various practical uses in finding coordinates of major points in a triangle such as Midpoint of a line segment, centroid, incenter, circumcenter, etc. The midpoint formula is used to locate a point (its coordinate values) in a plane that is exactly between two other points. The formula has a wide range of applications in geometry. By referring to this, Selina Concise Maths Solution Class 10 Chapter 13, students will improve their analytical and logical thinking abilities of geometry and the above-mentioned concepts.

Exercises in Selina Concise Mathematics Class 10 Solutions Chapter 13 - Section and Midpoint Formula:

Students should attempt to solve the following exercises to strengthen their understanding of Chapter 13 - Section and Midpoint formula

• Exercise 13 (A) Solutions

• Exercise 13 (B) Solutions

• Exercise 13 (C) Solutions

Tips to prepare for Exams using Selina Concise Maths Solution for Class 10 Chapter 13

Chapter 13 is all about formulas, concepts, and definitions, so keep them handy at all times. You can read them when you're on the go. This technique is extremely beneficial when doing last-minute revisions.

1. It is helpful to experience various types of problems, but you must also ensure that you solve them for yourself. It is easy to learn theories and concepts, but it is more difficult to learn how to apply them. So, if you want to get maximum marks in Mathematics, you must solve and question independently at least three to four times.

2. When you go through the answers, make sure to pay close attention to the steps that helped you get the answer. Since you can't just write the answer and get maximum marks in Math, just paying attention to the figures is a waste of time. Rather than all of this, learn the steps involved. You will certainly get some marks for each step.

3. Understand your strengths and weaknesses, and work to improve both.

4. If you notice any questions that seem to be critical when practicing, make a note of them. You must solve the question again later when revising this chapter; this will help you brush up on your concepts.

5. Using graphs and figures with focus and neatness will also help you achieve full marks.

Conclusion

The ICSE Mathematics Class 10 Solutions Chapter 13 prepared by Vedantu experts covers all important concepts according to the syllabus. A lot of research has been done on the solutions to provide a fun learning environment for students. The free PDF provided by Vedantu on Selina Concise Maths Solution Class 10 Chapter 13 also includes plenty of exercises and practice problems so that students can be more confident about their subject knowledge.