CBSE Physics Experiment To Measure Diameter of a Given Wire Using Screw Gauge

Measurement is a common problem in both physics and engineering. Many times we are required to accurately measure extremely small lengths such as the diameter of a thin wire, the thickness of a sheet, etc. in construction and blueprint services. Any small miscalculation might lead to large errors in the measurement. Therefore, it becomes essential to get a simple hands-on way to measure the diameter of a given wire using a screw gauge.

Table of Contents

• Aim

• Theory

• Procedure

• Observations

• Result

Aim

To measure the diameter of a given wire using a screw gauge.

Apparatus required

• Given wire

• Screw gauge

• Magnifying glass

Theory

A screw gauge works using a main and a circular scale. The distance covered on the main scale by the circular scale after completing one full rotation is known as the pitch of the circular scale or pitch of screw gauge. In this experiment, we put the wire between the two rods of the main scale and gently tighten the rods using the screw of the circular scale. The corresponding readings on the main and circular scales give the measurement of the diameter of the wire.

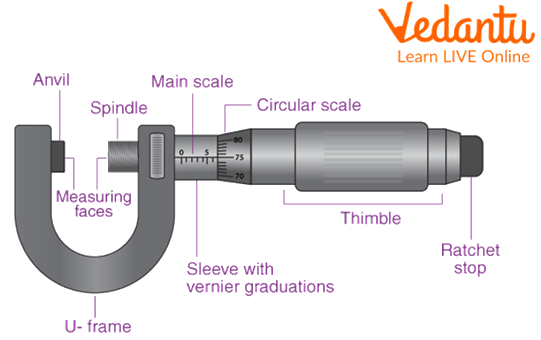
Schematic Diagram of Screw Gauge with its Components

Procedure

1. Rotate the circular scale so that it traverses towards the fixed end of the gauge, till it comes in contact with the end (Please refer to the image given above).

2. Check if the zero of circular scale coincides with the zero of main scale. If not, note the circular scale division that coincides best with the main engraved scale.

3. Now rotate the circular scale exactly once and note the division on the main scale with which the circular scale coincides to get the pitch.

4. Divide this distance by the number of divisions on a circular scale to get the least count.

5. Now, rotate the circular scale using a screw in the opposite direction and hold the wire between the two rods of the main scale. Hold the wire gently between the rods till the screw stops rotating.

6. Note the main scale reading where the circular scale lies using a magnifying glass.

7. Note the circular scale reading, which coincides with the main scale.

8. Loosen the circular scale screw and note both readings in a similar fashion two other times. Note the observations.

Observations

Pitch of the screw gauge = 1 mm

Number of divisions on circular scale = 100

Least count = \[\dfrac{\text{Pitch}}{\text{Number of divisions}}\; = \dfrac{{1\;mm}}{{100}} = 0.01\;mm\]

Observation Table

Result

Average diameter of the wire, 

D =\[\dfrac{{D_1 + D_2 + D_3}}{3} = …………\]

Precautions

1. Note the zero error very carefully.

2. Do not hold the wire using the gauge too tightly or too loosely.

3. Only note the circular scale division which coincides best with the main scale using magnifying glass. If no division is coinciding, note the preceding division.

Lab Manual Questions

1. Out of two screw gauges having 100 and 300 divisions respectively, which should be preferred for taking readings and why?

Ans: Out of these two screw gauges, the one with 300 divisions on the circular scale should be preferred for taking readings. This is because the least count of a screw gauge is inversely proportional to the circular scale divisions, and more accuracy can be reached with decreasing the least count.

2. How to solve the instrumental error arising when the linear distance moved by the screw is not proportional to the rotation given to it?

Ans: In such situations, the screw becomes torn out from the inside and develops a lot of irregularities. It is advisable to replace the screw.

3. Explain the scales of the screw gauge? How does a zero error arise?

Ans: A screw gauge has two scales - one is the main scale and another one is a circular scale with 100 divisions engraved on it. When the zero error of the circular scale does not coincide with the zero of the main scale, zero error arises.

4. Why does a screw gauge develop a backlash error after some time?

Ans: Due to wear and tear of the instrument, a screw gauge develops a backlash error after some time due to the development of numerous irregularities inside the circular scale.

Viva Questions

1. Explain the working principle of a screw gauge.

Ans: A screw gauge is based on the principle of a rotating screw. As the screw rotates, it covers a linear distance on the main scale. This gives us the pitch and least count and hence the required accuracy for measurement.

2. What are the orders of length a screw gauge is suitable for measuring?

Ans: A screw gauge is capable of precisely measuring lengths up to 0.01 mm.

3. Why is a screw gauge called a micrometer gauge?

Ans: The precision up to which a screw gauge can measure is 0.01 mm and it is equivalent to the 10 µm, therefore, as we can see it lies in the range of micrometer the screw gauge is also called a micrometer gauge.

4. Write three commercial applications of a screw gauge.

Ans: Screw gauge finds commercial applications in precisely determining the diameter of thin wires, the thickness of a paper sheet and the thickness of a given experimental metallic chip used in communication devices.

5. Explain the formula for the calculation of least count.

Ans: Least count is calculated by dividing the distance covered by the circular scale on its one full rotation on the main scale (pitch) by the number of divisions on the circular scale.

6. Explain zero error. How to determine zero error?

Ans: A zero error is the error which arises in the final result when the zeroes of the main scale and circular scale do not coincide. It is determined by noting the main scale division with which the circular scale coincides at the full range of rotation of the circular scale.

7. How is a screw gauge better than a vernier calliper?

Ans: A screw gauge has a greater precision of 0.01 mm of measuring lengths compared to vernier calipers (0.1 mm). Hence, the lengths measured by a screw gauge are more accurate to a second decimal than a vernier calliper.

8. Give the working formula of a screw gauge.

Ans: The final reading is given by the sum of main scale and circular scale readings, which is given by the product of the number of coinciding circular scale divisions and the least count of the instrument.

9. What is pitch?

Ans: The length covered by the circular scale over the main scale on one complete rotation of the circular scale is known as the pitch of the instrument. It is roughly equal to 1 mm.

10. Name two other examples that can be used alternatively in the above experiment.

Ans: The thickness of the sheet of paper and the diameter of a thin stick can also be used in the above experiment.

Practical Based Questions

1. Least count of screw gauge is:

1. 1 mm

2. 0.1 mm

3. 0.01 mm

4. 0.001 mm

Ans: (C) The least count of a screw gauge is 0.01 mm.

2. How many screws are there in a screw gauge?

1. 1

2. 2

3. 3

4. 4

Ans: (A) A screw gauge has 1 screw for the movable hinge.

3. How many scales does a screw gauge have?

1. 2

2. 3

3. 5

4. 6

Ans: (A) A screw gauge has 2 scales

4. The ratio of the least counts of the centimeter scale to that of a screw gauge is:

1. 1

2. 10

3. 100

4. 1000

Ans: (C) The least count of a centimeter scale is 1 mm, while that of a screw gauge is 0.01 mm. Hence the ratio is 100.

5. Screw gauge is ideal for measuring:

1. Edge of a dice

2. Thickness of a wire

3. Radius of curvature

4. Length of a notebook

Ans: (B) A screw gauge can be used to accurately measure the thickness of a wire.

6. A screw gauge can be manufactured by a combination of:

1. Copper and tin

2. Aluminum

3. Stainless steel and iron

4. None of the above

Ans: (C) A screw gauge can be manufactured by a combination of stainless steel and iron.

7. The error that arises when the zeroes of the main scale and the circular scale do not coincide is called:

1. Systematic error

2. Random error

3. Backlash error

4. Zero error

Ans: (D) The error that arises when the zeroes of main and circular scales do not coincide is called zero error.

8. Accuracy of measurement can be increased by:

1. Increasing the number of divisions on circular scale

2. Using a magnifying glass

3. Using a thick wire for measuring diameter

4. Using more circular scales

Ans: (A) The accuracy of measurement can be increased by increasing the number of divisions on a circular scale.

9. How many types of zero errors are there?

1. One

2. Two

3. Three

4. Four

Ans: (B) There are two types of zero errors - positive and negative.

10. Which of the following is not suitable for measurement by a screw gauge?

1. Diameter of a thin wire

2. Thickness of a fine slab

3. Depth of a vessel

4. Thickness of a semiconductor chip

Ans: (C) Depth of a vessel is not suitable for measurement by a screw gauge.

Conclusion

From this experiment, we can conclude that screw gauge finds immense applications in the field of experimental physics in order to accurately measure the diameter of thin wires, the thickness of a sheet etc. They find various commercial applications in numerous engineering and medical fields in the society.

Throughout this experiment, we have taken utmost care in teaching the novice about the very idea, and the basic parameters should have been crystal clear in his/ her mind.

We hope that the reader is now enlightened regarding the very concept of the same and is motivated to explore the field in the time to come.