NCERT Exemplar for Class 8 Maths Solutions Chapter 8 Exponents & Powers

Solved examples

1. Multiplicative inverse of 27 is

(a) 2–7 

(b) 72 

(c) – 27 

(d) – 27

Ans: The Correct answer is (a).

Multiplicative inverse of ${2^7} = \dfrac{1}{{{2^7}}} = {2^{ - 7}}$

2. The human body has about 100 billion cells. This number can be written in exponential form as

(a) 10–11 

(b) 1011 

(c) 109 

(d) 10–9

Ans: The correct answer is (b).

100 billion = 100,000,000,000 = 1011

In questions 3 to 5, fill in the blanks to make the statements true.

3. ${\left( { - 4} \right)^4} \times {\left( {\dfrac{5}{4}} \right)^4} = \_\_\_\_\_$

Ans: 54

${\left( { - 4} \right)^4} \times \dfrac{{{5^4}}}{{{4^4}}} = {4^4} \times \dfrac{{{5^4}}}{{{4^4}}} = {5^4}$

4. ${\left( {{2^{ - 3}}} \right)^2} \times {\left( {{3^{ - 2}}} \right)^3} = \_\_\_\_\_$

Ans: 6–6

${\left( {{2^{ - 3}}} \right)^2} \times {\left( {{3^{ - 2}}} \right)^2} = {2^{ - 6}} \times {3^{ - 6}}$

=${\left( {2 \times 3} \right)^{ - 6}} = {6^{ - 6}}$ 

5. The distance between earth and sun is 150 million kilometers which can be written in exponential form as _______.

Ans: 1.5 × 108 km

1 million km = 1000000 km

150 million km = 150000000 km = 1.5 × 108 km 

In questions 6 and 7, state whether the statements are true (T) or false (F):

6. Very small numbers can be expressed in standard form using positive exponents.

Ans: False.

7. (–10) × (–10) × (–10) × (–10) = 10–4

Ans: False.

(–10) × (–10) × (–10) × (–10) = (-10)4 or (10)4

8. Simplify $\dfrac{{{{\left( { - 2} \right)}^3} \times {{\left( { - 2} \right)}^7}}}{{3 \times {4^6}}}$

Ans: $\dfrac{{{{\left( { - 2} \right)}^3} \times {{\left( { - 2} \right)}^7}}}{{3 \times {4^6}}} = \dfrac{{{{\left( { - 2} \right)}^{3 + 7}}}}{{3 \times {{\left( {{2^2}} \right)}^6}}} = \dfrac{{{{\left( { - 2} \right)}^{3 + 7}}}}{{3 \times {2^{12}}}}$

= $\dfrac{{{{\left( { - 2} \right)}^{3 + 7}}}}{{3 \times {2^{12}}}} = \dfrac{{{{\left( { - 2} \right)}^{10}}}}{{3 \times {2^{12}}}} = \dfrac{{{2^{10}}}}{{3 \times {2^{12}}}}$

= $\dfrac{{{2^{10 - 12}}}}{3} = \dfrac{{{2^{ - 2}}}}{3} = \dfrac{1}{{3 \times {2^2}}} = \dfrac{1}{{12}}$

9. Find x so that (–5)x+1 × (–5)5 = (–5)7

Ans: (–5)x+1 × (–5)5 = (–5)7

(–5)x+1+5 = (–5)7 {As am × an = am+n}

(–5)x+6 = (–5)7

On both sides, powers have the same base, so their exponents must be equal.

Therefore, x + 6 = 7

x = 7 – 6 = 1

So, x = 1

Hence, the value of x is 1.

Exercise

In questions 1 to 33, out of the four options, only one is correct. Write the correct answer.

1. In 2n, n is known as

(a) Base 

(b) Constant 

(c) Exponent 

(d) Variable

Ans: Option (c) is correct.

2 is a rational number as base in expression, and n is the power of that base which is called an exponent or power or index.

2. For a fixed base, if the exponent decreases by 1, the number becomes

(a) One-tenth of the previous number.

(b) Ten times of the previous number.

(c) Hundredth of the previous number.

(d) Hundred times of the previous number.

Ans: Option (a) is correct.

If the exponent is decreased by 1, then for the

fixed base, the number becomes one-tenth of the previous

number.

e.g.- For 104, exponent decreases by 1

104-1 = 103

$\Rightarrow \dfrac{{{{10}^3}}}{{{{10}^4}}} = \dfrac{1}{{10}}$

3. 3–2 can be written as

(a) 32 

(b) $\dfrac{1}{{{3^2}}}$

(c) $\dfrac{1}{{{3^{ - 2}}}}$

(d) $ - \dfrac{2}{3}$

Ans: Option (b) is correct.

Use, law of exponent ${a^{ - m}} = \dfrac{1}{{{a^m}}}$ where a is a non zero integer.

Thus, ${3^{ - 2}} = \dfrac{1}{{{3^2}}}$

4. The value of $\dfrac{1}{{{4^{ - 2}}}}$ is

(a) 16

(b) 8

(c) $\dfrac{1}{{16}}$

(d) $\dfrac{1}{8}$

Ans: Option (a) is correct.

Use, law of exponent ${a^{ - m}} = \dfrac{1}{{{a^m}}}$ where a is a non zero integer.

Thus, $\dfrac{1}{{{4^{ - 2}}}} = \dfrac{1}{{\dfrac{1}{{{4^2}}}}} = {4^2} = 16$

5. The value of 35 ÷ 3–6 is

(a) 35 

(b) 3–6 

(c) 311 

(d) 3–11 

Ans: Option () is correct.

Use, law of exponent ${a^m} \div {a^n} = {a^{m - n}}$ where a is a non zero integer.

Thus, ${3^5} \div {3^{ - 6}} = {3^{5 - \left( { - 6} \right)}} = {3^{5 + 6}} = {3^{11}}$.

6. The value of ${\left( {\dfrac{{\mathbf{2}}}{{\mathbf{5}}}} \right)^{{\mathbf{ - 2}}}}$ is

(a) $\dfrac{4}{5}$

(b) $\dfrac{4}{{25}}$

(c) $\dfrac{{25}}{4}$

(d) $\dfrac{5}{2}$

Ans: Option (c) is correct.

Use, law of exponent ${a^{ - m}} = \dfrac{1}{{{a^m}}}$ where a is a non zero integer.

Thus, ${\left( {\dfrac{2}{5}} \right)^{ - 2}} = \dfrac{1}{{{{\left( {\dfrac{2}{5}} \right)}^2}}} = \dfrac{1}{{\dfrac{4}{{25}}}} = \dfrac{{25}}{4}$

7. The value of ${\left( {\dfrac{{\mathbf{2}}}{{\mathbf{5}}}} \right)^{{\mathbf{ - }}1}}$ is

(a) $\dfrac{2}{5}$

(b) $\dfrac{5}{2}$

(c) $ - \dfrac{5}{2}$

(d) $ - \dfrac{2}{5}$

Ans: Option (b) is correct.

Use the law of exponent ${a^{ - m}} = \dfrac{1}{{{a^m}}}$, where a is a non zero integer.

Thus, ${\left( {\dfrac{2}{5}} \right)^{ - 1}} = \dfrac{1}{{{{\left( {\dfrac{2}{5}} \right)}^1}}} = \dfrac{1}{{\dfrac{2}{5}}} = \dfrac{5}{2}$

8. The multiplicative inverse of 10-100 is

(a) 10

(b) 100

(c) 10100

(d) 10-100

Ans: Option (c) is correct.

For multiplicative inverse, let a be the multiplicative of 10-100

So,  

$a \times {10^{ - 100}} = 1$

$\Rightarrow a = \dfrac{1}{{{{10}^{ - 100}}}} = {10^{100}}$

9. The value of (-2)2×3-1 is

(a) 32

(b) 64

(c) -32

(d) -64

Ans: Option (c) is correct.

For (-a)m, if m is odd, then (-a)m is negative

(-2)2×3-1 = (-2)6–1 = (-2)5

= (-2) × (-2) × (-2) × (-2) × (-2) = - 32

10. The value of ${\left( {\dfrac{{ - 2}}{3}} \right)^4}$ is equal to

(a) $\left( {\dfrac{{16}}{{81}}} \right)$

(b) $\left( {\dfrac{{81}}{{16}}} \right)$

(c) $\left( {\dfrac{{ - 16}}{{81}}} \right)$

(d) $\left( {\dfrac{{81}}{{ - 16}}} \right)$

Ans: Option (a) is correct.

For (-a)m, if m is even, then (-a)m is positive.

${\left( { - \dfrac{2}{3}} \right)^4} = \left( { - \dfrac{2}{3}} \right) \times \left( { - \dfrac{2}{3}} \right) \times \left( { - \dfrac{2}{3}} \right) \times \left( { - \dfrac{2}{3}} \right) = \dfrac{{16}}{{81}}$

11. The multiplicative inverse of ${\left( { - \dfrac{5}{9}} \right)^{ - 99}}$ is

(a) ${\left( { - \dfrac{5}{9}} \right)^{99}}$

(b) $\left( {{{\dfrac{5}{9}}^{99}}} \right)$

(c) ${\left( {\dfrac{9}{{ - 5}}} \right)^{99}}$

(d) ${\left( {\dfrac{9}{5}} \right)^{99}}$

Ans: Option (a) is correct.

For multiplicative inverse, a is called multiplicative inverse of b, if a x b = 1.

Thus,

$\Rightarrow a \times {\left( {\dfrac{{ - 5}}{9}} \right)^{ - 99}} = 1$

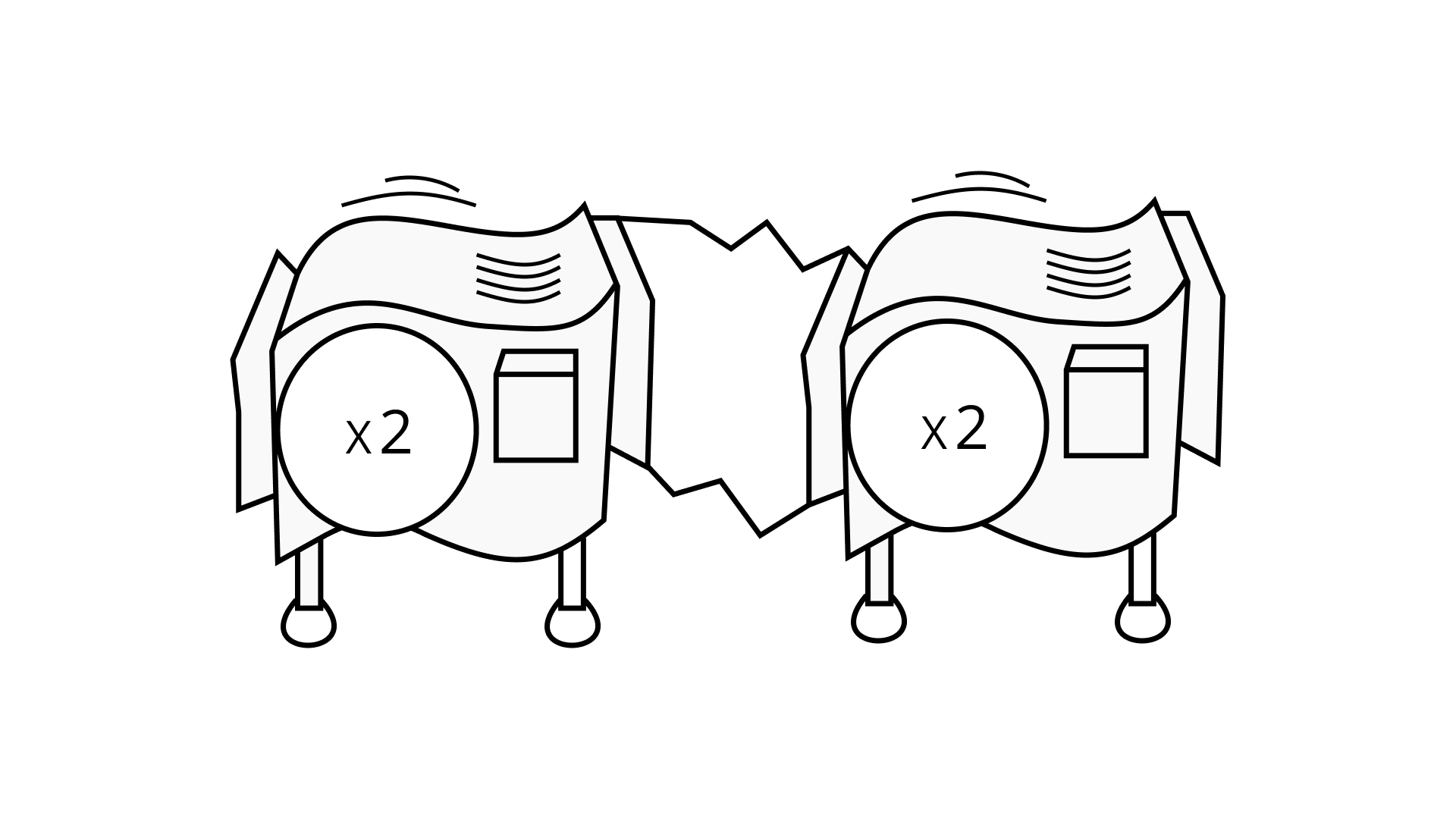
$\Rightarrow a = \dfrac{1}{{{{\left( {\dfrac{{ - 5}}{9}} \right)}^{ - 99}}}} = {\left( { - \dfrac{5}{9}} \right)^{99}}$

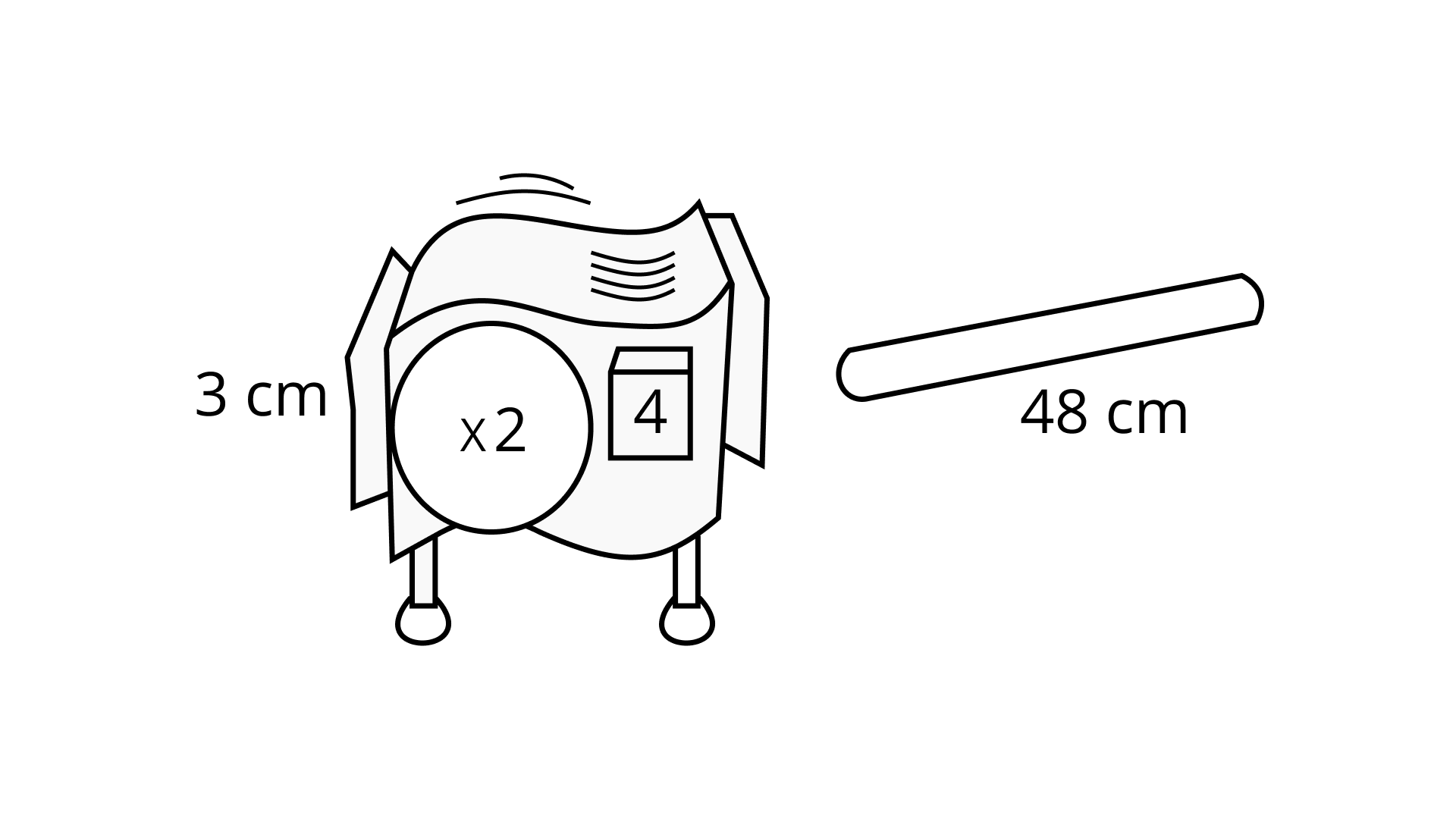
12. If x be any non-zero integer and m, n be negative integers, then xm $\times$ xn is equal to

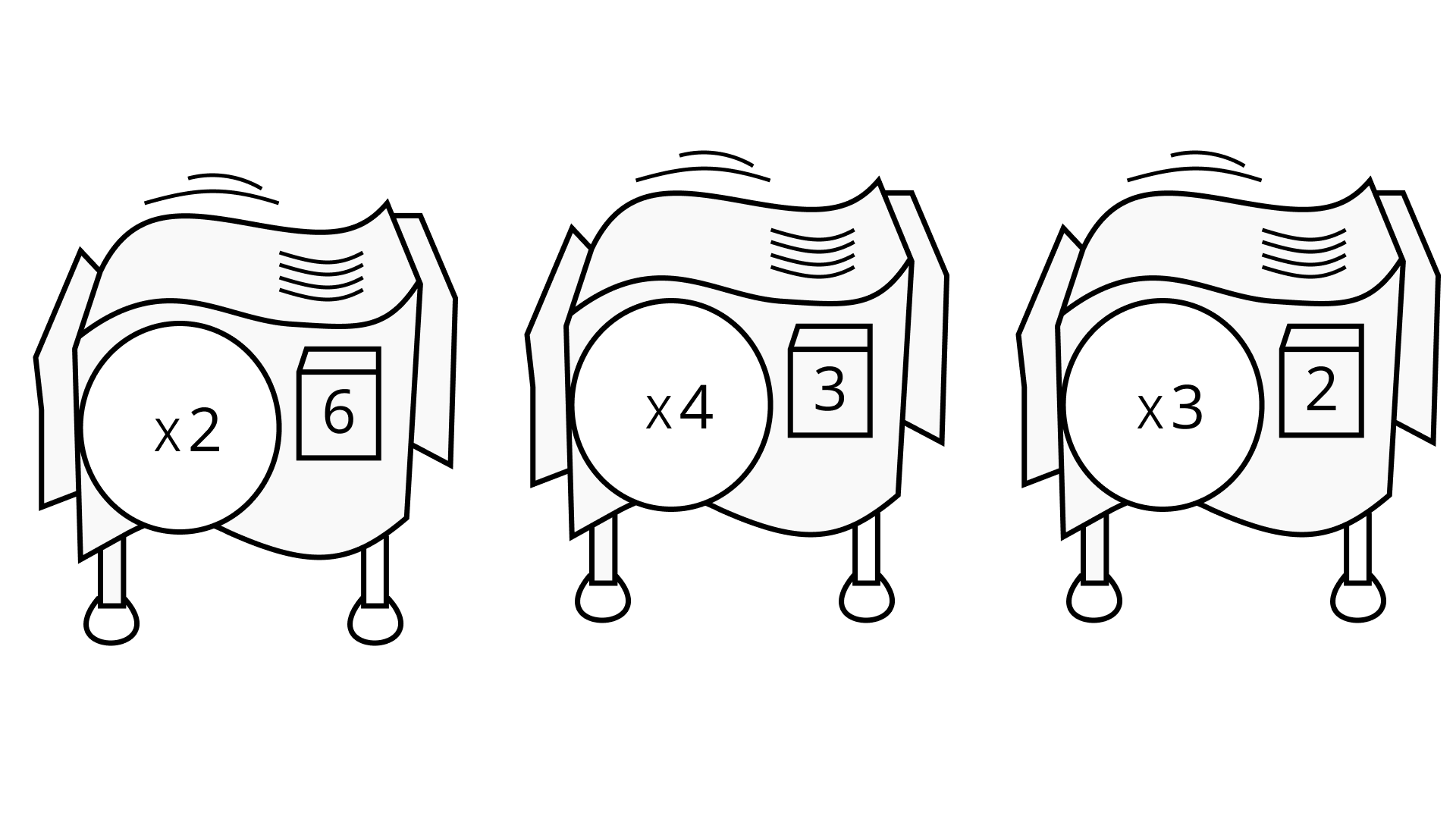
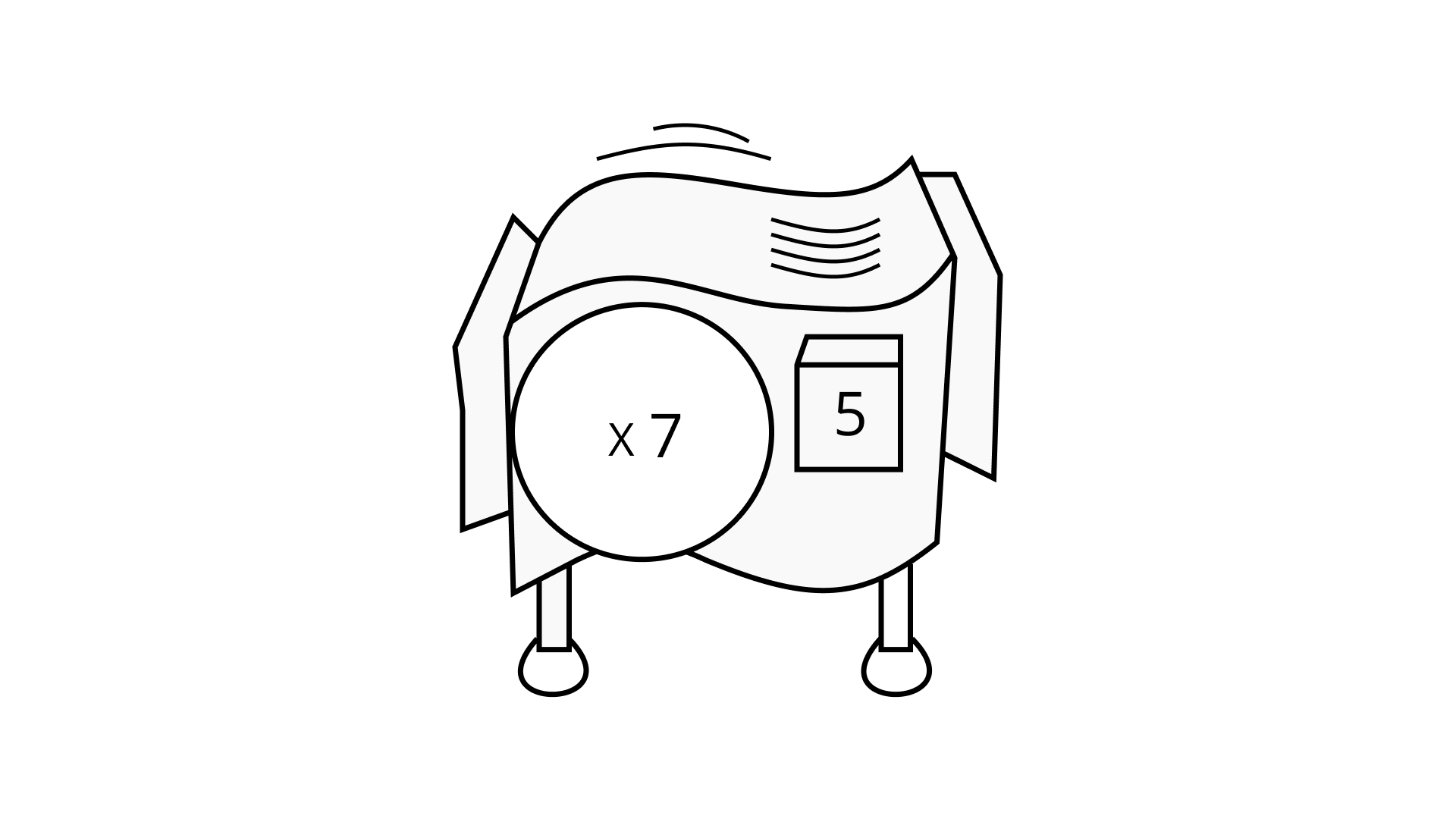
(a) xm 

(b) xm+n 

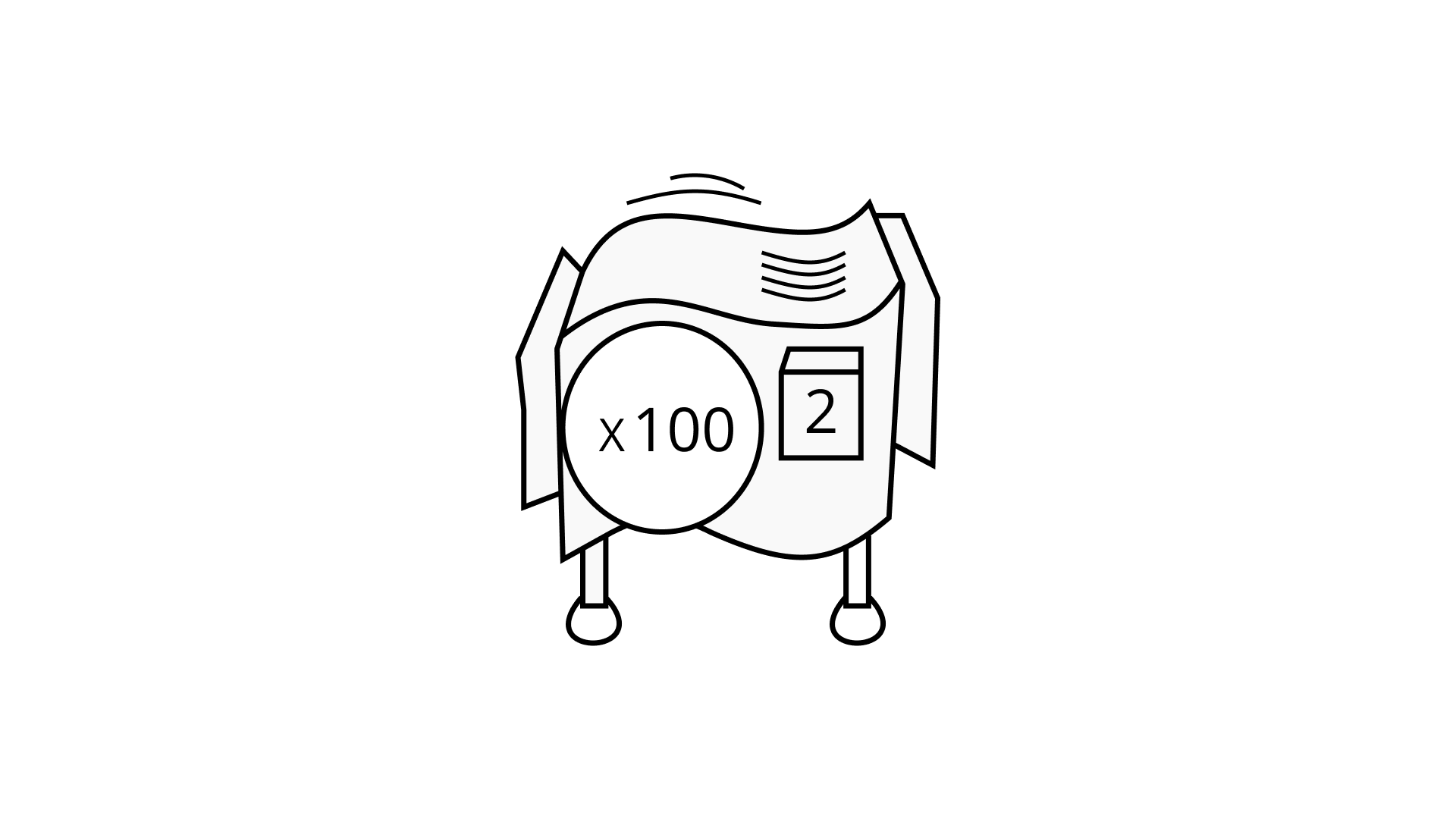
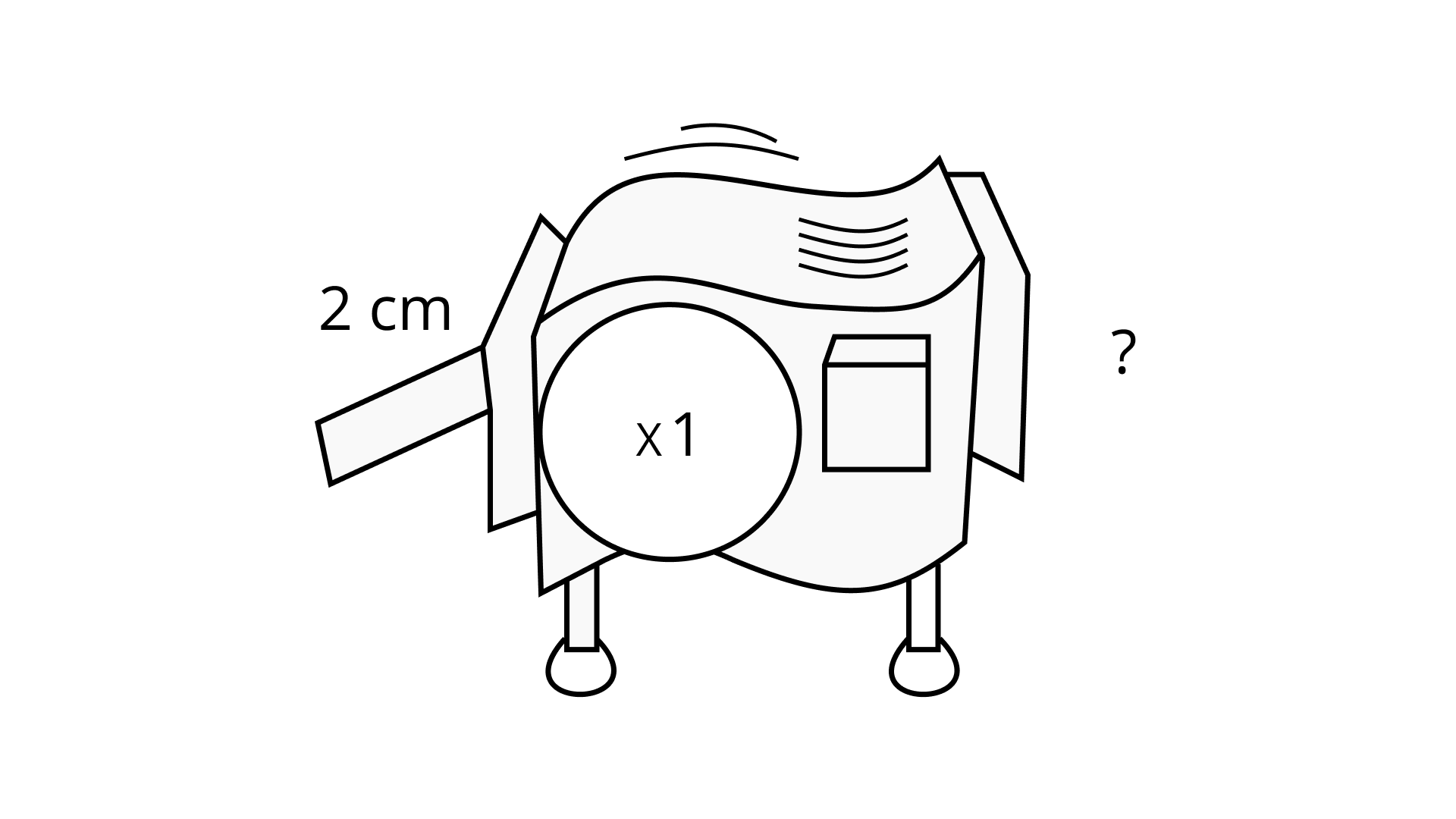
(c) xn 

(d) xm–n

Ans: Option (b) is correct.

Using law of exponents, am × an = (a)m+n (Where, a is a non-zero integer)

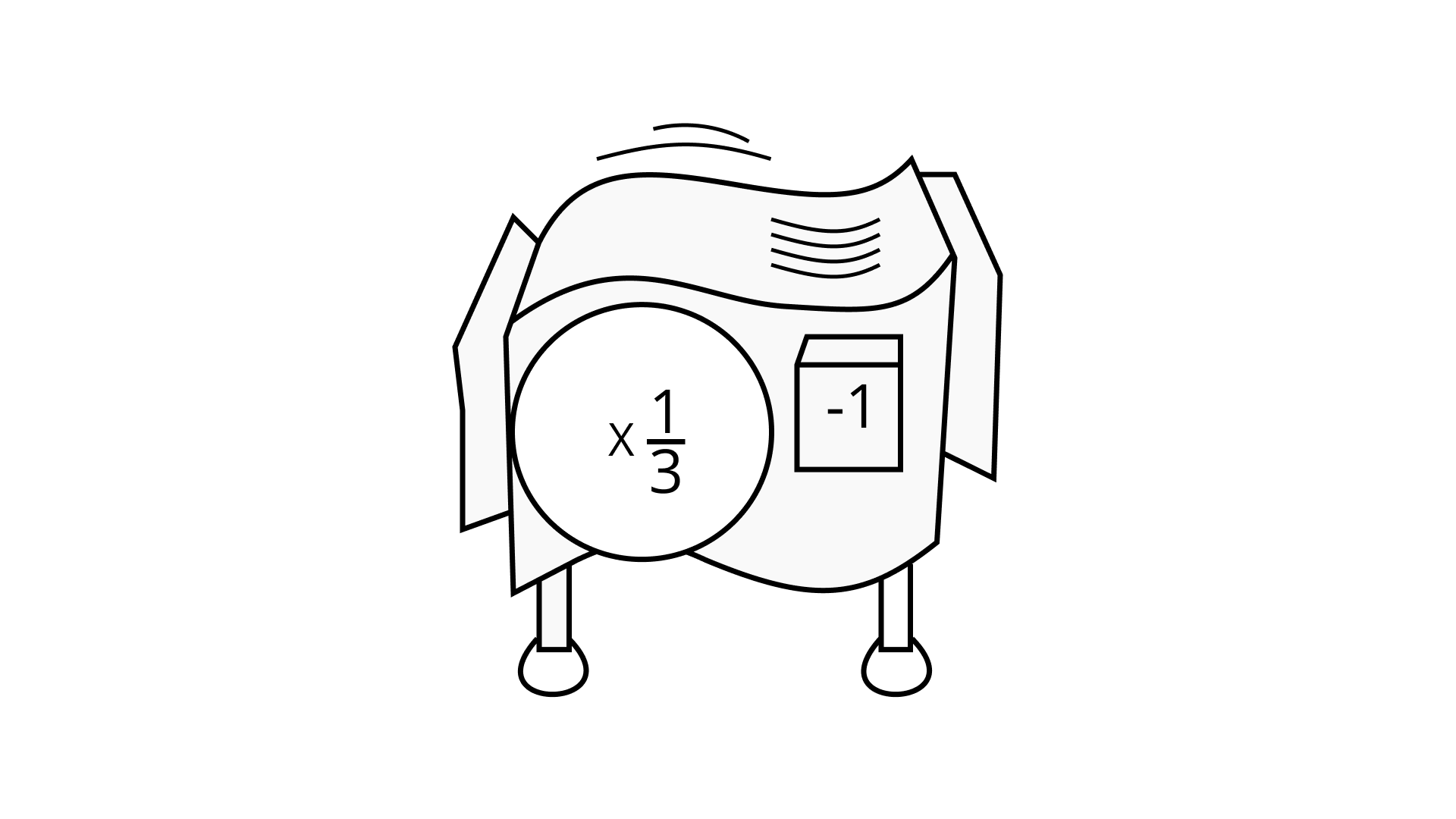
Similarly, xm$\times$xn = (x)m+n

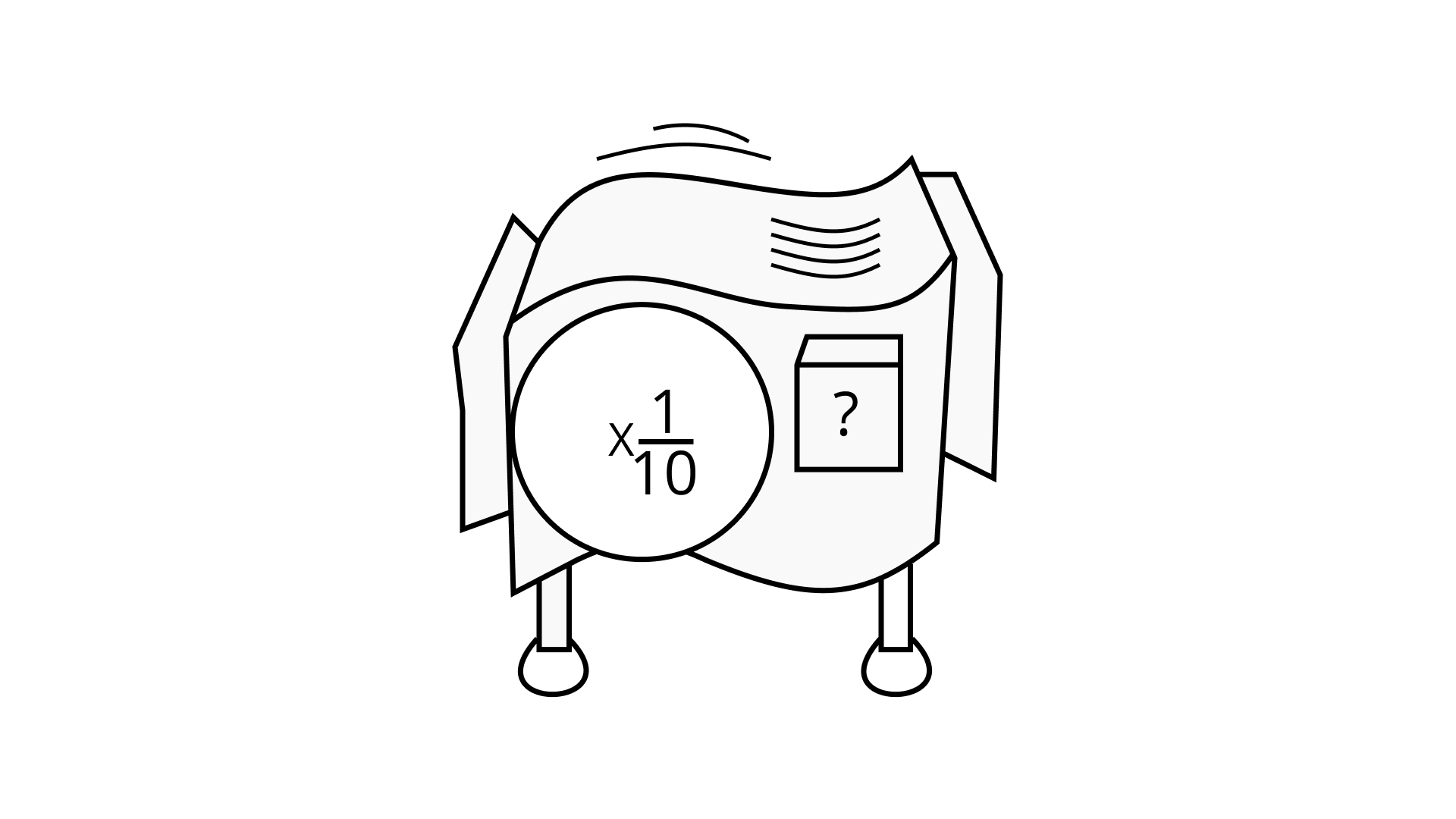
13. If y be any non-zero integer, then y0 is equal to

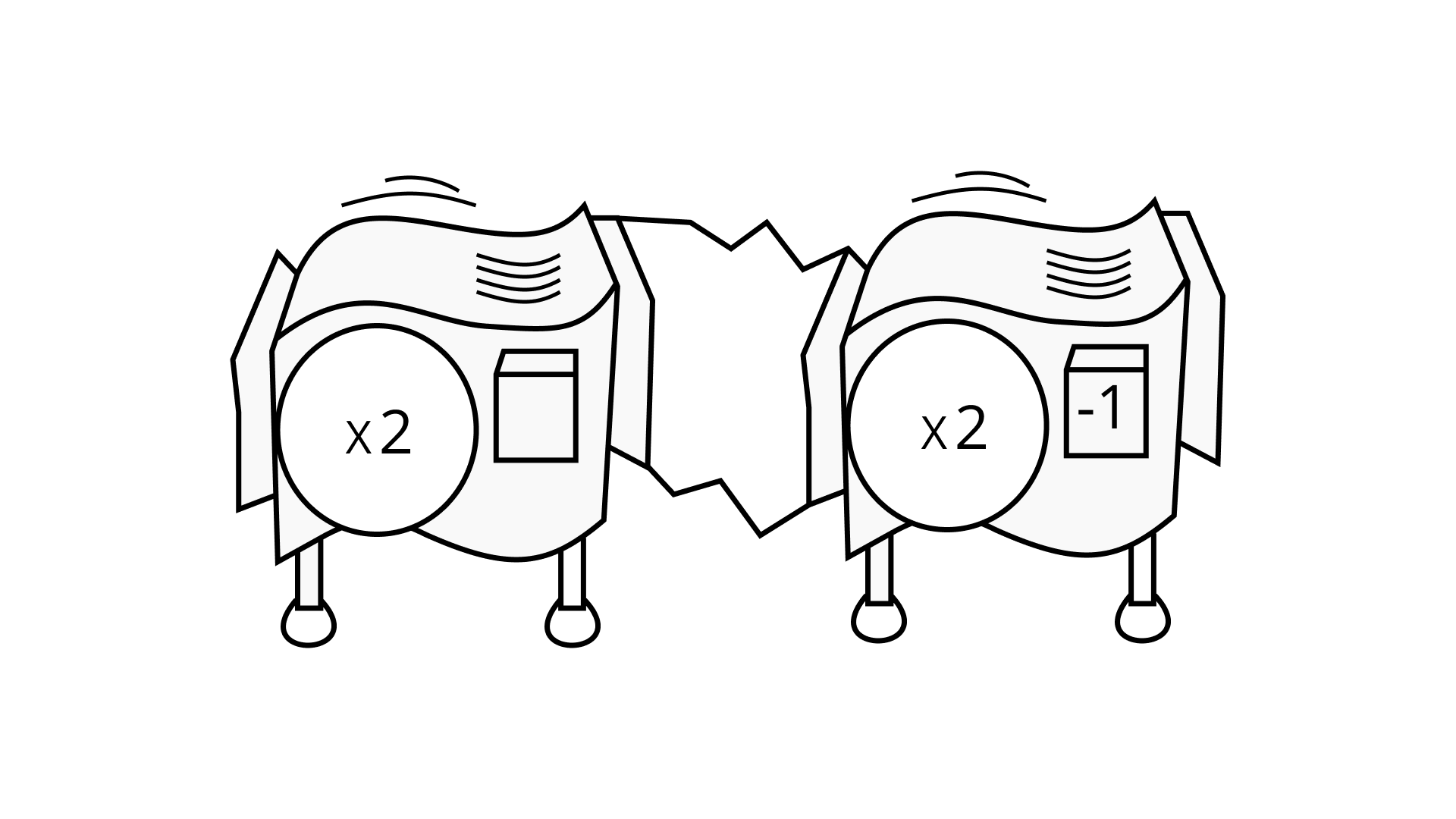
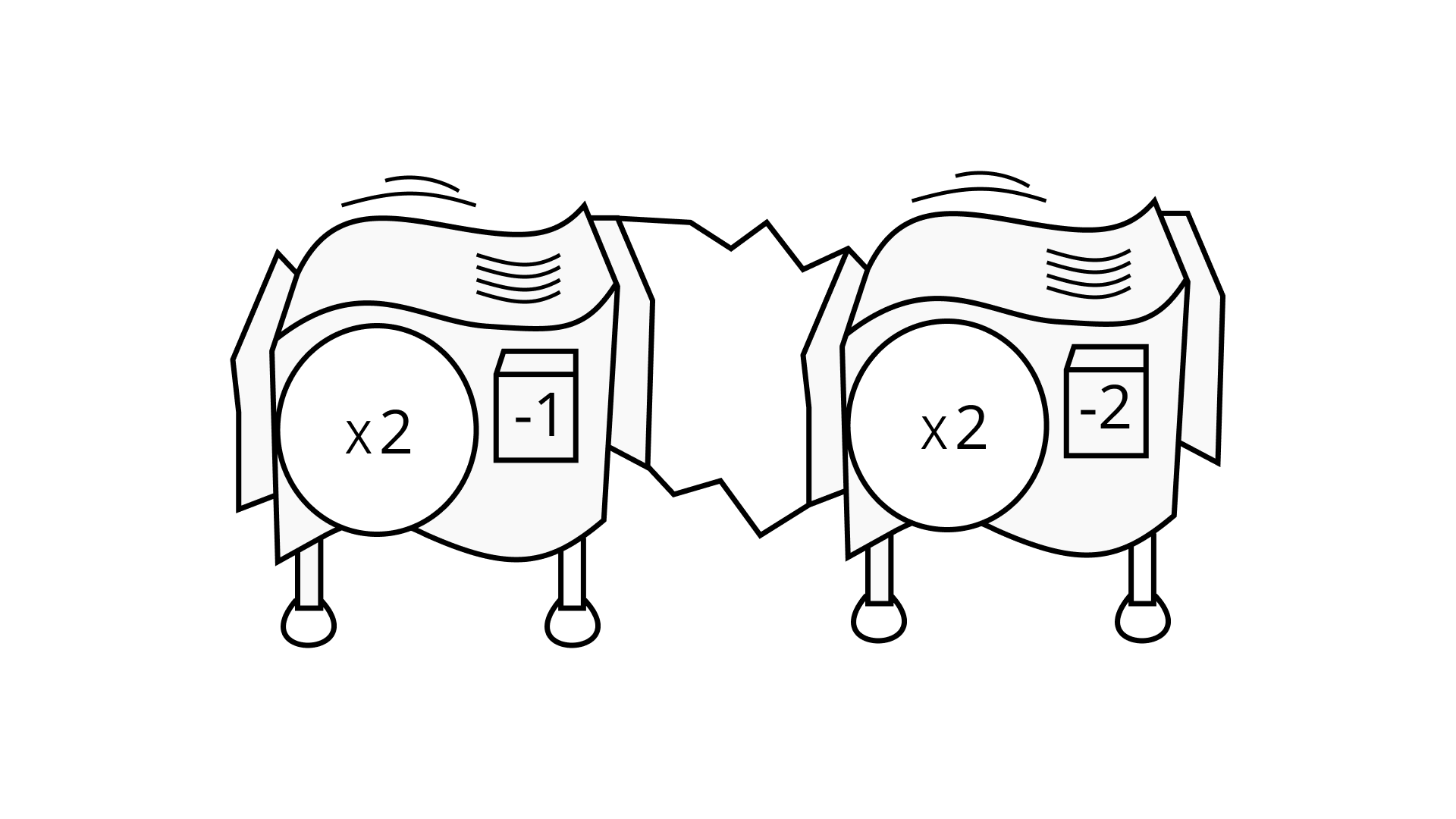
(a) 1 

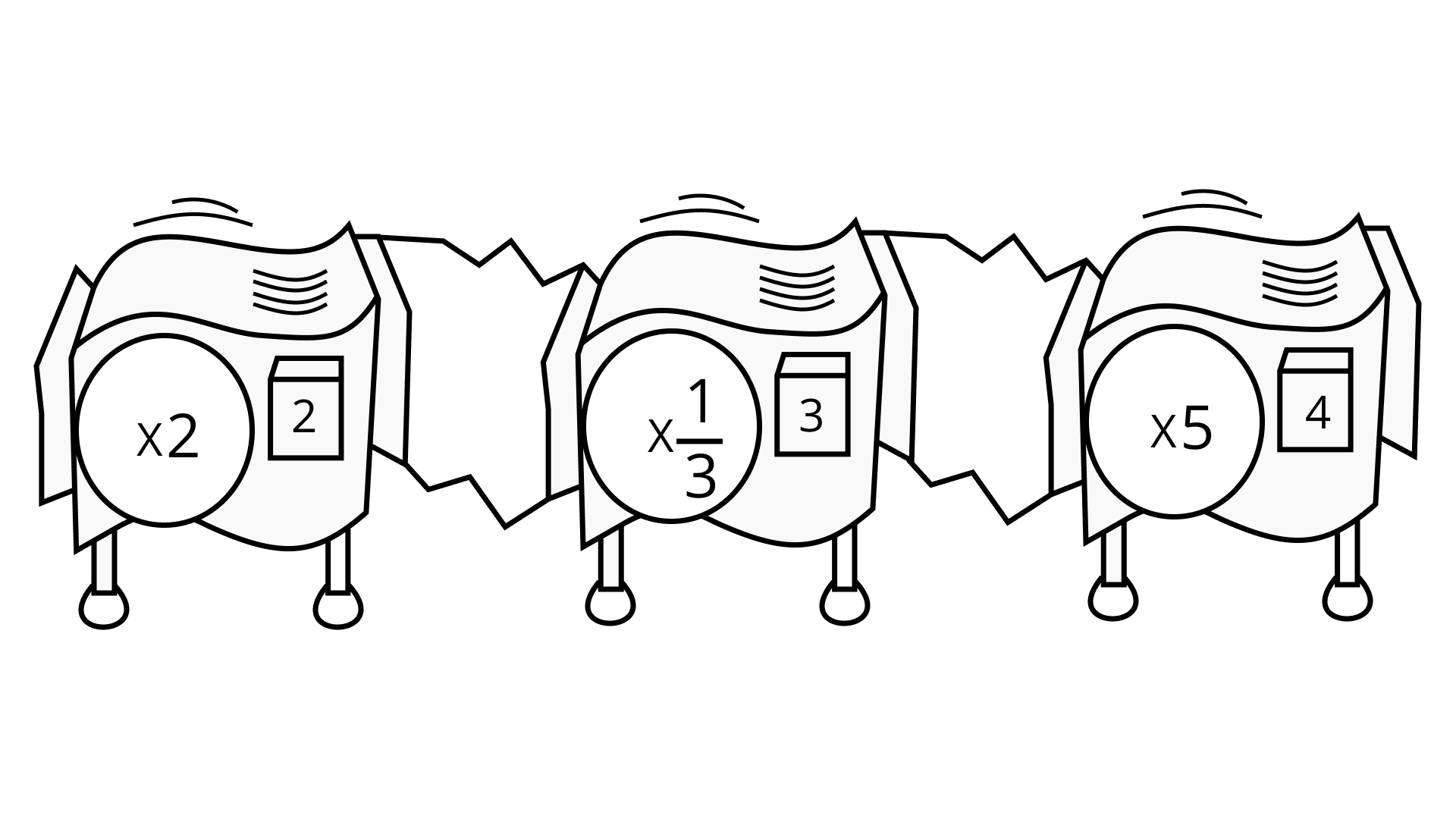
(b) 0 

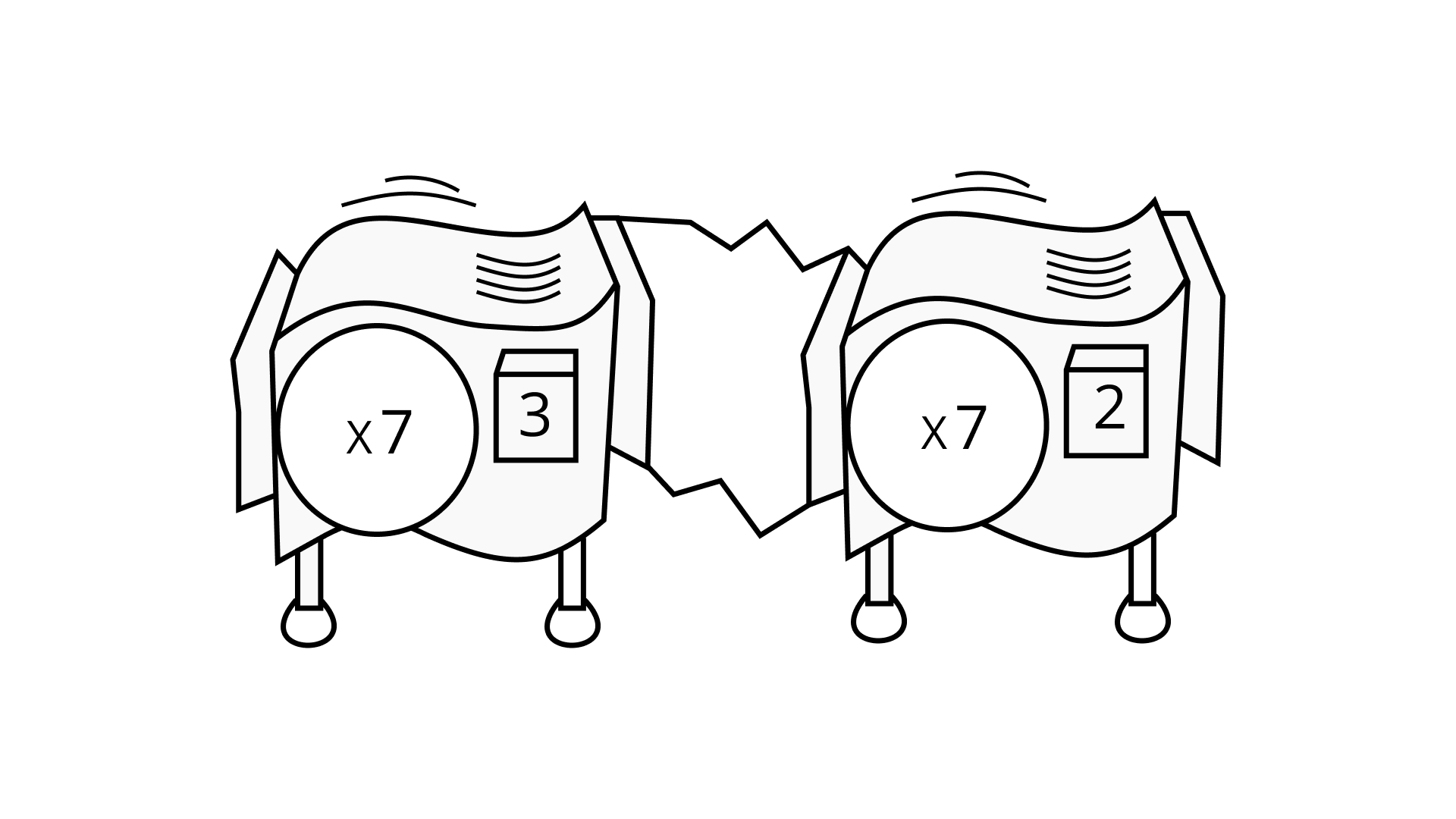
(c) – 1 

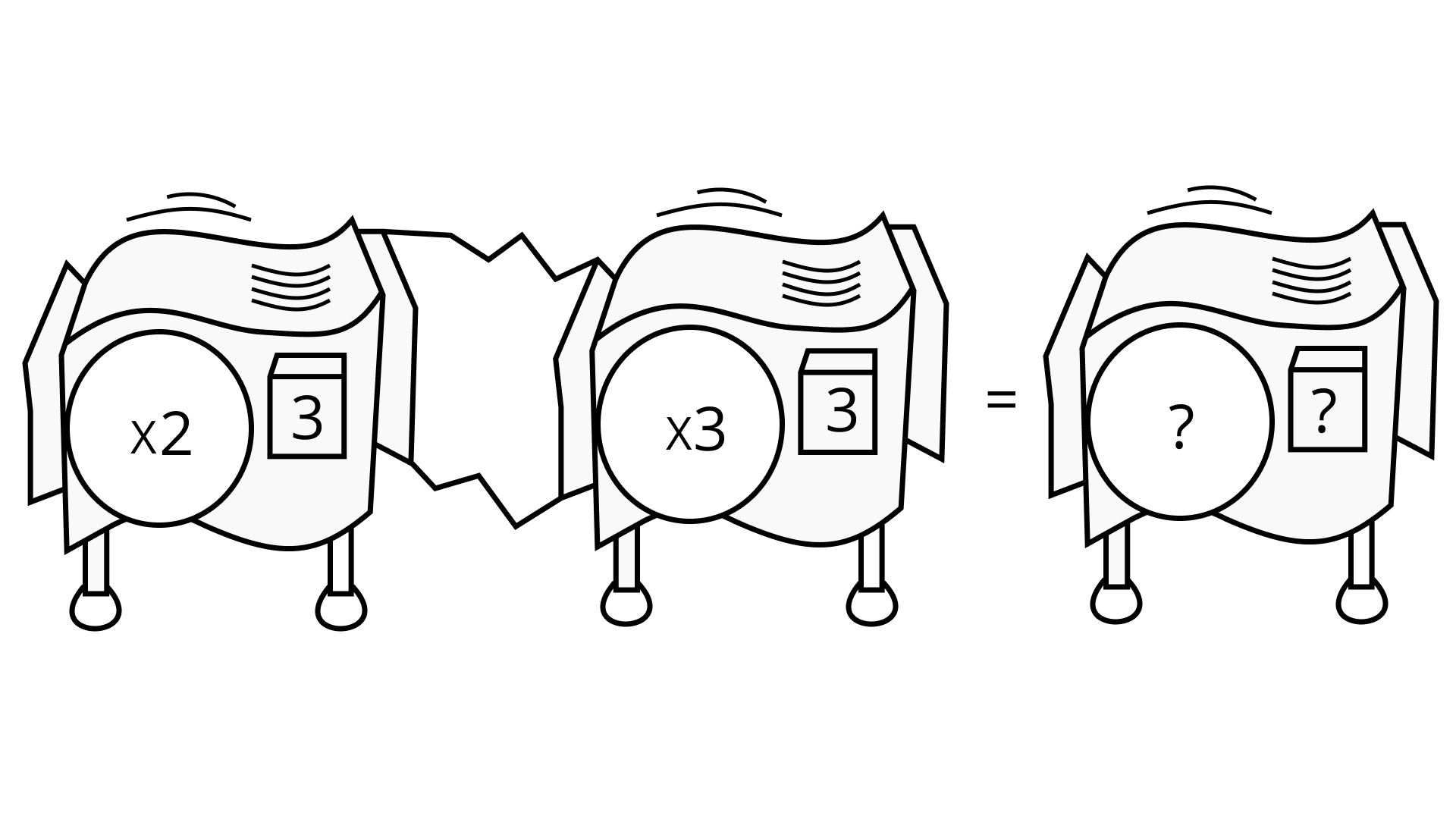
(c) Not defined

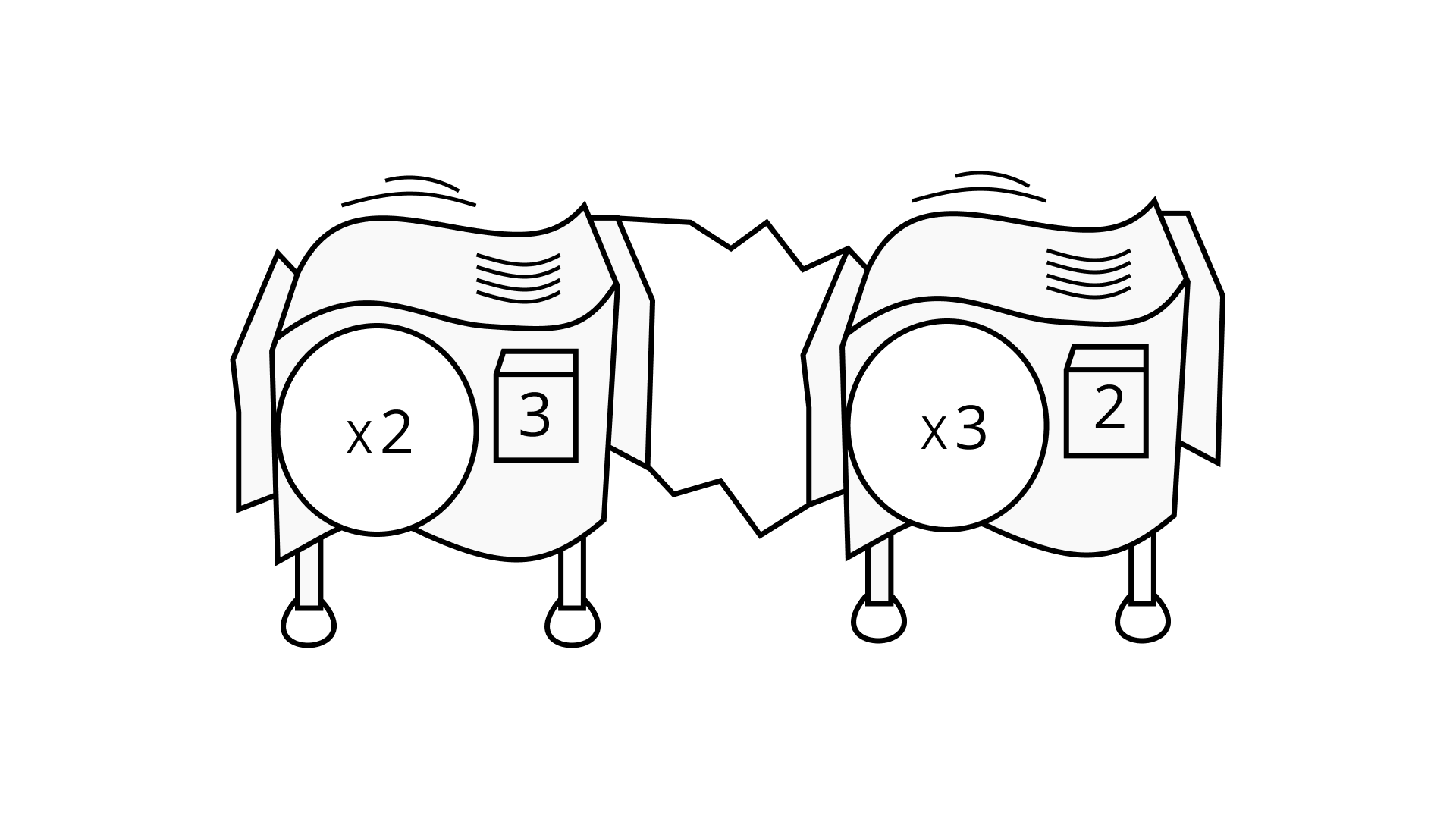
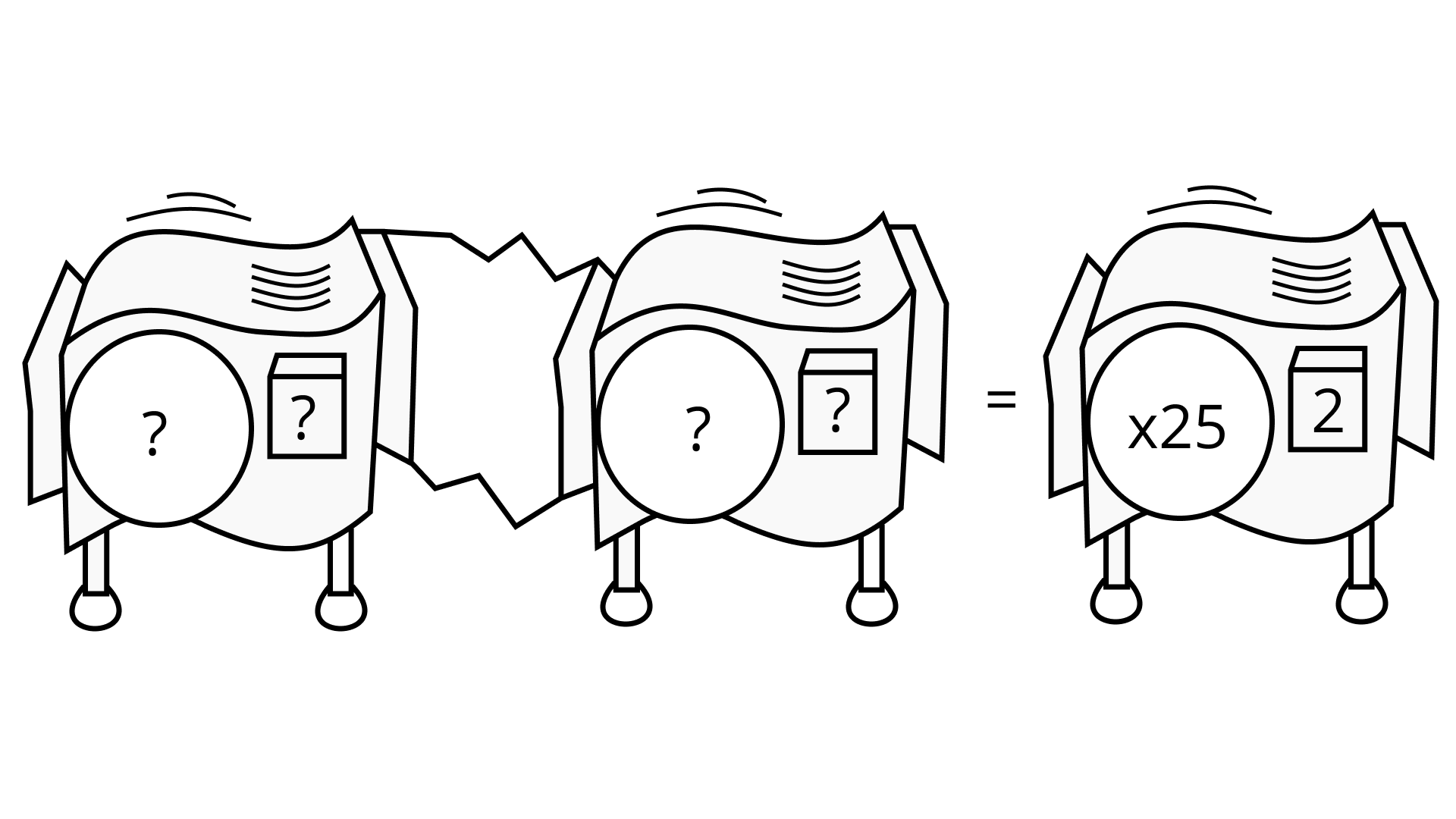
Ans: Option (a) is correct.

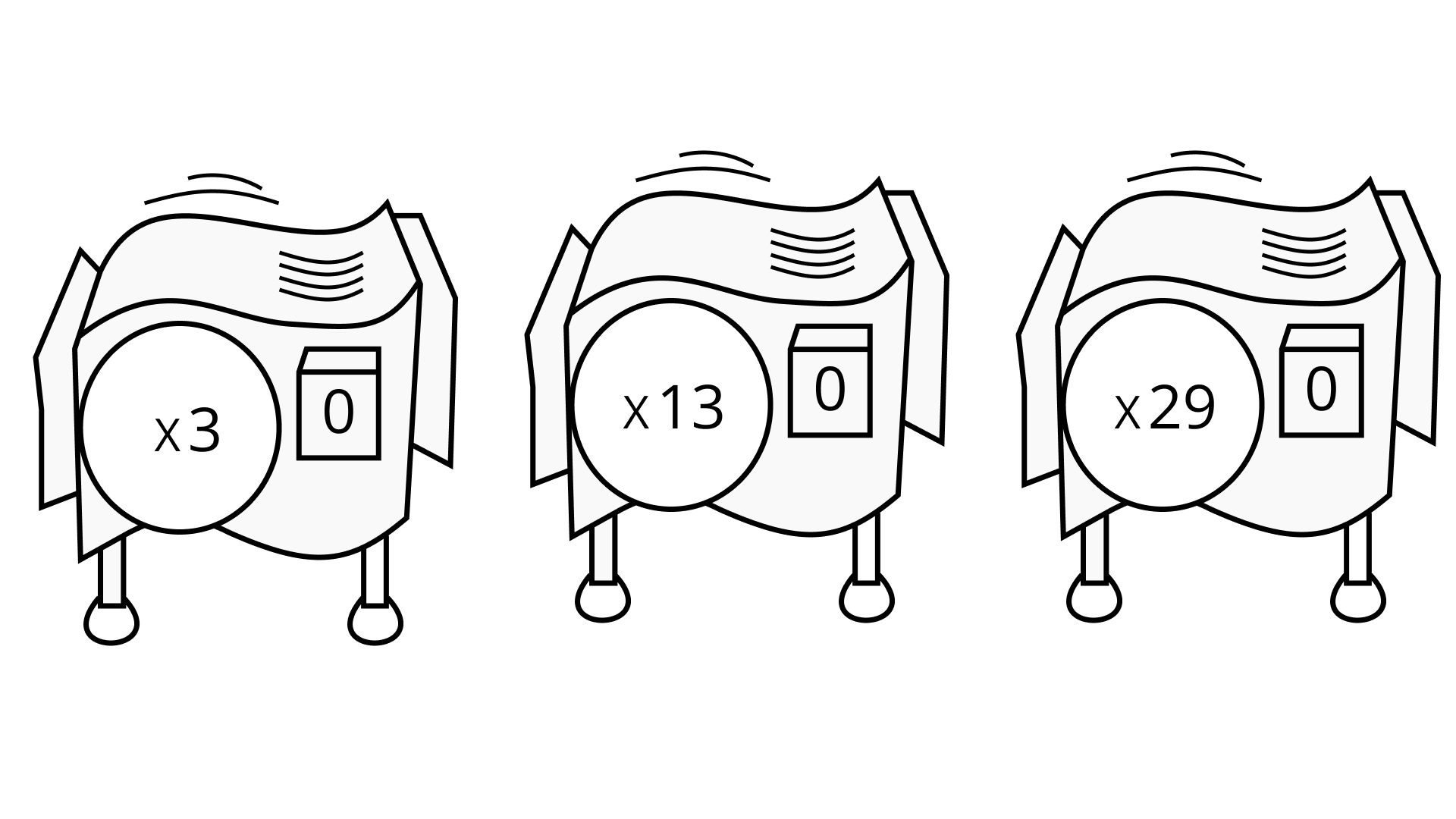
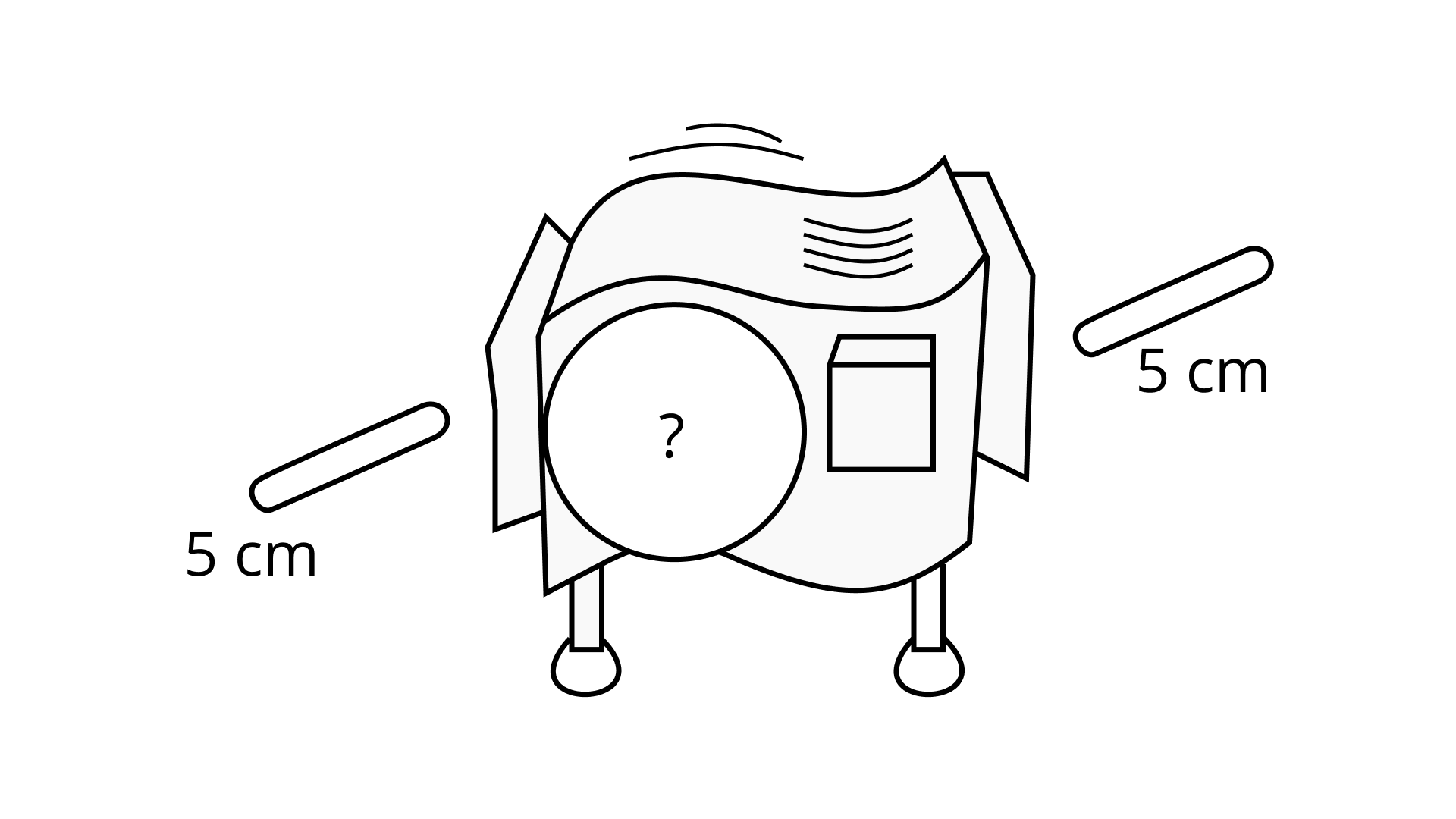
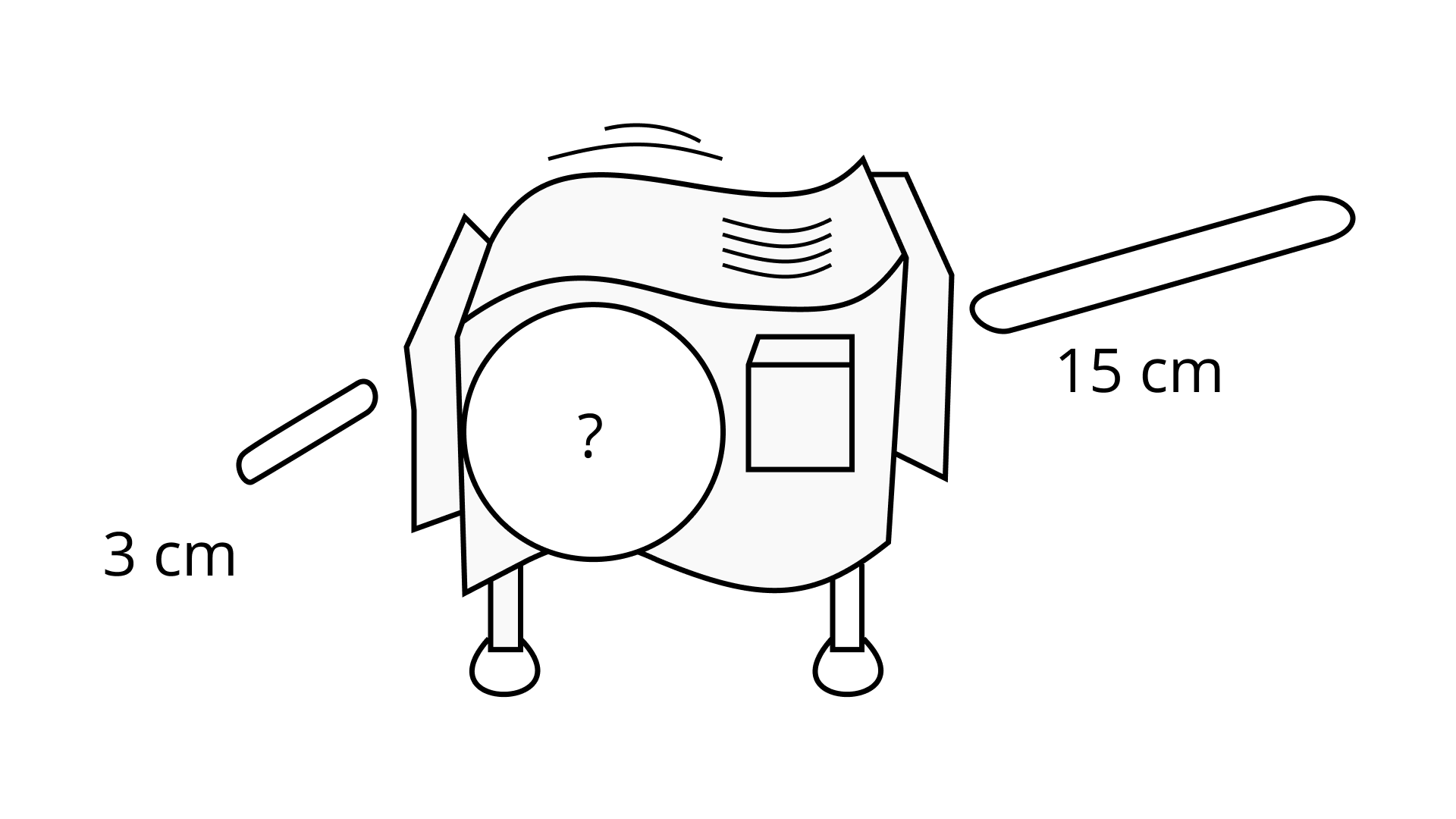
Using law of exponents, a0 = 1

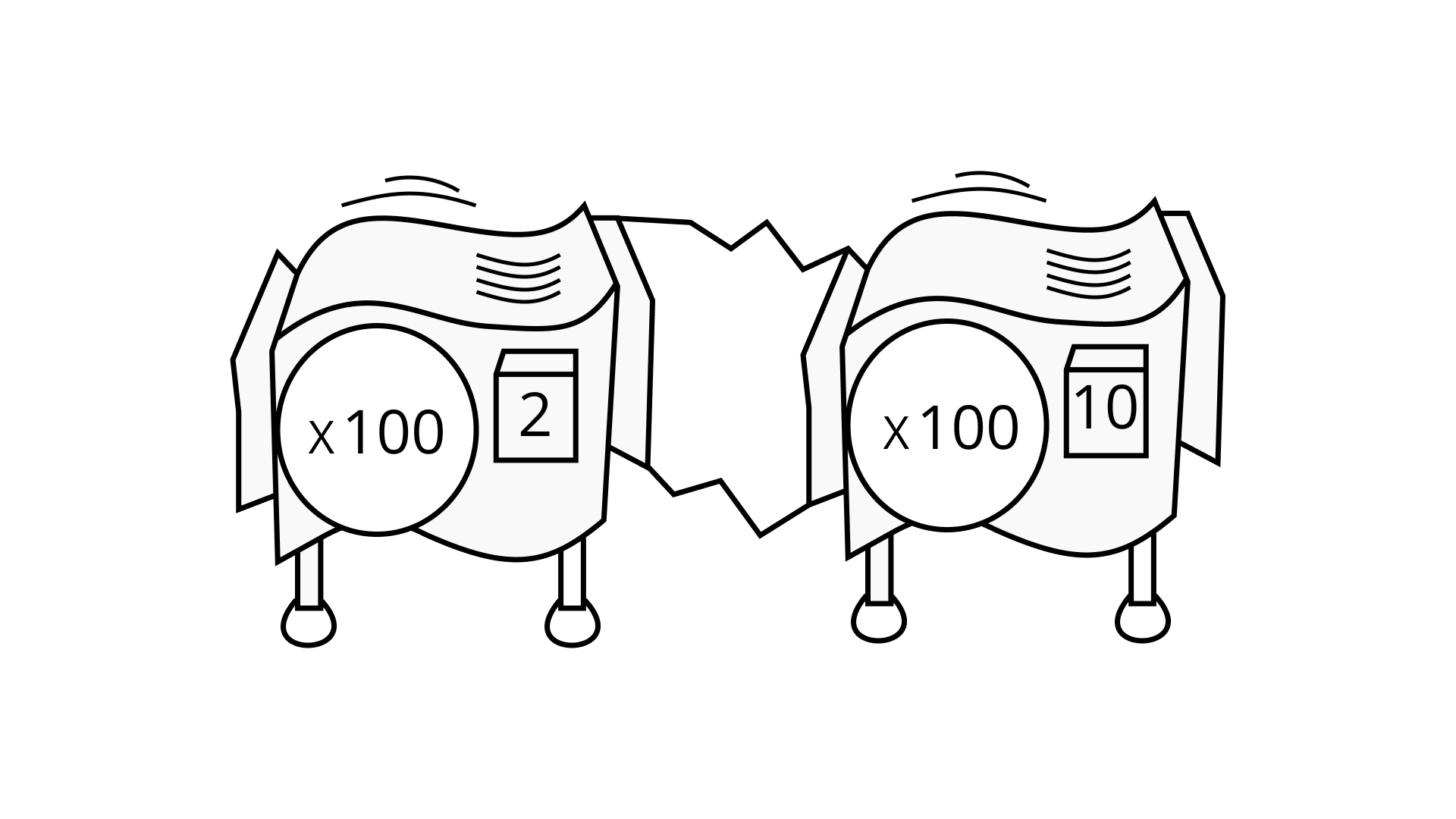
Similarly, y0 = 1.

14. If x be any non-zero integer, then x–1 is equal to

(a) x

(b) $\dfrac{1}{x}$

(c) -x

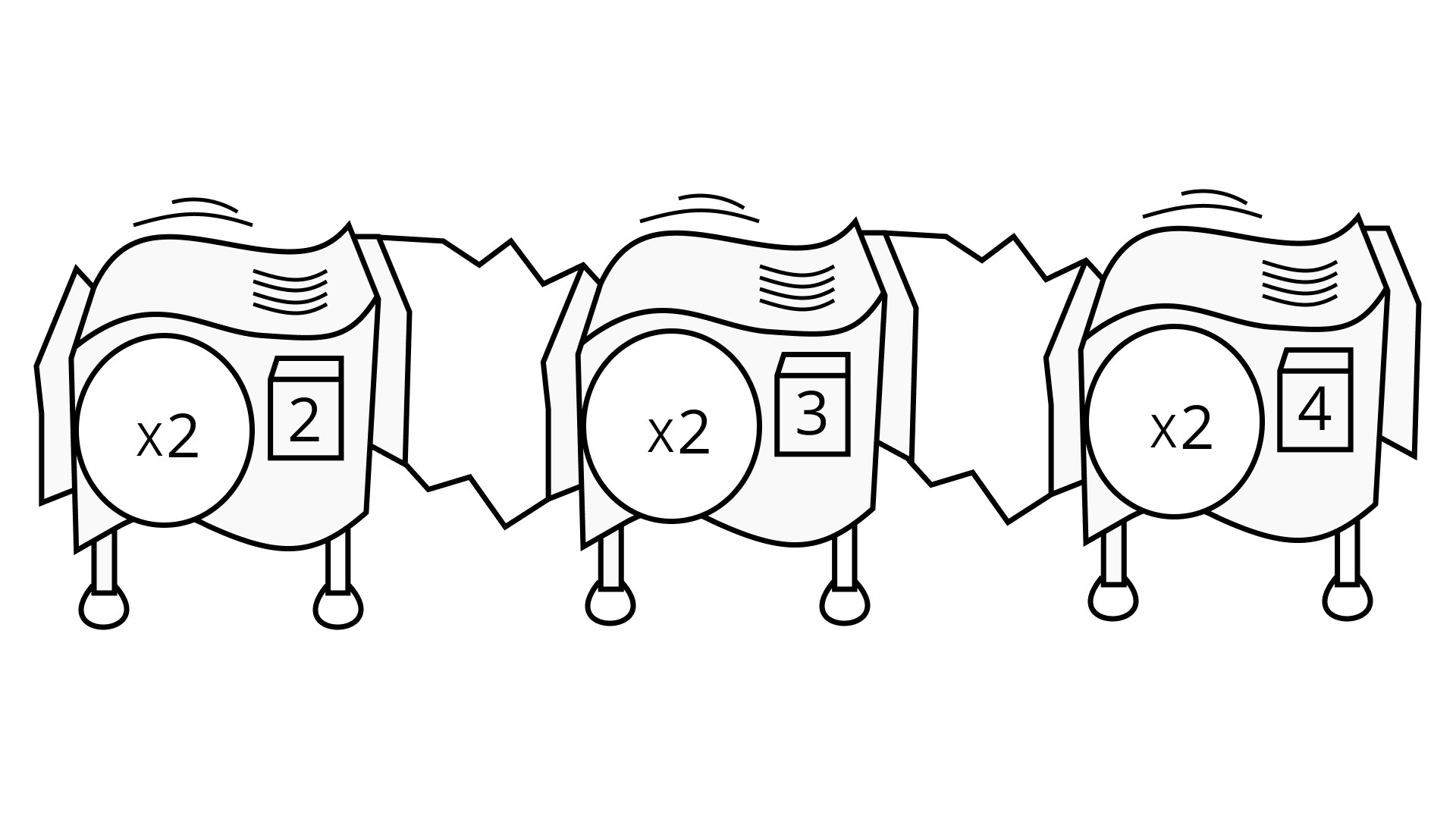
(d) $\dfrac{{ - 1}}{x}$

Ans: Option (b) is correct.

Use the law of exponent ${a^{ - m}} = \dfrac{1}{{{a^m}}}$, where a is a non zero integer.

Thus, ${x^{ - 1}} = \dfrac{1}{{{x^1}}} = \dfrac{1}{x}$

15. If x be any integer different from zero and m be any positive integer, then x–m is equal to

(a) xm

(b) -xm

(c) $\dfrac{1}{{{x^m}}}$

(d) $\dfrac{{ - 1}}{{{x^m}}}$

Ans: Option (c) is correct.

Use the law of exponent ${a^{ - m}} = \dfrac{1}{{{a^m}}}$, where a is a non zero integer.

Thus, ${x^{ - m}} = \dfrac{1}{{{x^m}}}$

16. If x be any integer different from zero and m, n be any integers, then

(xm)n is equal to

(a) xm+n 

(b) xmn 

(c) ${x^{\dfrac{m}{n}}}$

(d) ${x^{m - n}}$

Ans: Option (b) is correct.

Use the law of exponent ${\left( {{a^m}} \right)^n} = {\left( a \right)^{m \times n}}$, where a is a non zero integer.

Thus, ${\left( {{x^m}} \right)^n} = {\left( x \right)^{m \times n}} = {x^{mn}}$.

17. Which of the following is equal to ${\left( { - \dfrac{3}{4}} \right)^{ - 3}}$?

(a) ${\left( {\dfrac{3}{4}} \right)^{ - 3}}$

(b) $ - {\left( {\dfrac{3}{4}} \right)^{ - 3}}$

(c) ${\left( {\dfrac{4}{3}} \right)^3}$

(d) ${\left( { - \dfrac{4}{3}} \right)^3}$

Ans: Option (d) is correct.

Use the law of exponent ${a^{ - m}} = \dfrac{1}{{{a^m}}}$, where a is a non zero integer.

Thus, ${\left( {\dfrac{{ - 3}}{4}} \right)^{ - 3}} = \dfrac{1}{{{{\left( {\dfrac{{ - 3}}{4}} \right)}^3}}} = {\left( { - \dfrac{4}{3}} \right)^3}$

18. ${\left( { - \dfrac{5}{7}} \right)^{ - 5}}$ is equal to

(a) ${\left( {\dfrac{5}{7}} \right)^{ - 5}}$

(b) ${\left( {\dfrac{7}{5}} \right)^5}$

(c) ${\left( {\dfrac{7}{5}} \right)^5}$

(d) ${\left( { - \dfrac{7}{5}} \right)^5}$

Ans: Option (d) is correct.

Use the law of exponent ${a^{ - m}} = \dfrac{1}{{{a^m}}}$, where a is a non zero integer.

Thus, ${\left( {\dfrac{{ - 5}}{7}} \right)^{ - 5}} = \dfrac{1}{{{{\left( {\dfrac{{ - 5}}{7}} \right)}^5}}} = {\left( { - \dfrac{7}{5}} \right)^5}$

19. ${\left( {\dfrac{{ - 7}}{5}} \right)^{ - 1}}$ is equal to

(a) $\dfrac{5}{7}$

(b) $ - \dfrac{5}{7}$

(c) $\dfrac{7}{5}$

(d) $\dfrac{{ - 7}}{5}$

Ans: Option (b) is correct.

Use the law of exponent ${a^{ - m}} = \dfrac{1}{{{a^m}}}$, where a is a non zero integer.

Thus, ${\left( {\dfrac{{ - 7}}{5}} \right)^{ - 1}} = \dfrac{1}{{{{\left( {\dfrac{{ - 7}}{5}} \right)}^1}}} = \left( { - \dfrac{5}{7}} \right)$

20. (–9)3 ÷ (–9)8 is equal to

(a) (9)5 

(b) (9)–5 

(c) (– 9)5 

(d) (– 9)–5

Ans: Option (d) is correct.

Use law of exponent $\dfrac{{{a^m}}}{{{a^n}}} = {\left( a \right)^{m - n}}$, where a is a non zero integer.

Thus, $\dfrac{{{{\left( { - 9} \right)}^3}}}{{{{\left( { - 9} \right)}^8}}} = {\left( { - 9} \right)^{3 - 8}} = {\left( { - 9} \right)^{ - 5}}$

21. For a non-zero integer x, x7 ÷ x12 is equal to

(a) x5 

(b) x19 

(c) x–5 

(d) x–19

Ans: Option (c) is correct.

Use law of exponent $\dfrac{{{a^m}}}{{{a^n}}} = {\left( a \right)^{m - n}}$, where a is a non zero integer.

Thus, $\dfrac{{{x^7}}}{{{x^{12}}}} = {x^{7 - 12}} = {x^{ - 5}}$.

22. For a non-zero integer x, (x4)–3 is equal to

(a) x12 

(b) x–12 

(c) x64 

(d) x–64

Ans: Option (b) is correct.

Use law of exponent ${\left( {{x^m}} \right)^n} = {\left( x \right)^{m \times n}} = {\left( x \right)^{mn}}$, where a is a non zero integer.

Thus, ${\left( {{x^4}} \right)^{ - 3}} = {x^{4 \times \left( { - 3} \right)}} = {x^{ - 12}}$

23. The value of (7–1 – 8–1)–1 – (3–1 – 4–1)–1 is

(a) 44 

(b) 56 

(c) 68 

(d) 12

Ans: Option (a) is correct.

Use the law of exponent ${a^{ - m}} = \dfrac{1}{{{a^m}}}$, where a is a non zero integer.

Thus, 

${\left( {\dfrac{1}{7} - \dfrac{1}{8}} \right)^{ - 1}} - {\left( {\dfrac{1}{3} - \dfrac{1}{4}} \right)^{ - 1}} = {\left( {\dfrac{{8 - 7}}{{56}}} \right)^{ - 1}} - {\left( {\dfrac{{4 - 3}}{{12}}} \right)^{ - 1}}$

= ${\left( {\dfrac{1}{{56}}} \right)^{ - 1}} - {\left( {\dfrac{1}{{12}}} \right)^{ - 1}} = 56 - 12 = 44$

24. The standard form for 0.000064 is

(a) 64 × 104 

(b) 64 × 10–4 

(c) 6.4 × 105 

(d) 6.4 × 10–5

Ans: Option (d) is correct.

Given, 0.000064 = 0.64 × 10-4 = 6.4 × 10-5

25. The standard form for 234000000 is

(a) 2.34 × 108 

(b) 0.234 × 109 

(c) 2.34 × 10–8 

(d) 0.234 × 10–9

Ans: Option (a) is correct.

234000000 = 234 x 106 = 2.34 x 102+6

= 2.34 x 108

26. The usual form for 2.03 × 10–5

(a) 0.203 

(b) 0.00203 

(c) 203000 

(d) 0.0000203

Ans: Option (d) is correct.

Use the law of exponent ${a^{ - m}} = \dfrac{1}{{{a^m}}}$, where a is a non zero integer.

Thus, 

$2.03 \times {10^{ - 5}} = \dfrac{{2.03}}{{{{10}^5}}} = 0.0000203$

27. ${\left( {\dfrac{1}{{10}}} \right)^0}$is equal to

(a) 0

(b) $\dfrac{1}{{10}}$

(c) 1

(d) 10

Ans: Option (c) is correct.

Use the law of exponent ${a^0} = 1$, where a is a non zero integer.

Thus, 

${\left( {\dfrac{1}{{10}}} \right)^0} = 1$

28. ${\left( {\dfrac{3}{4}} \right)^5} \div {\left( {\dfrac{5}{3}} \right)^5}$is equal to

(a) ${\left( {\dfrac{3}{4} \div \dfrac{5}{3}} \right)^5}$

(b) ${\left( {\dfrac{3}{4} \div \dfrac{5}{3}} \right)^1}$

(c) ${\left( {\dfrac{3}{4} \div \dfrac{5}{3}} \right)^0}$

(d) ${\left( {\dfrac{3}{4} \div \dfrac{5}{3}} \right)^{10}}$

Ans: Option (a) is correct.

Use the law of exponent ${a^m} \div {b^m} = {\left( {a \div b} \right)^m}$, where a is a non zero integer.

Thus, 

${\left( {\dfrac{3}{4}} \right)^5} \div {\left( {\dfrac{5}{3}} \right)^5} = {\left( {\dfrac{3}{4} \div \dfrac{5}{3}} \right)^5}$

29. For any two non-zero rational numbers x and y, x4 ÷ y4 is equal to

(a) (x ÷ y)0 

(b) (x ÷ y)1 

(c) (x ÷ y)4 

(d) (x ÷ y)8

Ans: Option (c) is correct.

Use the law of exponent ${a^m} \div {b^m} = {\left( {a \div b} \right)^m}$, where a is a non zero integer.

Thus, 

${x^4} \div {y^4} = {\left( {\dfrac{x}{y}} \right)^4} = {\left( {x \div y} \right)^4}$

30. For a non-zero rational number p, p13 ÷ p8 is equal to

(a) p5 

(b) p21 

(c) p–5 

(d) p–19

Ans: Option (a) is correct.

Use the law of exponent ${a^m} \div {a^n} = {\left( a \right)^{m - n}}$, where a is a non zero integer.

Thus, 

${p^{13}} \div {p^8} = {\left( p \right)^{13 - 8}} = {p^5}$

31. For a non-zero rational number z, (z-2)3 is equal to

(a) z6 

(b) z–6 

(c)z1 

(d) z4

Ans: Option (b) is correct.

Use the law of exponent ${\left( {{a^m}} \right)^n} = {\left( a \right)^{mn}}$, where a is a non zero integer.

Thus, 

${\left( {{z^{ - 2}}} \right)^3} = {z^{ - 2 \times 3}} = {z^{ - 6}}$

32. Cube of $-\dfrac{1}{2}$ is 

(a) $\dfrac{1}{8}$

(b) $\dfrac{1}{{16}}$

(c) $-\dfrac{1}{8}$

(d) $-\dfrac{1}{{16}}$

Ans: Option (c) is correct.

For (-a)m, if m is odd, then (-a)m is negative.

${\left( { - \dfrac{1}{2}} \right)^3} = \left( { - \dfrac{1}{2}} \right) \times \left( { - \dfrac{1}{2}} \right) \times \left( { - \dfrac{1}{2}} \right) = \left( { - \dfrac{1}{8}} \right)$

33. Which of the following is not the reciprocal of ${\left( {\dfrac{2}{3}} \right)^4}$?

(a) ${\left( {\dfrac{3}{2}} \right)^4}$

(b) ${\left( {\dfrac{3}{2}} \right)^{ - 4}}$

(c) ${\left( {\dfrac{2}{3}} \right)^{ - 4}}$

(d) $\dfrac{{{3^4}}}{{{2^4}}}$

Ans: Option (b) is correct.

Reciprocal of a is $\dfrac{{\text{1}}}{{\text{a}}}.$

${\left( {\dfrac{2}{3}} \right)^4} = {\left( {\dfrac{2}{3}} \right)^{ - 4}} = {\left( {\dfrac{3}{2}} \right)^4}$

$\Rightarrow \dfrac{{{3^4}}}{{{2^4}}} \ne {\left( {\dfrac{3}{2}} \right)^{ - 4}}$

In questions 34 to 65, fill in the blanks to make the statements true.

34. The multiplicative inverse of 1010 is ___________.

Ans: 10-10

Multiplicative inverse is the reciprocal of a number. Thus,

${10^{10}} = \dfrac{1}{{{{10}^{10}}}} = {10^{ - 10}}$

35. a3 × a–10 = __________.

Ans: ${a^3} \times {a^{ - 10}} = {a^{ - 7}}$

$\Rightarrow {a^m} \times {a^n} = {a^{m + n}}$

$\Rightarrow {a^3} \times {a^{ - 10}} = {a^{3 - 10}} = {a^{ - 7}}$

36. 50 = __________.

Ans: 1

As, a0 =1, so 50 = 1.

37. 55 × 5–5 = __________.

Ans: -1

As, xm × xn = (x)m+n

${5^5} \times {5^{ - 5}} = {\left( 5 \right)^{5 - 5}} = {\left( 5 \right)^0} = 1$

38. The value of ${\left( {\dfrac{1}{{{2^3}}}} \right)^2}$is equal to _________.

Ans: $\left( {\dfrac{1}{{{2^6}}}} \right)$

As, (xm) n = (x)mn

${\left( {\dfrac{1}{{{2^3}}}} \right)^2} = {\left( {\dfrac{{{1^3}}}{{{2^3}}}} \right)^2} = {\left( {\dfrac{1}{2}} \right)^{3 \times 2}} = {\left( {\dfrac{1}{2}} \right)^6} = \dfrac{1}{{{2^6}}}$

39. The expression for 8–2 as a power with the base 2 is _________.

Ans: (2)-6

In 8-2, 8 is the base and -2 is the power.

${8^{ - 2}} = \dfrac{1}{{{8^2}}} = \dfrac{1}{{64}}$

${2^6} = 2 \times 2 \times 2 \times 2 \times 2 \times 2 = 64$

$\Rightarrow \dfrac{1}{{64}} = \dfrac{1}{{{2^6}}} = {2^{ - 6}}$

40. Very small numbers can be expressed in standard form by using _________ exponents.

Ans: negative.

41. Very large numbers can be expressed in standard form by using _________ exponents.

Ans: positive.

42. By multiplying (10)5 by (10)–10 we get ________. 

Ans: ${\left( {10} \right)^{ - 5}}$

As, xm × xn = (x)m+n

${10^5} \times {10^{ - 10}} = {\left( {10} \right)^{5 - 10}} = {\left( {10} \right)^{ - 5}}$

43. ${\left[ {{{\left( {\dfrac{2}{{13}}} \right)}^{ - 6}} \div {{\left( {\dfrac{2}{{13}}} \right)}^3}} \right]^3} \times {\left( {\dfrac{2}{{13}}} \right)^{ - 9}} = \_\_\_\_$

Ans: ${\left( {\dfrac{2}{{13}}} \right)^{ - 36}}$

Use the law of exponent ${a^m} \div {a^n} = {\left( a \right)^{m - n}}$, where a is a non zero integer.

Thus, 

${\left( {{{\left( {\dfrac{2}{{13}}} \right)}^{ - 6}} \div {{\left( {\dfrac{2}{{13}}} \right)}^3}} \right)^3} \times {\left( {\dfrac{2}{{13}}} \right)^{ - 9}} = {\left( {{{\left( {\dfrac{2}{{13}}} \right)}^{ - 6 - 3}}} \right)^3} \times {\left( {\dfrac{2}{{13}}} \right)^{ - 9}}$

= ${\left( {{{\left( {\dfrac{2}{{13}}} \right)}^{ - 9}}} \right)^3} \times {\left( {\dfrac{2}{{13}}} \right)^{ - 9}}$

= ${\left( {\dfrac{2}{{13}}} \right)^{ - 27}} \times {\left( {\dfrac{2}{{13}}} \right)^{ - 9}} = {\left( {\dfrac{2}{{13}}} \right)^{ - 27 - 9}} = {\left( {\dfrac{2}{{13}}} \right)^{ - 36}}$

44. Find the value [4–1 +3–1 + 6–2]–1.

Ans: $\dfrac{{18}}{{11}}$

Use the law of exponent ${a^{ - m}} = \dfrac{1}{{{a^m}}}$, where a is a non zero integer.

Thus, 

${\left( {{4^{ - 1}} + {3^{ - 1}} + {6^{ - 2}}} \right)^{ - 1}} = {\left( {\dfrac{1}{4} + \dfrac{1}{3} + \dfrac{1}{{{6^2}}}} \right)^{ - 1}}$

= ${\left( {\dfrac{1}{4} + \dfrac{1}{3} + \dfrac{1}{{36}}} \right)^{ - 1}} = {\left( {\dfrac{{9 + 12 + 1}}{{36}}} \right)^{ - 1}}$

= ${\left( {\dfrac{{22}}{{36}}} \right)^{ - 1}} = \dfrac{{36}}{{22}} = \dfrac{{18}}{{11}}$

45. [2–1 + 3–1 + 4–1]0 = ______

Ans: 1

Use the law of exponent ${a^0} = 1$, where a is a non zero integer.

Thus, 

${\left( {{2^{ - 1}} + {3^{ - 1}} + {4^{ - 1}}} \right)^0} = 1$

46. The standard form of $\left( {\dfrac{1}{{{\mathbf{100000000}}}}} \right)$ is ______.

Ans:  1 × 10-8

Standard form, $\dfrac{1}{{100000000}} = \dfrac{1}{{1 \times {{10}^8}}} = {10^{ - 8}}$

47. The standard form of 12340000 is ______.

Ans: 1.234 x 107

For standard form of 12340000= 1234 x 104

= 1.234 x 104 x 103 = 1.234 x 107

48. The usual form of 3.41 × 106 is _______.

Ans: 3410000

So, 3.41 x 106 = 3.41 x 10 x 10 x 10 x 10 x 10 x 10

= 3.41 x 106 = 3410000

49. The usual form of 2.39461 × 106 is _______.

Ans: 2394610

So, 2.39461 × 106 = 2.39461x 10 x 10 x 10 x 10 x 10 x 10

= 2.39461 x 106 = 2394610

50. If 36 = 6 × 6 = 62, then $\dfrac{1}{{36}}$ expressed as a power with the base 6 is ________.

Ans: ${6^{ - 2}}$

Since 36 = 6 × 6 = 62

Then $\dfrac{1}{{36}} = \dfrac{1}{{6 \times 6}} = \dfrac{1}{{{6^2}}} = {6^{ - 2}}$

51. By multiplying ${\left( {\dfrac{5}{3}} \right)^4}$ by ________ we get 54.

Ans: ${3^4}$

Let a to be multiplied.

${\left( {\dfrac{5}{3}} \right)^4} \times a = {5^4}$

$\Rightarrow \dfrac{{{5^4}}}{{{3^4}}} \times a = {5^4}$

$\Rightarrow a = {3^4}$

52. 35 ÷ 3–6 can be simplified as __________.

Ans: ${3^{11}}$

Use the law of exponent ${a^m} \div {a^n} = {\left( a \right)^{m - n}}$, where a is a non zero integer.

Thus, 

${3^5} \div {3^{ - 6}} = {3^{5 - \left( { - 6} \right)}} = {3^{5 + 6}} = {3^{11}}$

53. The value of 3 × 10-7 is equal to ________.

Ans: 0.0000003

Given, 3 x 10-7   = 3.0 x 10-7   
Now, placing the decimal seven places towards the left of the original position, we get 0.0000003. Hence, the value of 3 x 10-7 is equal to 0.0000003.

54. To add the numbers given in standard form, we first convert them into numbers with __ exponents.

Ans: equal

To add the numbers given in standard form, we first convert them into numbers with equal exponents.
e.g. 2.46 x 106   + 24.6 x 105 = 2.46 x 105 + 2.46 x 106 = 4.92 x 106

55. The standard form for 32,50,00,00,000 is __________.

Ans: For standard form, 32500000000 = 3250 x 102 x 102 x 103

= 3250 x 107 = 3.250 x 1010 or 3.25 x 1010

Hence, the standard form for 32500000000 is 3.25 x 1010.

56. The standard form for 0.000000008 is __________.

Ans: 8.0 x 10-9

For standard form, 0.000000008 = 0.8 x 10-8 = 8 x 10-9 = 8.0 x 10-9

Hence, the standard form for 0.000000008 is 8.0 x 10-9.

57. The usual form for 2.3 × 10-10 is ____________.

Ans: 0.00000000023

For usual form, 2.3 x 10-10 = 0.23 x 10-11
= 0.00000000023
Hence, the usual form for 2.3 x 10-10 is 0.00000000023.

58. On dividing 85 by _________ we get 8.

Ans: 84

Since $\dfrac{{{8^5}}}{{{8^4}}} = 8$.

59. On multiplying _________ by 2–5 we get 25.

Ans: 210

As ${2^{10}} \times {2^{ - 5}} = {2^{10 - 5}} = {2^5}$

60. The value of [3–1 × 4–1]2 is _________.

Ans: $\dfrac{1}{{{3^2} \times {4^2}}}$

As, ${\left( {{3^{ - 1}} \times {4^{ - 1}}} \right)^2} = {\left( {\dfrac{1}{3} \times\dfrac{1}{4}} \right)^2} = \dfrac{1}{{{3^2} \times {4^2}}}$

61. The value of [2–1 × 3–1]–1 is _________.

Ans: $\dfrac{1}{6}$

As, ${\left( {{2^{ - 1}} \times {3^{ - 1}}} \right)^{ - 1}} = {\left( {\dfrac{1}{2} \times \dfrac{1}{3}} \right)^{ - 1}} = {\left( {\dfrac{1}{6}} \right)^{ - 1}} = 6$

62. By solving (60 – 70) × (60 + 70) we get ________.

Ans: 0

$\left( {{6^0} - {7^0}} \right) \times \left( {{6^0} + {7^0}} \right) = \left( {1 - 1} \right) \times \left( {1 - 1} \right) = 0 \times 0 = 0$

63. The expression for 35 with a negative exponent is _________.

Ans: $\dfrac{1}{{{3^{ - 5}}}}$

Expression can be written as ${3^5} = \dfrac{1}{{{3^{ - 5}}}}$

64. The value for (–7)6 ÷ 76 is _________.

Ans: 1

$\dfrac{{{{\left( { - 7} \right)}^6}}}{{{{\left( 7 \right)}^6}}} = \dfrac{{{{\left( { - 1 \times 7} \right)}^6}}}{{{{\left( 7 \right)}^6}}} = \dfrac{{{{\left( { - 1} \right)}^6} \times {{\left( 7 \right)}^6}}}{{{{\left( 7 \right)}^6}}} = {\left( { - 1} \right)^6} = 1$

65. The value of [1–2 + 2–2 + 3–2] × 62 is ________.

Ans: $\dfrac{{36}}{1} + \dfrac{{36}}{4} + \dfrac{{36}}{9}$

$\left( {{1^{ - 2}} + {2^{ - 2}} + {3^{ - 2}}} \right) \times {6^2} = \left( {\dfrac{1}{{{1^2}}} + \dfrac{1}{{{2^2}}} + \dfrac{1}{{{3^2}}}} \right) \times 36$

= $\left( {\dfrac{1}{1} + \dfrac{1}{4} + \dfrac{1}{9}} \right) \times 36$

=$\dfrac{{36}}{1} + \dfrac{{36}}{4} + \dfrac{{36}}{9}$

=$36+9+4=49$

In questions 66 to 90, state whether the given statements are true (T) or false (F).

66. The multiplicative inverse of (– 4)–2 is (4)–2.

Ans: False.

LHS = ${\left( { - 4} \right)^{ - 2}} = \dfrac{1}{{{{\left( { - 4} \right)}^2}}} = \dfrac{1}{{16}}$

RHS = ${\left( 4 \right)^{ - 2}} = \dfrac{1}{{{{\left( 4 \right)}^2}}} = \dfrac{1}{{16}}$

LHS = RHS. Hence, these numbers are the same and not multiplicative.

67. The multiplicative inverse of ${\left( {\dfrac{3}{2}} \right)^2}$ is not equal to ${\left( {\dfrac{2}{3}} \right)^{ - 2}}$.

Ans: True.

${\left( {\dfrac{3}{2}} \right)^2} \times {\left( {\dfrac{2}{3}} \right)^{ - 2}} = {\left( {\dfrac{3}{2}} \right)^2} \times {\left( {\dfrac{3}{2}} \right)^2}$

68. ${10^{ - 2}} = \dfrac{1}{{100}}$ 

Ans: True.

Use ${x^{ - m}} = \dfrac{1}{{{x^m}}}$.

${10^{ - 2}} = \dfrac{1}{{{{10}^2}}} = \dfrac{1}{{100}}$

69. 24.58 = 2 × 10 + 4 × 1 + 5 × 10 + 8 × 100

Ans: False

R H S = 2 x 10+ 4 x 1+ 5 x 10+ 8 x 100 = 20 + 4 + 50 + 800 = 874 

So, L H S ≠ R H S

70. 329.25 = 3 × 102 + 2 × 101 + 9 × 100 + 2 × 10–1 + 5 × 10–2

Ans: True

RHS = 3 x 102 + 2 x 101 + 9 x 100 + 2 x 10-1 + 5 x 10-2

= 3 x 10 + 2 x 10 + 9 x 10 + $\dfrac{2}{{10}} + \dfrac{5}{{10 \times 10}}$

Therefore, LHS = RHS.

71. (–5)–2 × (–5)–3 = (–5)–6

Ans: False

LHS = (- 5)-2 x (-5)-3

Using law of exponents, am × an = am+n

Therefore, (–5)–2 × (–5)–3 = (–5)–5

72. (–4)–4 × (4)–1 = (4)5

Ans: False

LHS = (-4)-4 x (4)-1

Using law of exponents, am × an = am+n

(-4)-4 × (4)-1 = (4)-5

73. ${\left( {\dfrac{2}{3}} \right)^{ - 2}} \times {\left( {\dfrac{2}{3}} \right)^{ - 5}} = {\left( {\dfrac{2}{3}} \right)^{10}}$

Ans: False

${\text{LHS  = }}{\left( {\dfrac{2}{3}} \right)^{ - 2}} \times {\left( {\dfrac{2}{3}} \right)^{ - 5}} = {\left( {\dfrac{2}{3}} \right)^{ - 2 - 5}} = {\left( {\dfrac{2}{3}} \right)^{ - 7}}$

So, L H S ≠ R H S

74. 50 = 5

Ans: False.

Using law of exponent = a0 = 1

50 = 1.

75. (–2)0 = 2

Ans: False.

Using law of exponent = a0 = 1

(-2)0 = 1.

76. ${\left( { - \dfrac{8}{2}} \right)^0} = 0$

Ans: False.

Using law of exponent = a0 = 1

${\left( { - \dfrac{8}{2}} \right)^0} = 1$

77. (–6)0 = –1

Ans: False.

Using law of exponent = a0 = 1

(-6)0 = 1.

78. (–7)–4 × (–7)2 = (–7)–2

Ans: True.

LHS = (-7)4 x (-7)2

Using law of exponents, am × an = am+n

Therefore, (-7)-4 x (-7)-2 = (-7)-4+2 = (-7)-2

LHS = RHS

79. The value of $\dfrac{1}{{{4^{ - 2}}}}$ is equal to 16.

Ans: True

Using law of exponents, ${x^{ - m}} = \dfrac{1}{{{x^m}}}$

Thus, $\dfrac{1}{{{4^{ - 2}}}} = {4^2} = 4 \times 4 = 16$

80. The expression for 4–3 as a power with the base 2 is 26.

Ans: False

Using law of exponents, ${x^{ - m}} = \dfrac{1}{{{x^m}}}$

Thus,${4^{ - 3}} = \dfrac{1}{{{4^3}}} = \dfrac{1}{{{{\left( {{2^2}} \right)}^3}}} = \dfrac{1}{{{2^6}}}$ 

81. ap × bq = (ab)pq

Ans: False.

RHS = (ab)pq

Using law of exponents, am × an = am+n

Therefore, (ab)pq = (a)pq x (b)pq

L H S ≠ R H S

82. $\dfrac{{{x^m}}}{{{y^m}}} = {\left( {\dfrac{y}{x}} \right)^{ - m}}$

Ans: True

${\text{RHS  = }}{\left( {\dfrac{y}{x}} \right)^{ - m}} = {\left( {\dfrac{x}{y}} \right)^m} = \dfrac{{{x^m}}}{{{y^m}}} = {\text{LHS}}$

83. ${a^m} = \dfrac{1}{{{a^{ - m}}}}$

Ans: True

Using law of exponents, ${x^{ - m}} = \dfrac{1}{{{x^m}}}$

${a^m} = \dfrac{1}{{{a^{ - m}}}}$

84. The exponential form for (–2)4 × ${\left( {\dfrac{5}{2}} \right)^4}$ is 54.

Ans: True

${\left( { - 2} \right)^4} \times {\left( {\dfrac{5}{2}} \right)^4} = {\left( 2 \right)^4} \times {\left( {\dfrac{5}{2}} \right)^4}$

= ${2^4} \times \dfrac{{{5^4}}}{{{2^4}}} = {5^4}$

85. The standard form for 0.000037 is 3.7 × 10–5.

Ans: True
For standard form, 0.000037 = 0.37 x 10-4= 3.7 x 10-5

86. The standard form for 203000 is 2.03 × 105

Ans: True
For standard form, 203000 = 203 x 10 x 10 x 10 = 203 x 103
= 2.03 x 102 x 103= 2.03 x 105

87. The usual form for 2 × 10–2 is not equal to 0.02.

Ans: False

As, $2 \times {10^{ - 2}} = 2 \times \dfrac{1}{{{{10}^2}}} = 2 \times \dfrac{1}{{100}} = 0.02$

88. The value of 5–2 is equal to 25.

Ans: False

As, ${5^{ - 2}} = \dfrac{1}{{{5^2}}} = \dfrac{1}{{25}} \ne 25$

89. Large numbers can be expressed in the standard form by using positive exponents.

Ans: True
e.g. 2350000 = 235 x 10 x 10 x 10 x 10 = 235 x 104
= 2.35 x 104 x 102 =2.35 x 106

90. am × bm = (ab)m

Ans: True

LHS = am × bm = (a × b)m = (ab)m

91. Solve the following:

(i) 100–10 

Ans: Use ${x^{ - m}} = \dfrac{1}{{{x^m}}}$

So, ${100^{ - 10}} = \dfrac{1}{{{{100}^{10}}}}$

(ii) 2–2 × 2–3 

Ans: Using law of exponents, am × an = am+n

${2^{ - 2}} \times {2^{ - 3}} = {2^{ - 2 - 3}} = {2^{ - 5}}$

(iii) ${\left( {\dfrac{1}{2}} \right)^{ - 2}} \div {\left( {\dfrac{1}{2}} \right)^{ - 3}}$

Ans: Use ${a^m} \div {a^n} = {a^{m - n}}$

${\left( {\dfrac{1}{2}} \right)^{ - 2}} \div {\left( {\dfrac{1}{2}} \right)^{ - 3}} = {\left( {\dfrac{1}{2}} \right)^{ - 2 - \left( { - 3} \right)}} = {\left( {\dfrac{1}{2}} \right)^1} = \dfrac{1}{2}$

92. Express 3–5 × 3–4 as a power of 3 with positive exponent.

Ans: Using law of exponents, am × an = am+n

${3^{ - 5}} \times {3^{ - 4}} = {3^{ - 5 - 4}} = {3^{ - 9}} = \dfrac{1}{{{3^9}}}$

93. Express 16–2 as a power with the base 2.

Ans: Since $2 \times 2 \times 2 \times 2 = 16 = {2^4}$,

${16^{ - 2}} = {\left( {{2^4}} \right)^{ - 2}} = {\left( 2 \right)^{4 \times  - 2}} = {2^{ - 8}}$

94. Express $\dfrac{{27}}{{64}}$ and $\dfrac{{ - 27}}{{64}}$ as powers of a rational number.

Ans: 27 = 3 × 3 × 3 = 33

-27 = -3 × -3 × -3 = (-3)3

64 = 4 × 4 × 4 = 43

Now use ${\left( {\dfrac{a}{b}} \right)^m} = \dfrac{{{a^m}}}{{{b^m}}}$,

$\dfrac{{27}}{{64}} = \dfrac{{{3^3}}}{{{4^3}}} = {\left( {\dfrac{3}{4}} \right)^3}$

$\Rightarrow \dfrac{{ - 27}}{{64}} = \dfrac{{{{\left( { - 3} \right)}^3}}}{{{4^3}}} = {\left( {\dfrac{{ - 3}}{4}} \right)^3}$

95. Express $\dfrac{{16}}{{81}}$ and $\dfrac{{ - 16}}{{81}}$ as powers of a rational number.

Ans: 16 = 4 × 4 = (4)2

81 = 9 × 9 = 92

Now use ${\left( {\dfrac{a}{b}} \right)^m} = \dfrac{{{a^m}}}{{{b^m}}}$,

$\dfrac{{16}}{{81}} = \dfrac{{{4^2}}}{{{9^2}}} = {\left( {\dfrac{4}{9}} \right)^2}$

$\Rightarrow \dfrac{{ - 16}}{{81}} = \dfrac{{ - {{\left( 4 \right)}^2}}}{{{9^2}}} =  - {\left( {\dfrac{4}{9}} \right)^2}$

96. Express as a power of a rational number with a negative exponent.

(a) ${\left( {{{\left( {\dfrac{{ - 3}}{2}} \right)}^{ - 2}}} \right)^{ - 3}}$

Ans: Use ${\left( {{a^m}} \right)^n} = {a^{mn}}$ and ${a^{ - m}} = \dfrac{1}{{{a^m}}}$

${\left( {{{\left( {\dfrac{{ - 3}}{2}} \right)}^{ - 2}}} \right)^{ - 3}} = {\left( {\dfrac{{ - 3}}{2}} \right)^{ - 2 \times \left( { - 3} \right)}} = {\left( {\dfrac{{ - 3}}{2}} \right)^6} = {\left( {\dfrac{2}{3}} \right)^{ - 6}}$

(b) (25 ÷ 28) × 2–7

Ans: Use ${a^m} \div {a^n} = {a^{m - n}}$ and ${a^m} \times {a^n} = {a^{m + n}}$

$\left( {{2^5} \div {2^8}} \right) \times {2^{ - 7}} = \left( {{2^{5 - 8}}} \right) \times {2^{ - 7}}$

= ${2^{ - 3}} \times {2^{ - 7}} = {2^{ - 3 - 7}} = {2^{ - 10}}$

97. Find the product of the cube of (–2) and the square of (+4).

Ans: Since, cube of (-2)= (-2)3

And square of (+4)= (+4)2

Therefore, the product= (-2)3 x (4)2 = (-8) x 16 = -128

98. Simplify:

(i) ${\left( {\dfrac{1}{4}} \right)^{ - 2}} + {\left( {\dfrac{1}{2}} \right)^{ - 2}} + {\left( {\dfrac{1}{3}} \right)^{ - 2}}$

Ans: Use ${a^{ - m}} = \dfrac{1}{{{a^m}}}$,

${\left( {\dfrac{1}{4}} \right)^{ - 2}} + {\left( {\dfrac{1}{2}} \right)^{ - 2}} + {\left( {\dfrac{1}{3}} \right)^{ - 2}} = {4^2} + {2^2} + {3^2} = 16 + 4 + 9 = 29$

(ii) ${\left( {{{\left( {\dfrac{{ - 2}}{3}} \right)}^{ - 2}}} \right)^{3}} \times {\left( {\dfrac{1}{3}} \right)^{ - 4}} \times {3^{ - 1}} \times \dfrac{1}{6}$

Ans: Use ${a^m} \div {a^n} = {a^{m - n}}$

${\left( {{{\left( {\dfrac{{ - 2}}{3}} \right)}^{ - 2}}} \right)^3} \times {\left( {\dfrac{1}{3}} \right)^{ - 4}} \times {3^{ - 1}} \times \dfrac{1}{6} = {\left( {\dfrac{{ - 2}}{3}} \right)^{ - 2 \times 3}} \times {3^4} \times \dfrac{1}{3} \times \dfrac{1}{6}$

= ${\left( {\dfrac{{ - 2}}{3}} \right)^{ - 6}} \times {3^4} \times \dfrac{1}{3} \times \dfrac{1}{{2 \times 3}}$

= $\dfrac{{{3^6}}}{{{2^6}}} \times {3^4} \times \dfrac{1}{3} \times \dfrac{1}{{2 \times 3}}$

= $\dfrac{{{3^{10 - 2}}}}{{{2^{6 + 1}}}} = \dfrac{{{3^8}}}{{{2^7}}}$

(iii) $\dfrac{{49 \times {z^{ - 3}}}}{{{7^{ - 3}} \times 10 \times {z^{ - 5}}}}{\text{   }}\left( {z \ne 0} \right)$

Ans: Use ${a^m} \div {a^n} = {a^{m - n}}$ 

$\dfrac{{49 \times {z^{ - 3}}}}{{{7^{ - 3}} \times 10 \times {z^{ - 5}}}} = \dfrac{{{7^2} \times {z^{ - 3}}}}{{{7^{ - 3}} \times 10 \times {z^{ - 5}}}} = \dfrac{{{7^{2 + 3}} \times {z^{ - 3 + 5}}}}{{10}}$

= $\dfrac{{{7^5} \times {Z^2}}}{{10}} = \dfrac{{{7^{^5}}}}{{10}}{z^2}$

(iv) (25 ÷ 28) × 2-7

Ans: Use ${a^m} \div {a^n} = {a^{m - n}}$ 

$\left( {{2^5} \div {2^8}} \right) \times {\left( 2 \right)^{ - 7}} = {\left( 2 \right)^{5 - 8}}{\left( 2 \right)^{ - 7}}$

= ${2^{ - 3}} \times {2^{ - 7}} = {2^{ - 3 - 7}} = {2^{ - 10}} = \dfrac{1}{{{2^{10}}}} = \dfrac{1}{{1024}}$

99. Find the value of x so that

(i) ${\left( {\dfrac{5}{3}} \right)^{ - 2}} \times {\left( {\dfrac{5}{3}} \right)^{ - 14}} = {\left( {\dfrac{5}{3}} \right)^{8x}}$

Ans: Use ${a^m} \times {a^n} = {a^{m + n}}$,

${\left( {\dfrac{5}{3}} \right)^{ - 2}} \times {\left( {\dfrac{5}{3}} \right)^{ - 14}} = {\left( {\dfrac{5}{3}} \right)^{8x}}$

$\Rightarrow {\left( {\dfrac{5}{3}} \right)^{ - 2 - 14}} = {\left( {\dfrac{5}{3}} \right)^{8x}}$

$\Rightarrow {\text{Compare }}{\text{both }}{\text{sides,}}$

$\Rightarrow - 16 = 8x$

$\Rightarrow x =  - 2$

(ii) ${\left( { - 2} \right)^3} \times {\left( { - 2} \right)^{ - 6}} = {\left( { - 2} \right)^{2x - 1}}$

Ans: Use, am × an = am+n

Then, (-2)3 x (-2)-6 = (-2)2x-1

(-2)3-6 = (-2)2x-1

(-2)-3 = (-2)2x-1

Compare both the sides and the result is=

$-3 = 2x – 1$

$\Rightarrow 2 x = -3 + 1$

$\Rightarrow 2x = -2$

$\Rightarrow x= -1$

(iii) ${\left( {{2^{ - 1}} + {4^{ - 1}} + {6^{ - 1}} + {8^{ - 1}}} \right)^x} = 1$

Ans: Use ${a^{ - m}} = \dfrac{1}{{{a^m}}}$,

${\left( {{2^{ - 1}} + {4^{ - 1}} + {6^{ - 1}} + {8^{ - 1}}} \right)^x} = 1$

$\Rightarrow {\left( {\dfrac{1}{2} + \dfrac{1}{4} + \dfrac{1}{6} + \dfrac{1}{8}} \right)^x} = 1$

$\Rightarrow {\left( {\dfrac{{12 + 6 + 4 + 3}}{{24}}} \right)^x} = 1$

$\Rightarrow {\left( {\dfrac{{25}}{{24}}} \right)^x} = 1$

This can be possible only if x = 0 because a0 = 1.

100. Divide 293 by 10,00,000 and express the result in standard form.

Ans: Use ${a^{ - m}} = \dfrac{1}{{{a^m}}}$,

1000000 = 106

$\Rightarrow \dfrac{{293}}{{{{10}^6}}} = 293 \times {10^{ - 6}}$

$= 2.93 \times {10^{ - 6}} \times {10^2} = 2.93 \times {10^{ - 4}}$

101. Find the value of x–3 if x = (100)1–4 ÷ (100)0.

Ans: Use ${a^m} \div {a^n} = {a^{m - n}}$ and ${a^m} \times {a^n} = {a^{m + n}}$

$x = {\left( {100} \right)^{ - 3}} \div {\left( {100} \right)^0}$

$\Rightarrow x = {\left( {100} \right)^{ - 3 - 0}}$

$\Rightarrow x = {\left( {100} \right)^{ - 3}}$

Thus,

$\Rightarrow {x^{ - 3}} = {\left( {{{\left( {100} \right)}^{ - 3}}} \right)^{ - 3}} = {\left( {100} \right)^{ 9}}$

102. By what number should we multiply (–29)0 so that the product becomes (+29)0.

Ans: Let x be multiplied with (–29)0 to get (+29)0

So, 

$x \times {\left( { - 29} \right)^0} = {\left( {29} \right)^0}$

$\Rightarrow x \times 1 = 1$

$\Rightarrow x = 1$

103. By what number should (–15)–1 be divided so that quotient may be equal to 

(–15)–1?

Ans: Let (–15)–1 be divided by x to get quotient (–15)–1.

So,

$\dfrac{{{{\left( { - 15} \right)}^{ - 1}}}}{x} = {\left( { - 15} \right)^{ - 1}}$

$\Rightarrow x = \dfrac{{{{\left( { - 15} \right)}^{ - 1}}}}{{{{\left( { - 15} \right)}^{ - 1}}}}$

$\Rightarrow x = 1$ 

104. Find the multiplicative inverse of (–7)–2 ÷ (90)–1.

Ans: a is called multiplicative inverse of b, if a x b= 1.

${\left( { - 7} \right)^{ - 2}} \div {\left( {90} \right)^{ - 1}} = \dfrac{1}{{{{\left( 7 \right)}^2}}} \div \dfrac{1}{{{{\left( {90} \right)}^1}}} = \dfrac{1}{{49}} \times 90 = \dfrac{{90}}{{49}}$

Put $b = \dfrac{{90}}{{49}}$

$\Rightarrow a \times \dfrac{{90}}{{49}} = 1$

$\Rightarrow a = \dfrac{{49}}{{90}}$

105. If 53x–1 ÷ 25 = 125, find the value of x.

Ans: Given, 53x–1 ÷ 25 = 125

Since, 25 = 5 x 5 = 52

And 125 = 5 x 5 x 5 = 53

Therefore, 53x–1 ÷ (5)2 = (5)3

So, (5)3x–1-2 = (5)3 [As am ÷ an = (a)m-n ] 

(5)3x–3 = (5)3

On comparing both sides, we get

⇒3x – 3 = 3

⇒3x = 6

⇒x = 2

106. Write 39,00,00,000 in the standard form.

Ans: For standard form,

39,00,00,000 = 39 x 10 x 10 x 10 x 10 x 10 x 10 x 10

= 39 x 107 = 3.9 x 101 x 107

Use the law of exponent am × an = am+n

Thus, 39,00,00,000= 3.9 x 108

Therefore, the standard form of 39,00,00,000 = 3.9 x 108

107. Write 0.000005678 in the standard form.

Ans: For standard form, 

0.000005678 = 0.5678 x 10-5 = 5.678 x 10-5 x 10-1

= 5.678 x 10-6 

Hence, 5.678 x 10-6 is the standard form of 0.000005678.

108. Express the product of 3.2 × 106 and 4.1 × 10–1 in the standard form.

Ans: Product of 3.2 × 106 and 4.1 × 10–1 = (3.2 x 106) (4.1x 10-1)

= (3.2 x 4.1) x 106 x 10-1

= 13.12 x 105 = 1.312 x 105 x 101 [As am × an = am+n]

= 1.312 x 106

109. Express $\dfrac{{1.5 \times {{10}^6}}}{{2.5 \times {{10}^{ - 4}}}}$ in the standard form.

Ans: Use am ÷ an = (a)m-n,

$\dfrac{{1.5 \times {{10}^6}}}{{2.5 \times {{10}^{ - 4}}}} = \dfrac{{15}}{{25}} \times {10^{6 + 4}} = \dfrac{3}{5} \times {10^{10}}$

= $0.6 \times {10^{10}}$

= $6 \times {10^{ - 1}} \times {10^{10}} = 6 \times {10^9}$

110. Some migratory birds travel as much as 15,000 km to escape the extreme climatic conditions at home. Write the distance in metres using scientific notation.

Ans: Total distance traveled by migratory bird = 15000 km.

= 15000 x 1000 m [As 1 km= 1000 m]

= 15000000 m

= 15 x 106 m

Scientific notation of 15 x 106 = 1.5 x 107 m.

111. Pluto is 59,1,30,00, 000 m from the sun. Express this in the standard form.

Ans: Distance between Pluto and Sun = 59,1,30,00, 000

Standard form of 59,1,30,00, 000 = 5913 x 106

= 5.913 x 106 x 103

Use, am × an = am+n

Therefore, 5.913 x 106 x 103 = 5.913 x 109

112. Special balances can weigh something as 0.00000001 gram. Express this number in the standard form.

Ans: Weight = 0.00000001 g

Standard form= 0.00000001 = 0.1 x 10-7 g

= 1 x 10-7 x 10-1 g [Use, am × an = am+n]

= 1.0 x 10-8 g

113. A sugar factory has annual sales of 3 billion 720 million kilograms of sugar. Express this number in the standard form.

Ans: Annual sales of a sugar factory = 3 billion 720

million kilograms = 3720000 kg

Standard form of-

3720000 = 372 x 10 x 10 x 10 x 10 = 372 x 104 kg

Use am × an = am+n

= 372 x 104 x 102 = 3.72 x 106 kg.

114. The number of red blood cells per cubic millimetre of blood is approximately 5.5 million. If the average body contains 5 litres of blood, what is the total number of red cells in the body? Write the standard form. (1 litre = 1,00,000 mm3)

Ans: The average body contains 5 L of blood.
Also, the number of red blood cells per cubic millimetre of blood is approximately 5.5 million.
Blood contained by body = 5 L = 5 x 100000 mm3
Red blood cells = 5 x 100000 mm3
Blood = 5.5 x 1000000 x 5 x 100000= 55 x 5 x 105 + 5
= 275 x 1010 = 2.75 x 1010 x 102 = 2.75 x 1012

115. Express each of the following in standard form:

(a) The mass of a proton in gram is $\dfrac{{1673}}{{{\mathbf{1000000000000000000000000000}}}}$

Ans: Standard form = $\dfrac{{1673}}{{{{10}^{27}}}} = 1673 \times {10^{ - 27}}g$

= $1.673 \times {10^{ - 27}} \times {10^3}g$

= $1.673 \times {10^{ - 27 + 3}}g$

= $1.673 \times {10^{ - 24}}g$

(b) A Helium atom has a diameter of 0.000000022 cm.

Ans: Standard form= 0.22 x 10-7 cm = 2.2 x 10-1 x 10-7

Using the law of exponent am × an = am+n,

= 2.2 x 10-1-7 = 2.2 x 10-8 cm

Therefore, the standard form is 2.2 x 10-8 cm. 

(c) Mass of a molecule of hydrogen gas is about 0.00000000000000000000334 tons.

Ans: Standard form = 0.334 x 10-20 = 3.34 x 10-20 x 10-1

[Use am × an = am+n]

3.34 x 10-20 x 10-1 = 3.34 x 10-21

(d) Human body has 1 trillion of cells which vary in shape and size.

Ans: Cells in human body = 1 trillion

As, 1 trillion = 1000000000000

Standard form of 1000000000000 = 10 x 10 x 10 x 10 x 10 x

10 x 10 x 10 x 10 x 10 x 10 x 10 = 1012 

(e) Express 56 km in m.

Ans: Given, 56 km = 56 x 1000 m= 56000 m

Standard form of 56000 m = 56 x 103 = 5.6 x 103 x 101 = 5.6 x 104 m

(f) Express 5 tons in g.

Ans: Given, 5 tons = 5 x 100 kg = 5 x 100 x 1000 g = 500000g

Standard form of 500000

= 5 x 10 x 10 x 10 x 10 x 10 = 5 x 105

(g) Express 2 years in seconds.

Ans: 2 yr = 2 x 365 days

= 2 x 365 x 24h

= 2 x 365 x 24 x 60min

= 2 x 365 x 24 x 60 x 60s

= 63072000 s

Standard form of

63072000 = 63072 x 10 x 10 x 10 = 63072 x 103

63072 x 103 = 6.3072 x 104 x 103

Since, am × an = am+n

6.3072 x 104 x 103 = 6.3072 x 107 s 

(h) Express 5 hectares in cm2 (1 hectare = 10000 m2)

Ans: 5 hec = 5 x 10000 m2

= 5 x 10000 x 100 x 100 cm2

= 5 x 104+2+2 [Use am × an = am+n]

= 5 x 108 cm2

116. Find x so that ${\left( {\dfrac{2}{9}} \right)^3} \times {\left( {\dfrac{2}{9}} \right)^{ - 6}} = {\left( {\dfrac{2}{9}} \right)^{2x - 1}}$

Ans: Use am × an = am+n

$\Rightarrow {\left( {\dfrac{2}{9}} \right)^3} \times {\left( {\dfrac{2}{9}} \right)^{ - 6}} = {\left( {\dfrac{2}{9}} \right)^{2x - 1}}$

$\Rightarrow {\left( {\dfrac{2}{9}} \right)^{3 - 6}} = {\left( {\dfrac{2}{9}} \right)^{2x - 1}}$

$\Rightarrow {\left( {\dfrac{2}{9}} \right)^{ - 3}} = {\left( {\dfrac{2}{9}} \right)^{2x - 1}}$

$\Rightarrow - 3 = 2x - 1$

$\Rightarrow 2x =  - 3 + 1$

$\Rightarrow x = \dfrac{{ - 2}}{2} =  - 1$

117. By what number should ${\left( {\dfrac{{ - 3}}{2}} \right)^{ - 3}}$ be divided so that the quotient may be

${\left( {\dfrac{4}{{27}}} \right)^{ - 2}}$?

Ans: Let ${\left( {\dfrac{{ - 3}}{2}} \right)^{ - 3}}$ is divided by x to get quotient ${\left( {\dfrac{4}{{27}}} \right)^{ - 2}}.$

Then,

$\Rightarrow {\left( {\dfrac{{ - 3}}{2}} \right)^{ - 3}} \div x = {\left( {\dfrac{4}{{27}}} \right)^{ - 2}}$

$\Rightarrow {\left( {\dfrac{2}{{ - 3}}} \right)^3} \times \dfrac{1}{x} = {\left( {\dfrac{{27}}{4}} \right)^2}$

$\Rightarrow x = \dfrac{{{2^3} \times {4^2}}}{{{{\left( { - 3} \right)}^3} \times {{\left( {27} \right)}^2}}} = \dfrac{{{2^3} \times {{\left( {{2^2}} \right)}^2}}}{{ - {{\left( 3 \right)}^3} \times {{\left( {{3^3}} \right)}^2}}} = \dfrac{{{2^{3 + 4}}}}{{ - {3^{3 + 6}}}} = \dfrac{{{2^7}}}{{ - {3^9}}}$

In questions 118 and 119, find the value of n.

118. $\dfrac{{{6^n}}}{{{6^{ - 2}}}} = {6^3}$

Ans: Use ${a^m} \div {a^n} = {\left( a \right)^{m - n}}$

$\dfrac{{{6^n}}}{{{6^{ - 2}}}} = {6^3}$

$\Rightarrow {6^{n - \left( { - 2} \right)}} = {6^3}$

$\Rightarrow {6^{n + 2}} = {6^3}$

On comparing both sides

n + 2= 3

n = 1

Therefore, the value of n is 1.

119. $\dfrac{{{2^n} \times {2^6}}}{{{2^{ - 3}}}} = {2^{18}}$

Ans: Use ${a^m} \times {a^n} = {\left( a \right)^{m + n}}$, ${a^m} \div {a^n} = {\left( a \right)^{m - n}}$ and ${a^{ - m}} = \dfrac{1}{{{a^m}}}$.

$\Rightarrow \dfrac{{{2^n} \times {2^6}}}{{{2^{ - 3}}}} = {2^{18}}$

$\Rightarrow {2^{n + 6 - \left( { - 3} \right)}} = {2^{18}}$

$\Rightarrow {2^{n + 9}} = {2^{18}}$

On comparing both sides,

⇒n + 9 = 18

⇒n = 9

120. $\dfrac{{125 \times {x^{ - 3}}}}{{{5^{ - 3}} \times 25 \times {x^{ - 6}}}}$

Ans: Use ${a^m} \times {a^n} = {\left( a \right)^{m + n}}$, ${a^m} \div {a^n} = {\left( a \right)^{m - n}}$ and ${a^{ - m}} = \dfrac{1}{{{a^m}}}$.

$\dfrac{{125 \times {x^{ - 3}}}}{{{5^{ - 3}} \times 25 \times {x^{ - 6}}}} = \dfrac{{{5^3} \times {x^{ - 3}}}}{{{5^{ - 3}} \times {5^2} \times {x^{ - 6}}}}$

= ${5^{3 + 3 - 2}} \times {x^{ - 3 + 6}}$

= ${5^4} \times {x^3} = 625{x^3}$

121. $\dfrac{{16 \times {{10}^2} \times 64}}{{{2^4} \times {4^2}}}$

Ans: Use ${a^m} \times {a^n} = {\left( a \right)^{m + n}}$, ${a^m} \div {a^n} = {\left( a \right)^{m - n}}$ and ${a^{ - m}} = \dfrac{1}{{{a^m}}}$.

$\dfrac{{16 \times {{10}^2} \times 64}}{{{2^4} \times {4^2}}} = {\left( 4 \right)^2} \times {10^2} \times {2^{ - 4}} \times {4^3} \times {4^{ - 2}}$

= ${\left( {{2^2}} \right)^2} \times {10^2} \times {\left( {{2^2}} \right)^{ - 2}} \times {4^3} \times {4^{ - 2}}$

= ${4^2} \times {10^2} \times {4^{ - 2}} \times {4^3} \times {4^{ - 2}}$

= ${4^{2 - 2 + 3 - 2}} \times {10^2}$

= ${4^1} \times {10^2} = 400$

122. If $\dfrac{{{5^m} \times {5^3} \times {5^{ - 2}}}}{{{5^{ - 5}}}} = {5^{12}}$, find m.

Ans: Use ${a^m} \times {a^n} = {\left( a \right)^{m + n}}$, ${a^m} \div {a^n} = {\left( a \right)^{m - n}}$ and ${a^{ - m}} = \dfrac{1}{{{a^m}}}$.

$\Rightarrow {5^{m + 3 + \left( { - 2} \right) - \left( { - 5} \right)}} = {5^{12}}$

$\Rightarrow {5^{m + 3 - 2 + 5}} = {5^{12}}$

$\Rightarrow {5^{m + 6}} = {5^{12}}$

On comparing both sides,

⇒m + 6 = 12

⇒n = 6

123. A new born bear weighs 4 kg. How many kilograms might a five-year-old bear weigh if its weight increases by the power of 2 in 5 years?

Ans: Weight of new born bear = 4 kg
Weight increases by the power of 2 in 5 yr.
Weight of bear in 5 yr = (4)2 = 16 kg

124. The cells of a bacteria double in every 30 minutes. A scientist begins with a single cell. How many cells will be there after-

(a) 12 hours 

Ans: The bacteria cell in every 30 min= 2

So, cell of a bacterium in 1h = 22 $[$As (2+2) in 1h$]$

cell of a bacterium in 12h = 22 x 22 x 22 x 22 x22 x 22 x 22 x

22 x 22 x 22 x 22 x 22 = 224 

(b) 24 hours

Ans: Similarly, bacteria in 24 h = 224 x 224 = 224+24 = 248

125. Planet A is at a distance of 9.35 × 106 km from Earth and planet B is 6.27 × 107 km from Earth. Which planet is nearer to Earth?

Ans: Distance between planet A and Earth = 9.35 x 106 km Distance between planet B and Earth = 6.27 x 107 km
For finding difference between above two distances, we have to change both in same exponent of 10, i.e. 9.35 x 106 = 0.935 x 107, clearly 6.27 x 107 is greater.
So, planet A is nearer to Earth.

126. The cells of a bacteria double itself every hour. How many cells will there be after 8 hours, if initially we start with 1 cell. Express the answer in powers.

Ans: The cell of a bacteria double itself every hour = 1 + 1

= 2 = 21

Since, the process started with 1 cell.

As, am × an = am+n

Therefore, total no. of cell in 8h = 21 x 21 x 21 x 21 x 21 x 21 x

21 x 21 = 28

127. An insect is on the 0 point of a number line, hopping towards 1. She covers half the distance from her current location to 1 with each hop. So, she will be at $\dfrac{1}{2}$ after one hop, $\dfrac{3}{4}$after two hops, and so on.

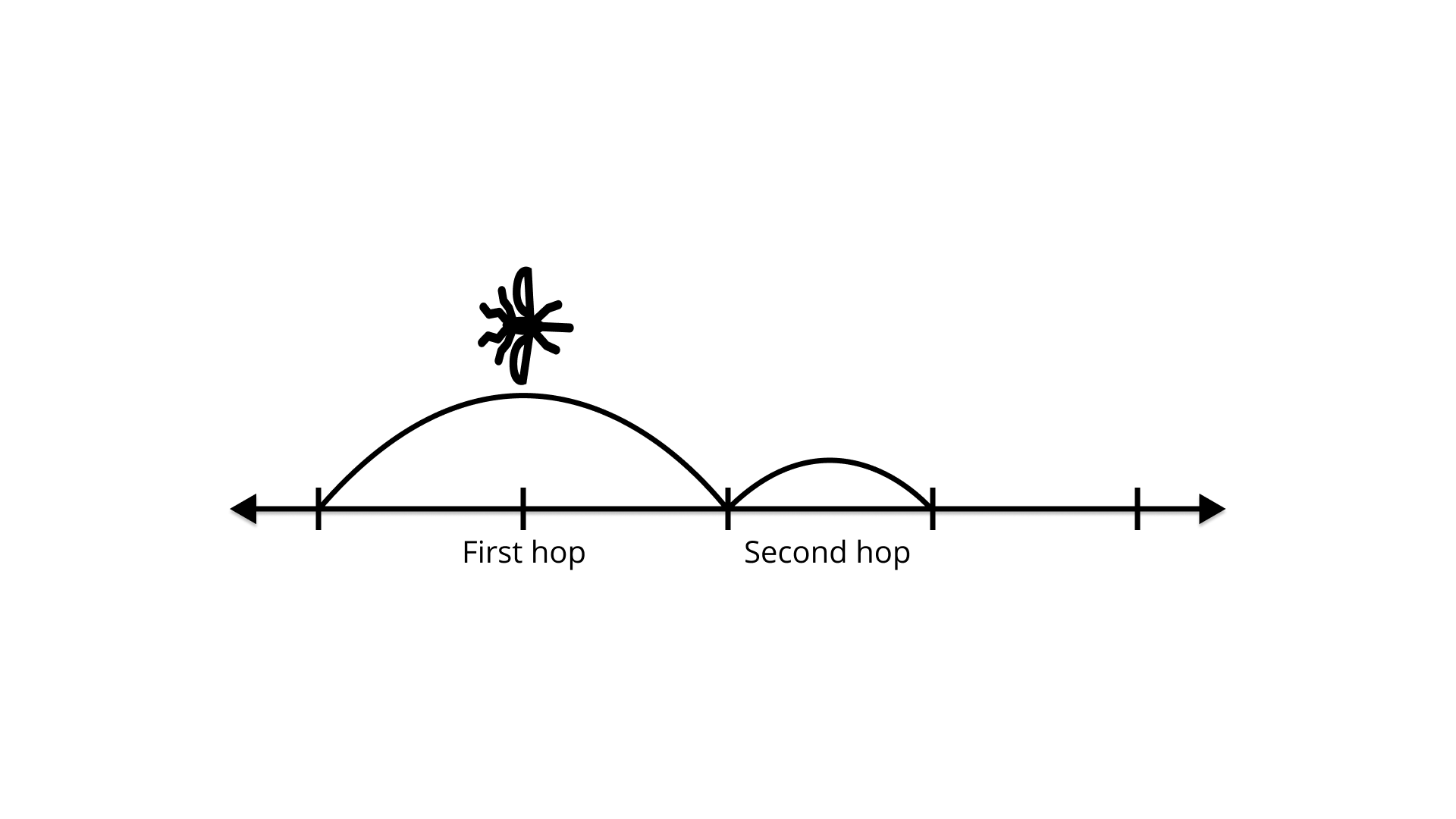
(a) Make a table showing the insect’s location for the first 10 hops.

Ans: On the basis of given information in the question, we can arrange the following table which shows the insect’s location for the first 10 hops.

(b) Where will the insect be after n hops?

Ans: If we see the distance covered in each hops

Distance covered in 1st hops = $1-\dfrac{1}{2}$

Distance covered in 2nd hops = $1-\dfrac{1}{4}$

Distance covered in 3rd hops = $1-\dfrac{1}{8}$

---------------------------------------------------------------------------

Distance covered in n hops = $1-{\left( {\dfrac{1}{2}} \right)^n}$

(c) Will the insect ever get to 1? Explain.

Ans: No, because for reaching 1, ${\left( {\dfrac{1}{2}} \right)^n}$ has to be zero for finite n

which is not possible.

128. Predicting the ones digit, copy and complete this table and answer the questions that follow.

(a) Describe patterns you see in the ones digits of the powers.

Ans: On the basis of given pattern in 1x and 2x , we can make more patterns for 3x 4x , 5x ,6x , 7x , 8x , 9x , 10x .
Thus, we have the following table which shows all details about the patterns.

(b) Predict the ones digit in the following:

1. 412                  

Ans: Ones digit in 412 is 6.

2. 920   

Ans: Ones digit in 920 is 1.

3. 317

Ans: Ones digit in 317 is 3.

 4. 5100 

Ans: Ones digit in 5100 is 5.

 4. 10500 

Ans: Ones digit in 10500 is 0.

(c) Predict the ones digit in the following:

1. 3110                

Ans: Ones digit in 3110 is 1.

2. 1210 

Ans:  Ones digit in 1210 is 4.

3. 1721    

Ans:  Ones digit in 1721 is 7.

4. 2910

Ans:  One digit in 2910 is 1.

129. Astronomy The table shows the mass of the planets, the sun and the moon in our solar system.

(a) Write the mass of each planet and the Moon in scientific notation.

Ans: Using law of exponents am × an = am+n

Sun= 199 x 1028 = 1.99 x 1028 x 102 = 1.99 x 1030

Mercury= 33 x 1022 = 3.3 x 1022 x 10 = 3.3 x 1023

Venus= 487 x 1022 = 4.87 x 1022 x 102 = 4.87 x 1024

Earth= 597 x 1022 = 5.97 x 1022 x 102 = 5.97 x 1024

Mars= 642 x 1027 = 6.42 x 1027 x 102 = 6.42 x 1029

Jupiter= 19 x 1026 = 1.9 x 1026 x 10= 1.9 x 1027

Saturn= 568 x 1024 = 5.68 x 1024 x 102 = 5.68 x 1026

Uranus= 868 x 1023 = 8.68 x 1023 x 102 = 8.68 x 1025

Neptune= 102 x 1024 = 1.02 x 1024 x 102 = 1.02 x 1026

Pluto= 127 x 1024 = 1.27 x 1020 x 102 = 1.27 x 1022

Moon= 795 x 1020 = 7.95 x 1020 x 102 = 7.95 x 1022

(b) Order the planets and the moon by mass, from least to greatest.

Ans: Order of mass of all planets and Moon from least to greatest.

Pluto < Moon < Mercury < Venus < Earth < Uranus < Neptune < Saturn < Jupiter < Mars

(c) Which planet has about the same mass as earth?

Ans: Venus has the mass similar to Earth.

130. Investigating the Solar System The table shows the average distance from each planet in our solar system to the sun.

(a) Complete the table by expressing the distance from each planet

to the Sun in scientific notation.

Ans: Scientific notation of distance from Sun to

Earth= 149600000 = 1496 x 105 = 1.496 x 108

Jupiter= 778300000 = 7783 x 105 = 7.783 x 108

Mars= 227900000 = 2279 x 105 = 2.279 x 108

Mercury= 57900000 = 579 x 105 = 5.97 x 107

Neptune= 4497000000 = 4497 x 105 = 4.497 x 108

Pluto= 5900000000 = 59 x 108 = 5.9 x 109

Saturn= 1427000000= 1427 x 106 = 1.427 x 109

Venus= 108200000 = 1082 x 105 = 1.082 x 108

(b) Order the planets from closest to the sun to farthest from the sun.

Ans: Order of planet from closest to the Sun to farthest from the

sun is given by

Mercury < Venus < Earth < Mars < Jupiter < Saturn < Uranus

< Neptune < Pluto.

131. This table shows the mass of one atom for five chemical elements. Use it to answer the question given.

(a) Which is the heaviest element?

Ans: The heaviest element is Lead = 34.4 × 10–26 

(b) Which element is lighter, Silver or Titanium?

Ans: Silver = 17.9 × 10–26 and Titanium= 7.95 × 10–26, therefore,

Titanium is lighter.

(c) List all five elements in order from lightest to heaviest.

Ans: Arrangement of elements from lightest to heaviest-

Hydrogen < Lithium < Titanium < Silver < Lead

132. The planet Uranus is approximately 2,896,819,200,000 metres away from the Sun. What is this distance in standard form?

Ans: Distance between the planet Uranus and the Sun is 2896819200000 m.
Standard form of 2896819200000 = 28968192 x 10 x 10 x 10 x 10 x 10
= 28968192 x 105 = 2.8968192 x 1012 m

133. An inch is approximately equal to 0.02543 metres. Write this distancein standard form.

Ans: Standard form of 0.02543 m = 0.2543 x 10-1 m = 2.543 x 10-2 m Hence,’ standard form of 0.02543 is 2.543 x 10-2 m.

134. The volume of the Earth is approximately 7.67 × 10–7 times the volume of the Sun. Express this figure in usual form.

Ans: Given, volume of the Earth = 7.67 × 10–7 times the volume of the Sun.

Usual form of 7.67 × 10–7 = 0.000000767

We have placed decimal 7 places towards the left of the original position.

135. An electron’s mass is approximately 9.1093826 × 10–31 kilograms. What is this mass in grams?

Ans: Mass of electron = 9.1093826 × 10–31

= 9.1093826 × 10–31 x 1000 g

(Use, am × an = (a)m+n)

= 9.1093826 × 10–31 x 103 = 9.1093826 × 10–28 g.

136. At the end of the 20th century, the world population was approximately 6.1 × 109 people. Express this population in usual form. How would you say this number in words?

Ans: Given, at the end of the 20th century, the world population was 6.1 x 109 (approx). People population in usual form = 6.1 x 109 = 6100000000 

Hence, the population in its usual form was six thousand one hundred million.

137. While studying her family’s history. Shikha discovers records of ancestors 12 generations back. She wonders how many ancestors she has had in the past 12 generations. She starts to make a diagram to help her figure this out. The diagram soon becomes very complex.

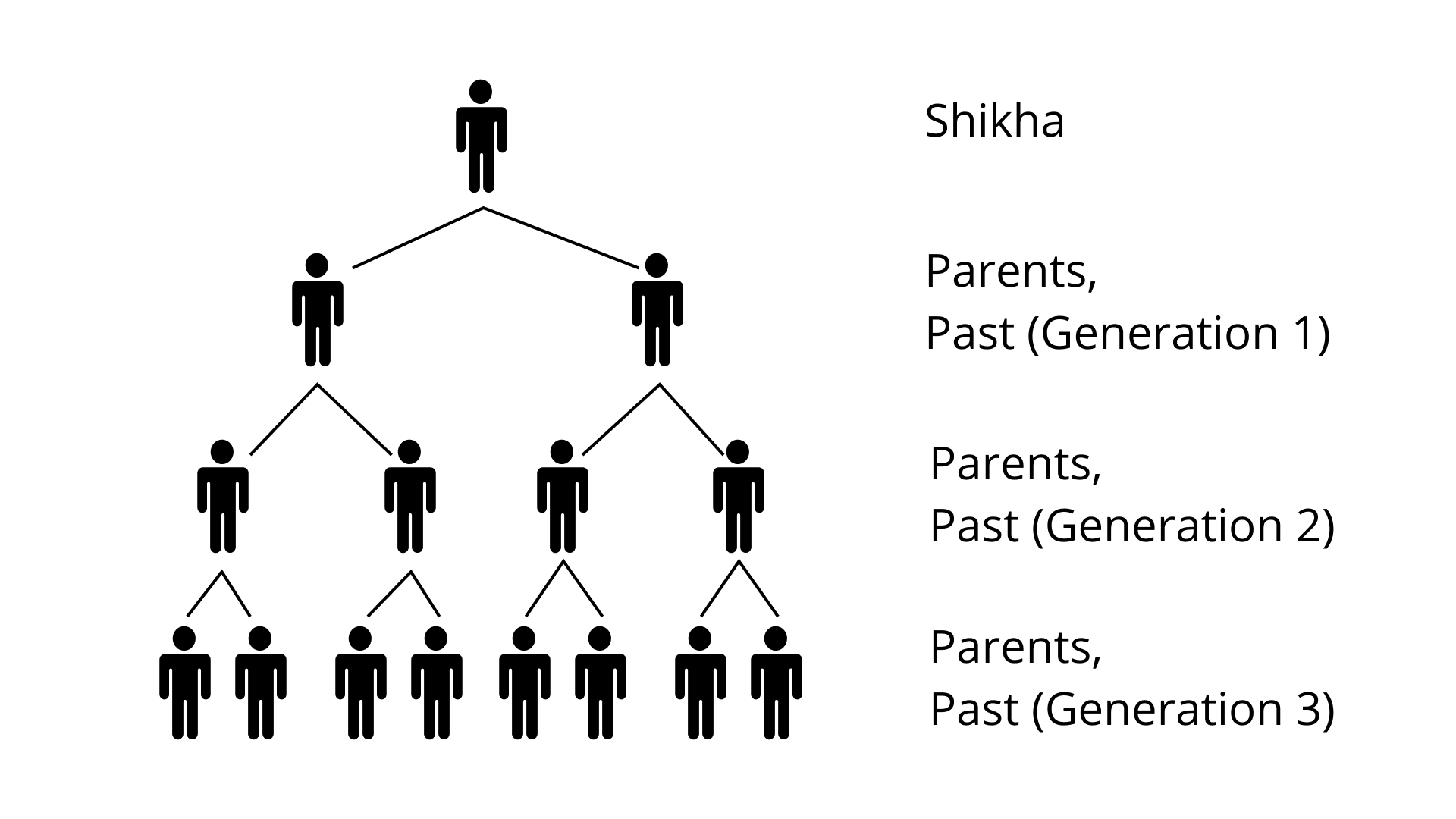
(a) Make a table and a graph showing the number of ancestors in each of the 12 generations.

Ans: On the basis of the given diagram, we can make a table that shows the number of ancestors in each of the 12 generations.

Hence, we can also make a graph that shows the relation between generation and ancestor.

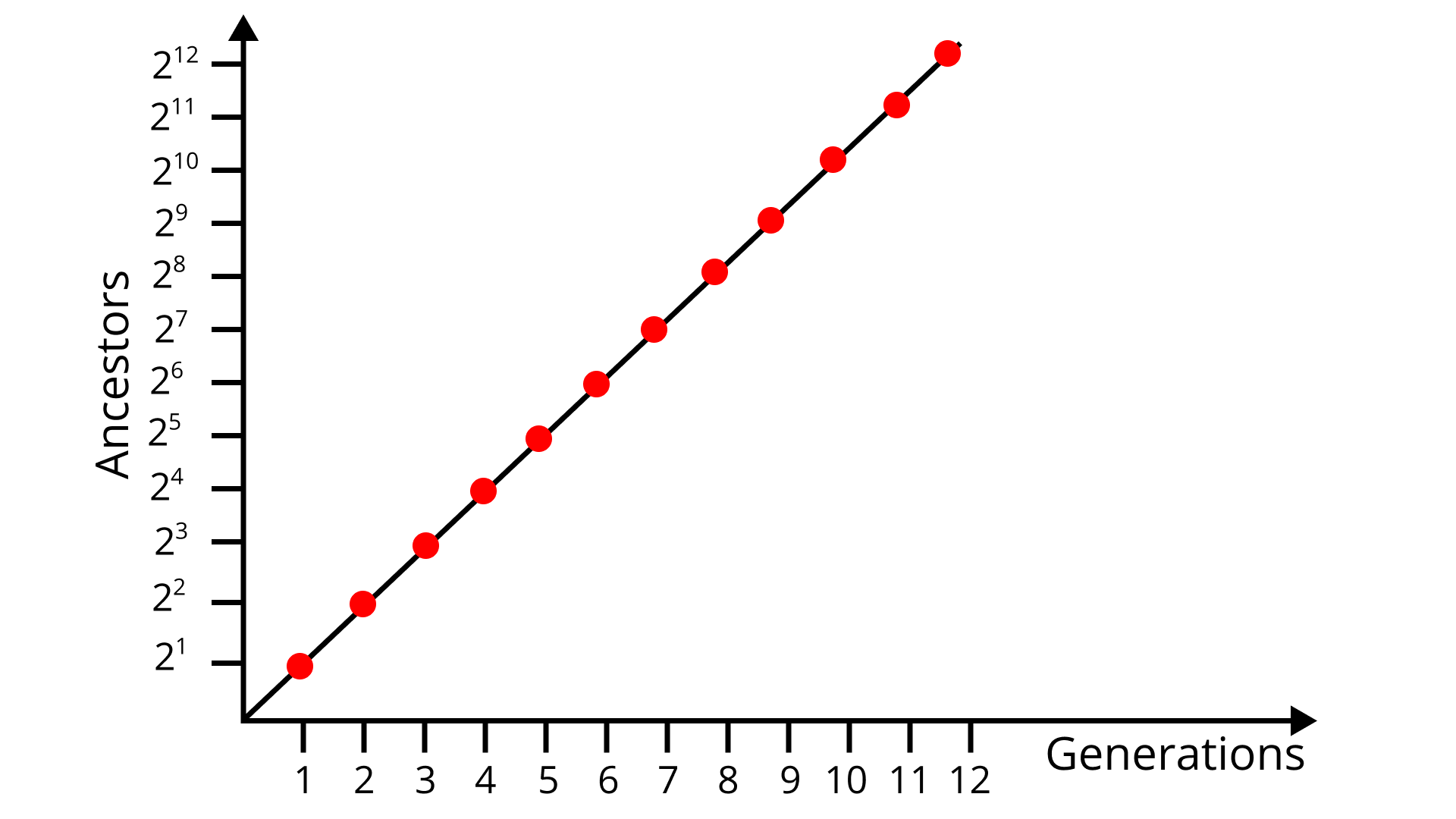
(b) Write an equation for the number of ancestors in a given generation n.

Ans: On the basis of the generation-ancestor graph, the numbers of ancestors in n generations will be 2n.

138. About 230 billion litres of water flows through a river each day. How many litres of water flows through that river in a week? How many litres of water flows through the river in an year? Write your answer in standard notation.

Ans: Water flows through a river in each day = 230000000000 = 230 billion

Water flows through the river in a week = 7 x 230000000000

= 1610000000000 = 1610 billion = 1.61 x 1012 L

Water flows through the river in a year= 230000000000 x 365

= 8395000000000000 = 8.395 x 1013 L.

139. A half-life is the amount of time that it takes for a radioactive substance to decay to one half of its original quantity. 

Suppose radioactive decay causes 300 grams of a substance to decrease to 300 × 2–3 grams after 3 half-lives. Evaluate 300 × 2–3 to determine how many grams of the substance are left. 

Explain why the expression 300 × 2–n can be used to find the amount of the substance that remains after n half-lives.

Ans: Since, 300 g of a substance decreases to 300 x 2-3 g

after 3 half-lives.

So, we have to evaluate 300 x 2-3 = $\dfrac{{300}}{8}$ = 37.5 g

140. Consider a quantity of a radioactive substance. The fraction of this quantity that remains after t half-lives can be found by using the expression 3–t. 

(a) What fraction of substance remains after 7 half-lives?

Ans: Since, 3-t expression is used for finding the fraction of the quality that remains after t half-lives.

Hence, the fraction of substance remains after 7 half-lives will be equal to 3-7 i.e., $\dfrac{1}{{{3^7}}}.$

(b) After how many half-lives will the fraction be $\dfrac{1}{{243}}$ of the original?

Ans: Given, t half-lives = 3-t

So, $\dfrac{1}{{{3^5}}} = \dfrac{1}{{{3^t}}}$

And t = 5.

On comparing both sides, we get t = 5 half-lives.

141. One Fermi is equal to 10–15 metre. The radius of a proton is 1.3 Fermis. Write the radius of a proton in metres in standard form.

Ans: The radius of a proton is 1.3 fermi.
One fermi is equal to 10-15 m.
So, the radius of the proton is 1.3 x 10-15 m.
Hence, standard form of radius of the proton is 1.3 x 10-15 m.

142. The paper clip below has the indicated length. What is the length in standard form?

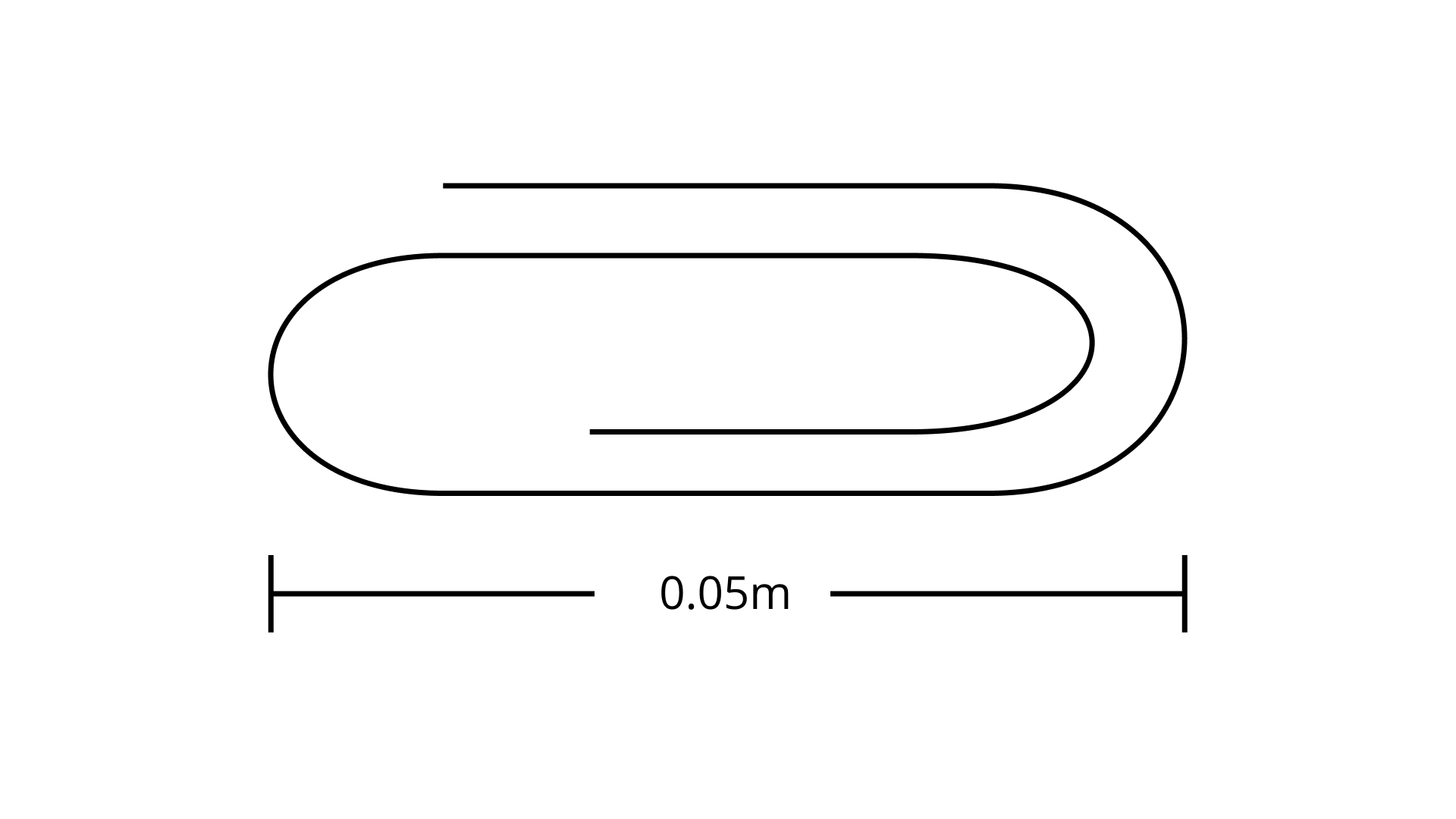
Ans: Length of the paper clip = 0.05 m
In standard form, 0.05 m = 0.5 x 10-1 = 5.0 x 10-2 m
Hence, the length of the paper clip in standard form is 5.0 x 10-2 m

143. Use the properties of exponents to verify that each statement is true.

(a) $\dfrac{1}{4}\left( {{2^n}} \right) = {2^{n - 2}}$

Ans: ${\text{LHS  =  }}\dfrac{1}{4}\left( {{2^n}} \right) = \dfrac{1}{{{2^2}}} \times {2^n} = {2^{n - 2}} = {\text{RHS}}$

(b) ${4^{n - 1}} = \dfrac{1}{4}{\left( 4 \right)^n}$

Ans: ${\text{RHS  =  }}\dfrac{1}{4}{\left( 4 \right)^n} = \dfrac{1}{4} \times {4^n} = {4^{n - 1}} = {\text{LHS}}$

(c) 25(5n–2) = 5n

Ans: ${\text{LHS  =  25}}\left( {{5^{n - 2}}} \right) = {5^2}{5^{n - 2}} = {5^{2 + n - 2}} = {5^n} = {\text{RHS}}$

144. Fill in the blanks

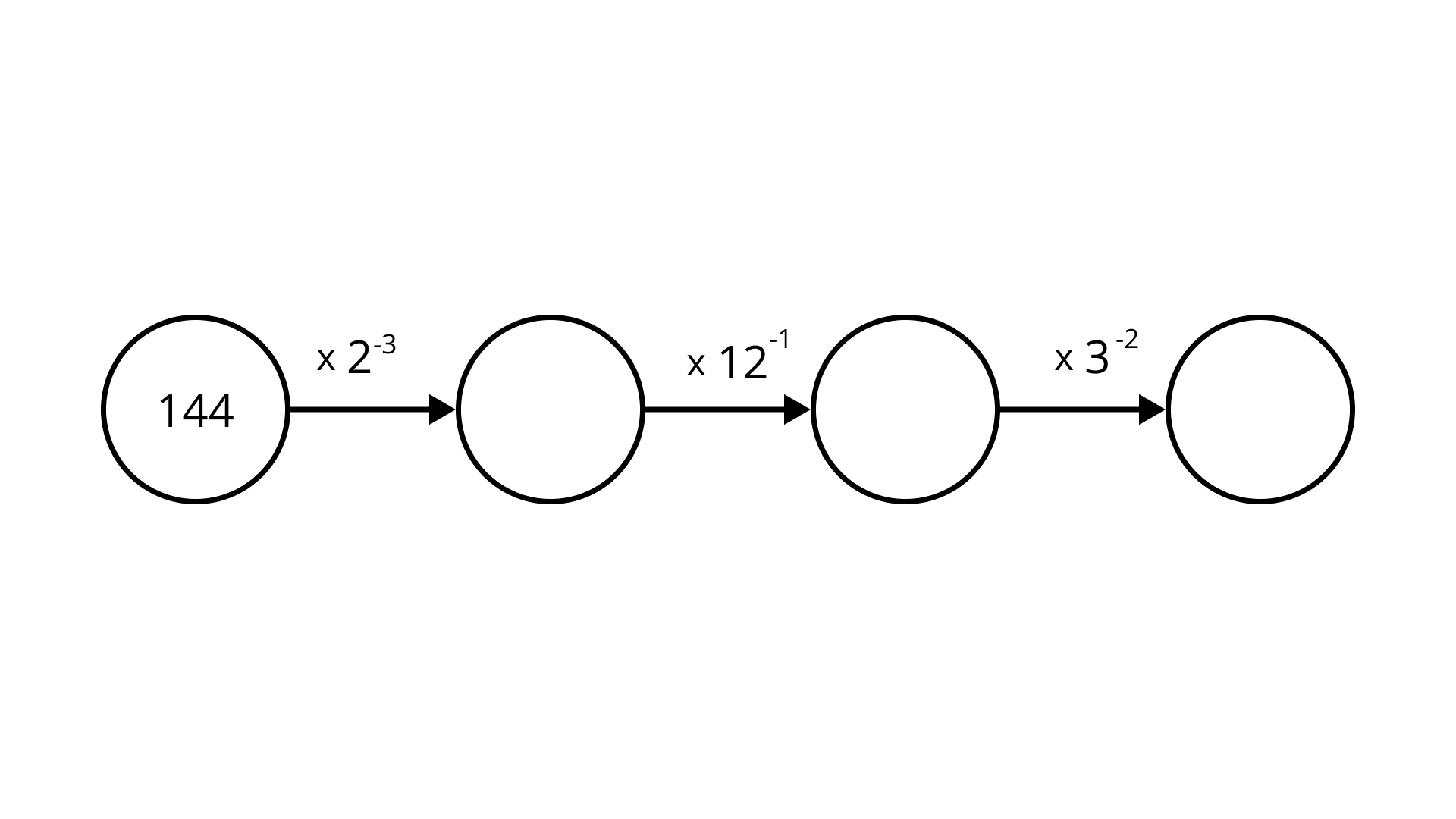
Ans: $144 \times {2^{ - 3}} = 144 \times \dfrac{1}{8} = 18$

$18 \times {2^{ - 1}} = 18 \times \dfrac{1}{12} = \dfrac{3}{2}$

$\dfrac{3}{2} \times {3^{ - 2}} = \dfrac{3}{2} \times \dfrac{1}{{{3^2}}} = \dfrac{1}{{2 \times 3}} = \dfrac{1}{6}$

145. There are 864,00 seconds in a day. How many days long is a second? Express your answer in scientific notation.

Ans: Total seconds in a day = 86400
So, a second is long as $\dfrac{1}{{86400}} = 0.000011574$
Scientific notation of 0.000011574= 1.1574 x 10-5days

146. The given table shows the crop production of a State in the year 2008 and 2009. Observe the table given below and answer the given questions.

(a) For which crop(s) did the production decrease?

Ans: From the given table we can figure out that bajra, jowar and rice crop’s production decreased.

(b) Write the production of all the crops in 2009 in their standard form.

Ans: The production of all crops in 2009

Bajra= 1.4 x 103 – 0.1 x 103 = 1.3 x 103

Jowar= 1.7 x 106 – 44 x 104

= 1.7 x 106 – 0.44 x 106 = 1.26 x 106

Rice= 3.7 x 103 – 0.1 x 103 = 3.6 x 103

Wheat= 5.1 x 105 + 19 x 104

= 5.1 x 105 + 1.9 x 105 = 7 x 105

(c) Assuming the same decrease in rice production each year as in 2009, how many acres will be harvested in 2015? Write in standard form.

Ans: Incomplete information.

147. Stretching Machine Suppose you have a stretching machine which could stretch almost anything. For example, if you put a 5 metre stick into a (× 4) stretching machine (as shown below), you get a 20 metre stick. Now if you put a 10 cm carrot into a (× 4) machine, how long will it be when it comes out?

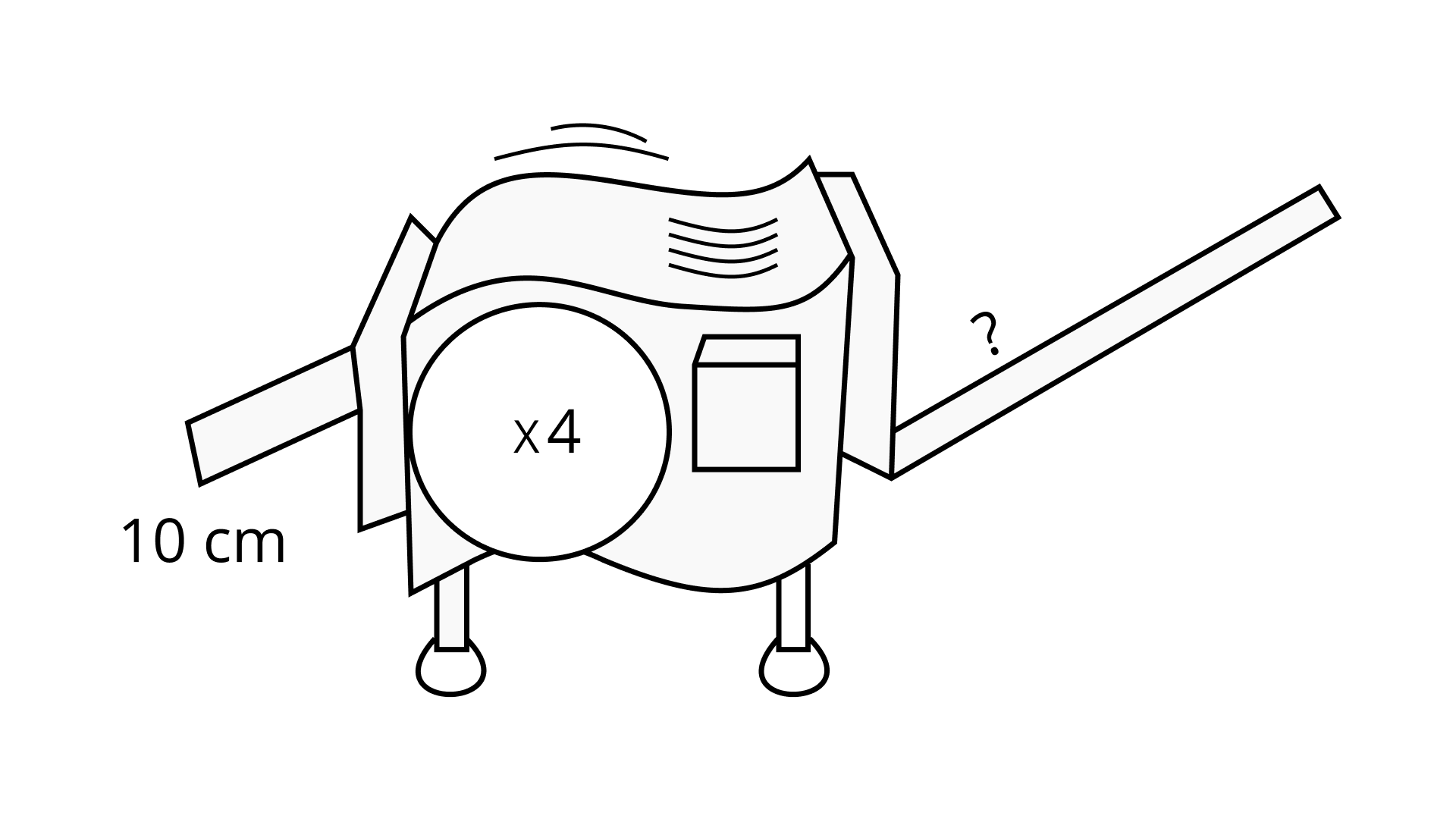
Ans: According to the question, if we put a 5 m stick into a (x 4) stretching machine, then the machine produces 20 m sticks.
Similarly, if we put 10 cm carrots into a (x 4) stretching machine, then the machine produces 10 x 4 = 40 cm sticks.

148. Two machines can be hooked together. When something is sent through this hook up, the output from the first machine becomes the input for the second.

(a) Which two machines hooked together do the same work a (× 102) machine does? Is there more than one arrangement of two machines that will work?

Ans: 

To get the same work in (x102) machine, hook (x 22) and (x 52) machine.

So, x 102 = x 100

Now, we get,

22 x 52 = 4 x 25 = 100

(b) Which stretching machine does the same work as two (× 2) machines hooked together?

Ans: 

The same work would be produced by a (x 4) single machine when two machines (x 2) and (x 2) are hooked together.

149. Repeater Machine Similarly, a repeater machine is a hypothetical machine which automatically enlarges items several times. For example, sending a piece of wire through a (× 24) machine is the same as putting it through a (× 2) machine four times. So, if you send a 3 cm piece of wire through a (× 24) machine, its length becomes 3 × 2 × 2 × 2 × 2 = 48 cm. It can also be written that a base (2) machine is being applied 4 times.

Ans: According to the question, if we put a 3 cm piece of wire through a (x 24) machine, its length becomes 3 x 2 x 2 x 2 x 2 = 48 cm.
Similarly, a 4 cm long strip becomes 4 x 2 x 2 x 2 x 2 = 64 cm.

150. For the following repeater machines, how many times the base machine is applied and how much the total stretch is?

(a)

Ans: In the first machine that is (a), (x1002) = 10000 stretch. Because it is twice the base machine. 

(b)

Ans: In machine (b), (x 75) = 16807 stretch.
Since, it is fair times the base machine.

(c)

Ans: In machine (c), (x 57) = 78125 stretch.
Since, it is 7 times the base machine.

151. Find three repeater machines that will do the same work as a (×64) machine. Draw them, or describe them using exponents.

Ans: We know that, the possible factors of 64 are 2, 4, 8. :

If 26 =64, 43 =64 and 82 =64

Hence, three repeater machines that would work as a (x 64) will be (x 26), (x 43) and (x 82). The diagram of (x 26), (x 43) and (x 82) is given below.

152. What will the following machine do to a 2 cm long piece of chalk?

Ans: The machine produce x 1100 = 1
So, if we insert a 2 cm long piece of chalk in that machine, the piece of chalk remains the same.

153. In a repeater machine with 0 as an exponent, the base machine is applied 0 times.

(a) What do these machines do to a piece of chalk?

Ans: Use the law of exponent a0 = 1.

Since, 30 = 1, 130 = 1, 290 = 1

So, machine (x 30), (x 130) and (x 290) produce nothing on not changing the piece 7 chalk. 

(b) What do you think the value of 60 is?

Ans: Use law of exponent a0 = 1,

Similarly, (x 60) machine does not change the piece.

154. Shrinking Machine

In a shrinking machine, a piece of stick is compressed to reduce its length. If 9 cm long sandwich is put into the shrinking machine below, how many cm long will it be when it emerges?

Ans: According to the question, in a shrinking machine, a piece of stick is compressed to reduce its length. If a 9 cm long sandwich is put into the shrinking machine, then the length of the sandwich will be $9 \times \dfrac{1}{{{3^{ - 1}}}}$= 9 x 3 = 27 cm.

155. What happens when 1 cm worms are sent through these hook-ups?

(i)

Ans: If you put 1 cm worms through ( x21) and (x2-1)

machine, the result will be = 1 x 2 x $\dfrac{1}{2}$ = 1cm.

(ii)

Ans: If we send 1 cm worms through hooked machines (x 2-1) and (x 2)-2, result will be-

$1 \times \dfrac{1}{2} \times \dfrac{1}{{2 \times 2}} = \dfrac{1}{{2 \times 4}} = \dfrac{1}{8}{\text{ cm  =  0}}{\text{.125 cm}}$

156. Sanchay put a 1cm stick of gum through a (1 × 3–2) machine. How long was the stick when it came out?

Ans: Length of the stick of gum that Sanchay put through the (1 x 3-2) machine = 1 cm

Negation (-) sign in power states that the given machine is a

shrinking machine.

Hence $1 \times \dfrac{1}{{{3^2}}} = 1 \times \dfrac{1}{9} = \dfrac{1}{9}{\text{ cm}}$

Therefore, the length of the stick when it came out is $\dfrac{1}{9}{\text{ cm}}$.

157. Ajay had a 1cm piece of gum. He put it through the repeater machine given below and it came out $\dfrac{1}{{{\mathbf{100}},{\mathbf{000}}}}$cm long. What is the missing value?

Ans: The 1 cm piece of gum that Ajay put came out as $\dfrac{1}{{100000}}$.

From this we can conclude that the machine is a shrinking

machine.

Therefore, the type of shrinking machine is ${\left( { \times \dfrac{{{1}}}{{10}}} \right)^5}$. 

Hence, the value missing is 5.

158. Find a single machine that will do the same job as the given hook-up.

(a) a (× 23) machine followed by (× 2–2) machine.

Ans: If (x23) machine is followed by a (x2-2) machine,

the result will be- $2 \times 2 \times 2 \times \dfrac{1}{2} \times \dfrac{1}{2} = {2^1}$

Thus, a single machine (x 21) will also work as the given hook-up.

(b) a (× 24) machine followed by $\left( { \times {{\left( {\dfrac{1}{2}} \right)}^2}}\right)$ machine.

Ans: A (x24) machine is followed by a $\left[ {{{\left( {\dfrac{1}{2}} \right)}^2}} \right]$ machine.

Therefore, the result will be $2 \times 2 \times 2 \times 2 \times \dfrac{1}{2} \times \dfrac{1}{2} = 4$

(c) a (× 599) machine followed by a (5–100) machine.

Ans: A (×599) machine is followed by a (x5–100) machine.

Therefore, the result will be ${5^{99}} \times \dfrac{1}{{{5^{100}}}} = \dfrac{1}{5}$

Thus, a $\left( { \times \dfrac{1}{5}} \right)$ machine will work as the given hook-up.

159. Find a single repeater machine that will do the same work as each hook-up.

(a)

Ans: The work that can be performed by the repeater machine is

equal to 22 x 23 x 24 = 29.

Hence, (x 29) single machine can perform the same amount of work. 

(b)

Ans: The work that can be performed by the repeater machine is equal to 1002 x 10010.

Hence, (x 10012) single machine can perform the same amount of work.

(c)

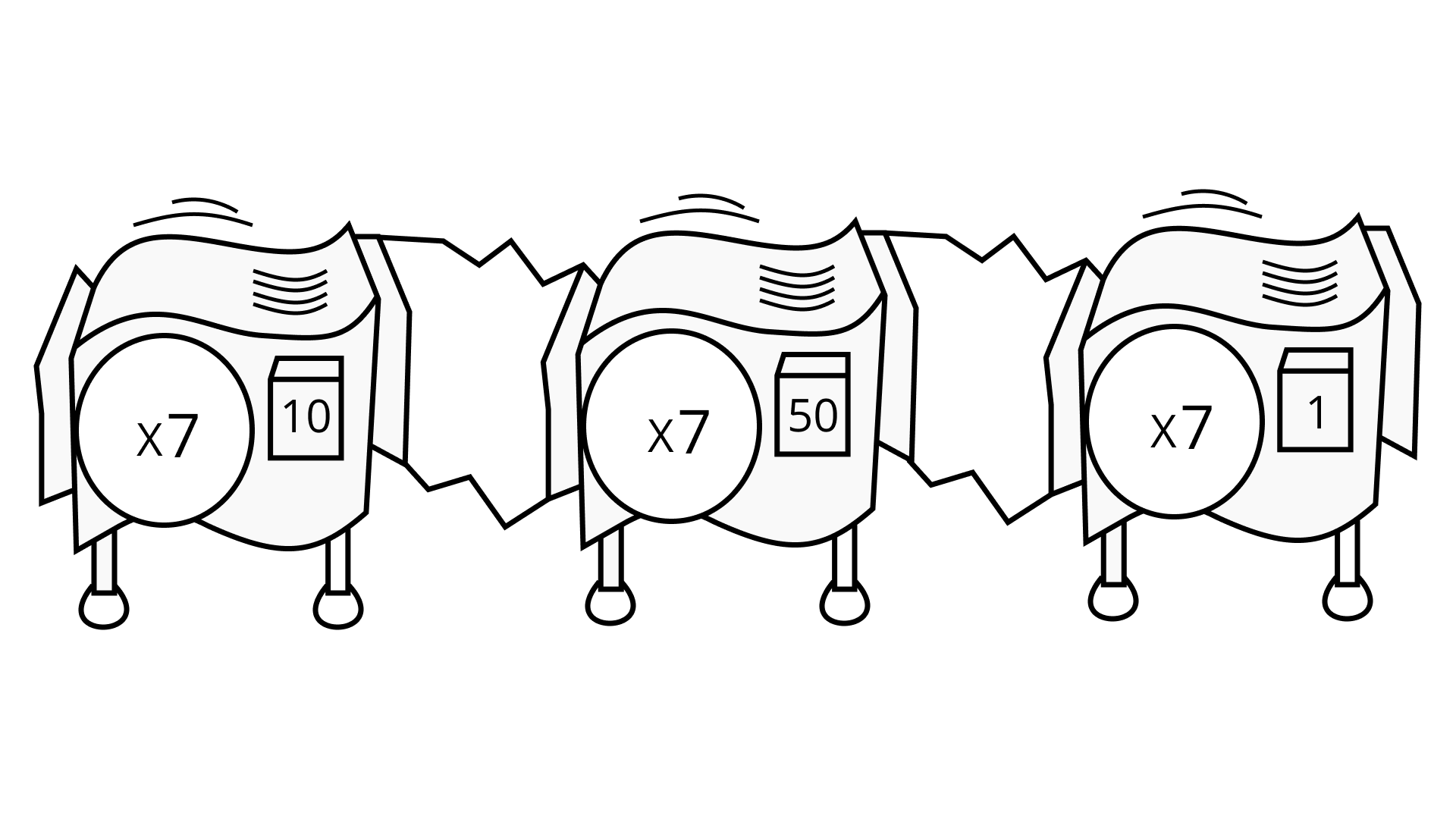
Ans: The work that can be performed by the repeater machine is equal to 710 x 750 x 71 = 761

Hence, (x761) single machine can perform the same amount of work.

(d)

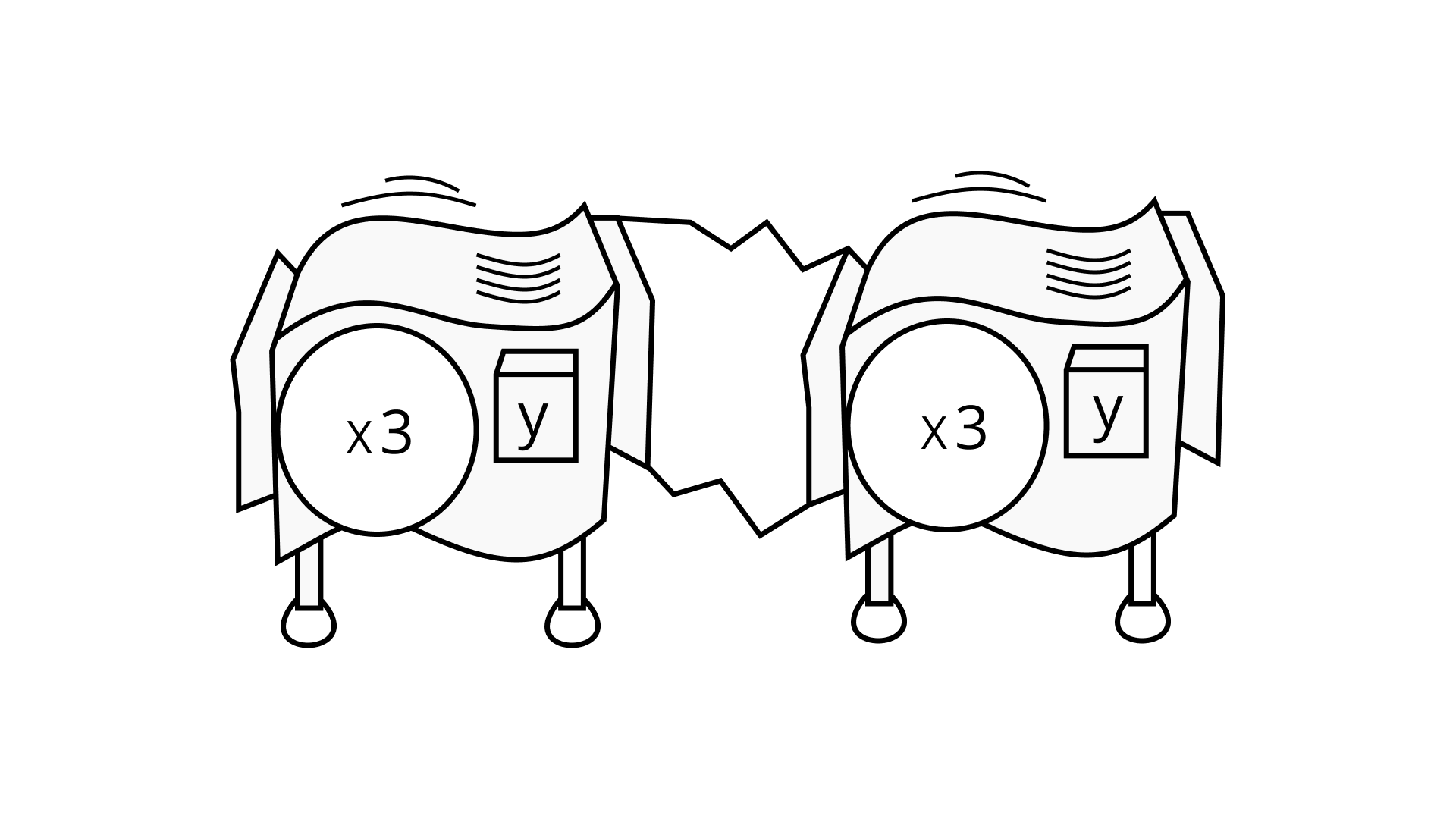
Ans: The work that can be performed by the repeater machine is equal to 3y x 3y = 32y

Hence, (32y) single machine can perform the same amount of work.

(e)

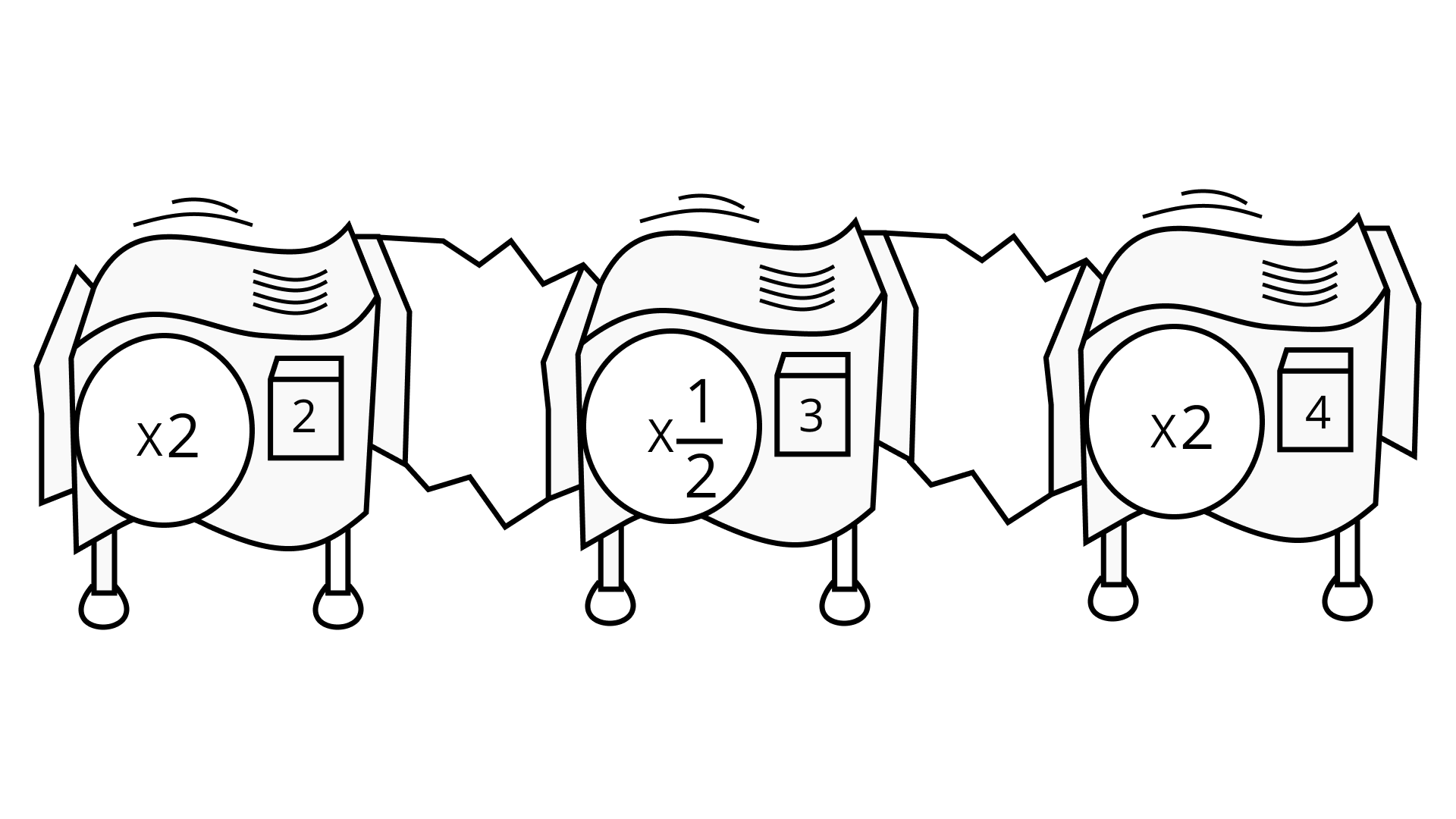
Ans: The work that can be performed by the repeater machine is equal to ${2^2} \times {\left( {\dfrac{1}{2}} \right)^3} \times {2^4} = {2^6} \times \dfrac{1}{{{2^3}}} = {2^3}$

Hence, (x23) single machines can perform the same amount of work.

(f)

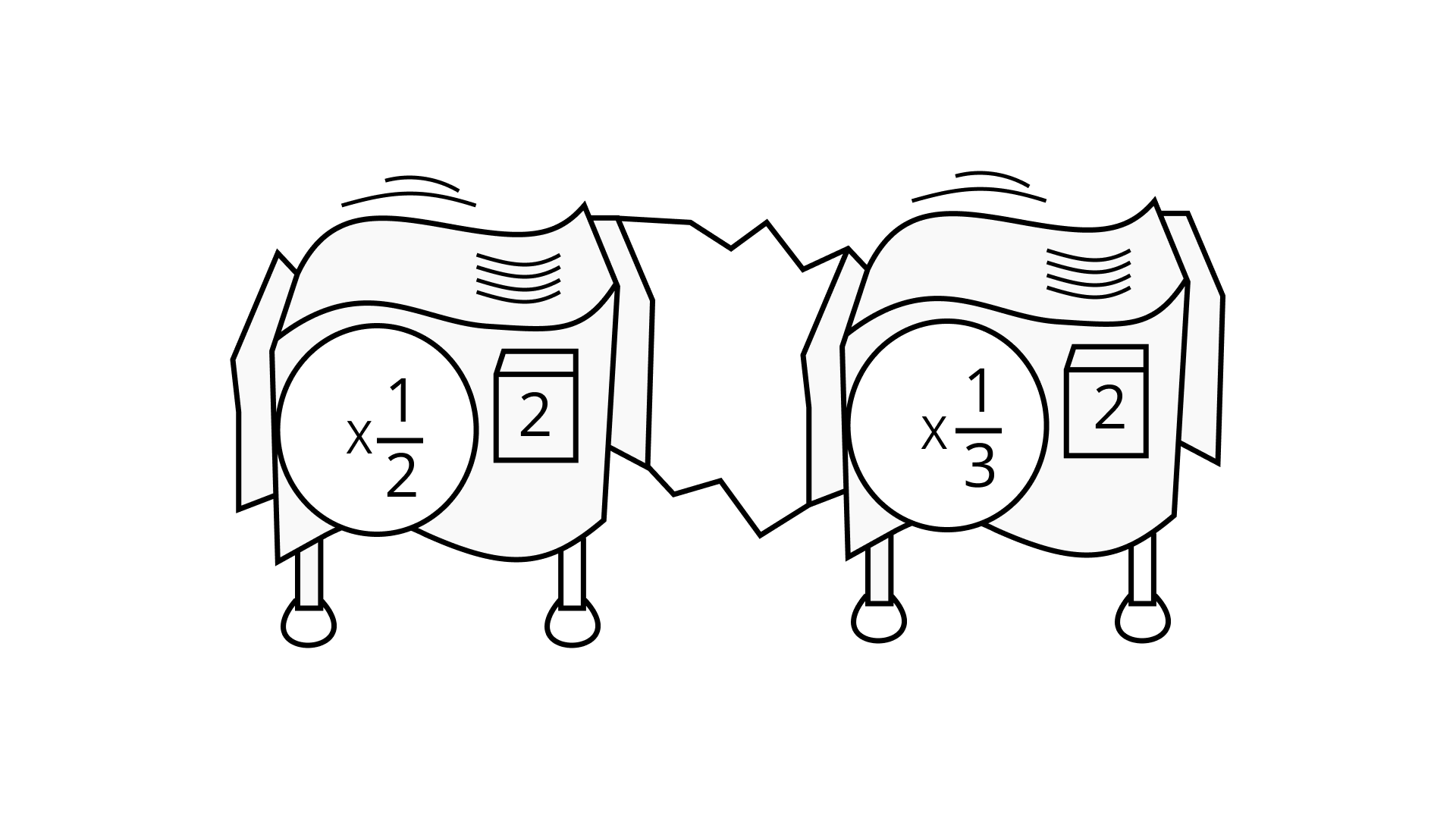
Ans: The work that can be performed by the repeater machine is equal to ${\left( {\dfrac{1}{2}} \right)^2} \times {\left( {\dfrac{1}{3}} \right)^2} = \dfrac{1}{2} \times \dfrac{1}{2} \times \dfrac{1}{3} \times \dfrac{1}{3} = \dfrac{1}{{2 \times 3 \times 2 \times 3}} = \dfrac{1}{{{6^2}}}$

Hence, $\left[ {{{\left( { \times \dfrac{1}{6}} \right)}^2}} \right]$ single machine can perform the same amount of work.

160. For each hook-up, determine whether there is a single repeater machine that will do the same work. If so, describe or draw it.

(a)

Ans: The work that can be performed by the hook-up machine = 73 × 72 = 75

So, (x 75) single machine can perform the same amount of work.

The diagram of a (x 75) single machine can be shown as below:

(b)

Ans: The work that can be performed by the hook-up machine = 23 × 33 = 8 × 9 = 72

Hence, it is not possible that a single machine to perform the same amount of work as (x 82) = 64 and (x 92) = 81.

(c)

Ans: The work that can be performed by the hook-up machine = ${2^2} \times {\left( {\dfrac{1}{3}} \right)^3} \times {5^4} = 4 \times \dfrac{1}{{27}} \times 625$ = $\dfrac{{2500}}{{27}} = 92.59$

Hence, it is not possible that a single machine to perform the same amount of work.

(d)

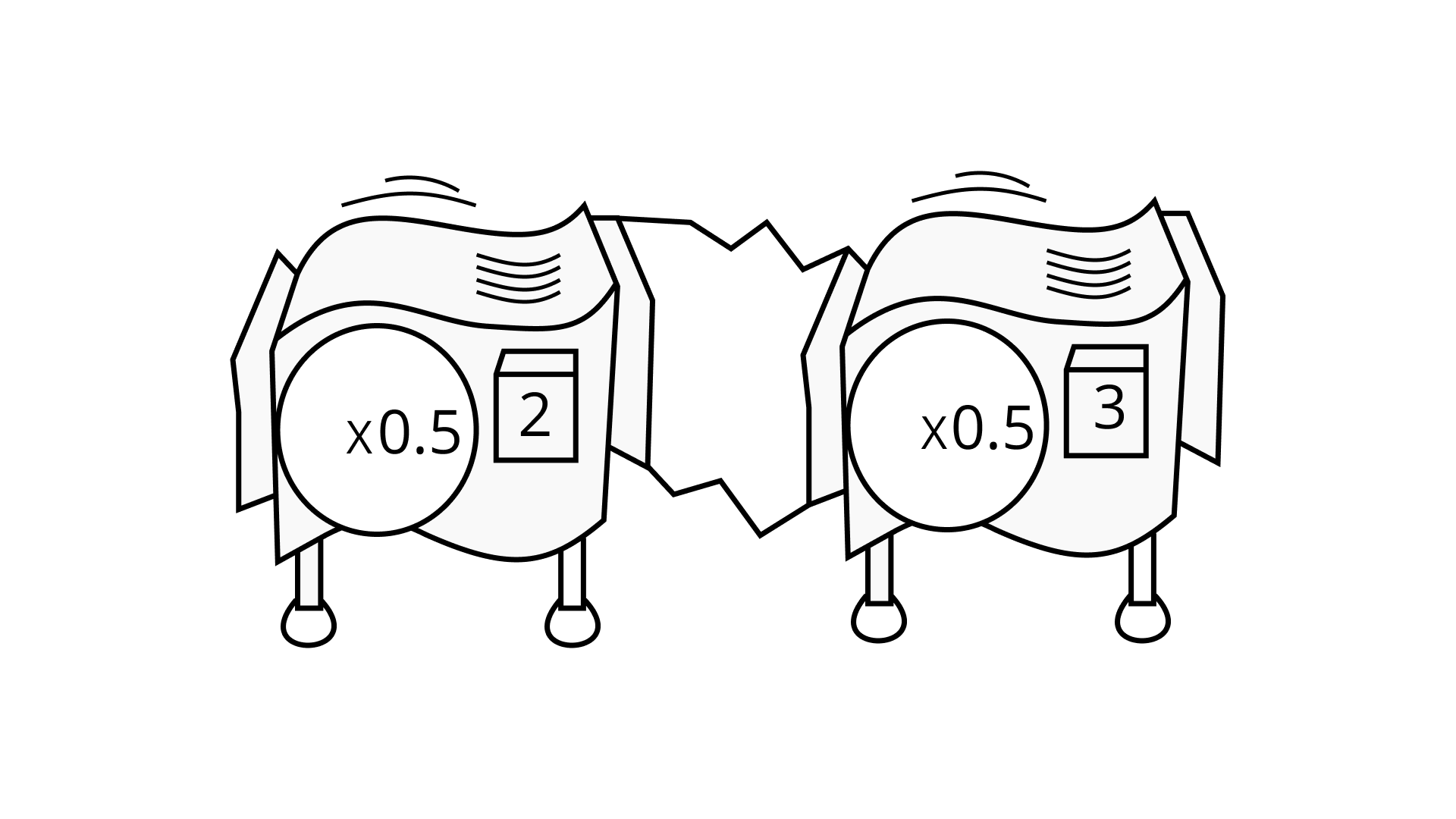
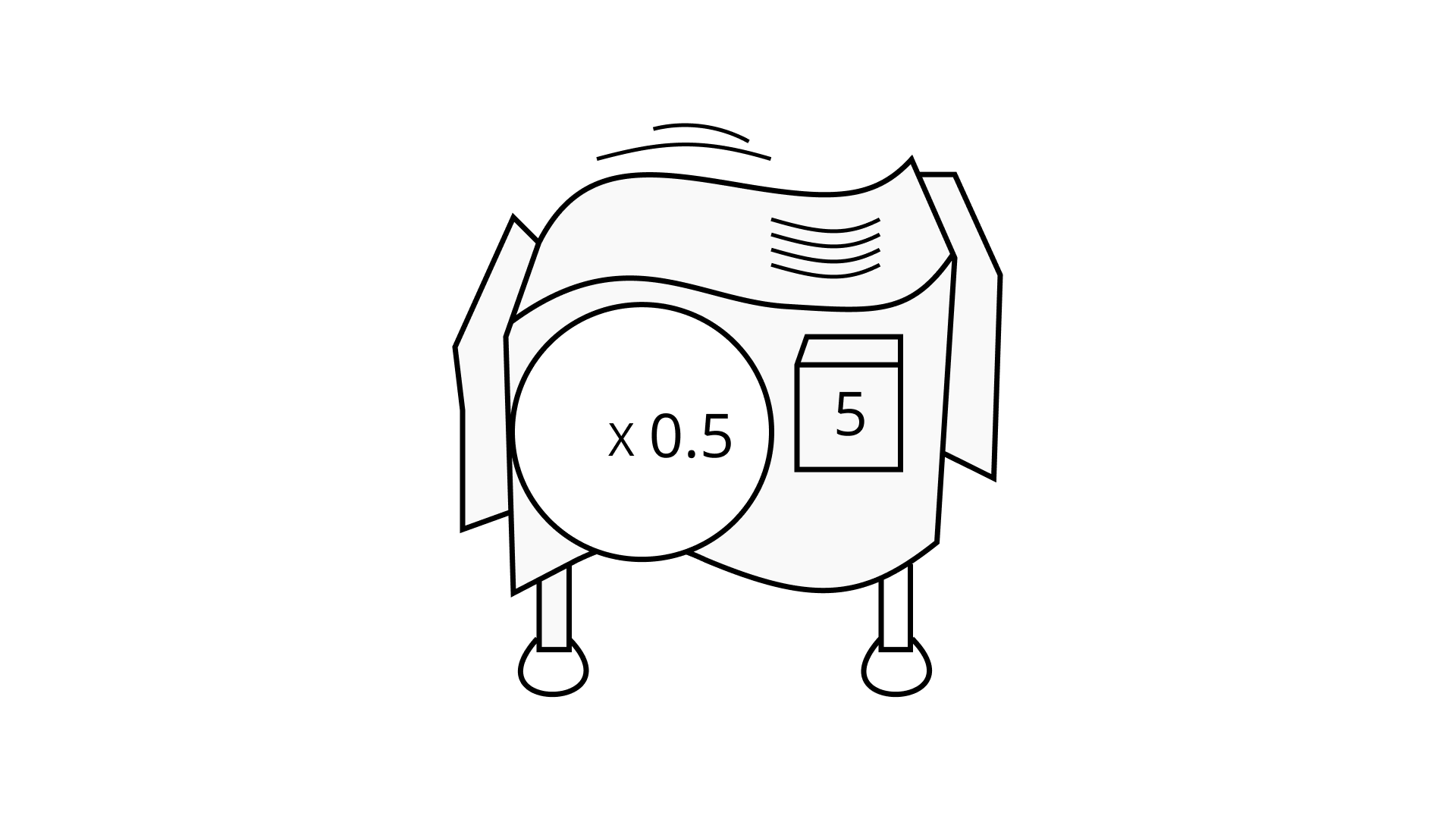
Ans: The work that can be performed by the hook-up machine = (0.5)2 x (0.5)3 = (0.5)5

So, (x (0.5)5) a single machine can perform the same amount of work.

The diagram of a (x 0.5)5 single machine can be shown as below:

(e)

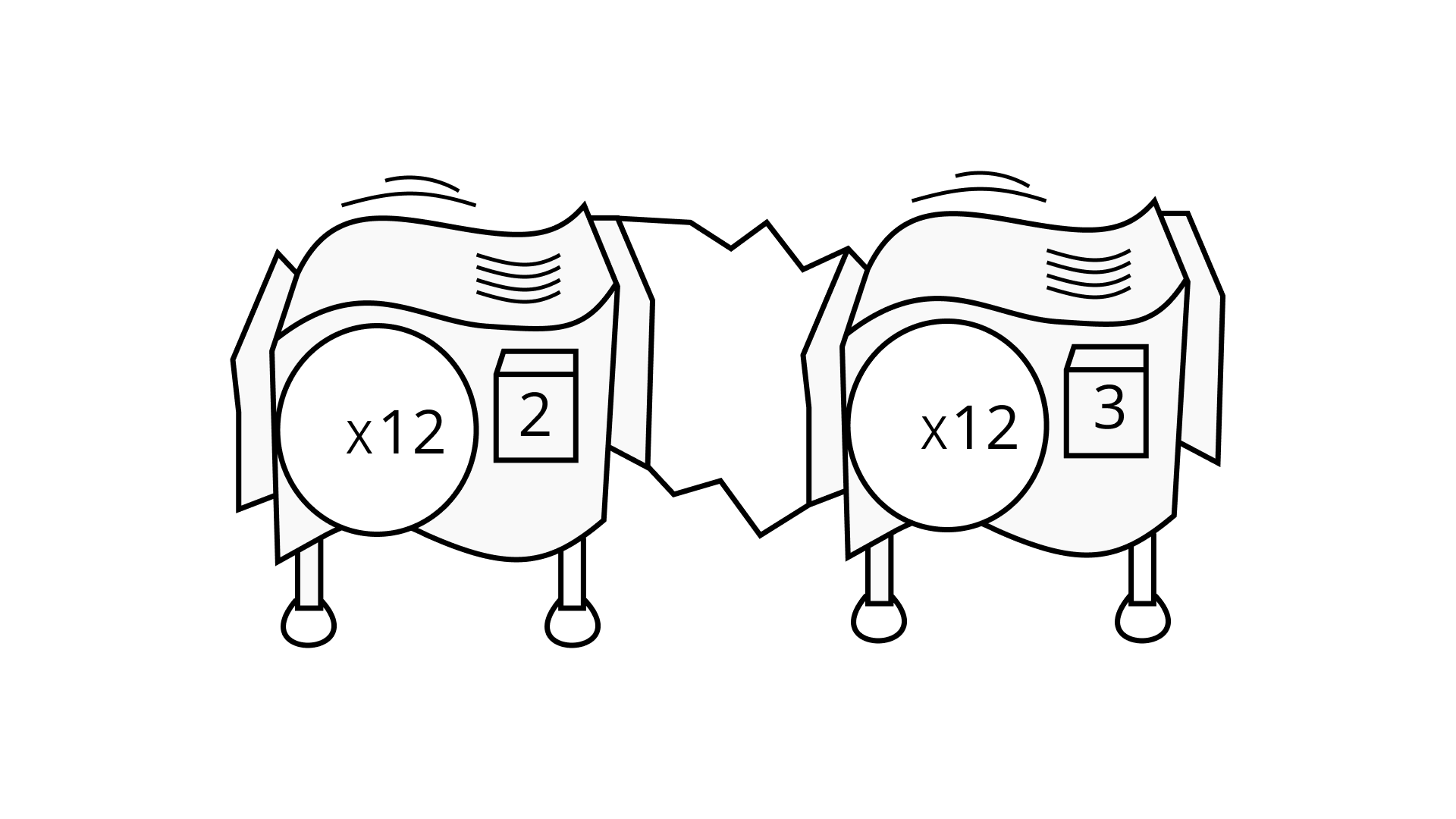
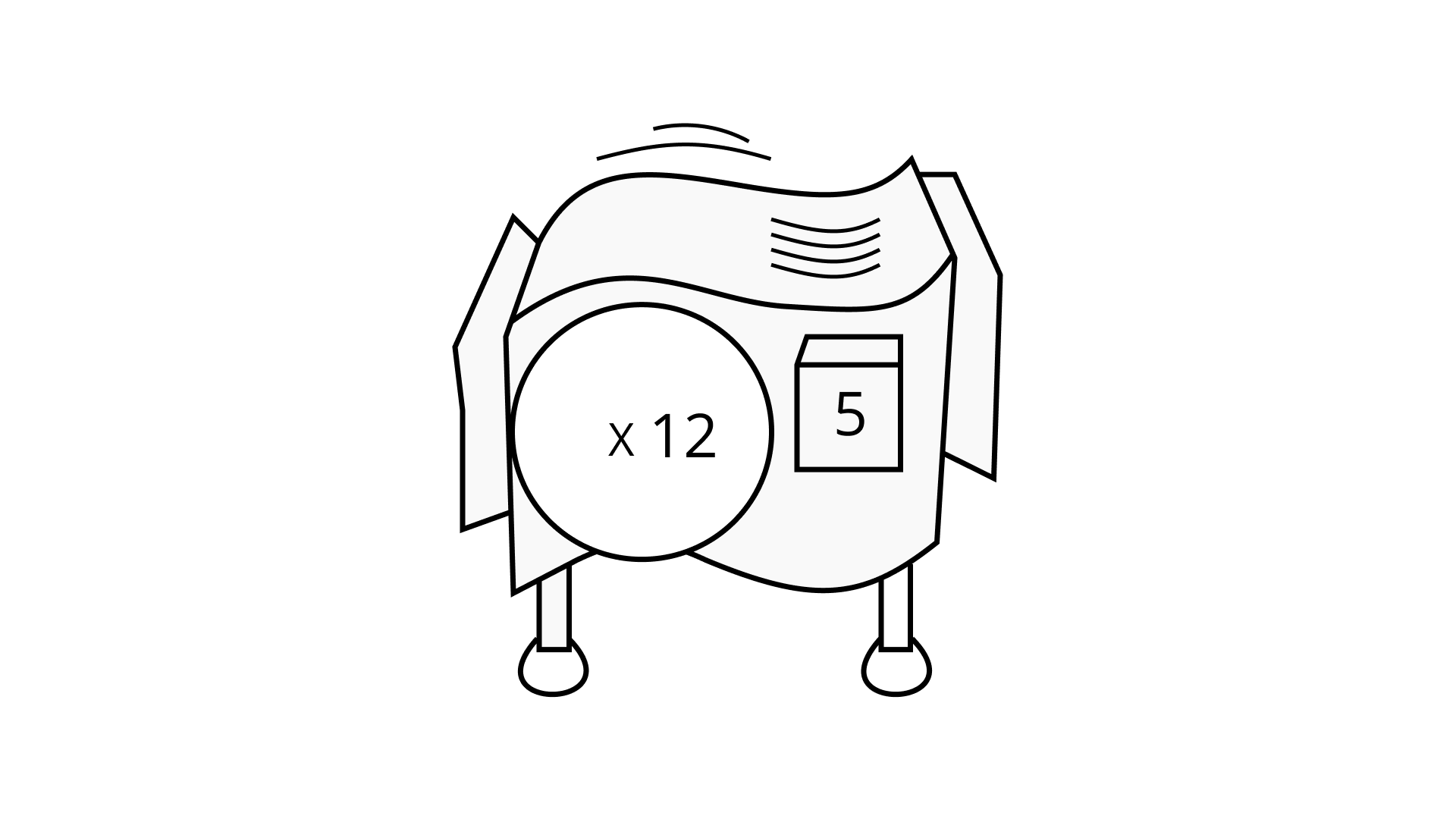
Ans: The work that can be performed by the hook-up machine = 122 x 123 = 125

So, (x 125) single machine can perform the same amount of work.

The diagram of a (x 125) single machine can be shown as below:

161. Shikha has an order from a golf course designer to put palm trees through a (× 23) machine and then through a (× 33) machine. She thinks she can do the job with a single repeater machine. What single repeater machine should she use?

Ans: The work done by hook-up machine is equal to 2 x 2 x 2 x 3 x 3 x 3 = 216 = 63 So, she should use (x 63) single machine for the purpose.

162. Neha needs to stretch some sticks to 252 times their original lengths, but her (×25) machine is broken. Find a hook-up of two repeater machines that will do the same work as a (×252) machine. To get started, think about the hookup you could use to replace the (×25) machine.

Ans: Work done by single machine (x 252) = 25 x 25 = 625 or 5 x 5 x 5 x 5 or 52 x 52 Hence, (x 52) and (x 52) hook-up machine can replace the (x 25) machine.

163. Supply the missing information for each diagram.

(a)

Ans: When a piece of length 5 cm is inserted in a single machine, it produces a piece having the same length of 5 cm.

Hence, it is a (x 1) repeated machine.

Therefore, the value of ? = 1.

(b)

Ans: When a piece of length 3 cm is inserted in a single machine, it produces a piece having the length 15 cm.

Hence, it is a (x 5) repeated machine.

Therefore, the value of ? = 5.

(c)

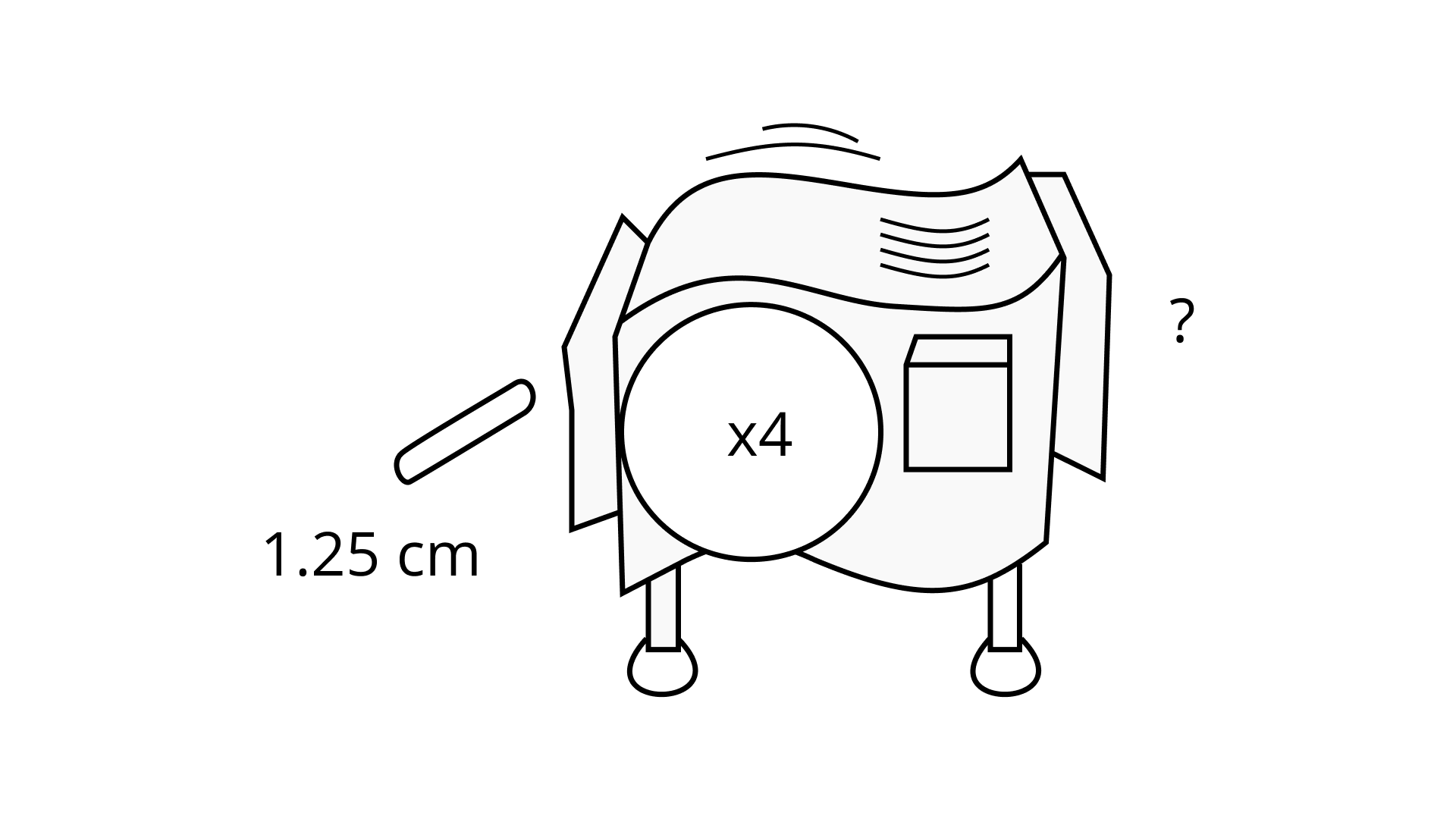
Ans: When a piece of length 1.25 cm is inserted in a (x 4) repeated machine, it will produce a piece that is 1.25 x 4 = 10 cm in length.

Therefore, the value of ? = 10 cm

(d)

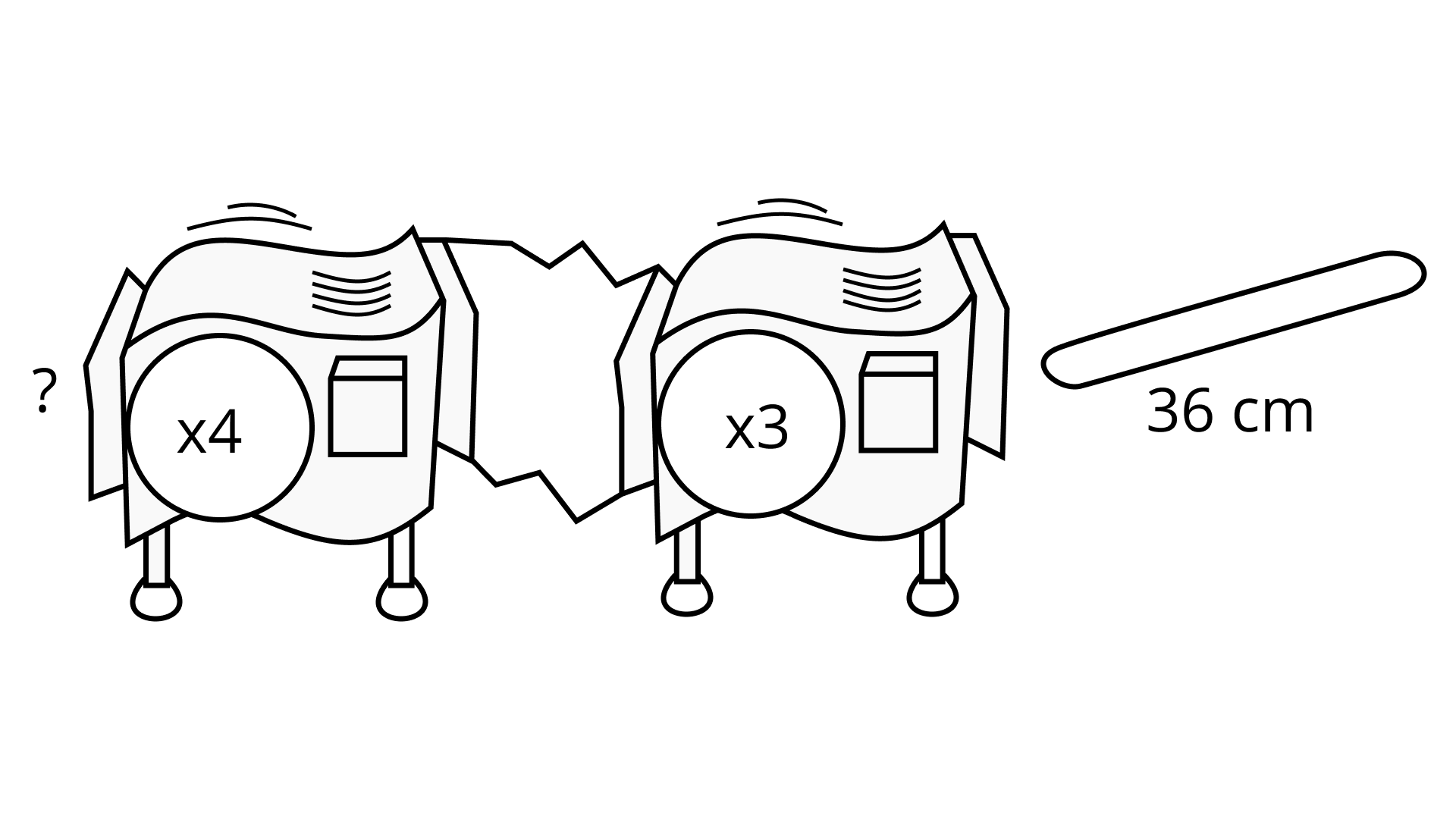
Ans: When a piece of length x cm is inserted in (x 4) and (x 3)

hooked machine, it will produce a piece that is 36 cm in

length.

Hence, $x \times 4 \times 3 = 36$

$\dfrac{{{\text{Output}}}}{{{\text{Input}}}} = 12$

$\dfrac{{36}}{{12}} = 3{\text{ cm}}$ 

164. If possible, find a hook-up of a prime base number machine that will do the same work as the given stretching machine. Do not use (× 1) machines.

(a) 

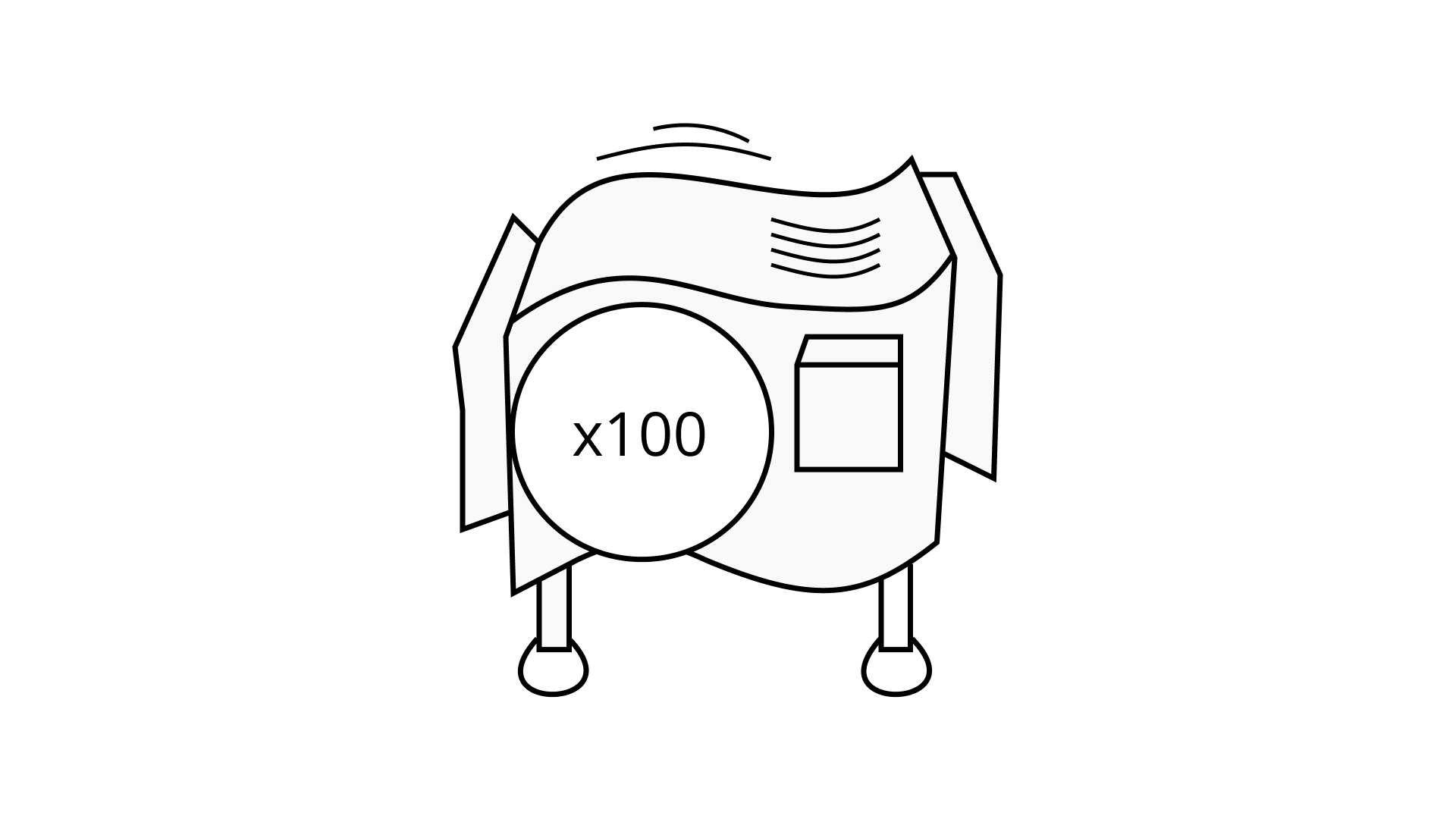
Ans: Single machine work = 100
Hook-up machine of prime base number that do the same work down by x 100
= 22 x 52
= 4 × 25
= 100

(b) 

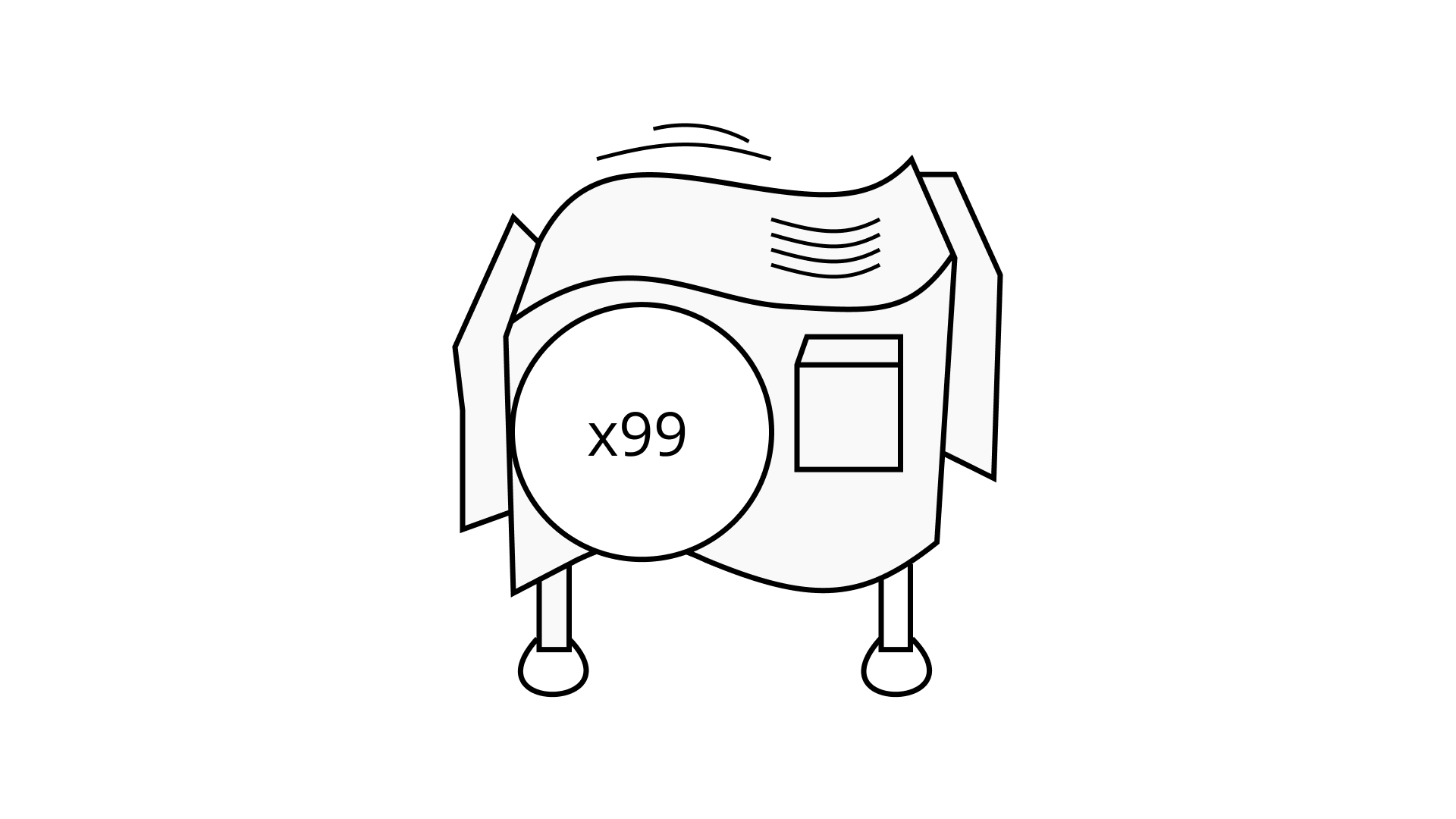
Ans: x 99 = 32 x 111 hook-up machine.

(c) 

Ans: x 37 machine cannot do the same work.

(d) 

Ans: x 1111 = 101 x 11 hook-up machine.

165. Find two repeater machines that will do the same work as a (× 81) machine.

Ans: Two repeater machines that do the same work as (x 81) are (x 34) and (x 92).
Since, factor of 81 are 3 and 9.

166. Find a repeater machine that will do the same work as a $\left( { \times \dfrac{1}{8}} \right)$ machine.

Ans: The repeater machine that performs the same

amount of work: $\dfrac{1}{8}$ are $\dfrac{1}{2},\dfrac{1}{2},\dfrac{1}{2}$

Hence, $\dfrac{1}{8} = \dfrac{1}{2} \times \dfrac{1}{2} \times \dfrac{1}{2} = {\left( {\dfrac{1}{2}} \right)^3}$

Thus, $\left( { \times \dfrac{1}{{{2^3}}}} \right)$ repeater machine can perform the same work as a $\left( { \times \dfrac{1}{8}} \right)$ machine.

167. Find three machines that can be replaced with hook-ups of (× 5) machines.

Ans: Since, 52 = 25, 53 = 125, 54 = 625
Hence, (x 52), (x 53) and (x 54) machines can replace (x 5) hook-up machines.

168. The left column of the chart lists the lengths of input pieces of ribbon. Stretching machines are listed across the top. The other entries are the outputs for sending the input ribbon from that row through the machine from that column. Copy and complete the chart.

Ans: In the given table, the left column of the chart list is the length of the input piece of ribbon. Thus, the outputs for sending the input ribbon are given in the following table.

169. The left column of the chart lists the lengths of input chains of gold. Repeater machines are listed across the top. The other entries are the outputs you get when you send the input chain from that row through the repeater machine from that column. Copy and complete the chart.

Ans: In the given table, the left column of the chart lists the length of input chains of gold. Thus, the output we get when we send the input chain from the row through the repeater machine are detailed in the following table.

170. Long back in ancient times, a farmer saved the life of a king’s daughter. The king decided to reward the farmer with whatever he wished. The farmer, who was a chess champion, made an unusual request:

“I would like you to place 1 rupee on the first square of my chessboard, 2 rupees on the second square, 4 on the third square, 8 on the fourth square, and so on, until you have covered all 64 squares. 

Each square should have twice as many rupees as the previous square.” The king thought this to be too less and asked the farmer to think of some better reward, but the farmer didn’t agree. How much money has the farmer earned?

Hint: The following table may help you. What is the first square on which the king will place at least Rs 10 lakh?

Ans: A grid of dimensions 8 x 8 is provided

We find the sum of each row-

e.g. The sum of the 1st row = 20 + 21 + 22 + 23 + 24 + 25 + 26 + 27 =

255

The sum of the 2nd row= 28 + 29 + 210 + 211 + 212 + 213 + 214 +

215

= 28 (20 + 21 + 22 + 23 + 24 + 25 + 26 + 27)

= 28 x 255 = 256 x 255 = 65280

The sum of the 3rd row= 216 x 255 = 16711680

171. The diameter of the Sun is 1.4 × 109 m and the diameter of the Earth is 1.2756 × 107 m. Compare their diameters by division.

Ans: Given,

Sun’s diameter = 1.4 × 109 m

Earth’s diameter = 1.2756 × 107 m

For comparing, we need to change the diameters of both sun

and earth in the same powers of 10, i.e. 1.2756 x 107 = 0.012756 x 109

Now, if the diameter of sun is divided by the diameter of the earth = $\dfrac{{1.4 \times {{10}^9}}}{{0.012756 \times {{10}^9}}} = 110$

Therefore, the sun’s diameter is 110 times the earth’s diameter.

172. Mass of Mars is 6.42 × 1029 kg and the mass of the Sun is 1.99 × 1030 kg. What is the total mass?

Ans: Mass of Mars = 6.42 x 1029 kg

Mass of the Sun = 1.99 x 1030 kg 

Total mass of Mars and Sun together = 6.42 x 1029 + 1.99 x 1030 

= 6.42 x 1029 + 19.9 x 1029 = 26.32 x 1029 kg

173. The distance between the Sun and the Earth is 1.496 × 108 km and the distance between the Earth and the Moon is 3.84 × 108 m. During a solar eclipse the Moon comes in between the Earth and the Sun. What is the distance between the Moon and the Sun at that particular time?

Ans: The distance between the Sun and the Earth is 1.496 x 108 km

= 1.496 x 108 x 103 m = 1496 x 108 m

The distance between the Earth and the Moon is 3.84 x108 m.

The distance between the Moon and the Sun at particular time (solar eclipse) = (1496 x 108 – 3.84 x 108)m = 1492.16 x 108 m

174. A particular star is at a distance of about 8.1 × 1013 km from the Earth. Assuring that light travels at 3 × 108 m per second, find how long does light take from that star to reach the Earth.

Ans: Total distance between the earth and the star = 8.1 x 1013 km = 8.1 x 1013 x 103 m

Speed of light = 3 x 108 m per second.

Hence, time that light would take to reach the earth = $\dfrac{{8.1 \times {{10}^{13}} \times {{10}^3}}}{{3 \times {{10}^8}}}$

= $\dfrac{{8.1 \times {{10}^{16}}}}{{3 \times {{10}^8}}}$

= $\dfrac{{8.1}}{3} \times {10^8}$

= $2.7 \times {10^8}s$ 

175. By what number should (–15)–1 be divided so that the quotient may be equal to (–5)–1?

Ans: Let the number be x.

Hence,

${\left( { - 15} \right)^{ - 1}} \div x = {\left( { - 5} \right)^{ - 1}}$

$\Rightarrow \dfrac{1}{{ - 15}} \times \dfrac{1}{x} = \dfrac{1}{{ - 5}}$

$\Rightarrow x = \dfrac{{ - 15}}{{ - 5}} = 3$

Therefore, the required number is 3.

176. By what number should (–8)–3 be multiplied so that the product may be equal to (–6)–3?

Ans: Let the number be x.

Hence,

$x \times {\left( { - 8} \right)^{ - 3}} = {\left( { - 6} \right)^{ - 3}}$

$\Rightarrow x = \dfrac{{{{\left( { - 6} \right)}^{ - 3}}}}{{{{\left( { - 8} \right)}^{ - 3}}}} = \dfrac{{{{\left( { - 8} \right)}^3}}}{{{{\left( { - 6} \right)}^3}}} = \dfrac{{ - {8^3}}}{{ - {6^3}}}$

= $\dfrac{{512}}{{216}} = \dfrac{{64}}{{27}}$

Therefore, the required number is $\dfrac{{64}}{{27}}$.