
Class 7 Maths NCERT Exemplar Solutions Chapter 5 Lines & Angles
Free PDF download of NCERT Exemplar for Class 7 Maths Chapter - 5 Lines & Angles solved by expert Maths teachers on Vedantu.com as per NCERT (CBSE) Book guidelines. All Chapter - 5 Lines & Angles exercise questions with solutions to help you to revise the complete syllabus and score more marks in your examinations.
Download NCERT Solutions PDF and opt to cross-refer post-answering questions to score subject-best marks. Subjects like Science, Maths, English, Social Science, Hindi will become easy to study if you have access to NCERT Solution for Class 7 Science, Maths solutions and solutions of other subjects. You can also download NCERT Solutions for Class 7 Maths to help you to revise the complete syllabus and score more marks in your examinations.
Lines and Angles Chapter 5 Class 7
SOLVED EXAMPLES
In each of the Examples 1 to 4, there are four options, out of which one option is correct. Write the correct one.
Example 1: The angles between North and East and North and West are:
(a) complementary angles
(b) supplementary angles
(c) both acute angles
(d) both obtuse angles
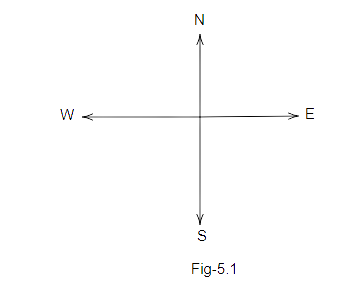
Ans: Option (b) is correct.
From the diagram, it is very evident that the angles between North and East and North and West are supplementary angles.
Example 2: Which of the following pair of angles are supplementary?
(a) \[{48^o},{42^0}\]
(b) \[{60^o},{60^o}\]
(c) \[{75^o},{105^o}\]
(d) \[{179^o},{2^o}\]
Ans: Option (c) is correct.
Sum of \[{75^o}and{105^o}\] is equal to \[{180^o}\] i.e. Supplementary.
Example 3: In Fig. 5.2, a pair of corresponding angles is
(a) \[\angle 1,\angle 2\]
(b) \[\angle 3,\angle 6\]
(c) \[\angle 3,\angle 5\]
(d) \[\angle 3,\angle 7\]
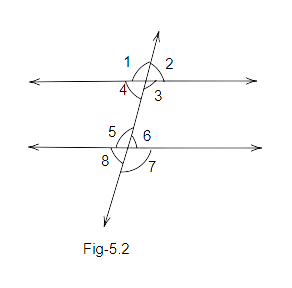
Ans: Option (d) is correct.
From the figure, we can see that \[\angle 3\,and\,\angle 7\] is a pair of corresponding angles.
Example 4: If two lines are intersected by a transversal, then the number of pairs of interior angles on the same side of the transversal is
(a) \[1\]
(b) \[2\]
(c) \[3\]
(d) \[4\]
Ans: Option (b) is correct.
If two lines are intersected by a transversal, then the number of pairs of interior angles on the same side of the transversal is \[2\].
In Examples 5 to 7, fill in the blanks to make the statements true.
Example 5: Two lines in a plane which never meet at any point are called _________.
Ans: Correct answer is parallel lines
Example 6: Angles of a linear pair are _________ as well as ________.
Ans: Correct answer is adjacent, supplementary
Example 7: Adjacent angles have a common vertex, a common __________ and no-common _________.
Ans: Correct answer is arm, interior points.
In Examples 8 to 11, state whether the statements are True or False.
Example 8: The sum of two complementary angles is 180°.
Ans: False
Explanation: Because the sum of two complementary angles is \[{90^o}\].
Example 9: Sum of two supplementary angles is \[{180^o}\].
Ans: True
The Sum of two supplementary angles is supplementary.
Example 10: Sum of interior angles on the same side of a transversal with two parallel lines is 90°.
Ans: False
Explanation: Sum of interior angles on the same side of a transversal with two parallel lines is \[{180^o}\]
Example 11: Vertically opposite angles are equal.
Ans: True
Example 12: In Fig. \[5.3\], four-line segments PQ, QR, RS, and ST are making the letter W, PQ||RS and QR||ST. If the angle between PQ and QR is \[{39^o}\], find the values of x and y.
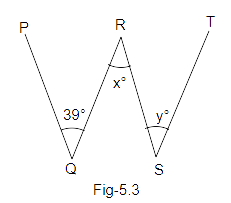
Ans: since, we know that, \[PQ\parallel RS\] and QR is a transversal.
So, \[x = \angle PQR = {39^o}\] (Alternate interior angles)
Also, QR \[\parallel \]ST and RS is a transversal.
Therefore, \[x = y = {39^o}\] (Alternate interior angles)
Example 13: In Fig. \[5.4\], are the angles \[1\] and \[2\] of the letter N forming a pair of adjacent angles? Give reasons.
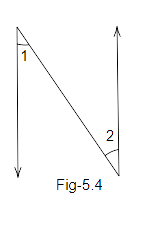
Ans: No, angles \[1\] and \[2\] of the letter N are not forming a pair of adjacent angles as they do not have a common vertex. Angles \[1\] and \[2\] of the letter N are Alternate interior angles.
Example 14: In Fig. 5.5, the points A, O and B are collinear. Ray OC ⊥ ray OD. Check whether:
(i) \[\angle \]AOD and \[\angle \]BOC are complementary,
(ii) \[\angle \]AOC and \[\angle \]BOC are supplementary.
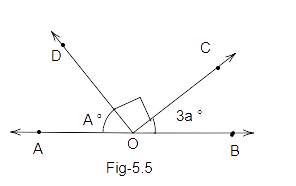
Ans: (i) The points A, O and B are collinear i.e. AOB is a straight line.
So, we can write:
\[\angle \]AOD \[ + \]\[\angle \]DOC \[ + \]\[\angle \]BOC \[ = {180^o}\]
\[\angle \]AOD \[ + \] \[{90^o}\;\]\[ + \]\[\angle \]BOC \[ = {180^o}\]
\[\angle \]AOD \[ + \] \[\angle \]BOC \[ = {90^o}\;\]
Therefore, \[\angle \]AOD and \[\angle \]BOC are complementary angles.
(ii) The points A, O, and B are collinear i.e. AOB is a straight line.
So, we can write:
\[\angle \]AOC \[ + \] \[\angle \]BOC \[ = {180^o}\]
Therefore, \[\angle \]AOC and \[\angle \]BOC are supplementary angles.
Example 15: In Fig. \[5.6\], AB \[\parallel \]EF, ED\[\parallel \]CB and \[\angle \]APE is \[{39^o}\]. Find \[\angle \]CQF.
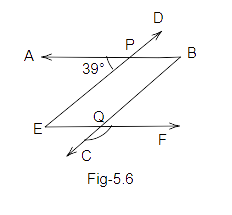
Ans: We know that ED is parallel to BC and AB is a transversal.
Therefore, we can write:
\[\angle \]QBP \[ = \]\[\angle \]APE \[ = \]\[{39^o}\] (Corresponding angles)
Also, AB is parallel to EF and BC is a transversal.
Therefore, we can write:
\[\angle \]QBP \[ = \]\[\angle \]FQB \[ = \] \[{39^o}\] (Alternate interior angles)
Also, we know that BQC is a straight line.
So, \[\angle \]CQF \[ + \]\[\angle \]FQB \[ = {180^o}\] (Linear pairs)
\[\angle \]CQF \[ + \]\[{39^o}\] \[ = {180^o}\]
\[\angle \]CQF \[ = {180^o}\]\[ - {39^o}\]
\[\angle \]CQF \[ = {141^o}\]
Example 16: Out of a pair of complementary angles, one is two-third of the other. Find the angles.
Ans: Suppose, the one angle is ‘y’ and the other is \[{90^o} - y\].
Now, according to the question,
\[\dfrac{2}{3}y = {90^o} - y\]
\[2y = 3({90^o} - y)\]
\[2y = {270^o} - 3y\]
\[2y + 3y = {270^o}\]
\[5y = {270^o}\]
\[y = \dfrac{{{{270}^o}}}{5}\]
\[y = {54^o}\]
Therefore, the angles are:
\[ \Rightarrow y = {54^o} \]
\[ \Rightarrow {90^o} - y = {90^o} - {54^o} = {36^o}\]
Example 17: In Fig. \[5.7\], CD intersects the line AB at F, \[\angle \]CFB \[ = \]\[{50^o}\] and \[\angle \]EFA \[ = \]\[\angle \]AFD. Find the measure of \[\angle \]EFC.
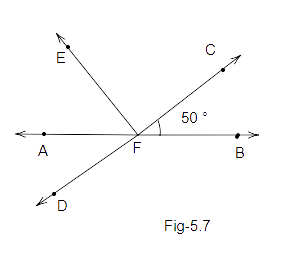
Ans: suppose \[\angle \]EFA \[ = y\]
Therefore, \[\angle \]EFA \[ = \]\[\angle \]AFD \[ = y\]\[ = {50^o}\] \[.....(i)\]
Also, we know that line CD intersects line AB at point F.
Therefore, \[\angle AFD = CFB = y = {50^o}\] (Vertically opposite angles)
Since, AB is a straight line, so we can write:
\[\angle EFA + CFB + \angle EFC = {180^o}\]
\[{50^o} + {50^o} + \angle EFC = {180^o}\] (From equation(i))
\[{100^o} + \angle EFC = {180^o}\]
\[\angle EFC = {180^o} - {100^o}\]
\[\angle EFC = {80^o}\]
Example 18 In the given figure, find out which pair of lines are parallel.
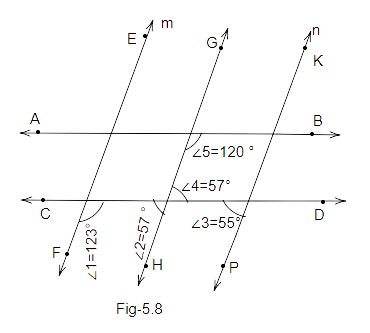
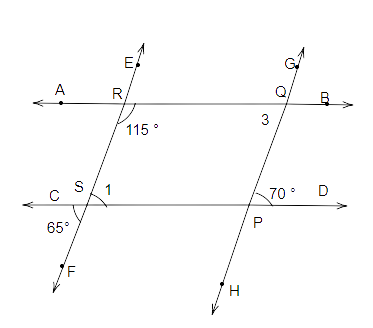
Ans: First let’s check lines EF and GH, taking CD as transversal,
So, we can write:
\[\angle 1 + \angle 2 = {180^o}\] (Interior angles)
\[{123^o} + {57^o} = {180^o}\]
\[{180^o} = {180^o}\]
Since the sum of interior angles on the same side of the transversal is \[{180^o}\], therefore we can say that line ‘EF’ is parallel to line ‘GH’.
Next let’s check lines GH and KP, taking CD as transversal,
Now, \[\angle 2and\angle 3\] are corresponding angles.
But, \[\angle 2{\text{ }} = {\text{ }}57^\circ ,{\text{ }}\angle 3{\text{ }} = {\text{ }}55^\circ \]
So, \[\angle 2 \ne \angle 3\]
Therefore, lines GH and KP are not parallel lines.
Similarly, for lines EF and KP, taking CD as transversal
\[\angle 1 + \angle 3 = {180^o}\] (interior angles on the same side of a transversal)
\[{123^o} + {55^o} = {180^o}\]
\[{178^o} \ne {180^o}\]
Therefore, lines EF and KP are not parallel lines.
Also suppose for lines AB and CD, taking GH as a transversal
\[\angle 5 + \angle 4 = {180^o}\] (interior angles)
\[{122^o} + {57^o} = {180^o}\]
\[{179^o} \ne {180^o}\]
Therefore, AB is not parallel to GH
EXERCISE
1. The angles between North and West and South and East are
(a) complementary
(b) supplementary
(c) both are acute
(d) both are obtuse
Ans: Option (b) is correct.
we know that the angle made by the North and the west is the right angle. Also similarly the angle made by south and east is the right angle. Therefore the angles between North and West and South and East are supplementary
2. Angles between South and West and South and East are
(a) vertically opposite angles
(b) complementary angles
(c) making a linear pair
(d) adjacent but not supplementary
Ans: Option (c) is correct.
we know that the angle made by the North and the west is the right angle. Also similarly the angle made by south and east is the right angle. Therefore the angles between North and West and South and East are making a linear pair.
3. In Fig., PQ is a mirror, AB is the incident ray and BC is the reflected ray. If \[\angle ABC = {46^0}\], then \[\angle ABP\] is equal to.
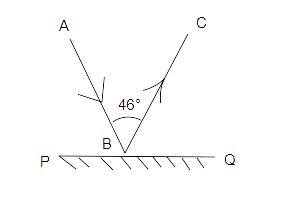
(a) \[{44^o}\] (b) \[{67^o}\]
(c) \[{13^o}\] (d) \[{62^o}\]
Ans: Option (b) is correct.
As we know that PQ is a straight line, so we can write:
\[\angle ABP + \angle ABC + \angle CBQ = {180^O}\]
Also, angle of incidence is equal to angle of reflection i.e. \[\angle ABP = \angle CBQ\]Therefore on putting this value in the above equation we get:
\[2\angle ABP + \angle ABC + = {180^O}\]
\[2\angle ABP + {46^o} = {180^o}\]
\[2\angle ABP = {180^o} - {46^o}\]
\[\angle ABP = \dfrac{{{{134}^o}}}{{{{46}^o}}}\]
\[\angle ABP = {67^o}\]
4. If the complement of an angle is \[{79^o}\], then the angle will be of
(a) \[{1^o}\]
(b) \[{11^o}\]
(c) \[{79^o}\]
(d) \[{101^o}\]
Ans: Option (b) is correct.
We know that the sum of two complementary angles is \[{90^o}\].
Let’s assume the angle is ‘y’.
Therefore we can write:
\[y + {79^o} = {180^o}\]
\[y = {180^o} - {79^o}\]
\[y = {11^o}\]
5. Angles that are both supplementary and vertically opposite are
(a) \[{95^o},{85^o}\]
(b) \[{90^o},{90^o}\]
(c) \[{100^o},{80^o}\]
(d) \[{45^o},{45^o}\]
Ans: Option (b) is correct.
we know that vertically opposite angles are equal so let’s assume each angle to be ‘x’.
\[x + x = {180^o}\]
\[2x = {180^o}\]
\[x = {90^o}\]
6. The angle which makes a linear pair with an angle of \[{61^o}\] is of
(a ) \[{29^o}\]
(b) \[{61^o}\]
(c) \[{122^o}\]
(d) \[{119^o}\]
Ans: Option (d) is correct.
Sum of linear pairs accounts to \[{180^o}\]
Suppose the other angle is ‘y’.
\[y + {61^o} = {180^o}\]
\[y = {180^o} - {61^o}\]
\[y = {119^o}\]
7. The angles x and \[{90^o} - x\] are
(a) supplementary (b) complementary
(c) vertically opposite (d) making a linear pair
Ans: Option (b) is correct.
The angles x and \[{90^o} - x\] are complementary angles.
8. The angles \[x - {10^o}\] and \[{190^o} - x\] are:
(a) interior angles on the same side of the transversal
(b) making a linear pair
(c) complementary
(d) supplementary
Ans: Option (d) is correct.
we know that
\[x - {10^o} = x + {190^o} - x\]
\[x = {180^o}\]
Therefore, The angles \[x - {10^o}\] and \[{190^o} - x\] are supplementary angles.
9. In Fig. the value of x is
(a) \[{110^o}\] (b) \[{46^o}\]
(c) \[{64^o}\] (d) \[{150^o}\]
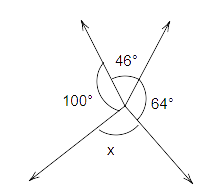
Ans: Option (d) is correct
we know that the sum of the angle made around a point is
Therefore,
\[x + {64^o} + {46^o} + {100^o} = {360^o}\]
\[x + {210^o} = {360^o}\]
\[x = {360^o} - {210^o}\]
\[x = {150^o}\]
10. In Fig, if AB || CD, \[\angle APQ = {50^o}\] and \[\angle PRD = {130^O}\] , then \[\angle QPR\] is:
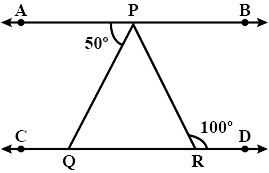
(a) \[{130^O}\] (b) \[{50^o}\]
(c) \[{80^O}\] (d) \[{30^O}\]
Ans: Option (c) is correct
Here we know that lines AB are parallel to line CD and PR is the transversal.
Thus we can say that \[\angle APR = \]\[\angle PRD = {130^O}\] (Alternate angles)
Therefore,
\[\angle QPR + \angle APQ = {130^O}\]
\[\angle QPR + {50^o} = {130^O}\]
\[\angle QPR = {80^O}\]
11. In Fig, lines l and m intersect each other at a point. Which of the following is false?
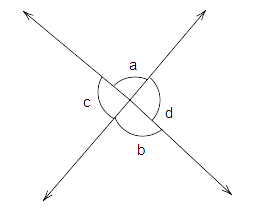
(a) \[\angle a = \angle b\] (b)\[\angle d = \angle c\]
(c) \[\angle a + \angle d = {180^O}\] (d)\[\angle a = \angle d\]
Ans: Option (d) is correct.
\[\angle a\] and \[\angle d\] are linear pairs. So they cannot be equal.
12. If angle P and angle Q are supplementary and the measure of angle P is 60°, then the measure of angle Q is
(a) \[{120^O}\] (b) \[{60^O}\] (c) \[{30^O}\] (d) \[{20^O}\]
Ans: Option (a) is correct.
\[\angle P + \angle Q = {180^O}\]
\[{60^O} + \angle Q = {180^O}\]
\[\angle Q = {180^O} - {60^O}\]
\[\angle Q = {120^O}\]
13. In Fig, POR is a line. The value of a is
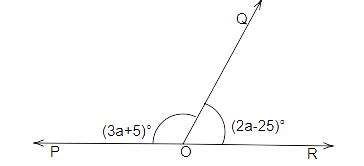
(a) \[{40^o}\] (b) \[{45^o}\]
(c) \[{55^o}\] (d) \[{60^O}\]
Ans: Option (a) is correct.
Since, POR is a straight line.
\[\angle POQ + \angle QOR = {180^O}\]
\[{(3a + 5)^O} + {(2a - 25)^o} = {180^O}\]
\[5a - {20^o} = {180^O}\]
\[a = \dfrac{{{{200}^o}}}{5}\]
\[a = {40^o}\]
14. In Fig. 5.14, POQ is a line. If \[x = {30^O}\], then \[\angle QOR\] is
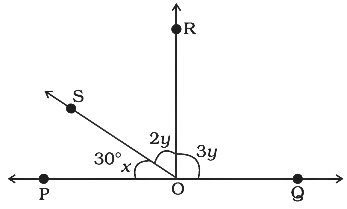
(a) \[{90^O}\] (b) \[{30^O}\]
(c) \[{150^O}\] (d) \[{60^O}\]
Ans: Option (a) is correct.
Since PQ is a straight line:
\[x + 2y + 3y = {180^O}\]
\[{30^O} + 5y = {180^O}\]
\[y = {30^o}\]
\[now{\text{ we know that }}\angle QOR = 3y\]
\[{\text{Put the value of 'y' in the above equation, we get}}\]
\[\angle QOR = 3 \times {30^o}\]
\[\angle QOR = {90^o}\]
15. The measure of an angle which is four times its supplement is
(a) \[{36^o}\] (b) \[{144^o}\]
(c) \[{16^o}\] (d) \[{64^o}\]
Ans: Option (b) is correct.
Suppose ‘x’ be the angle and its supplement be \[{180^O} - x\]
Therefore,
\[x = 4({180^O} - x)\]
\[x = {720^o} - 4x\]
\[5x = {720^o}\]
\[x = \dfrac{{{{720}^o}}}{5}\]
\[x = {144^o}\]
16. In Fig, the value of y is

(a) \[{30^O}\] (b) \[{15^o}\]
(c) \[{20^o}\] (d) \[{22.5^o}\]
Ans: Option (c) is correct.
It is a straight line.
Therefore,
\[6y + y + 2y = {180^O}\]
\[9y = {180^O}\]
\[y = \dfrac{{{{180}^O}}}{9}\]
\[y = {20^o}\]
17. In Fig, PA, BC, DT are parallel to each other and AB is parallel to DC . Then, the values of a and b are respectively. ,
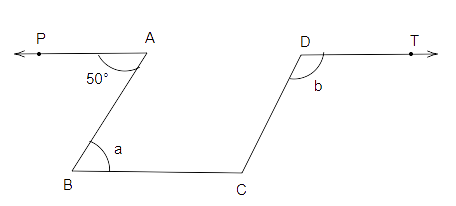
(a) \[{60^o}\], \[{120^o}\] (b) \[{50^o},{130^o}\]
(c) \[{70^o},{110^o}\] (d) \[{80^o},{100^o}\]
Ans: Option (b) is correct
Since PA is parallel to BC and AB is a transversal.
Therefore,
\[\angle PAB = \angle ABC = a = {50^o}\] (Alternate angles)
Also, AB is parallel to CD.
Thus,
\[\angle ABC + \angle BCD = {180^O}\]
\[{50^o} + \angle BCD = {180^O}\]
\[\angle BCD = {180^O} - {50^O}\]
\[\angle BCD = {130^O}\]
Also,
$\angle BCD = \angle CDT = b = {130^ \circ }$ (Alternate angles)
18. The difference of two complementary angles is 30°. Then, the angles are
(a) \[{60^o},{30^o}\] (b) \[{70^o},{40^o}\]
(c) \[{20^o},{50^o}\] (d) \[{75^o},{105^o}\]
Ans: Option (a) is correct.
Lets consider the pair of complementary angle is \[({90^o} - x)and{\text{ }}x\]
Then according to the question:
\[({90^o} - x) - x = {30^o}\]
\[{90^o} - 2x = {30^o}\]
\[{90^o} - {30^o} = 2x\]
\[{60^o} = 2x\]
\[x = {30^o}\]
The value of other complementary angle is
\[({90^o} - x) = ({90^o} - {30^o}) = {60^o}\]
19. In Fig. 5.17, PQ || SR and SP || RQ. Then, angles a and b are respectively:
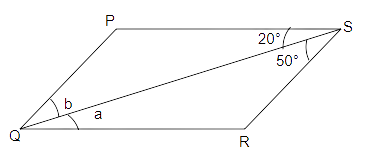
(a) \[{20^o},{50^o}\] (b) \[{50^o},{20^o}\] (c) \[{30^o},{50^o}\] (d) \[{45^o}{35^o}\]
Ans: Option (a) is correct.
SR is parallel to PQ and the line RP is a transversal.
Thus,
\[\;b = {50^o}\;\;\;\left( {Alternate{\text{ }}angles} \right)\]
\[a = {20^o}\;\left( {Alternate{\text{ }}angles} \right)\]
20. In Fig. 5.18, a and b are
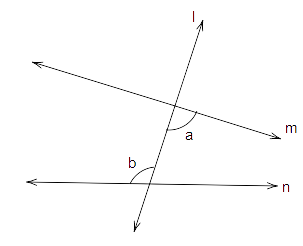
(a) alternate exterior angles
(b) corresponding angles
(c) alternate interior angles
(d) vertically opposite angles
Ans: a correct answer is an option (c).
Line ‘m’ and ‘n’ are parallel lines and ‘l’ is the transversal. Therefore angles ‘a’ and ‘b’ are alternate angles.
Due to their interior position Therefore angles ‘a’ and ‘b’ are interior alternate angles.
21. If two supplementary angles are in the ratio \[1:2\], then the bigger angle is
(a) \[{120^o}\] (b) \[{125^o}\]
(c) \[{110^o}\] (d) \[{90^o}\]
Ans: Option (a) is correct.
lets consider two angles are 1x and 2x.
since they are supplementary angles, their sum will be:
\[1x + 2x = {180^o}\]
\[3x = {180^o}\]
\[x = \dfrac{{{{180}^o}}}{3}\]
\[x = {60^o}\]
\[Now{\text{ the bigger angle is 2x = 2}} \times {60^o} = {120^o}\]
22. In Fig. 5.19, \[\angle \]ROS is a right angle and \[\angle \]POR and \[\angle \]QOS are in the ratio \[1:5\]. Then, ∠QOS measures
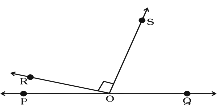
(a) \[{150^o}\] (b) \[{75^o}\]
(c) \[{45^o}\] (d) \[{60^o}\]
Ans: Option (b) is correct.
We know that ‘PQ’ is a straight line.
According to the question: \[5\angle POR = \angle QOS....(i)\]
Also, we know that,
\[\angle POR + \angle ROS + \angle QOS = {180^O}\]
\[1x + {90^o} + 5x = {180^O}\]
\[6x = {180^O} - {90^o}\]
\[6x = {90^o}\]
\[x = \dfrac{{{{90}^o}}}{6}\]
\[x = {15^o}\]
Now, from the equation (i):
$5\angle POR = \angle QOS = 5\angle POR = 5 \times {15^ \circ } = {75^ \circ }$
23. Statements a and b are as given below:
a: If two lines intersect, then the vertically opposite angles are equal.
b: If a transversal intersects, two other lines, then the sum of two interior angles on the same side of the transversal is \[{180^o}\].
Then
(a) Both a and b are true
(b) a is true and b is false
(c) a is false and b is true
(d) both a and b are false
Ans: Option (b) is correct.
If two lines intersect, then the vertically opposite angles are equal. Hence statement ‘a’ is true.
When a transversal intersects two parallel lines, the angle made on the interior same side is \[{180^o}\]. Hence, statement ‘b’ is false.
24. For Fig. 5.20, statements p and q are given below:
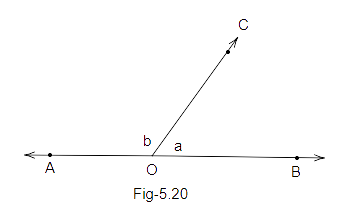
p: a and b are forming a linear pair.
q: a and b are forming a pair of adjacent angles.
Then,
(a) both p and q are true
(b) p is true and q is false
(c) p is false and q is true
(d) both p and q are false
Ans: Option (a) is correct.
AB is a straight line. Therefore a and b are forming a linear pair and is a pair of adjacent angles.
25. In Fig, \[\angle \] AOC and \[\angle \]BOC form a pair of:
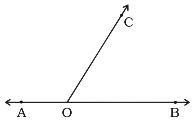
(a) vertically opposite angles
(b) complementary angles
(c) alternate interior angles
(d) supplementary angles
Ans: Option (d) is correct.
\[\angle \] AOC and \[\angle \]BOC are supplementary angles.
26. In Fig, the value of a is:
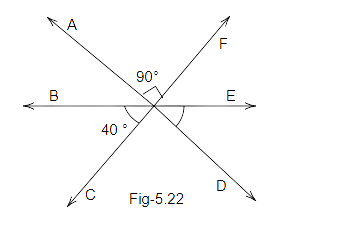
\[{20^o}\] (b) \[{15^o}\]
(c) \[{5^o}\] (d) \[{10^o}\]
Ans: Option (d) is correct.
We know that \[\angle AOF = \angle COD = {90^o}\] (Vertically opposite angles)
Also, BE is a straight line:
Therefore,
\[\angle BOC + \angle COD + \angle DOE = {180^O}\]
\[{40^O} + {90^o} + 5a = {180^O}\]
\[5a = {180^O} - {130^o}\]
\[5a = {50^o}\]
\[a = \dfrac{{{{50}^o}}}{5}\]
\[a = {10^o}\]
27. In Fig. 5.23, if QP || SR, the value of a is
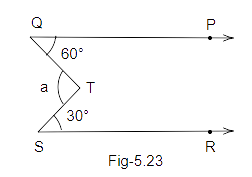
\[{40^o}\] (b) \[{30^O}\]
(c) \[{90^o}\] (d) \[{80^O}\]
Ans: Option (c) is correct.
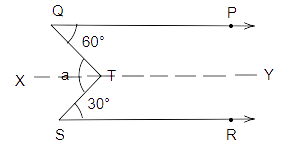
Here QP is parallel to XY.
Therefore \[\angle \]PQT \[ = \] \[\angle \]
XTQ \[ = {60^o}\] \[....(i)\]
Similarly, SR is parallel to XY.
Therefore, \[\angle \]STX \[ = \]\[\angle \]RST \[
= \]\[{30^O}\] \[....(ii)\]
Also, we know that.
$a = \angle XTQ + \angle STX$
$ \Rightarrow a = {60^ \circ } + {30^ \circ }$
$ \Rightarrow a = {90^ \circ }$
28. In which of the following figures, a and b are forming a pair of adjacent angles?
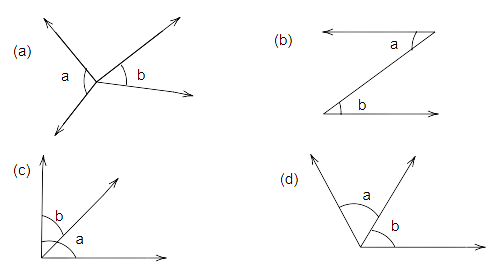
Ans: Option (d) is correct
Angles ‘a’ and ‘b’ have a common vertex and arm. So they are adjacent angles.
29. In a pair of adjacent angles, (i) vertex is always common, (ii) one arm is always common, and (iii) uncommon arms are always opposite rays:
Then
(a) All (i), (ii) and (iii) are true
(b) (iii) is false
(c) (i) is false but (ii) and (iii) are true
(d) (ii) is false
Ans: Option (b) is correct.
In a pair of adjacent angles, the vertex is always common and one arm is always common. While the statement(iii) is false.
30. In Fig. 5.25, lines PQ and ST intersect at O. If \[\angle POR = {90^o}\] and \[x:y = 3:2\] , then z is equal to
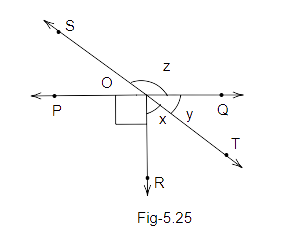
(a) \[{126^o}\] (b) \[{144^o}\]
(c) \[{136^o}\] (d) \[{154^o}\]
Ans: Option (b) is correct.
\[\angle POR + x + y = {180^O}\]
\[{90^o} + x + y = {180^O}\]
\[x + y = {90^o}....(i)\]
\[also,\dfrac{x}{y} = \dfrac{3}{2}\]
\[let{\text{ x = 3k}}\]
\[{\text{y = 2k}}\]
\[put{\text{ value in euation (i)}}\]
\[{\text{3k + 2k = 9}}{{\text{0}}^o}\]
\[k = {18^o}\]
Therefore, now\[{\text{ y = 2k = 2}} \times {\text{1}}{{\text{8}}^o} = {36^o}\]
Also, ST is a straight line and ‘z’ and ‘y’ are adjacent angles:
Therefore,
\[z + y = {180^o}\]
\[z + {36^o} = {180^o}\]
\[z = {144^o}\]
31. In Fig. 5.26, POQ is a line, then a is equal to
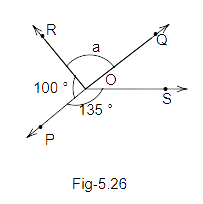
\[{35^o}\] (b) \[{100^o}\]
(c) \[{80^o}\] (d) \[{135^o}\]
Ans: Option (c) is correct answer.
We can see that ‘PQ’ is a straight line. Therefore \[\angle \]POR and \[\angle \]ROQ forms linear pair.
Thus, we can write,
\[POR{\text{ + }}ROQ = {180^o}\]
\[{100^o} + a = {180^o}\]
\[a = {180^o} - {100^o}\]
\[a = {80^o}\]
32. Vertically opposite angles are always
(a) supplementary
(b) complementary
(c) adjacent
(d) equal
Ans: Option (d) is correct.
we know that the vertically opposite angles are always equal. It’s a theorem.
33. In Fig, a = 40°. The value of b is

(a) \[{20^o}\] (b) \[{24^o}\]
(c) \[{36^o}\] (d) \[{120^o}\]
Ans: Option (a) is correct.
We know that, we can write:
\[5b + 2a = {180^o}\]
Also, since value of \[a = \]\[{40^o}\]
So on putting the value of a, we will get:
\[5b + 2 \times {40^o} = {180^o}\]
\[5b + {80^o} = {180^o}\]
\[5b = {180^o} - {80^o}\]
\[5b = {100^o}\]
\[b = \dfrac{{{{100}^o}}}{5}\]
\[b = {20^o}\]
34. If an angle is \[{60^o}\] less than two times of its supplement, then the greater angle is
(a) \[{100^o}\] (b) \[{80^o}\]
(c) \[{60^o}\] (d) \[{120^o}\]
Ans: Option (a) is correct.
Lets say the angles be \[x\] and \[{180^o} - x\]
Now according to the conditions given in the question, we can write:
\[x = 2({180^o} - x) - {60^o}\]
\[x = {360^o} - 2x - {60^o}\]
\[x + 2x = {360^o} - {60^o}\]
\[3x = {300^o}\]
\[x = \dfrac{{{{300}^o}}}{3}\]
\[x = {100^o}\]
35. In Fig 5.28, PQ || RS.
If \[\angle 1 = {(2a + b)^o}\] and \[\angle 6 = {(3a - b)^o}\] then the measure of \[\angle 2\] in terms of b is
(a) \[{(3 - b)^o}\] (b) \[{(3 - b)^o}\]
(c) \[{(108 - b)^o}\] (d) \[{(180 - b)^o}\]
Ans: Option (c) is correct.
In this figure, we know that PQ is parallel to RS and ‘l’ is transversal.
\[\angle 2 = \angle 6 = {(34 - b)^o}......(i)\] (Corresponding angle)
Also, \[\angle 1 + \angle 2 = {180^o}\]
\[{(2a + b)^o} + \angle 2 = {180^o}\] (Since, given \[\angle 1 = {(2a + b)^o}\])
\[\angle 2 = {180^o} - {(2a + b)^o}.........(ii)\]
Now putting the value of equation (i) in equation (ii).
Thus we get:
\[{(3a - b)^o} = {180^o} - {(2a + b)^o}\]
\[3a - b + 2a + b = {180^o}\]
\[5a = {180^o}\]
\[a = {36^o}\]
Now we will put the value of ‘a’ in the equation:
\[\angle 2 = {(3a - b)^o}\]
\[\angle 2 = {(3 \times {36^o} - b)^o}\]
\[\angle 2 = {180^o}\]
36. In Fig, PQ||RS and \[a:b = 3:2\] Then, f is equal to
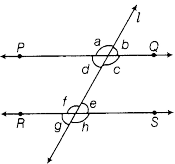
(a) \[{36^o}\] (b) \[{108^o}\]
(c) \[{72^o}\] (d) \[{144^o}\]
Ans: Option (b) is correct.
We know that \[a:b = 3:2\]
Thus, we can write: \[a = 3x\] and \[b = 2x\]
Also,
\[a + b = {180^o}\]
\[3x + 2x = {180^o}\]
\[5x = {180^o}\]
\[x = \dfrac{{{{180}^o}}}{5}\]
\[x = {36^o}\]
And $a = 3x$
Thus, $a = 3 \times {36^ \circ }$
So, we get, $a = {108^ \circ }$
Also, we know that PQ is parallel to RS and ‘l’ is transversal.
$a = f = {108^ \circ }$ as a and f are corresponding angles.
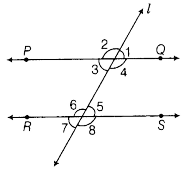
37. In Fig 5.30, line l intersects two parallel lines PQ and RS. Then, which one of the following is not true?
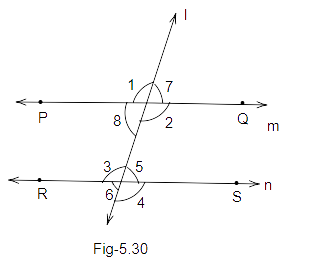
(a) \[\angle 1 = \angle 3\] (b) \[\angle 2 = \angle 4\]
(c) \[\angle 6 = \angle 7\] (d) \[\angle 4 = \angle 8\]
Ans: Option (d) is correct.
We know that, PQ is parallel to RS and ‘l’ is the transversal.
So, \[\angle 1 = \angle 3\] as they are corresponding angle.
\[\angle 2 = \angle 4\] as they are also corresponding angle.
\[\angle 6 = \angle 7\] as they are alternate angles.
38. In Fig. 5.30, which one of the following is not true?
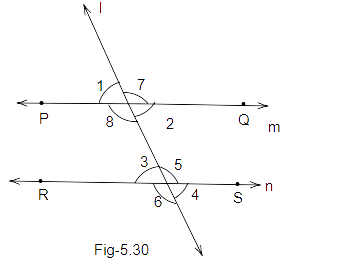
(a) \[\angle 1 + \angle 5 = {180^o}\]
(b) \[\angle 2 + \angle 5 = {180^o}\]
(c) \[\angle 3 + \angle 8 = {180^o}\]
(d) \[\angle 2 + \angle 3 = {180^o}\]
Ans: Option (d) is correct.
We know that, PQ is parallel to RS and ‘l’ is the transversal.
Also, \[\angle 2 = \angle 5....(i)\] (Co-interior angles)
Similarly, \[\angle 3 = \angle 8.....(ii)\] (Co-interior angles)
Also, \[\angle 1 = \angle 2.....(iii)\] (Vertically opposite angles)
Now, by comparing equations (i), (ii), (iii).
We get: \[\angle 1 + \angle 5 = {180^o}\] (since, \[\angle 2 = \angle 3\]as alternate interior angles)
So we can write, \[\angle 2 + \angle 3 = {180^o}\] is false. It cannot be true.
39. In Fig. 5.30, which of the following is true?
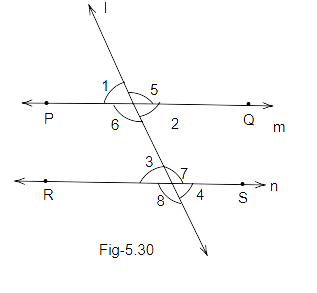
(a) \[\angle 1 = \angle 5\] (b) \[\angle 4 = \angle 8\]
(c) \[\angle 5 = \angle 8\] (d) \[\angle 3 = \angle 7\]
Ans: Option (c) is correct.
We know that PQ is parallel to RS and ‘l’ is the transversal.
Therefore, \[\angle 5 = \angle 8\] as they are alternate interior angles.
40. In Fig, PQ||ST. Then, the value of x + y is
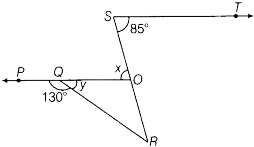
(a) \[{125^o}\] (b) \[{135^o}\]
(c) \[{145^o}\] (d) \[{120^o}\]
Ans: Option (b) is correct.
We know that, PQ is parallel to ST and SO is the transversal.
\[x = {85^o}\] (Alternate angles)
Since PO is a straight line.
Therefore,
\[\angle PQR + \angle OQR = {180^o}\]
\[{130^o} + y = {180^o}\]
\[y = {180^o} - {130^o}\]
\[y = {50^o}\]
Now,
\[x + y = {85^o} + {50^o}\]
\[x + y = {135^o}\]
41. In Fig. 5.32, if PQ||RS and QR||TS, then the value a is
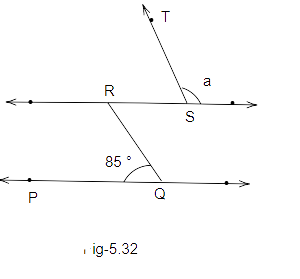
(a) \[{95^o}\] (b) \[{90^o}\]
(c) \[{85^o}\] (d) \[{75^o}\]
Ans: Option (a) is correct.
We know that RS is parallel to PQ and RQ is a transversal.
\[\angle PQR = \angle QRS = {85^O}{\text{ (alternate interior angles)}}\]
Also, RQ is parallel to ST and RS is transversal.
So, \[\angle QRS = \angle RST = {85^O}{\text{ (alternate interior angles)}}\]
And, RS is a straight line, thus,
\[\angle RST + a = {180^o}\]
\[{85^o} + a = {180^o}\]
\[a = {180^o} - {85^o}\]
\[a = {95^o}\]
In questions \[42{\text{ to 56}}\], fill in the blanks to make the statements true.
42. If the sum of measures of two angles is \[{90^o}\], then the angles are _______.
Ans: Correct answer is Complementary
43. If the sum of measures of two angles is \[{180^o}\], then they are________.
Ans: Correct answer is Supplementary
44. A transversal intersects two or more than two lines at _________ points.
Ans: Correct answer is Distinct
If a transversal intersects two parallel lines, then (Q. \[45to48\]).
45. the sum of interior angles on the same side of a transversal is ________.
Ans: Correct answer is \[{180^o}\]
46. alternate interior angles have one common ________.
Ans: Correct answer is Arm
47. corresponding angles are on the ________side of the transversal.
Ans: Correct answer is the Same
48. alternate interior angles are on the________ side of the transversal.
Ans: Correct answer is Opposite
49. Two lines in a plane that do not meet at a point anywhere are ________called lines.
Ans: Correct answer is Parallel
50. Two angles forming a __________ pair are supplementary.
Ans: Correct answer is Linear
51. The supplement of an acute is always _________ angle.
Ans: Correct answer is Obtuse
52. The supplement of a right angle is always ______ angle.
Ans: Correct answer is Right
53. The supplement of an obtuse angle is always ___ angle.
Ans: Correct answer is Acute
54. In a pair of complementary angles, each angle cannot be more than_____.
Ans: Correct answer is \[{90^o}\]
55. An angle is \[{45^o}\]. Its complementary angle will be ______.
Ans: Let the complementary angle be x
\[{45^o} + x = {90^o}\]
\[x = {90^o} - {45^o}\]
\[x = {55^o}\]
56. An angle which is half of its supplement is of ___.
Ans: Correct answer is \[{60^o}\]
Suppose, the angle is ‘y’ and its supplement is \[({180^o} - y)\]
Now, according to the question:
\[y = \dfrac{{({{180}^o} - y)}}{2}\]
\[2y = {180^o} - y\]
\[2y + y = {180^o}\]
\[3y = {180^o}\]
\[y = \dfrac{{{{180}^o}}}{3}\]
\[y = {60^o}\]
In questions \[57 - 71\], state whether the statements are True or False.
57. Two right angles are complementary to each other.
Ans: Correct answer is False
As we are aware of the fact that the sum of two right angles is supplementary and not complementary.
58. One obtuse angle and one acute angle can make a pair of complementary angles.
Ans: Correct answer is False
A complementary angle can be made by the sum of two acute angles.
59. Two supplementary angles are always obtuse angles.
Ans: Correct answer is False
60. Two right angles are always supplementary to each other.
Ans: Correct answer is True.
As we can see, \[{90^o} + {90^o} = {180^o}\]
61. One obtuse angle and one acute angle can make a pair of supplementary angles.
Ans: Correct answer is True
62. Both angles of a pair of supplementary angles can never be acute angles.
Ans: Correct answer is True.
63. Two supplementary angles always form a linear pair.
Ans: Correct answer is True.
64. Two angles making a linear pair are always supplementary.
Ans: Correct answer is True
65. Two angles making a linear pair are always adjacent angles.
Ans: Correct answer is True
66. Vertically opposite angles form a linear pair.
Ans: Correct answer is False
It is not mandatory that vertically opposite angles form a linear pair.
67. Interior angles on the same side of a transversal with two distinct parallel lines are complementary angles.
Ans: Correct answer is False
A supplementary angle is formed by interior angles on the same side of a transversal with two distinct parallel lines.
68. Vertically opposite angles are either acute angles or both obtuse angles.
Ans: True
Because vertically opposite angles are always equal. Thus, these angles are either acute angles or both obtuse angles.
69. A linear pair may have two acute angles.
Ans: Correct answer is False.
For a linear pair to form, one obtuse angle and one acute angle is needed.
70. An angle is more than \[{45^o}\]. Its complementary angle must be less than \[{45^o}\].
Ans: Correct answer is True.
Let’s suppose two angles be ‘x’ and ‘y’.
Suppose, \[x = {45^o}\]
Also, \[x + y = {180^o}\]
Now on putting the value of ‘x’, we will get:
\[x + y = {90^o}\]
\[{45^o} + y = {90^o}\]
\[y = {90^o} - {45^o}\]
\[y = {45^o}\]
Therefore, if an angle is more than \[{45^o}\]. Its complementary angle must be less than \[{45^o}\].
71. Two adjacent angles always form a linear pair.
Ans: Correct answer is False.
Adjacent angles do not always form a linear pair.
72. Write down each pair of adjacent angles shown in the following figures:
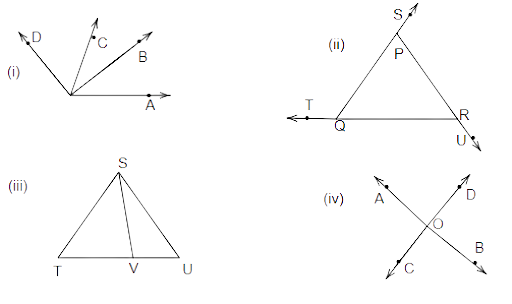
(i). Adjacent angles in figure (i) are:
\[\angle AOB{\text{ }}and{\text{ }}\angle BOC;\]
\[\angle AOC{\text{ }}and{\text{ }}\angle COD;{\text{ }}\]
\[\angle BOC{\text{ }}and{\text{ }}\angle COD{\text{ }}\]
\[\angle AOB{\text{ }}and{\text{ }}\angle BOD;{\text{ }}\]
(ii). Adjacent angles in the figure (ii) are:
\[\angle PQT{\text{ }}and{\text{ }}\angle PQR;{\text{ }}\]
\[\angle PQT{\text{ }}and{\text{ }}\angle PQR;{\text{ }}\]
\[\angle ORU{\text{ }}and{\text{ }}\angle QRP;{\text{ }}\]
(iii). Adjacent angles in figure (iii) are:
\[\angle TSV{\text{ }}and{\text{ }}\angle USV;\]
\[\angle SVT{\text{ }}and{\text{ }}\angle SVU;\]
(iv). Adjacent angles in the figure (iv) are:
\[\angle AOC{\text{ }}and{\text{ }}\angle AOD;\]
\[\angle BOC{\text{ }}and{\text{ }}\angle BOD;{\text{ }}\]
\[\angle AOC{\text{ }}and{\text{ }}\angle BOC;{\text{ }}\]
\[\angle AOD{\text{ }}and{\text{ }}\angle BOD\]
73. In each of the following figures, write, if any, (i) each pair of vertically opposite angles, and (ii) each linear pair.
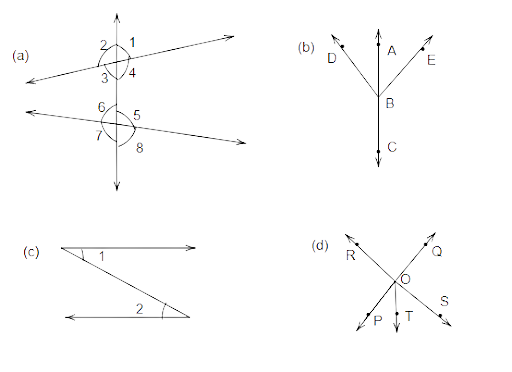
Ans: (a).
Pair of vertically opposite angles are:
\[\angle 1{\text{ }}and{\text{ }}\angle 3;{\text{ }}\]
\[\angle 2{\text{ }}and{\text{ }}\angle 4;\]
\[\angle 5{\text{ }}and{\text{ }}\angle 7{\text{ }}\]
\[\angle 6{\text{ }}and{\text{ }}\angle 8{\text{ }}\]
And pair of linear angles are:
\[\angle 1{\text{ }}and{\text{ }}\angle 2,\angle 1{\text{ }}and{\text{ }}\angle 4,\angle 2{\text{ }}and{\text{ }}\angle 3,{\text{ }}\angle 3{\text{ }}and{\text{ }}\angle 4,{\text{ }},\angle 5{\text{ }}and{\text{ }}\angle 6,{\text{ }},\angle {\text{ }}5{\text{ }}and{\text{ }}\angle 8,{\text{ }},\angle {\text{ }}6{\text{ }}and{\text{ }}\angle 7,{\text{ }},\angle 7{\text{ }}and{\text{ }}\angle 8\]
(b). Vertically opposite angles are not present in this figure.
And pair of linear angles are:
\[\angle ABD{\text{ }}and{\text{ }}\angle DBC;{\text{ }}\]
\[\angle ABE{\text{ }}and{\text{ }}\angle CBE\]
(c). In this figure, there are no vertically opposite angles. Also, it does not have linear angles.
(d). Pair of vertically opposite angles are:
\[\angle POR{\text{ }}and{\text{ }}\angle QOS;{\text{ }}\]
\[\angle ROQ{\text{ }}and{\text{ }}\angle POS\]
And pair of linear angles are:
\[\angle POR{\text{ }}and{\text{ }}\angle ROQ;{\text{ }}\]
\[\angle ROQ{\text{ }}and{\text{ }}\angle OOS;\]
\[\angle OOS{\text{ }}and\angle SOP;{\text{ }}\]
\[\angle SOP{\text{ }}and{\text{ }}\angle POR;\]
\[\angle ROT{\text{ }}and{\text{ }}\angle TOS;\]
\[\angle OOT{\text{ }}and{\text{ }}\angle POT\]
74. Name the pairs of supplementary angles in the following figures:
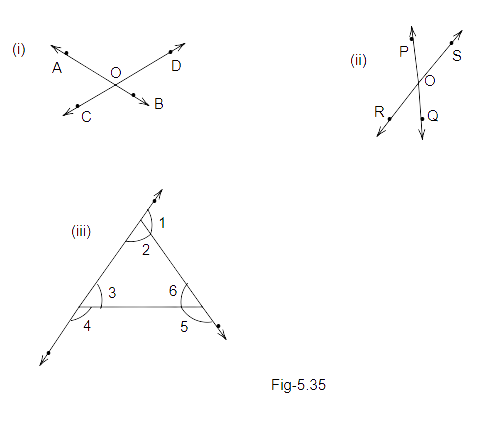
(i). Pairs of supplementary angles are:
\[\angle AOD{\text{ }}and{\text{ }}\angle DOB;{\text{ }}\]
\[\angle DOB{\text{ }}and{\text{ }}\angle BOC;\]
\[\angle BOC{\text{ }}and{\text{ }}\angle AOC;{\text{ }}\]
\[\angle AOC{\text{ }}and\angle AOD\]
(ii). Pairs of supplementary angles are:
\[\angle POS{\text{ }}and{\text{ }}\angle SOQ,{\text{ }}\]
\[\angle POR{\text{ }}and{\text{ }}\angle ROQ,{\text{ }}and{\text{ }}\]
\[\angle RPS{\text{ }}and{\text{ }}\angle RPQ.{\text{ }}\]
(iii). Pairs of supplementary angles are:
\[\angle 1{\text{ }}and{\text{ }}\angle 2,\]
\[\angle 3{\text{ }}and{\text{ }}\angle 4,{\text{ }}\]
\[\angle 5{\text{ }}and{\text{ }}\angle 6.\]
75. In Fig, PQ || RS, TR || QU and \[\angle PTR = {40^O}\]. Find \[\angle \]QUR
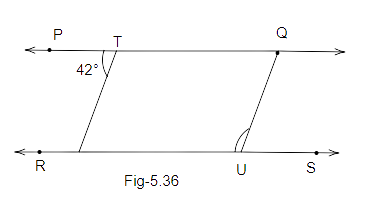
Ans: As we know that, PQ is parallel to RS and TR is a transversal.
Therefore, \[\angle PTR = \angle TRU = {42^O}\] (Alternate Interior angles)
\[\angle TRU + \angle QUR = {180^o}\] (co-interior angles)
\[\angle TRU + \angle QUR = {180^o}\]
\[{42^O} + \angle QUR = {180^o}\]
\[{42^O} + \angle QUR = {180^o}\]
\[\angle QUR = {138^o}\]
76. The drawings below (Fig), show angles formed by the goalposts at different positions of a football player. The greater the angle, the better chance the player has of scoring a goal. For example, the player has a better chance of scoring a goal from Position A than from Position B.
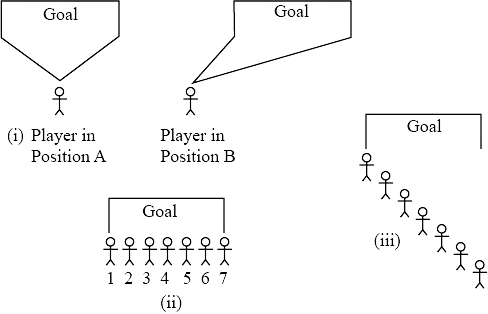
In Parts (a) and (b) given below, it may help to trace the diagrams and draw and measure angles.
(a) Seven football players are practicing their kicks. They are lined up in a straight line in front of the goalpost [Fig.(ii)]. Which player has the best (the greatest) kicking angle?
(b) Now the players are lined up as shown in Fig. (iii). Which player has the best kicking angle?
(c) Estimate at least two situations such that the angles formed by different positions of two players are a complement to each other.
Ans: (a). The ‘player number \[{4^{th}}\] ‘ has the highest degree of angle to kick. Thus, he has the best (the greatest) kicking angle.
(b). The ‘player number \[{4^{th}}\] ‘ has the highest degree of angle to kick. Thus, he has the best (the greatest) kicking angle.
(c). Two players in the game are in such types of different positions that they formed two pairs of angle’ \[({45^o},{45^o})\] and \[({60^o},{30^o})\] that are a complement to each other.
As, \[{60^o} + {30^o} = {90^o}\]
\[{45^o} + {45^o} = {90^o}\]
Thus, the answer is clear.
77. The sum of two vertically opposite angles is \[{166^o}\]. Find each of the angles.
Ans: We know that the two vertically opposite angles are equal.
So let’s suppose the angle is ‘x’
\[x + x = {166^o}\]
\[2x = {166^o}\]
\[x = \dfrac{{{{166}^o}}}{2}\]
\[x = {83^o}\]
78. In Fig. 5.38, l ||m||n. \[\angle \] QPS \[ = \] \[{35^o}\] and \[\angle \] QRT \[ = \] \[{55^o}\]. Find \[\angle \] PQR.
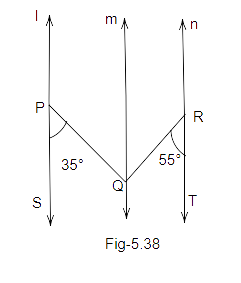
Ans: We know that ‘l’ is parallel to ‘m’ and P is a transversal.
Therefore, \[\angle SPQ = \angle PQM = {35^O}\] (Alternate interior angles)
Also, ‘m’ is parallel to ‘n’ and QR is a transversal.
Therefore, \[\angle MQR = \angle QRT = {55^O}\] (Alternate interior angles)
Thus,
\[\angle \;PQR = \angle PQM + \angle MQR\]
\[\angle \;PQR = {35^O} + {55^O}\]
\[\angle \;PQR = {90^O}\]
79. In Fig., P, Q and R are collinear points and TQ \[ \bot \] PR, Name;
(a) pair of complementary angles
(b) two pairs of supplementary angles.
(c) four pairs of adjacent angles.
Ans:
(a) $\angle TOS$ and $\angle SQR$ is pair of complementary angles.
(b) $\angle PQT$ and $\angle TOR$, $\angle SQR$ and $\angle PQS$ are the two pairs of supplementary angles.
(c) $\angle PQT$ and $\angle TQS$, $\angle TQS$ and $\angle SQR$, $\angle PQT$ and $\angle TOR$, and $\angle PQS$ and $\angle SQR$ are four pairs of adjacent angles.
80. In Fig 5.40, OR \[ \bot \] OP.
(i) Name all the pairs of adjacent angles.
(ii) Name all the pairs of complementary angles.
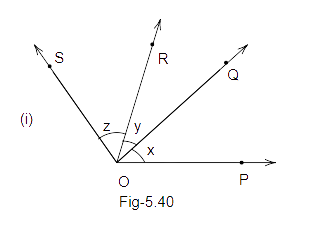
Ans: (i) four pair of adjacent angles are:
\[\angle x{\text{ }}and{\text{ }}y,{\text{ }}\]
\[\angle x{\text{ }}and\angle y{\text{ }} + {\text{ }}\angle z,{\text{ }}\]
\[\angle y{\text{ }}and{\text{ }}\angle z,{\text{ }}\]
\[\angle z{\text{ }}and{\text{ }}\angle x{\text{ }} + {\text{ }}\angle y.\]
(ii) As we know that \[\angle x{\text{ }}and{\text{ }}\angle y\] are complementary angles.
Therefore we can say that, \[\angle x{\text{ = }}\angle y = \angle z{\text{ }}\]
Thus, The pair of complementary angles are:
\[\angle x{\text{ }}and\angle y\]
\[\angle y{\text{ and }}\angle z\]
\[\angle z{\text{ }}and{\text{ }}\angle x\].
81. If two angles have a common vertex and their arms form opposite rays (Fig. ), Then,
(a) how many angles are formed?
(b) how many types of angles are formed?
(c) write all the pairs of vertically opposite angles.
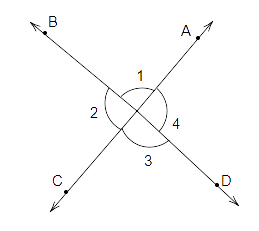
(a). In the above given figure \[13\] angles are formed.
(b) ‘Four’ types of angles are formed. Linear pairs, adjacent angles, vertically opposite angles and supplementary angles.
(c). \[\angle 1{\text{ }}and{\text{ }}3,{\text{ }}\angle 2{\text{ }}and{\text{ }}\angle 4\] are the pairs of vertically opposite angles.
82. In (Fig 5.42) are the following pairs of angles adjacent? Justify your answer.
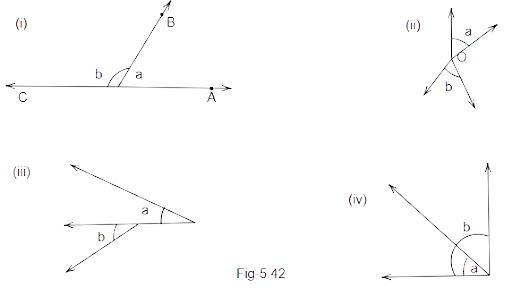
Ans: (i) a and b are adjacent angles as they share a common arm.
(ii) a and b are not adjacent angles as they do not share a common arm.
(iii) a and b are not adjacent angles as they do not share a common vertex.
(iv) a and b are not adjacent angles as they do not share a common arm and lie on the same side of the common arm.
83. In Fig. 5.43, write all the pairs of supplementary angles.
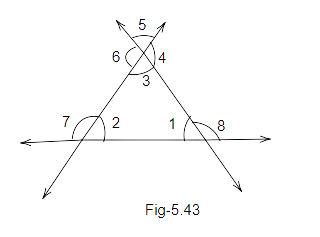
Ans: Pairs of supplementary angles formed are:
\[\angle 1{\text{ }}and{\text{ }}\angle 8,{\text{ }}\]
\[\angle 2{\text{ }}and{\text{ }}\angle 7,{\text{ }}\]
\[\angle {\text{ }}3{\text{ }}and{\text{ }}\angle 4,{\text{ }}\]
\[\angle 4{\text{ }}and{\text{ }}\angle 5,{\text{ }}\]
\[\angle 5{\text{ }}and{\text{ }}\angle 6,{\text{ }}\]
\[\angle 3{\text{ }}and{\text{ }}\angle 6.\]
84. What is the type of other angles of a linear pair if
(a) one of its angles is acute?
(b) one of its angles is obtuse?
(c) one of its angles is right?
Ans: (a) In a linear pair, if one of its angles is acute, then the other angle must be obtuse.
In a linear pair, if one of its angle is obtuse, then the other angle must be acute.
In a linear pair, if one of its angles is right, then the other angle must be the right angle.
85. Can two acute angles form a pair of supplementary angles? Give a reason in support of your answer.
Ans: No, two acute angles cannot form a pair of supplementary angles.as acute angles are those angles that are less than \[{90^o}\]
Therefore, \[{89^o} + {89^o} \ne {180^o}\]
86. Two lines AB and CD intersect at O (Fig. 5.44). Write all the pairs of adjacent angles by taking angles 1, 2, 3, and 4 only.
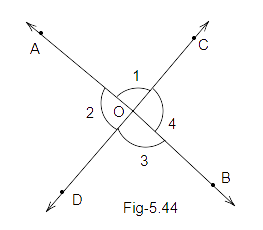
Ans: There are four pairs of adjacent angles in the above figure.
And these adjacent angles are as follows:
\[\angle 1{\text{ }}and{\text{ }}\angle 2,{\text{ }}\]
\[\angle 1{\text{ }}and{\text{ }}\angle 4,{\text{ }}\]
\[\angle 2{\text{ }}and{\text{ }}\angle 3,{\text{ }}\]
\[\angle 3{\text{ }}and{\text{ }}\angle 4.\]
87. If the complement of an angle is \[{62^o}\], then find its supplement.
Ans: Let ‘x’ be the angle and its complement will be \[{90^o} - x\].
Now, according to the conditions given in the question, we can write:
\[{90^o} - x = {62^o}\]
\[x = {90^o} - {62^o}\]
\[x = {28^o}\]
Now, the supplement of the angle will be: \[ \Rightarrow {180^o} - {28^o} \Rightarrow {152^o}\]
88. A road crosses a railway line at an angle of \[{30^0}\] as shown in Fig.5.45. Find the values of a, b and c.

Ans:
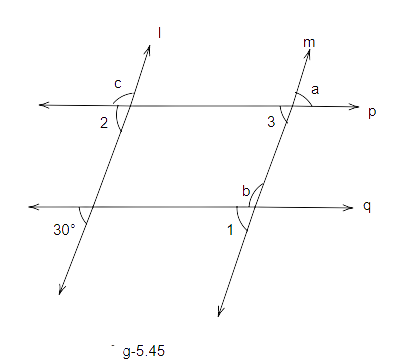
Ans: ‘l’ is parallel to ‘m’ and ‘q’ is the transversal.
Therefore, \[\angle 1 = {30^0}\] (corresponding angles)
Also, ‘m’ is a straight line, so:
\[\angle 1 + b = {180^o}\]
\[{30^0} + b = {180^o}\]
\[b = {180^o} - {30^o}\]
\[b = {150^o}..........(i)\]
Now, we know that ‘p’ is parallel to ‘q’ and ‘m’ is the transversal.
Therefore, \[\angle 1 = \angle 3 = {30^0}\] (corresponding angle)
So, \[\angle 3 = a = {30^0}.....(ii)\] (Vertically opposite angles)
Now, ‘p’ is parallel to ‘q’ and ‘l’ is the transversal.
So, \[\angle 2 = {30^0}\] (corresponding angles)
Also, ‘l’ is a straight line.
So,
\[\angle 2 + c = {180^o}\]
\[{30^0} + c = {180^o}\]
\[c = {180^o} - {30^o}\]
\[c = {150^o}.......(iii)\]
89. The legs of a stool make an angle of 35° with the floor as shown in Fig. 5.46. Find the angles x and y.

Ans:
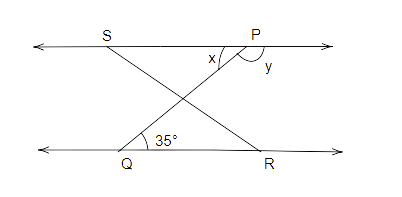
In this figure, ‘l’ is parallel to ’m’ and PQ is a transversal.
Therefore, \[x = {35^o}\] (alternate interior angles).
Also, ‘l’ is a straight line.
So,
\[x + y = {180^o}\]
\[{35^o} + y = {180^o}\]
\[y = {180^o} - {35^o}\]
\[y = {145^o}\]
Thus, \[x = {35^o}\] and \[y = {145^o}\].
90. Iron rods a, b, c, d, e, and f are making a design in a bridge as shown in Fig. 5.47, in which a ||b, c ||d, e || f. Find the marked angles between
(i) b and c
(ii) d and e.
(iii) d and f
(iv) c and f
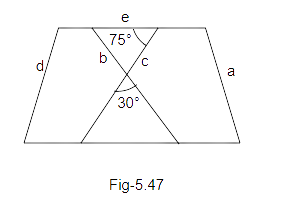
Ans:
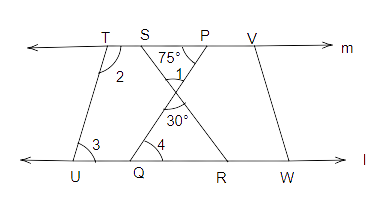
(a). Suppose the angle between b and c is ‘\[1\]’.
Therefore, \[\angle 1 = {30^o}\] (vertically opposite angles)
(b). Suppose the angle between d and e is ‘\[2\]’.
Also, we know that TU is parallel to YW and ‘m’ is the transversal.
So,
\[\angle 2 + {75^0} = {180^o}{\text{ (Co - interior angles)}}\]
\[\angle 2 = {180^o} - {75^0}\]
\[\angle 2 = {105^o}\]
(c). Suppose the angle between d and f is 3
So,
\[\angle 2 + \angle 3 = {180^o}{\text{ (Co - interior angles)}}\]
\[{105^o} + \angle 3 = {180^o}{\text{ (}}\because \angle 2 = {105^o})\]
\[\angle 3 = {180^o} - {105^o}\]
\[\angle 3 = {75^o}\]
(d). Suppose the angle between c and f is \[4\]
So, we know that SP is parallel to QR and ‘PQ’ is the transversal.
Therefore, \[\angle 4 = {75^o}\] (alternate interior angles).
91. Amisha makes a star with the help of line segments a, b, c, d, e, and f, in which a || d, b || e, and c || f. Chhaya marks an angle as 120° as shown in Fig. 5.48 and asks Amisha to find the \[\angle \]x, \[\angle \]y and \[\angle \]z. Help Amisha in finding the angles.
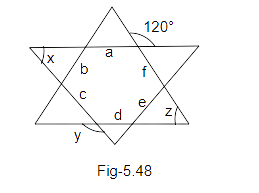
Ans: Let’s suppose angle \[1,2\]as shown in the figure below:
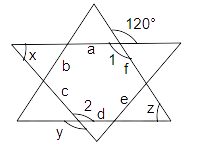
we know that,
\[\angle 1 = {120^o}\] (Vertically opposite angles)
Also, ‘f’ is parallel to ‘c’, and ‘a’ is a transversal.
\[x + \angle 1 = {180^o}{\text{ (co - interior angles)}}\]
\[x + {120^o} = {180^o}\]
\[x = {60^o}\]
Also, ‘a’ is parallel to ‘d’ and ‘c’ is a transversal.
Therefore,
\[x + \angle 2 = {180^o}{\text{ (co - interior angles)}}\]
\[{60^o} + \angle 2 = {180^o}\]
\[\angle 2 = {180^o} - {60^o}\]
\[\angle 2 = {120^o}\]
And, \[y = \angle 2 = {120^o}\] (Vertically opposite angles)
Again, ‘a’ is parallel to ‘d’ and ‘f’ is a transversal.
So,
\[z + \angle 1 = {180^o}{\text{ (co - interior angles)}}\]
\[z + {120^o} = {180^o}\]
\[z = {180^o} - {120^o}\]
\[z = {60^o}\]
Thus, the values of x,y, and z are:
\[x = {60^0}\]
\[y = {120^o}\]
\[z = {60^o}\]
92. In Fig. 5.49, AB||CD, AF||ED, \[\angle AFC = {68^\circ}\] and \[\angle FED = {42^\circ}\] . Find \[\angle EFD\].
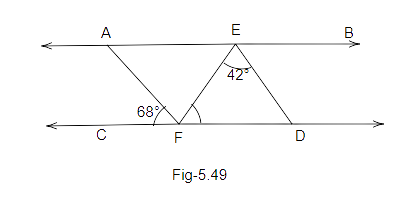
Ans: let's do the marking on the figure as shown below:
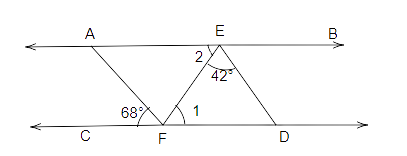
We know that AF is parallel to ED and FD is a transversal.
So, \[\angle 3 = {68^\circ}\] (corresponding angles)
Also, we know that the sum of all the angles of a triangle is .
Therefore,
\[\angle 1 + {42^\circ} + \angle 3 = {180^\circ}\]
\[\angle 1 + {42^\circ} + {68^\circ} = {180^\circ}(from{\text{ equation(i))}}\]
\[\angle 1 + {110^\circ} = {180^\circ}\]
\[\angle 1 = {180^\circ} - {110^\circ}\]
\[\angle 1 = {70^\circ}\]
Thus, \[\angle EFD = \angle 1 = {70^\circ}\].
93. In Fig. 5.50, OB is perpendicular to OA and \[\angle BOC = {49^o}\]. Find ∠ AOD.
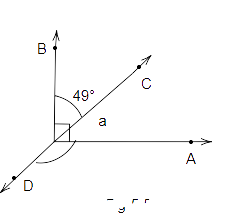
Ans: We know that OB is perpendicular to OA.
Therefore, \[\angle AOB = {90^O}\]
Also we know that, \[\angle BOC = {49^o}\]
So,
\[\angle BOC + \angle AOC = \angle AOB\]
\[{49^o} + \angle AOC = {90^o}\]
\[\angle AOC = {90^o} - {49^o}\]
\[\angle AOC = {41^o}...(i)\]
Again, CD is a straight line:
\[\angle AOD + \angle AOC = {180^o}\]
\[\angle AOD + {41^o} = {180^o}\]
\[\angle AOD = {180^o} - {41^o}\]
\[\angle AOD = {139^O}\]
94. Three lines AB, CD and EF intersect each other at O. If \[\angle AOE = {30^o}\] and \[\angle DOB = {40^O}\] (Fig. 5.51), find ∠ COF.
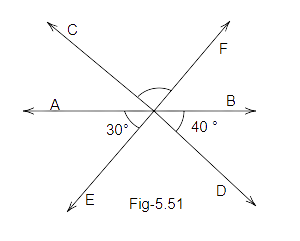
Ans: We know that AB is a straight line, so:
\[\angle AOE + \angle EOD + \angle DOB = {180^O}\]
\[{30^o} + \angle EOD + {40^o} = {180^o}\]
\[\angle EOD + {70^o} = {180^o}\]
\[\angle EOD = {180^o} - {70^o}\]
\[\angle EOD = {110^o}\]
Now, \[\angle EOD + \angle COF = {110^o}\] (Vertically opposite angles).
95. Measures (in degrees) of two complementary angles are two consecutive even integers. Find the angles.
Ans: suppose two consecutive even integers complementary angles are \[2x{\text{ and (2x + 2)}}\]
Now, according to the question:
\[2x{\text{ + (2x + 2) = 9}}{{\text{0}}^o}\]
\[4x + 2 = {90^o}\]
\[4x = {90^o} - {2^o}\]
\[4x = {88^o}\]
\[x = \dfrac{{{{88}^o}}}{4}\]
\[x = {22^o}\]
Now, the value of angles are:
\[ \Rightarrow 2x = 2 \times {22^o} = {44^o}\]
\[ \Rightarrow 2x + 2 \Rightarrow 2 \times {22^o} + 2 \Rightarrow {46^o}\]
96. If a transversal intersects two parallel lines, and the difference of two interior angles on the same side of a transversal is \[{20^o}\], find the angles.
Ans: Suppose the two angles are ‘a’ and ‘b’.
we know that the supplementary angles are: \[a + b = {180^o} - - - (i)\]
Also, given in the question that: \[a - b = {20^o} - - - (ii)\]
Now, on adding the equation (i) and (ii), we will get:
\[a + b + a - b = {180^o} + {20^o}\]
\[2a = {200^o}\]
\[a = \dfrac{{{{200}^o}}}{2}\]
\[a = {100^o}\]
Now, on substituting the value of ‘a’ in equation (ii) we will get:
\[a - b = {20^o}\]
\[{100^o} - b = {20^o}\]
\[{100^0} - {20^o} = b\]
\[b = {80^o}\]
Therefore the value of angles are,
\[a = {100^0}\]
\[b = {80^o}\]
97. Two angles are making a linear pair. If one of them is one-third of the other, find the angles.
Ans: We know that sum of pair of linear angles is equal to \[{180^o}\].
So, let's suppose, one angle be ‘x’, then the other angles will be \[{180^o} - x\].
Now it is given in the question that, \[x = \dfrac{1}{2}({180^o} - x)\]
Now, on solving this we will get:
\[x = \dfrac{1}{3}({180^o} - x)\]
\[3x = {180^o} - x\]
\[3x + x = {180^o}\]
\[4x = {180^o}\]
\[x = \dfrac{{{{180}^o}}}{4}\]
\[x = {45^o}\]
Therefore, the angles are: \[x = {45^o}\]
Other angles are: \[ \Rightarrow {180^o} - x \Rightarrow {180^o} - {45^o} \Rightarrow {135^o}\]
98. Measures (in degrees) of two supplementary angles are consecutive odd integers. Find the angles.
Ans: Suppose the two supplementary angles that are consecutive odd integers be \[2x + 1\] and \[2x + 3\].
Now, according to the question,
\[2x + 3 + 2x + 1 = {180^o}\]
\[4x + 4 = {180^o}\]
\[4x = {180^o} - {4^o}\]
\[4x = {176^o}\]
\[x = \dfrac{{{{176}^o}}}{4}\]
\[x = {44^o}\]
Therefore the values of angles are:
\[ \Rightarrow 2x + 1 \Rightarrow 2 \times {44^o} + 1 \Rightarrow {89^o}\]
\[ \Rightarrow 2x + 3 \Rightarrow 2 \times {44^o} + 3 \Rightarrow {91^o}\]
99. In Fig. 5.52, AE || GF || BD, AB || CG || DF and ∠ CHE \[ = {120^o}\]. Find \[\angle \]ABC and \[\angle \]CDE.
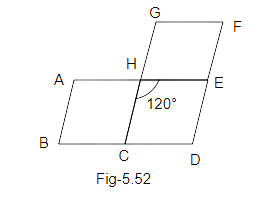
Ans: Ans: we know that AE is parallel to BD and HC is a transversal.
Therefore, \[\angle CHE = \angle BCH...(i)\] (alternate angles).
Also, CH is parallel to DE and CD is a transversal.
\[\angle BCH = \angle CDE = {120^O}....(ii)\]
Also, we know that AB is parallel to DE and BC is a transversal.
\[\angle ABD + \angle BDE = {180^O}(Co - {\text{ interior angles}})\]
\[\angle ABD + {120^o} = {180^O}\]
\[\angle ABD = {180^O} - {120^o}\]
\[\angle ABD = {60^o}...(iii)\]
Therefore, the angles are \[\angle ABC = {60^o}\] and \[CDE = {120^o}\]
100. In Fig. 5.53, find the value of \[\angle \]BOC, if points A, O and B are collinear.
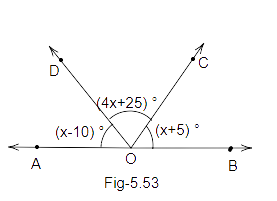
Ans: We know that AOB is a straight line.
So,
\[\angle AOD + \angle DOC + \angle BOC = {180^O}\]
\[x - 10 + 4x + 25 + x + 5 = {180^O}\]
\[6x - {30^o} = {180^O}\]
\[6x = {180^o} + {30^o}\]
\[6x = {210^o}\]
\[x = \dfrac{{{{210}^o}}}{6}\]
\[x = {35^o}\]
Now, the value of angle \[\angle \]BOC \[ = \]\[x + 5\]
\[\angle BOC = x + 5\]
\[\angle BOC = {35^o} + 5\]
\[\angle BOC = {40^o}\]
101. In Fig. 5.54, if l ||m, find the values of a and b.
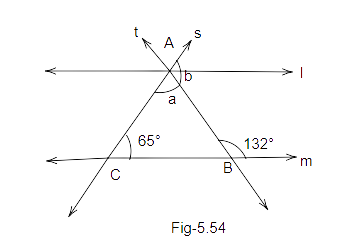
Ans: We know that ‘l’ is parallel to ‘m’ and AB is a transversal.
Therefore,
\[{132^o} + b = {180^o}....(co - {\text{ interior angles}})\]
\[b = {180^o} - {132^o}\]
\[b = {48^o}\]
Also, \[\angle ABC = b = {180^o}....(alternate{\text{ angles}})\]
And we know that the sum of all angles of a triangle is \[{180^o}\].
Thus,
\[a + {65^o} + \angle ABC = {180^o}\]
\[a + {65^o} + {48^o} = {180^o}\]
\[a + {113^o} = {180^o}\]
\[a = {180^o} - {113^o}\]
\[a = {67^o}\]
Therefore, the values of a and b are:
\[a = {67^o}\]
\[b = {48^o}\]
102. In Fig. 5.55, l ||m and a line t intersect these lines at P and Q, respectively. Find the sum \[2a + b\].
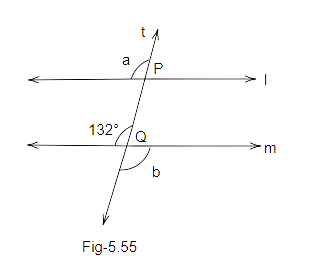
Ans: we know that, l is parallel to m and PQ is a transversal.
Therefore, \[b = {132^o}\] (vertically opposite angles)
Also, \[a = {132^o}\] (corresponding angle)
Now according to the question, value of \[2a + b\] is:
\[ \Rightarrow 2a + b \Rightarrow 2 \times {132^o} + {132^o} \Rightarrow {264^o} + {132^o} \Rightarrow {396^o}\]
103. In Fig. 5.56, QP || RS. Find the values of a and b.
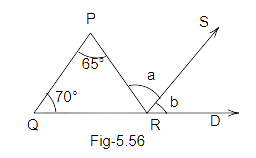
Ans: as we know that QP is parallel to RS and PR is a transversal.
So, \[a = {65^o}\] (alternate angles).
Also, QP is parallel to RS and QR is a transversal.
Therefore, \[b = {70^o}\] (corresponding angles)
Thus, the value of a and b are:
\[a = {65^o}\]
\[b = {70^o}\]
104. In Fig. 5.57, PQ || RT. Find the value of \[a + b\].
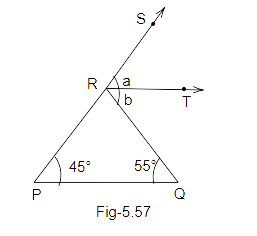
Ans: we know that RT is parallel to PQ and RQ is a transversal.
Therefore, \[b = {55^o}...(i)\] (alternate interior angles)
Also, RT is parallel to PQ and PR is a transversal.
So, \[a = {45^o}...(ii)\] (corresponding angles)
Now, according to the question, value of \[a + b\].
\[ \Rightarrow a + b = {45^o} + {55^o} \Rightarrow a + b = {100^o}\]
105. In Fig 5.58, PQ, RS, and UT are parallel lines.
(i) If \[c = {57^o}\] and \[a = \dfrac{c}{3}\] , find the value of d.
(ii) If \[c = {57^o}\] and \[a = \dfrac{2}{5}c\] , find b.
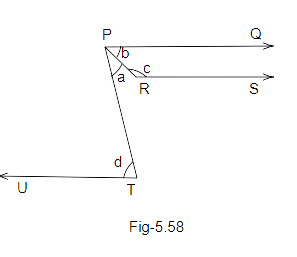
Ans: (i) we know that in the figure PQ is parallel to UT and PT is a transversal.
Therefore, \[a + b = c\] (alternate angles)
On solving this we will get:
\[b = c - a\]
\[b = {57^o} - \dfrac{c}{3}\]
\[b = {57^o} - \dfrac{{{{57}^o}}}{3}\]
\[b = {57^o} - {19^o}\]
\[b = {38^o}.....(i)\]
Also, in the figure PQ is parallel to RS and PR is a transversal.
\[b + d = {180^o}\]
\[{38^o} + d = {180^o}...(from{\text{ eq (i))}}\]
\[d = {180^o} - {38^o}\]
\[d = {142^o}\]
(ii). we know that in the figure PQ is parallel to UT and PT is a transversal.
Therefore, \[a + b = c\] (alternate angles)
On solving this we will get:
\[b = c - a\]
\[b = {75^o} - \dfrac{2}{5}c\]
\[b = {75^o} - \dfrac{2}{3} \times {75^o}\]
\[b = {75^o} - {30^o}\]
\[b = {45^o}.....(ii)\]
106. In Fig. 5.59, AB||CD. Find the reflex \[\angle \]EFG.
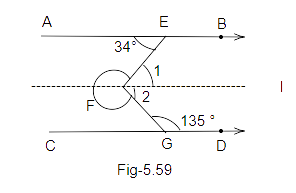
Ans: in the above figure, AB is parallel to ‘l’ and EF is a transversal.
\[\angle 1 = {34^o}...(i)\] (alternate angles)
Also, In the figure, ‘l’ is parallel to CD and FG is a transversal.
\[\angle 2 + {135^o} = {180^o}...(co - {\text{ interior angles)}}\]
\[\angle 2 = {180^o} - {135^o}\]
\[\angle 2 = {45^o}...(ii)\]
Thus, from eq (i) and (ii)
\[\angle EFG = \angle 1 + \angle 2\]
\[\angle EFG = {34^o} + {45^o}\]
\[\angle EFG = {79^o}\]
Also, the reflex of angle \[\angle EFG\]is ,
\[\angle EFG = {360^o} - {79^o}\]
\[\angle EFG = {281^o}\]
107. In Fig. 5.60, two parallel lines l and m are cut by two transversals n and p. Find the values of x and y.
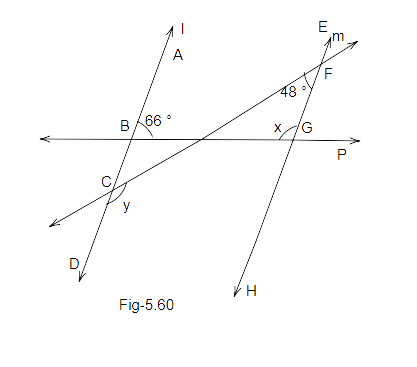
Ans: in the figure above, we know that ‘l’ is parallel to ‘m’ and BG is a transversal.
So,
\[x + {66^o} = {180^o}...(co - {\text{ interior angles)}}\]
\[x = {180^o} - {66^o}\]
\[x = {114^o}\]
Also, ‘l’ is parallel to ‘m’ and FC is a transversal.
\[y + {48^o} = {180^o}..(co - {\text{ interior angles}})\]
\[y = {180^o} - {48^o}\]
\[y = {132^o}\]
Thus, values of x and y is:
\[x = {114^o}\]
\[y = {132^o}\]
108. In Fig. 5.61, l, m, and n are parallel lines, and the lines p and q are parallel. Find the values of a, b and c.
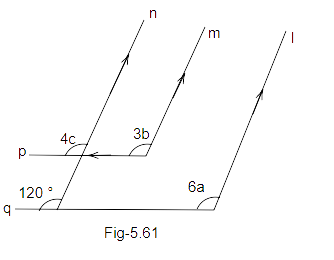
Ans: From the above figure, we know that ‘p’ is parallel to ‘q’ and ‘n’ is a transversal.
\[4c = {120^o}...(corresponding{\text{ }}angles)\]
\[c = \dfrac{{{{120}^o}}}{4}\]
\[c = {30^o}....(i)\]
Also, we know that ‘n’ is parallel to ‘l’ and ‘q’ is a transversal.
So,
\[6a = {120^o}.....(corresponding{\text{ angles)}}\]
\[a = \dfrac{{{{120}^o}}}{6}\]
\[a = {20^o}....(ii)\]
Again, ‘n’ is parallel to ‘m’ and ‘p’ is a transversal.
So,
\[4c = 3b.....(corresponding{\text{ angles)}}\]
\[{\text{From eq (i) and (ii)}}\]
\[{\text{4}} \times {\text{3}}{{\text{0}}^o} = 3 \times b\]
\[{120^o} = 3b\]
\[b = \dfrac{{{{120}^o}}}{3}\]
\[b = {40^o}\]
Therefore, the value of a, b and c are:
\[a = {20^o}\]
\[b = {40^o}\]
\[c = {30^o}\]
109. In Fig. 5.62, state which pair of lines are parallel. Give reason.
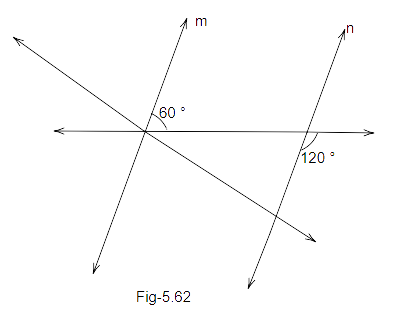
Ans: In the figure given below:
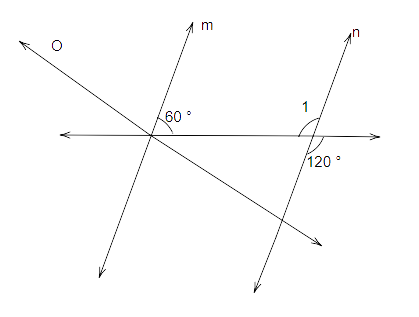
\[\angle 1 = {120^o}...(i)\] (vertically opposite angles)
Now, \[ \Rightarrow {60^o} + \angle 1 = {60^o} + {120^o} \Rightarrow {180^o}\]
Therefore, the sum of co-interior angles on the same side of transversal is equal to \[{180^o}\].
Hence, this proves that ‘m’ is parallel to ’n’ and ‘l’ is a transversal.
110. In Fig. 5.63, examine whether the following pairs of lines are parallel or not:
(i) EF and GH
(ii) AB and CD
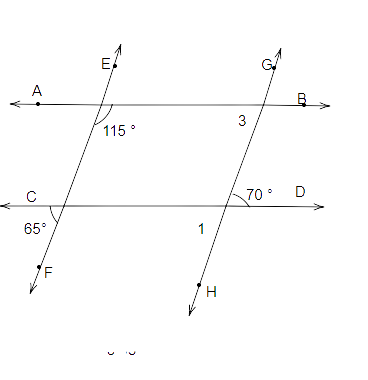
Ans: In the figure given below:
(i). \[\angle 1 = {65^o}\] (vertically opposite angles)
But, \[\angle 1 = {65^o} \ne \angle QPD = {70^0}\]
Therefore, EF and GH is not parallel to each other.
(ii). In this case \[\angle 1 + {115^o}\] must be equal to \[{180^o}\], as they are co-interior angles.
Therefore, from eq (i), on putting the value of \[\angle 1\], we will get:
\[ \Rightarrow \angle 1 + {115^o} \Rightarrow {65^o} + {115^o} \Rightarrow {180^o}\]
Thus, it is equal to \[{180^o}\].
Therefore, AB and CD are parallel to each other.
111. In Fig. 5.64, find out which pair of lines are parallel:
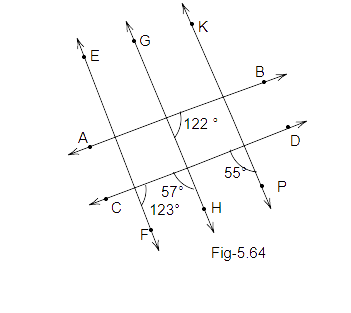
Ans: In the figure given below:
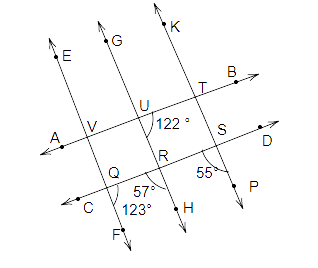
We know that,
\[ \Rightarrow \angle FQR + \angle HRQ \Rightarrow {123^o} + {57^o} \Rightarrow {180^o}\]
Therfore, EF is parallel to GH as sum of angles on the same side of transversal is \[{180^o}\].
Also, \[ \Rightarrow \angle TUR + \angle UVQ \Rightarrow {122^o}\]
So, EF is parallel to GH and AB is a transversal.
As, \[ \Rightarrow \angle UVQ \ne \angle FQR\]
Therefore, AB and CD are not parallel lines.
112. In Fig. 5.65, show that
(i)AB || CD
(ii) EF || GH

Ans: (i) \[\angle PQC = {50^o}\] (vertically opposite angles)
Now, \[ \Rightarrow \angle APQ + \angle PQC \Rightarrow {130^o} + {50^o} \Rightarrow {180^o}\]
So, it proves that \[\angle APQ{\text{ and }}\angle PQC\] are supplementary angles.
Therefore, AB is parallel to CD.
(ii) \[\angle APQ{\text{ and }}\angle RPE = {130^o}\] (Vertically opposite angles)
\[ \Rightarrow \angle RPE + \angle GRP = {130^o} + {50^o} \Rightarrow {180^o}\]
So, it proves that \[\angle RPE{\text{ }}and{\text{ }}\angle {\text{GRP}}\] are supplementary angles.
113. In Fig. 5.66, two parallel lines l and m are cut by two transversals p and q. Determine the values of x and y.
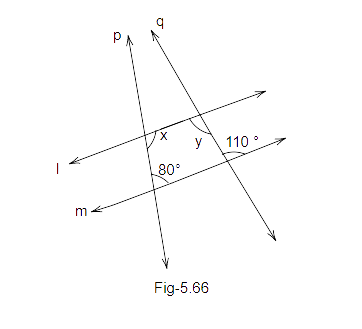
Ans: In the above figure, ‘l’ is parallel to ‘m’ and ‘q’ is a transversal.
\[x = {110^o}\] (vertically opposite angles)
Also, ‘l’ is parallel to ‘m’ and ‘p’ is a transversal.
So,
\[y + {80^o} = {180^o}....{\text{ (co - interior angles)}}\]
\[{\text{y}} = {180^o} - {80^o}\]
\[y = {100^o}\]
Thus, the values of x and y are:
\[x = {110^o}\]
\[y = {100^o}\]
Lines and Angles Chapter 5 Class 7
Lines and Angles chapter falls in the geometry unit of Class 7 Chapter contains the following topics.
Introduction to Lines and Angles
Related Angles
Complementary Angles
Supplementary Angles
Adjacent Angles
Linear Pair
Vertically Opposite Angles
Pairs of lines
Intersecting Lines
Transversal
Angles made by a Transversal
Transversal of Parallel Lines
Checking of parallel lines
You learn about different terms like a line segment, collinear points, non-collinear points and many more. This chapter covers the basics of geometry that helps you in higher classes.
Download Solutions of NCERT Exemplar Class 7 Maths
Download solutions of NCERT exemplar class 7 Lines and Angles to match your answers and correct all your mistakes to score excellent marks in your maths exam. These solutions are from Vedantu, and you need to sign up with an email id or mobile number to download them.
NCERT doesn’t provide solutions to the exemplar problems, the best maths faculties working with Vedantu created these answers to help students to make their concept more clear. Students can download solutions of textbook exercise and other subjects exemplar from the Vedantu or our mobile app available on the google play store.
FAQs on NCERT Exemplar for Class 7 Maths Solutions Chapter 5 Lines & Angles
1. How to find the best study material for class 7 maths?
Vedantu provides the best study material for class 7 maths to make your exam preparation easy and fun. Solutions of NCERT exemplar and textbooks are made available by the best maths teachers. You can join our online class for maths to learn from them and clear your doubts in a face to face interaction. Class 7 maths covers crucial topics, for instance, lines and angles, that help you in the long term for solving geometry problems.
2. What are the types of angles covered in Chapter 5 Class 7 Maths?
Angle forms between the two rays originated from the common point called the vertex. In the Lines and Angles chapter, you will learn different types of angles, for example, complementary angles, supplementary angles, adjacent angles. When two angles together make a sum of 90 degrees, they are called complementary angles. When the two angles sum 180 degrees, they are called supplementary angles. Adjacent angles are those that have a common vertex or arms. When two lines intersect at a common point, it forms vertical opposite angles.
3. Is it relevant to read lines and angles from NCERT?
Yes, it is. The lines and angles chapter helps you understand geometry in the higher classes, and its relevance occurs in learning different shapes and planes. Class 7 NCERT textbook provides a detailed explanation of each topic and gives you a space to test your learning with exercise questions and exemplar problems. Vedantu brings you answers to these questions. Every chapter has relevance when it comes to maths. You always learn new expressions or formulas from them.
4. How many questions are there in NCERT Exemplar Class 7 Chapter Lines and Angles?
NCERT Exemplar Class 7 chapter lines and angles have plenty of questions to test your learning. It contains 40 Multiple Choice Questions (MCQs), thorough knowledge of all the concepts is needed to answer them. There are 17 questions on fill in the blanks type and 13 true or false. The remaining ones cover numerical in total this chapter comprises 100 questions, and to solve them, you need your concepts clear.
5. What are the key reasons to choose Vedantu online tuition for maths class 7?
Vedantu brings you a lot of facilities after joining our online tuition class. The first thing that makes us different from others is, we give you excellent teachers and their guidance at a minimal cost, and you can access all the premium resources from your device at any time from anywhere. Maths plays a crucial role in your education, and to advance it, Vedantu helps you with animated and practical examples. We provide solutions of NCERT textbook and exemplar under CBSE guidelines.























