NCERT Exemplar for Class 7 Maths Solutions Chapter 4 Simple Equations

Solved Examples

In examples $1$ to $3$, there are four options, out of which one is correct. Choose the correct one.

Example 1: The solution of the equation \[3x + 5 = 0\] is

a) $\dfrac{5}{3}$ 

b) $ - 5$ 

c) $ - \dfrac{5}{3}$ 

d) $5$ 

Ans: The correct answer is option (c) $ - \dfrac{5}{3}$

Given equation, \[3x + 5 = 0\]

$ \Rightarrow 3x =  - 5$ 

Divide the equation by $3$ 

$ \Rightarrow \dfrac{{3x}}{3} =  - \dfrac{5}{3}$

$ \Rightarrow x =  - \dfrac{5}{3}$

Example 2: $ - 1$ is not a solution of the equation

a) $x + 1 = 0$ 

b) $x - 1 = 2$ 

c) $2y + 3 = 1$ 

d) $2p + 7 = 5$ 

Ans: The correct answer is option (b) $x - 1 = 2$

a) $x + 1 = 0$ 

Transpose $1$ to the RHS

$ \Rightarrow x =  - 1$

Hence, $ - 1$ is solution of equation $x + 1 = 0$

b) $x - 1 = 2$ 

Transpose $ - 1$ to the RHS

$ \Rightarrow x = 2 + 1$

$ \Rightarrow x = 3$

Hence, $ - 1$ is not a solution of equation $x - 1 = 2$

c) $2y + 3 = 1$ 

Transpose $3$ to the RHS

$ \Rightarrow 2y = 1 - 3$

$ \Rightarrow 2y =  - 2$

Divide the equation by $2$ 

$ \Rightarrow \dfrac{{2y}}{2} =  - \dfrac{2}{2}$

$ \Rightarrow y =  - 1$

Hence, $ - 1$ is solution of equation $2y + 3 = 1$

d) $2p + 7 = 5$ 

Transpose $7$ to the RHS

$ \Rightarrow 2p = 5 - 7$

$ \Rightarrow 2p =  - 2$

Divide the equation by $2$ 

$ \Rightarrow \dfrac{{2p}}{2} =  - \dfrac{2}{2}$

$ \Rightarrow p =  - 1$

Hence, $ - 1$ is solution of equation $2p + 7 = 5$

Example 3: Which of the following equations can be formed using the expression $x = 5$

a) $2x + 3 = 13$ 

b) $3x + 2 = 13$ 

c) $x - 5 = 1$ 

d) $4x - 9 = 21$ 

Ans: The correct is option (a) $2x + 3 = 13$ 

Given that, $x = 5$

Multiply both sides by $2$ 

$ \Rightarrow 2 \times x = 2 \times 5$

$ \Rightarrow 2x = 10$

Add $3$ to both the sides,

$ \Rightarrow 2x + 3 = 10 + 3$

$ \Rightarrow 2x + 3 = 13$

In examples $4$ to $6$, fill in the blanks to make it a true statement.

Example 4: Any value of the variable which makes both sides of an equation equal, is known as a _____ of the equation.

Ans: Solution

Example 5: The root of the equation $y - 13 = 9$ is _____.

Ans: $22$ 

Given equation, $y - 13 = 9$

Transpose $ - 13$ to the RHS

$ \Rightarrow y = 9 + 13$ 

$ \Rightarrow y = 22$

Example 6: $2x + $ ____ $ = 11$ has the solution $ - 4$.

Ans: $19$ 

Let the filler be $y$ 

We are given that the equation has solution $ - 4$, it means $x =  - 4$ 

$ \Rightarrow 2\left( { - 4} \right) + y = 11$ 

$ \Rightarrow  - 8 + y = 11$

Transpose $ - 8$ to the RHS

$ \Rightarrow y = 11 + 8$ 

$ \Rightarrow y = 19$

In examples $7$ to $10$, state whether the statements are True or False.

Example 7: $12$ is a solution of the equation $4x - 5 = 3x + 10$.

Ans: False

Given equation, $4x - 5 = 3x + 10$

$ \Rightarrow 4x - 3x = 10 + 5$

$ \Rightarrow x = 15$

Hence, the given statement is false.

Example 8: A number $x$ divided by $7$ gives $2$ can be written as $\dfrac{{x + 1}}{7} = 2$.

Ans: False

Given number = $x$ 

On dividing it by $7$, it becomes $\dfrac{x}{7}$ 

According to question,

$ \Rightarrow \dfrac{x}{7} = 2$ 

Hence, the given statement is false.

Example 9: $x + 2 = 5$ and $3x - 1 = 8$ have the same solutions.

Ans: True

Let us first the solution of $x + 2 = 5$

Transpose $2$ to the RHS

$ \Rightarrow x = 5 - 2$

$ \Rightarrow x = 3$

Now we will find the solution of $3x - 1 = 8$

Transpose $ - 1$ to the RHS

$ \Rightarrow 3x = 8 + 1$

$ \Rightarrow 3x = 9$

$ \Rightarrow x = 3$

Hence, the given statement is true.

Example 10: The equation $3x + 7 = 10$ has $1$ as its solution.

Ans: True

Given equation, $3x + 7 = 10$

Transpose $7$ to the RHS

$ \Rightarrow 3x = 10 - 7$

$ \Rightarrow 3x = 3$

$ \Rightarrow x = 1$

In each of the examples $11$ to $13$, form an equation for each statement.

Example 11: One fourth of a number is $20$ less than the number itself.

Ans: Let $x$ be the number.

Thus, one fourth of the number = $\dfrac{x}{4}$ 

Given that, $\dfrac{x}{4}$ is $20$ less than the number itself. 

Therefore, the required equation is $\dfrac{x}{4} = x - 20$.

Example 12: On subtracting $13$ from $3$ times of a number, the result is $8$.

Ans: Let $x$ be the number.

Thus, three time of the number = $3x$ 

On subtracting $13$, it becomes $3x - 13$ 

Therefore, the required equation is $3x - 13 = 8$.

Example 13: Two times a number increased by $5$ equals $9$.

Ans: Let $x$ be the number.

Thus, two times the number $x$ = $2x$ 

When increased by $5$, it becomes $2x + 5$

Therefore, the required equation is $2x + 5 = 9$.

Example 14: $9$ added to twice a number gives $13$. Find the number.

Ans: Let $x$ be the number.

So, twice the number = $2x$

When $9$ is added, it becomes $2x + 9$

According to the question,

$ \Rightarrow 2x + 9 = 13$ 

Transpose $9$ to the RHS

$ \Rightarrow 2x = 13 - 9$

$ \Rightarrow 2x = 4$

Divide the equation by $2$ 

$ \Rightarrow x = 2$

Therefore, the required number is $2$.

Example 15: $1$ subtracted from one third of a number gives $1$. Find the number.

Ans: Let $x$ be the number.

So, one third of the number = $\dfrac{x}{3}$ 

According to the question,

$ \Rightarrow \dfrac{x}{3} - 1 = 1$ 

Transpose $ - 1$ to the RHS

$ \Rightarrow \dfrac{x}{3} = 1 + 1$

$ \Rightarrow \dfrac{x}{3} = 2$

On cross multiplication, we get

$ \Rightarrow x = 6$

Therefore, the required number is $6$.

Example 16: Correct the incorrect equation written in Roman numerals by moving only one tooth pick.

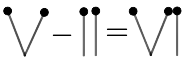
Ans: By moving one vertical tooth pick from the left hand side, change the minus sign to plus. Hence, we get 

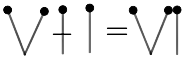
Example 17: Solve the riddle “What is too much fun for one, enough for two, and means nothing to three?” The answer to this is hidden in the equations given below.

a) If $4c = 16$, then $c = $ ?

b) If $2r - 3 = 7$, then $r = $ ?

c) If $2s + 4 = 4s$, then $s = $ ?

d) If $4e + 8 = 20$, then $e = $ ?

e) If $3t + 8 = 29$, then $t = $ ?

To get the answer substitute the numbers for the letters it equals in the following manner: $\dfrac{{}}{2},\dfrac{{}}{3},\dfrac{{}}{4},\dfrac{{}}{5},\dfrac{e}{{}},\dfrac{{}}{7}$ 

Ans:

a) If $4c = 16$, then $c = $ ?

Divide both the sides by $4$ 

$ \Rightarrow c = 4$

b) If $2r - 3 = 7$, then $r = $ ?

We have, $2r - 3 = 7$

Transpose $ - 3$ to the RHS

$ \Rightarrow 2r = 7 + 3$

$ \Rightarrow 2r = 10$

Divide both the sides by $2$ 

$ \Rightarrow r = 5$

c) If $2s + 4 = 4s$, then $s = $ ?

We have, $2s + 4 = 4s$

Transpose $2s$ to the RHS

$ \Rightarrow 4 = 4s - 2s$

$ \Rightarrow 4 = 2s$

$ \Leftrightarrow 2s = 4$

Divide both the sides by $2$ 

$ \Rightarrow s = 2$

d) If $4e + 8 = 20$, then $e = $ ?

We have, $4e + 8 = 20$

Transpose $8$ to the RHS

$ \Rightarrow 4e = 20 - 8$

$ \Rightarrow 4e = 12$

Divide both the sides by $4$ 

$ \Rightarrow e = 3$

e) If $3t + 8 = 29$, then $t = $ ?

We have, $3t + 8 = 29$

Transpose $8$ to the RHS

$ \Rightarrow 3t = 29 - 8$

$ \Rightarrow 3t = 21$

Divide both the sides by $3$ 

$ \Rightarrow t = 7$

On replacing the solutions by corresponding letters we get,

$ \Rightarrow \dfrac{s}{2},\dfrac{e}{3},\dfrac{c}{4},\dfrac{r}{5},\dfrac{e}{3},\dfrac{t}{7}$

Example 18: Solve the following equation: $10 = 4 + 3\left( {t + 2} \right)$ 

Ans: Given equation, $10 = 4 + 3\left( {t + 2} \right)$

On opening the brackets, we get

$ \Rightarrow 10 = 4 + 3t + 6$

$ \Rightarrow 10 = 3t + 10$

Transpose $10$ to the RHS

$ \Rightarrow 10 - 10 = 3t$

$ \Rightarrow 0 = 3t$

$ \Leftrightarrow 3t = 0$

Divide the equation by $3$ 

$ \Rightarrow t = 0$

Exercise

In the Questions $1$ to $18$, there are four options out of which, one is correct. Choose the correct one. 

1. The solution of the equation $ax + b = 0$ is

a) $\dfrac{a}{b}$ 

b) $ - b$

c) $ - \dfrac{b}{a}$

d) $\dfrac{b}{a}$ 

Ans: The correct answer is option (c) $ - \dfrac{b}{a}$

Given equation, $ax + b = 0$

$ \Rightarrow ax =  - b$

Divide both sides by $a$

$ \Rightarrow x =  - \dfrac{b}{a}$

2. If $a$ and $b$ are positive integers, then the solution of the equation $ax = b$ will always be a

a) Positive number 

b) Negative number 

c) $1$

d) $0$ 

Ans: The correct answer is option (a) positive number.

We know that numbers greater than zero are positive integers. So, let $a = 3$ and $b = 5$.

Now, we will substitute these values in the given equation, $ax = b$

$ \Rightarrow 3 \times x = 5$

$ \Rightarrow \dfrac{{3x}}{3} = \dfrac{5}{3}$

$ \Rightarrow x = \dfrac{5}{3}$

Hence, the solution of the equation $ax = b$ will always be a positive number.

3. Which of the following is not allowed in a given equation? 

a) Adding the same number to both sides of the equation. 

b) Subtracting the same number from both sides of the equation. 

c) Multiplying both sides of the equation by the same non-zero number.  

d) Dividing both sides of the equation by the same number. 

Ans: The correct answer is option (d) dividing both sides of the equation by the same number.

Dividing both sides of the equation by a non-zero number is allowed.

4. The solution of which of the following equations is neither a fraction nor an integer? 

a) $2x + 6 = 0$ 

b) $3x - 5 = 0$ 

c) $5x - 8 = x + 4$ 

d) $4x + 7 = x + 2$ 

Ans: The correct answer is option (d) $4x + 7 = x + 2$

a) $2x + 6 = 0$ 

Transpose $6$ to the RHS.

$ \Rightarrow 2x =  - 6$

$ \Rightarrow x =  - 3$

$ - 3$ is an integer.

b) $3x - 5 = 0$ 

Transpose $ - 5$ to the RHS.

$ \Rightarrow 3x = 5$$ \Rightarrow x = \dfrac{5}{3}$

$\dfrac{5}{3}$ is a fraction.

c) $5x - 8 = x + 4$ 

Transpose $ - 8$ to the RHS and $x$ to the LHS

$ \Rightarrow 5x - x = 4 + 8$

$ \Rightarrow 4x = 12$

$ \Rightarrow x = 3$

$3$ is an integer.

d) $4x + 7 = x + 2$ 

Transpose $7$ to the RHS and $x$ to the LHS

\[ \Rightarrow 4x - x = 2 - 7\]

$ \Rightarrow 3x =  - 5$

$ \Rightarrow x =  - \dfrac{5}{3}$

$ - \dfrac{5}{3} $ is neither a fraction nor an integer.

5. The equation which cannot be solved in integers is 

a) $5y - 3 =  - 18$ 

b) $3x - 9 = 0$ 

c) $3z + 8 = 3 + z$ 

d) $9y + 8 = 4y - 7$ 

Ans: The correct answer is option (c) $3z + 8 = 3 + z$

a) $5y - 3 =  - 18$ 

Transpose $ - 3$ to the RHS.

\[ \Rightarrow 5y =  - 18 + 3\]

\[ \Rightarrow 5y =  - 15\]

$ \Rightarrow x =  - 3$

$ - 3$ is an integer.

b) $3x - 9 = 0$ 

Transpose $ - 9$ to the RHS.

\[ \Rightarrow 3x = 9\]

$ \Rightarrow x = 3$

$3$ is an integer.

c) $3z + 8 = 3 + z$ 

Transpose $8$ to the RHS and $z$ to the LHS

$ \Rightarrow 3z - z = 3 - 8$

$ \Rightarrow 2z =  - 5$

$ \Rightarrow z =  - \dfrac{5}{2}$

$ - \dfrac{5}{2}$ is not an integer.

d) $9y + 8 = 4y - 7$ 

Transpose $8$ to the RHS and $4y$ to the LHS

\[ \Rightarrow 9y - 4y =  - 7 - 8\]

$ \Rightarrow 5y =  - 15$

$ \Rightarrow y =  - \dfrac{{15}}{5}$

$ - 3$ is an integer.

6. If $7x + 4 = 25$, then $x$ is equal to 

a) $\dfrac{{29}}{7}$ 

b) $\dfrac{{100}}{7}$ 

c) $2$ 

d) $3$ 

Ans: The correct answer is option (d) $3$

Given equation, $7x + 4 = 25$

Transpose $4$ to the RHS.

\[ \Rightarrow 7x = 25 - 4\]

\[ \Rightarrow 7x = 21\]

$ \Rightarrow x = 3$

Hence the value of $x$ is $3$.

7. The solution of the equation $3x + 7 =  - 20$ is

a) $\dfrac{{17}}{7}$ 

b) $ - 9$ 

c) $9$ 

d) $\dfrac{{13}}{3}$ 

Ans: The correct answer is option (b) $ - 9$

Given equation, $3x + 7 =  - 20$

Transpose $7$ to the RHS.

\[ \Rightarrow 3x =  - 20 - 7\]

\[ \Rightarrow 3x =  - 27\]

$ \Rightarrow x =  - 9$

Therefore the solution of $3x + 7 =  - 20$ is $ - 9$.

8. The value of $y$ for which the expressions $\left( {y - 15} \right)$ and $\left( {2y + 1} \right)$ become equal is 

a) $0$ 

b) $16$ 

c) $8$ 

d) $ - 16$ 

Ans: The correct answer is option (d) $ - 16$

To find the value of $y$ for which the expressions are equal, we will equate both expressions.

$ \Rightarrow y - 15 = 2y + 1$ 

Transpose $ - 15$ to the RHS and $2y$ to the LHS.

\[ \Rightarrow y - 2y = 1 + 15\]

\[ \Rightarrow  - y = 16\]

$ \Rightarrow y =  - 16$

9. If $k + 7 = 16$, then the value of $8k - 72$ is

a) $0$ 

b) $1$ 

c) $112$ 

d) $56$

Ans: The correct answer is option (a) $0$

Given equation, $k + 7 = 16$

Transpose $7$ to the RHS.

\[ \Rightarrow k = 16 - 7\]

\[ \Rightarrow k = 9\]

Now, we will substitute the value of $k$ in $8k - 72$.

$ \Rightarrow 8 \times 9 - 72$

$ \Rightarrow 72 - 72 = 0$

10. If $43m = 0.086$, then the value of $m$ is

a) $0.002$ 

b) $0.02$ 

c) $0.2$ 

d) $2$

Ans: The correct answer is option (a) $0.002$

Given equation, $43m = 0.086$

Divide the equation by $43$.

\[ \Rightarrow \dfrac{{43m}}{{43}} = \dfrac{{0.086}}{{43}}\]

On division, we get

$ \Rightarrow m = 0.002$

11. $x$ exceeds $3$ by $7$, can be represented as

a) $x + 3 = 2$ 

b) $x + 7 = 3$ 

c) $x - 3 = 7$ 

d) $x - 7 = 3$

Ans: The correct answer is option (c) $x - 3 = 7$

Exceeds means greater.

Since, $x$ is greater than $3$ by $7$. So, we can say that if we subtract $3$ from $x$, we would get $7$.

Therefore, the required answer is $x - 3 = 7$.

12. The equation having $5$ as a solution is:

a) $4x + 1 = 2$ 

b) $3 - x = 8$ 

c) $x - 5 = 3$ 

d) $3 + x = 8$

Ans: The correct answer is option (d) $3 + x = 8$

a) $4x + 1 = 2$ 

Transpose $1$ to the RHS.

\[ \Rightarrow 4x = 2 - 1\]

\[ \Rightarrow 4x = 1\]

Divide the equation by $4$.

$ \Rightarrow x = \dfrac{1}{4}$

b) $3 - x = 8$ 

Transpose $3$ to the RHS.

\[ \Rightarrow  - x = 8 - 3\]

\[ \Rightarrow  - x = 5\]

Divide the equation by $ - 1$.

$ \Rightarrow x =  - 5$

c) $x - 5 = 3$ 

Transpose $ - 5$ to the RHS.

\[ \Rightarrow x = 3 + 5\]

\[ \Rightarrow x = 8\]

d) $3 + x = 8$

Transpose $3$ to the RHS.

\[ \Rightarrow x = 8 - 3\]

\[ \Rightarrow x = 5\]

Hence, equation $3 + x = 8$ has the answer $5$.

13. The equation having $ - 3$ as a solution is: 

a) $x + 3 = 1$ 

b) $8 + 2x = 3$ 

c) $10 + 3x = 1$ 

d) $2x + 1 = 3$ 

Ans: The correct answer is option (c) $10 + 3x = 1$

a) $x + 3 = 1$

Transpose $3$ to the RHS.

\[ \Rightarrow x = 1 - 3\]

\[ \Rightarrow x =  - 2\]

b) $8 + 2x = 3$ 

Transpose $8$ to the RHS.

\[ \Rightarrow 2x = 3 - 8\]

\[ \Rightarrow 2x =  - 5\]

Divide the equation by $2$.

$ \Rightarrow x =  - \dfrac{5}{2}$

c) $10 + 3x = 1$ 

Transpose $10$ to the RHS.

\[ \Rightarrow 3x = 1 - 10\]

\[ \Rightarrow 3x =  - 9\]

Divide the equation by $3$.

$ \Rightarrow x =  - 3$

d) $2x + 1 = 3$ 

Transpose $1$ to the RHS.

\[ \Rightarrow 2x = 3 - 1\]

\[ \Rightarrow 2x = 2\]

Divide the equation by $2$.

$ \Rightarrow x = 1$

Hence, equation $10 + 3x = 1$ has the solution $ - 3$.

14. Which of the following equations can be formed starting with $x = 0$ ?

a) $2x + 1 =  - 1$ 

b) $\dfrac{x}{2} + 5 = 7$ 

c) $3x - 1 =  - 1$ 

d) $3x - 1 = 1$ 

Ans: The correct answer is option (c) $3x - 1 =  - 1$

a) $2x + 1 =  - 1$ 

Transpose $ - 1$ to the RHS.

\[ \Rightarrow 2x =  - 1 - 1\]

\[ \Rightarrow 2x =  - 2\]

Divide the equation by $2$.

$ \Rightarrow x =  - 1$

Thus, our solution is $ - 1$. So, we can’t form the equation $2x + 1 =  - 1$ starting with $x = 0$.

b) $\dfrac{x}{2} + 5 = 7$ 

Transpose $5$ to the RHS.

\[ \Rightarrow \dfrac{x}{2} = 7 - 5\]

\[ \Rightarrow \dfrac{x}{2} = 2\]

On cross multiplication, we get

$ \Rightarrow x = 4$

Thus, our solution is $4$. So, we can’t form the equation $\dfrac{x}{2} + 5 = 7$ starting with $x = 0$.

c) $3x - 1 =  - 1$ 

Transpose $ - 1$ to the RHS.

\[ \Rightarrow 3x =  - 1 + 1\]

\[ \Rightarrow 3x = 0\]

Divide the equation by $3$.

$ \Rightarrow x = \dfrac{0}{3}$

$ \Rightarrow x = 0$

Thus, our solution is $0$. So, we can form the equation $3x - 1 =  - 1$ starting with $x = 0$.

d) $3x - 1 = 1$ 

Transpose $ - 1$ to the RHS.

\[ \Rightarrow 3x = 1 + 1\]

\[ \Rightarrow 3x = 2\]

Divide the equation by $3$.

$ \Rightarrow x = \dfrac{2}{3}$

Thus, our solution is $\dfrac{2}{3}$. So, we can’t form the equation $3x - 1 = 1$ starting with $x = 0$.

Hence, the correct answer is $3x - 1 =  - 1$.

15. Which of the following equations cannot be formed using the equation $x = 7$ ?

a) $2x + 1 = 15$ 

b) $7x - 1 = 50$ 

c) $x - 3 = 4$ 

d) $\dfrac{x}{7} - 1 = 0$ 

Ans: The correct answer is option (b) $7x - 1 = 50$

a) $2x + 1 = 15$ 

Transpose $1$ to the RHS.

\[ \Rightarrow 2x = 15 - 1\]

\[ \Rightarrow 2x = 14\]

Divide the equation by $2$.

$ \Rightarrow x = 7$

This equation can be formed.

b) $7x - 1 = 50$ 

Transpose $ - 1$ to the RHS.

\[ \Rightarrow 7x = 50 + 1\]

\[ \Rightarrow 7x = 51\]

Divide the equation by $7$.

$ \Rightarrow x = \dfrac{{51}}{7}$

This equation can’t be formed.

c) $x - 3 = 4$ 

Transpose $ - 3$ to the RHS.

\[ \Rightarrow x = 4 + 3\]

\[ \Rightarrow x = 7\]

This equation can be formed.

d) $\dfrac{x}{7} - 1 = 0$ 

Transpose $1$ to the RHS.

\[ \Rightarrow \dfrac{x}{7} = 1\]

On cross multiplication, we get

\[ \Rightarrow x = 7\]

This equation can be formed.

16. If $\dfrac{x}{2} = 3$, then the value of $3x + 2$ is

a) $20$ 

b) $11$ 

c) $\dfrac{{13}}{2}$ 

d) $8$ 

Ans: The correct answer is option (a) $20$

Given that, $\dfrac{x}{2} = 3$

On cross multiplication, we get

$ \Rightarrow x = 3 \times 2$

$ \Rightarrow x = 6$

Now, we will substitute the value of $x$ in $3x + 2$

$ \Rightarrow 3 \times 6 + 2$ 

$ \Rightarrow 18 + 2$

$ \Rightarrow 20$

17. Which of the following numbers satisfy the equation $ - 6 + x =  - 12$ ?

a) $2$ 

b) $6$ 

c) $ - 6$ 

d) $ - 2$ 

Ans: The correct answer is option (c) $ - 6$

Given that, $ - 6 + x =  - 12$

Transpose $ - 6$ to the RHS.

\[ \Rightarrow x =  - 12 + 6\]

\[ \Rightarrow x =  - 6\]

18. Shifting one term from one side of an equation to another side with a change of sign is known as 

a) Commutativity 

b) Transposition 

c) Distributivity 

d) Associativity  

Ans: The correct answer is option (b) Transposition.

In Questions $19$ to $48$, fill in the blanks to make the statements true. 

19. The sum of two numbers is $60$ and their difference is $30$.

a) If smaller number is $x$, the other number is _____.(use sum) 

Ans: Let $x$ be the smaller number. Hence, the other number would be $60 - x$.

b) The difference of numbers in terms of $x$ is _____. 

Ans: The difference of two numbers is $ 60 - x - x$

$ \Rightarrow 60 - 2x$

c) The equation formed is _____. 

Ans: According to question,

The difference of two numbers is $30$

$ \Rightarrow 60 - x - x = 30$

$ \Rightarrow 60 - 2x = 30$

Transpose $60$ to the RHS

$ \Rightarrow  - 2x = 30 - 60$

$ \Rightarrow  2x - 30 = 0$

d) The solution of the equation is _____. 

Ans: Obtained equation is $ \Rightarrow  2x - 30 = 0$

$ \Rightarrow  - 2x = - 30$

Divide the equation by $ - 2$

$ \Rightarrow x = 15$

e) The numbers are _____ and _____. 

Ans: The other number is $60 - x$.

$ \Rightarrow 60 - 15 = 45$

So the numbers are $15$ and $45$.

20. Sum of two numbers is $81$. One is twice the other.

a) If the smaller number is $x$, the other number is ____.

Ans: Let the smaller number be $x$ 

Hence, the other number = $81 - x$ or $2x$ 

b) The equation formed is ____.

Ans: According to the question,

$ \Rightarrow x + 2x = 81$ 

$ \Rightarrow 3x = 81$

c) The solution of the equation is ____.

Ans: Obtained equation $ \Rightarrow 3x = 81$

Divide the equation by $3$.

$ \Rightarrow \dfrac{{3x}}{3} = \dfrac{{81}}{3}$

$ \Rightarrow x = 27$

d) The numbers are ____ and ____.

Ans: Smaller number = $27$ 

Thus, other number = $2x$ 

$ \Rightarrow 2 \times 27 = 54$

21. In a test Abha gets twice the marks as that of Palak. Two times Abha’s marks and three times Palak’s marks make $280$.

a) If palak gets $x$ marks, Abha gets ____ marks.

Ans: Let the marks obtained by Palak be $x$ 

Thus, Abha gets $2x$ marks

b) The equation formed is____.

Ans: According to the question,

$ \Rightarrow 4x + 3x = 280$ 

$ \Rightarrow 7x = 280$

c) The solution of the equation is ____.

Ans: Obtained equation $ \Rightarrow 7x = 280$

Divide the equation by $7$ 

$ \Rightarrow \dfrac{7}{7}x = \dfrac{{280}}{7}$

$ \Rightarrow x = 40$

d) Marks obtained by Abha are____.

Ans: Marks obtained by Palak = $40$ 

Therefore, marks obtained by Abha = $2x$ 

$ \Rightarrow 2 \times 40 = 80$ 

22. The length of a rectangle is two times its breadth. Its perimeter is $60cm$.

a) If the breadth of the rectangle is $x{\text{ c}}m$, the length of the rectangle is ____.

Ans: Let the breadth of rectangle be $x$ 

Thus, the length of the rectangle becomes $2x$.

b) Perimeter in terms of $x$ is ____.

Ans: Therefore, perimeter = $2\left( {2x + x} \right) = 6x$ 

c) The equation formed is ____.

Ans: According to the question,

$ \Rightarrow 6x = 60$ 

d) The solution of the equation is ____.

Ans: Obtained equation $ \Rightarrow 6x = 60$ 

Divide the equation by $6$.

$ \Rightarrow x = 10$

23. In a bag there are $5$ and $2$ rupee coins. If they are equal in number and their worth is Rs. $70$, then

a) The worth of $x$ coins of Rs. $5$ each ____.

Ans: There are $x$ coins of Rs. $5$ then worth is $5x$.

b) The worth of $x$ coins of Rs. $2$ each ____.

Ans: There are $x$ coins of Rs. $2$ then worth is $2x$.

c) The equation formed is ____.

Ans: Let the number of two rupees coins be $x$ 

As two rupee and five rupee coins are in equal numbers. Therefore, five rupees are also $x$.

According to the question,

$ \Rightarrow 2x + 5x = 70$ 

$ \Rightarrow 7x = 70$

d) There are ____ $5$ rupee coins and ____ $2$ rupee coins.

Ans: Obtained equation $ \Rightarrow 7x = 70$

Divide the equation by $7$ 

$ \Rightarrow x = 10$

So, there are $10$, $5$ rupee coins and $10$, $2$ rupee coins.

24. In a Mathematics quiz, $30$ prizes consisting of $1st$ and $2nd$ prizes only are to be given. $1st$ and $2nd$ prizes are worth Rs. $2000$ and Rs. $1000$, respectively. If the total prize money is Rs. $52,000$ then show that:

a) If $1st$ prizes are $x$ in number the number of $2nd$ prizes are ____.

Ans: Let the number of $1st$ prizes be $x$ 

Thus, the number of $2nd$ prizes are $30 - x$ 

b) The total value of prizes in terms of $x$ are ____.

Ans: $2000x + 1000\left( {30 - x} \right)$ 

c) The equation formed is ____.

Ans:According to the question,

$ \Rightarrow 2000x + 1000\left( {30 - x} \right) = 52000$ 

On multiplication, we get

$ \Rightarrow 2000x + 30000 - 1000x = 52000$

d) The solution of the equation is ____.

Ans: Obtained equation $ \Rightarrow 2000x + 30000 - 1000x = 52000$

Transpose $30000$ to the RHS

$ \Rightarrow 2000x - 1000x = 52000 - 30000$

$ \Rightarrow 1000x = 22000$

Divide by equation by $1000$ 

$ \Rightarrow \dfrac{{1000}}{{1000}}x = \dfrac{{22000}}{{1000}}$

$ \Rightarrow x = 22$

e) The number of $1st$ prizes are ____ and the number of $2nd$ prizes are ____.

Ans: Number of first prizes are 22.

Now, we will find the number of second prizes = $30 - x$ 

$ \Rightarrow 30 - 22$

$ \Rightarrow 8$

25. If $z + 3 = 5$, then $z$ = _____ .

Ans: Given equation, $z + 3 = 5$

Transpose $3$ to the RHS

$ \Rightarrow z = 5 - 3$

$ \Rightarrow z = 2$

Therefore, the value of $z$ is $2$.

26. ____ is the solution of the equation $3x - 2 = 7$.

Ans: Given equation, $3x - 2 = 7$

Transpose $ - 2$ to the RHS

$ \Rightarrow 3x = 7 + 2$

$ \Rightarrow 3x = 9$

Divide the equation by $3$.

$ \Rightarrow x = 3$

Therefore, the solution of the given equation is $3$.

27. _____ is the solution of $3x + 10 = 7$.

Ans: Given equation, $3x + 10 = 7$

Transpose $10$ to the RHS

$ \Rightarrow 3x = 7 - 10$

$ \Rightarrow 3x =  - 3$

Divide the equation by $3$.

$ \Rightarrow x =  - 1$

Therefore, the solution of the given equation is $ - 1$.

28. If $2x + 3 = 5$, then the value of $3x + 2$ is _____ .

Ans: Given equation, $2x + 3 = 5$

Transpose $3$ to the RHS

$ \Rightarrow 2x = 5 - 3$

$ \Rightarrow 2x = 2$

Divide the equation by $2$.

$ \Rightarrow x = 1$

Now, we will substitute the value of $x$ in $3x + 2$

$ \Rightarrow 3 \times 1 + 2$

$ \Rightarrow 3 + 2 = 5$

Therefore, the value of $3x + 2$ is $5$.

29. In integers, $4x - 1 = 8$ has _____ solution.

Ans: Given equation, $4x - 1 = 8$

Transpose $ - 1$ to the RHS

\[ \Rightarrow 4x = 8 + 1\]

$ \Rightarrow 4x = 9$

Divide the equation by $4$.

$ \Rightarrow x = \dfrac{9}{4}$

Thus, in integer, the given equation has no solution.

30. In natural numbers, $4x + 5 =  - 7$ has ____ solution.

Ans: Given equation, $4x + 5 =  - 7$

Transpose $5$ to the RHS

\[ \Rightarrow 4x =  - 7 - 5\]

$ \Rightarrow 4x =  - 12$

Divide the equation by $4$.

$ \Rightarrow x =  - 3$

$ - 3$ is not a natural number. Thus, the equation has no natural solution.

31. In natural numbers, $x - 5 =  - 5$ has ____ solution.

Ans: Given equation, $x - 5 =  - 5$

Transpose $ - 5$ to the RHS

$ \Rightarrow x =  - 5 + 5$

$ \Rightarrow x = 0$

We know that $0$ is not a natural number. Thus, the given equation has no solution.

32. In whole numbers, $x + 8 = 12 - 4$ has ____ solution.

Ans: Given equation, $x + 8 = 12 - 4$

$ \Rightarrow x + 8 = 8$

Transpose $8$ to the RHS

\[ \Rightarrow x = 8 - 8\]

$ \Rightarrow x = 0$

We know that $0$ is a whole number. Thus, the given equation has one solution which is $0$.

33. If $5$ are added to three times a number, it becomes the same as $7$ are subtracted from four times the same number. This fact can be represented as ____.

Ans: Let the number be $x$.

Three times of number = $3 \times x$ 

$ \Rightarrow 3x$ 

Four times of number = $4 \times x$ 

$ \Rightarrow 4x$ 

According to the question, 

$ \Rightarrow 3x + 5 = 4x - 7$ 

This is our required answer.

34. $x + 7 = 10$ has the solution ____.

Ans: Given equation, $x + 7 = 10$

Transpose $7$ to the RHS.

$ \Rightarrow x = 10 - 7$

$ \Rightarrow x = 3$

35. $x - 0 = $ ____; when $3x = 12$.

Ans: Given equation, $3x = 12$

Divide the equation by $3$.

$ \Rightarrow x = \dfrac{{12}}{3}$

$ \Rightarrow x = 4$

Now, we will substitute the value of $x$ in $x - 0$

$ \Rightarrow 4 - 0 = 4$

Thus, $4$ is the solution.

36. $x - 1 = $ ____; when $2x = 2$ 

Ans: Given that, $2x = 2$

Divide the equation by $2$.

$ \Rightarrow x = 1$

Now, we will substitute the value of $x$ in $x - 1$

$ \Rightarrow 1 - 1 = 0$

Thus, $0$ is the solution.

37. $x - \_\_\_ = 15$; when $\dfrac{x}{2} = 6$.

Ans: Given that, $\dfrac{x}{2} = 6$

On cross multiplication, we get

$ \Rightarrow x = 6 \times 2$

$ \Rightarrow x = 12$

Let the required number = $y$ 

$\therefore 12 - y = 15$ 

Transpose $12$ to the RHS

$ \Rightarrow  - y = 15 - 12$

$ \Rightarrow  - y = 3$

Divide the equation by $ - 1$ 

$ \Rightarrow y =  - 3$ 

38. The solution of the equation $x + 15 = 19$ is ____.

Ans: Given equation, $x + 15 = 19$

Transpose $15$ to the RHS

$ \Rightarrow x = 19 - 15$

$ \Rightarrow x = 4$

Therefore, the solution of the equation $x + 15 = 19$ is $4$.

39. Finding the value of a variable in a linear equation that ____ the equation is called a ____ of the equation.

Ans: Satisfies; root

40. Any term of an equation may be transposed from one side of the equation to the other side of the equation by changing the ____ of the term.

Ans: Sign

41. If $\dfrac{9}{5}x = \dfrac{{18}}{5}$, then $x$ = ____

Ans: Given equation, $\dfrac{9}{5}x = \dfrac{{18}}{5}$

Transpose $\dfrac{9}{5}$ to the RHS

$ \Rightarrow x = \dfrac{{18}}{5} \times \dfrac{5}{9}$

On canceling the common terms, we get

$ \Rightarrow x = 2$

Therefore, the value of $x$ is $2$.

42. If $3 - x =  - 4$ then $x$ = ____.

Ans: Given equation, $3 - x =  - 4$

Transpose $3$ to the RHS

$ \Rightarrow  - x =  - 4 - 3$

$ \Rightarrow  - x =  - 7$

Divide the equation by $ - 1$ 

$ \Rightarrow x = 7$

Therefore, the value of $x$ is $7$.

43. If $x - \dfrac{1}{2} =  - \dfrac{1}{2}$ then $x$ = ____.

Ans: Given equation, $x - \dfrac{1}{2} =  - \dfrac{1}{2}$

Transpose $ - \dfrac{1}{2}$ to the RHS

$ \Rightarrow x =  - \dfrac{1}{2} + \dfrac{1}{2}$

$ \Rightarrow x = 0$

Therefore, the value of $x$ is $0$.

44. If $\dfrac{1}{6} - x = \dfrac{1}{6}$ then $x$ = ____.

Ans: Given equation, $\dfrac{1}{6} - x = \dfrac{1}{6}$

Transpose $\dfrac{1}{6}$ to the RHS

$ \Rightarrow  - x = \dfrac{1}{6} - \dfrac{1}{6}$

$ \Rightarrow  - x = 0$

$ \Rightarrow x = 0$

Therefore, the value of $x$ is $0$.

45. If $10$ less than a number is $65$, then the number is ____.

Ans: Let the number be $x$.

According to the question, we have

$ \Rightarrow x - 10 = 65$ 

Transpose $ - 10$ to the RHS.

$ \Rightarrow x = 65 + 10$

$ \Rightarrow x = 75$

Hence, the number is $75$.

46. If a number is increased by $20$, it becomes $45$. Then the number is ____.

Ans: Let the number be $x$ 

The number is increased by $20$. Therefore, we get

$ \Rightarrow x + 20$ 

According to question, 

$ \Rightarrow x + 20 = 45$

Transpose $20$ to the RHS.

$ \Rightarrow x = 45 - 20$

$ \Rightarrow x = 25$

Hence, the number is $25$.

47. If $84$ exceeds another number by $12$, then the other number is ____.

Ans: Let $x$ be the number.

According to the question,

$ \Rightarrow 84 = x + 12$ 

Transpose $12$ to the LHS.

 $ \Rightarrow 84 - 12 = x$

$ \Rightarrow 72 = x$

Or

$ \Rightarrow x = 72$

Hence, the number is $72$.

48. If $x - \dfrac{7}{8} = \dfrac{7}{8}$ then $x$ = ____.

Ans: Given equation, $x - \dfrac{7}{8} = \dfrac{7}{8}$

Transpose $ - \dfrac{7}{8}$ to the RHS

$ \Rightarrow x = \dfrac{7}{8} + \dfrac{7}{8}$

$ \Rightarrow x = \dfrac{{7 + 7}}{8}$

$ \Rightarrow x = \dfrac{{14}}{8}$

$ \Rightarrow x = \dfrac{7}{4}$

Therefore, the value of $x$ is $\dfrac{7}{4}$.

In Questions $49$ to $55$, state whether the statements are True or False.

49. $5$ is the solution of the equation $3x + 2 = 17$.

Ans: True

Given equation, $3x + 2 = 17$

Transpose $2$ to the RHS

\[ \Rightarrow 3x = 17 - 2\]

$ \Rightarrow 3x = 15$

Divide the equation by $3$.

$ \Rightarrow x = 5$

Therefore, the solution of equation $3x + 2 = 17$ is $5$.

50. $\dfrac{9}{5}$ is the solution of the equation $4x - 1 = 8$.

Ans: False

Given equation, $4x - 1 = 8$

Transpose $ - 1$ to the RHS

\[ \Rightarrow 4x = 8 + 1\]

\[ \Rightarrow 4x = 9\]

Divide the equation by $4$.

$ \Rightarrow x = \dfrac{9}{4}$

Therefore, the solution of equation $3x + 2 = 17$ is $\dfrac{9}{4}$ not $\dfrac{9}{5}$.

51. $4x - 5 = 7$ does not have an integer as its solution.

Ans: False

Given equation, $4x - 5 = 7$

Transpose $ - 5$ to the RHS

\[ \Rightarrow 4x = 7 + 5\]

\[ \Rightarrow 4x = 12\]

Divide the equation by $3$.

$ \Rightarrow x = 3$

The solution of the given equation is $3$ and it is an integer.

52. One third of a number added to itself gives $10$, can be represented as $\dfrac{x}{3} + 10 = x$.

Ans: False

Let the number be $x$.

Therefore, one third of the number = $\dfrac{x}{3}$.

According to the question,

$ \Rightarrow \dfrac{x}{3} + x = 10$ 

Hence, the given representation of the statement is false.

53. $\dfrac{3}{2}$ is the solution of the equation $8x - 5 = 7$.

Ans: True

Given equation, $8x - 5 = 7$

Transpose $ - 5$ to the RHS

\[ \Rightarrow 8x = 7 + 5\]

\[ \Rightarrow 8x = 12\]

Divide the equation by $8$.

$ \Rightarrow x = \dfrac{{12}}{8}$

$ \Rightarrow x = \dfrac{3}{2}$

The solution of the given equation $8x - 5 = 7$ is $\dfrac{3}{2}$.

54. If $4x - 7 = 11$, then $x = 4$.

Ans: False

Given, equation, $4x - 7 = 11$

Transpose $ - 7$ to the RHS

\[ \Rightarrow 4x = 11 + 7\]

\[ \Rightarrow 4x = 18\]

Divide the equation by $4$.

$ \Rightarrow x = \dfrac{{18}}{4}$

$ \Rightarrow x = \dfrac{9}{2}$

The value of $x$ is $\dfrac{9}{2}$ not $4$.

55. If $9$ is the solution of the variable $x$ in the equation $\dfrac{{5x - 7}}{2} = y$, then the value $y$ is $28$.

Ans: False 

Given that, $x = 9$.

Now, we will substitute value of $x$ in equation $\dfrac{{5x - 7}}{2} = y$

$ \Rightarrow \dfrac{{5 \times 9 - 7}}{2} = y$

$ \Rightarrow \dfrac{{45 - 7}}{2} = y$

$ \Rightarrow y = \dfrac{{38}}{2}$

$ \Rightarrow y = 19$

The value of $y$ is $19$ not $28$

56. Match each of the entries in Column I with the appropriate entries in Column II.

Ans: i. $x + 5 = 9$ 

Transpose $5$ to the RHS.

$x = 9 - 5$

$x = 4$

$\therefore \left( i \right) \to (C)$ 

ii. $x - 7 = 4$ 

Transpose $ - 7$ to the RHS.

$x = 4 + 7$

$x = 11$

$\therefore \left( {ii} \right) \to (E)$

iii. $\dfrac{x}{{12}} =  - 5$ 

On cross multiplication, we get

$ \Rightarrow x =  - 5 \times 12$

$ \Rightarrow x =  - 60$

$\therefore \left( {iii} \right) \to (F)$

iv. $5x = 30$ 

Divide the equation by $5$.

$ \Rightarrow x = 6$

$\therefore \left( {iv} \right) \to (D)$

v. The value of $y$ which satisfies $3y = 5$ 

Divide the equation by $3$.

$ \Rightarrow x = \dfrac{5}{3}$

$\therefore \left( v \right) \to (B)$

vi. If $p = 2$, then the value of $\dfrac{1}{3}\left( {1 - 3p} \right)$ 

We will substitute the value of $p$ in equation $\dfrac{1}{3}\left( {1 - 3p} \right)$.

$ \Rightarrow \dfrac{1}{3}\left( {1 - 3 \times 2} \right)$

$ \Rightarrow \dfrac{1}{3}\left( {1 - 6} \right)$

$ \Rightarrow \dfrac{1}{3}\left( { - 5} \right)$

$ \Rightarrow \dfrac{{ - 5}}{3}$

$\therefore \left( {vi} \right) \to (A)$

In Questions $57$ to $67$, express each of the given statements as an equation.

57. $13$ subtracted from twice of a number gives $3$.

Ans: Let the number be $x$.

Two times of the number = $2x$

Then, $13$ is subtracted from it = $2x - 13$ 

The required equation: $2x - 13 = 3$

58. One-fifth of a number is $5$ less than that number.

Ans: Let $y$ be the number.

One-fifth of the number = $\dfrac{y}{5}$ 

The required equation = $\dfrac{y}{5} = y - 5$

59. A number is $7$ more than one-third of itself.

Ans: Let $y$ be the number.

One-third of the number = $\dfrac{y}{3}$ 

As $7$ is more, then we get = $\dfrac{y}{3} + 7$

Therefore, $y = \dfrac{y}{3} + 7$ is the required equation.

60. Six times a number is $10$ more than the number.

Ans: Let $x$ be the number.

Six times of the number = $6x$ 

Therefore, the required equation is $6x = x + 10$.

61. If $10$ is subtracted from half a number, the result is $4$.

Ans: Let the number be $x$ 

Then, half of the number = $\dfrac{x}{2}$

Therefore, the required equation is $\dfrac{x}{2} - 10 = 4$

62. Subtracting $5$ from $p$, the result is $2$.

Ans: Subtract $5$ from $p$ = $p - 5$ 

Therefore, the required equation is $p - 5 = 2$

63. Five times a number increased by $7$ is $27$.

Ans: Let the number be $x$ 

Five-times of the number = $5x$ 

It is increased by $7$. So, we get $5x + 7$ 

Therefore, the required equation is $5x + 7 = 27$

64. Mohan is $3$ years older than Sohan. The sum of their ages is $43$ years.

Ans: Let the age of Sohan be $x$ years.

Therefore, Mohan’s age = $\left( {x + 3} \right)$ years

Sum of Mohan’s and Sohan’s age = $x + \left( {x + 3} \right)$ years

Therefore, the required equation is $x + \left( {x + 3} \right) = 43$

65. If $1$ is subtracted from a number and the difference is multiplied by $\dfrac{1}{2}$, the result is $7$.

Ans: Let $x$ be the number

On subtraction of $1$, we get $x - 1$ 

After multiplication of $\dfrac{1}{2}$, we get $\dfrac{1}{2}\left( {x - 1} \right)$

Therefore, the required equation is $\dfrac{1}{2}\left( {x - 1} \right) = 7$

66. A number divided by $2$ and then increased by $5$ is $9$.

Ans: Let the number be $x$ 

Dividing the number by $2$ = $\dfrac{x}{2}$ 

It has increased by $5$. Therefore, we get

$ \Rightarrow \dfrac{x}{2} + 5$ 

Therefore, the required equation is $\dfrac{x}{2} + 5 = 9$

67. The sum of twice a number and $4$ is $18$.

Ans: Let the number be $x$ 

Twice of the number = $2x$ 

$4$ is added, then the expression becomes = $2x + 4$ 

Therefore, the required equation is $2x + 4 = 18$

68. The age of Sohan Lal is four times that of his son Amit. If the difference of their ages is $27$ years, find the age of Amit.

Ans: Let age of Amit be $x$ years.

Thus, age of Sohan Lal = $4x$ 

According to the question, 

$ \Rightarrow 4x - x = 27$ 

$ \Rightarrow 3x = 27$

Divide the equation by $3$.

$ \Rightarrow x = \dfrac{{27}}{3}$

$ \Rightarrow x = 9$

Thus, Amit's age is $9$ years.

69. A number exceeds the other number by $12$. If their sum is $72$, find the numbers.

Ans: Let the number be $x$ 

Therefore, other number will be $x + 12$ 

According to the question, 

$ \Rightarrow x + x + 12 = 72$ 

$ \Rightarrow 2x + 12 = 72$

Transpose $12$ to the RHS

$ \Rightarrow 2x = 72 - 12$

$ \Rightarrow 2x = 72 - 12$

$ \Rightarrow 2x = 60$

Divide the equation by $2$ 

$ \Rightarrow x = 30$

Other number = $x + 12$. 

$ \Rightarrow 30 + 12$ 

$ \Rightarrow 42$

Hence, the numbers are $30$ and $42$.

70. Seven times a number is $12$ less than thirteen times the same number. Find the number.

Ans: Let the number be $x$ 

Therefore, seven times of the number = $7x$ 

Similarly, thirteen times of the number = $13x$ 

According to question, 

$ \Rightarrow 7x = 13x - 12$ 

Transpose $12$ to the LHS and $7x$ to the RHS

$ \Rightarrow 12 = 13x - 7x$

$ \Rightarrow 12 = 6x$

Divide the equation by $6$.

$ \Rightarrow 2 = x$

Or 

$ \Rightarrow x = 2$

Therefore, $2$ is our required number.

71. The interest received by Karim is Rs. $30$ more than Ramesh. If the total interest received by them is Rs. $70$, find the interest received by Ramesh.

Ans: Let Rs. $x$ be the interest received by Ramesh

Thus, interest received by Karim = Rs. $\left( {30 + x} \right)$ 

According to the question,

$ \Rightarrow x + x + 30 = 70$ 

Transpose $30$ to the RHS

$ \Rightarrow 2x = 70 - 30$

$ \Rightarrow 2x = 40$

Divide the equation by $2$.

$ \Rightarrow x = 20$

Hence, the interest received by Ramesh was of Rs. $20$.

72. Subramaniam and Naidu donate some money in a Relief fund. The amount paid by Naidu is Rs $125$ more than that of Subramaniam. If the total money paid by them is Rs $975$, find the amount of money donated by Subramaniam.

Ans: Let the amount donated by Subramanian be Rs $x$.

Therefore, the amount paid by Naidu = Rs $\left( {x + 125} \right)$ 

According to the question,

$ \Rightarrow x + x + 125 = 975$ 

Transpose $125$ to the RHS

$ \Rightarrow 2x = 975 - 125$

$ \Rightarrow 2x = 850$

Divide equation by $2$.

$ \Rightarrow x = 425$

Therefore, Subramanian donated Rs $425$.

73. In a school, the number of girls is $50$ more than the number of boys. The total number of students is $1070$. Find the number of girls.

Ans: Let the number of girls be $x$ 

Therefore, the number of boys = $x - 50$ 

According to the question,

$ \Rightarrow x + x - 50 = 1070$ 

Transpose $50$ to the RHS

$ \Rightarrow 2x = 1070 + 50$

$ \Rightarrow 2x = 1120$

Divide the equation by $2$ 

$ \Rightarrow x = \dfrac{{1120}}{2}$

$ \Rightarrow x = 560$

Hence, number of girls = $560$

74. Two times a number increased by $5$ equals $9$. Find the number.

Ans: Let the number be $x$ 

Therefore, two times of the number = $2x$ 

After increment of $5$, we get $2x + 5$ 

According to the question,

$ \Rightarrow 2x + 5 = 9$

Transpose $5$ to the RHS

$ \Rightarrow 2x = 9 - 5$

$ \Rightarrow 2x = 4$

Divide the equation by $2$ 

$ \Rightarrow x = 2$

Therefore, $2$ is our required number.

75. $9$ added to twice a number gives $13$. Find the number.

Ans: Let the number be $x$ 

Thus, two times of the number = $2x$ 

On addition of $9$, we get

$ \Rightarrow 2x + 9$ 

According to the question,

$ \Rightarrow 2x + 9 = 13$

Transpose $9$ to the RHS

$ \Rightarrow 2x = 13 - 9$

$ \Rightarrow 2x = 4$

Divide the equation by $2$ 

$ \Rightarrow x = 2$

Therefore, $2$ is our required number.

76. $1$ subtracted from one-third of a number gives $1$. Find the number.

Ans: Let the number be $x$ 

Thus, one-third of the number = $\dfrac{x}{3}$ 

On subtraction of $1$, we get

$ \Rightarrow \dfrac{x}{3} - 1$

According to the question,

$ \Rightarrow \dfrac{x}{3} - 1 = 1$

Transpose $ - 1$ to the RHS

$ \Rightarrow \dfrac{x}{3} = 1 + 1$

$ \Rightarrow \dfrac{x}{3} = 2$

On cross multiplication, we get

$ \Rightarrow x = 2 \times 3$

$ \Rightarrow x = 6$

Therefore, $6$ is our required number.

77. After $25$ years, Rama will be $5$ times as old as he is now. Find his present age.

Ans: Let the present age of Rama be $x$ years.

Thus, five times of his age = $5x$ 

According to the question,

$ \Rightarrow 5x = x + 25$  

Transpose $x$ to the LHS

$ \Rightarrow 5x - x = 25$

$ \Rightarrow 4x = 25$

Divide the equation by $4$ 

$ \Rightarrow x = \dfrac{{25}}{4}$

Now, we will write it in mixed fraction,

$ \Rightarrow x = 6\dfrac{1}{4}$

Therefore, Ram is $6\dfrac{1}{4}$ years old.

78. After $20$ years, Manoj will be $5$ times as old as he is now. Find his present age.

Ans: Let $x$ years be the present age of Manoj

Therefore, five times of his age = $5x$ 

Manoj’s age after $20$ years = $\left( {x + 20} \right)$ years

According to the question,

$ \Rightarrow 5x = x + 20$ 

Transpose $x$ to the LHS

$ \Rightarrow 5x - x = 20$

$ \Rightarrow 4x = 20$

Divide the equation by $4$ 

$ \Rightarrow x = \dfrac{{20}}{4}$

$ \Rightarrow x = 5$

Therefore, the present age of Manoj is $5$ years.

79. My younger sister’s age today is $3$ times, what it will be $3$ years from now minus $3$ times what her age was $3$ years ago. Find her present age.

Ans: Let $x$ years be the present age of my younger sister.

After $3$ years, her age will be $\left( {x + 3} \right)$ years.

Before $3$ years, her age was $\left( {x - 3} \right)$ years.

According to the question,

$ \Rightarrow x = 3\left( {x + 3} \right) - 3\left( {x - 3} \right)$ 

On multiplication, we get

$ \Rightarrow x = 3x + 9 - 3x + 9$

$ \Rightarrow x = 9 + 9$

$ \Rightarrow x = 18$

Therefore, present age of my younger sister = $18$ years

80. If $45$ is added to half a number, the result is triple the number. Find the number.

Ans: Let $x$ be the number.

Therefore, half of the number = $\dfrac{x}{2}$ 

After adding $45$, we get 

$ \Rightarrow \dfrac{x}{2} + 45$

According to the question, 

$ \Rightarrow \dfrac{x}{2} + 45 = 3x$

Transpose $\dfrac{x}{2}$ to the RHS

$ \Rightarrow 45 = 3x - \dfrac{x}{2}$

Take LCM

$ \Rightarrow 45 = \dfrac{{6x - x}}{2}$

\[ \Rightarrow 45 = \dfrac{{5x}}{2}\]

On cross multiplication, we get

\[ \Rightarrow 5x = 45 \times 2\]

\[ \Rightarrow 5x = 90\]

\[ \Rightarrow x = \dfrac{{90}}{5}\]

\[ \Rightarrow x = 18\]

Therefore, the required number is $18$.

81. In a family, the consumption of wheat is $4$ times that of rice. The total consumption of the two cereals is $80kg$. Find the quantities of rice and wheat consumed in the family.

Ans: Let the quantity of the rice consumed be $x$ kg.

Therefore, the consumed quantity of wheat = $4x$ kg.

According to the question,

$ \Rightarrow x + 4x = 80$ 

$ \Rightarrow 5x = 80$

$ \Rightarrow x = \dfrac{{80}}{5}$

$ \Rightarrow x = 16$

Therefore, the quantity of rice consumed by the family = $16kg$

Quantity of wheat consumed = $4x$ 

$ \Rightarrow 4 \times 16$ 

$ \Rightarrow 64kg$

Thus, the quantity of wheat consumed by the family = $64kg$

82. In a bag, the number of one rupee coins is three times the number of two rupees coins. If the worth of the coins is Rs. $120$, find the number of $1$ rupee coins.

Ans: Let the number of two rupee coins be $x$ 

Therefore, the number of one rupee coin be $3x$ 

According to the question,

$ \Rightarrow 1\left( {3x} \right) + 2\left( x \right) = 120$ 

$ \Rightarrow 3x + 2x = 120$

$ \Rightarrow 5x = 120$

Divide the equation by $5$.

$ \Rightarrow x = \dfrac{{120}}{5}$

$ \Rightarrow x = 24$

Therefore, $3 \times 24 = 72$ 

Hence, the number of one rupee coins is $72$.

83. Anamika thought of a number. She multiplied it by $2$, added $5$ to the product and obtained $17$ as the result. What is the number she had thought of?

Ans: Let the number thought by Anamika be $x$ 

On multiplying it by $2$, we get $2x$ 

On addition of $5$, we get $2x + 5$ 

According to the question,

$ \Rightarrow 2x + 5 = 17$

Transpose $5$ to the RHS

$ \Rightarrow 2x = 17 - 5$

$ \Rightarrow 2x = 12$

Divide the equation by $2$ 

$ \Rightarrow x = 6$

Therefore, $6$ is our required number.

84. One of the two numbers is twice the other. The sum of the numbers is $12$. Find the numbers.

Ans: Let the number be $x$ 

Therefore, other number will be $2x$ 

According to the question,

$ \Rightarrow x + 2x = 12$

$ \Rightarrow 3x = 12$

Divide the equation by $3$ 

$ \Rightarrow x = 4$

Therefore, the other number will be $2 \times 4 = 8$ 

Hence, our required numbers are $4$ and $8$.

85. The sum of three consecutive integers is $5$ more than the smallest of the integers. Find the integers.

Ans: Let the smaller number be $x$ 

Therefore, the next two consecutive integers would be $x + 1$ and $x + 2$.

According to the question,

$ \Rightarrow x + x + 1 + x + 2 = x + 5$ 

$ \Rightarrow 3x + 3 = x + 5$

Transpose $3$ to the RHS and $x$ to the LHS.

$ \Rightarrow 3x - x = 5 - 3$

$ \Rightarrow 2x = 2$

Divide the equation by $2$ 

$ \Rightarrow x = 1$

Therefore, the next two consecutive integers would be $2$ and $3$.

Hence, our required integers are $1$, $2$ and $3$.

86. A number when divided by $6$ gives the quotient $6$. What is the number?

Ans: Let the number be $x$ 

When it is divided by $6$ it becomes $\dfrac{x}{6}$ 

According to the question,

$ \Rightarrow \dfrac{x}{6} = 6$ 

On cross multiplication, we get

$ \Rightarrow x = 6 \times 6$ 

$ \Rightarrow x = 36$

Therefore, $36$ is the required number.

87. The perimeter of a rectangle is $40m$. The length of the rectangle is $4m$ less than $5$ times its breadth. Find the length of the rectangle.

Ans: Let $x$ meter be the breadth of the rectangle.

Thus, five times to the breadth = $5x$ 

Therefore, length of the rectangle is $\left( {5x - 4} \right)$ meter

Given, perimeter of the rectangle is $40m$ 

According to the question,

$ \Rightarrow 2\left( {x + 5x - 4} \right) = 40$ 

$ \Rightarrow 2\left( {6x - 4} \right) = 40$

Divide the equation by $2$.

$ \Rightarrow 6x - 4 = 20$

Transpose $ - 4$ to the RHS.

$ \Rightarrow 6x = 20 + 4$

$ \Rightarrow 6x = 24$

Divide the equation by $6$.

$ \Rightarrow x = \dfrac{{24}}{6}$

$ \Rightarrow x = 4$

Now, for length we have

$ \Rightarrow \left( {5x - 4} \right)$

$ \Rightarrow 5 \times 4 - 4$

$ \Rightarrow 20 - 4 = 16m$

Therefore, length of rectangle is $16m$.

88. Each of the $2$ equal sides of an isosceles triangle is twice as large as the third side. If the perimeter of the triangle is $30cm$, find the length of each side of the triangle.

Ans: Let $2x{\text{ cm}}$ be the length of equal sides of an isosceles triangle.

So, length of the third side = $xcm$ 

Given, perimeter of the triangle = $30cm$ 

According to the question,

$ \Rightarrow x + 2x + 2x = 30$ 

$ \Rightarrow 5x = 30$

Divide the equation by $5$.

$ \Rightarrow x = \dfrac{{30}}{5}$

$ \Rightarrow x = 6$

Length of two equal sides = $2 \times 6 = 12cm$ 

Therefore, the sides of an isosceles triangle are $6cm$, $12cm$ and $12cm$.

89. The sum of two consecutive multiplies of $2$ is $18$. Find the numbers.

Ans: Let the first multiple of $2$ is $x$ 

Thus, the next multiple of $2$ would $be$ $x + 2$ 

According to the question,

$ \Rightarrow x + x + 2 = 18$ 

Transpose $2$ to the RHS

$ \Rightarrow 2x = 18 - 2$

$ \Rightarrow 2x = 16$

Divide the equation by $2$ 

$ \Rightarrow x = 8$

Therefore, $8$ and $10$ are our required numbers.

90. Two complementary angles differ by $20^\circ $. Find the angles.

Ans: Let one angle be $x$ 

Therefore, complementary of $x$ = $90^\circ  - x$ 

According to the question,

$ \Rightarrow x - \left( {90^\circ  - x} \right) = 20^\circ $ 

$ \Rightarrow x - 90^\circ  + x = 20^\circ $

Transpose $ - 90^\circ $ to the RHS

$ \Rightarrow 2x = 20^\circ  + 90^\circ $

$ \Rightarrow 2x = 110^\circ $

Divide the equation by $2$ 

$ \Rightarrow x = \dfrac{{110^\circ }}{2}$

$ \Rightarrow x = 55^\circ $

Now, complementary of $x$ 

$ \Rightarrow 90^\circ  - x$

$ \Rightarrow 90^\circ  - 55^\circ $

$ \Rightarrow 35^\circ $

Therefore, complementary angles are $35^\circ $ and $55^\circ $.

91. $150$ have been divided into two parts such that twice the first part is equal to the second part. Find the parts.

Ans: Let the first part be $x$ 

Thus, other part = $150 - x$ 

According to the question,

$ \Rightarrow 2x = 150 - x$ 

Transpose $ - x$ to the LHS

$ \Rightarrow 2x + x = 150$

$ \Rightarrow 3x = 150$

Divide the equation by $3$ 

$ \Rightarrow x = 50$

Now, for other part we have

$ \Rightarrow 150 - x$

$ \Rightarrow 150 - 50$

$ \Rightarrow 100$

Hence, $150$ is divided into $50$ and $100$.

92. In a class of $60$ students, the number of girls is one third the number of boys. Find the number of girls and boys in the class.

Ans: Let the number of boys in the class be $x$ 

Thus, the number of girls is $60 - x$ 

According to the question,

$ \Rightarrow 60 - x = \dfrac{x}{3}$

On cross multiplication, we get

$ \Rightarrow 3\left( {60 - x} \right) = x$

$ \Rightarrow 180 - 3x = x$

Transpose $ - 3x$ to the RHS.

$ \Rightarrow 180 = 4x$

Or 

$ \Rightarrow 4x = 180$

Divide the equation by $4$ 

$ \Rightarrow x = 45$

Therefore, there are $45$ boys in the class.

Hence, the number of girls = $60 - 45$ = $15$ 

93. Two-third of a number is greater than one-third of the number by $3$. Find the number.

Ans: Let the number be $x$

Therefore, two-third of the numbers = $\dfrac{2}{3} \times x$ 

According to the question,

$ \Rightarrow \dfrac{2}{3} \times x = \dfrac{1}{3}x + 3$ 

Transpose $\dfrac{1}{3}x$ to the RHS.

$ \Rightarrow \dfrac{{2x}}{3} - \dfrac{x}{3} = 3$

Take LCM

$ \Rightarrow \dfrac{{2x - x}}{3} = 3$

$ \Rightarrow \dfrac{x}{3} = 3$

On cross multiplication, we get

$ \Rightarrow x = 3 \times 3$

$ \Rightarrow x = 9$

Therefore, $9$ is the required number.

94. A number is as much greater than $27$ as it is less than $73$. Find the number.

Ans: Let the number be $x$ 

According to the question,

$ \Rightarrow x - 27 = 73 - x$ 

Transpose $ - x$ to the LHS and $ - 27$ to the RHS.

$ \Rightarrow x + x = 73 + 27$

$ \Rightarrow 2x = 100$

Divide the equation by $2$ 

$ \Rightarrow x = 50$

Therefore, $50$ is the required number.

95. A man travelled two fifth of his journey by train, one-third by bus, one-fourth by car and the remaining $3km$ on foot. What is the length of his total journey?

Ans: Let the length of the total journey be \[xkm\] 

Distance traveled by train = $\dfrac{2}{5}xkm$ 

Distance traveled by bus = $\dfrac{1}{3}xkm$ 

Distance traveled by car = $\dfrac{1}{4}xkm$ 

Therefore, total journey traveled by train, bus and car = \[\dfrac{2}{5}x{\text{ + }}\dfrac{1}{3}x{\text{ + }}\dfrac{1}{4}x\] 

Take LCM

\[ = \dfrac{{12 \times 2x + 20 \times x + 15 \times x}}{{60}}\]

\[ = \dfrac{{24x + 20x + 15x}}{{60}}\]

\[ = \dfrac{{59x}}{{60}}\]

Thus, remaining journey = $x - \dfrac{{59x}}{{60}}$ 

$ = \dfrac{{60x - 59x}}{{60}}$ 

$ = \dfrac{x}{{60}}$

Given that, the remaining journey is $3km$.

$\therefore \dfrac{x}{{60}} = 3$

On cross multiplication, we get

$ \Rightarrow x = 3 \times 60$

$ \Rightarrow x = 180$

Therefore, the length of the total journey is $180km$.

96. Twice a number added to half of itself equals $24$. Find the number.

Ans: Let the number be $x$ 

Twice of the number = $2x$ 

Thus, half of the number $x$ = $\dfrac{x}{2}$ 

According to the question,

$ \Rightarrow 2x + \dfrac{x}{2} = 24$ 

Take LCM

$ \Rightarrow \dfrac{{4x + x}}{2} = 24$

On cross multiplication, we get

$ \Rightarrow 5x = 24 \times 2$

$ \Rightarrow 5x = 48$

Divide the equation by $5$ 

$ \Rightarrow x = \dfrac{{48}}{5}$

$ \Rightarrow x = 9.6$

Therefore, $9.6$ is the required number.

97. Thrice a number decreased by $5$ exceeds twice the number by $1$. Find the number.

Ans: Let the number be $x$ 

Thus, three times of the number $x$ = $3x$ 

When it is decreased by $5$, it becomes $3x - 5$ 

According to the question,

$ \Rightarrow 3x - 5 = 2x + 1$ 

Transpose $2x$ to the LHS and $ - 5$ to the RHS.

$ \Rightarrow 3x - 2x = 1 + 5$

$ \Rightarrow x = 6$

Therefore, $6$ is the required number.

98. A girl is $28$ years younger than her father. The sum of their ages is $50$ years. Find the ages of the girl and her father.

Ans: Let the age of father be $x$ years.

So, age of girl = $\left( {x - 28} \right)$ years

According to the question,

$ \Rightarrow x + x - 28 = 50$ 

Transpose $ - 28$ to the RHS

$ \Rightarrow 2x = 50 + 28$

$ \Rightarrow 2x = 78$

Divide the equation by $2$ 

$ \Rightarrow x = 39$

Therefore, age of father is $39$ years.

Now, age of girl = $\left( {x - 28} \right)$ years

$ \Rightarrow \left( {39 - 28} \right)$ Years

$ \Rightarrow 11$ Years

Therefore, age of girl is $11$ years.

99. The length of a rectangle is two times its width. The perimeter of the rectangle is $180cm$. Find the dimensions of the rectangle.

Ans: Let $x$ be the width of the rectangle.

So, length of the rectangle = $2x$ 

Given, perimeter of the rectangle = $180cm$ 

$ \Rightarrow 2\left( {2x + x} \right) = 180$ 

Divide the equation by $2$ 

$ \Rightarrow 3x = 90$

Divide the equation by $3$.

$ \Rightarrow x = 30$

Therefore, the width of rectangle = $30cm$ 

Now, for length = $2x$ 

$ \Rightarrow 2 \times 30 = 60cm$ 

Therefore, the length of rectangle = $60cm$

100. Look at this riddle? 

If she answers the riddle correctly however will she pay for the pencils?

Ans: Let the cost of one pencil be $x$ rupees

Therefore, cost of $5$ pencils will be $5x$ rupees

Cost of seven pencils = $7x$ rupees

According to the question,

$ \Rightarrow 7x = 5x + 6$ 

Transfer $5x$ to the LHS

$ \Rightarrow 7x - 5x = 6$

$ \Rightarrow 2x = 6$

Divide the equation by $2$

$ \Rightarrow x = 3$

Therefore, cost of $10$ pencils = $3 \times 10$ rupees

$ \Rightarrow 30$ Rupees

101. In a certain examination, a total of $3768$ students secured first division in the years $2006$ and $2007$. The number of first division in $2007$ exceeded those in $2006$ by $34$. How many students got first division in $2006$ ?

Ans: Let the number of students that got first division in $2006$ be $x$.

Therefore, the number of students that got first division in $2007$ be $3768 - x$.

According to the question,

$ \Rightarrow 3768 - x = x + 34$

Transfer $ - x$ to the RHS and $34$ to the LHS.

$ \Rightarrow 3768 - 34 = x + x$ 

$ \Leftrightarrow 2x = 3734$

Divide the equation by $2$ 

$ \Rightarrow x = 1867$

Therefore, the number of students who got the first division in $2006$ are $1867$.

102. Radha got Rs. $17,480$ as her monthly salary and over-time. Her salary exceeds the over-time by Rs. $10,000$. What is her monthly salary?

Ans: Let the monthly salary of Radha be Rs. $x$ 

So, money got by her in over-time = Rs. $\left( {17480 - x} \right)$ 

According to the question,

$ \Rightarrow x = 17480 - x + 10000$ 

Transpose $ - x$ to the LHS

$ \Rightarrow x + x = 17480 + 10000$

$ \Rightarrow 2x = 27480$

Divide the equation by $2$ 

$ \Rightarrow x = \dfrac{{27480}}{2}$

$ \Rightarrow x = 13740$

Hence, Radha's monthly salary is $13740$ Rupees.

103. If one side of a square is represented by $18x - 20$ and the adjacent side is represented by $42 - 13x$, find the length of the side of the square. 

Ans: We know that all sides of the square are equal.

According to the question, 

$ \Rightarrow 18x - 20 = 42 - 13x$ 

Transpose $ - 13x$ to the LHS and $ - 20$ to the RHS.

$ \Rightarrow 18x + 13x = 42 + 20$

$ \Rightarrow 31x = 62$

Divide the equation by $31$ 

$ \Rightarrow x = \dfrac{{62}}{{31}}$

$ \Rightarrow x = 2$

Now, side of the square = $18x - 20$ 

$ \Rightarrow 18 \times 2 - 20$

$ \Rightarrow 36 - 20 = 16$

Therefore, the length of the side of the square is $16$ units.

104. Follow the directions and correct the given incorrect equation, written in Roman numerals: 

(a) Remove two of these matchsticks to make a valid equation: 

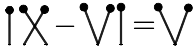
Ans: The correct equation after removing two matchsticks is:

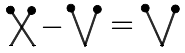
(b) Move one matchstick to make the equation valid. Find two different solutions.

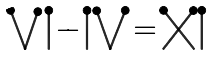
Ans: The correct equation after moving one matchstick is:

Or

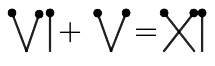
105. What does a duck do when it flies upside down? The answer to this riddle is hidden in the equation given below.

a) If $i + 69 = 70$, then $i = $ ?

b) If $8u = 6u + 8$, then $u = $ ?

c) If $4a =  - 5a + 45$, then $a = $ ?

d) If $4q + 5 = 17$, then $q = $ ?

e) If $ - 5t - 60 =  - 70$, then $t = $ ?

f) If $\dfrac{1}{4}s + 98 = 100$, then $s = $ ?

g) If $\dfrac{5}{3}p + 9 = 24$, then $p = $ ?

h) If $3c = c + 12$, then $c = $ ?

i) If $3\left( {k + 1} \right) = 24$, then $k = $ ?

For riddle answer: substitute the number for the letter it equals

$\dfrac{{}}{1}\dfrac{{}}{2}/\dfrac{{}}{3}\dfrac{{}}{4}\dfrac{{}}{5}\dfrac{{}}{6}\dfrac{{}}{7}\dfrac{{}}{8}/\dfrac{{}}{4}\dfrac{{}}{9}$ 

Ans: 

a) If $i + 69 = 70$, then $i = $ ?

Transpose $69$ to the RHS

$ \Rightarrow i = 70 - 69$

$ \Rightarrow i = 1$

b) If $8u = 6u + 8$, then $u = $ ?

Transpose $6u$ to the LHS

$ \Rightarrow 8u - 6u = 8$

$ \Rightarrow 2u = 8$

Divide the equation by $2$ 

$ \Rightarrow u = 4$

c) If $4a =  - 5a + 45$, then $a = $ ?

Transpose $ - 5a$ to the LHS

$ \Rightarrow 4a + 5a = 45$

$ \Rightarrow 9a = 45$

Divide the equation by $9$ 

$ \Rightarrow a = 5$

d) If $4q + 5 = 17$, then $q = $ ?

Transpose $5$ to the RHS

$ \Rightarrow 4q = 17 - 5$

$ \Rightarrow 4q = 12$

Divide the equation by $4$ 

$ \Rightarrow q = 3$

e) If $ - 5t - 60 =  - 70$, then $t = $ ?

Transpose $ - 60$ to the RHS

$ \Rightarrow  - 5t =  - 70 + 60$

$ \Rightarrow  - 5t =  - 10$

Divide the equation by $ - 2$ 

$ \Rightarrow t = 2$

f) If $\dfrac{1}{4}s + 98 = 100$, then $s = $ ?

Transpose $98$ to the RHS

$ \Rightarrow \dfrac{1}{4}s = 100 - 98$

$ \Rightarrow \dfrac{s}{4} = 2$

On cross multiplication, we get

$ \Rightarrow s = 2 \times 4$

$ \Rightarrow s = 8$

g) If $\dfrac{5}{3}p + 9 = 24$, then $p = $ ?

Transpose $9$ to the RHS

$ \Rightarrow \dfrac{5}{3}p = 24 - 9$

$ \Rightarrow \dfrac{5}{3}p = 15$

On cross multiplication, we get

$ \Rightarrow 5p = 15 \times 3$

$ \Rightarrow 5p = 45$

Divide the equation by $5$ 

$ \Rightarrow p = 9$

h) If $3c = c + 12$, then $c = $ ?

Transpose $c$ to the LHS

$ \Rightarrow 3c - c = 12$

$ \Rightarrow 2c = 12$

Divide the equation by $6$ 

$ \Rightarrow c = 6$

i) If $3\left( {k + 1} \right) = 24$, then $k = $ ?

On multiplication, we get

$ \Rightarrow 3k + 3 = 24$

Transpose $3$ to the RHS

$ \Rightarrow 3k = 24 - 3$

$ \Rightarrow 3k = 21$

Divide the equation by $3$.

$ \Rightarrow k = 7$

Therefore, we get

$ \Rightarrow i = 1$, $t = 2$, $q = 3$, $u = 4$, $a = 5$, $c = 6$, $k = 7$, $s = 8$ and $p = 9$.

Now, we will substitute the values in the equation. So, we get ‘it quacks up’.

$ \Rightarrow \dfrac{i}{1}\dfrac{t}{2}/\dfrac{q}{3}\dfrac{u}{4}\dfrac{a}{5}\dfrac{c}{6}\dfrac{k}{7}\dfrac{s}{8}/\dfrac{u}{4}\dfrac{p}{9}$

106. The three scales below are perfectly balanced if $ \bullet  = 3$. What are the values of $\vartriangle $ and $ * $ ?

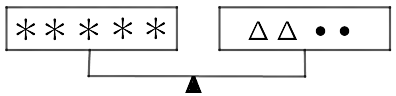
a) 

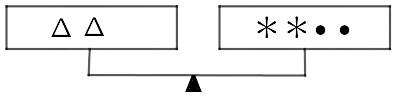
b)

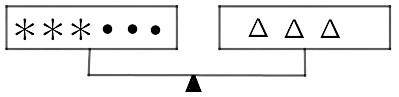
c) 

Ans: Given that, $ \bullet  = 3......\left( i \right)$ 

We have,

a) $5 *  = 2\vartriangle  + 2 \bullet ........\left( {ii} \right)$ 

b) $2\vartriangle  = 2 *  + 2 \bullet .......\left( {iii} \right)$ 

c) $3 *  + 3 \bullet  = 3\vartriangle .......\left( {iv} \right)$ 

Add equation $\left( {iii} \right)$ and $\left( {iv} \right)$ 

$ \Rightarrow 3\vartriangle  + 2\vartriangle  = 3 *  + 3 \bullet  + 2 *  + 2 \bullet $ 

$ \Rightarrow 5\vartriangle  = 5 *  + 5 \bullet $

By equation $\left( {ii} \right)$ we know that $5 *  = 2\vartriangle  + 2 \bullet $. Therefore, we get

$ \Rightarrow 5\vartriangle  = 2\vartriangle  + 2 \bullet  + 5 \bullet $

Transpose $5\vartriangle $ to the LHS

$ \Rightarrow 5\vartriangle  - 2\vartriangle  = 7 \bullet $

We know that $ \bullet  = 3$. Therefore, we get

$ \Rightarrow 3\vartriangle  = 7 \times 3$

$ \Rightarrow 3\vartriangle  = 21$

Divide the equation by $3$.

$ \Rightarrow \vartriangle  = 7$

Now, to find the value of $ * $, we will substitute the value of $ \bullet  = 3$ and $\vartriangle  = 7$ in the equation $\left( {ii} \right)$.

$ \Rightarrow 5 *  = 2\vartriangle  + 2 \bullet ........\left( {ii} \right)$

$ \Rightarrow 5 *  = 2 \times 7 + 2 \times 3$

$ \Rightarrow 5 *  = 14 + 6$

$ \Rightarrow 5 *  = 20$

Divide the equation by $4$.

$ \Rightarrow  *  = 4$

107. The given figure represents a weighing balance. The weights of some objects in the balance are given. Find the weight of each square and the circle.

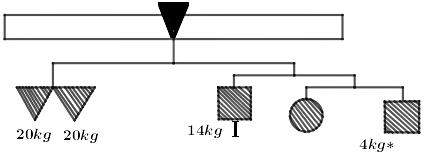
Ans: From the weighing balance, we get

$\bigcirc =  * + \square$

Therefore, we get

$\bigcirc = 4 +  \square  .....\left( i \right)$ 

And, $\vartriangle  + \vartriangle $ = $ \square $ + I + $ \bigcirc $ + $\square $ +  * 

Therefore, on substituting the values, we get

$ \Rightarrow 20 + 20 = 2 \times \square $ + 14 + $ \bigcirc $ + 4 

On addition, we get

$ \Rightarrow 40 = 2 \times \square $ + 14 + 4 + $ \square $ + 4 (Using $i$ )

$ \Rightarrow 40 = 3 \times \square  + 22$

Transpose $22$ to the LHS.

$ \Rightarrow 40 - 22 = 3 \times \square $

$ \Rightarrow 18 = 3 \times \square $

Divide the equation by $3$.

$ \Rightarrow 6 = \square $

Therefore, $\square  = 6kg$ 

From equation $\left( i \right) \bigcirc$ = $\left( {4 + 6} \right)kg$ = $10kg$ 

Simple Equations expresses two mathematical expressions with equal to between them. This category of equations consists of variables and constants. In the simplest terms, an ‘equal to’ sign; and a variable form an equation. Simple equations maintain the same value on either side of ‘equal to’.

Solving simple equations, think of the existing equation as a balance on either side of the ‘equal to’ sign that is the center. If you make any change, suppose you added a number on the left side, so, you have to add the same number on the other side to balance the equation.

E.g. x+6=10

The above example is a simple equation. To solve it, you need to isolate the ‘X’ variable to get its value. 

Download Class 7 Simple Equations NCERT Exemplar

NCERT provides an example for all subjects of Class 7. NCERT Exemplar contains a good amount of questions for practicing the topics. It builds your core knowledge strong; helps you solve surprising questions in the exams. Exemplar doesn’t have explained solutions to the questions. Vedantu presents detailed answers with helpful explanations solved by the best math teachers. Download it in PDF format after signing in.

Advantage of Using Exemplar 

NCERT is designed to give you more questions for practice, and with practice, you become familiar with your strongest and weakest points. These NCERT examples assist you in your preparation to do excellent in the examination.