NCERT Exemplar for Class 7 Maths Solutions Chapter 12 Practical Geometry Symmetry & Visualising Solid Shapes

In Examples 1 to 3, there are four options, out of which one is correct. Choose the correct one. 

Example 1. Which of the following is not a symmetrical figure?

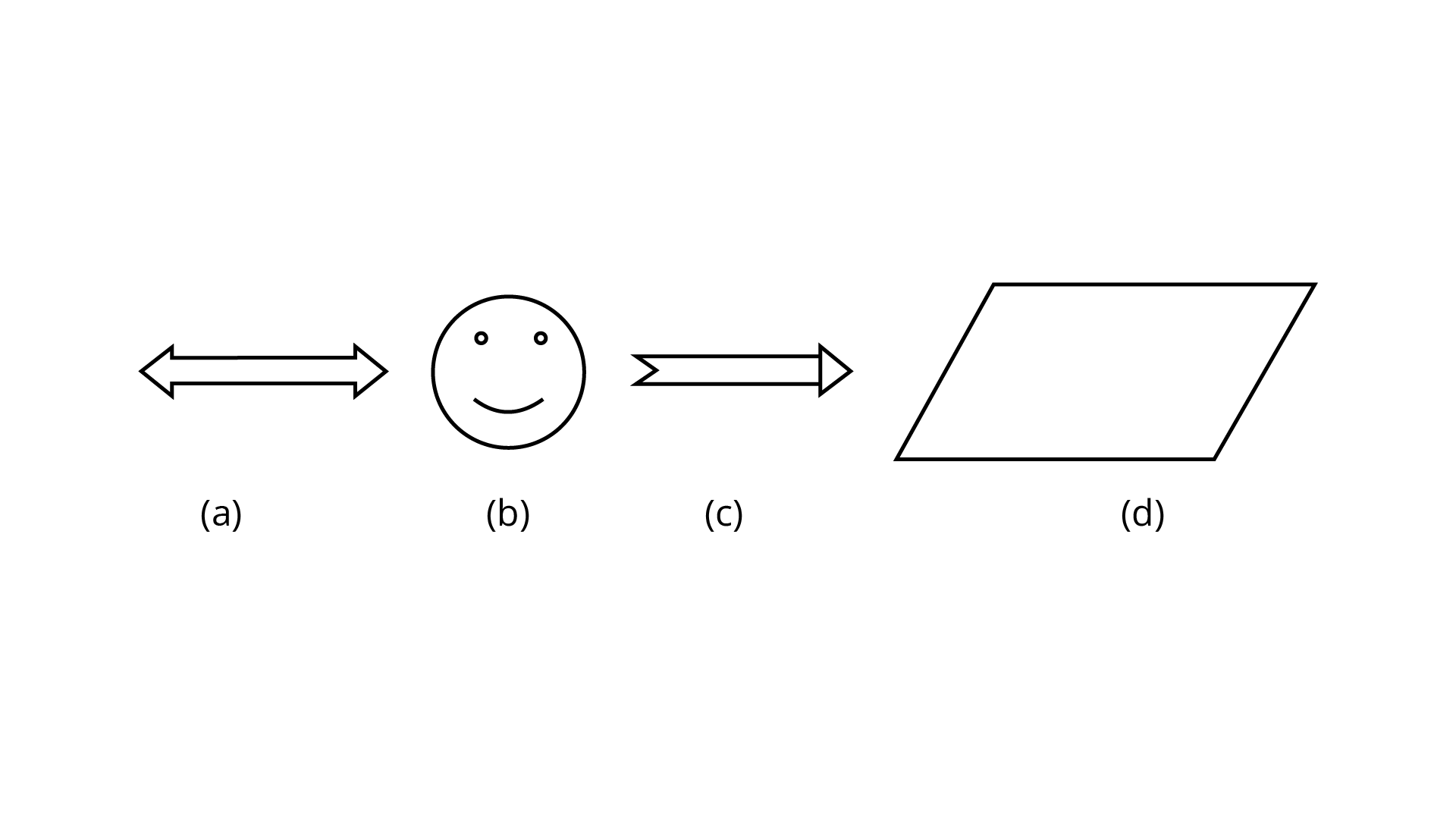
Ans: Option (d) is the correct answer.

If a figure can be folded or divided into half so that the two halves match exactly then such a figure is called a symmetric. Here, if we divide or fold the figure (d), the two halves do not match each other. So, it cannot be symmetric. Therefore, option (d) is the correct answer.

Example 2. In the word which of the following pairs of letters shows rotational symmetry 

(a) ${\mathbf{M}}$ and ${\mathbf{T}}$

(b) ${\mathbf{H}}$ and ${\mathbf{S}}$

(c) ${\mathbf{A}}$ and ${\mathbf{S}}$

(d)${\mathbf{T}}$ and ${\mathbf{S}}$

Ans: Option (b) is the correct answer.

In a complete turn of ${360^\circ }$, the number of times the figure coincides with its original position is called its order of rotational symmetry. In the word, H and S shows rotational symmetry. Therefore, option (b) is the correct answer.

Example 3. The angle of rotation for the figure 12.2 

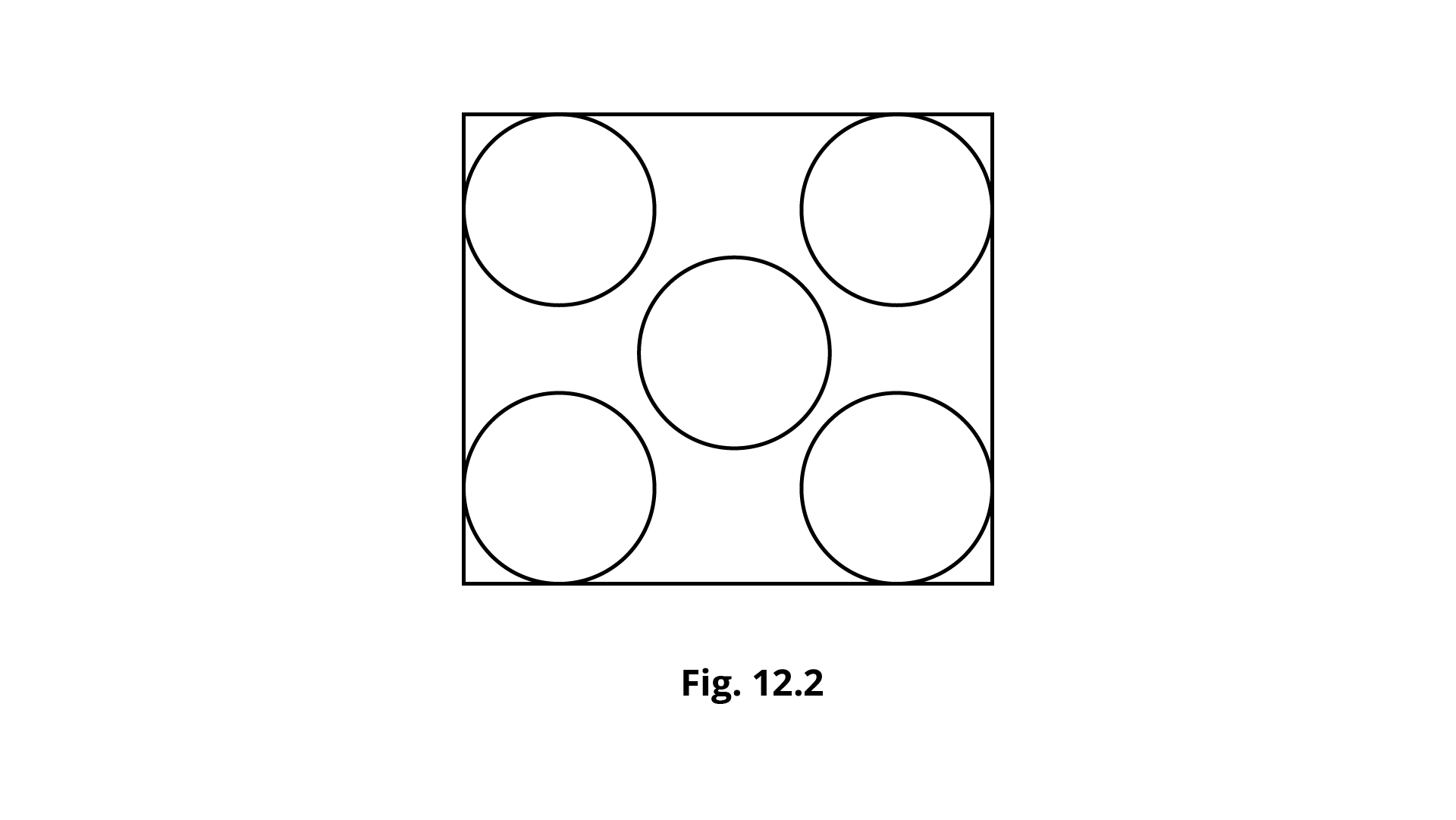
(a) ${\mathbf{45}}^\circ $

(b) ${\mathbf{60}}^\circ $

(c) ${\mathbf{90}}^\circ $

(d) ${\mathbf{180}}^\circ $

Ans: Option (c) is the correct answer.

An angle of rotation is the measure of the amount that a figure is rotated about a fixed point called a point of rotation. Here, the angle of rotation is ${{90^\circ }}$. Therefore, option (c) is the correct answer.

In Examples 4 to 6, fill in the blanks to make it a true statement.

Example 4. The figure 12.3 has ________ vertices, __________ edges and __________ faces.

Ans: The figure has $10$ vertices, $15$ edges and $7$ faces.

Example 5. The adjoining net in Fig. 12.4 represents a _________.

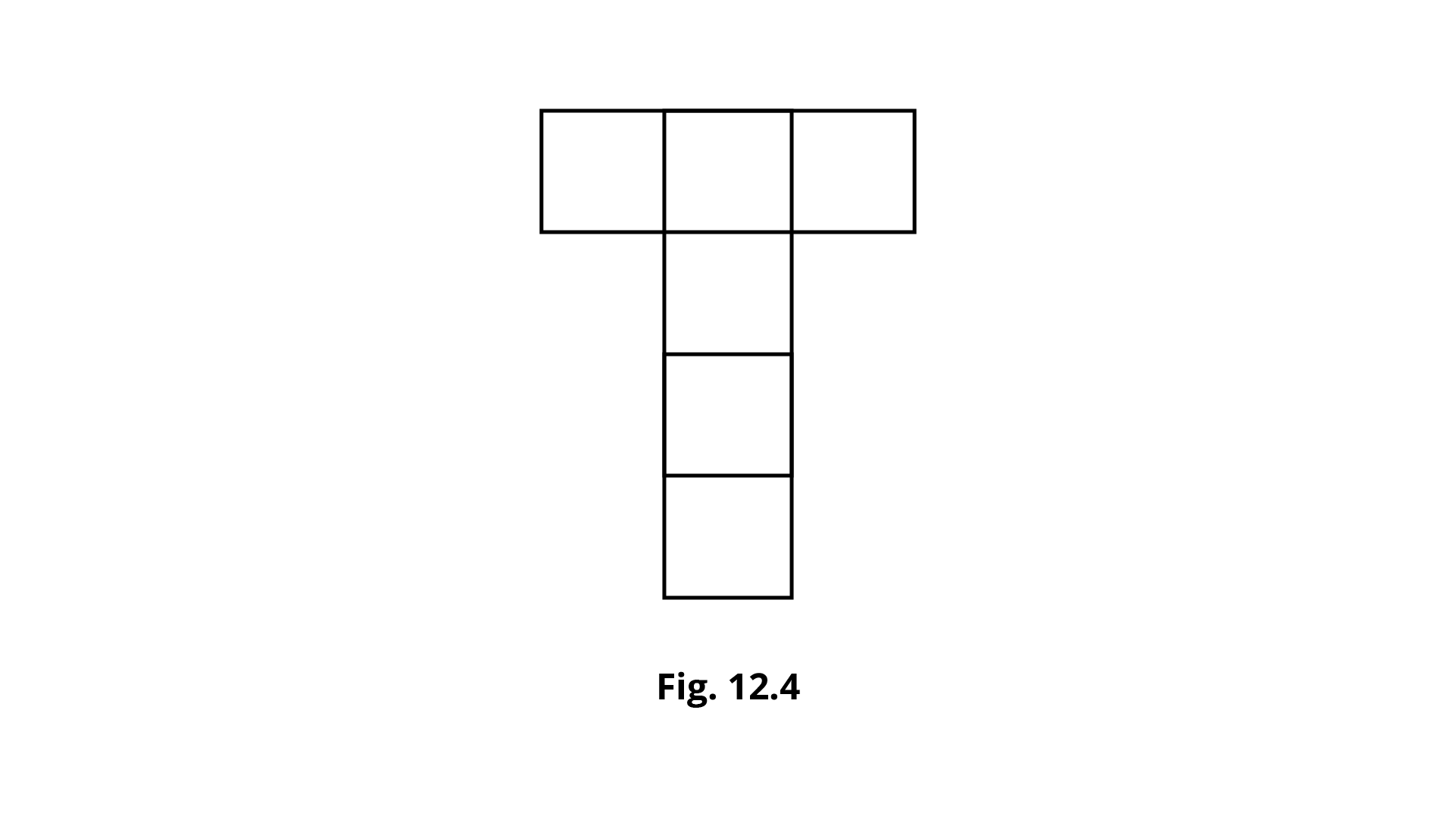
Ans: The adjoining net in Fig. 12.4 represents a cube.

Example 6. Rotation turns an object about a fixed point. This fixed point is called _______.

Ans: Rotation turns an object about a fixed point. This fixed point is called the center of rotation.

In Examples 7 to 9, state whether the statements are True or False. 

Example 7. A net of a ${\mathbf{3 - D}}$ shape is a sort of skeleton - outline in ${\mathbf{2 - D}}$, which, when folded results in the ${\mathbf{3 - D}}$ shape.

Ans: A skeleton outline of a solid that can be folded to make the solid is called a net of that solid. A net of a ${\mathbf{3 - D}}$ shape is a sort of skeleton - outline in ${\mathbf{2 - D}}$ which, when folded results in the ${\mathbf{3 - D}}$ shape. Therefore, the given statement is True.

Example 8. A regular pentagon has no lines of symmetry.

Ans: Any regular polygon has a line of symmetry equal to the number of sides. Therefore, the given statement is False.

Example 9. Order of rotational symmetry for the figure 12.5 is ${\mathbf{4}}$.

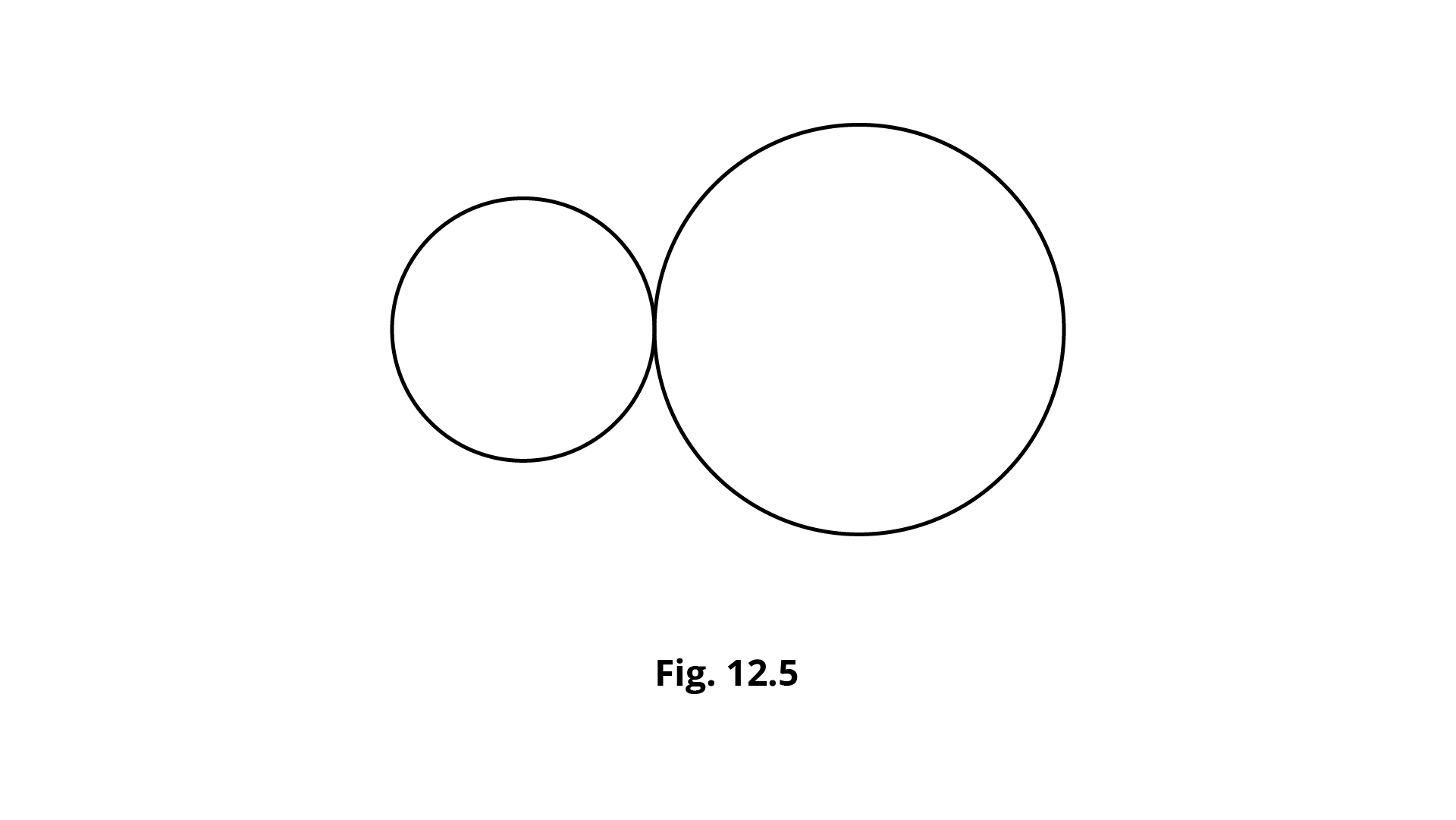
Ans: The order of rotational symmetry for a figure given the order of rotational symmetry of a shape is the number of times it can be rotated around a full circle and still look the same. Here, it is not $4$. 

Therefore, the given statement is false.

Example 10. Draw all the lines of symmetry for the following letters if they exist.

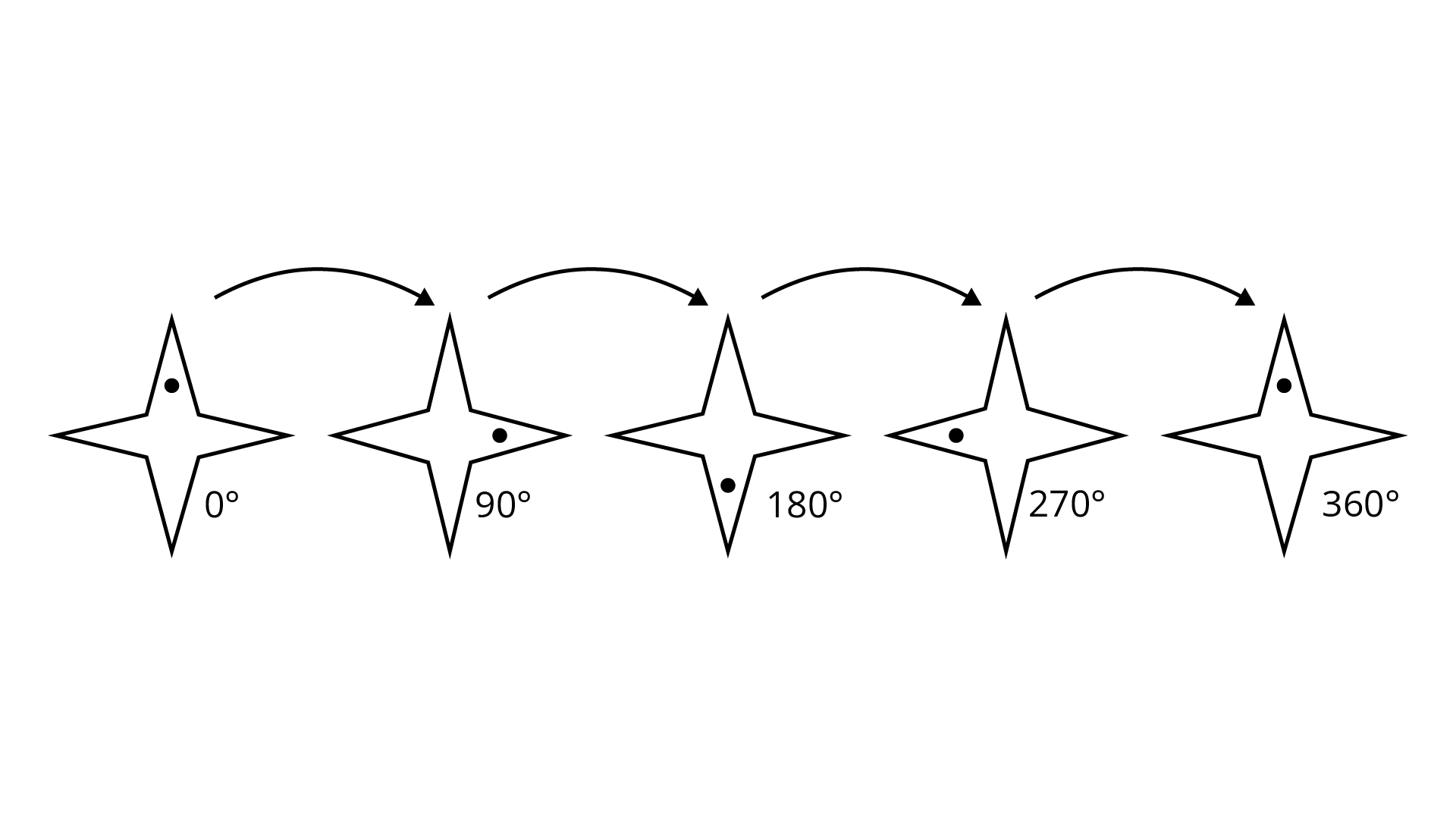
Example 11. State whether the figure 12.6 shows rotational symmetry. If yes, then what is the order of rotational symmetry?

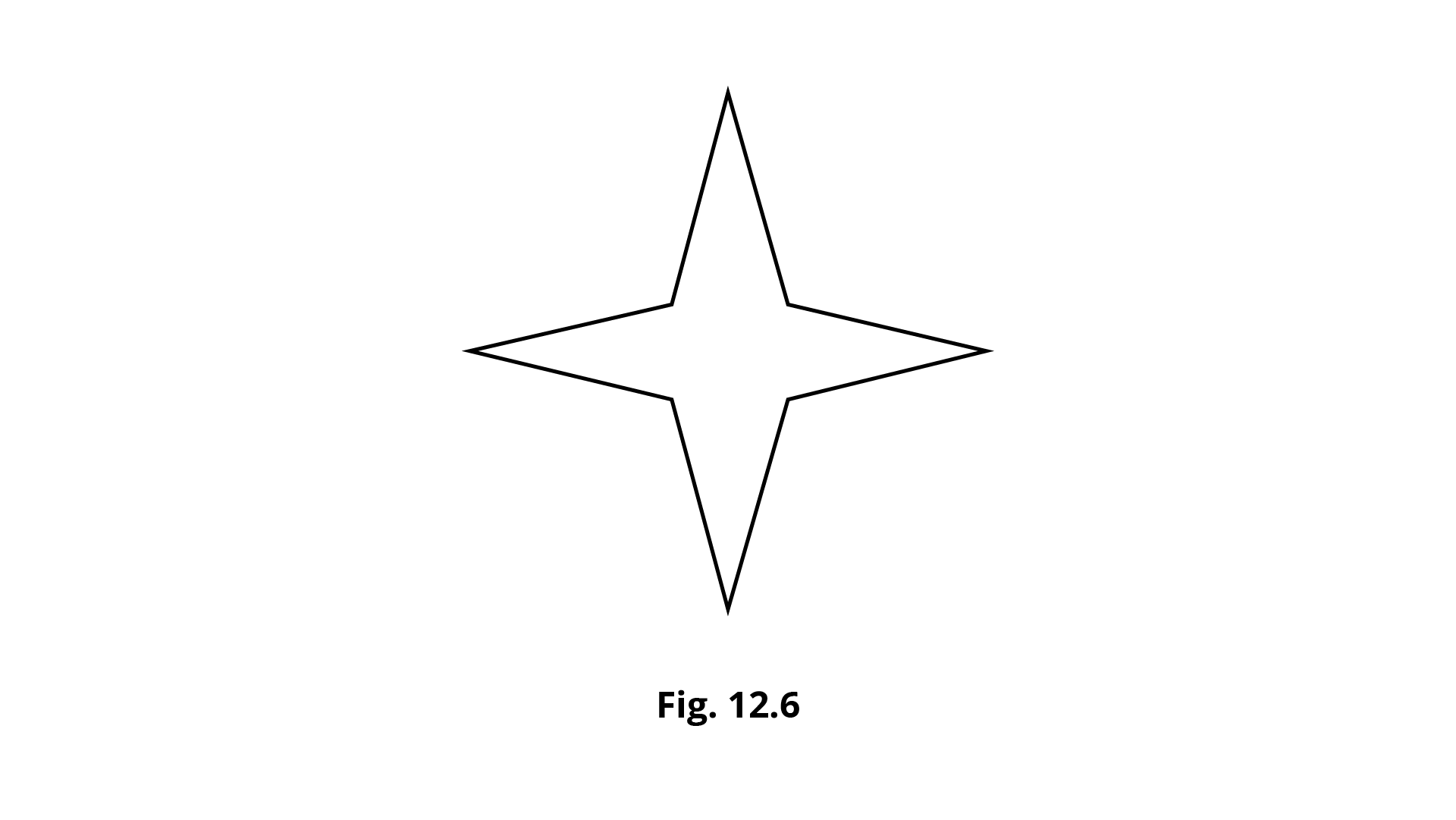
Ans: The given figure shows rotational symmetry. The order of symmetry $ = 4$, which is clear from the following figure:

Example 12: Identify the following figures:

(i)

Ans: The given figure is the Rectangular Pyramid.

(ii)

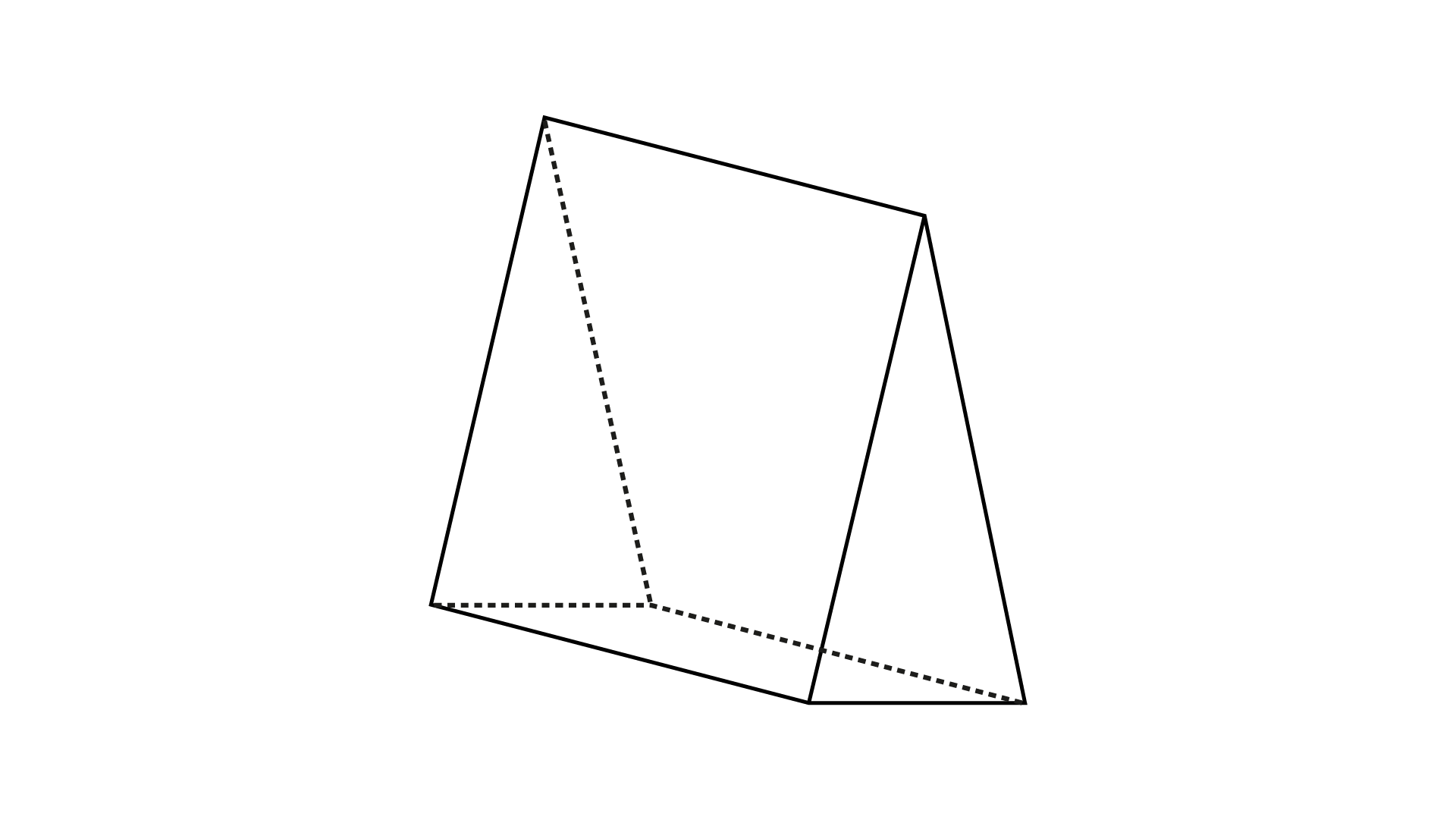
Ans: The given figure is Triangular Prism.

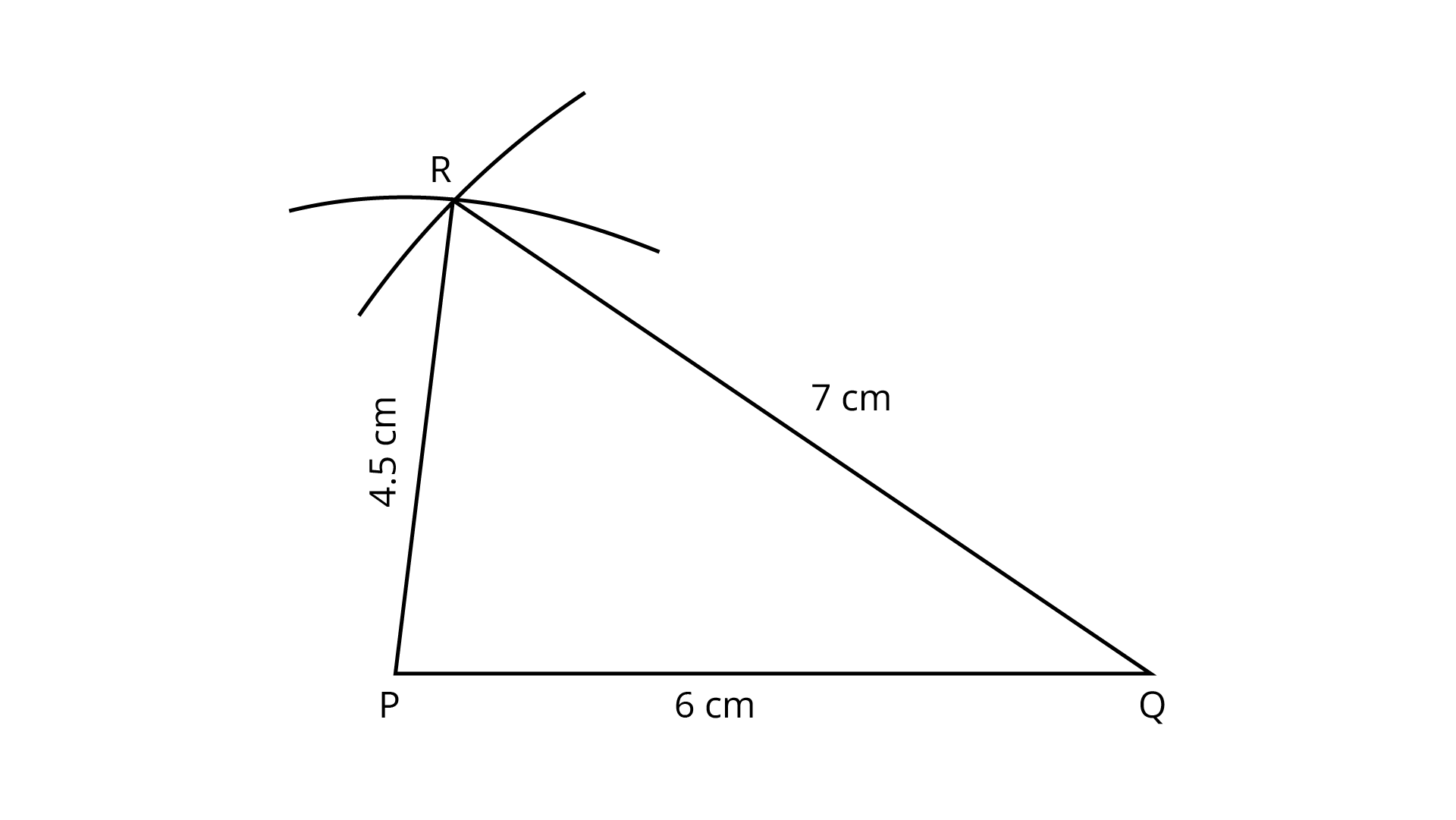
Example 13. Construct a triangle ${\mathbf{PQR}}$ such that ${\mathbf{PQ = 6cm}}$, ${\mathbf{QR = 7cm}}$ and ${\mathbf{PR = 4}}{\mathbf{.5cm}}$.

Ans: Steps of construction:

(1) Draw a line segment ${\text{PQ}}$ of length $6{\text{cm}}$.

(2) With P as center, draw an arc of radius $4.5{\text{cm}}$.

(3) With ${\text{Q}}$ as center, draw an arc of radius $7{\text{cm}}$ which intersects the previous arc at ${\text{R}}$.

(4) Join \[{\text{PR}}\] and \[{\text{QR}}{\text{.}}\]

Then $\Delta {\text{PQR}}$ is the required triangle.

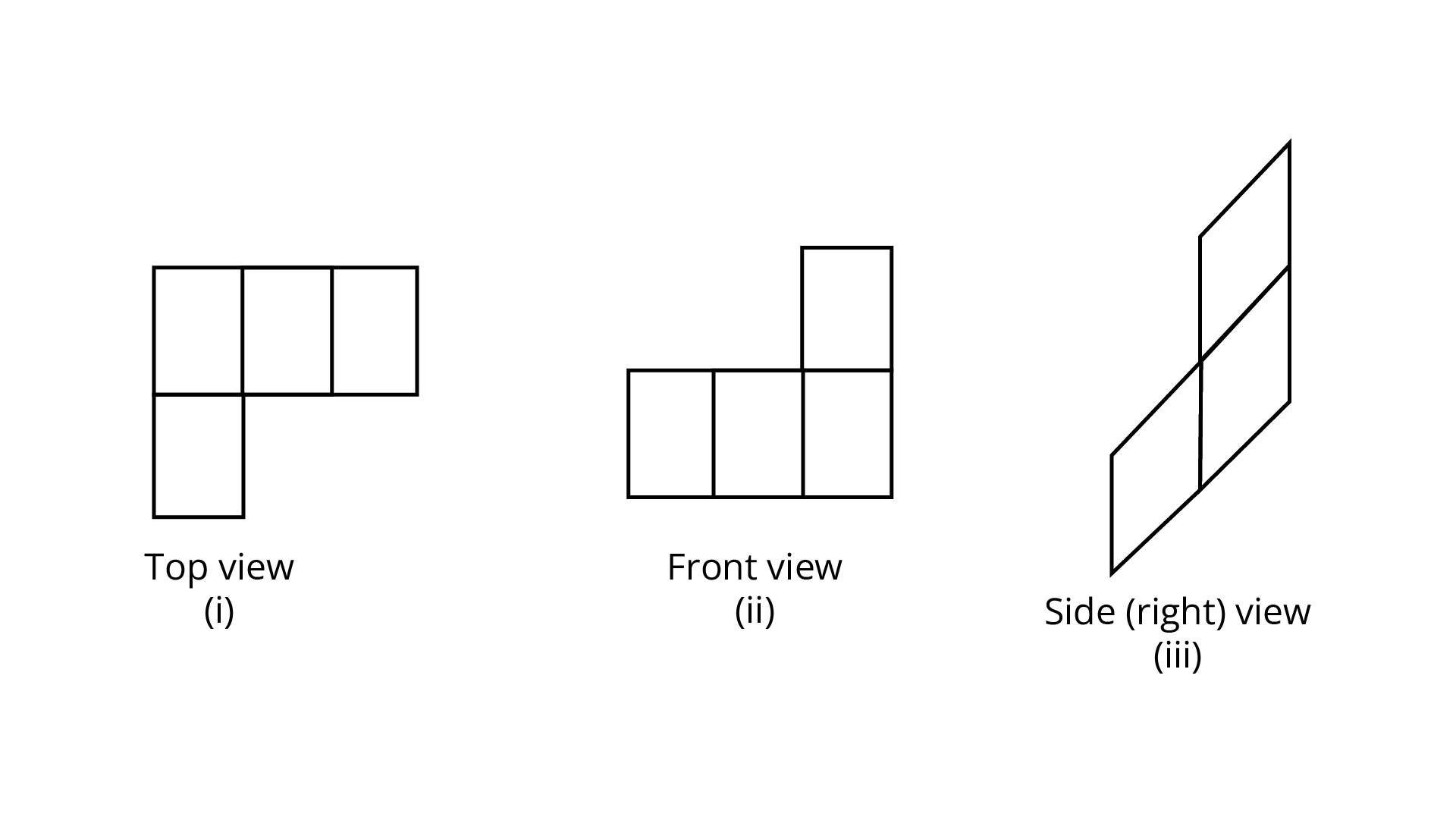
Example 14. Draw the top, the front and the side views of the following solid figure made up of cubes.

Ans: Desired views are shown in Figure,

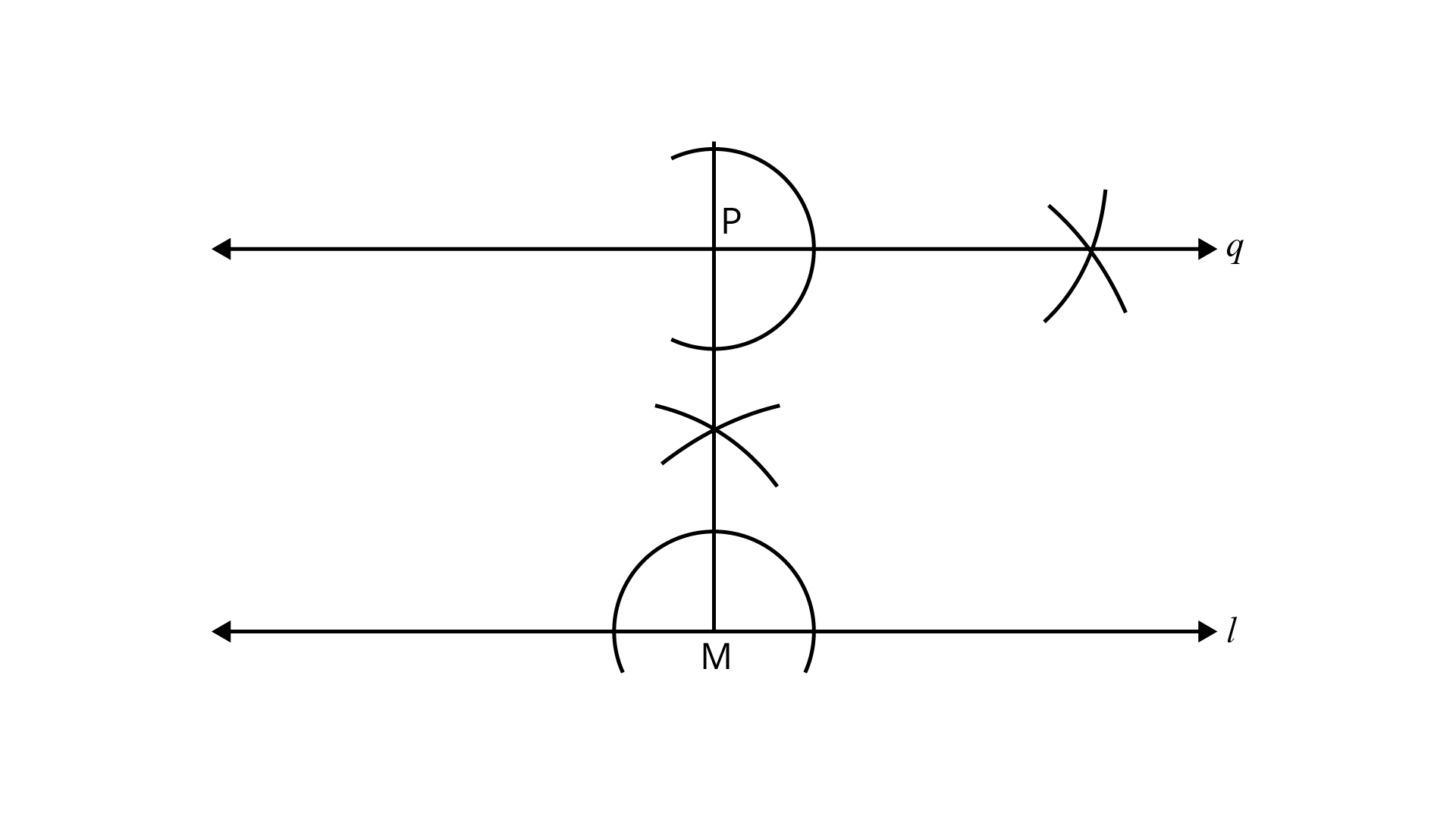
Example 15. Given a line ${\mathbf{l}}$ and a point ${\mathbf{M}}$ on it draw a perpendicular ${\mathbf{MP}}$ to ${\mathbf{l}}$ where${\mathbf{MP = 5}}{\mathbf{.2cm}}$ and a line ${\mathbf{q}}$ parallel to ${\mathbf{l}}$ through ${\mathbf{P}}$.

Ans: Steps of construction:

(1) Draw a line ${\text{l}}$.

(2) Take a point ${\text{M}}$ on it.

(3) Draw an angle of ${90^\circ }$ at ${\text{M}}$ with ${\text{l}}$ which is perpendicular to ${\text{l}}$ at ${\text{M}}$.

(4) With ${\text{M}}$ as center and radius $5.2{\text{cm}}$, draw an arc which intersects the above perpendicular at point ${\text{P}}$. MP is the required perpendicular.

(5) At $\text{P}$, draw an angle of ${90^\circ }$ with MP and produce a line $\text{q}$.

Line ${\text{q}}$ is the required line parallel to line ${\text{l}}$.

Example 16. Determine the number of edges, vertices and faces in the Fig. 12.12.

Ans: The different plain regions are called faces. Hence, there are $5$ faces.

The line segments formed, where the faces meet are called edges. Hence, there are $8$ edges.

Edges meet at a point which are called vertices. Hence, there are $5$ vertices.

Therefore, a square pyramid has $5$ faces, $5$ vertices and $8$ edges.

Exercise

1. A triangle can be constructed by taking its sides as:

(a) ${\mathbf{1}}{\mathbf{.8cm,2}}{\mathbf{.6cm,4}}{\mathbf{.4cm}}$

(b) ${\mathbf{2cm,3cm,4cm}}$

(c) ${\mathbf{2}}{\mathbf{.4cm,2}}{\mathbf{.4cm,6}}{\mathbf{.4cm}}$

(d) ${\mathbf{3}}{\mathbf{.2cm,2}}{\mathbf{.3cm,5}}{\mathbf{.5cm}}$

Ans:  Option (b) is the correct answer.

A triangle is possible, when the sum of two sides is greater than the third side. Use the hit and trial method and check the all options:

For option (a),

$1.8{\text{cm}} + 2.6{\text{cm}} = 4.4{\text{cm}}$, which is equal to third side

For option (b),

$2{\text{cm}} + 3{\text{cm}} = 5{\text{cm}}$, which is greater than third side

For option (c),

$2.4{\text{cm}} + 2.4{\text{cm}} = 4.8{\text{cm}}$, which is less than third side

For option (d),

$3.2{\text{cm}} + 2.3{\text{cm}} = 5.5{\text{cm}}$, which is equal to the third side.

Thus, only option (b) satisfies the condition. Therefore, option (b) is right.

2. A triangle can be constructed by taking two of its angles as:

(a) ${\mathbf{11}}{{\mathbf{0}}^{\mathbf{^\circ }}}{\mathbf{,4}}{{\mathbf{0}}^{\mathbf{^\circ }}}$

(b) \[{\mathbf{7}}{{\mathbf{0}}^{\mathbf{^\circ }}}{\mathbf{,11}}{{\mathbf{5}}^{\mathbf{^\circ }}}\]

(c) ${\mathbf{13}}{{\mathbf{5}}^{\mathbf{^\circ }}}{\mathbf{,4}}{{\mathbf{5}}^{\mathbf{^\circ }}}$

(d) ${\mathbf{9}}{{\mathbf{0}}^{\mathbf{^\circ }}}{\mathbf{,9}}{{\mathbf{0}}^{\mathbf{^\circ }}}$

Ans: Option (a) is the correct answer.

A triangle is possible, when the sum of all interior angles is equal to $180^{\circ}$. Use the hit and trial method and check the all options:

For option (a),

${110^\circ } + {40^\circ } = {150^\circ }$ and third angle is ${30^\circ }$

For option (b),

${70^\circ } + {115^\circ } = {185^\circ }$, is greater than ${180^\circ }$

For option (c),

${135^\circ } + {45^\circ } = {180^\circ }$, third angle is ${0^\circ }$

For option (d),

${90^\circ } + {90^\circ } = {180^\circ }$, third angle is ${0^\circ }$

Thus, only option (a) satisfies the condition.

Therefore, option (a) is the correct answer.

3. The number of lines of symmetry in the figure 12.13 given below is:

(a) ${\mathbf{4}}$

(b) ${\mathbf{8}}$

(c) ${\mathbf{6}}$

(d) infinitely many

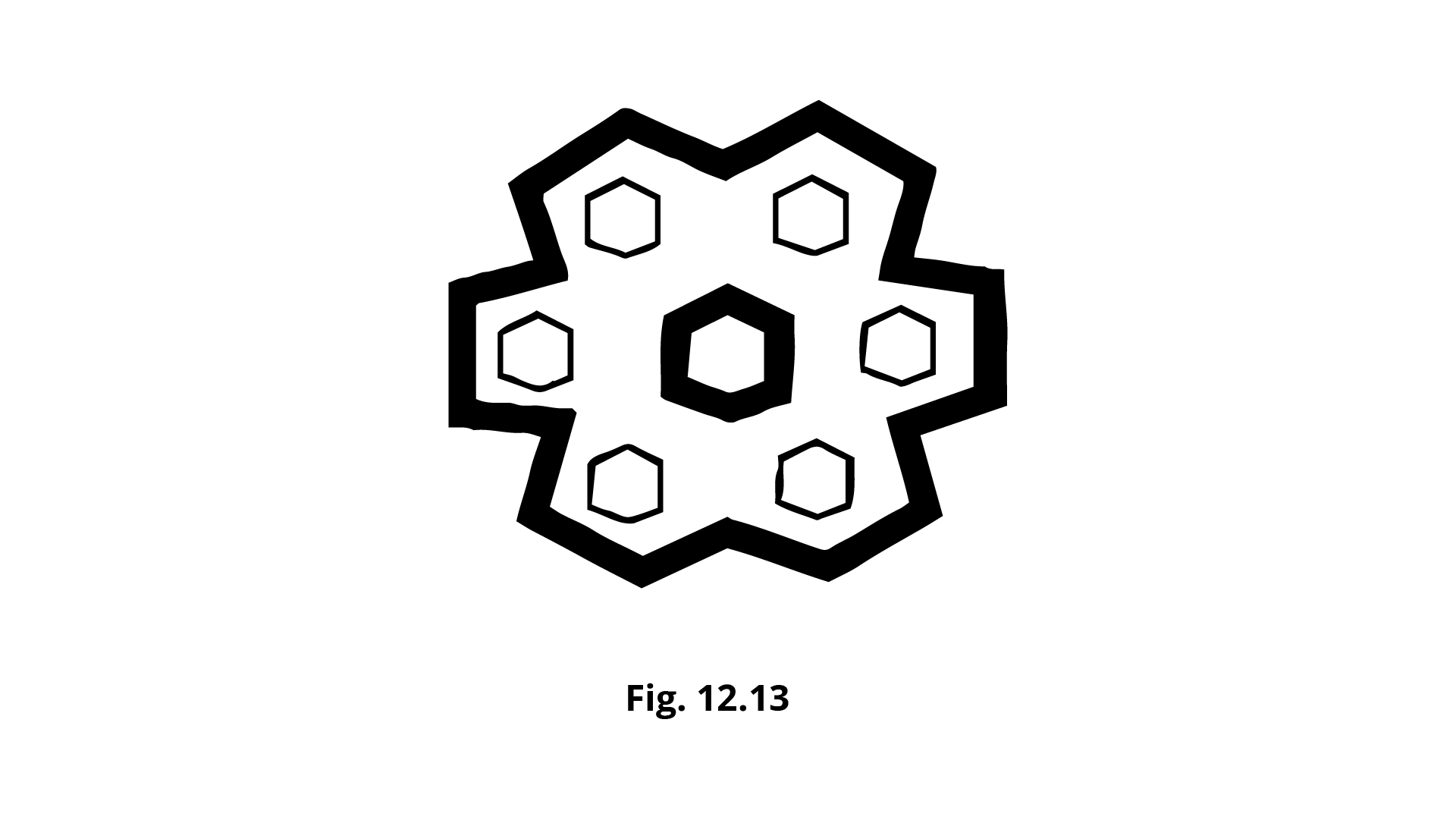
Ans: Option (c) is the correct answer.

Symmetrical line is the line which divides a figure into two equal parts.

Here, the figure has only $6$ line of symmetry. 

4. The number of lines of symmetry in figure 12.14 is:

(a) ${\mathbf{1}}$

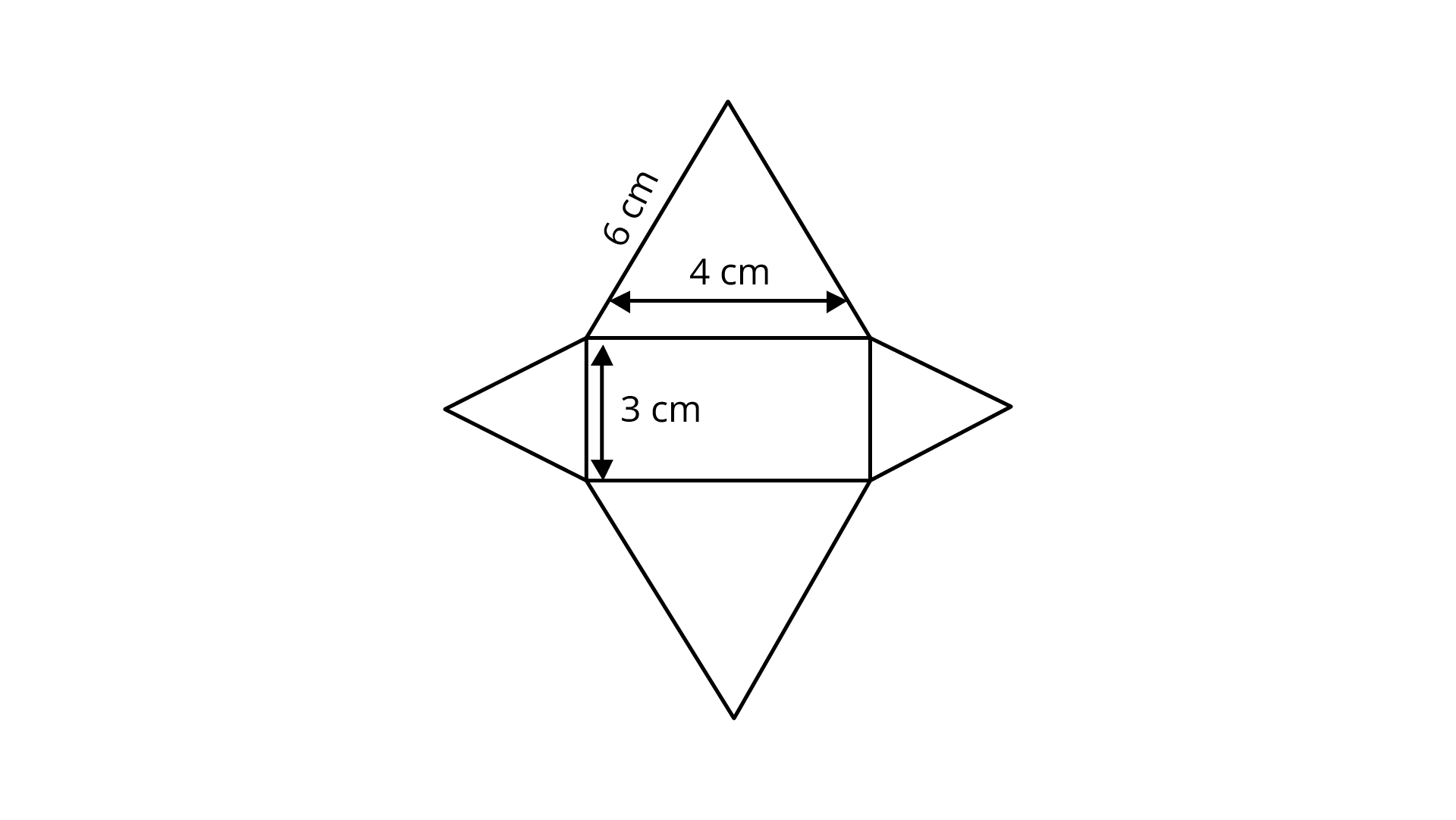
(b) ${\mathbf{3}}$

(c) ${\mathbf{6}}$

(d) infinitely many

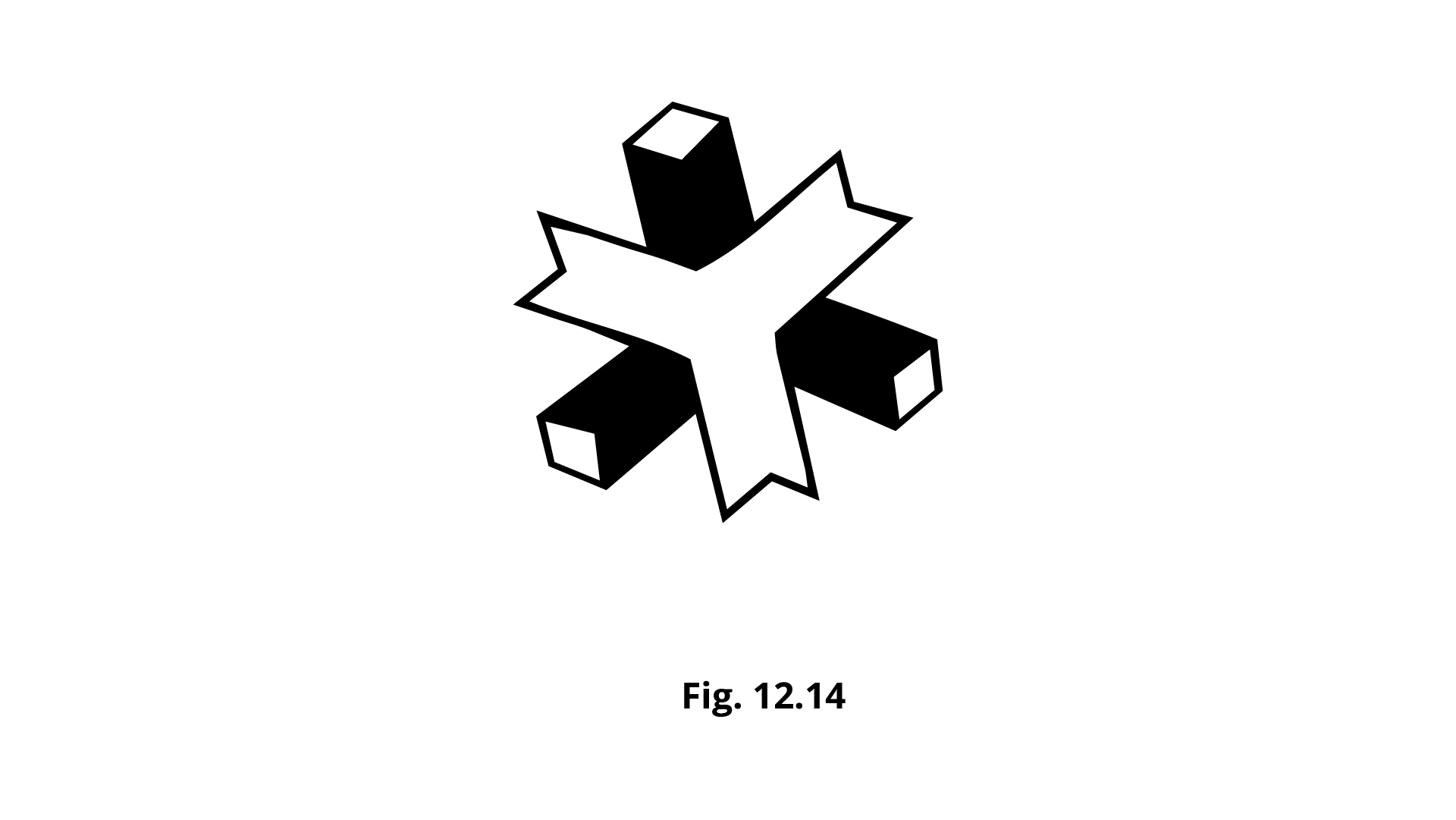
Ans: Option (b) is the correct answer.

Symmetrical line is the line which divides a figure into two equal parts.

Here, the figure has only a $3$ line of symmetry. Therefore, option (b) is the correct answer.

5. The order of rotational symmetry in the Fig. 12.15 given below is 

(a) ${\mathbf{4}}$

(b) ${\mathbf{8}}$

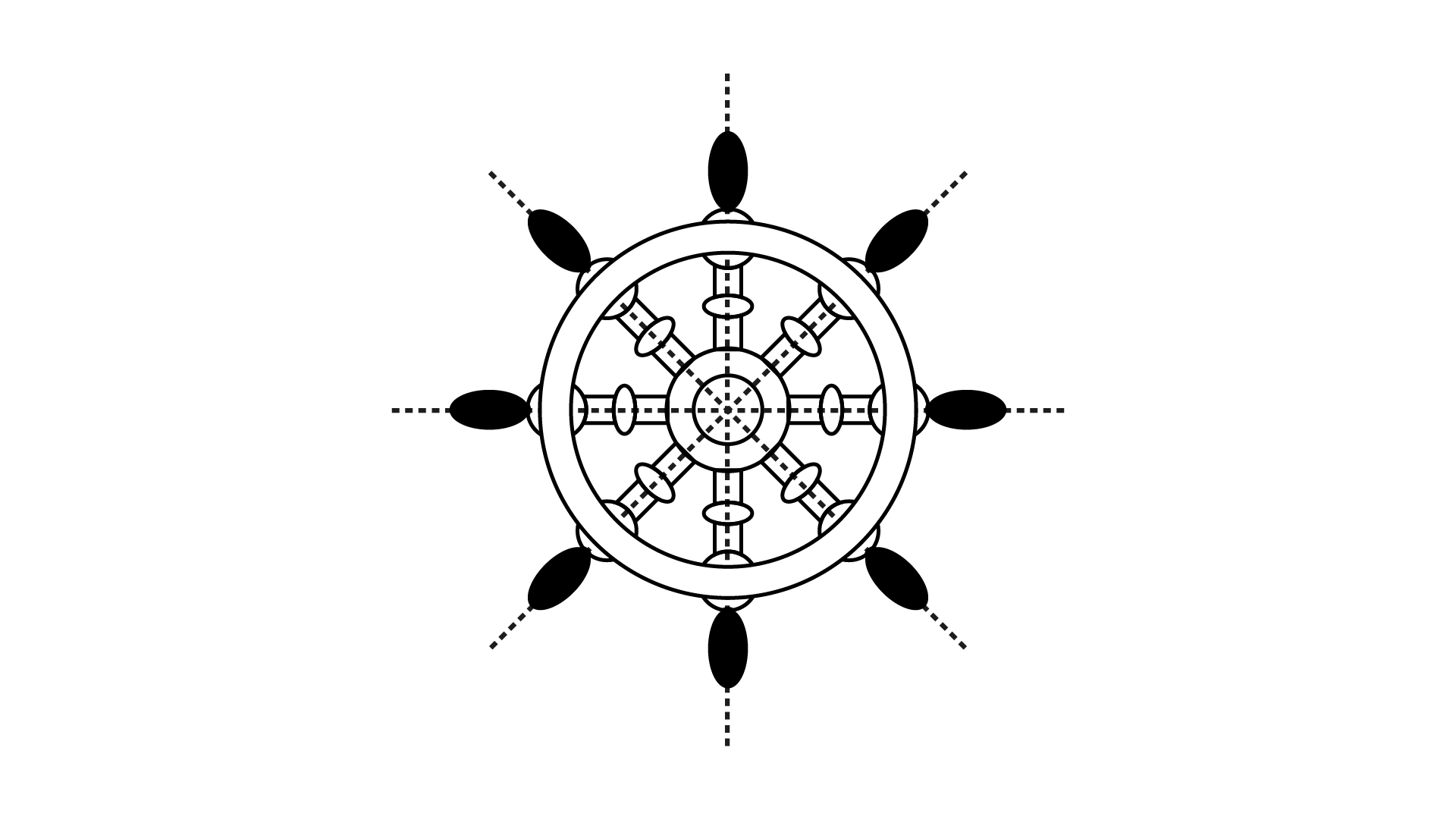
(c) ${\mathbf{6}}$

(d) Infinitely many

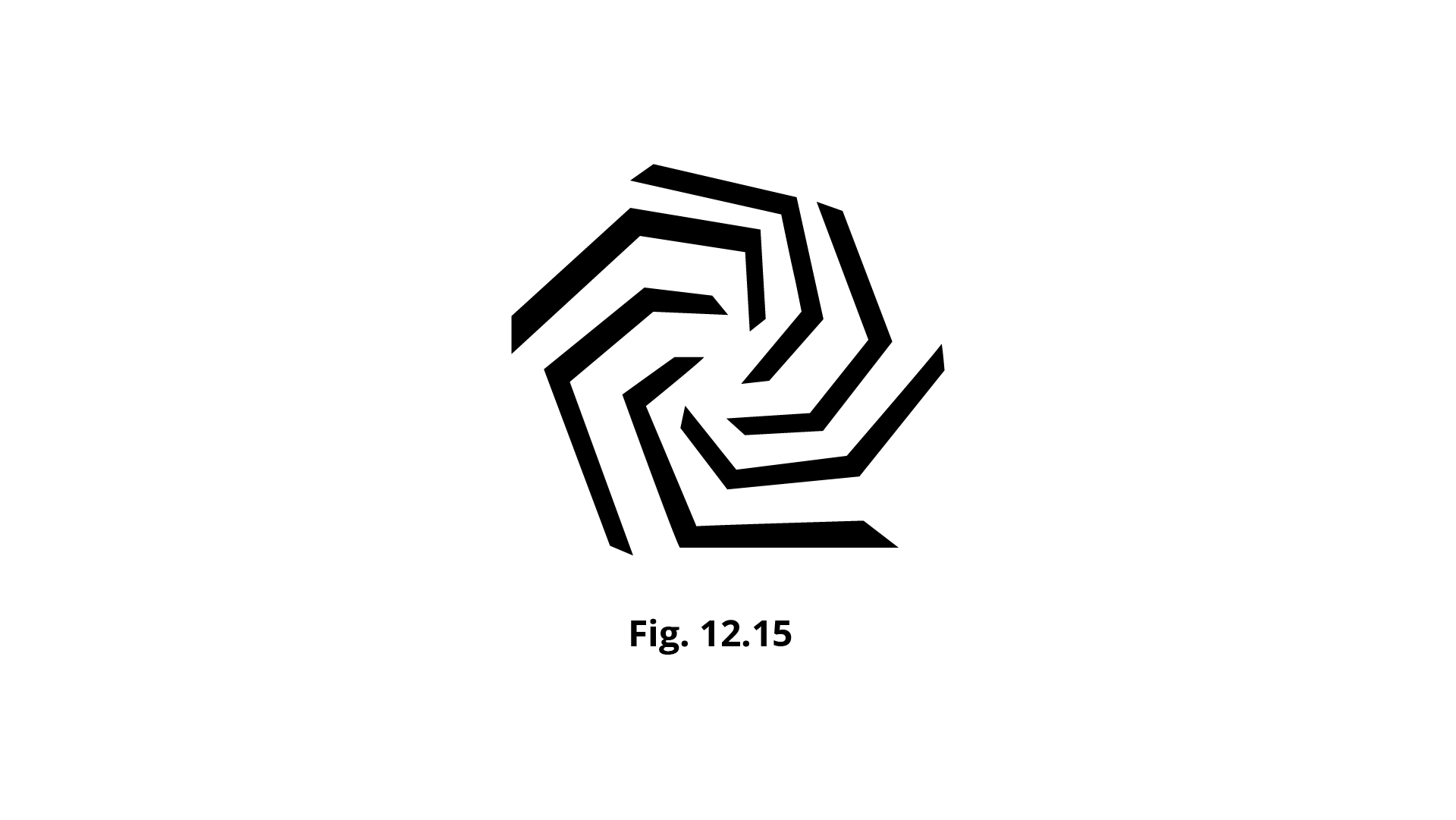
Ans: Option (c) is the correct answer.

In a complete turn of ${360^\circ }$, the number of times the figure coincides with its original position is called its order of rotational symmetry. Here, the order of rotational symmetry is $6$. Therefore, option (c) is the correct answer.

6. The order of rotational symmetry in the Fig. 12.16 given below is 

(a) ${\mathbf{4}}$

(b) ${\mathbf{2}}$

(c) ${\mathbf{1}}$

(d) Infinitely many

Ans: Option (b) is the correct answer.

In a complete turn of ${360^\circ }$, the number of times the figure coincides with its original position is called its order of rotational symmetry. Here, the order of rotational symmetry is $2$. Therefore, option (b) is the correct answer.

7. The name of the given solid in Fig 12.17 is: 

(a) triangular pyramid 

(b) rectangular pyramid 

(c) rectangular prism 

(d) triangular prism

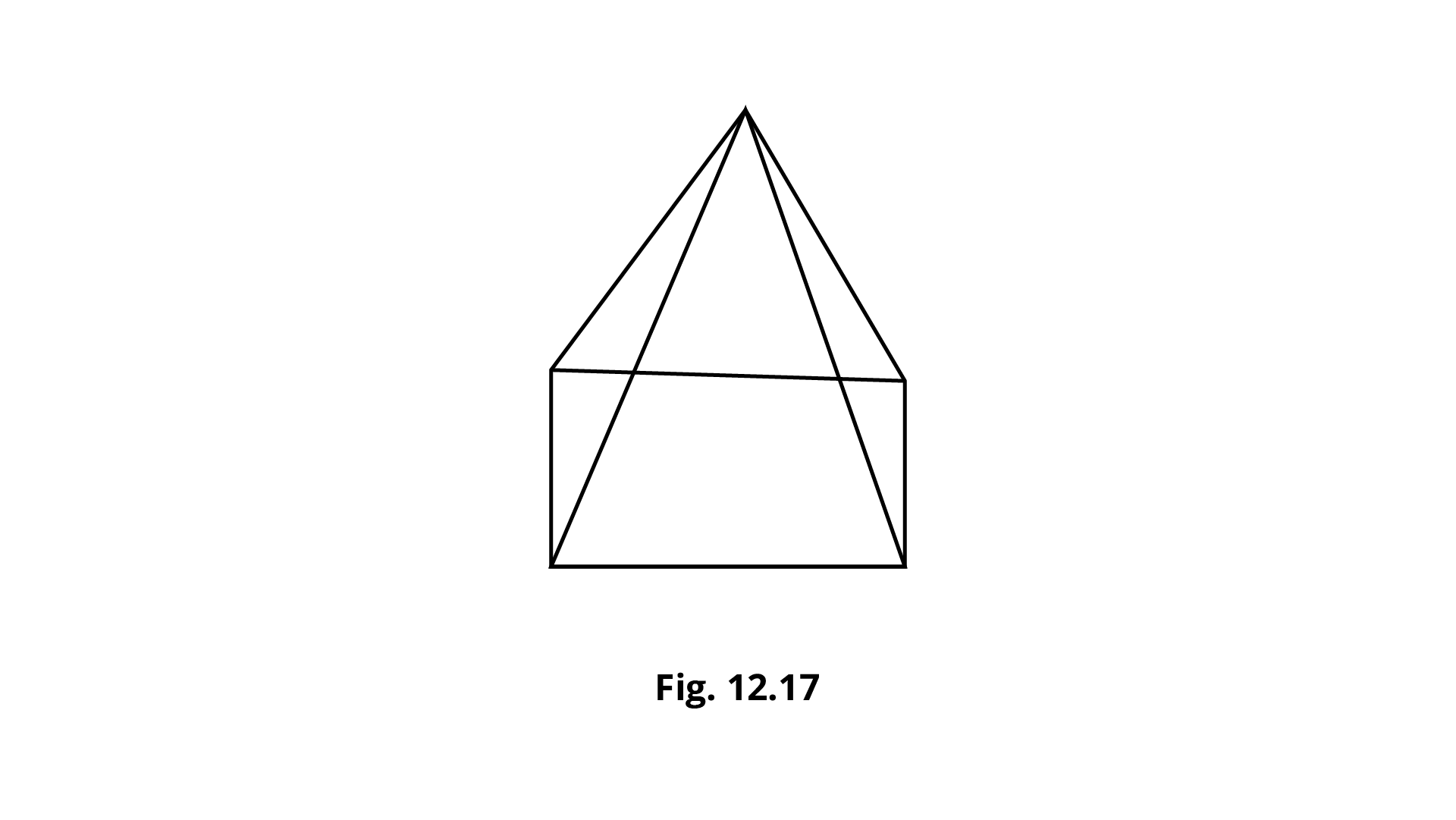
Ans: Option (b) is the correct answer.

A pyramid is a three dimensional polyhedron shaped structure with only one polygonal base and has triangular sides. A prism is a three dimensional polyhedron characterized by two bases which are polygonal in shape and rectangular sides perpendicular to the base. Here, the given figure contains rectangle base and triangle sides. Thus, the given figure is the combination of a rectangle and triangle called a rectangular pyramid. Therefore, option (b) is the correct answer.

8. The name of the given solid in Fig 12.18 is: 

(a) triangular pyramid 

(b) rectangular prism 

(c) triangular prism

(d) rectangular pyramid 

Ans: Option (c) is the correct answer.

A pyramid is a three dimensional polyhedron shaped structure with only one polygonal base and has triangular sides. A prism is a three dimensional polyhedron characterized by two bases which are polygonal in shape and rectangular sides perpendicular to the base. Here, the given figure contains parallelogram faces and triangle sides. Therefore, the given figure is the combination of parallelogram and triangle called triangular prism. 

9. All faces of a pyramid are always: 

(a) Triangular 

(b) Rectangular 

(c) Congruent 

(d) None of these

Ans: Option (d) is the correct answer.

The all faces of a pyramid are triangular except base as it depends on the type of pyramid. Therefore, option (d) is the correct answer.

10. A solid that has only one vertex is 

(a) Pyramid 

(b) Cube 

(c) Cone 

(d) Cylinder

Ans: Option (c) is the correct answer.

Vertex is defined as the common endpoint of two or more rays or line segments. And it typically means a corner or a point where lines meet. A pyramid is a three dimensional polyhedron shaped structure with only one polygonal base and has triangular sides and it has five vertices. A cube is a regular hexahedron and it has eight vertices. A cylinder has no vertex, since its faces never meet. A solid that has only one vertex is called a cone.

Therefore, option (c) is the correct answer.

11. Out of the following which is a ${\mathbf{3}}$-D figure? 

(a) Square 

(b) Sphere 

(c) Triangle 

(d) Circle

Ans: Option (b) is the correct answer.

The ${\text{3 - D}}$ figure is defined as the figure which has three dimensions, that is, length, width and height. Square, Triangle and Circle have only two dimensions. So, they are two dimensional figures. Therefore, option (b) is the correct answer.

12. Total number of edges a cylinder has 

(a) ${\mathbf{0}}$

(b) ${\mathbf{1}}$

(c) ${\mathbf{2}}$ 

(d) ${\mathbf{3}}$

Ans: Option (c) is the correct answer. 

A cylinder has 2 edges, 3 faces and 0 vertices.

13. A solid that has two opposite identical faces and other faces as parallelograms is a 

(a) prism 

(b) pyramid 

(c) cone 

(d) sphere

Ans: Option (a) is the correct answer.

A solid that has two opposite identical faces and other faces as parallelograms is a Prism.

Therefore, option (a) is the correct answer.

14. The solid with one circular face, one curved surface and one vertex is known as: 

(a) cone 

(b) sphere 

(c) cylinder 

(d) prism

Ans: Option (a) is the correct answer.

The solid with one circular face, one curved surface and one vertex is known as Cone.

Therefore, option (a) is the correct answer.

15. If three cubes each of edge ${\mathbf{4cm}}$ are placed end to end, then the dimensions of resulting solid are:

(a) ${\mathbf{12cm \times 4cm \times 4cm}}$

(b) ${\mathbf{4cm \times 8cm \times 4cm}}$

(c) ${\mathbf{4cm \times 8cm \times 12cm}}$

(d) ${\mathbf{4cm \times 6cm \times 8cm}}$

Ans: Option (a) is the correct answer.

If three cubes each of edge ${\mathbf{4cm}}$ are placed end to end, then the dimensions of the resulting solid are ${12cm \times 4cm \times 4cm}$. Therefore, option (a) is the correct answer.

16. When we cut a corner of a cube as shown in the figure 12.19, we get the cutout piece as:

(a) square pyramid 

(b) trapezium prism 

(c) triangular pyramid 

(d) a triangle

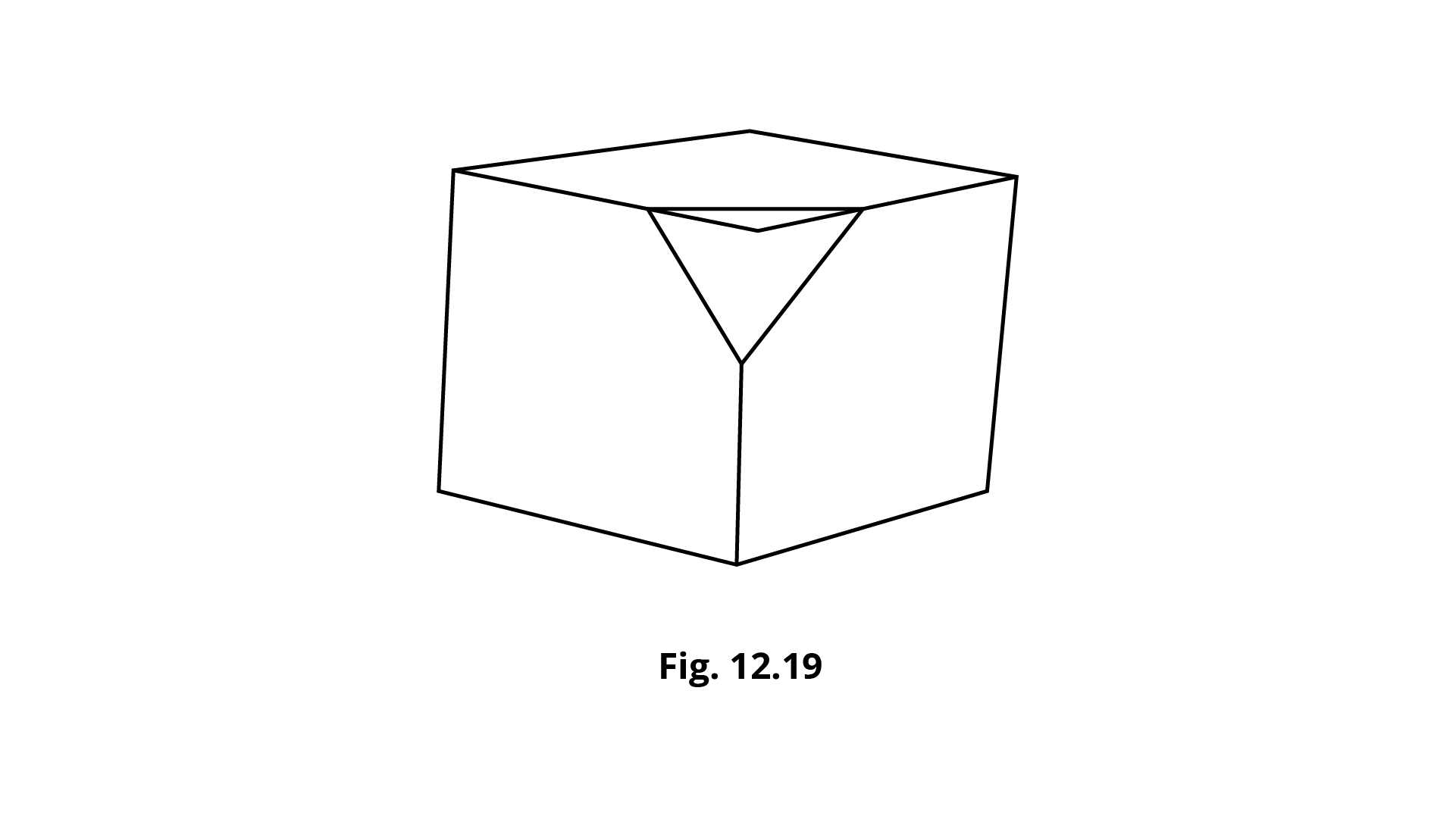
Ans: Option (c) is the correct answer.

When we cut a corner of a cube as shown in the figure, we get the cutout piece as a triangular pyramid. Therefore, option (c) is the correct answer.

17. If we rotate a right-angled triangle of height ${\mathbf{5cm}}$ and base ${\mathbf{3cm}}$ about its height a full turn, we get

(a) cone of height ${\mathbf{5cm}}$, base ${\mathbf{3cm}}$

(b) triangle of height ${\mathbf{5cm}}$, base ${\mathbf{3cm}}$

(c) cone of height ${\mathbf{5cm}}$, base ${\mathbf{6cm}}$

(d) triangle of height ${\mathbf{5cm}}$, base ${\mathbf{6cm}}$

Ans: Option (a) is the correct answer.

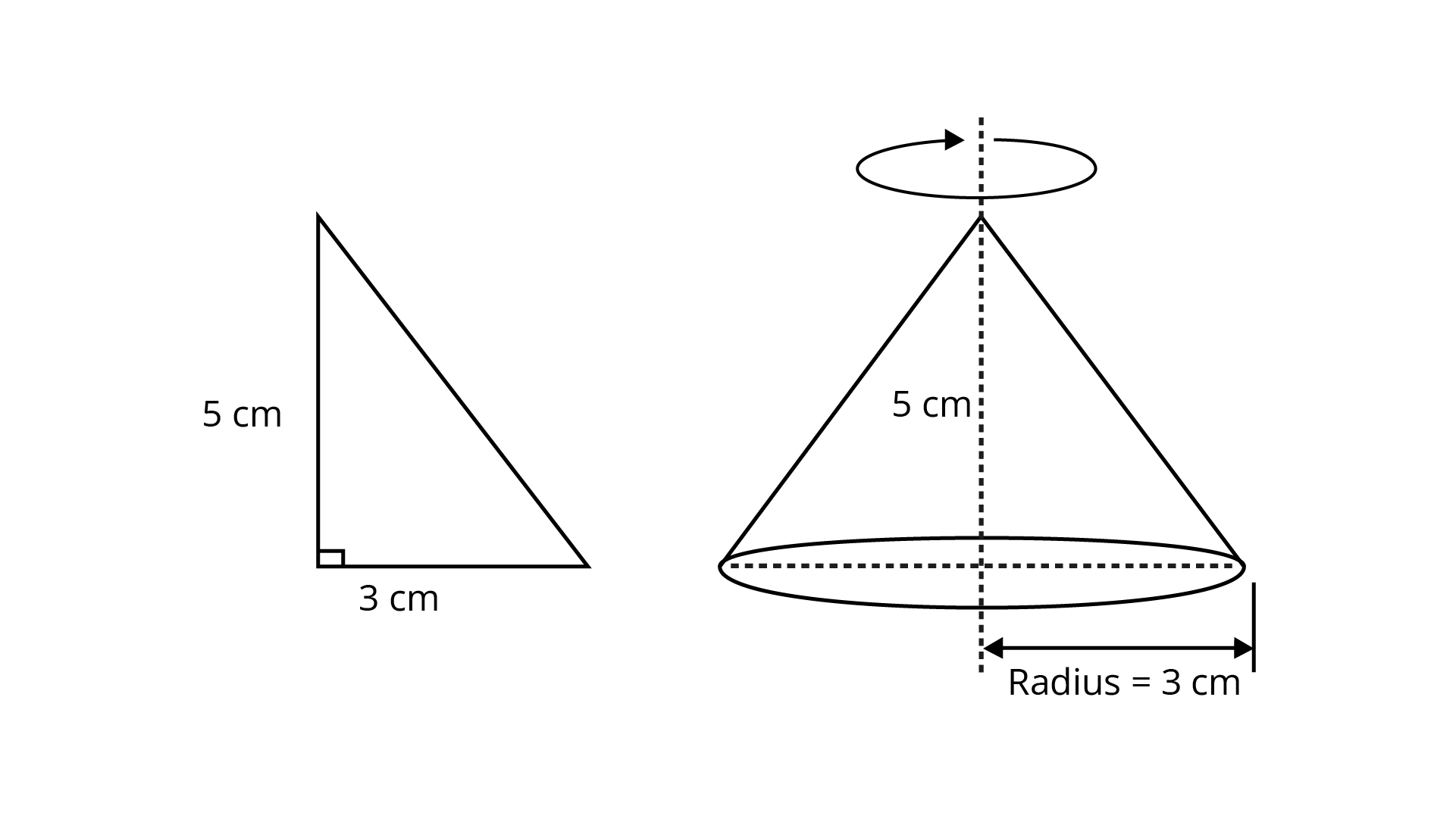
So, if we rotate a right-angled triangle of height ${\text{5cm}}$ and base ${\text{3cm}}$ about its height a full turn, we get cone of height ${\text{5cm}}$, base ${\text{3cm}}$. Therefore, option (a) is the correct answer.

18. If we rotate a right-angled triangle of height $5{\text{cm}}$ and base $3{\text{cm}}$ about its base, we get:

(a) cone of height ${\mathbf{3cm}}$ and base ${\mathbf{3cm}}$

(b) cone of height ${\mathbf{5cm}}$ and base ${\mathbf{5cm}}$

(c) cone of height ${\mathbf{5cm}}$ and base ${\mathbf{3cm}}$

(d) cone of height ${\mathbf{3cm}}$ and base ${\mathbf{5cm}}$

Ans: Option (d) is the correct answer.

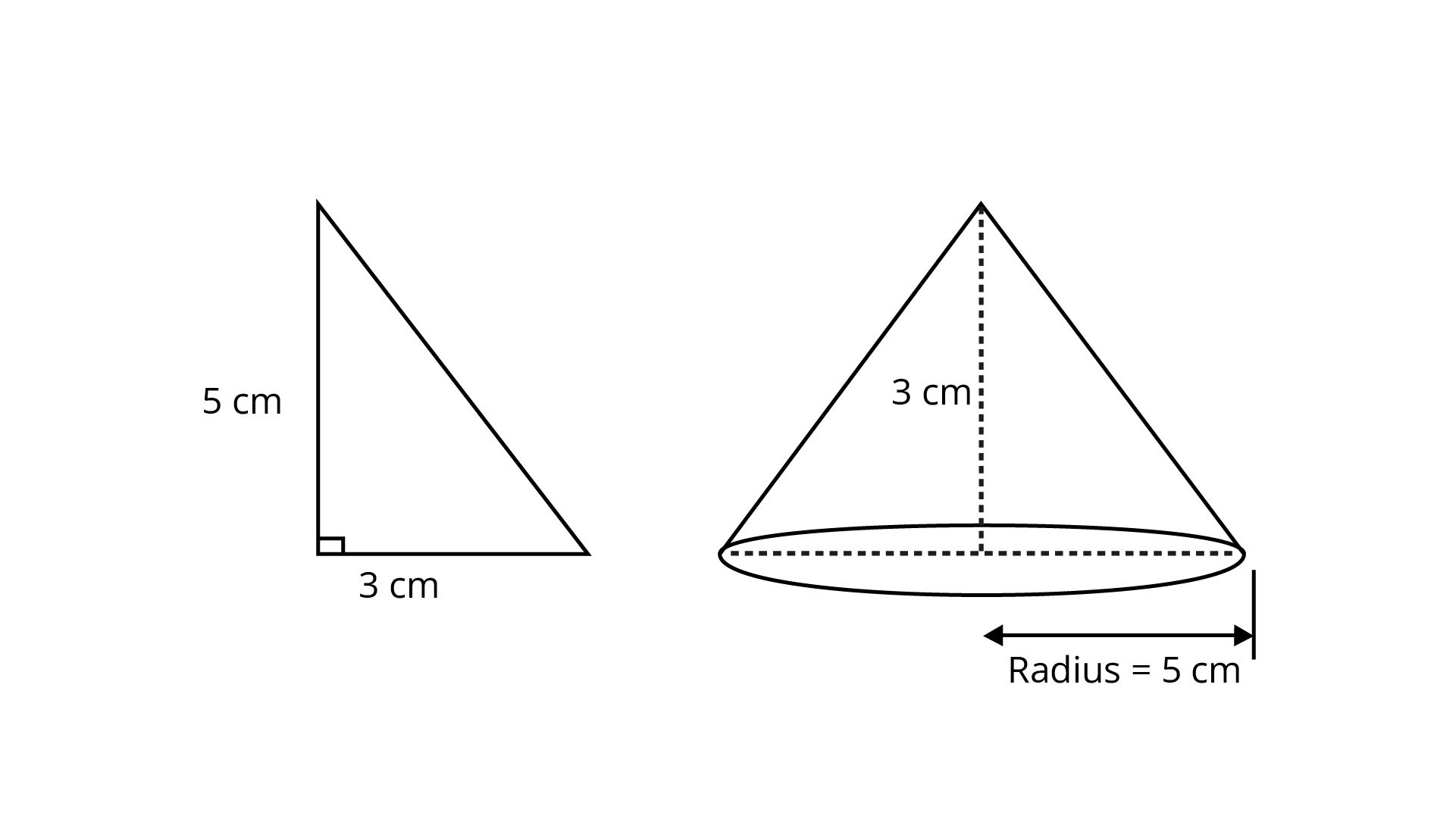
So, if we rotate a right-angled triangle of height $5{\text{cm}}$ and base $3{\text{cm}}$ about its base, we get cone of height $3{\text{cm}}$ and base $5{\text{cm}}$. Therefore, option (d) is the correct answer.

19. When a torch is pointed towards one of the vertical edges of a cube, you get a shadow of cube in the shape of

(a) square

(b) rectangle but not a square

(c) circle

(d) triangle

Ans: Option (b) is the correct answer.

The cube can cast a shadow in the form of a rectangle. So, when a torch is pointed towards one of the vertical edges of a cube, you get a shadow of the cube in the shape of a rectangle. Therefore, option (b) is the correct answer.

20. Which of the following sets of triangles could be the lengths of the sides of a right-angled triangle:

(a) ${\mathbf{3cm,4cm,6cm}}$

(b) ${\mathbf{9cm,16cm,26cm}}$

(c) ${\mathbf{1}}{\mathbf{.5cm,3}}{\mathbf{.6cm,3}}{\mathbf{.9cm}}$

(d) ${\mathbf{7cm,24cm,26cm}}$

Ans: Option (c) is the correct answer.

From the Pythagoras theorem,

Hypotenuse $^2 = $ base $^2 + $ height $^2$

Consider $3.9{\text{cm}}$ is the length of the hypotenuse.

Then, ${(3.9)^2} = {(1.5)^2} + {(3.6)^2}$

$15.21 = 2.25 + 12.96$

Add the numbers,

$15.21 = 15.21$

For option (a),

From the Pythagoras theorem,

Hypotenuse $^2 = $ base $^2 + $ height $^2$

Consider $6{\text{cm}}$ is the length of the hypotenuse.

Then, ${(6)^2} = {(4)^2} + {(3)^2}$

$36 = 16 + 9$

$36 \ne 25$

For option (b),

From the Pythagoras theorem,

Hypotenuse $^2 = $ base $^2 + $ height $^2$

Consider $26{\text{cm}}$ is the length of the hypotenuse.

Then,${(26)^2} = {(16)^2} + {(9)^2}$

$676 = 256 + 81$ 

$676 \ne 337$

For option (d),

From the Pythagoras theorem,

Hypotenuse $^2 = $ base $^2 + $ height $^2$

Consider $26{\text{cm}}$ is the length of the hypotenuse.

Then,${(26)^2} = {(24)^2} + {(7)^2}$

$676 = 576 + 49$ 

$676 \ne 625$

Therefore, option (c) is the correct answer.

21. In which of the following cases, a unique triangle can be drawn

(a) ${\mathbf{AB = 4cm,}}\,\,{\mathbf{BC = 8cm}}$ and ${\mathbf{CA = 2cm}}$

(b)  $BC=5.2 cm$ $\angle B = {90}^{\circ}$ and $\angle C = {110}^{\circ}$

(c) $XY=5 cm$ $\angle X = {45}^{\circ}$ and $\angle Y = {60}^{\circ}$

(d) An isosceles triangle with the length of each equal side ${\mathbf{6}}{\mathbf{.2cm}}$.

Ans: Option (c) is the correct answer. 

A triangle Is possible if:

(i) Sum of any two sides must be greater than the third side of the triangle.

(ii) Sum of all angles must be equal to $180^{\circ}$.

So, options (a) and (b) triangles are not possible because of the above points (i) and (ii) respectively.

In option (d) we can draw more than one isosceles triangle with side length $6.2$ $\mathrm{cm}$. So, triangles are not unique.

Thus, a unique triangle can be drawn only in option (c).

22. Which of the following has a line of symmetry?

(a)

Ans: Figure (c) has a line of symmetry.

A figure has line symmetry, if there is a line about which the figure may be folded so that the two parts of the figure will coincide with each other.

Therefore, figure (c) has a line of symmetry.

23. Which of the following are reflections of each other?

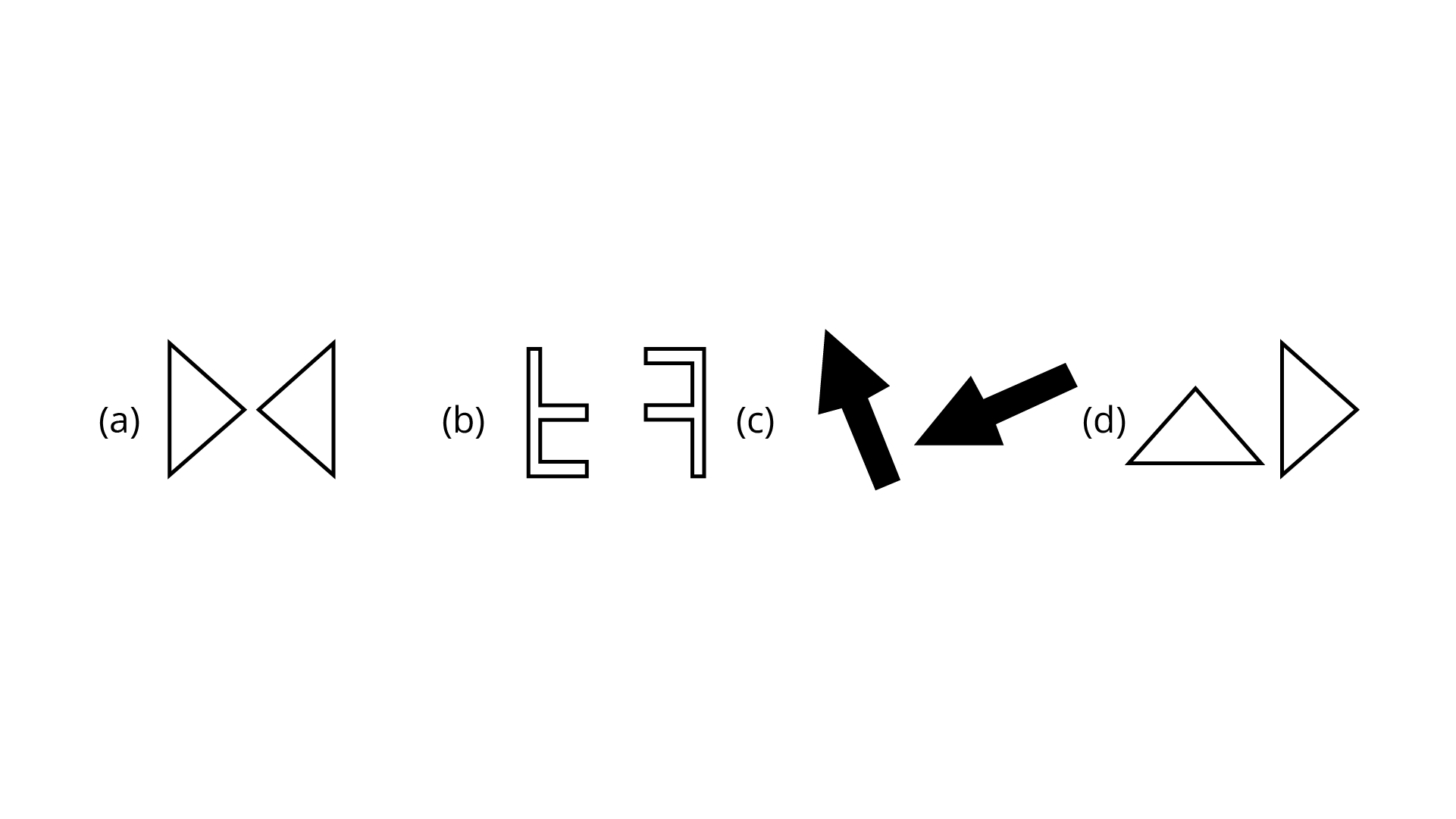
Ans: Figures in (a) are reflections of each other.

Mirror reflection leads to symmetry, under which the left-right orientation has to be taken care of. Therefore, option (a) is the correct answer.

24. Which of these nets is a net of a cube?

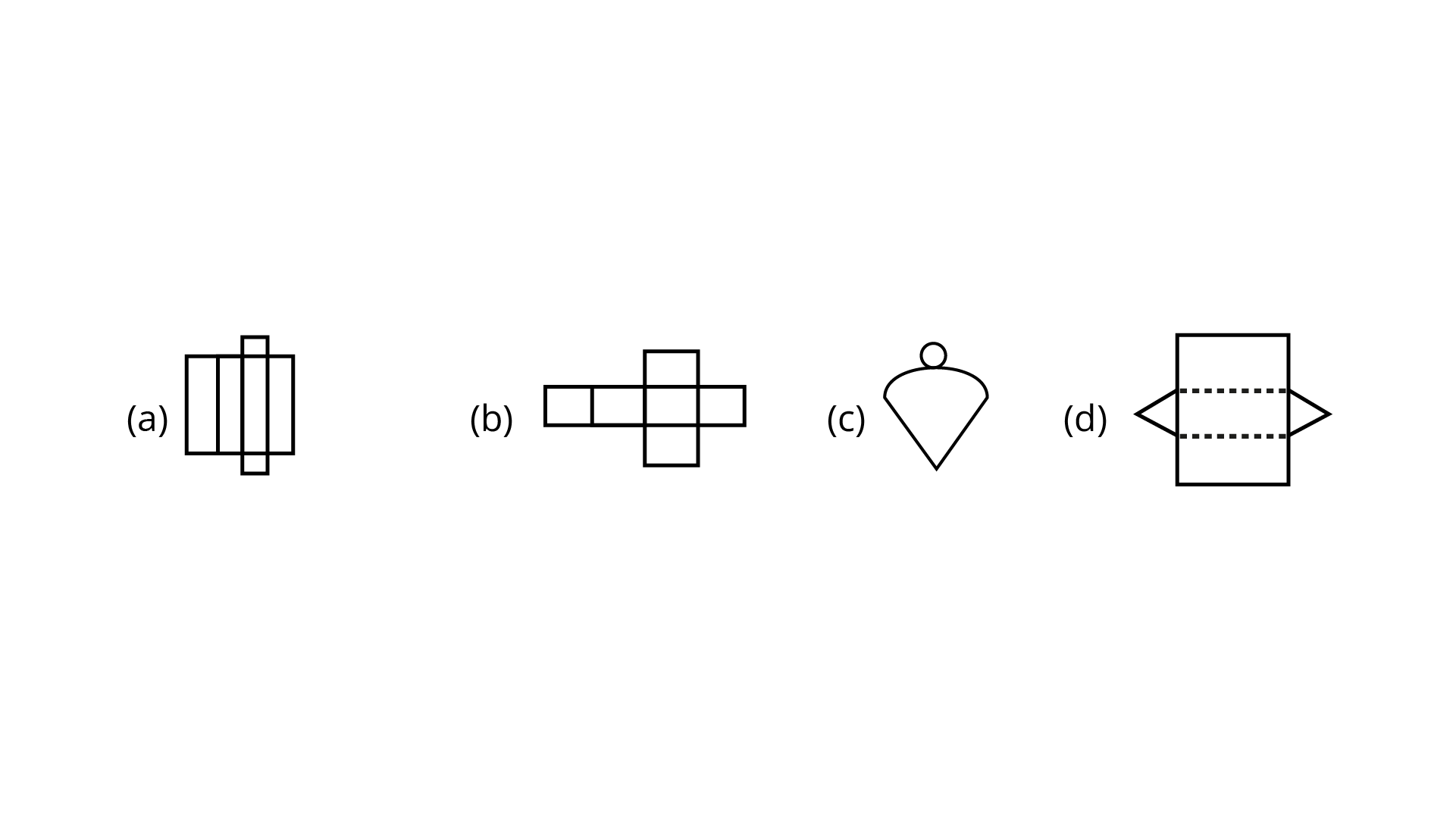
Ans: Option (b) is the correct answer.

Figure (b) is a net of cube.

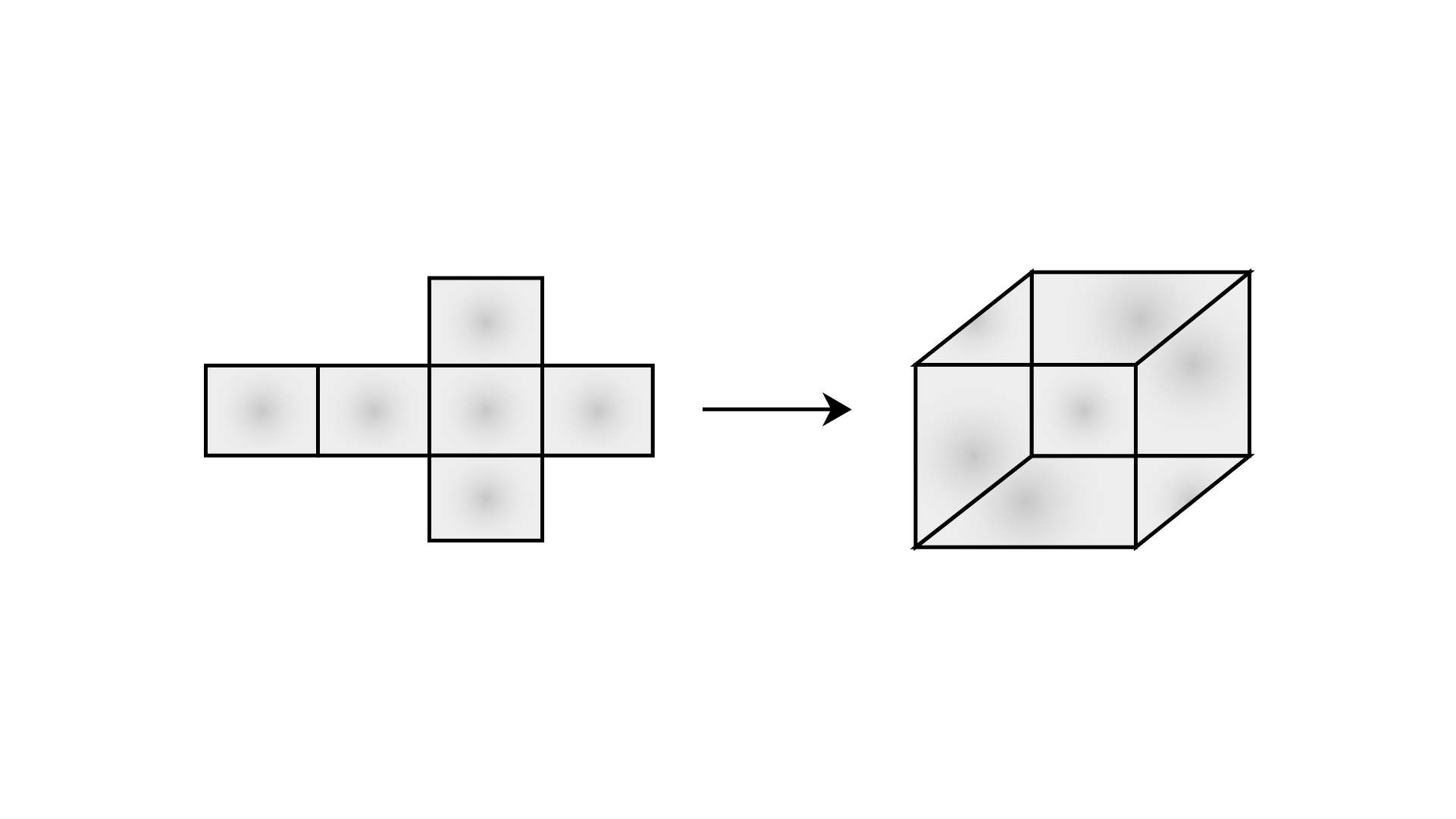
25. Which of the following nets is a net of a cylinder?

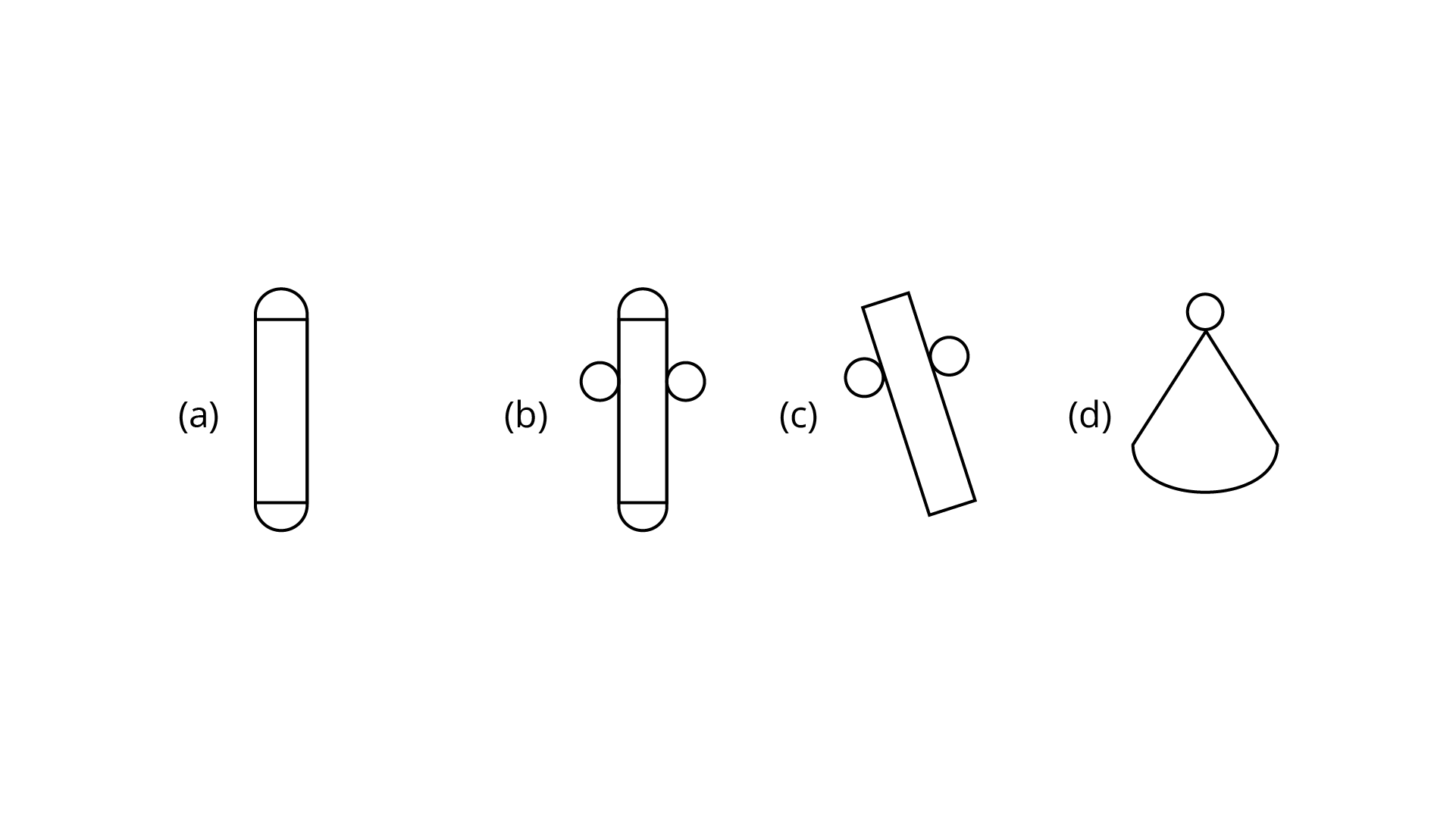
Ans: Option (b) is the correct answer.

Figure (c) is a net of a cylinder.

26. Which of the following letters of English alphabets have more than ${\mathbf{2}}$ lines of symmetry?

(a) Z

(b) O

(c) E

(d) H

Ans: Option (b) is the correct answer.

Figure (b) ‘O’ has more than $2$ lines of symmetry.

27. Take a square piece of paper as shown in figure (1). Fold it along its diagonals as shown in figure (2). Again fold it as shown in figure (3). Imagine that you have cut off ${\mathbf{3}}$ pieces in the form of congruent isosceles right-angled triangles out of it as shown in figure 4.

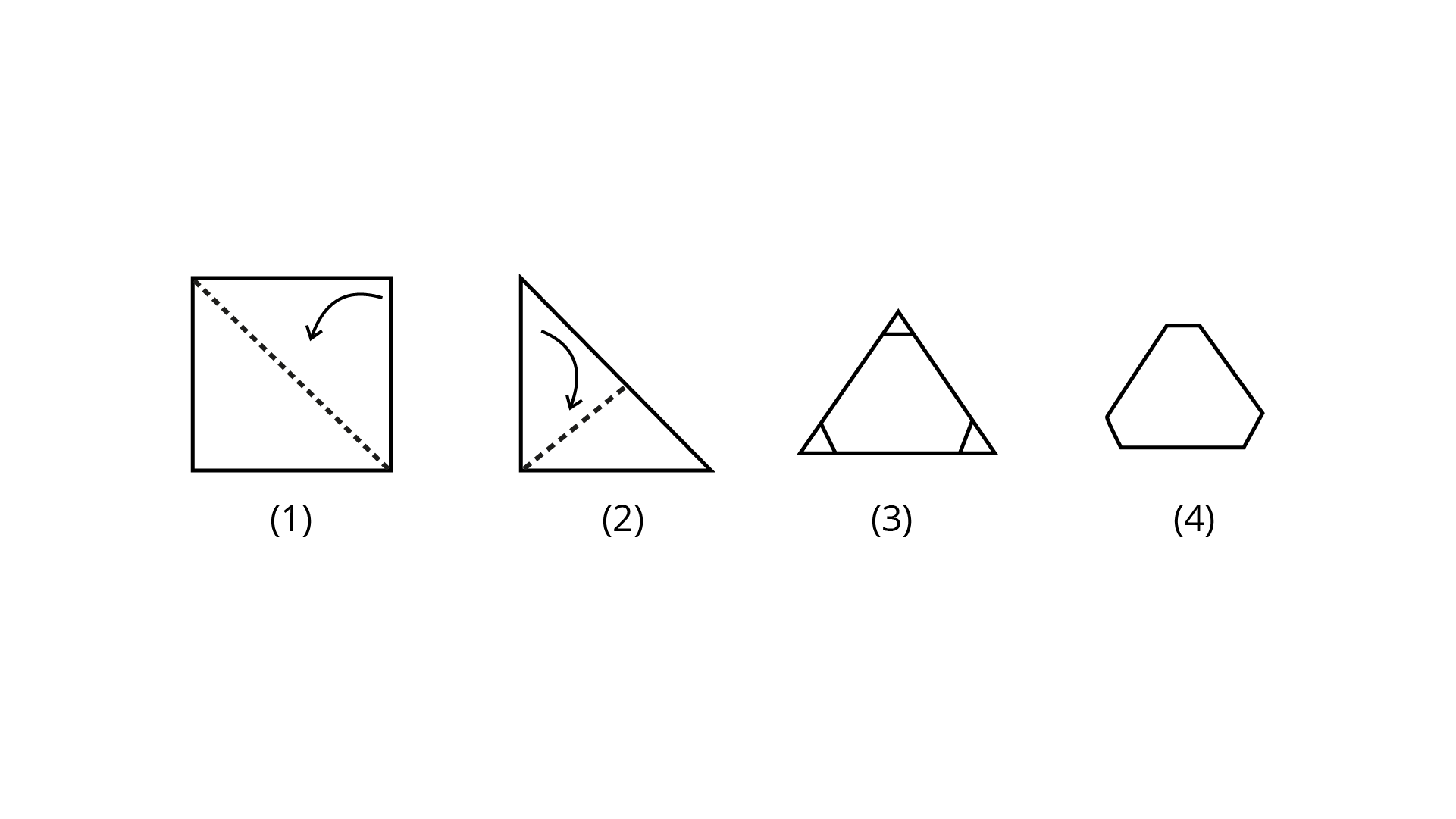
On opening the piece of paper which of the following shapes will you get?

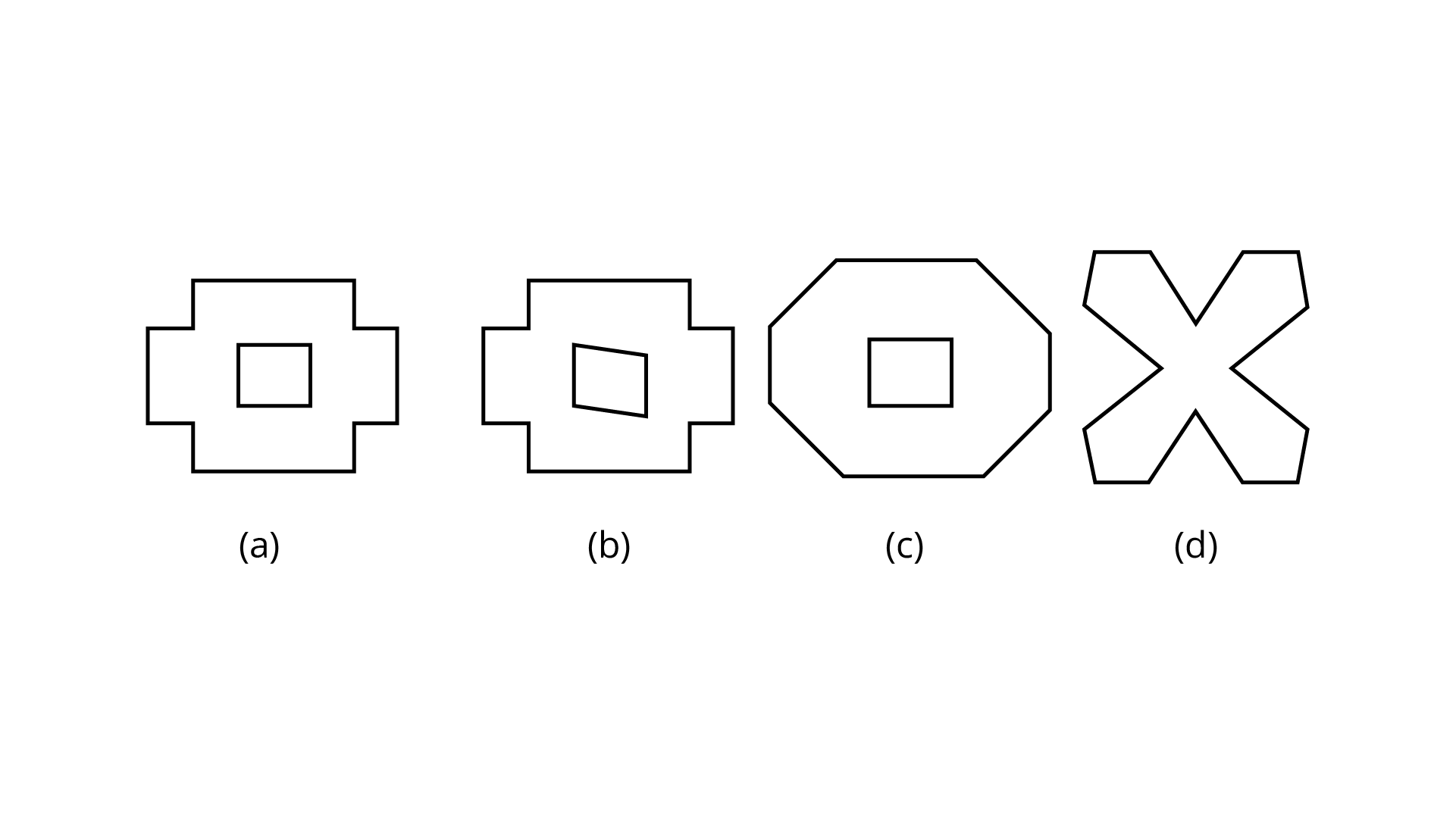
Ans: Option (a) is the correct answer.

On opening the piece of paper shapes, we get a shape like figure (a). 

28. Which of the following ${\mathbf{3}}$-dimensional figures has the top, side and front as triangles?

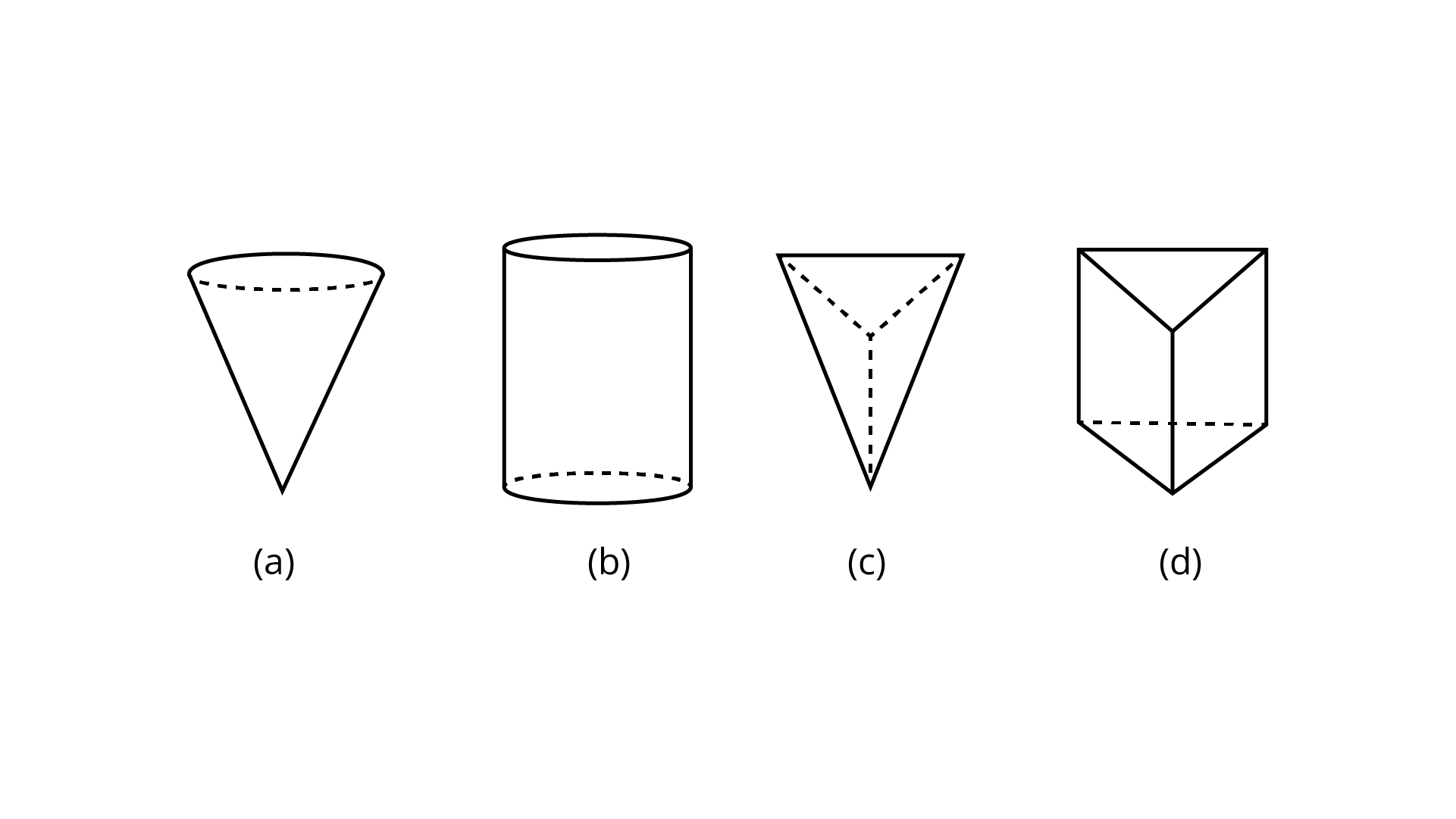
Ans: Figure (c) has a top, side and a front as triangles.

Therefore, option (c) is the correct answer.

In Questions 29 to 58, fill in the blanks to make the statements true.

29. In an isosceles right triangle, the number of lines of symmetry is ________.

Ans: The isosceles right triangle is given by,

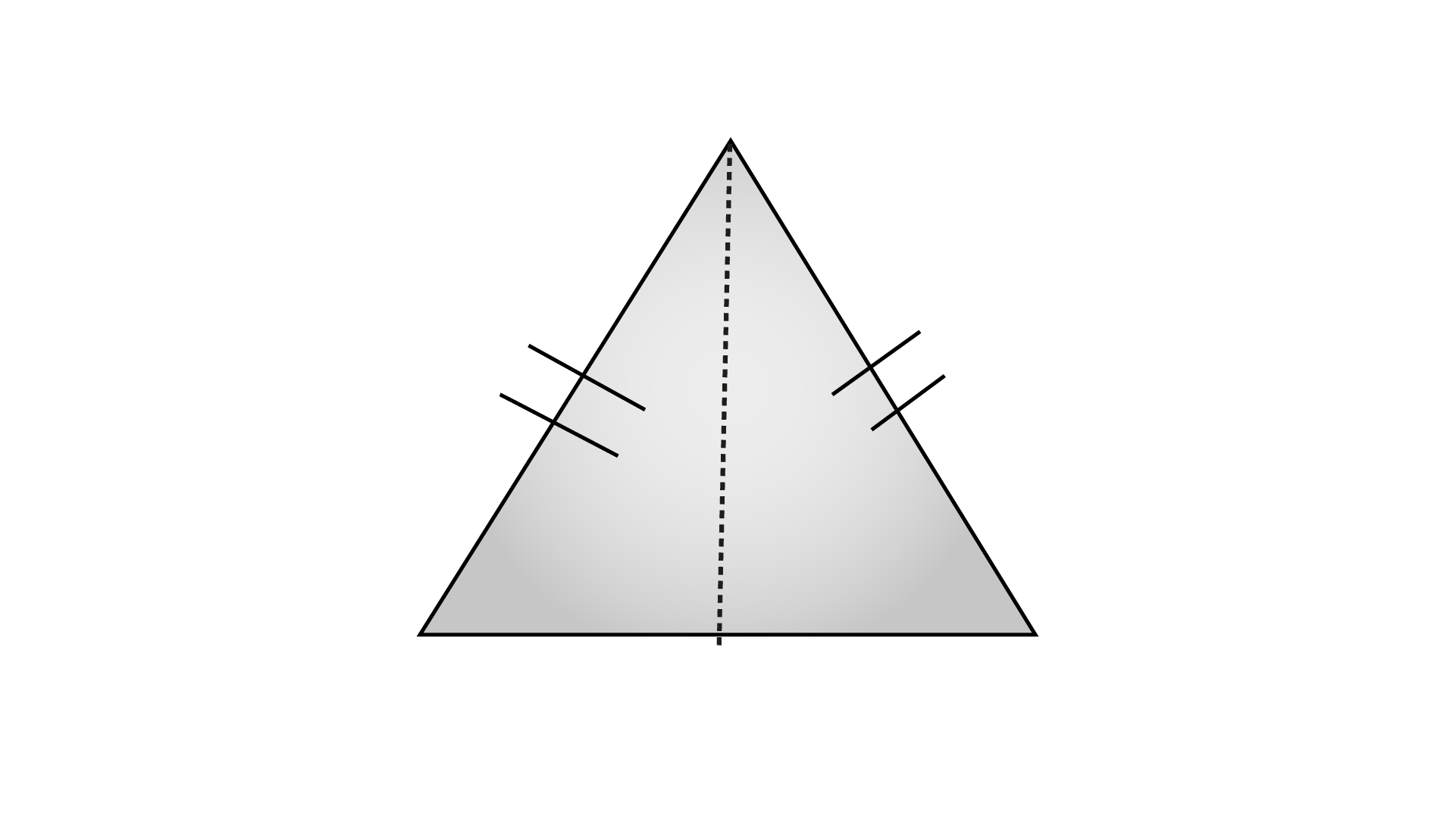
From the figure, it is clear that it has one line of symmetry. Therefore, In an isosceles right triangle, the number of lines of symmetry is one.

30. Rhombus is a figure that has ______lines of symmetry and has a rotational symmetry of order _______.

Ans: Rhombus is a figure that has two lines of symmetry and has a rotational symmetry of order two.

31. __________ triangle is a figure that has a line of symmetry but lacks rotational symmetry.

Ans: The triangle which has only one line of symmetry and no rotational symmetry is the isosceles triangle. Therefore, the Isosceles triangle is a figure that has a line of symmetry but lacks rotational symmetry.

32. __________ is a figure that has neither a line of symmetry nor a rotational symmetry.

Ans: The angles of a scalene triangle have different measures. Therefore, the Scalene triangle is a figure that has neither a line of symmetry nor a rotational symmetry.

33. __________ and __________ are the capital letters of English alphabets that have one line of symmetry but they interchange to each other when rotated through ${\mathbf{180^\circ }}$.

Ans: M and W are the capital letters of English alphabets that have one line of symmetry but they interchange to each other when rotated through ${\mathbf{180^\circ }}$.

34. The common portion of two adjacent faces of a cuboid is called __________.

Ans: Any two adjacent faces of a cuboid meet in a line segment, which is called an edge of the cuboid. Therefore, the common portion of two adjacent faces of a cuboid is called edge.

35. A plane surface of a solid enclosed by edges is called __________ .

Ans: A face is any of the individual flat surfaces of a solid object. Therefore, a plane surface of a solid enclosed by edges is called face.

36. The corners of solid shapes are called its __________.

Ans: Solid shapes have attributes like face, vertices, edges that describe them. Therefore, the corners of solid shapes are called its vertices.

37. A solid with no vertex is __________.

Ans: Sphere is the only solid figure with zero vertex, zero edge and one curved surface. 

Therefore, a solid with no vertex is a sphere.

38. A triangular prism has __________ faces, __________ edges and __________ vertices.

Ans: A triangular prism is polyhedron and a three-dimensional shape.

A triangular prism has $5$ faces, $9$ edges and $6$ vertices.

39. A triangular pyramid has __________ faces, __________ edges and __________vertices.

Ans: A triangular pyramid is a pyramid having a triangular base. A triangular pyramid has $4$ faces, $6$ edges and $4$ vertices.

40. A square pyramid has __________ faces, __________ edges and __________ vertices.

Ans: A square pyramid is a pyramid having a square base. A square pyramid has $5$ faces, $8$ edges and $5$ vertices.

41. Out of __________ faces of a triangular prism, __________are rectangles and __________ are triangles.

Ans: A triangular prism has five faces. Out of $5$ faces of a triangular prism, $3$ are rectangles and $2$ are triangles.

42. The base of a triangular pyramid is a __________.

Ans: A triangular pyramid is a geometric shape that has a triangular base and three triangular faces, having a common vertex. The base of a triangular pyramid is a triangle.

43. Out of __________ faces of a square pyramid, __________ are triangles and __________ is/are squares.

Ans: A square pyramid is a pyramid having a square base. It has $5$ faces, $8$ edges and $5$ vertices. Out of $5$ faces of a square pyramid,$4$ are triangles and $1$ is square.

44. Out of __________ faces of a rectangular pyramid __________ are triangles and base is __________.

Ans: It is known that if the base of a pyramid is rectangular, then it is called a rectangular pyramid. Out of $5$ faces of a rectangular pyramid, $4$ are triangles and base is rectangle.

45. Each of the letters ${\mathbf{H, N, S}}$ and ${\mathbf{Z}}$ has a rotational symmetry of order __________.

Ans: A shape has Rotational Symmetry when it still looks the same after some rotation. Each of the letters ${\mathbf{H, N, S}}$ and ${\mathbf{Z}}$ has a rotational symmetry of order two.

46. Order of rotational symmetry of a rectangle is __________.

Ans: In a complete turn (of ${360^\circ }$ ), the number of times the figure coincides with its original position is called its order of rotational symmetry. Order of rotational symmetry of a rectangle is two.

47. Order of rotational symmetry of a circle is __________.

Ans: In a complete turn (of ${360^\circ }$ ), the number of times the figure coincides with its original position is called its order of rotational symmetry. Order of rotational symmetry of a circle is infinite.

48. Each face of a cuboid is a __________.

Ans:

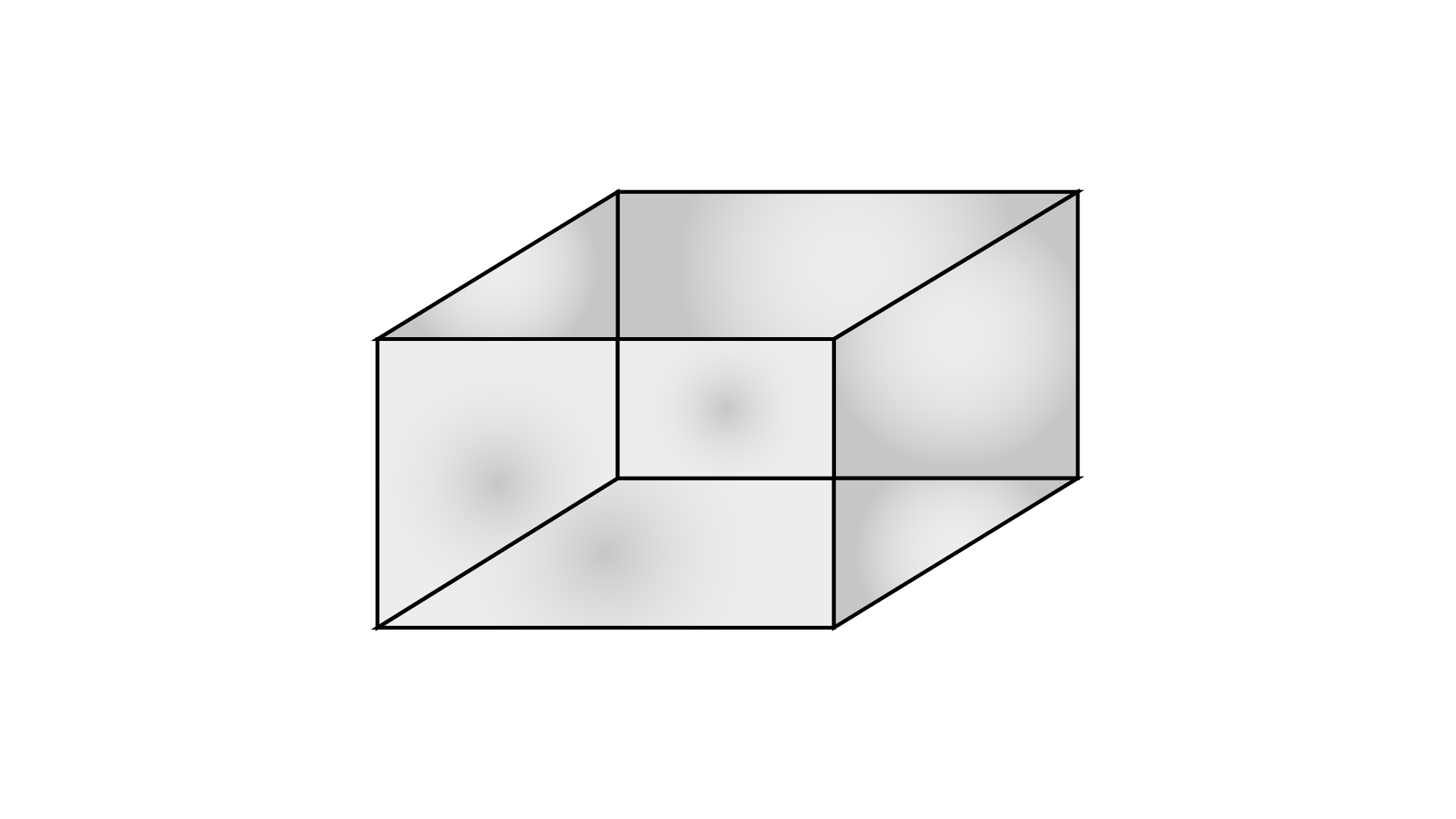
From the picture of cuboid, it is clear that,

Each face of a cuboid is a rectangle.

49. Line of symmetry for an angle is its __________.

Ans: Line of symmetry is an imaginary line that divides the figure in two equal halves. Therefore, the line of symmetry for an angle is its bisector.

50. A parallelogram has __________ line of symmetry.

Ans: There is no line of symmetry of a parallelogram along its length, breadth. There is no superimposition of one half on the other when folded along its half. The diagonals are not symmetrical. Therefore, a parallelogram has no line of symmetry.

51. Order of rotational symmetry of the following figure is_________.

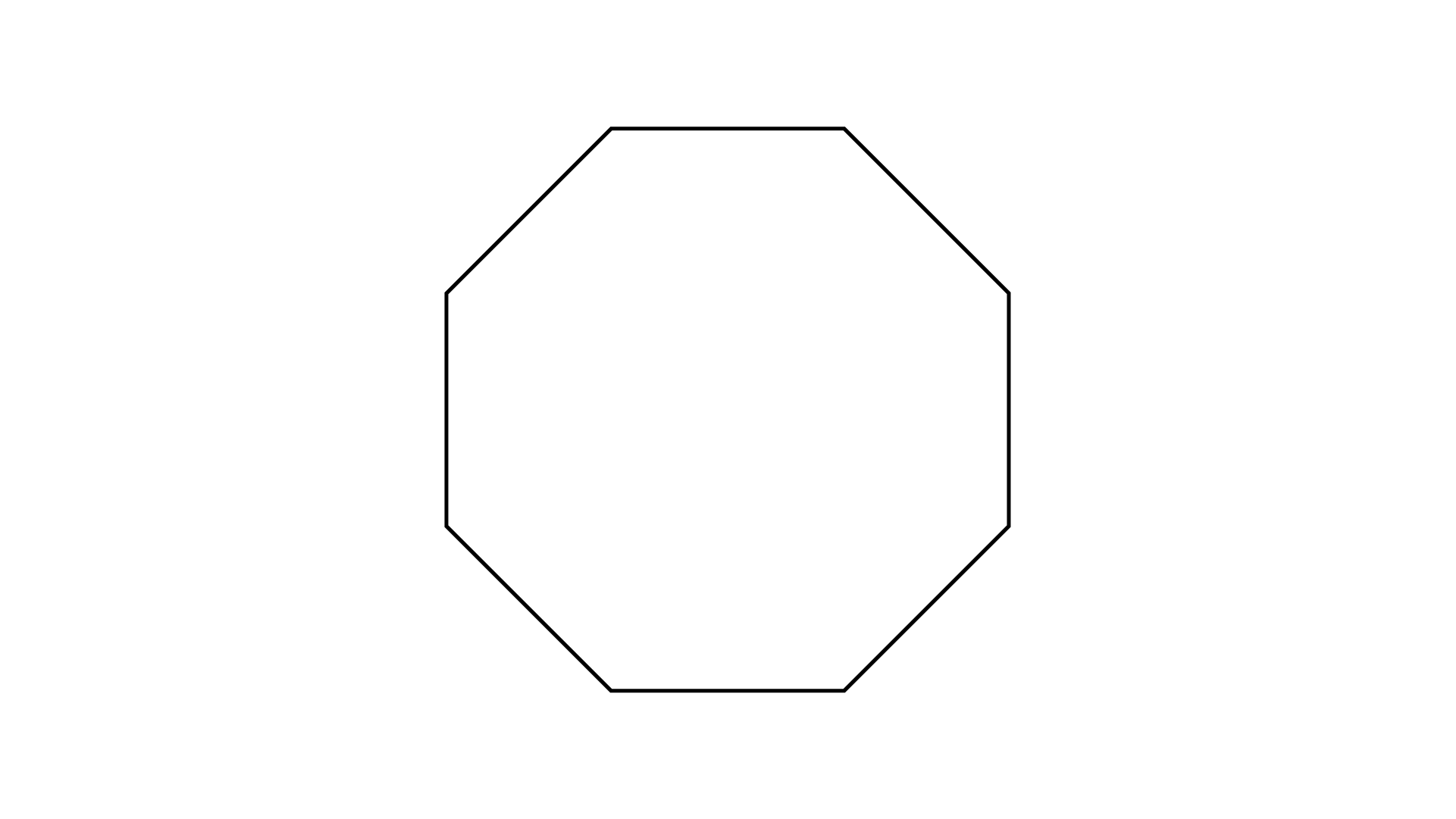
Ans: Octagon possesses eight orders of rotational symmetry.

Order of rotational symmetry is $8$.

52. A __________ triangle has no lines of symmetry.

Ans: In scalene triangle all sides and angles are unequal and so there is no line of symmetry. 

A Scalene triangle has no lines of symmetry.

53. Cuboid is a rectangular_________ .

Ans: Rectangular prism and cuboid refers to the same solid body. 

Cuboid is a rectangular prism.

54. A sphere has __________vertex, __________edge and __________curved surface.

Ans: Sphere is a solid body with zero vertex, zero edge and one curved surface. 

A sphere has $0$ vertex, $0$ edge and $1$ curved surface.

55. The following figure is a net of a __________.

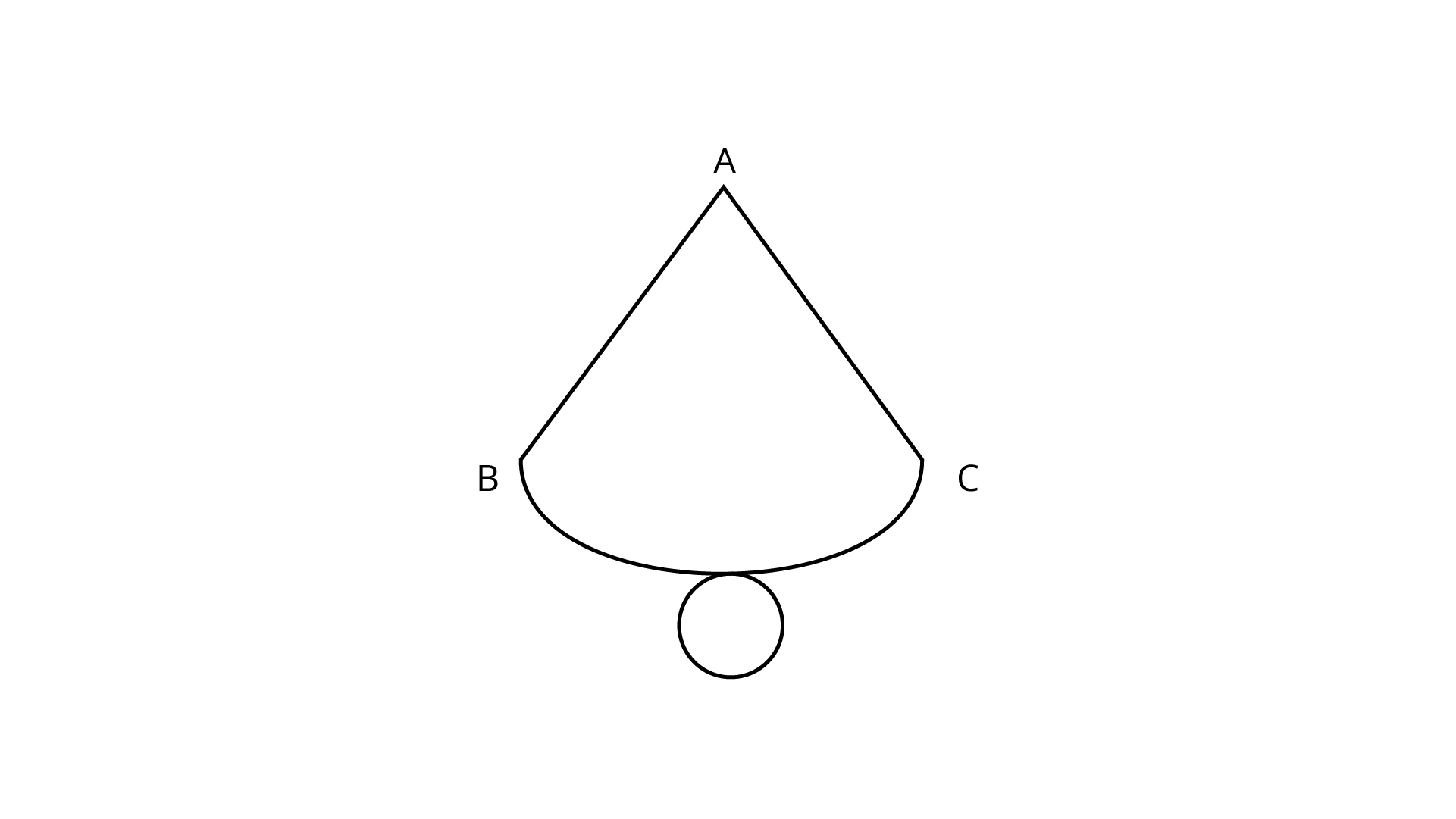
→ Circumference of circle = ______.

Ans: On observing the given figure, it represents a cone.

Therefore It is the net of a cone.

→ Circumference of circle ${\text{ =  2}}\pi r$.

56.  The following is a net of a __________.

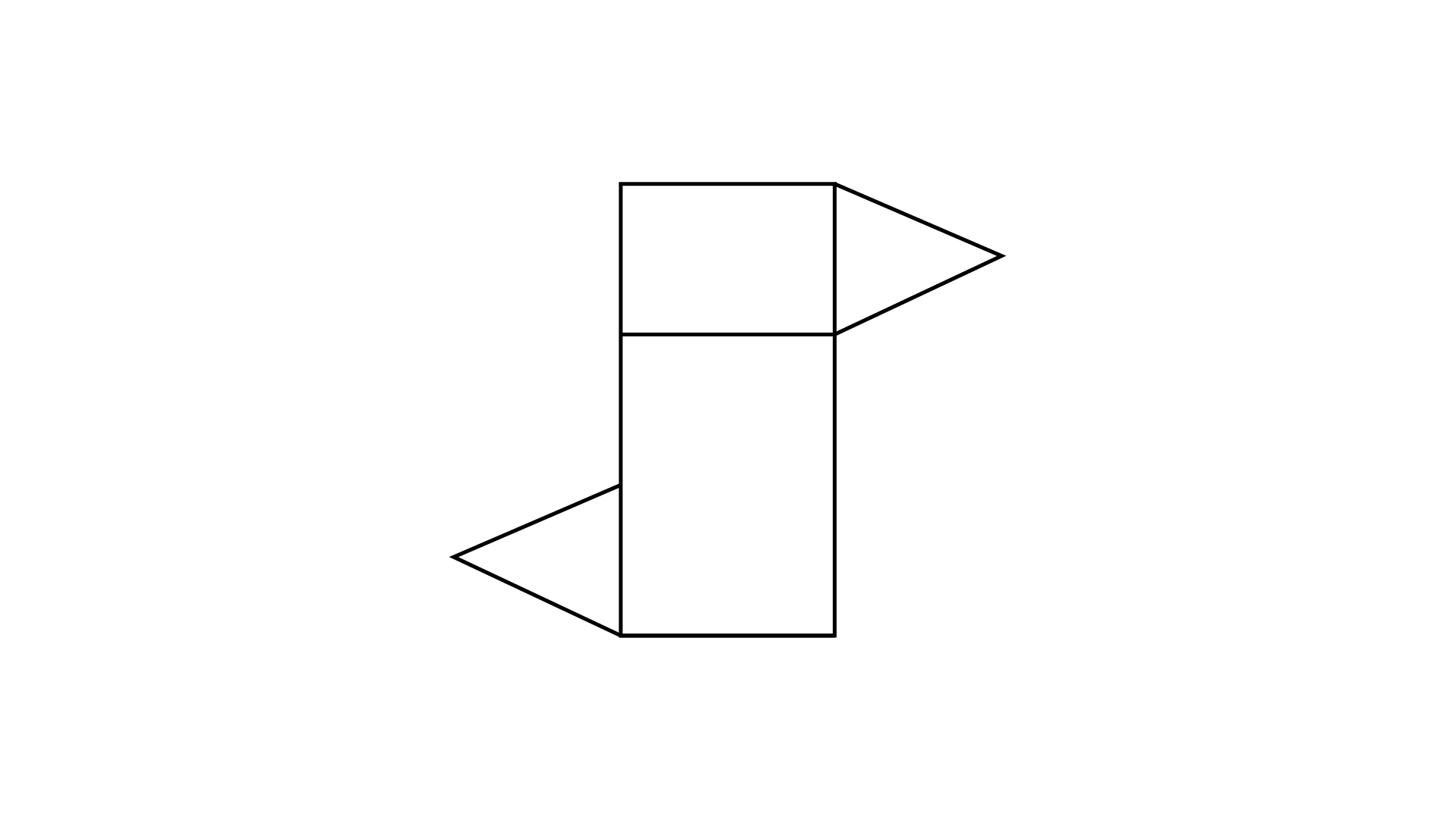
Ans: On observing the given figure, it represents a triangular prism.

Therefore it is a net of a triangular prism.

57. Order of rotational symmetry of the following figure is __________.

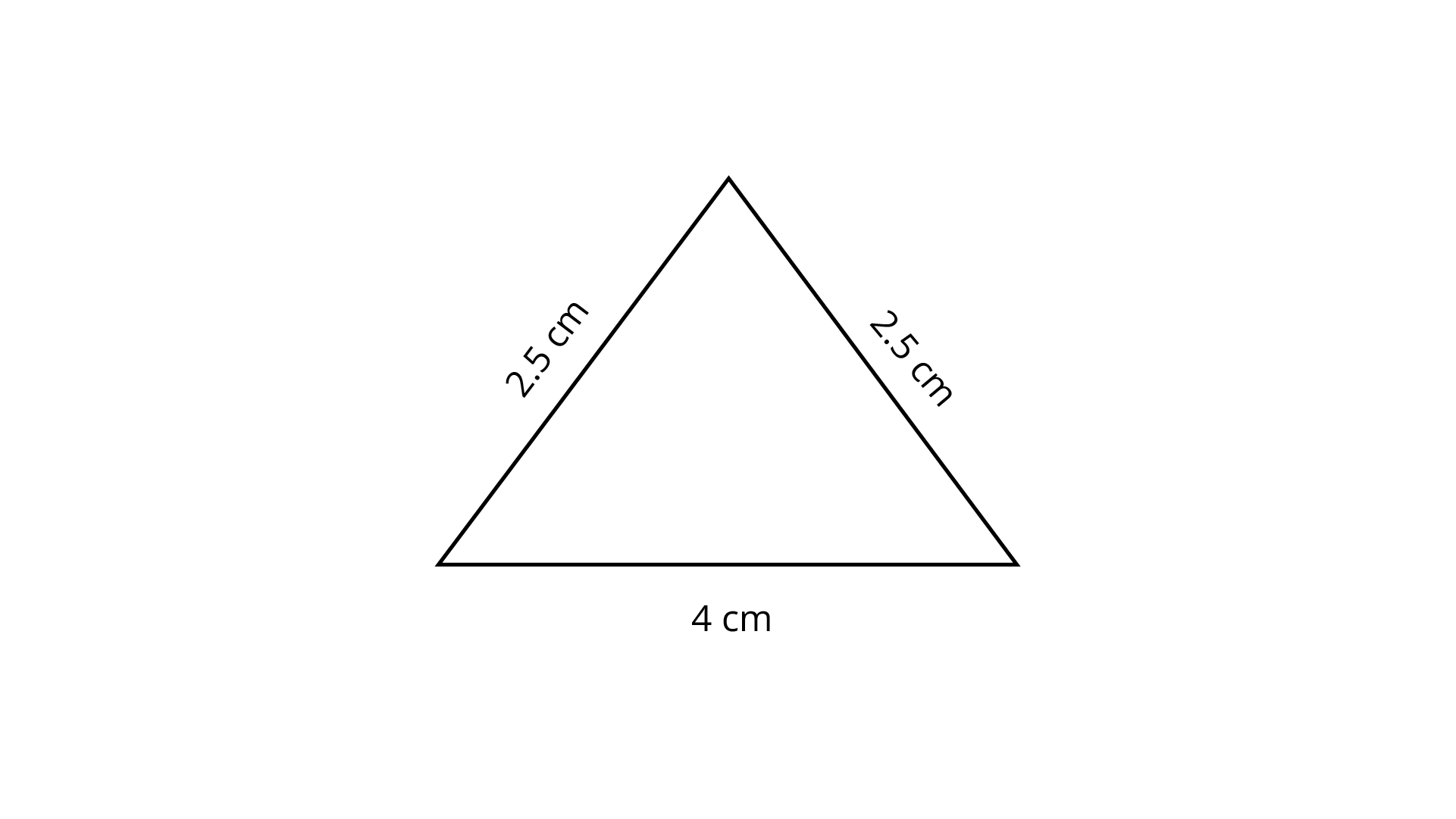
Ans: Given figure represents an isosceles triangle.

Isosceles triangle possesses one order of rotational symmetry.

Order of rotational symmetry is one.

58. Identical cubes are stacked in the corner of a room as shown below. The number of cubes that are not visible are _________.

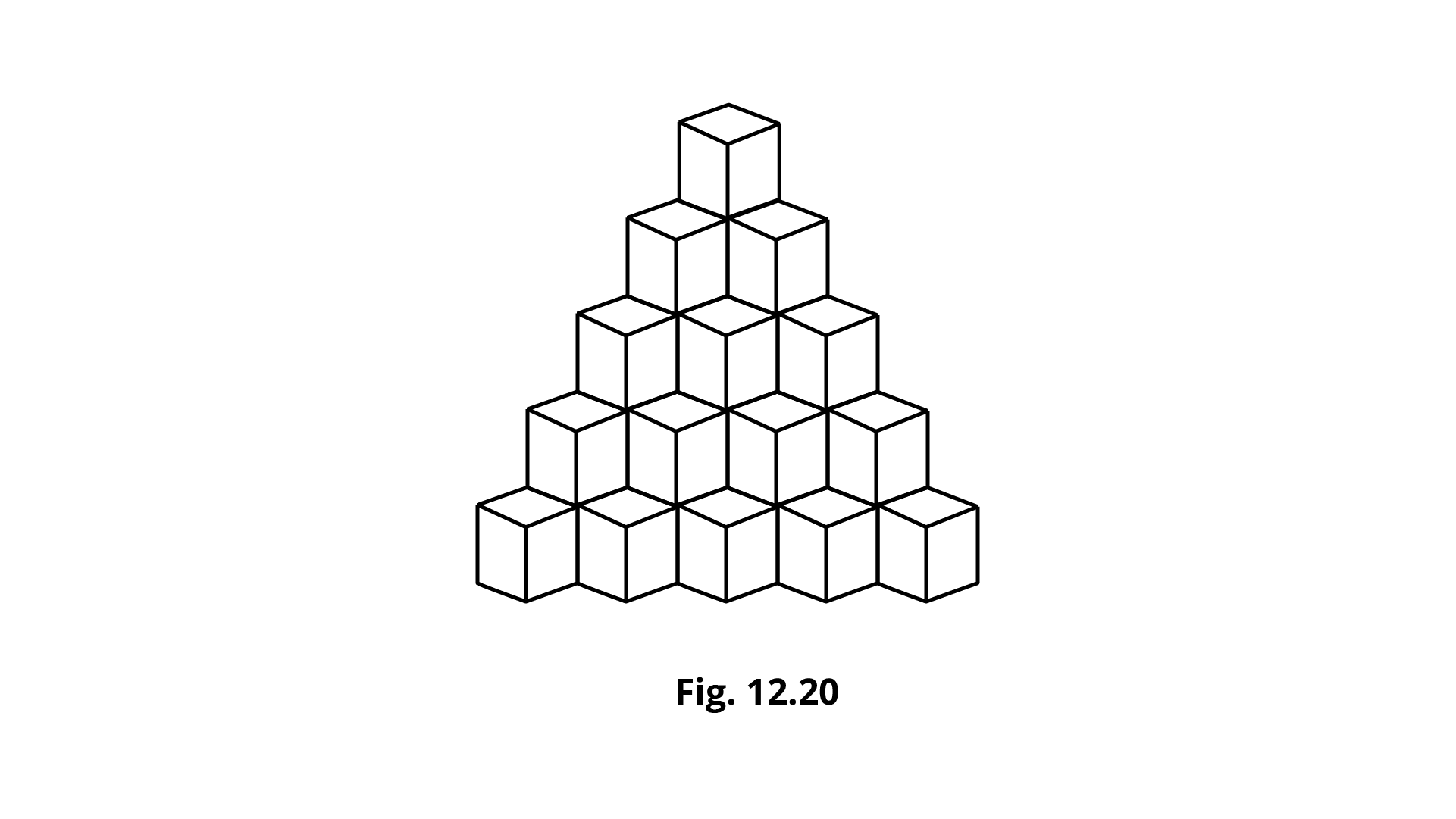
Ans: There are $20$ such cubes which are not visible.

Identical cubes are stacked in the corner of a room as shown below. The number of cubes that are not visible are $20$.

In Questions from 59 to 92, state whether the statements are True or False.

59. We can draw exactly one triangle whose angles are ${{70}^{\circ}, {30}^{\circ }}$ and ${\mathbf{80^\circ }}$.

Ans: This is not true exactly as there can be infinite number of triangles with angles ${70}^{\circ} ,{30}^{\circ} $ and ${80}^{\circ} $ with various different combinations of sides.

Therefore, the given statement is False.

60. The distance between the two parallel lines is the same everywhere.

Ans: The distance between the two parallel lines is always the same everywhere.

Therefore, the given statement is True.

61. A circle has two lines of symmetry.

Ans: Circle can have an infinite number of symmetries, not two.

Therefore, the given statement is False.

62. An angle has two lines of symmetry.

Ans: Bisector is only the line of symmetry of an angle.

Therefore, the given statement is False.

63. A regular hexagon has six lines of symmetry.

Ans: The number of lines of symmetry in a polygon is equal to its number of sides.

Therefore, the given statement is True.

64. An isosceles trapezium has one line of symmetry.

Ans: An isosceles trapezium has only one line of symmetry which is along the line joining the mid-points of the two opposite sides.

Therefore, the given statement is True.

65. A parallelogram has two lines of symmetry.

Ans: Parallelogram possesses zero line of symmetry.

Therefore, the given statement is False.

66. Order of rotational symmetry of a rhombus is four.

Ans: The order of rotational symmetry of a rhombus is only two not four.

Therefore, the given statement is False.

67. An equilateral triangle has six lines of symmetry.

Ans: An equilateral triangle has three lines of symmetry along the median of the triangle. 

Therefore, the given statement is False.

68. Order of rotational symmetry of a semi circle is two.

Ans: The order of rotational symmetry of a semicircle is only one.

Therefore, the given statement is False.

69. In an oblique sketch of the solid, the measurements are kept proportional.

Ans: The measurements are not kept proportional in the oblique sketch of the solid.

Therefore, the given statement is False.

70. An isometric sketch does not have proportional length.

Ans: An isometric sketch always possesses a proportional length.

Therefore, the given statement is False.

71. A cylinder has no vertex.

Ans: No vertex is present in the cylinder.

Therefore, the given statement is True.

72. All the faces, except the base of a square pyramid are triangular.

Ans: The base of a square pyramid is square and the rest of the faces are triangular.

A square pyramid has $4$ triangular faces and one square base.

Therefore, the given statement is True.

73. A pyramid has only one vertex.

Ans: There are at least four vertices in a pyramid.

Therefore, the given statement is False.

74. A triangular prism has ${\mathbf{5}}$ faces, ${\mathbf{9}}$ edges and ${\mathbf{6}}$ vertices.

Ans: A triangular prism is a prism that has two triangular bases and three rectangular sides. It has $6$vertices, $9$ edges, and $5$ faces.

Therefore, the given statement is True.

75. If the base of a pyramid is a square, it is called a square pyramid.

Ans: The name of a pyramid is based on the base of the pyramid. 

Thus, if the base of a pyramid is a square, then it is called a square pyramid.

Therefore, the given statement is True.

76. A rectangular pyramid has ${\mathbf{5}}$ rectangular faces.

Ans: A rectangular pyramid has in total $5$ faces, out of which $1$ is rectangular.

Therefore, the given statement is False.

77. Rectangular prisms and cuboids refer to the same solid.

Ans: A rectangular prism is also known as a cuboid.

So, a rectangular prism and cuboid represents the same solid.

Therefore, the given statement is True.

78. A tetrahedron has ${\mathbf{3}}$ triangular faces and ${\mathbf{1}}$ rectangular faces.

Ans: A tetrahedron has $4$ triangular faces.

Therefore, the given statement is False.

79. While a rectangle is a ${\mathbf{2 - D}}$ figure, a cuboid is a ${\mathbf{3 - D}}$ figure.

Ans: ${\text{2 - D}}$ shapes including rectangles, squares, circles and triangles. ${\text{3 - D}}$ shapes including cubes, cuboids, spheres etc.

Therefore, the given statement is True.

80. While the sphere is a ${\mathbf{2 - D}}$ figure, the circle is a ${\mathbf{3 - D}}$ figure.

Ans: ${\text{2 - D}}$ shapes including rectangles, squares, circles and triangles. ${\text{3 - D}}$ shapes including cubes, cuboids, spheres etc.

Therefore, the given statement is False.

81. Two dimensional figures are also called plane figures.

Ans: Two-dimensional figure is a figure that lies completely in one plane.

So, two dimensional figures are also known as plane figures.

Therefore, the given statement is True.

82. A cone is a polyhedron.

Ans: Polyhedrons are ${\text{3 - D}}$ figures with rectangular bases.

So, a cone is not a polyhedron.

Therefore, the given statement is False.

83. A prism has four bases.

Ans: A prism has only one base.

Therefore, the given statement is False.

84. The number of lines of symmetry of a regular polygon is equal to the vertices of the polygon.

Ans: It is true that the number of lines of symmetry of a regular polygon is equal to the vertices of the polygon.

Therefore, the given statement is True.

85. The order of rotational symmetry of a figure is ${\mathbf{4}}$ and the angle of rotation is ${\mathbf{180^\circ }}$ only.

Ans: If the order of rotational symmetry of a figure is $4$ then the angle of rotation must be ${90}^{\circ} $ only.

Therefore, the given statement is False.

86. After rotating a figure by ${\mathbf{120^\circ }}$ about its center, the figure coincides with its original position. This will happen again if the figure is rotated at an angle of ${\mathbf{240^\circ }}$.

Ans: It is true that after rotating a figure by $120^\circ $ about its center, the figure coincides with its original position. This will happen again if the figure is rotated at an angle of $240^\circ $.

Therefore, the given statement is True.

87. Mirror reflection leads to symmetry always.

Ans: Mirror reflection does not always lead to symmetry.

Therefore, the given statement is False.

88. Rotation turns an object about a fixed point which is known as the center of rotation.

Ans: The fixed point is the center of rotation. And the angle by which the object rotates is the angle of rotation.

Therefore, the given statement is True.

89. Isometric sheet divides the paper into small isosceles triangles made up of dots or lines.

Ans: Isometric sheet divides the paper into small equilateral triangles made up of dots or lines.

Therefore, the given statement is False.

90. The circle, the square, the rectangle and the triangle are examples of plane figures.

Ans: A plane figure is a flat figure with closed lines that stays in a single plane. The lines of the figure can be straight, curved or a combination. Some examples of plane figures are triangles, rectangles, squares, rhombuses, parallelograms, circles, ovals, hearts, pentagons and hexagons.

Therefore, the given statement is True.

91. The solid shapes are two-dimensional.

Ans: The solid shapes are three-dimensional. 

Examples of solid shapes are cone, cube etc.

Therefore, the given statement is False.

92. Triangle with length of sides as ${\mathbf{5cm}}$, ${\mathbf{6cm}}$ and ${\mathbf{11cm}}$ can be constructed.

Ans: Condition for constructing a triangle is that Sum of any two sides of a triangle should be greater than the third side.

But here, $6{\text{cm}} + 5{\text{cm}} = 11{\text{cm}}$ and the condition is not satisfied.

Therefore, the given statement is False.

93. Draw the top, side and front views of the solids given below in Figures 12.21 and 12.22:

(i) 

Ans: For the given figure,

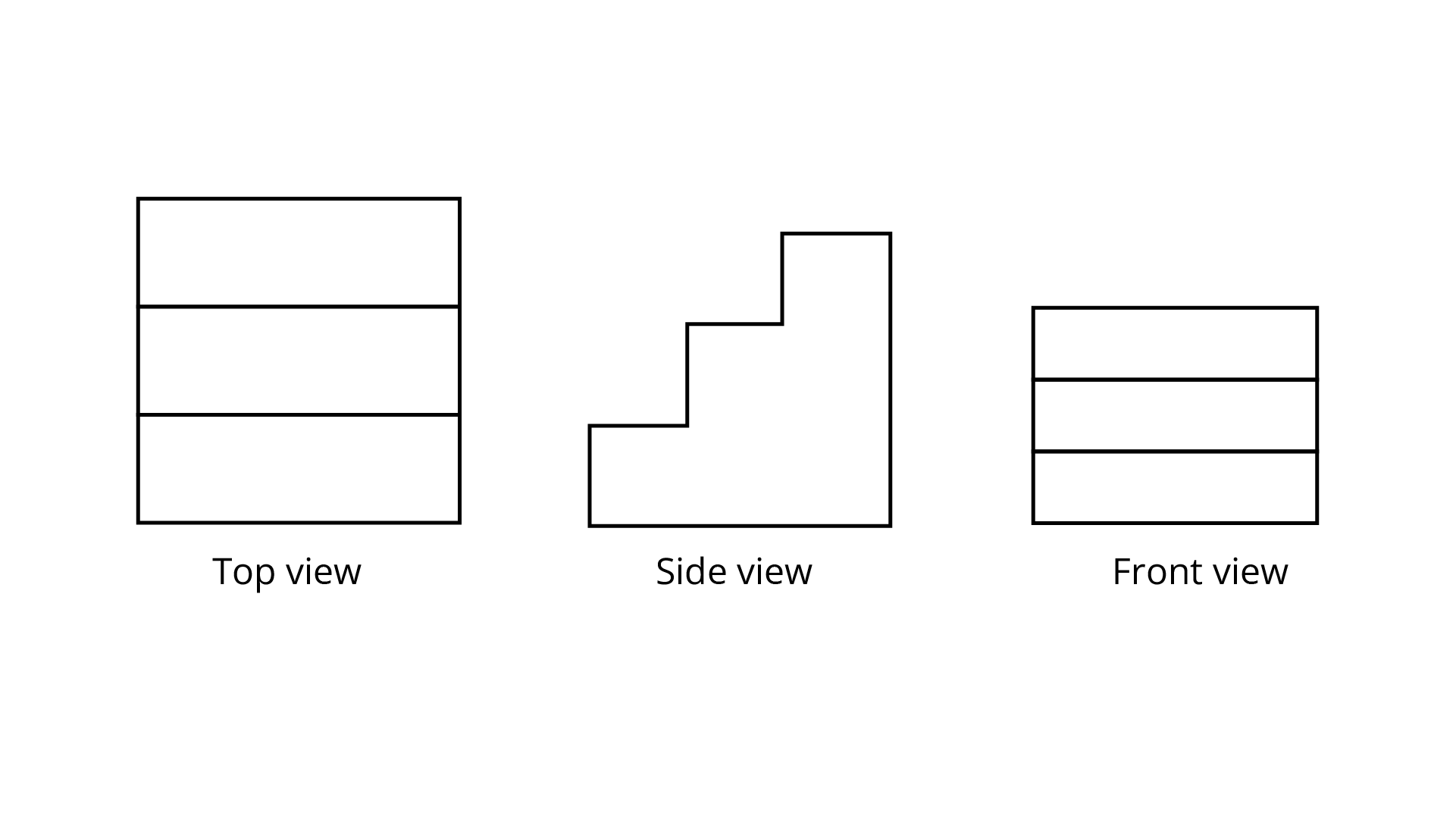
(ii) 

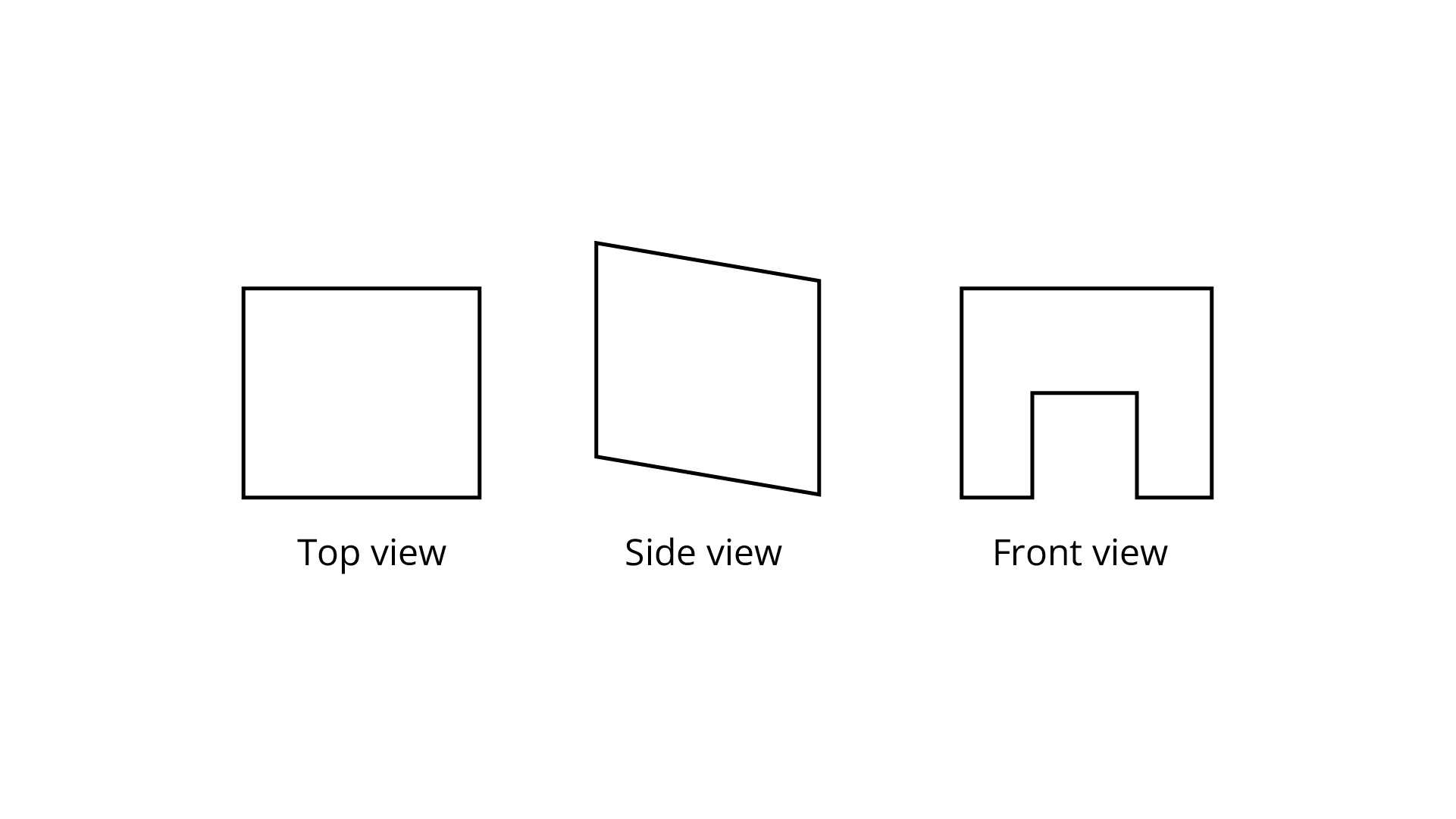
Ans:

94. Draw a solid using the top. side and front views as shown below. {Use Isometric dot paper}.

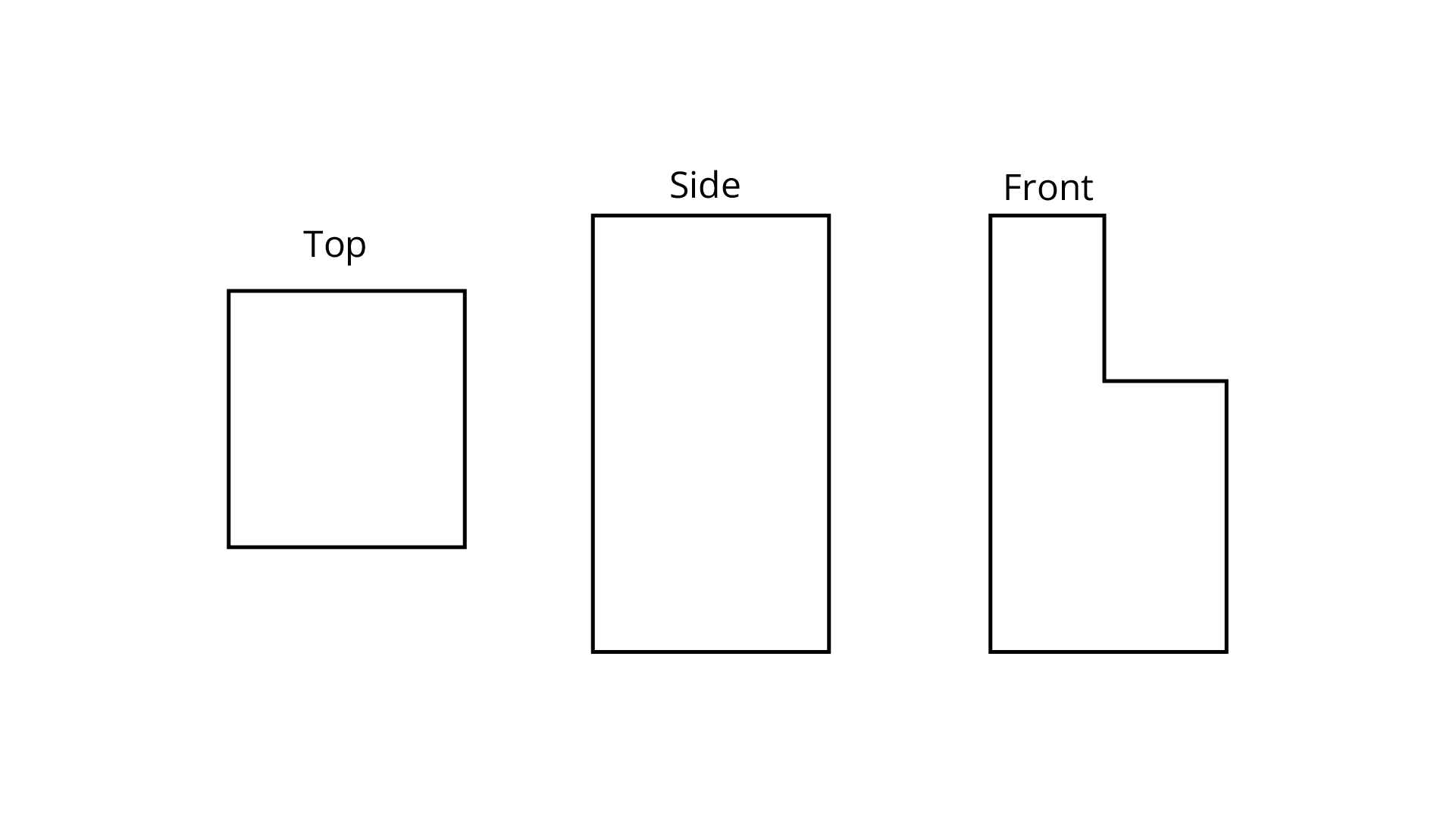
Ans:

95. Construct a right-angled triangle whose hypotenuse measures ${\mathbf{5 cm}}$ and one of the other sides measures ${\mathbf{3}}{\mathbf{.2 cm}}{\mathbf{.}}$

Ans: Steps of construction:
(1) Draw a line AB=  3.2 cm.
(2) Construct a right angle ${\mathbf{90}}^\circ $ at point B, that is $\angle {\text{ABY}  =  {90}^{\circ} }$.
(3) From point A, cut an arc 5 cm on BY at ${\text{C}}$
(4) Join ${\text{AC}}$.

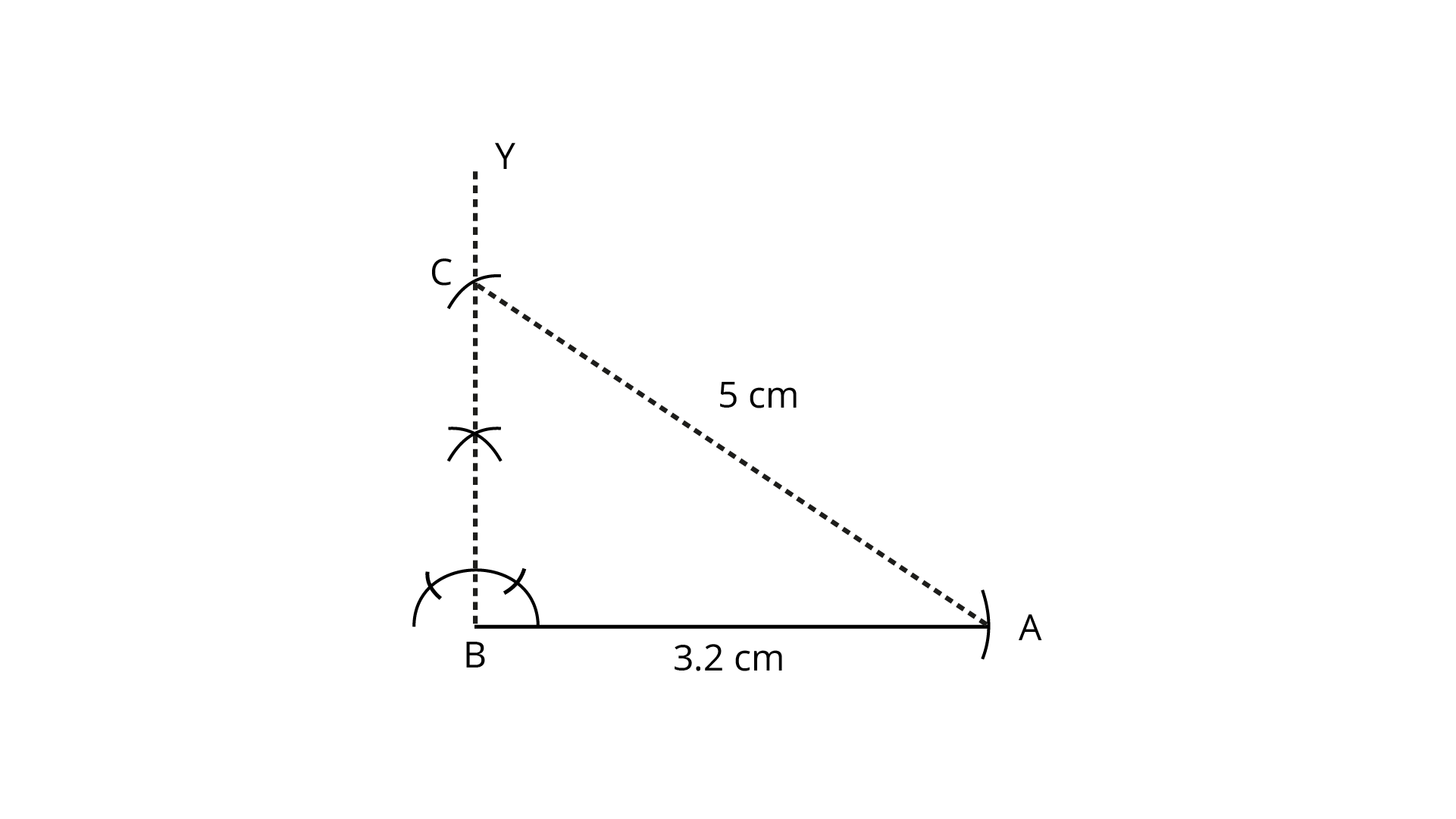
Therefore $\Delta {\text{ABC}}$ is the required triangle, having hypotenuse ${\text{AC  =  5 cm}}$ and ${\text{AB  =  3}}{\text{.2 cm}}{\text{.}}$

96. Construct a right-angled isosceles triangle with one side (other than hypotenuse) of length ${\mathbf{4}}{\mathbf{.5 cm}}$.

Ans: Steps of construction:
(1) Draw a line${\text{AB  =  4}}{\text{.5 cm}}$.
(2) Construct a right angle $\left( {90^\circ } \right)$ at point ${\text{B}}$, that is  $\angle ABY  =  {90}^{\circ}.$
(3) From point ${\text{B}}$, cut an arc ${\text{4}}{\text{.5 cm}}$ on ${\text{BY}}$ at ${\text{C}}$.
(4) Join ${\text{AC}}$.

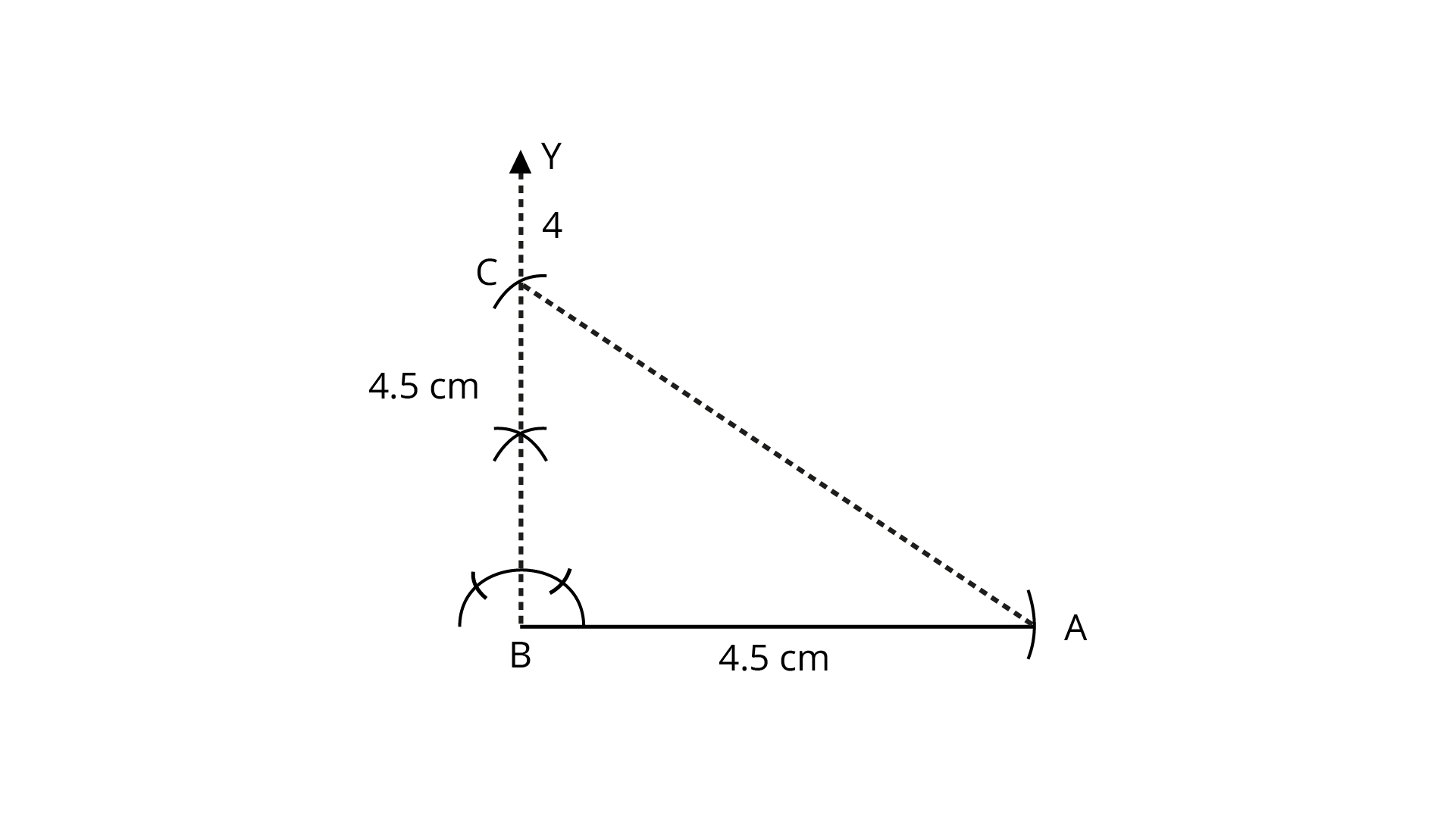
Therefore,$\Delta {\text{ABC}}$ is the required triangle with one side of length ${\text{4}}{\text{.5 cm}}$.

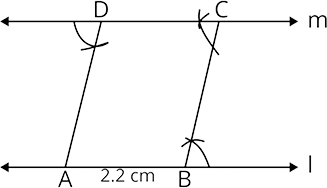
97. Draw two parallel lines at a distance of ${\mathbf{2}}{\mathbf{.2cm}}$ apart.

Ans: Steps of construction:
(1) Draw a line ${\text{l}}$ and mark a point ${\text{C}}$ outside it.

(2) Take a point ${\text{B}}$ on line ${\text{l}}$ and join ${\text{BC}}$.

(3) Draw a line parallel to the line ${\text{l}}$ passing through ${\text{C}}$.

(4) Mark a point ${\text{D}}$ on line ${\text{m}}$, at a distance of $2.2{\text{cm}}$ from ${\text{C}}$. 

(5) Mark angle arc at point D which should be equal to angle arc at point C.

(5) Through ${\text{D}}$ draw a line at the angle arc which will be parallel to the BC line.

98. Draw an isosceles triangle with each of equal sides of length ${\mathbf{3cm}}$ and the angle between them as ${\mathbf{45^\circ }}$.

Ans: Steps of construction: 

(1) Draw a line segment ${\text{AB}}$ of length $3{\text{cm}}$.

(2) Draw an angle of$45^\circ $ on point ${\text{B}}$ and produce it to ray ${\text{Y}}$.

(3) With ${\text{B}}$ as center, draw an arc of $3{\text{cm}}$ which intersects ray ${\text{BY}}$ at ${\text{C}}$.

(4) Join ${\text{AC}}$.

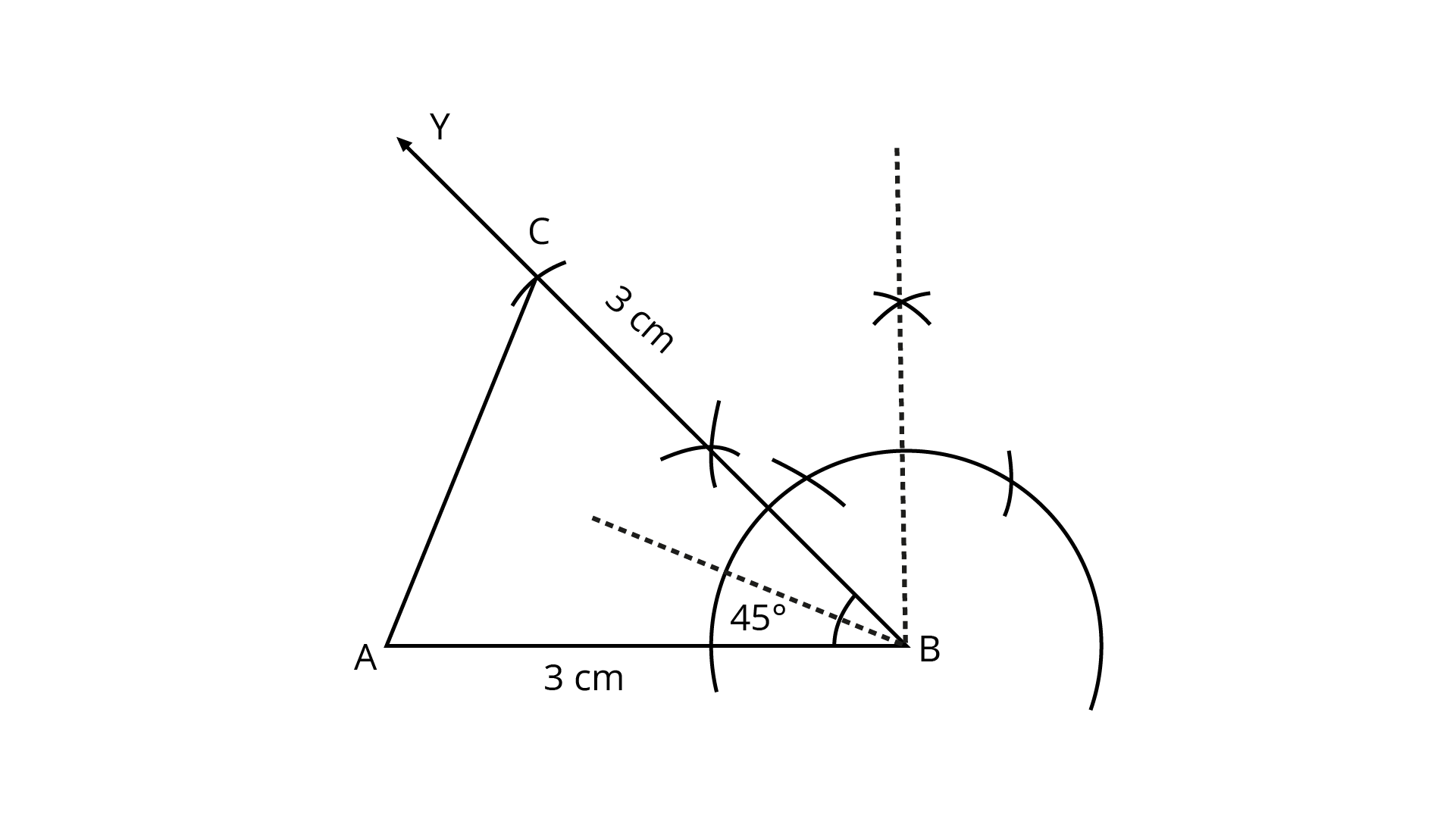
Thus,$\Delta {\text{ABC}}$ is the required isosceles triangle.

99. Draw a triangle whose sides are of lengths $4 cm, 5 cm$ and $7 cm$.

Ans: Let us assume that given sides are ${\text{BC  = 7 cm, AB  =  4 cm}}$ and ${\text{AC  =  5 cm}}$.

Steps of construction:

(1) Draw a line ${\text{BC  = 7 cm}}.$

(2) With center ${\text{B}}$ and radius ${\text{4 cm}}$ draw an arc.

(3) With center ${\text{C}}$ and radius ${\text{5 cm}},$ draw an arc which cuts the previous arc at ${\text{A}}$.

(4) Join ${\text{AB}} $ and ${\text{AC}}$.

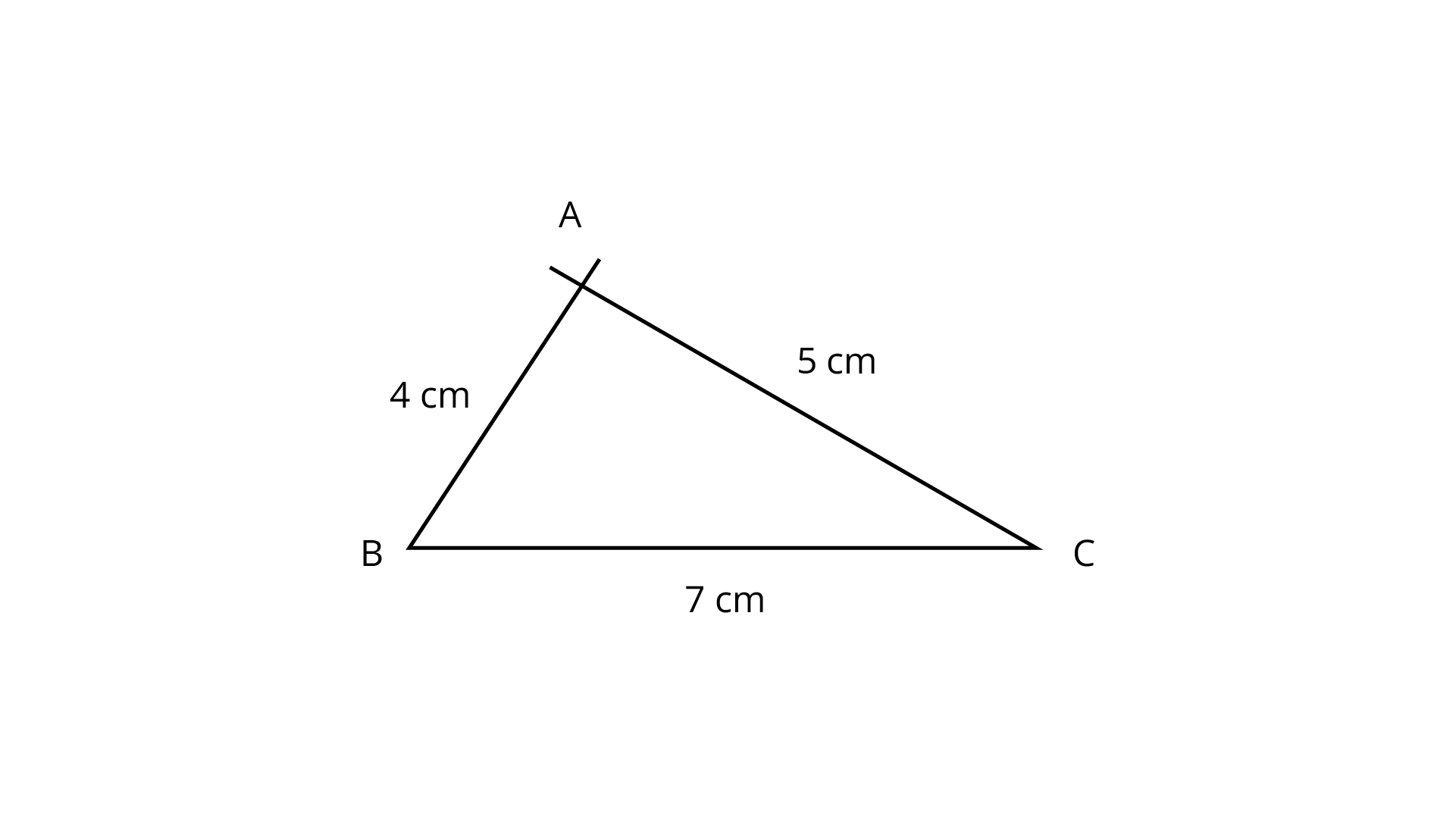
Hence,$\Delta {\text{ABC}}$ is the required triangle in which ${\text{BC  = 7 cm, AB  =  4 cm}}$ and ${\text{AC  =  5 cm}}.$

100. Construct an obtuse angled triangle which has a base of ${\mathbf{5}}{\mathbf{.5 cm}}$ and base angles of ${\mathbf{30^\circ }}$ and ${\mathbf{120^\circ }}$.

Ans: Steps of construction:

(1) Draw a line segment ${\text{BC}}$ of length ${\text{5}}{\text{.5 cm}}.$
(2) Draw an angle of $120^\circ $ on point ${\text{B}}$ and produce it to ray ${\text{Y}}$.
(3) Draw an angle of $30^\circ $ on point ${\text{C}}$ and produce it to ray ${\text{X}}$.
(4) Extend ${\text{BY}}$ and ${\text{CX}}$ to intersect at point ${\text{A}}$.

Hence, $\Delta {\text{ABC}}$ is the required triangle.

101. Construct an equilateral triangle ${\text{ABC}}$ of side ${\text{6}}\,{\text{cm}}$.

Ans: Steps of construction:
(1) Draw a line segment ${\text{AB = 6}}\,{\text{cm}}$ 

(2) Draw an arc of radius ${\text{6}}\,{\text{cm}}$ from point ${\text{A}}.$
(3) Now, draw another arc of radius ${\text{6}}\,{\text{cm}}$ from point ${\text{B}}$ to cut previous arc at ${\text{C}}.$
(4) Join ${\text{A}}$ to ${\text{C}}$ and ${\text{B}}$ to ${\text{C}}$.

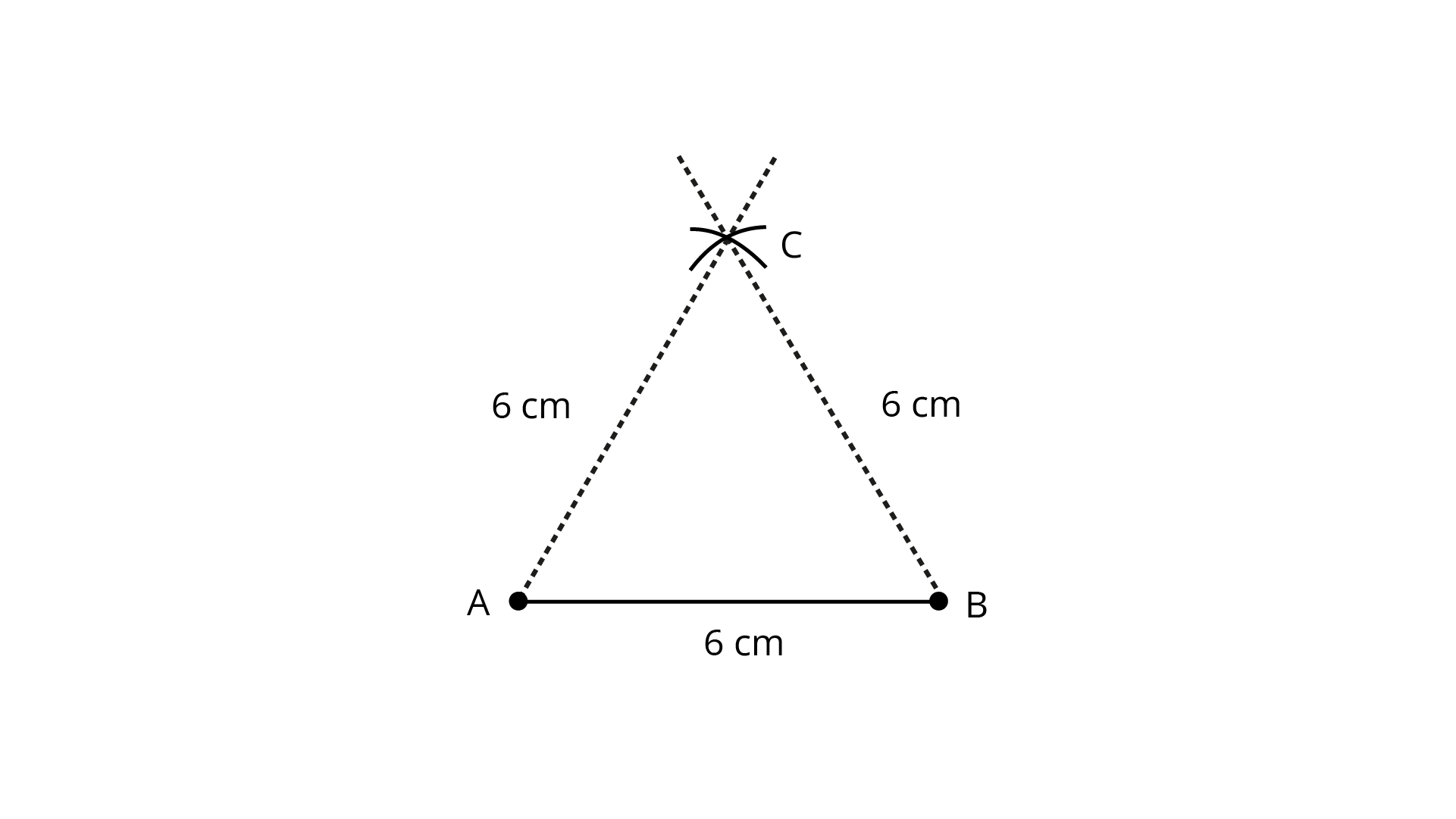
Hence, $\Delta {\text{ABC}}$ is the required triangle of side ${\text{6}}\,{\text{cm}}$.

102. By what minimum angle does a regular hexagon rotate so as to coincide with its original position for the first time?

Ans:

A regular hexagon must be rotated through a minimum angle of ${60}^{\circ} $. So, that it can coincide with its original position for the first time. Because the angle of rotation of hexagon is,

$\dfrac{{{{360}^\circ }}}{{{\text{ Number of sides }}}} = \dfrac{{{{360}^\circ }}}{6} = {60^\circ }$

103. In each of the following figures, write the number of lines of symmetry and order of rotational symmetry.

{Hint: Consider these as 2-D figures not as 3-D objects.}

(a)

Ans: The number of lines of symmetry is $1$. 

The order of rotational symmetry is $1$.

(b)

Ans: The number of lines of symmetry is $1$. 

The order of rotational symmetry is $1$.

(c)

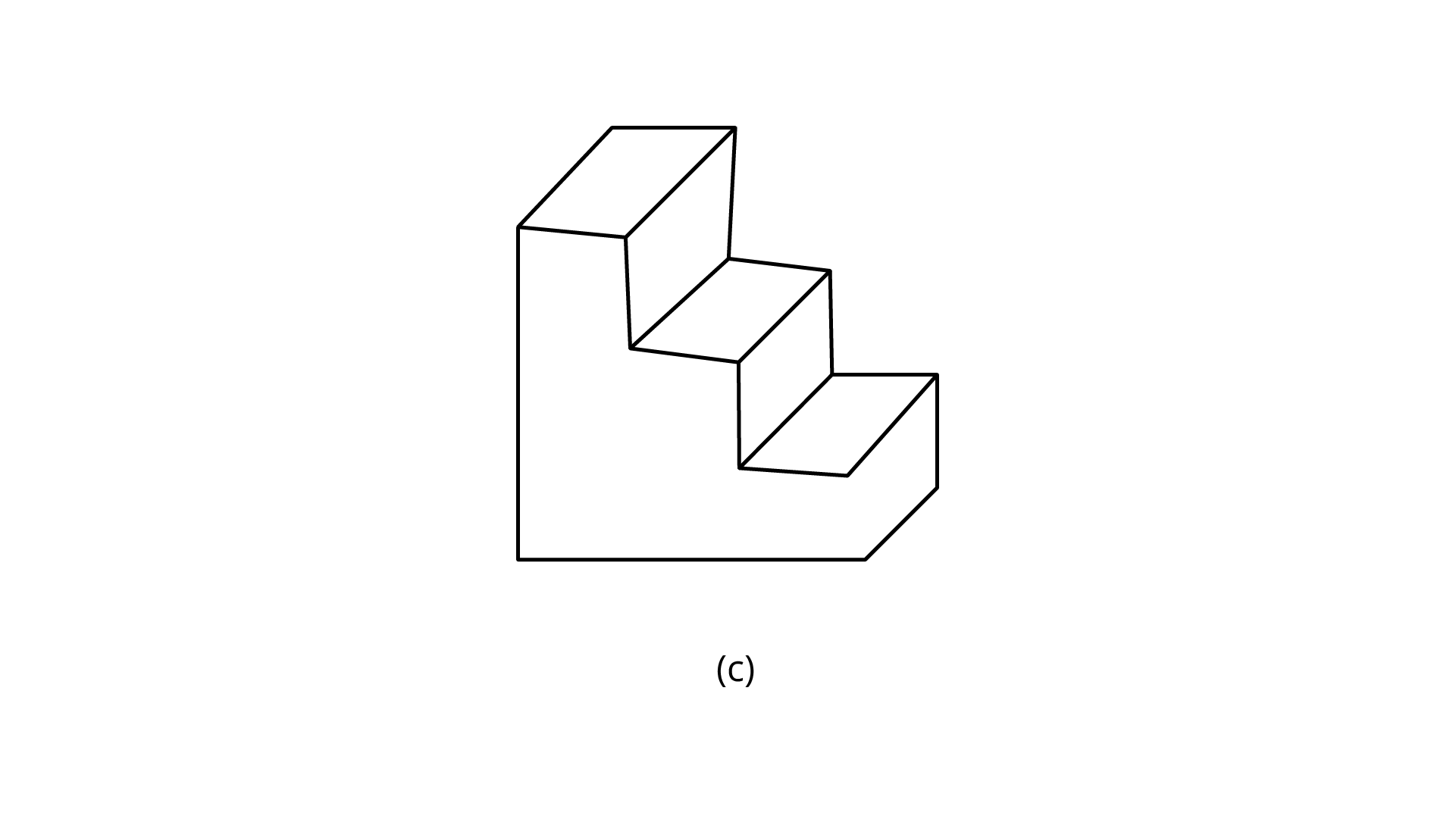
Ans: The number of lines of symmetry is $1$. 

The order of rotational symmetry is $1$.

(d)

Ans: The number of lines of symmetry is $2$. 

The order of rotational symmetry is $2$.

(e)

Ans: The number of lines of symmetry is $1$. 

The order of rotational symmetry is $1$.

(f)

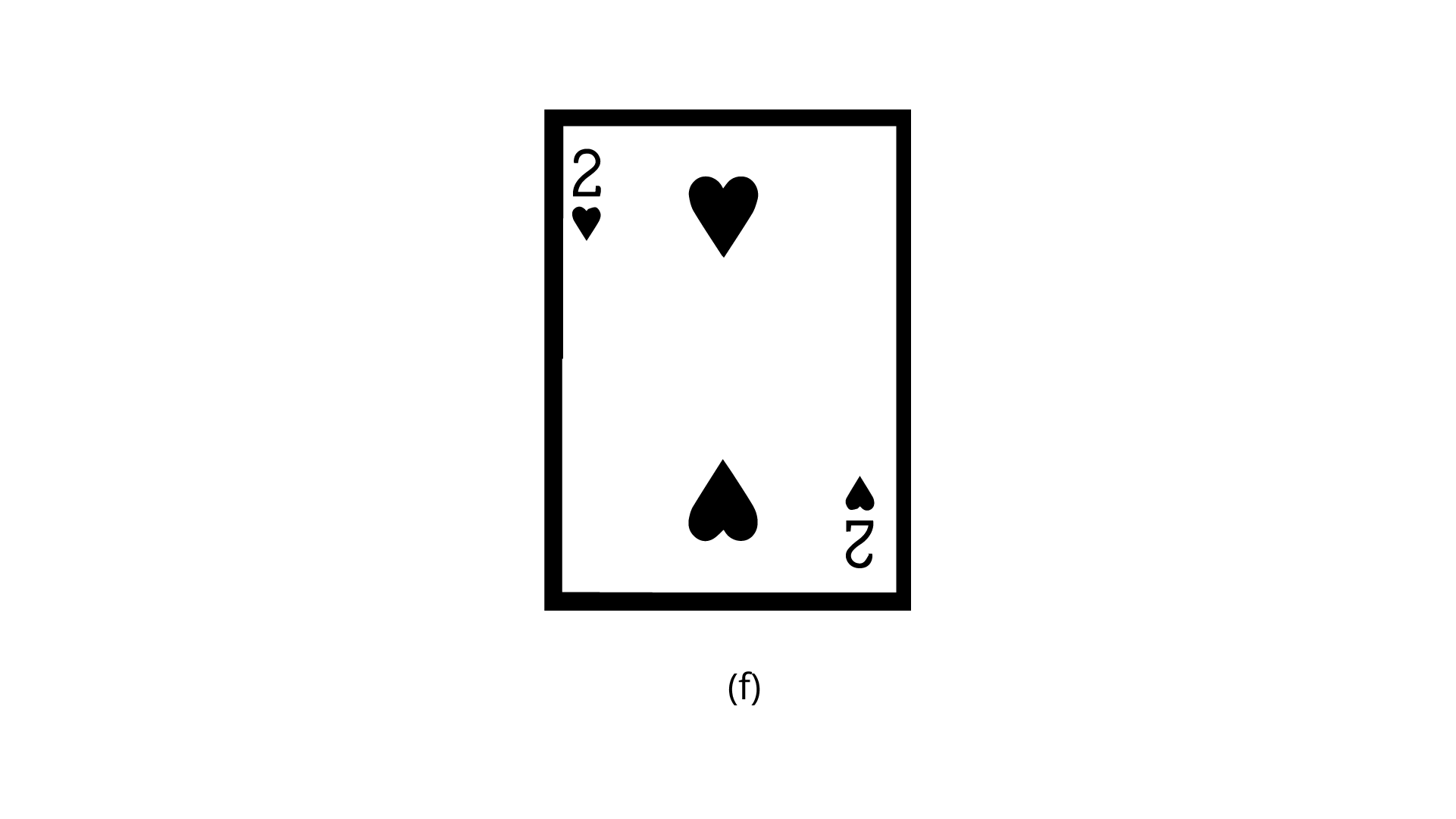
Ans: The number of lines of symmetry is $0$. 

The order of rotational symmetry is $1$.

(g)

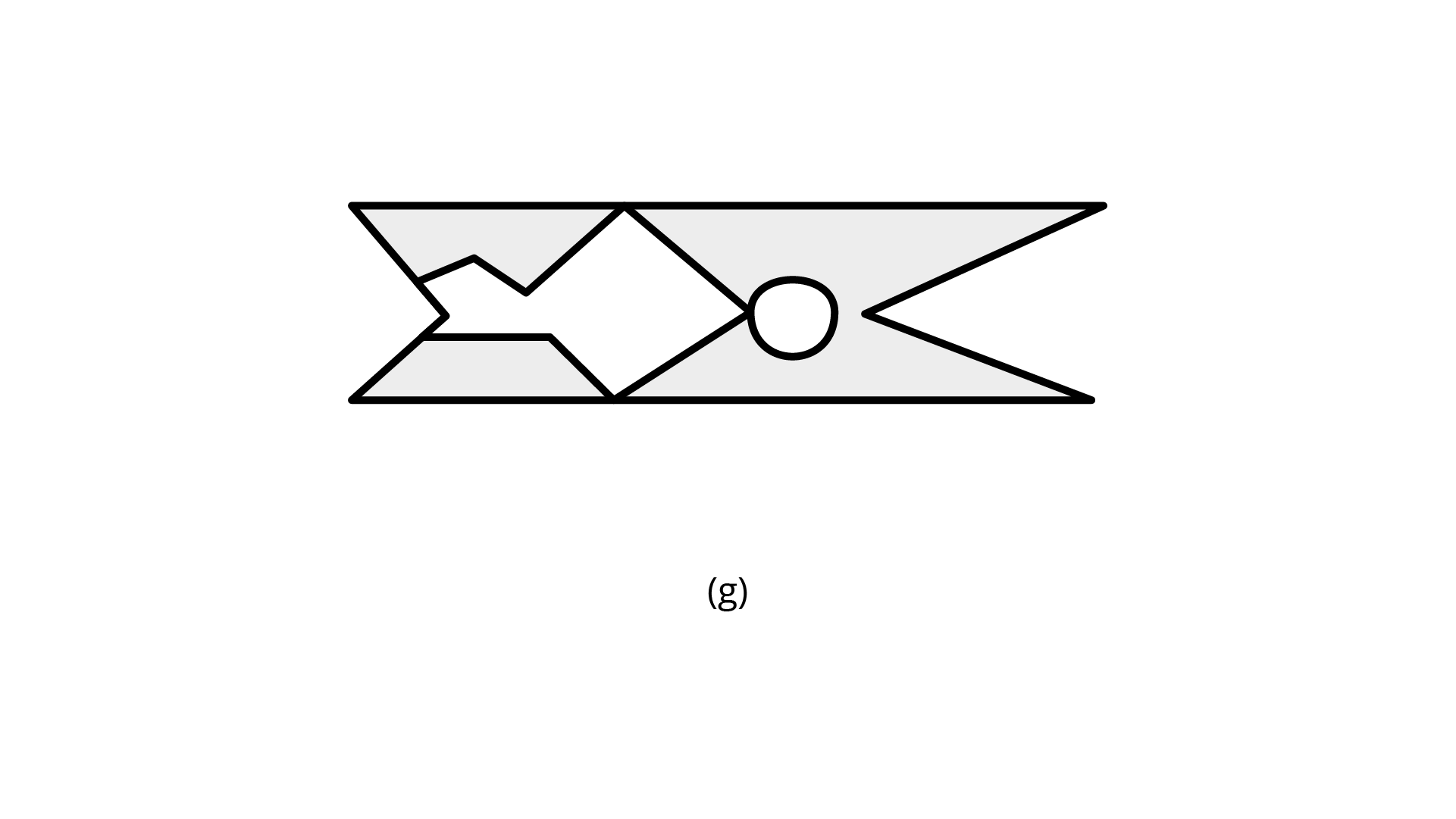
Ans: The number of lines of symmetry is $0$. 

The order of rotational symmetry is $1$.

(h)

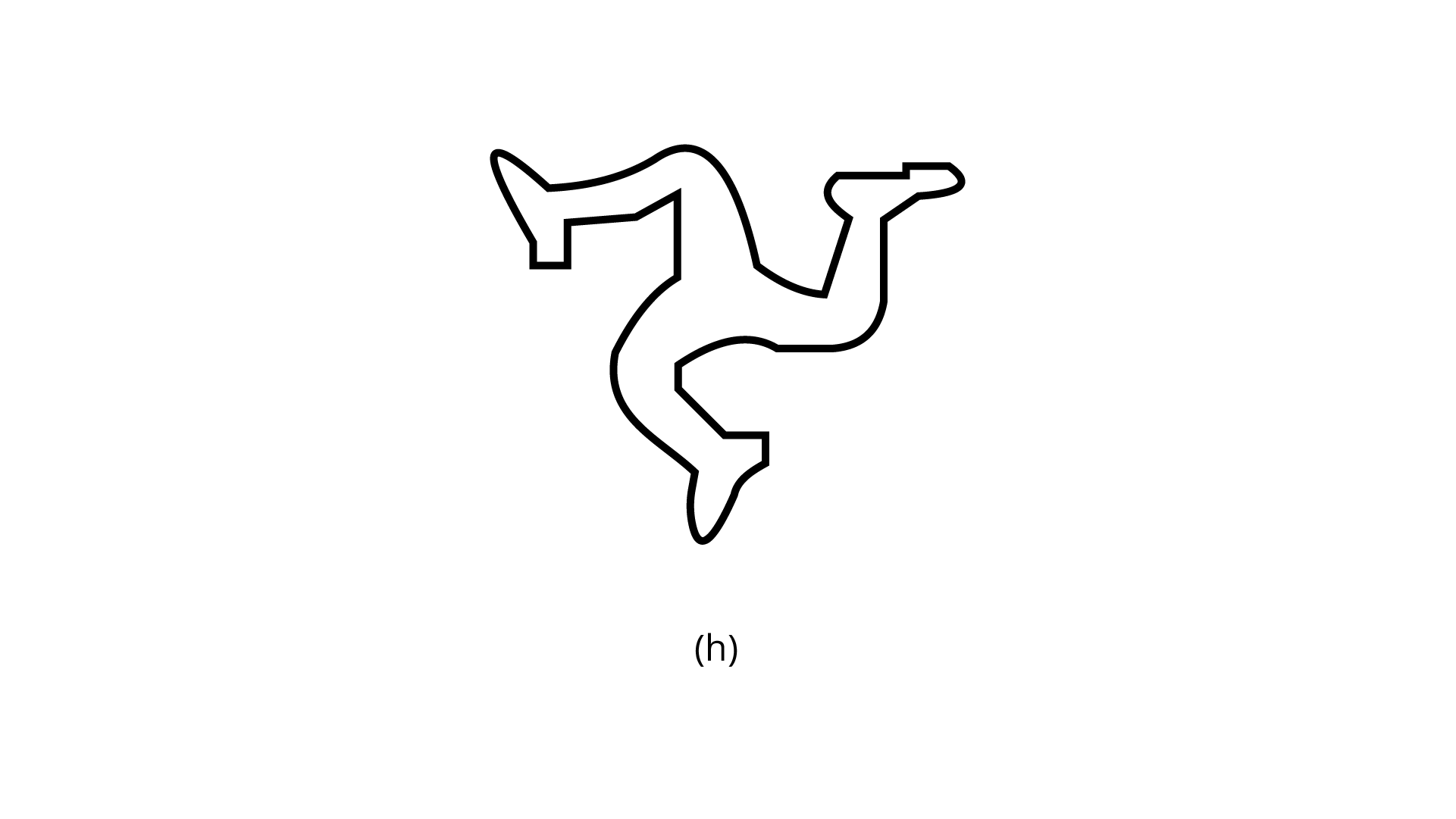
Ans: The number of lines of symmetry is $0$. 

The order of rotational symmetry is $3$.

(i)

Ans: The number of lines of symmetry is $4$. 

The order of rotational symmetry is $4$.

(j)

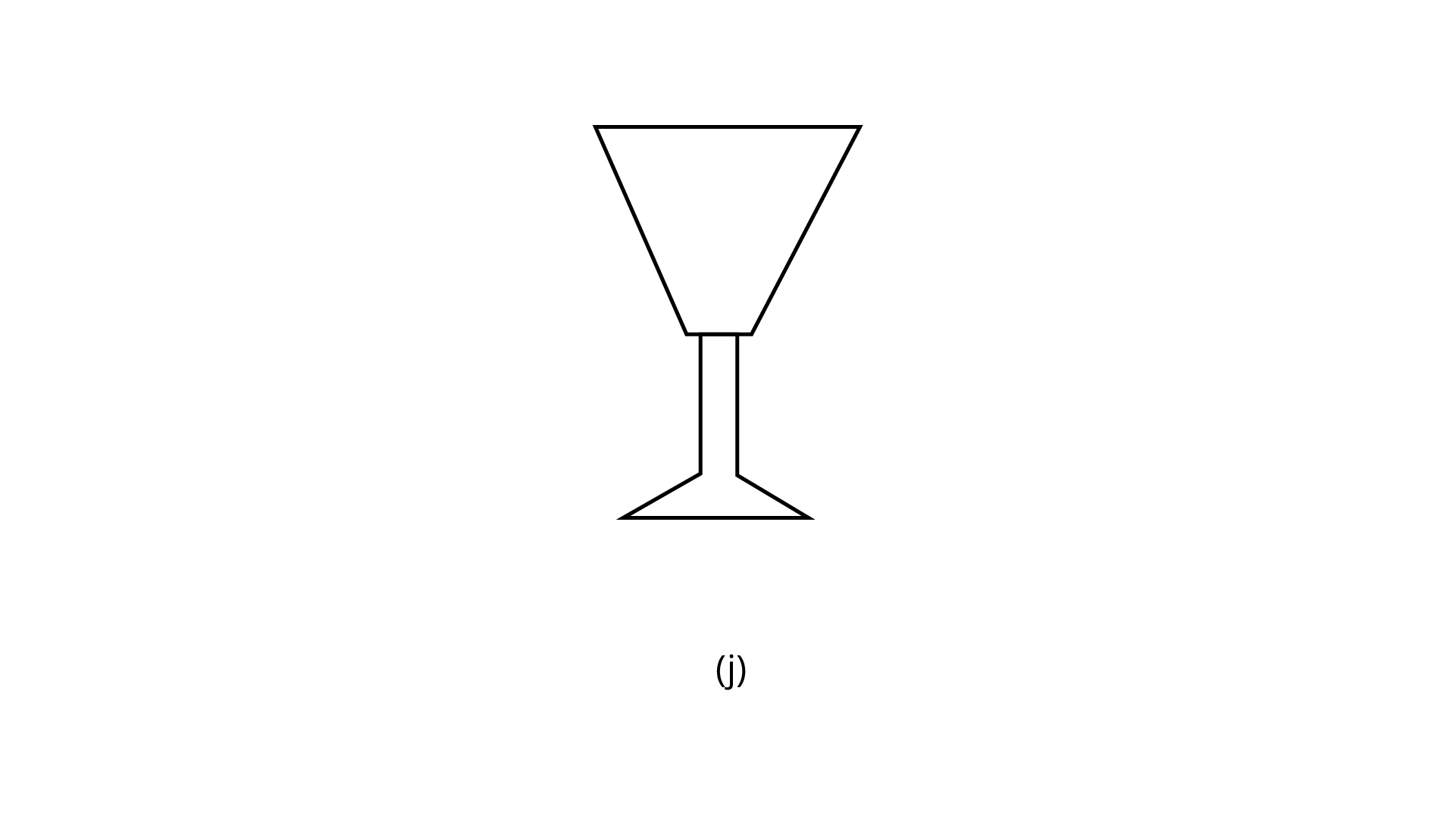
Ans: The number of lines of symmetry is $1$. 

The order of rotational symmetry is $1$.

(k)

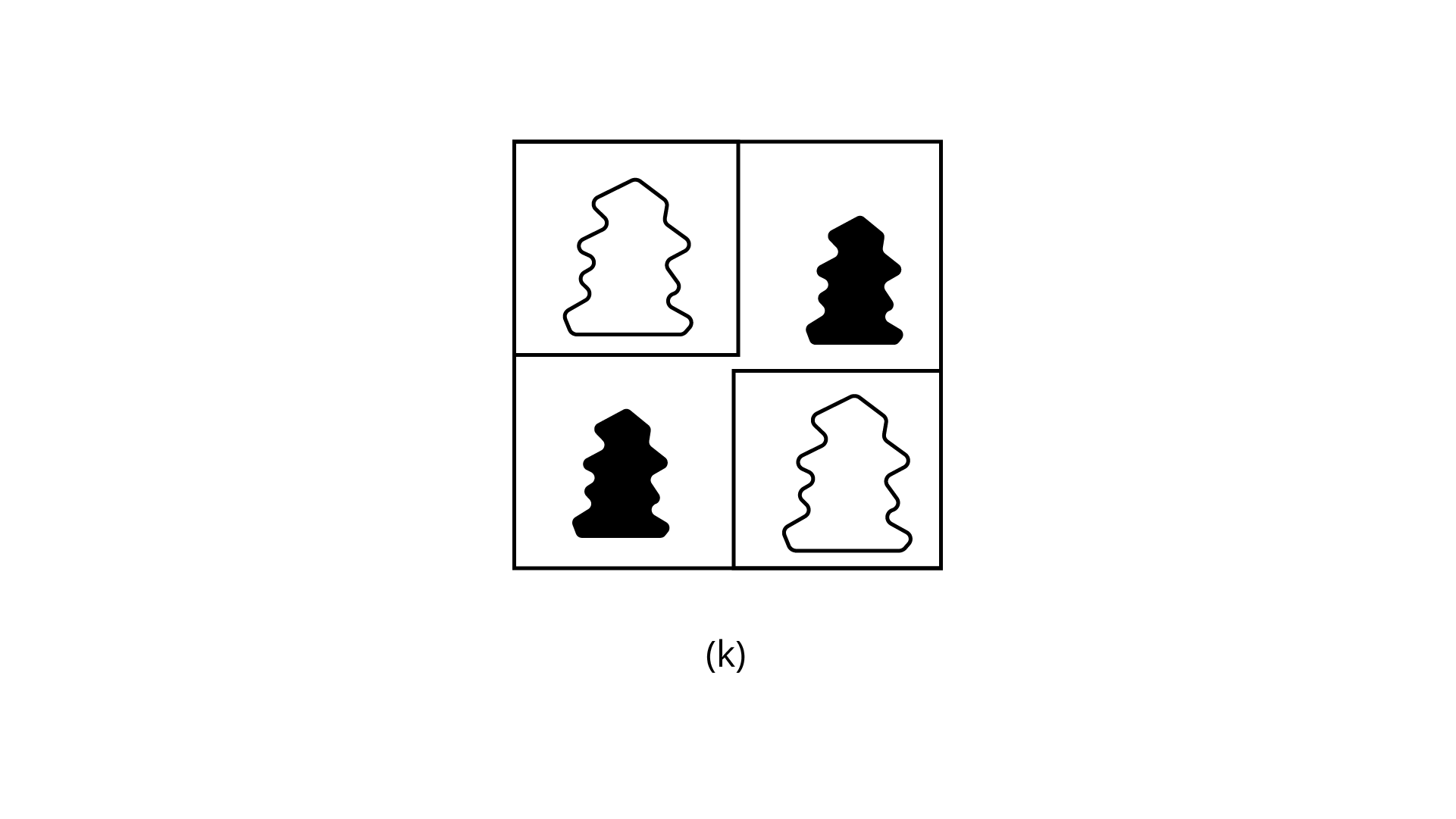
Ans: The number of lines of symmetry is $0$. 

The order of rotational symmetry is $1$.

(l)

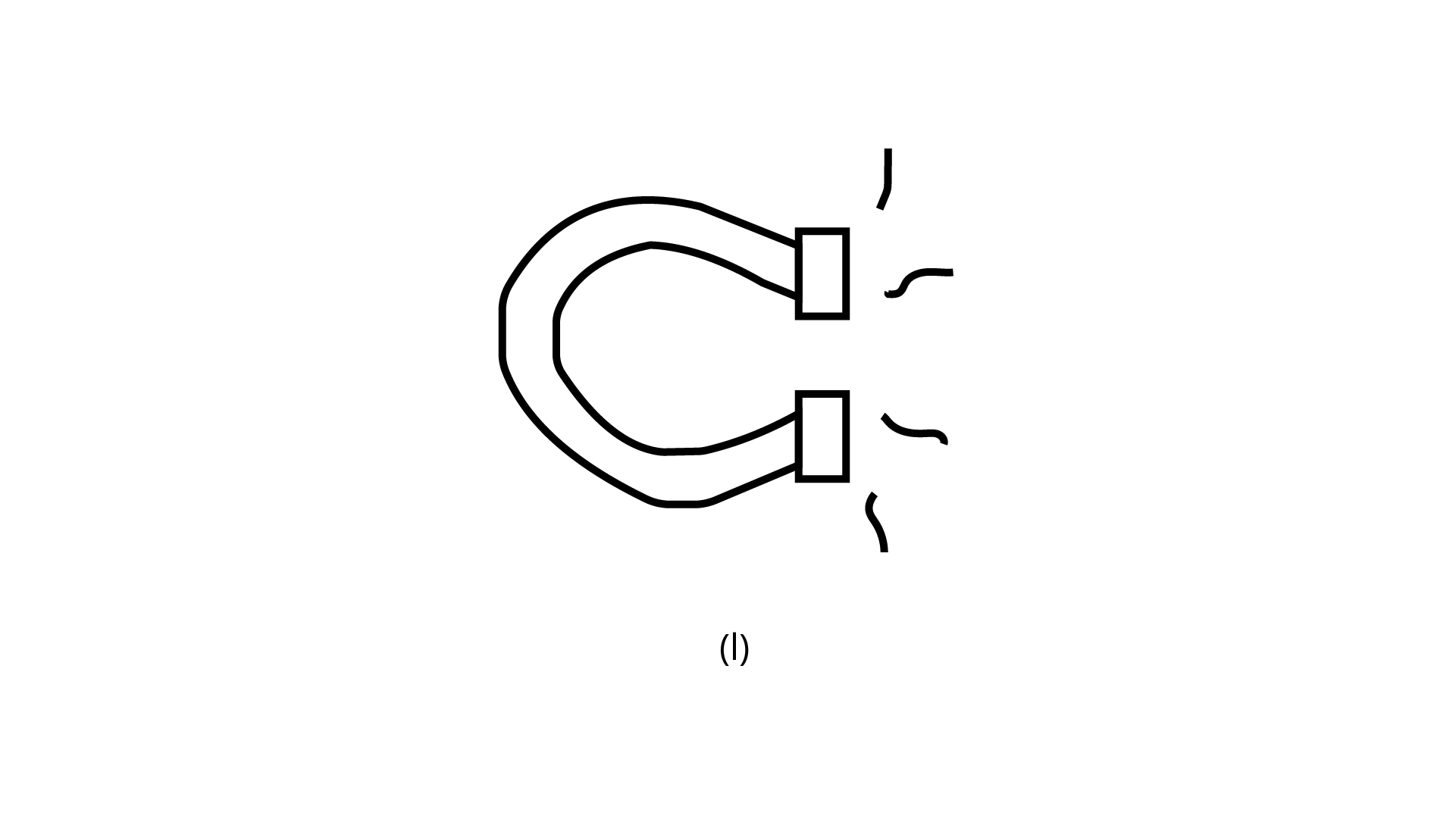
Ans: The number of lines of symmetry is $0$. 

The order of rotational symmetry is $1$.

(m)

Ans: The number of lines of symmetry is $0$. 

The order of rotational symmetry is $2$.

(n)

Ans: The number of lines of symmetry is $0$. 

The order of rotational symmetry is $1$.

(o)

Ans:The number of lines of symmetry is $1$. 

The order of rotational symmetry is $1$.

(p)

Ans: The number of lines of symmetry is $0$. 

The order of rotational symmetry is $1$.

(q)

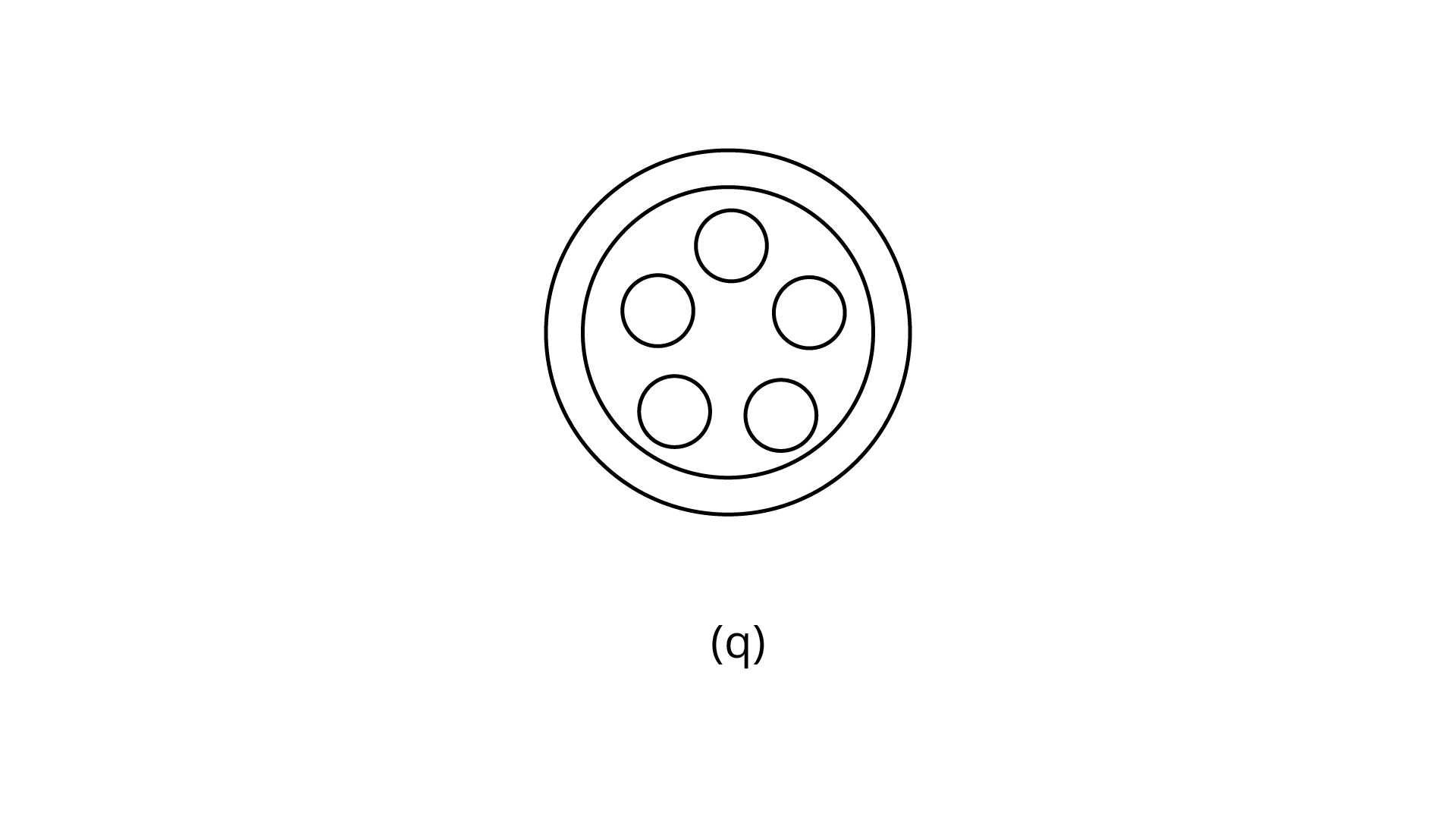
Ans: The number of lines of symmetry is $5$. 

The order of rotational symmetry is $5$.

(r)

Ans: The number of lines of symmetry is $0$. 

The order of rotational symmetry is $1$.

(s)

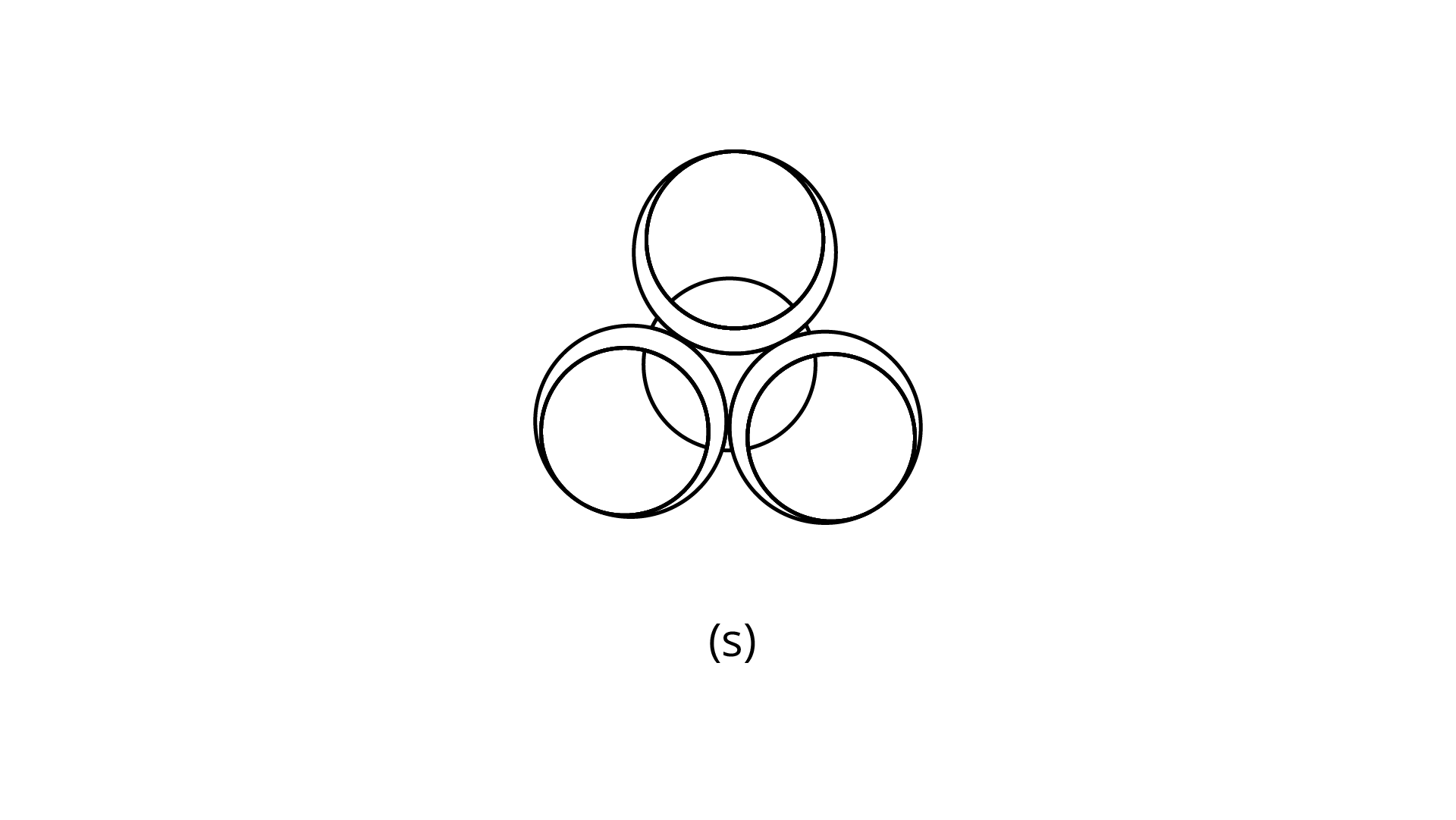
Ans: The number of lines of symmetry is $3$. 

The order of rotational symmetry is $3$.

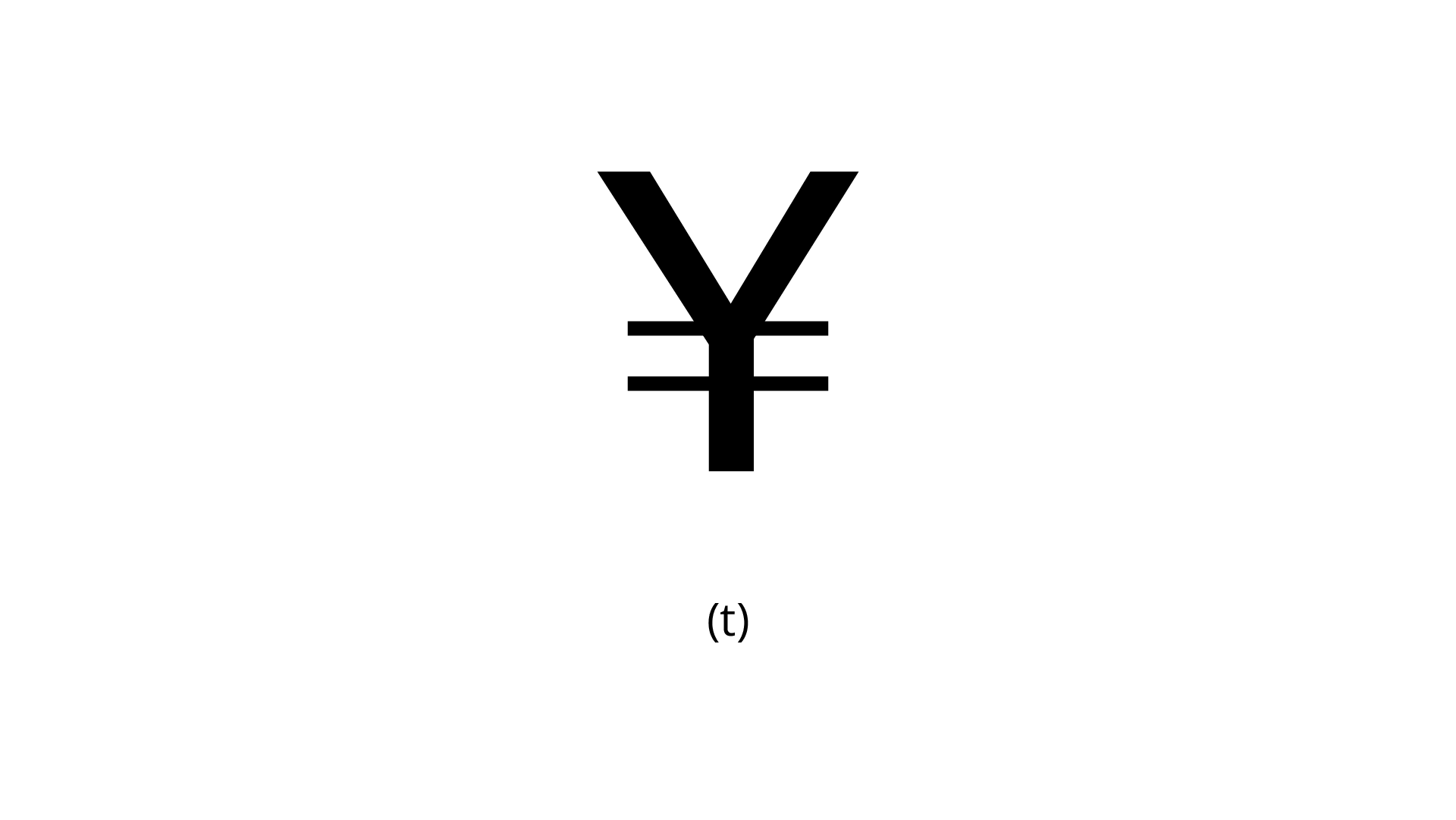
Ans: The number of lines of symmetry is $1$. 

The order of rotational symmetry is $1$.

(u)

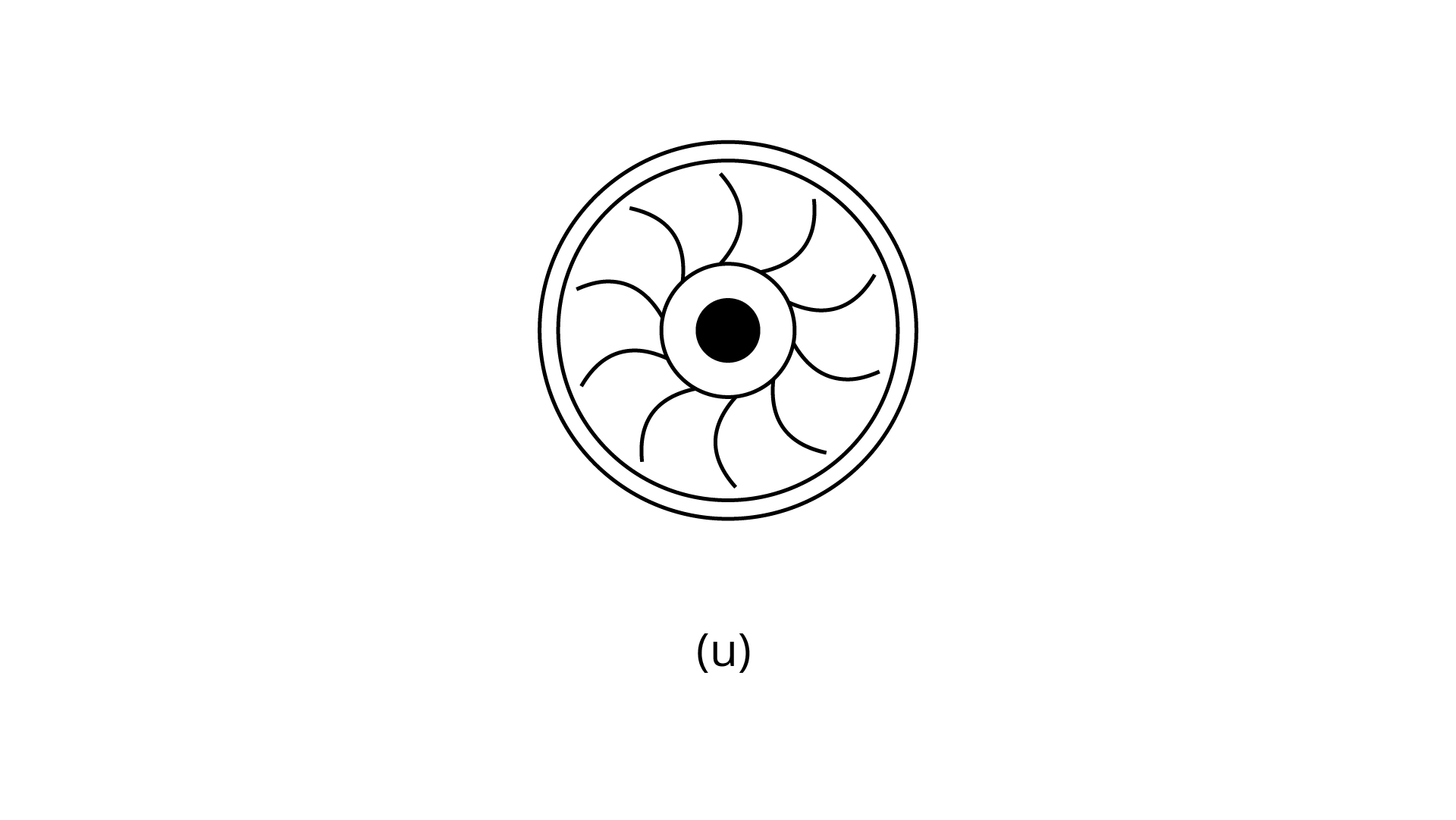
Ans: The number of lines of symmetry is $0$. 

The order of rotational symmetry is $10$.

(v)

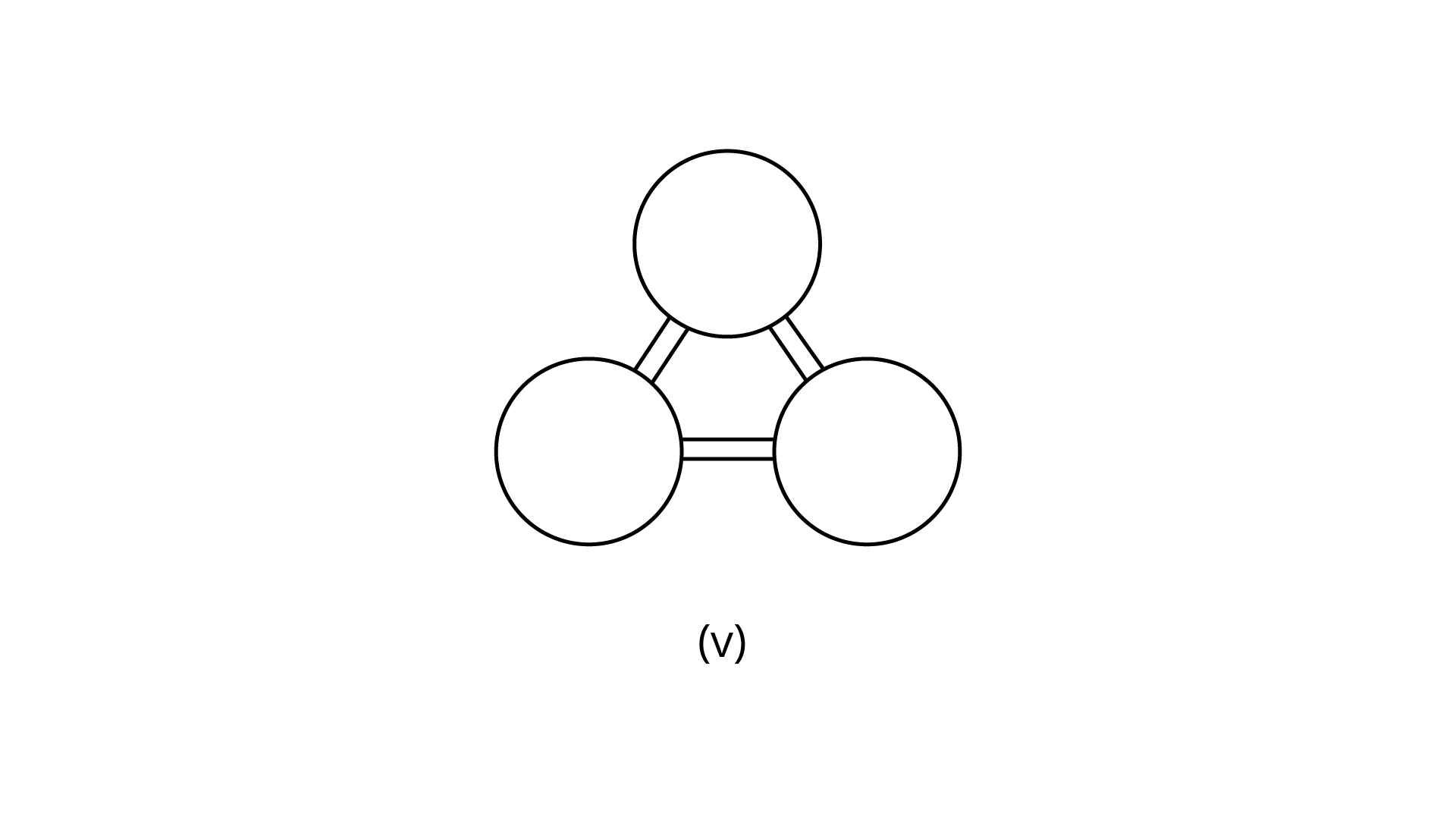
Ans: The number of lines of symmetry is $3$. 

The order of rotational symmetry is $3$.

(w)

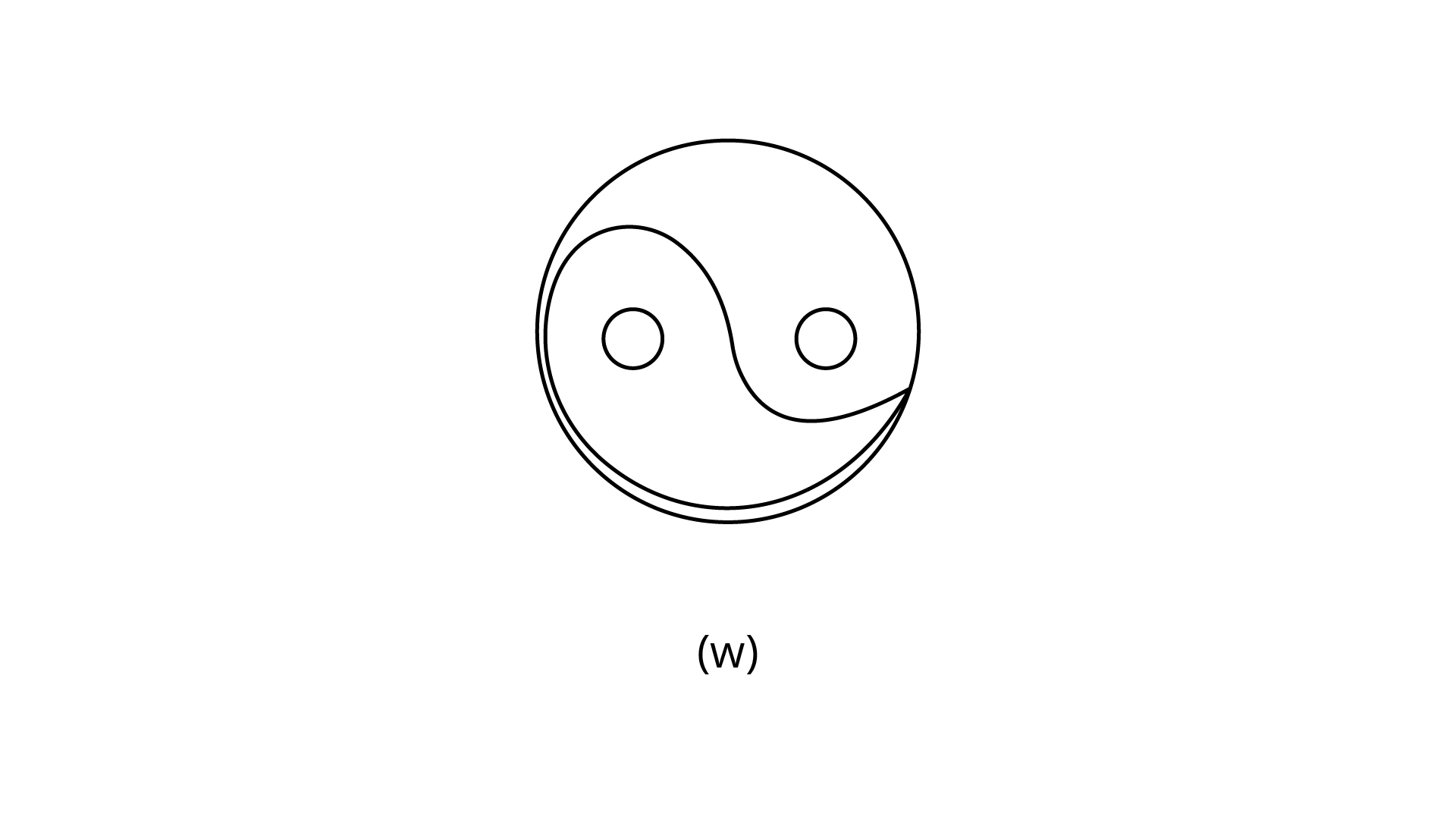
Ans: The number of lines of symmetry is $0$. 

The order of rotational symmetry is $1$.

104. In the figure 12.24 of a cube, 

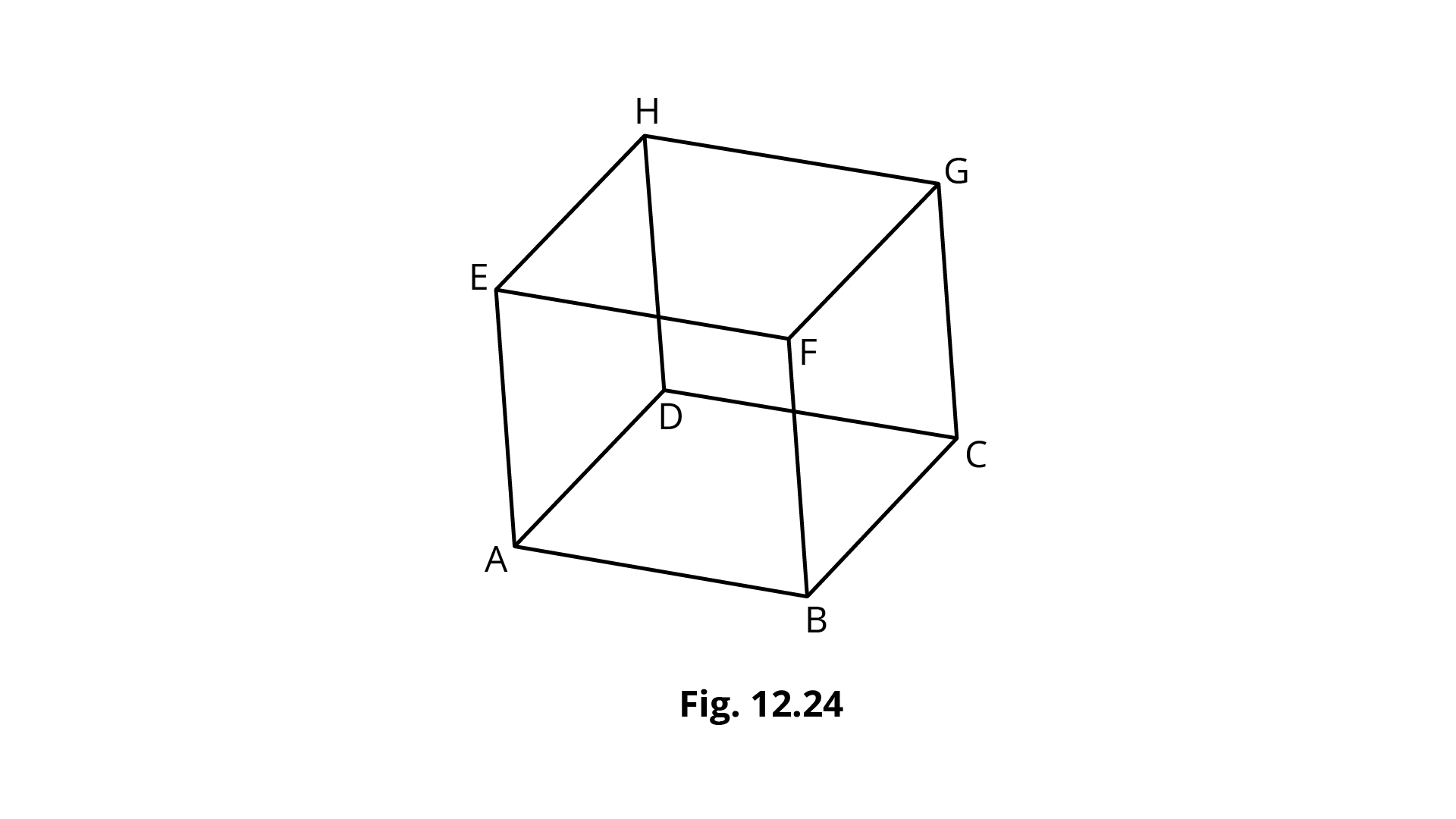
(i) Which edge is the intersection of faces ${\mathbf{{\rm E}FG{\rm H}}}$ and  ${\mathbf{EFBA}}$?

Ans: From the given figure, we can observe that ${\text{EF}}$ is the intersection of faces ${\text{EFGH}}$ and ${\text{EFBA}}{\text{.}}$

(ii) Which faces intersect at the edge ${\mathbf{FB}}$?

Ans: From the given figure, we can observe that faces ${\text{EFBA}}$ and ${\text{FBCG}}$ intersect at edge ${\text{FB}}{\text{.}}$

(iii) Which three faces form the vertex ${\mathbf{A}}$?

Ans:Faces ${\text{ABFE}},{\text{ADHE}}$ and ${\text{ABCD}}$ form the vertex ${\text{A}}$.

(iv) Which vertex is formed by the faces ${\mathbf{ABCD,ADHE}}$ and ${\mathbf{CDHG?}}$

Ans: Vertex ${\text{D}}$ is formed by the faces ${\text{ABCD}}$, ${\text{CDHG}}$ and ${\text{ADHE}}$.

(v) Give all the edges that are parallel to edge ${\mathbf{AB}}$.

Ans: The edges parallel to edge ${\text{AB}}$ are ${\text{CD}},{\text{EF}}$ and ${\text{HG}}$.

vi) Give the edges that are neither parallel nor perpendicular to edge ${\mathbf{BC}}$.

Ans: From the given figure, we can observe that edges ${\text{AE}},{\text{EF}},{\text{GH}}$ and ${\text{HD}}$ are neither parallel nor perpendicular to edge ${\text{BC}}$.

(vii) Give all the edges that are perpendicular to the edge ${\mathbf{AB}}$.

Ans: From the given figure, we can observe that edges ${\text{AE}},{\text{BF}},{\text{AD}}$ and ${\text{BC}}$ are perpendicular to edge ${\text{AB}}$.

(viii) Give four vertices that do not all lie in one plane.

Ans: Vertices ${\text{A}},{\text{B}},{\text{G}}$ and ${\text{H}}$ do not lie in one plane.

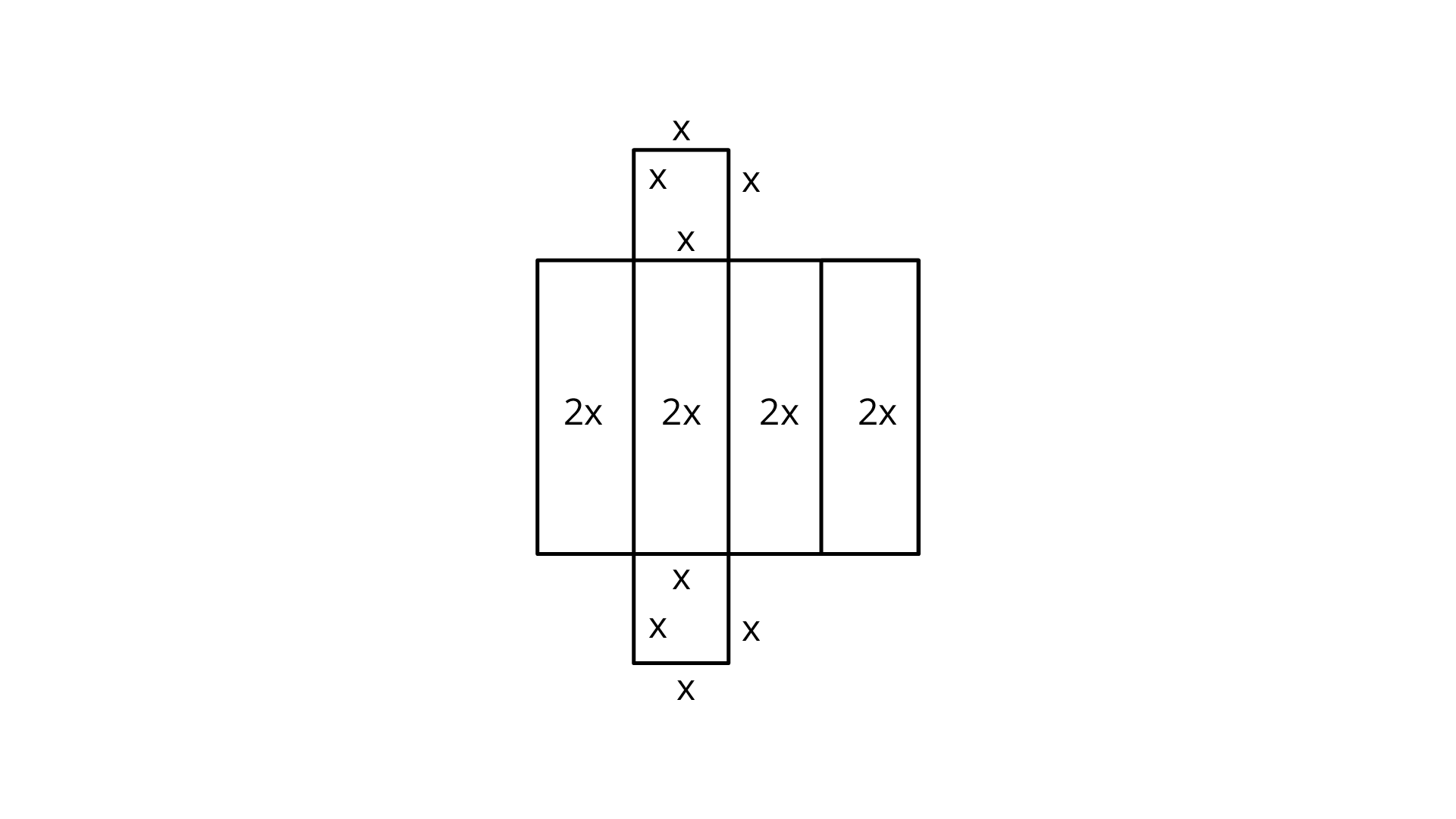
105. Draw a net of a cuboid having same breadth and height, but length double the breadth.

Ans: Let $x$ be the breadth and height.

Then, length is $2x.$

Required net of a cuboid will be,

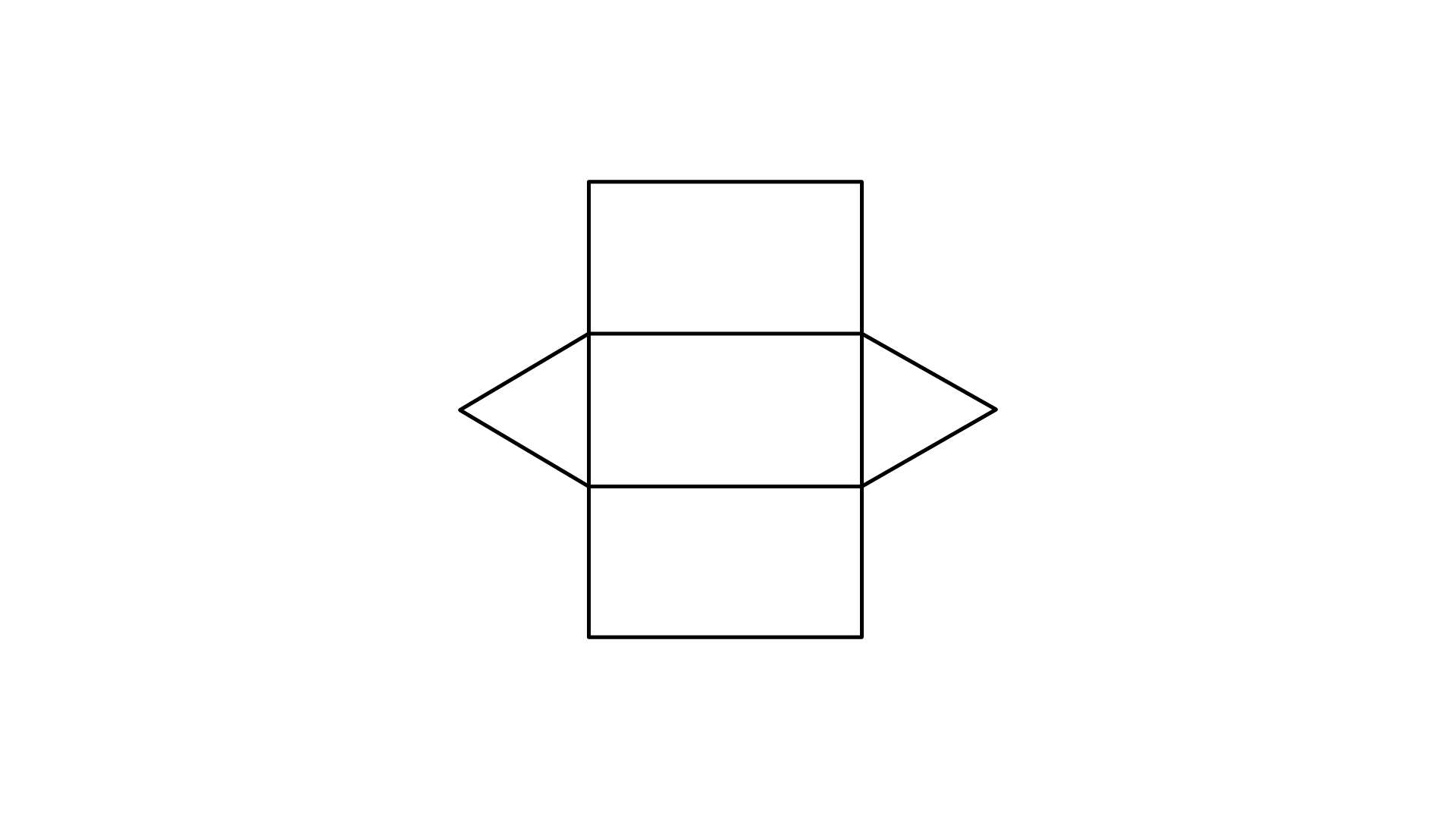
106. Draw the nets of the following: 

(i) Triangular prism 

Ans:

(ii) Tetrahedron 

Ans:

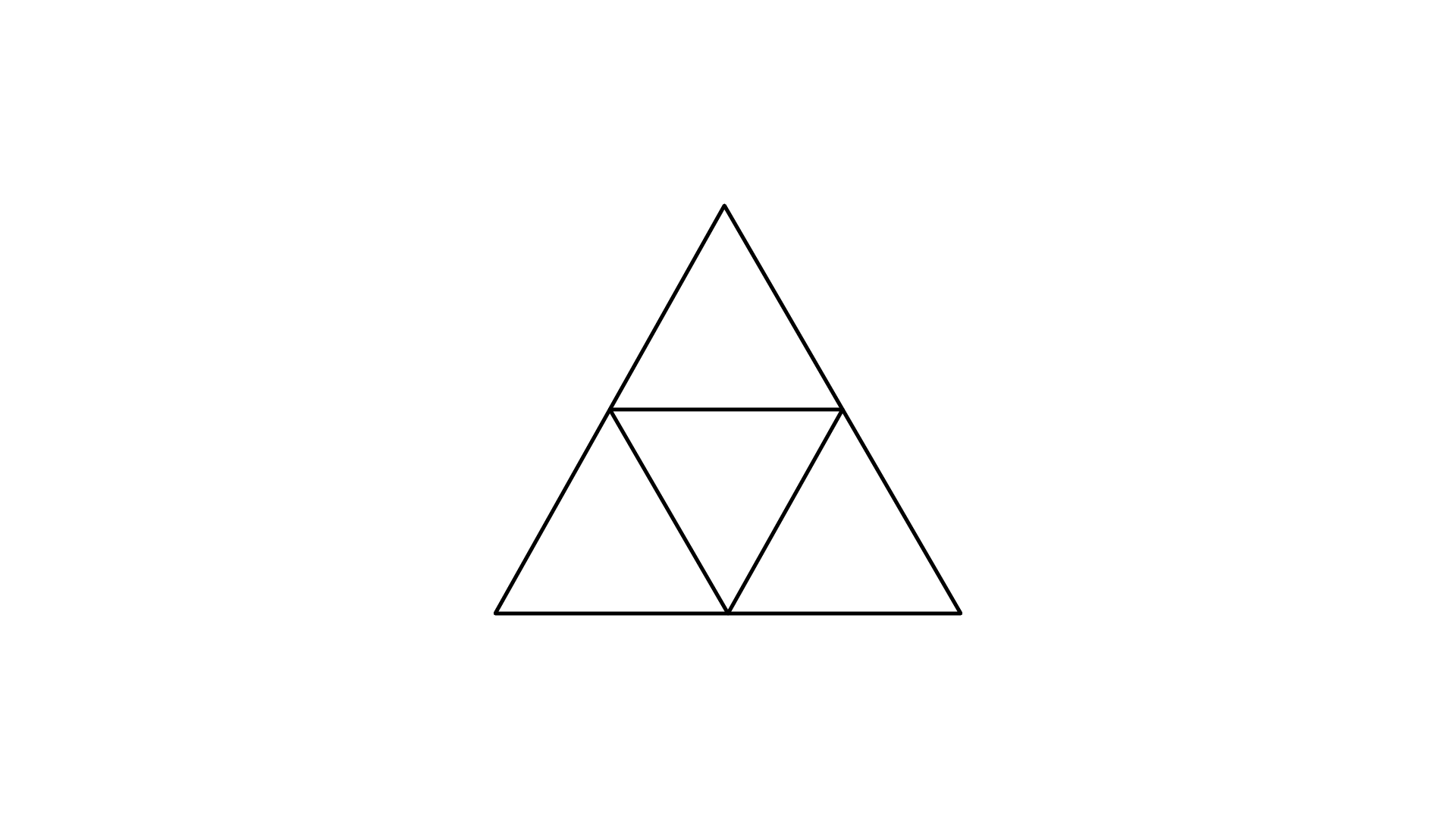
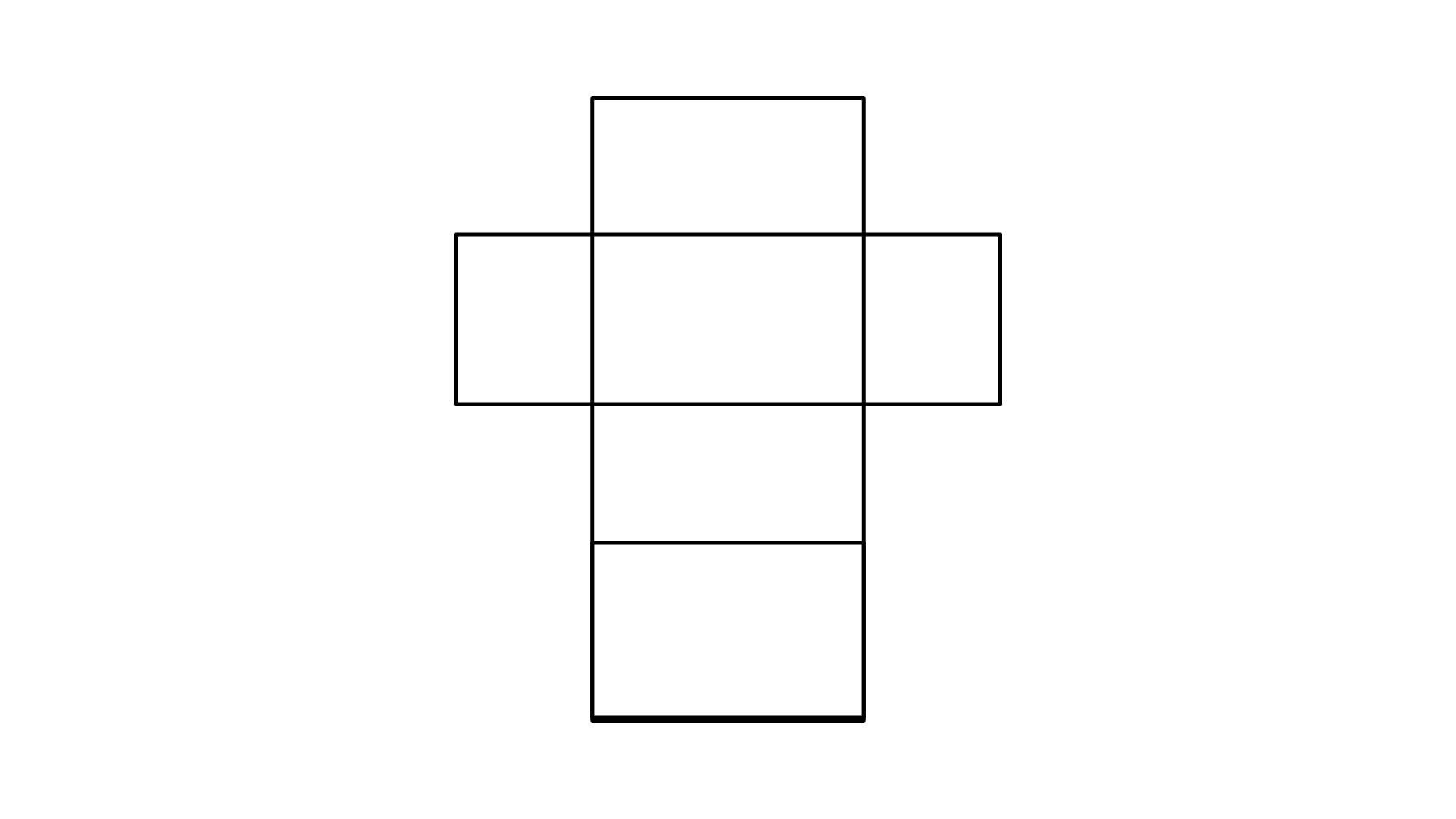
(iii) Cuboid

Ans:

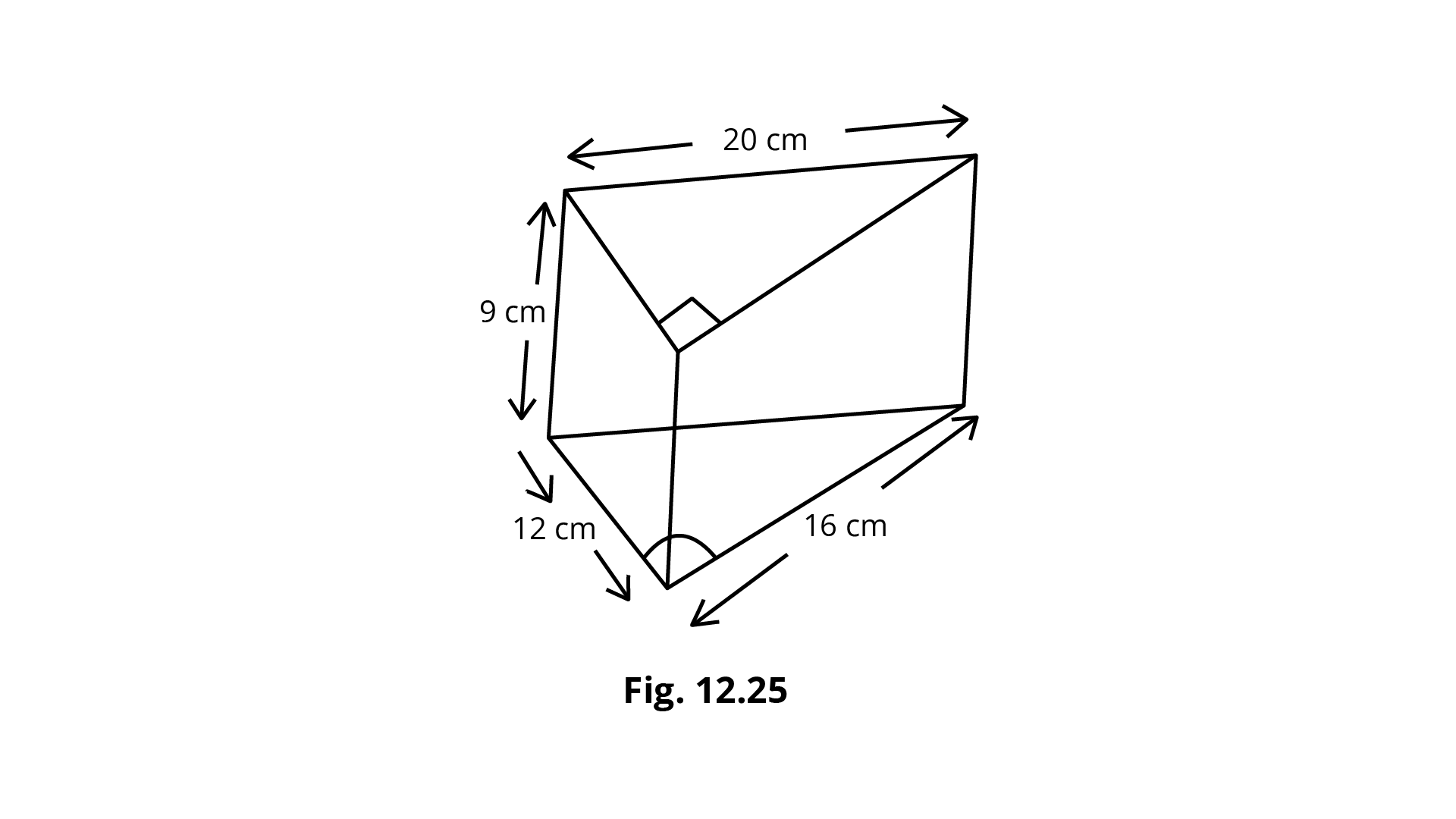
107. Draw a net of the solid given in the figure 12.25:

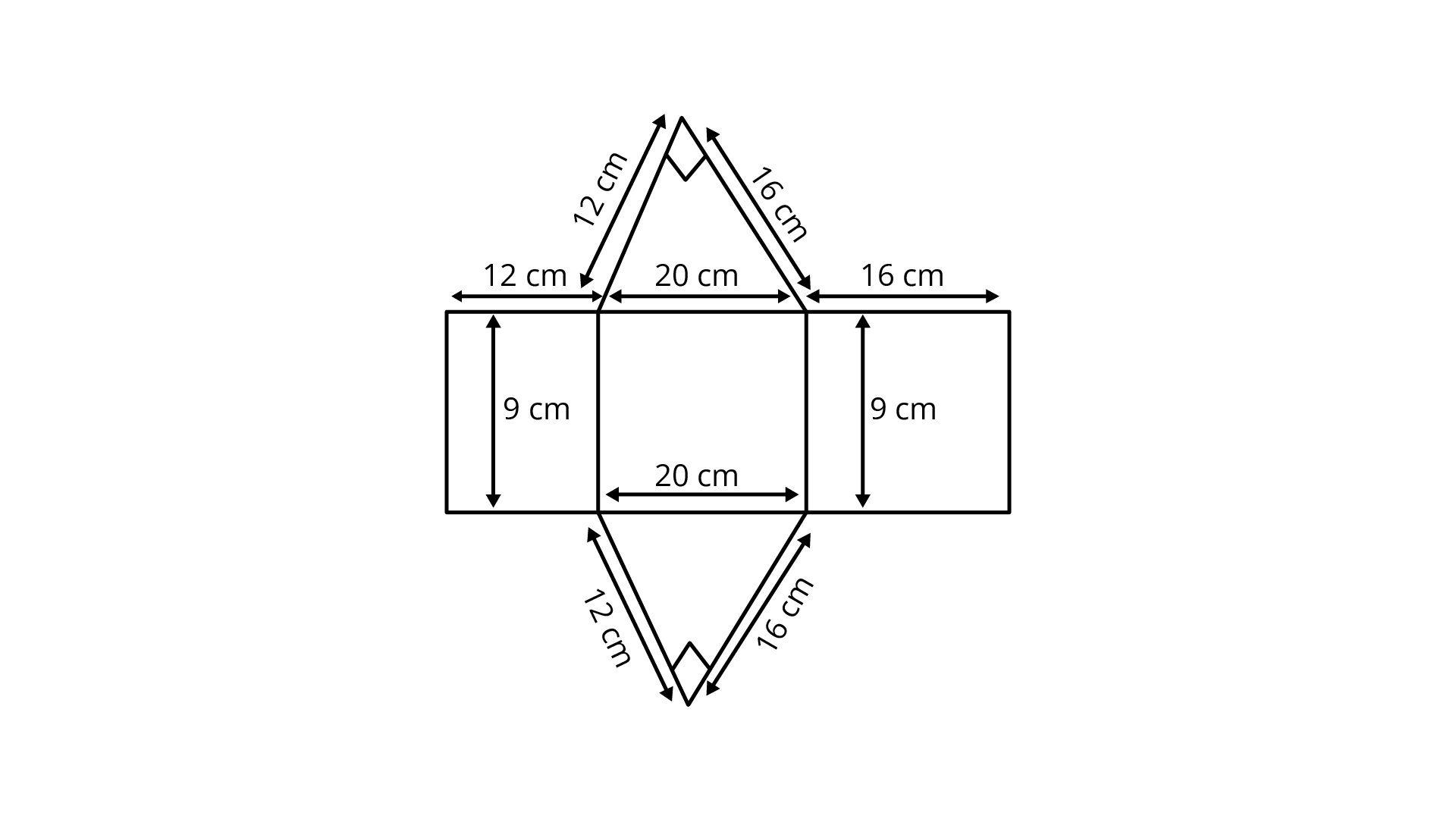
Ans: The net of the solid given in the figure is,

108. Draw an isometric view of a cuboid ${\mathbf{6 cm  \times  4 cm  \times  2 cm}}{\mathbf{.}}$

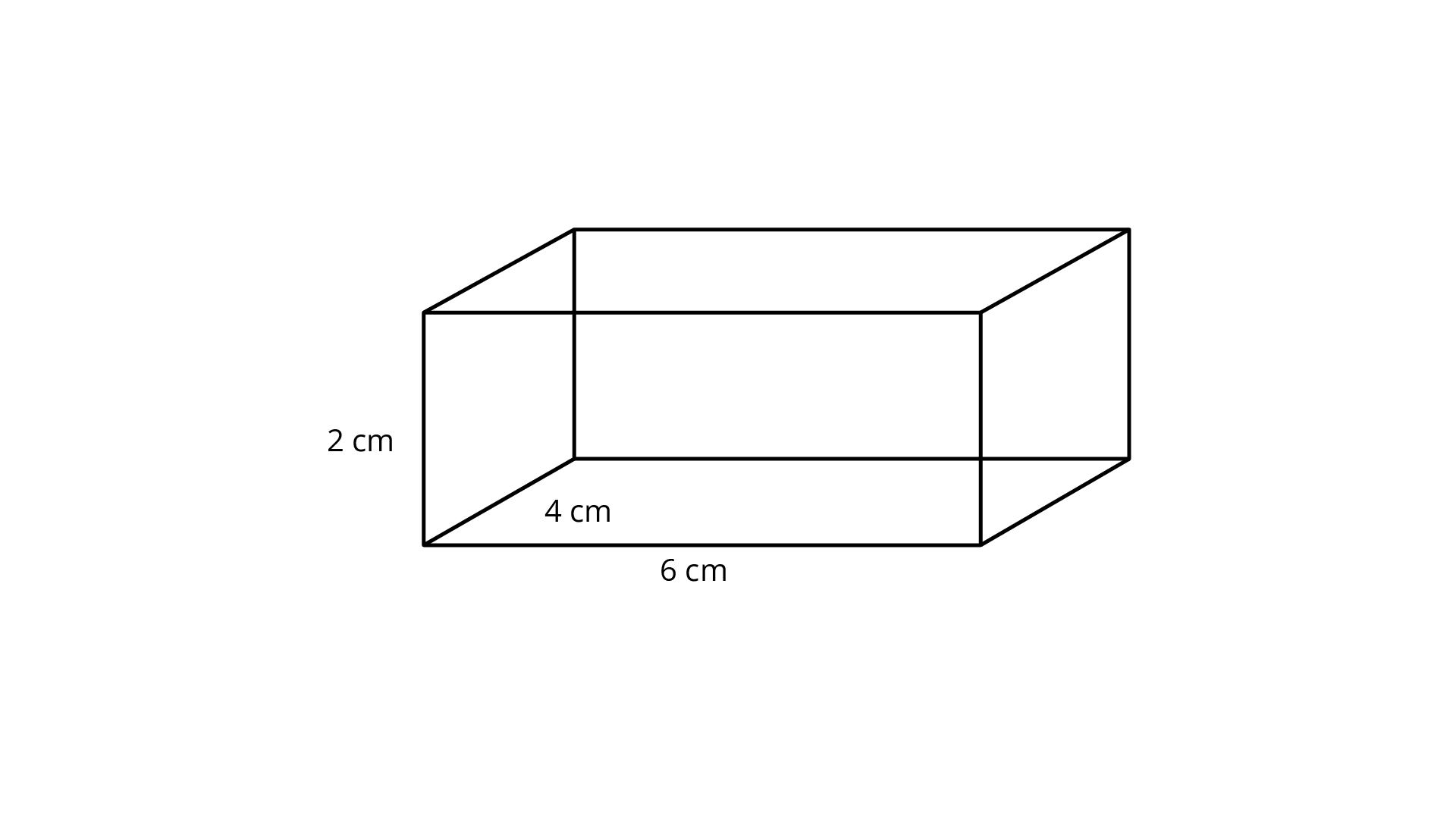
Ans:The isometric view of a cuboid ${6 cm  \times  4 cm  \times  2 cm}$ is,

109. The net given below in Fig. can be used to make a cube. 

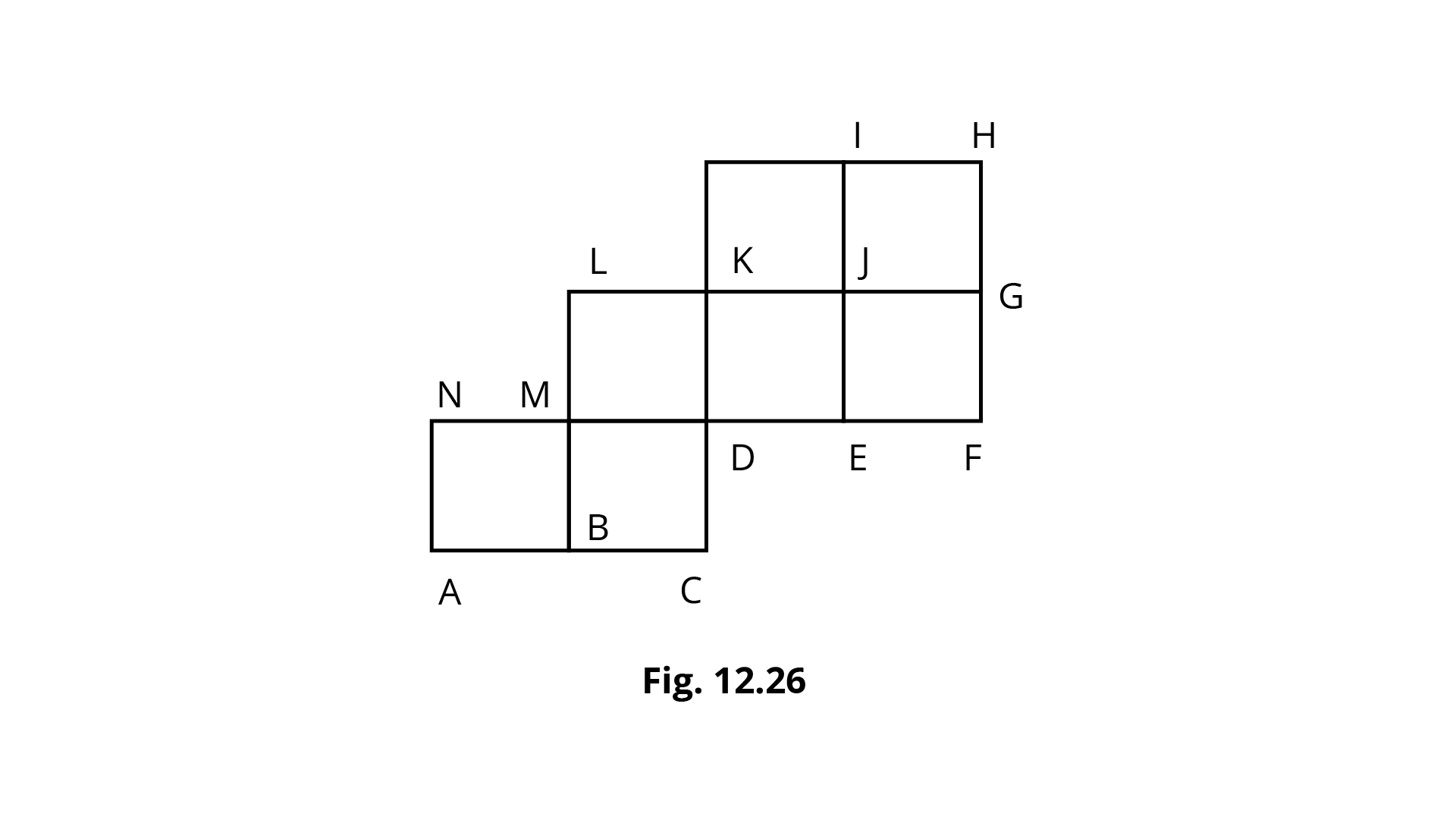
(i) Which edge meets ${\mathbf{AN}}$? 

Ans: The given net of a cube shows that edge ${\text{GH}}$ meets edge ${\text{AN}}$.

(ii) Which edge meets ${\mathbf{DE}}$?

Ans: The given net of a cube shows that edge ${\text{DC}}$ meets edge ${\text{DE}}$.

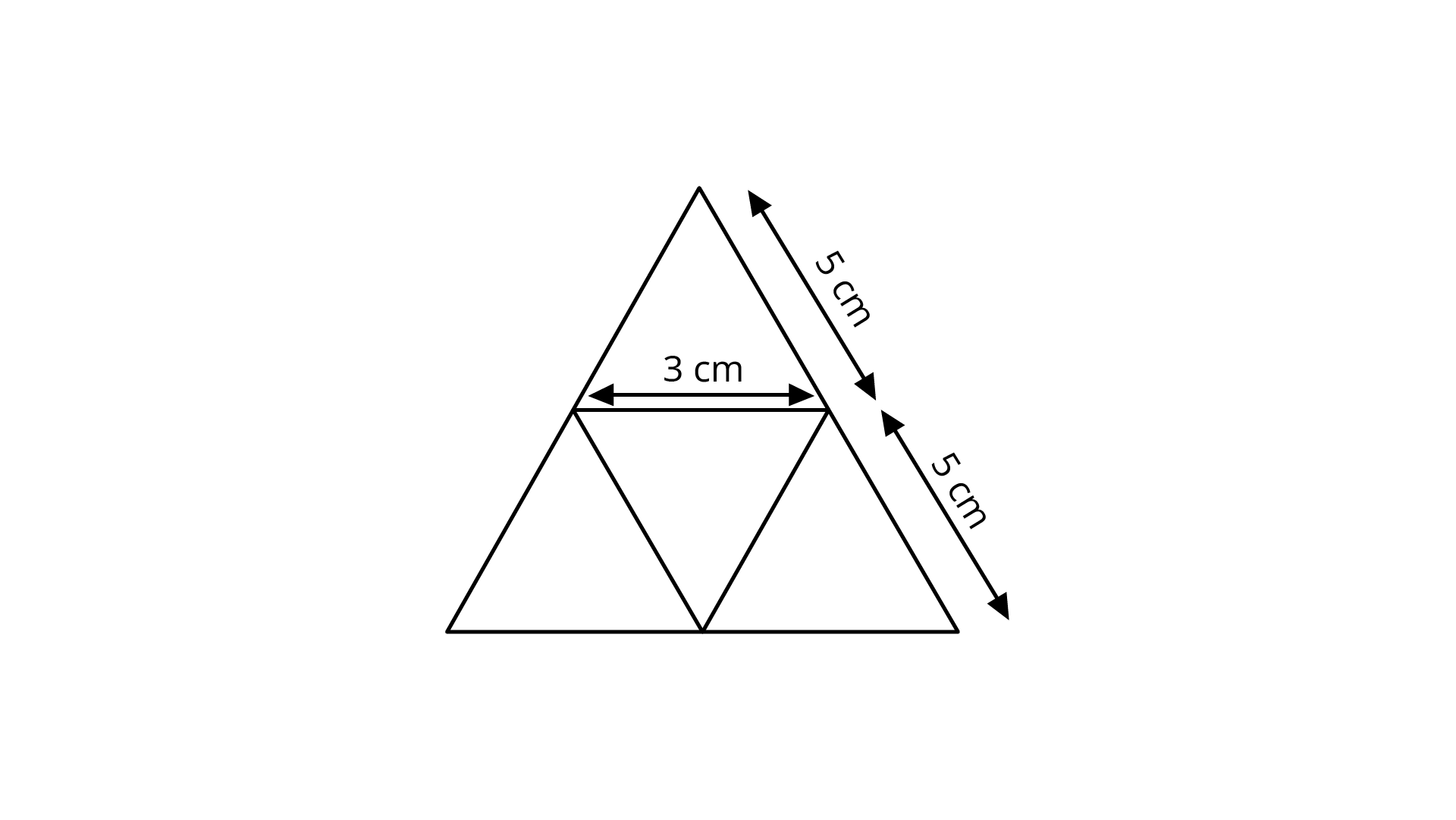
110. Draw the net of a triangular pyramid with base as equilateral triangle of side ${\mathbf{3 cm}}$ and slant edges ${\mathbf{5 cm}}$.

Ans: The net of such triangular pyramid will be,

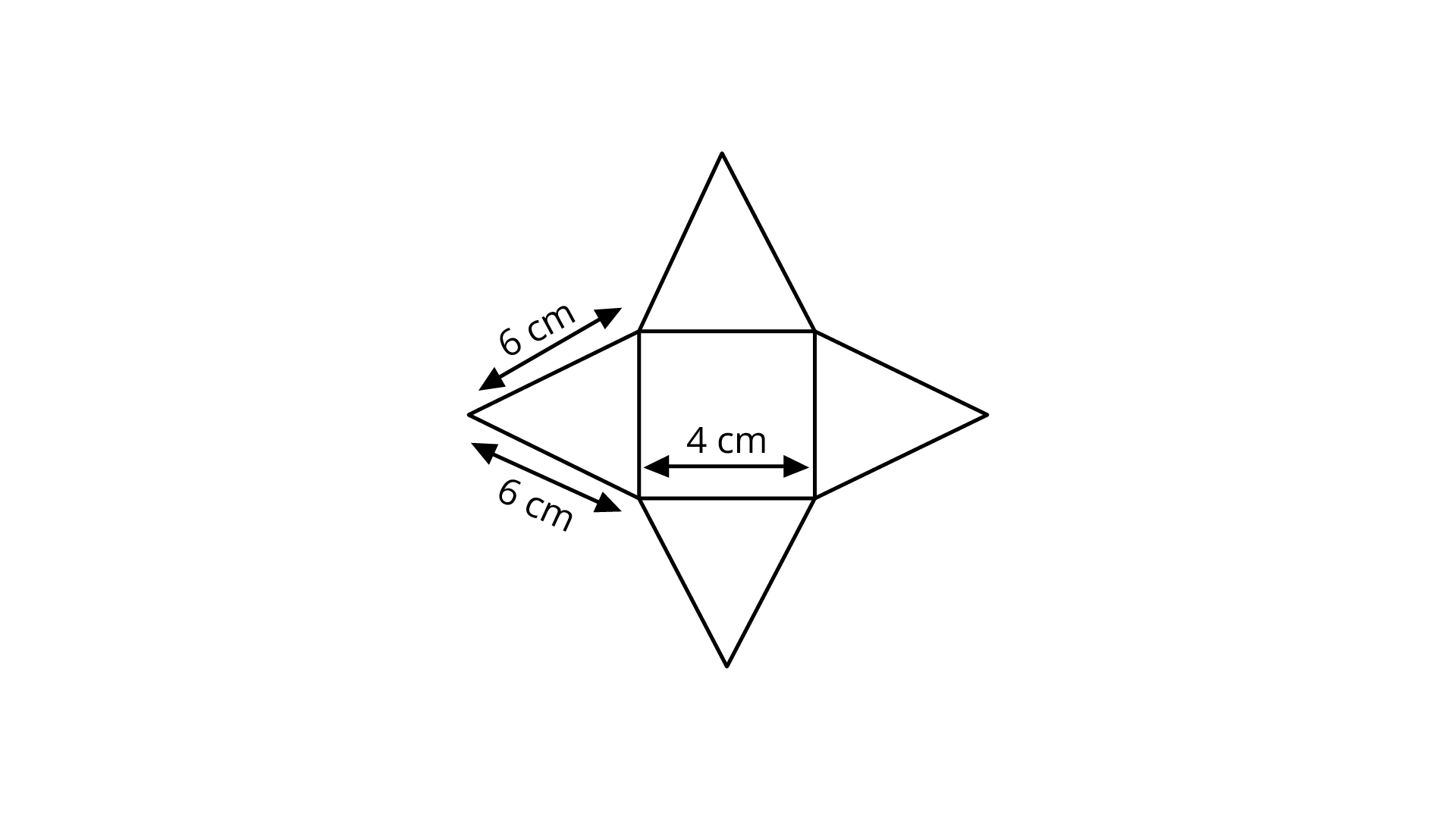
111. Draw the net of a square pyramid with base as square of side ${\mathbf{4cm}}$ and slant edges ${\mathbf{6cm}}$.

Ans: The net of such square pyramid will be,

112. Draw the net of rectangular pyramid with slant edge ${\mathbf{6cm}}$ and base as rectangle with length ${\mathbf{4cm}}$ and breadth ${\mathbf{3cm}}$.

Ans: The net of such rectangular pyramid will be,

113. Find the number of cubes in each of the following figures and in each case give the top, front, left side and right side view (arrow indicating the front view).

(a)

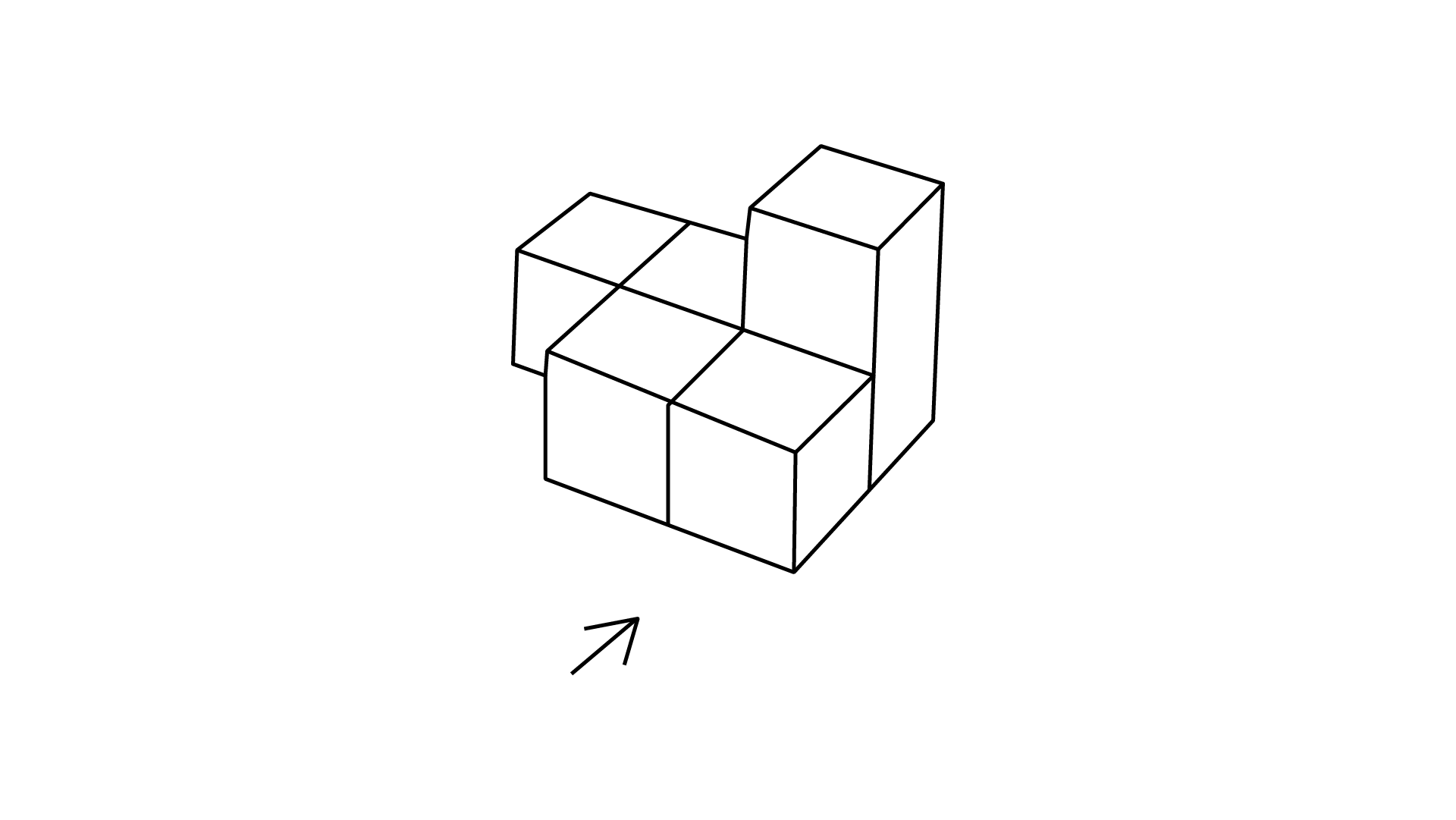
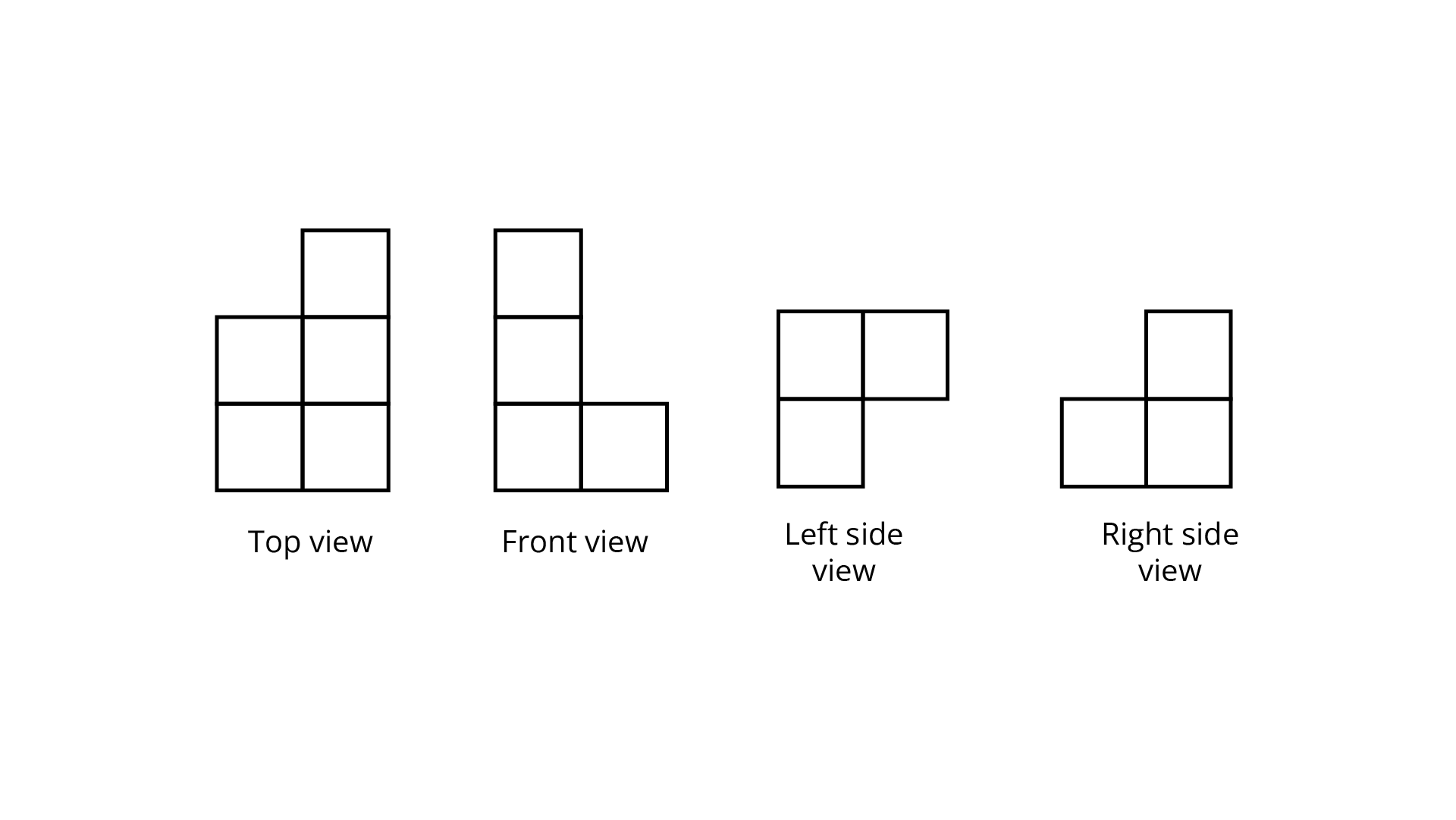
Ans: The number of cubes in given figure is $6.$

For the given figure,

(b)

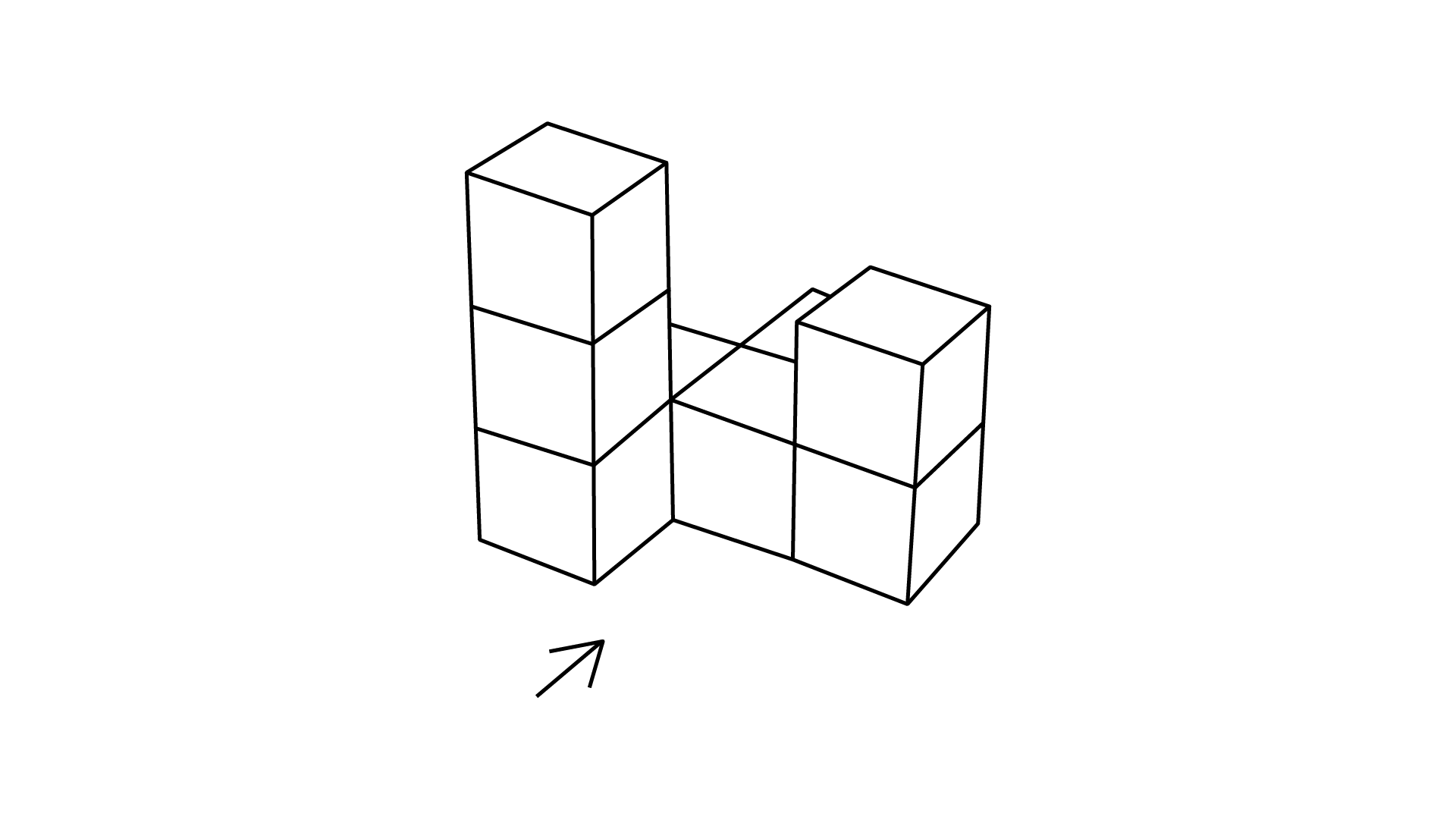
Ans: The number of cubes in given figure is $8.$

For the given figure,

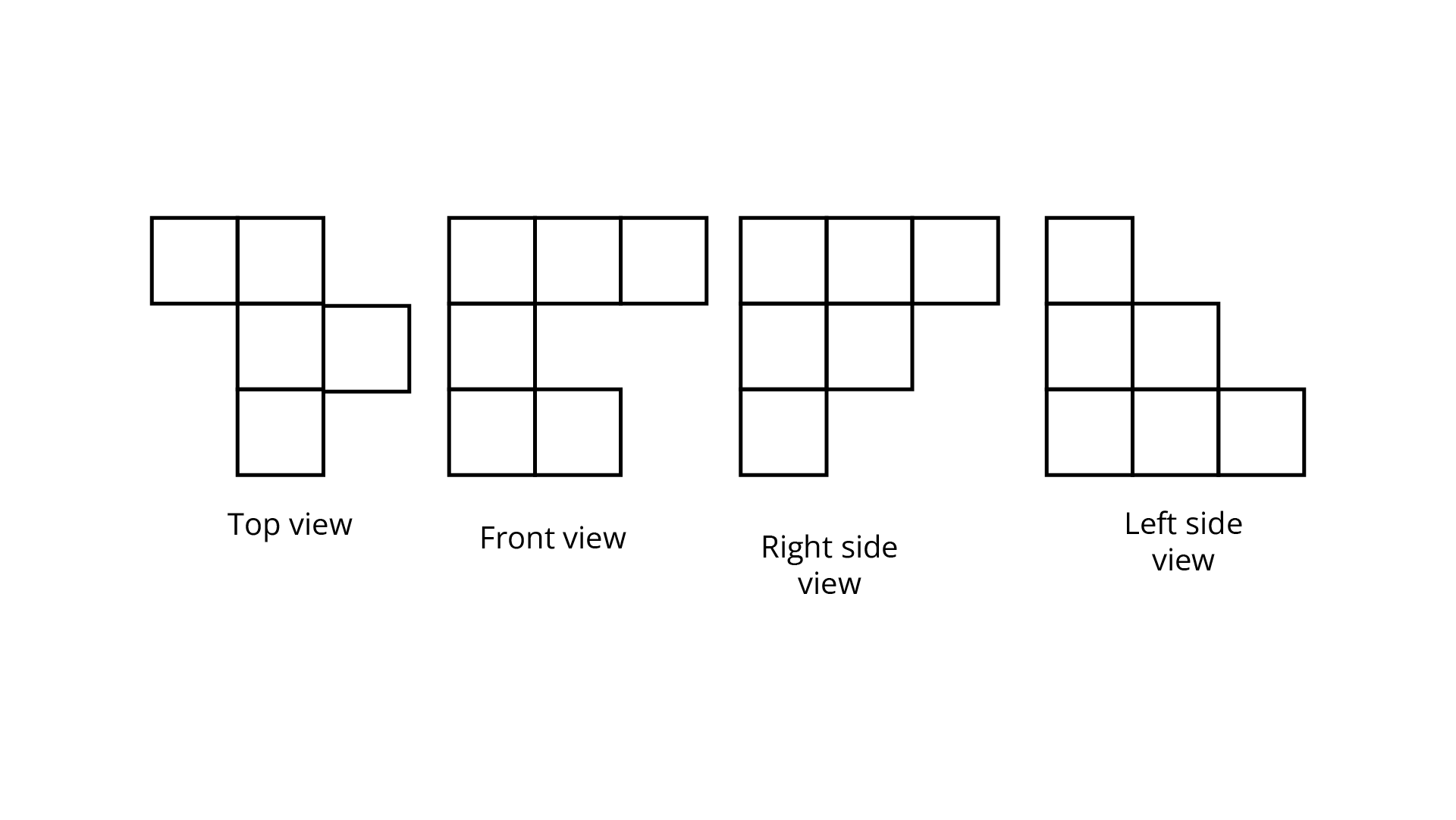
(c)

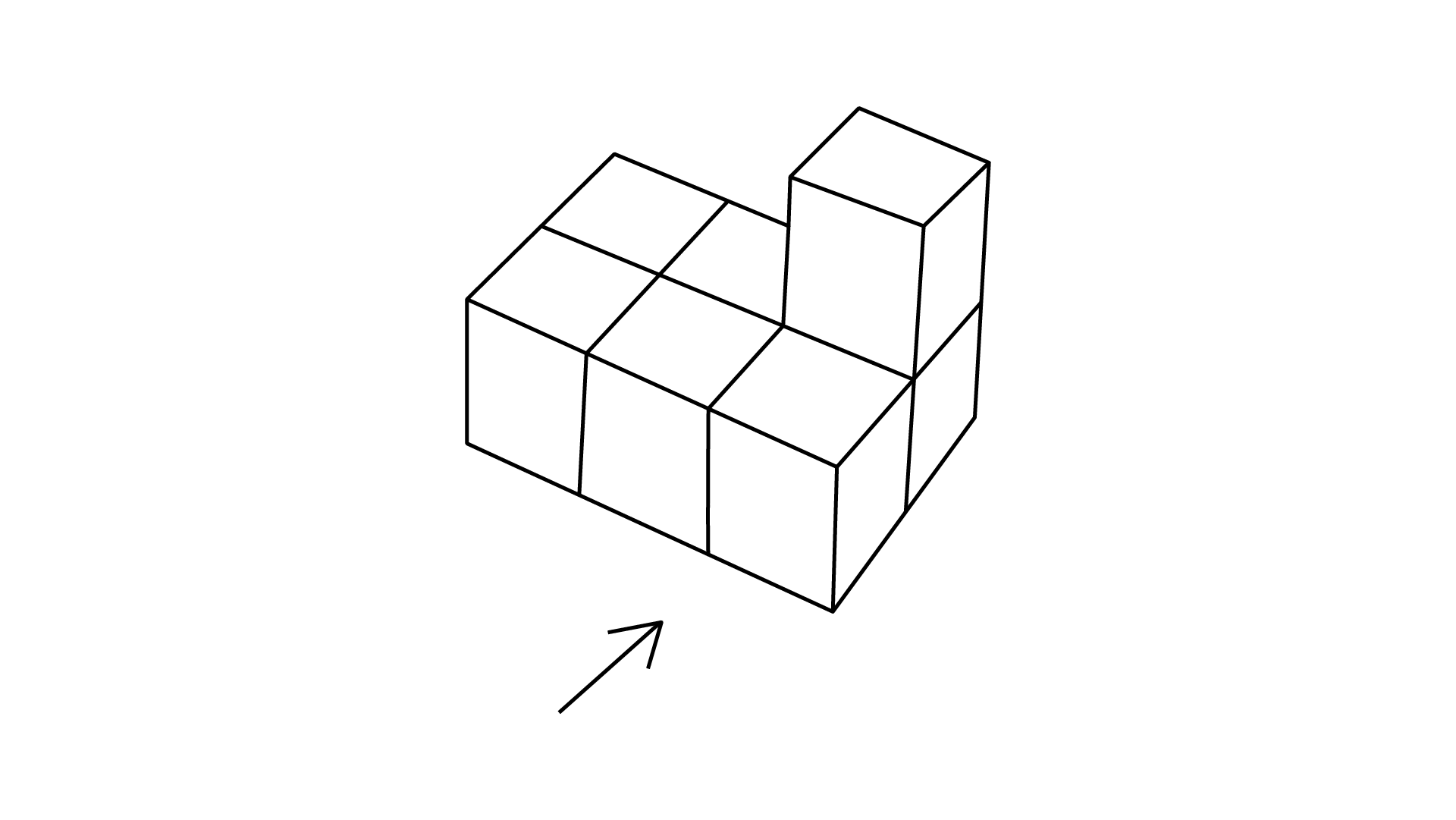
Ans: The number of cubes in given figure is $7.$

For the given figure,

(d)

Ans: The number of cubes in given figure is $8.$

For the given figure,

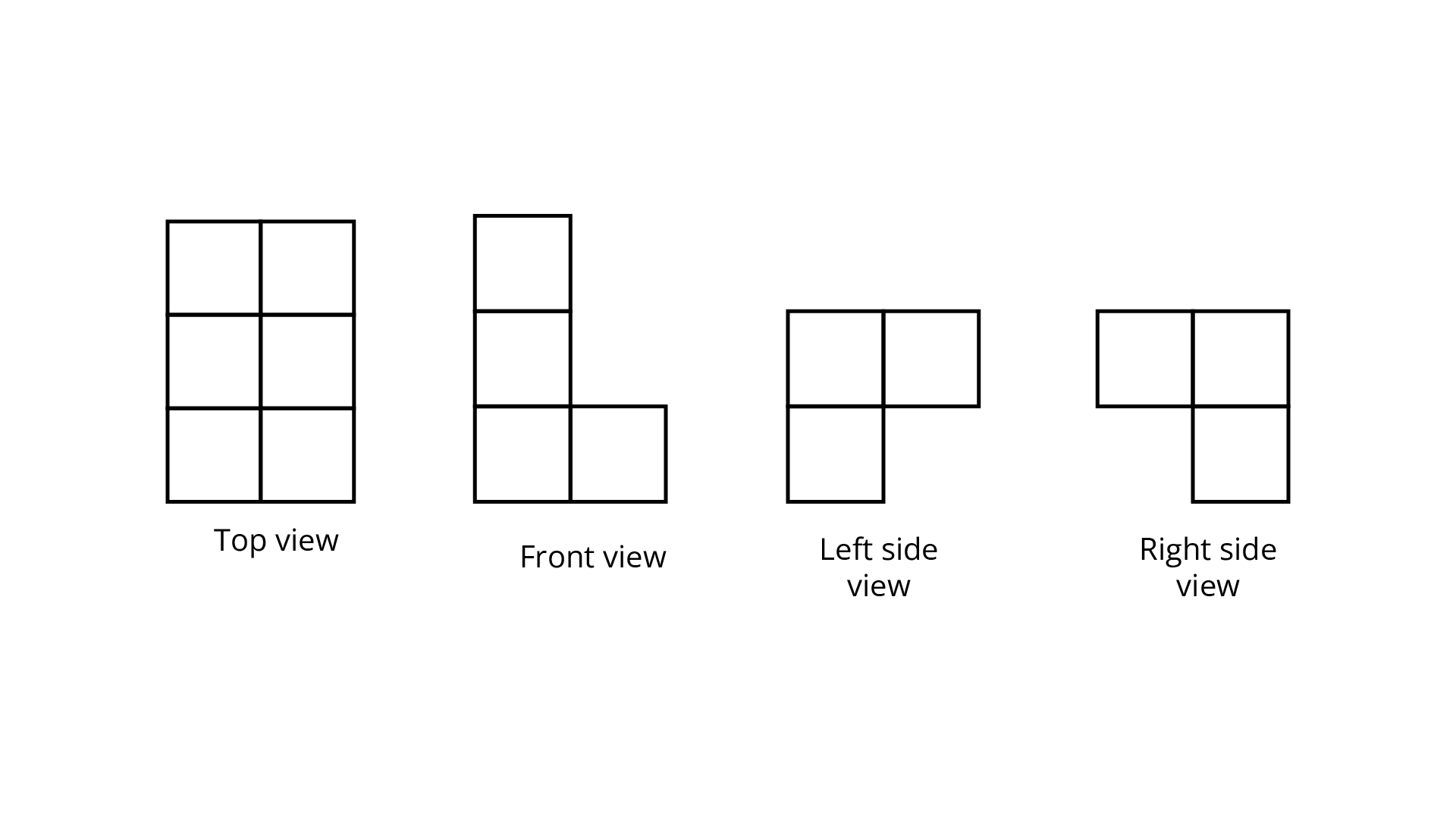
(e)

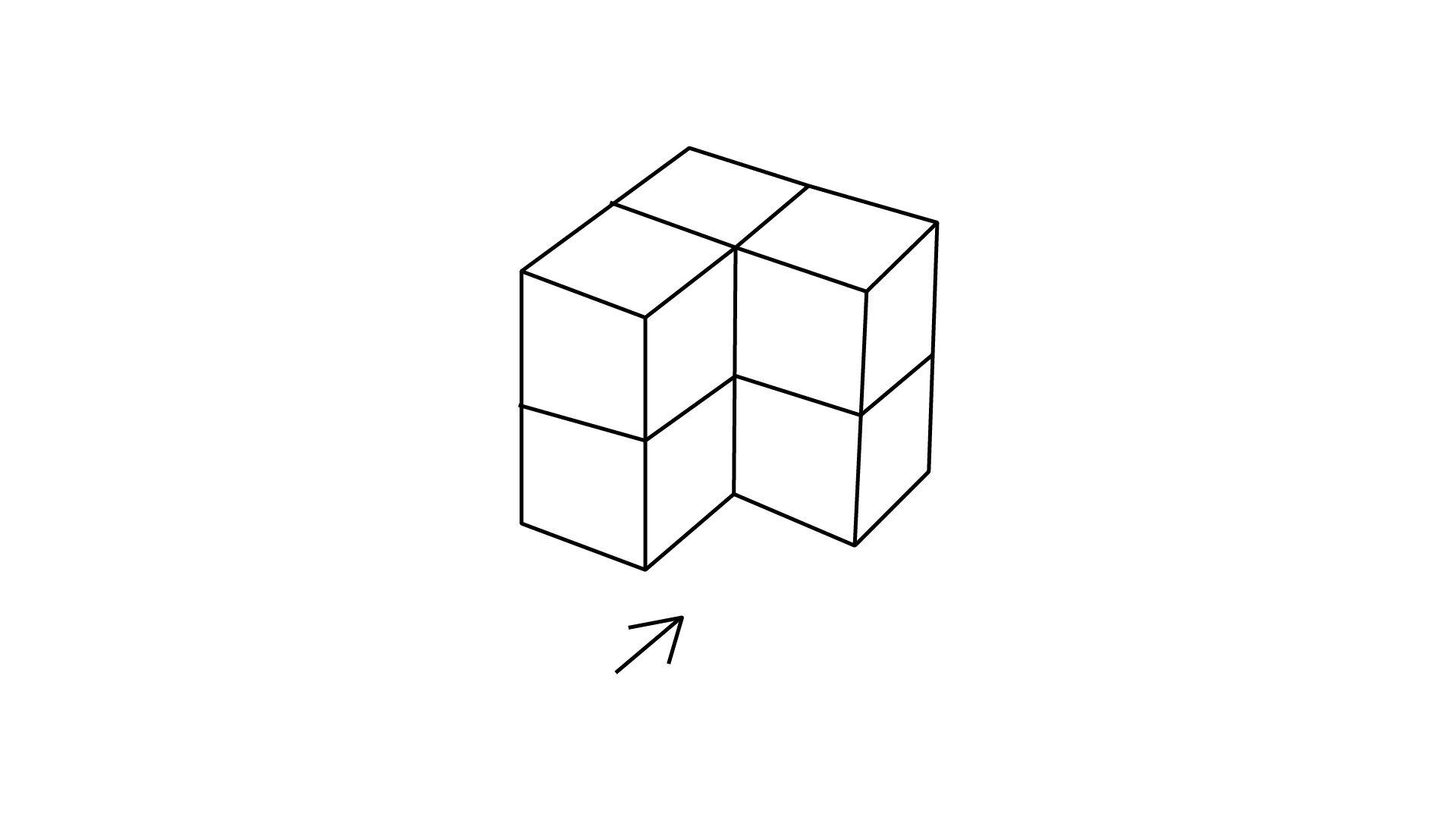
Ans: The number of cubes in given figure is $6.$

For the given figure,

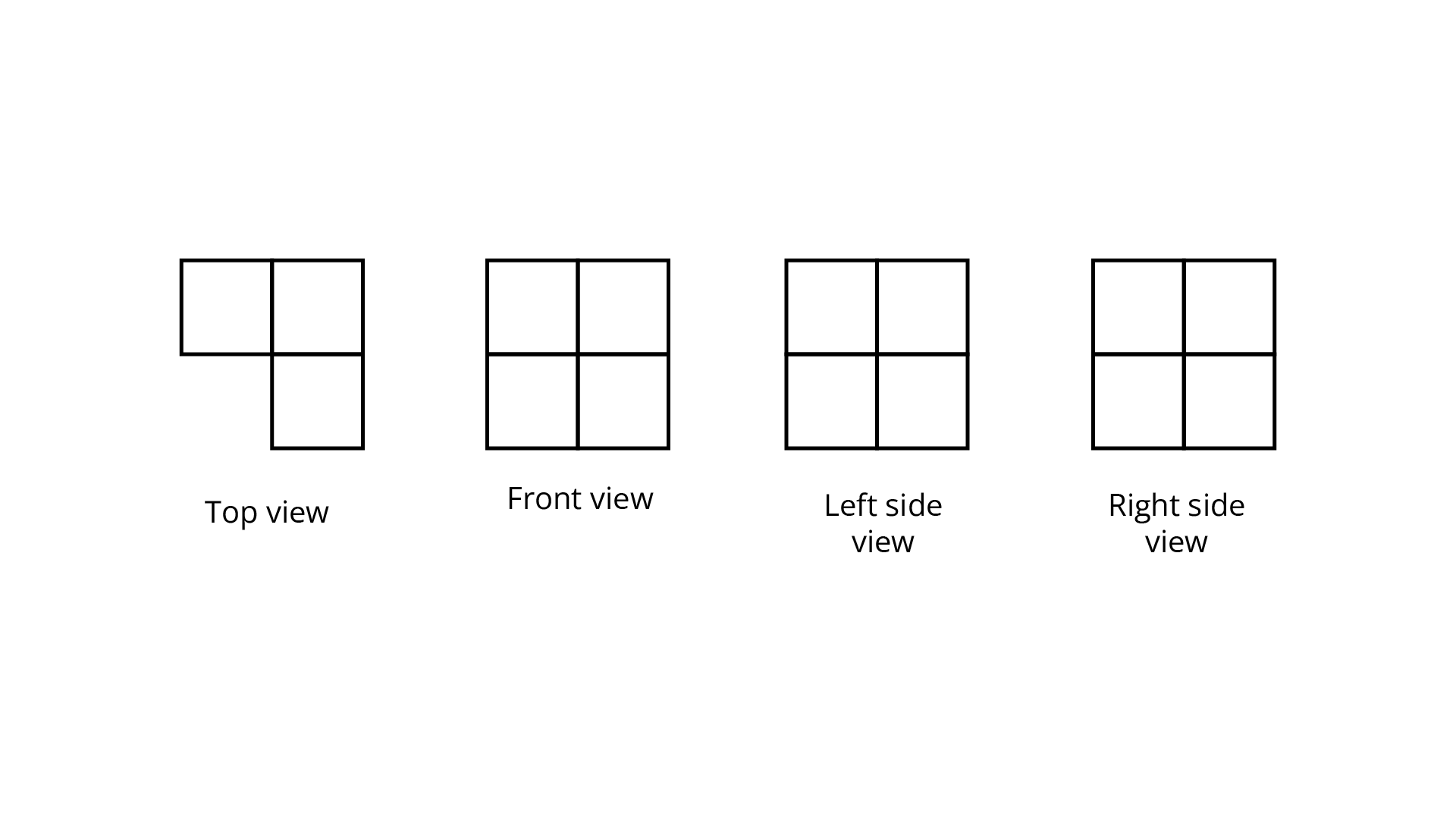
(f)

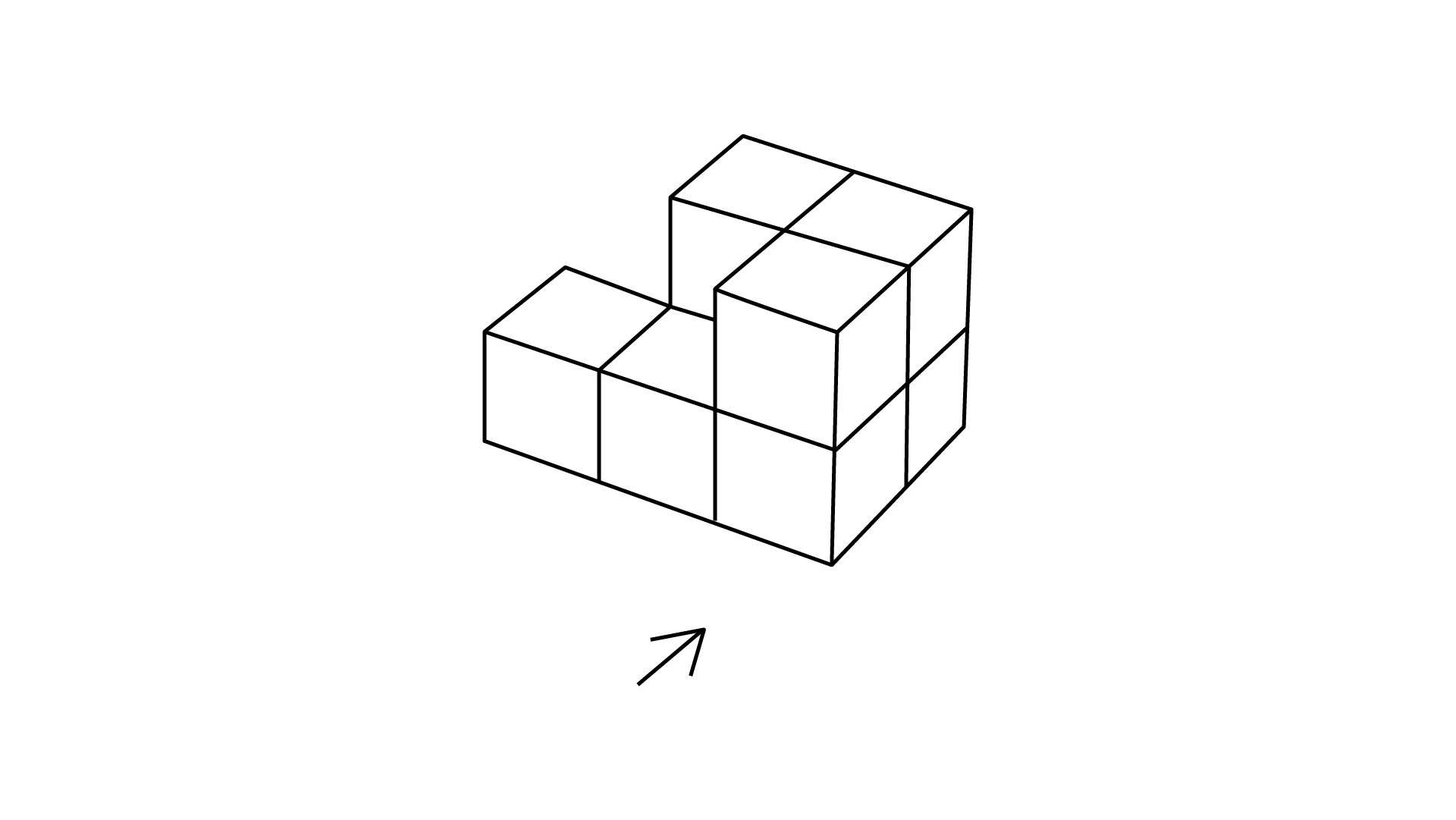
Ans: The number of cubes in given figure is $8.$

For the given figure,

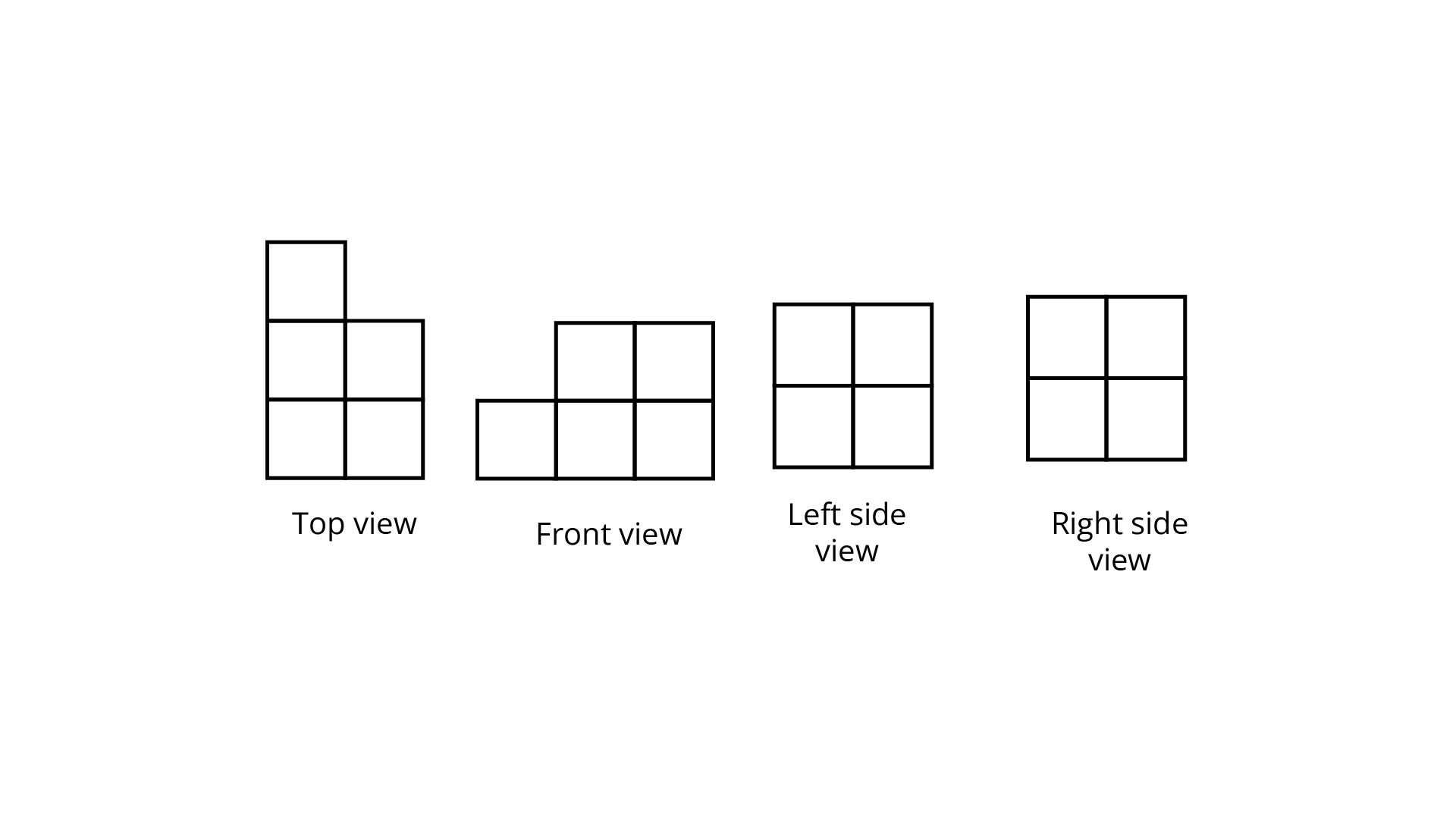
(g)

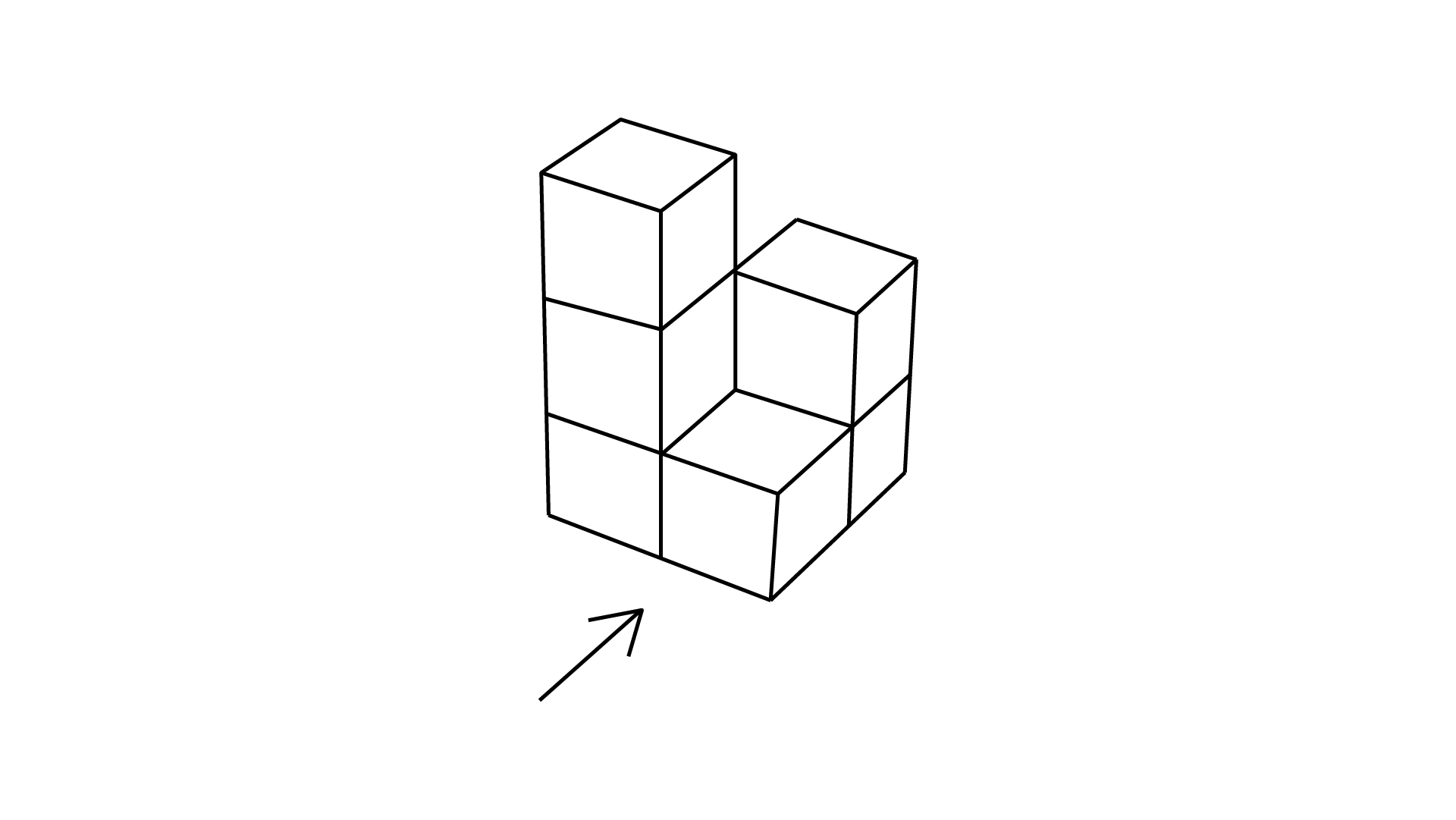
Ans: The number of cubes in given figure is $6.$

For the given figure,

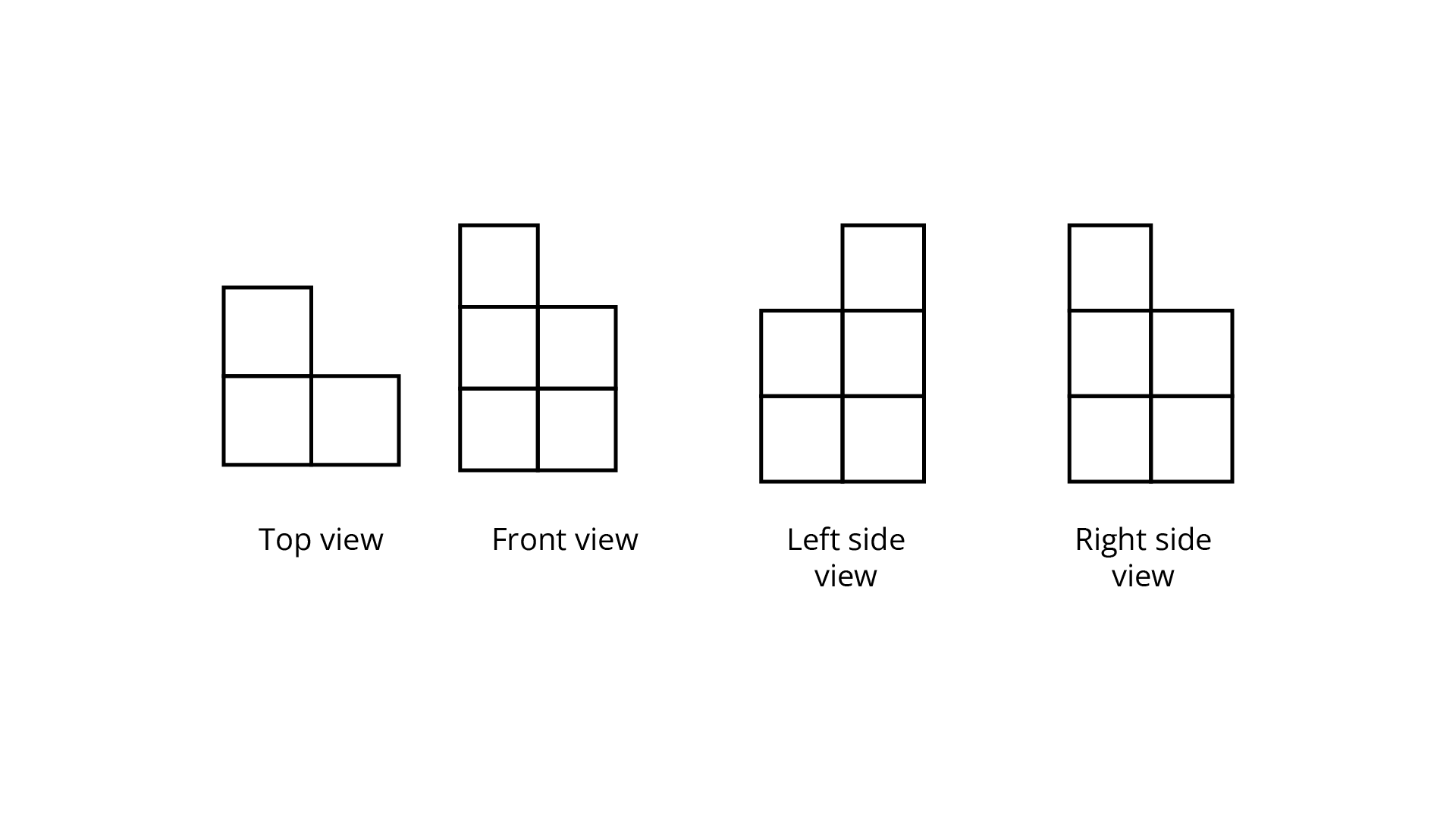
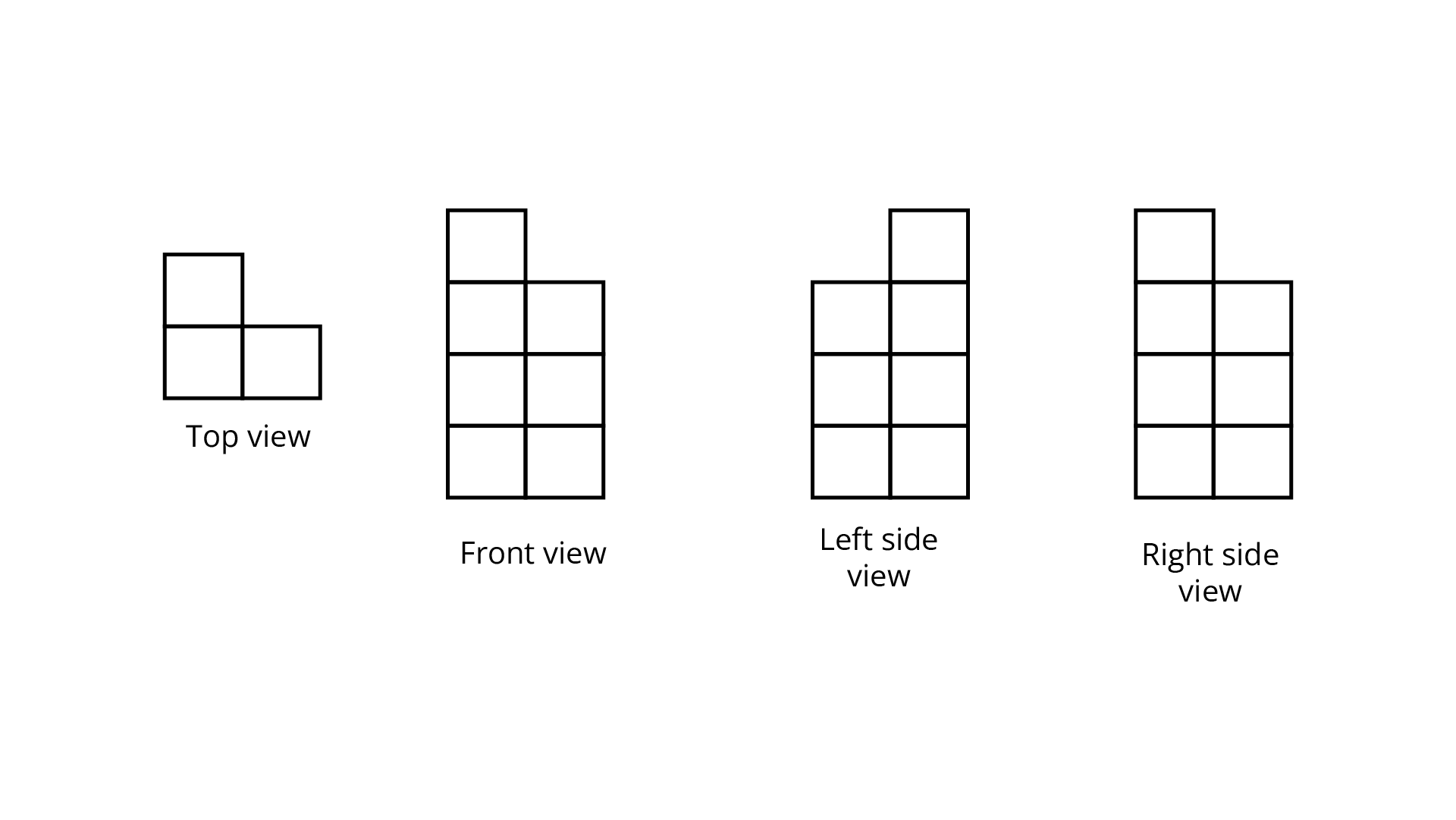
(h)

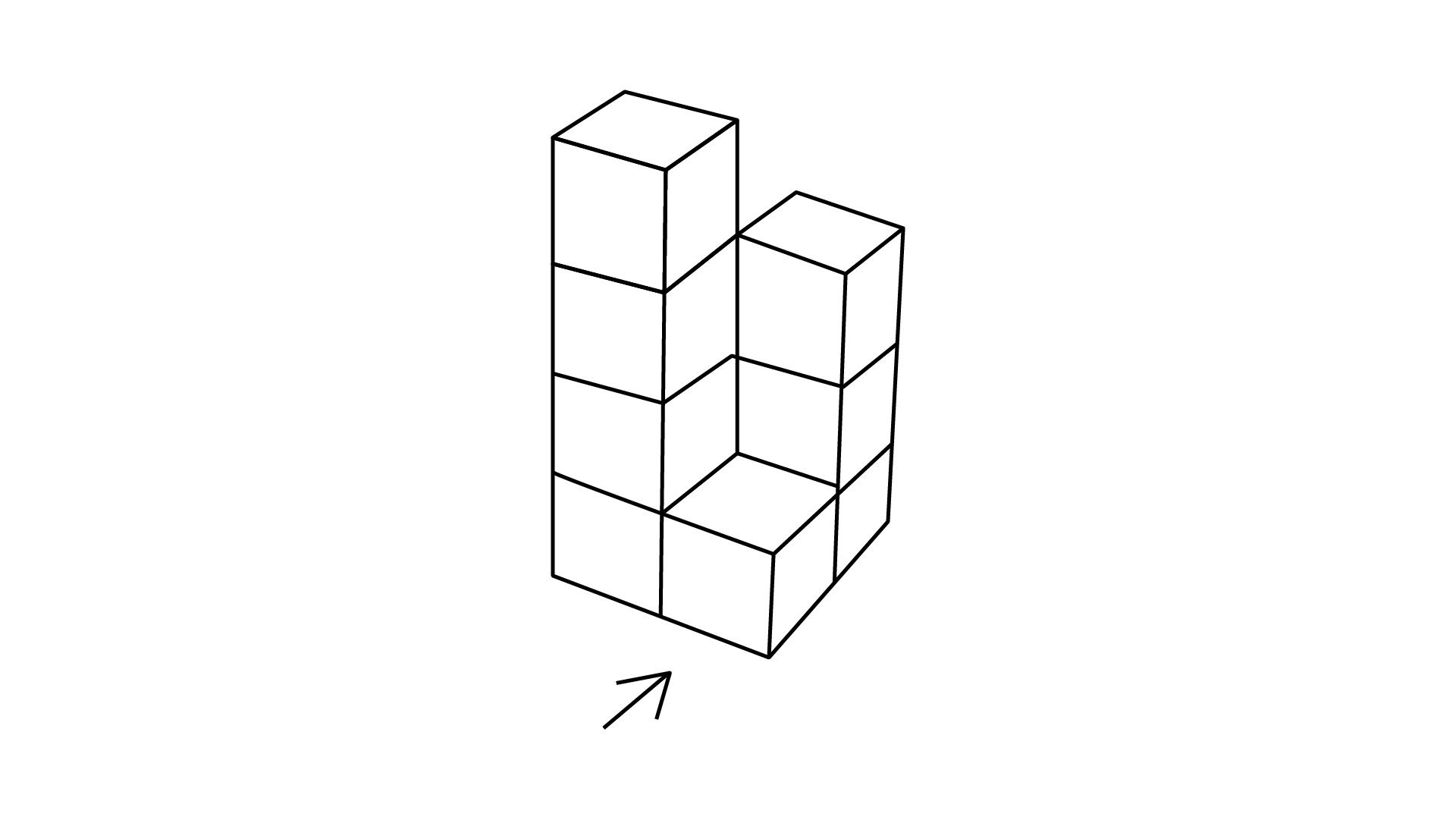
Ans: The number of cubes in given figure is $8.$

For the given figure,

114. Draw all lines of symmetry for each of the following figures as given below:

(a)

Ans: One line of symmetry.

(b)

Ans: It has no line of symmetry.

(c)

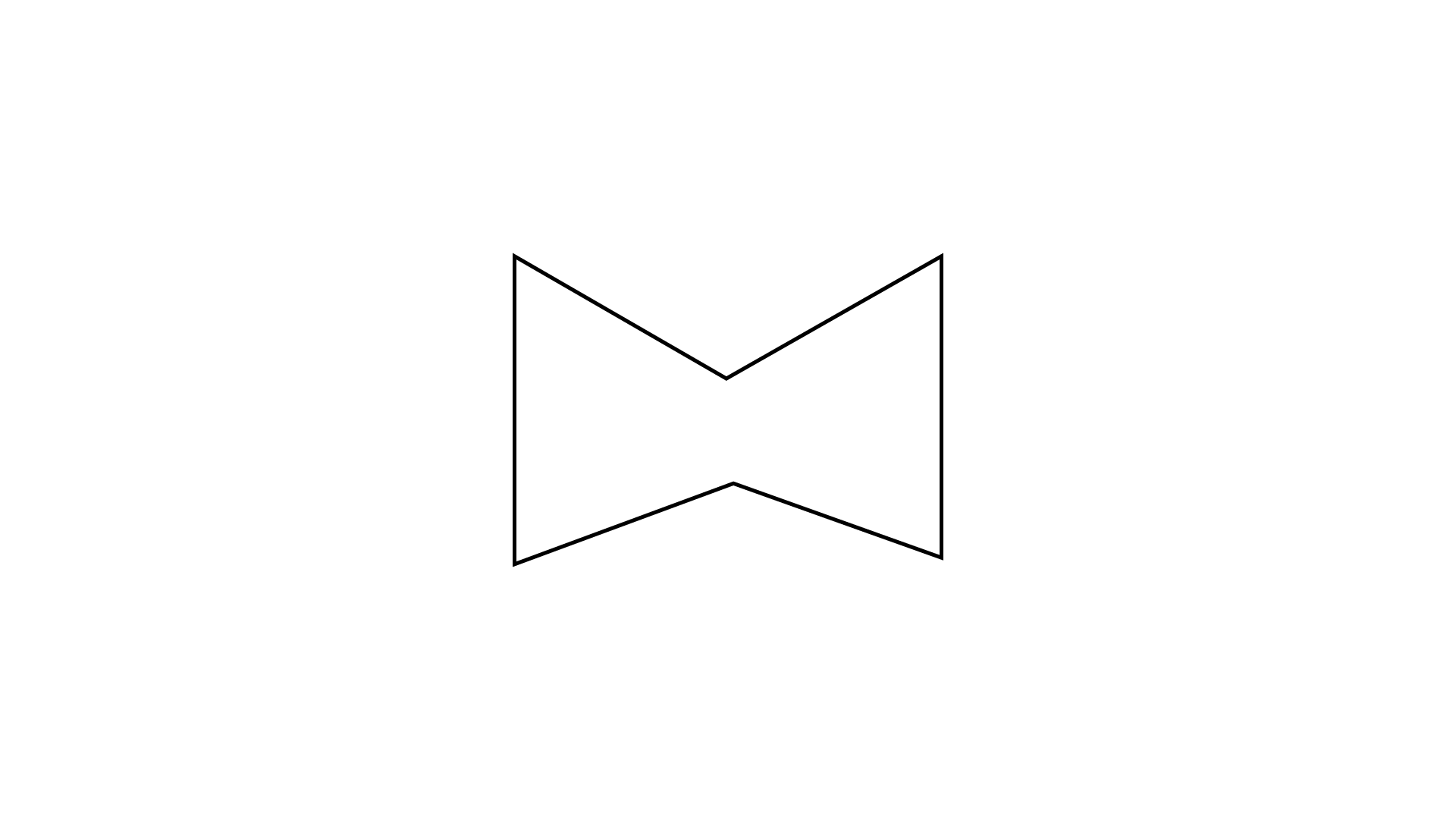
Ans: It has two lines of symmetry.

115. How many faces does Fig. 12.27 have?

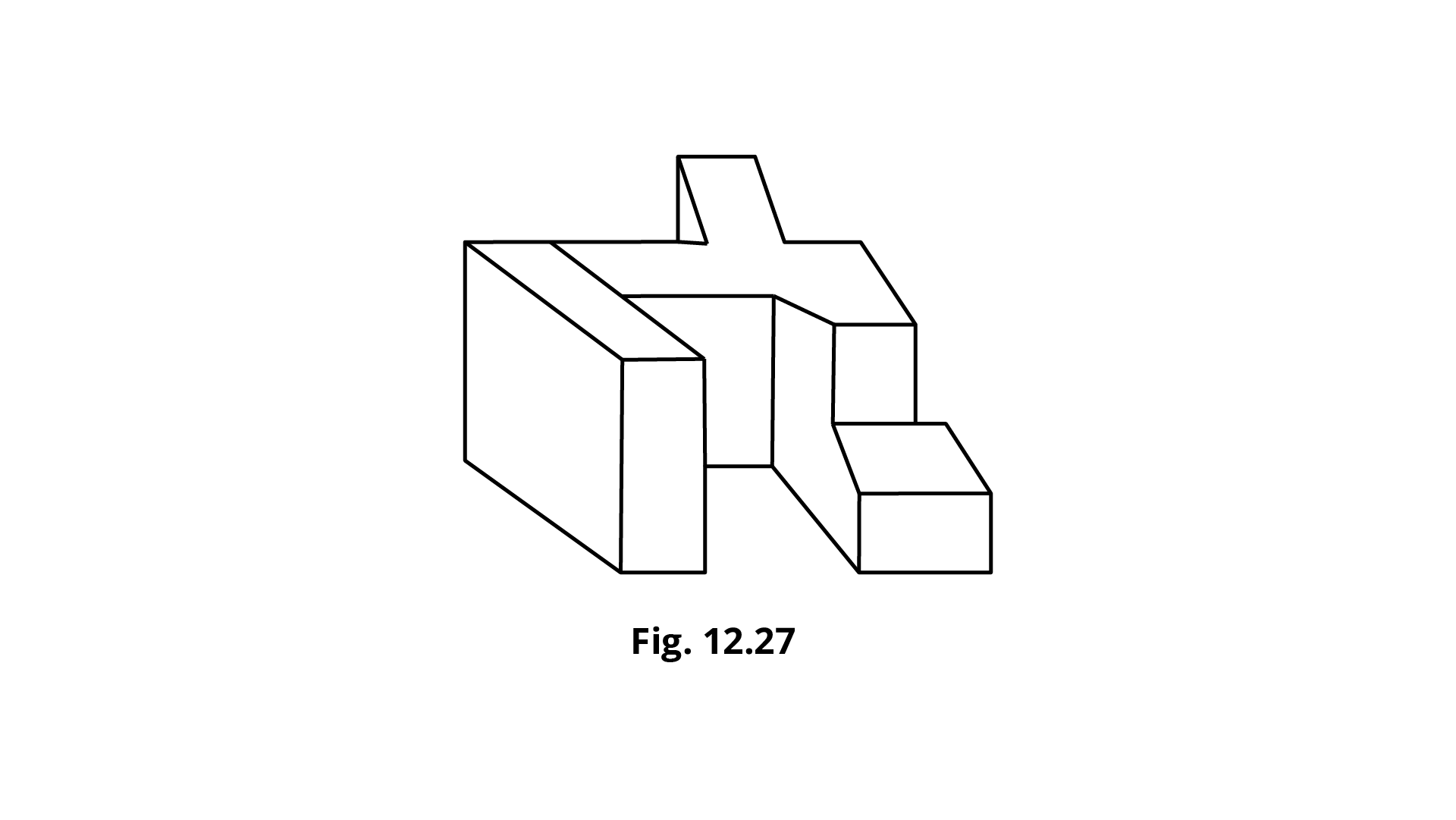
Ans: There are total \[16\] faces in the given figure.

116. Trace each figure. Then draw all lines of symmetry, if it has.

(a)

Ans:

It has two lines of symmetry.

(b)

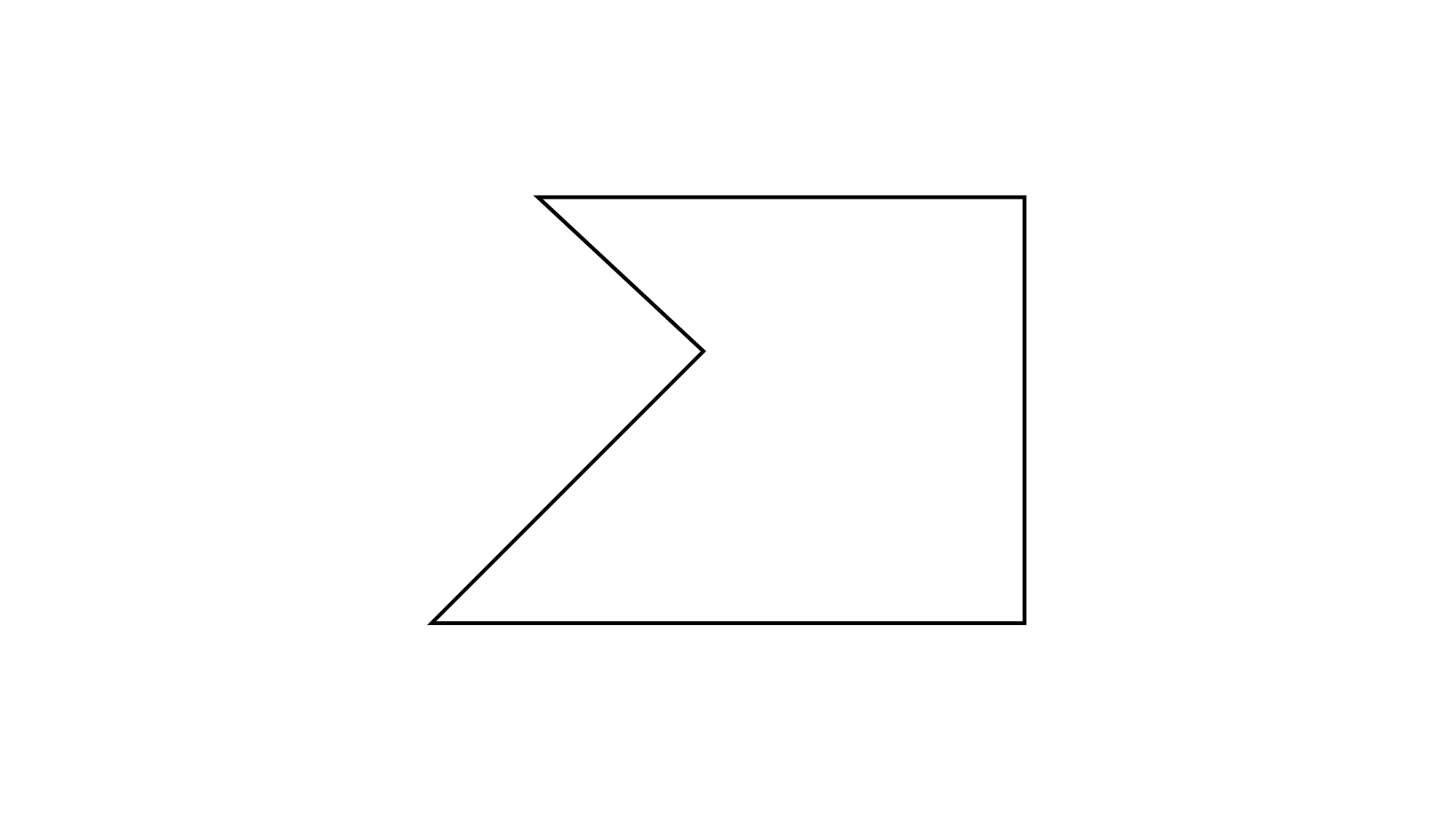
Ans:

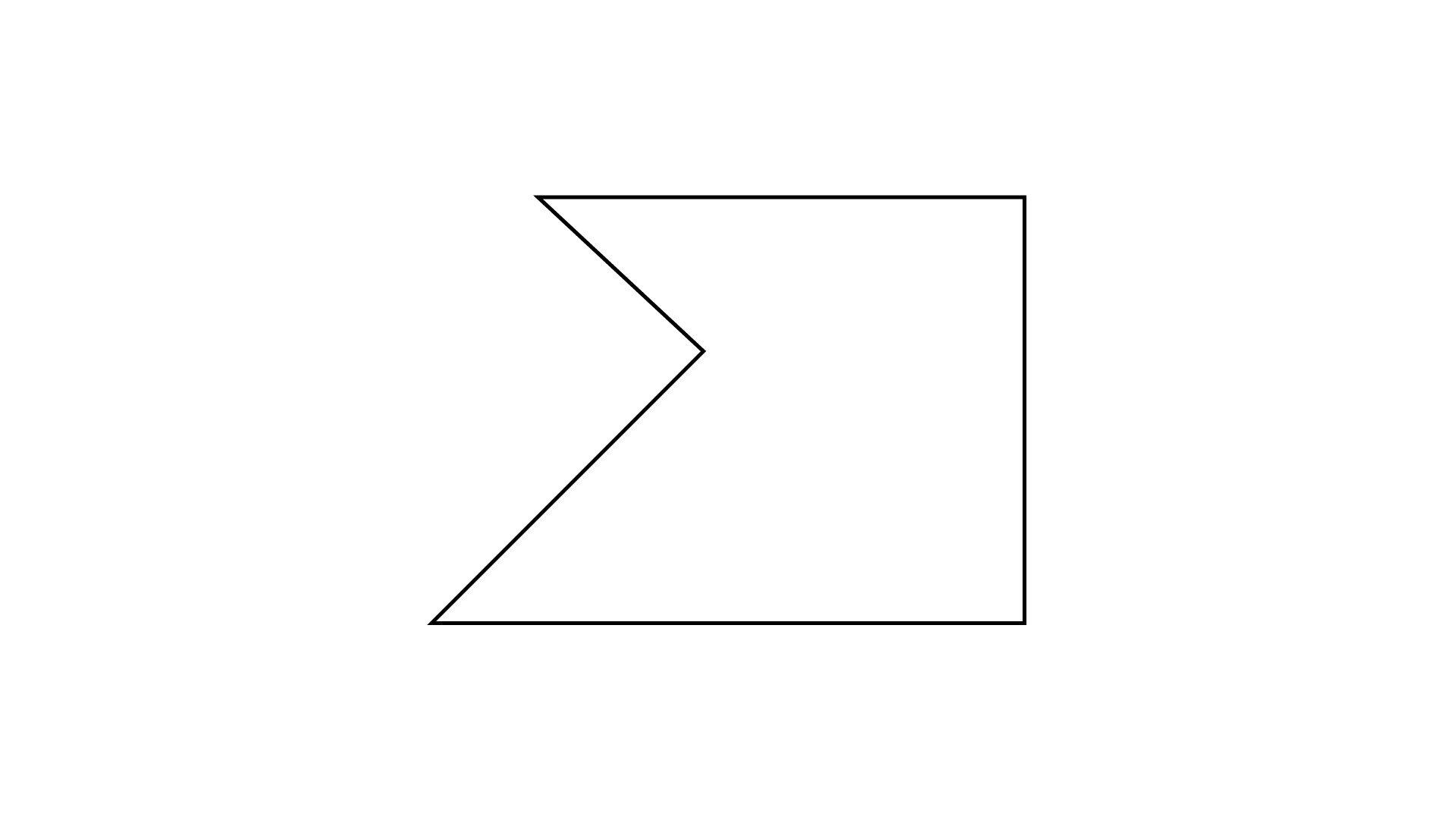
It has no line of symmetry.

(c)

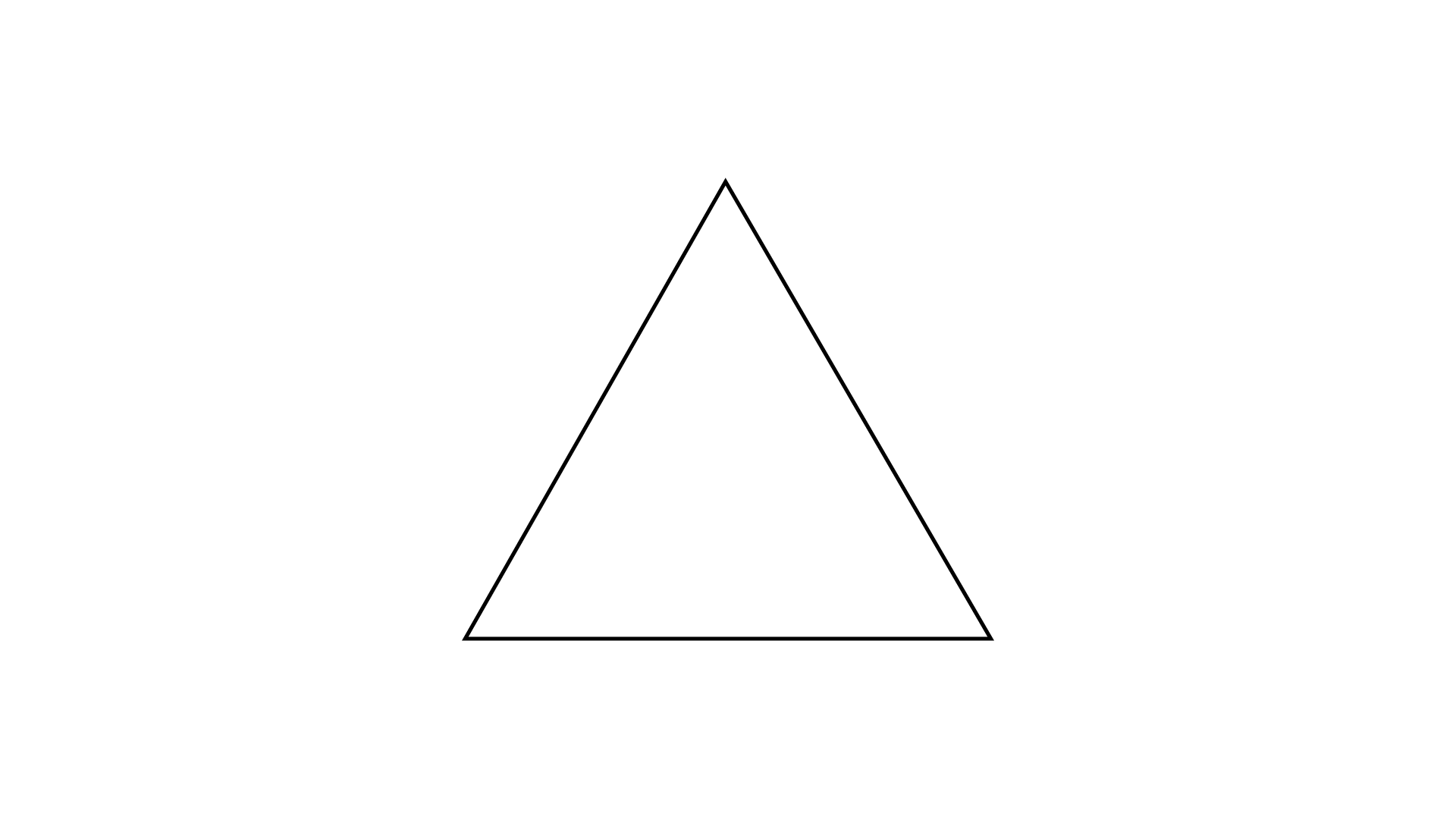
Ans:

It has three lines of symmetry.

117. Tell whether each figure has rotational symmetry or not.

(a)

Ans: The given figure has a rotational symmetry.

(b)

Ans:The given figure has no rotational symmetry.

(c)

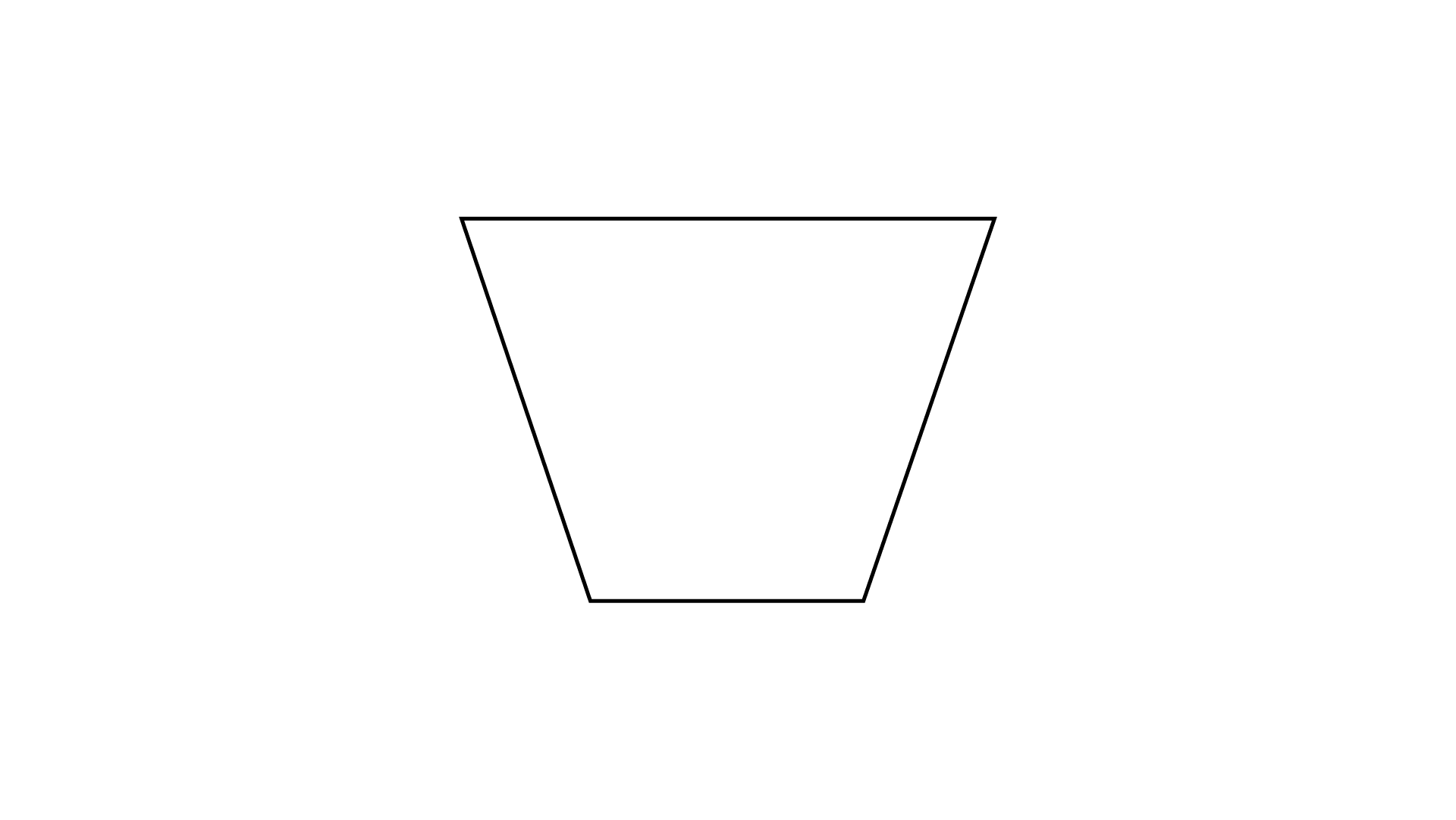
Ans: The given figure has no rotational symmetry.

(d)

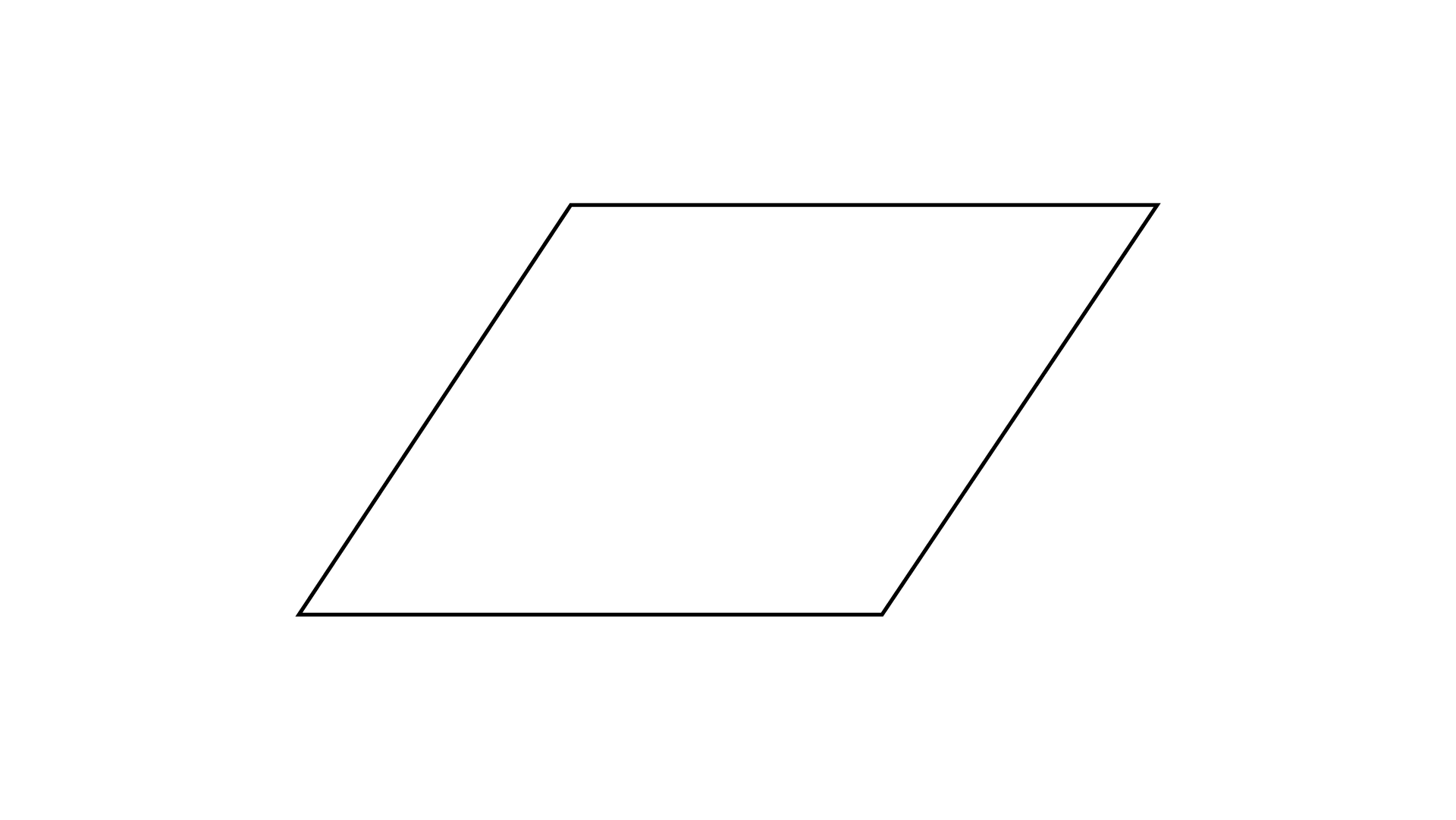
Ans: The given figure has a rotational symmetry.

(e)

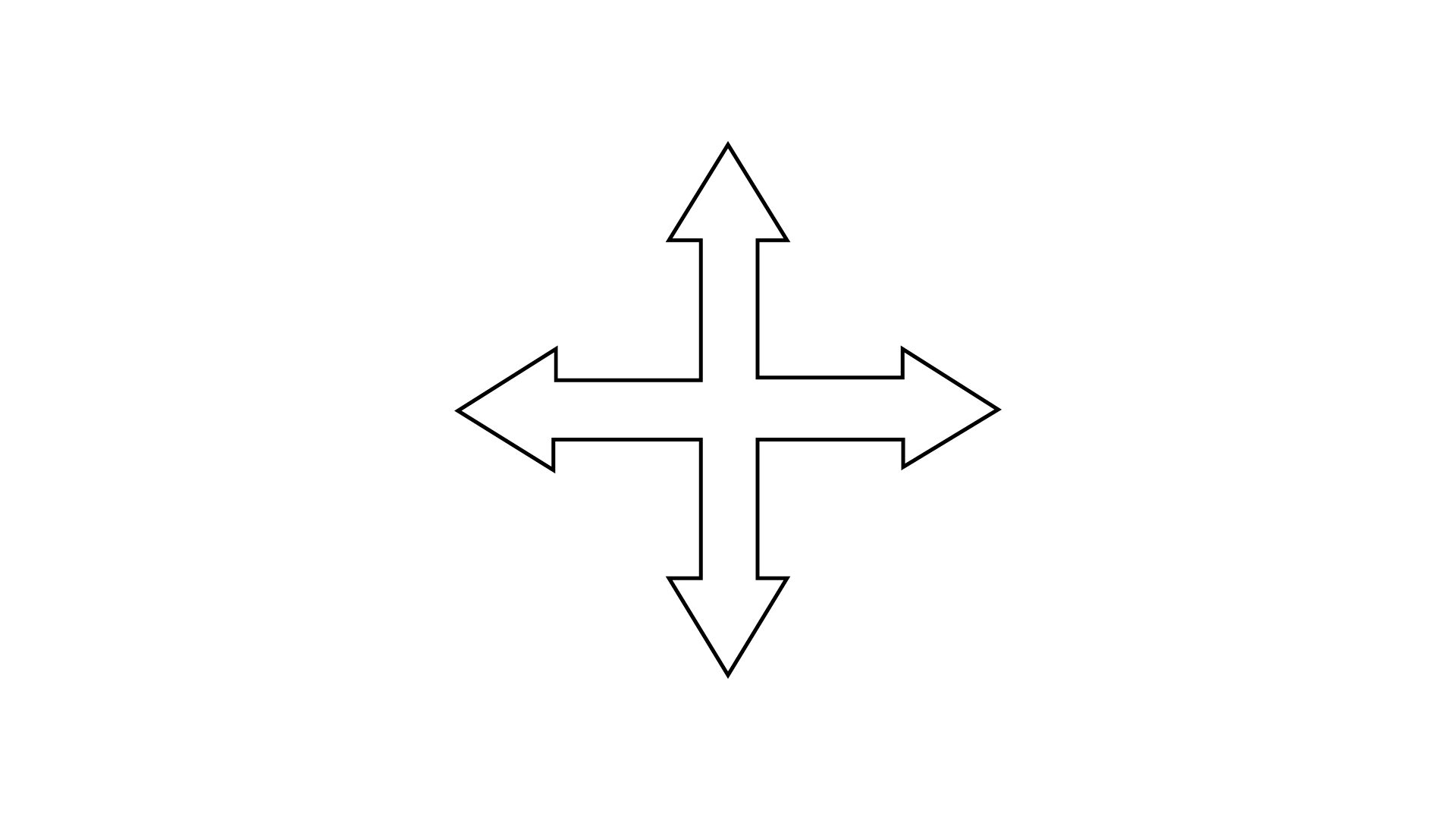
Ans: The given figure has a rotational symmetry.

(f)

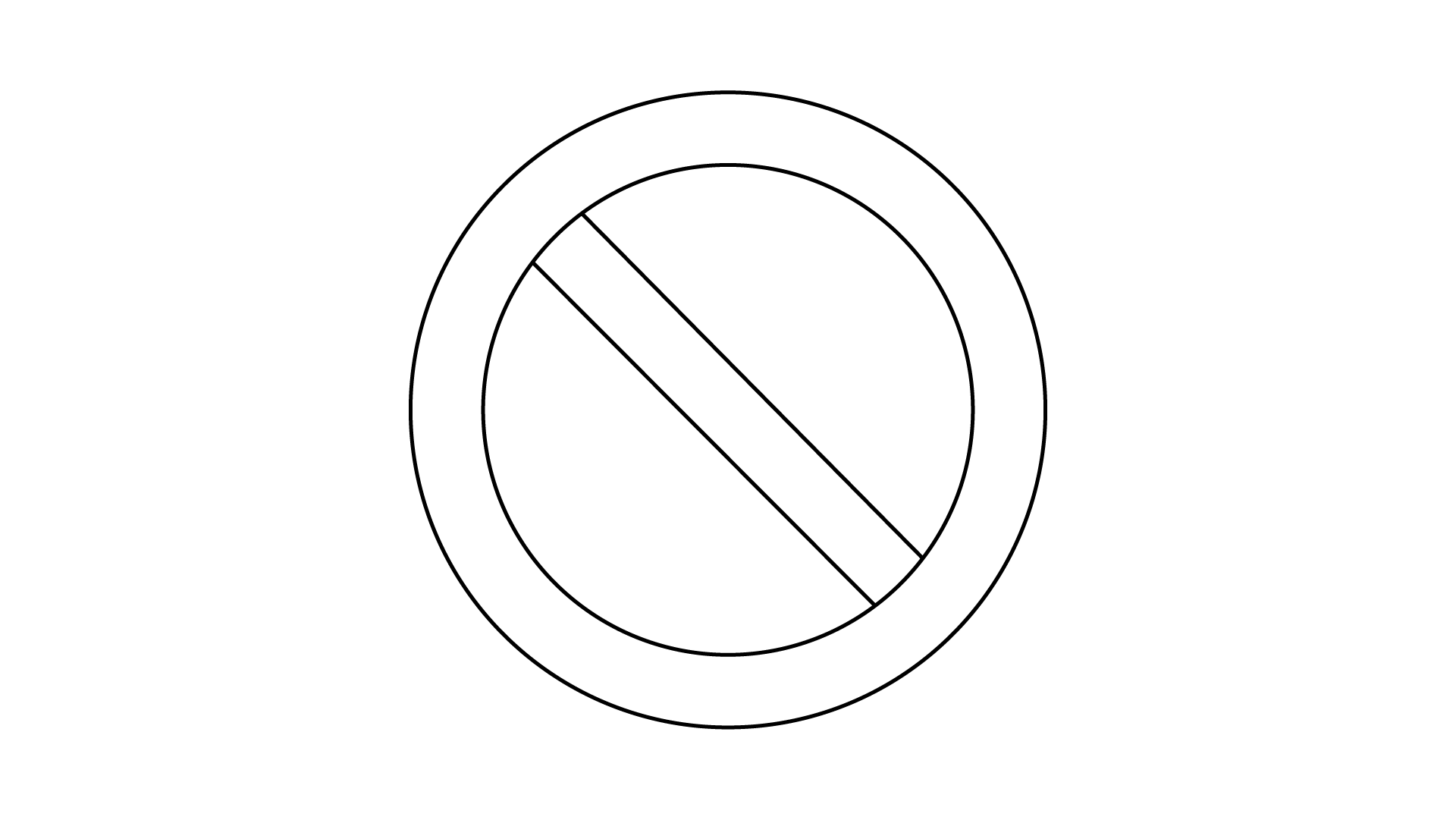
Ans: The given figure has a rotational symmetry.

118. Draw all lines of symmetry for each of the following figures.

(a)

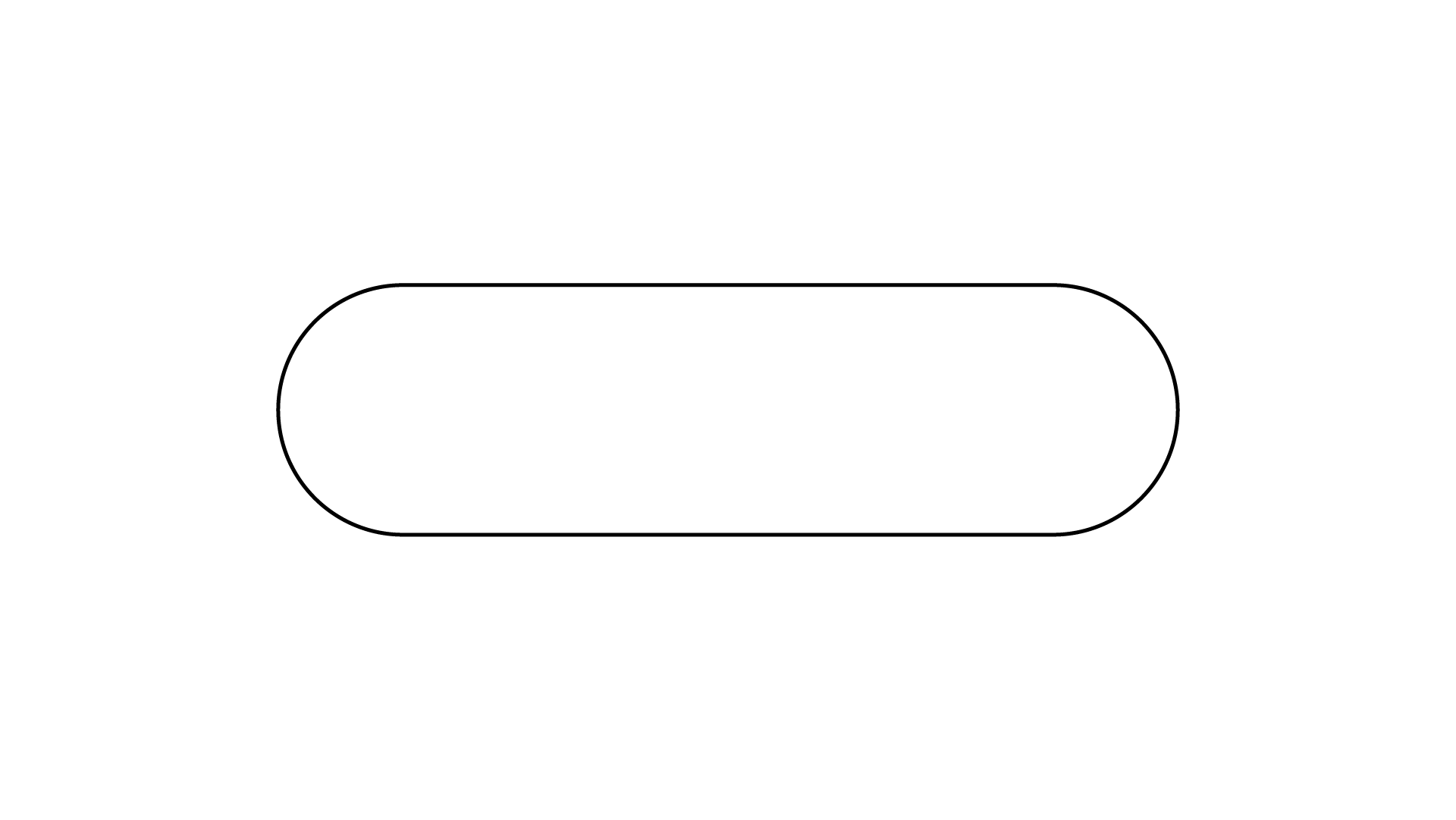
Ans:

It has two lines of symmetry.

(b)

Ans:

It has one line of symmetry.

(c)

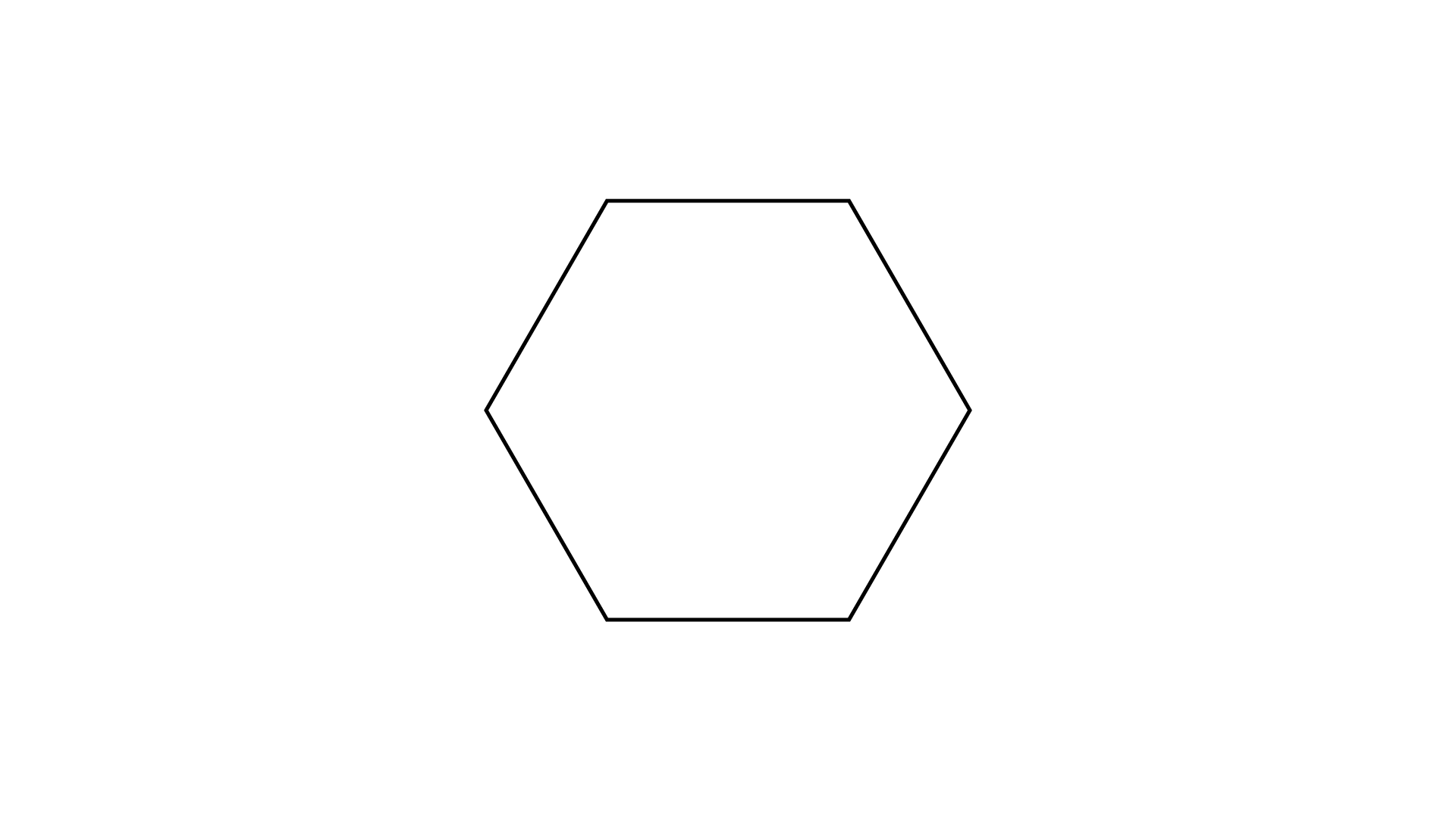
Ans:

It has six lines of symmetry.

(d)

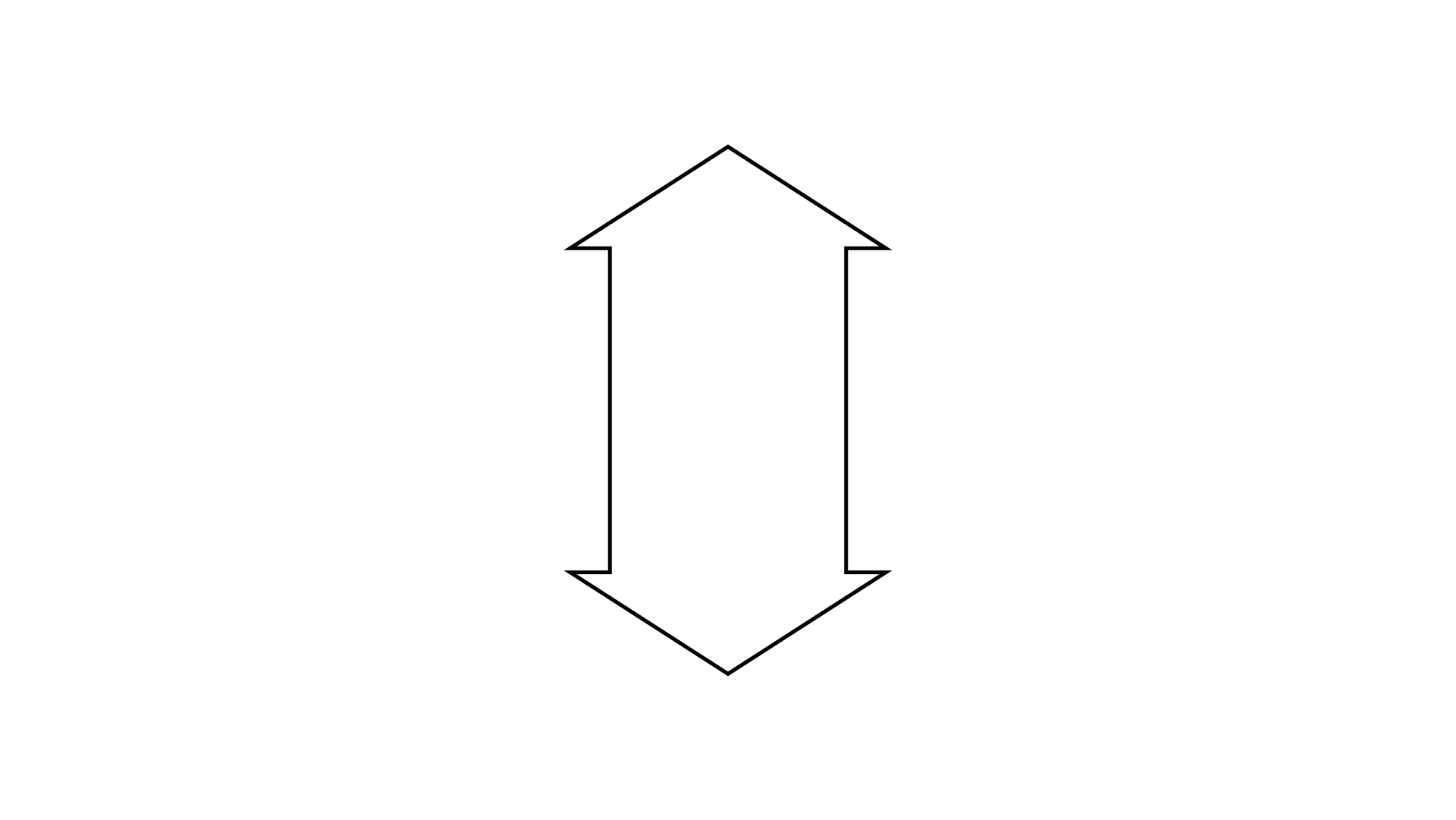
Ans:

It has two lines of symmetry.

(e)

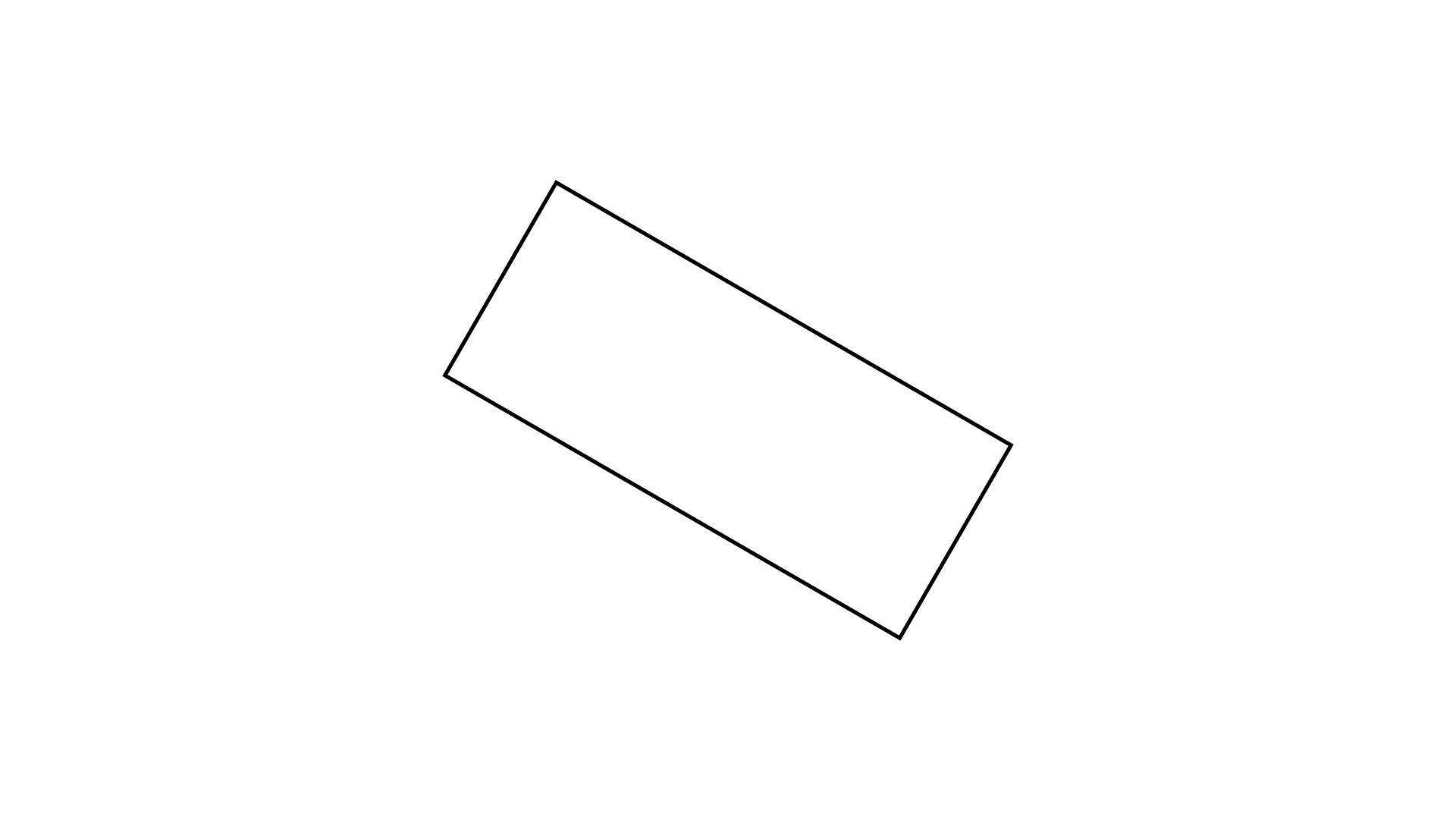
Ans:

It has two lines of symmetry.

(f)

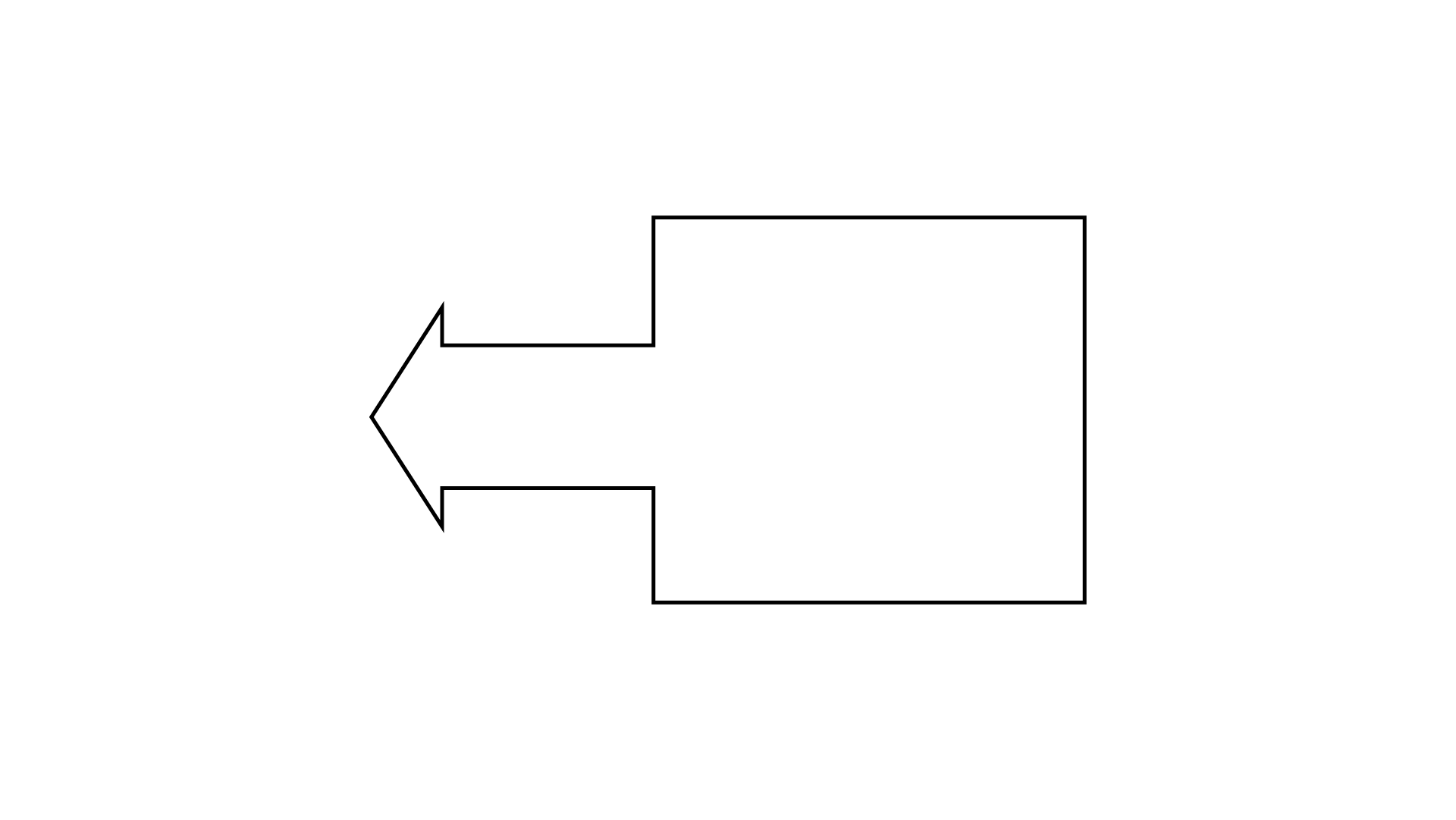
Ans:

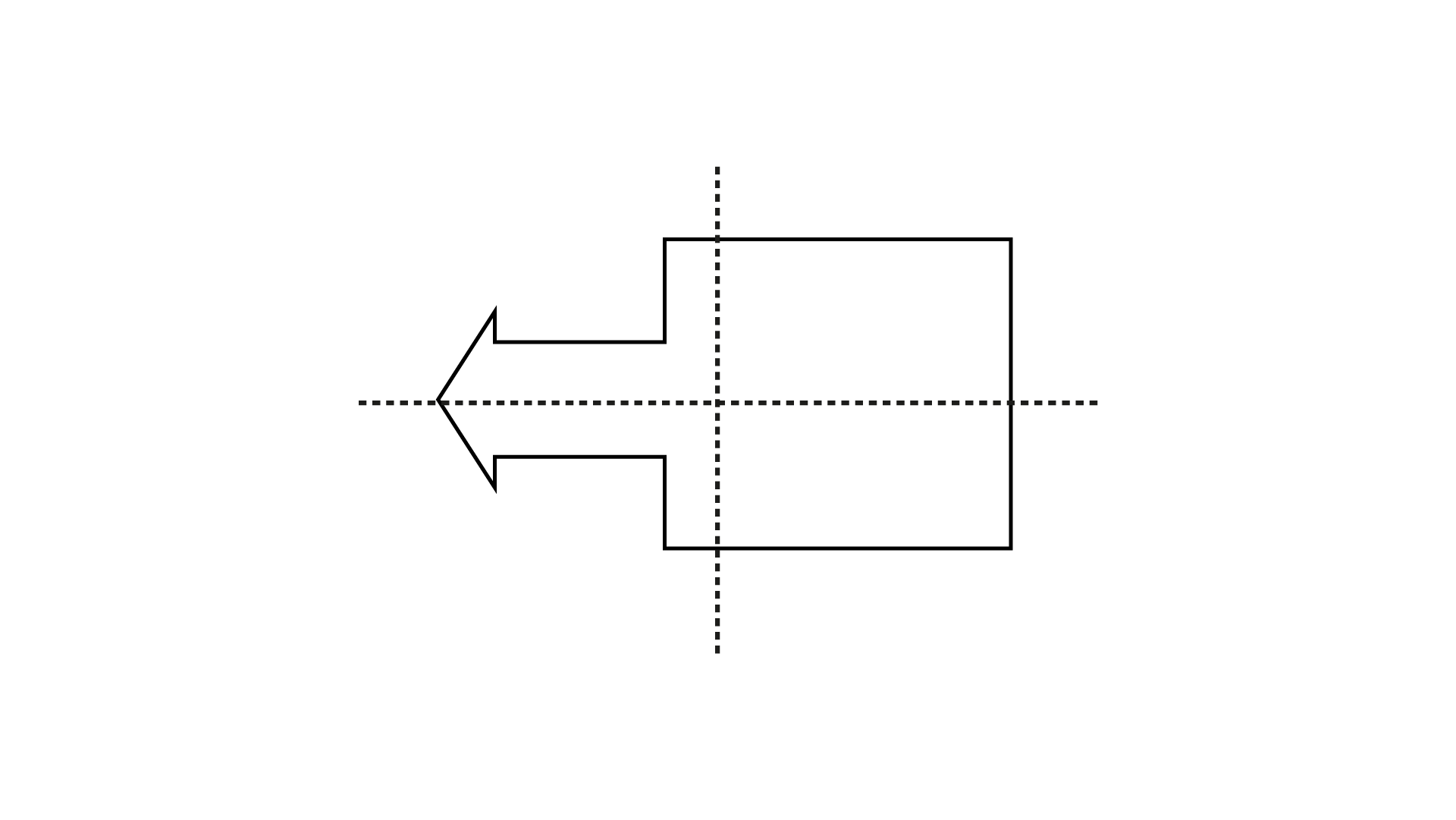
It has one line of symmetry.

119. Tell whether each figure has rotational symmetry. Write yes or no.

(a)

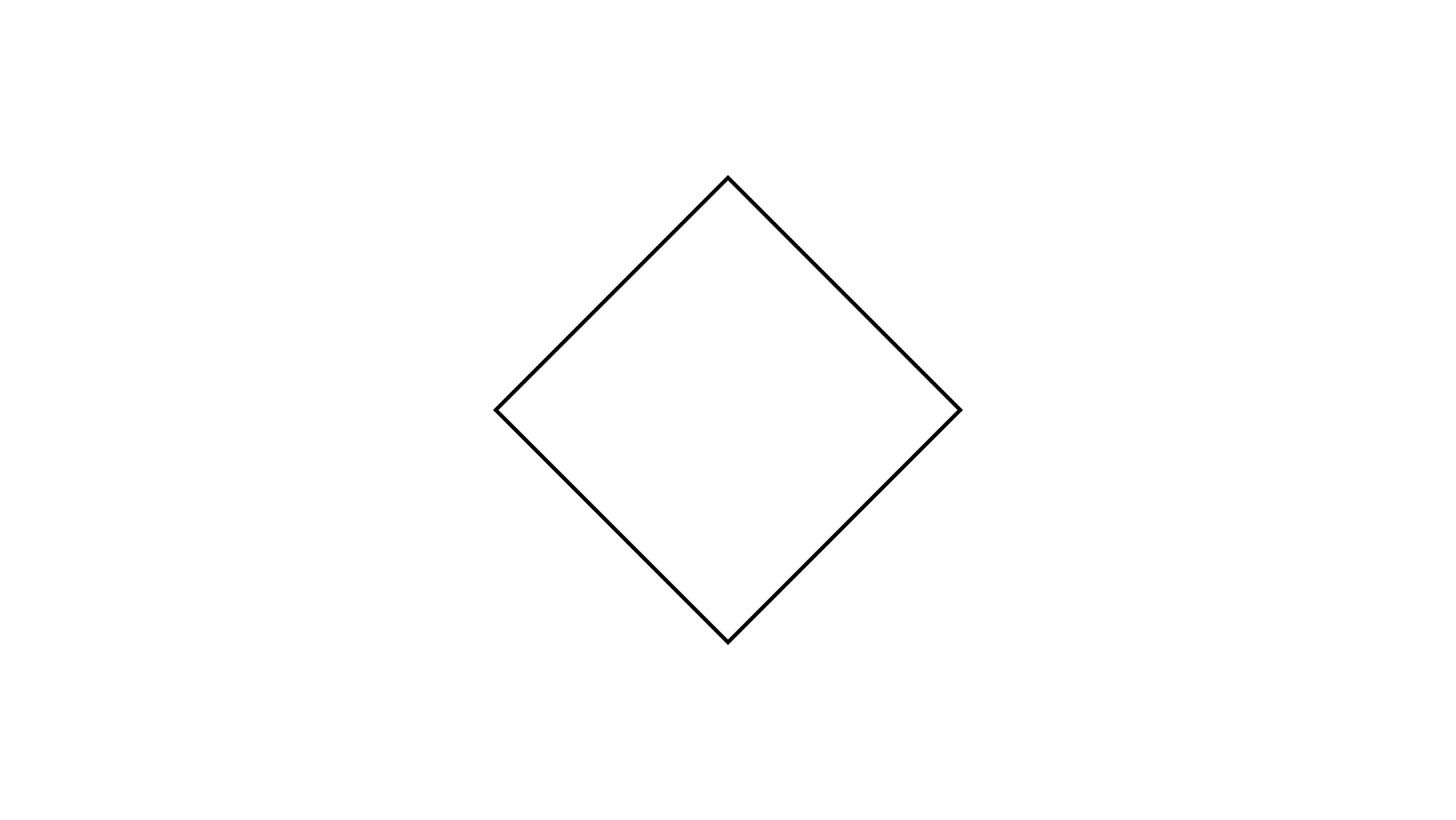
Ans: The given figure has rotational symmetry.

(b)

Ans: The given figure has rotational symmetry.

(c)

Ans: The given figure has no rotational symmetry.

(d)

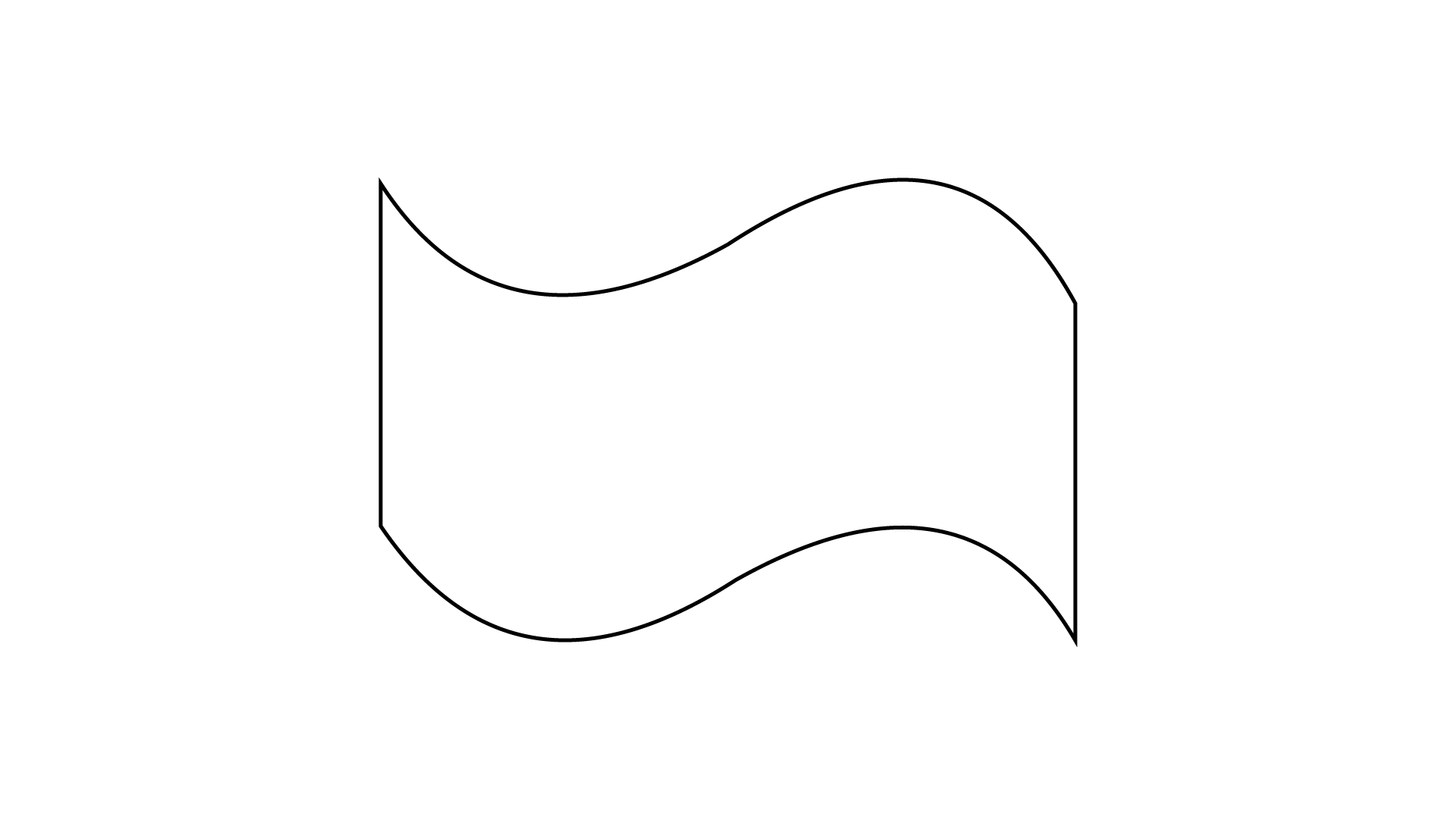
Ans: The given figure has rotational symmetry.

120. Does the Fig. 12.28 have rotational symmetry?

Ans: The given figure does not show rotational symmetry because one part of the design is un-darkened, whereas the other three parts are darkened. Hence, the design does not show symmetry.

121. The flag of Japan is shown below. How many lines of symmetry does the flag have?

Ans: The given flag has two lines of symmetry.

122. Which of the figures given below have both line and rotational symmetry?

(a)

(b)

(c)

(d)

Ans: Only (a) have both line and rotational symmetry. In the given figure, line of symmetry will be shown as,

Also, rotational symmetry will be shown as,

$\dfrac{{{{360}^\circ }}}{8} = {45^\circ }$, i.e. rotational angle is equal to ${45^\circ }$.

123. Which of the following figures do not have line symmetry?

(a)

Ans: The given figure has two lines of symmetry.

(b)

Ans:The given figure has one line of symmetry.

(c)

Ans: The given figure has two lines of symmetry.

(d)

Ans: The given figure has no lines of symmetry.

124. Which capital letters of the English alphabet have no line of symmetry?

Ans: The letters ${\text{F, G, J, L, N, R Q, R, S and Z}}$ have no line of symmetry.

Concepts To Learn From NCERT Exemplar Class 7 Math Solutions Chapter 12 Practical Geometry Symmetry & Visualizing Solid Shapes

As we all know geometry is all around our environment and can’t be ignored, similarly the chapter Practical Geometry Symmetry & Visualizing Solid Shapes cannot be ignored in the Class 7th Math syllabus. Understanding this chapter to its core is very important because it makes students learn how to measure the dimensions of a particular shape, how to recognize a shape to solve a problem, and more. In this chapter students also learn crucial visualization skills that are necessary to solve different NCERT problems and can be very easily also learned and organized through deep practice. 

This chapter includes a wide variety of exercise solutions to help students with all types of concepts that could be related to Practical geometry and visualizing solid shapes. Students might not realize but this chapter is of huge practical importance and it’s important to have clarity of it. Class 7th students will learn how to construct parallel lines, different triangles with essential conditions. In addition to that students will also learn about line and rotational symmetry in this chapter. One amazing thing children will learn in this chapter is about different solid shapes, their oblique nature and how they are represented isometrically. 

Important Topics In NCERT Exemplar Class 7 Math Solutions Chapter 12 Practical Geometry Symmetry & Visualizing Solid Shapes

Construction Of Triangle 

This chapter will make you aware of the important dimensions and measurements you should know to construct a triangle. 

Line Symmetry

Under this chapter students will also learn about what is line symmetry, how many lines of symmetry are there in different shapes and how to identify the symmetrical and asymmetrical shapes. 

Rotational Symmetry 

Rotational symmetry is a completely new topic that will be covered in this chapter. Students will learn what is the center of rotation, the angle of rotation and what does half and full-degree rotation mean. 

Solids 

As mentioned earlier, this chapter is practically very important because students will understand two types of sketches that are used to represent solid objects: Oblique sketches and Isometric sketches.