NCERT Exemplar for Class 6 Maths Solutions Chapter 7 Algebra

In examples 1 to 3, write the correct answer from the given four options:

Example 1: ${\mathbf{4a}}$ equals

(A) ${\mathbf{4}} + {\mathbf{a}}$

(B) ${\mathbf{4}} \times {\mathbf{a}}$

(C) ${\mathbf{a}} \times {\mathbf{a}} \times {\mathbf{a}} \times {\mathbf{a}}$

(D) ${\mathbf{4}} \div {\mathbf{a}}$

Ans: (b)

Example 2: ${\mathbf{8}}$ more than three times the number ${\mathbf{x}}$ can be represented as:

(A) ${\mathbf{8}} + {\mathbf{x}} + {\mathbf{3}}$

(B) ${\mathbf{3x}}-{\mathbf{8}}$

(C) ${\mathbf{3x}} + {\mathbf{8}}$

(D) ${\mathbf{8x}} + {\mathbf{3}}$

Ans: (c).

Example 3: Which of the following is an equation?

(A) ${\mathbf{x}} + {\mathbf{7}}$

(B) ${\mathbf{2y}} + {\mathbf{3}} = {\mathbf{7}}$

(C) ${\mathbf{2p}} < {\mathbf{10}}$

(D) ${\mathbf{12x}}$

Ans: (b)

Example 4: Fill in the blanks to make it a true statement:

${\mathbf{7}}$ times of ${\mathbf{y}}$ subtracted from ${\mathbf{50}}$ can be expressed as ________

Ans: $50-7{\text{y}}$

Example 5: State true or false:

${\mathbf{x}}$=${\mathbf{5}}$ is a solution of the equation ${\mathbf{3}}-{\mathbf{x}}$=${\mathbf{8}}$

Ans: False

Give an expression for each of the examples 6 to 8:

Example 6: ${\mathbf{13}}$ subtracted from thrice of a number.

Ans: If the number is ${\text{x}}$ then, thrice of the number will be $3{\text{x}}$.

If $13$ subtracted from it, then the expression is $3{\text{x - 13}}$.

Example 7: Megha’s age (in years) is ${\mathbf{2}}$ more than ${\mathbf{5}}$ times her daughter’s age.

Ans: If the daughter’s age is ${\text{x}}$ year then,

$5$ times the age of daughter’s age is $= 5{\text{x}}$.

And $2$ more than $5{\text{x}}$$= 5{\text{x}}{\text{ + }}{\text{2}}$.

Hence, the age of Megha (in years) $= 5{\text{x}}{\text{ + }}{\text{2}}$.

Example 8: Anagha, Sushant and Faizal are climbing the steps to a hilltop. Anagha is at the step p. Sushant is ${\mathbf{10}}$ steps ahead and Faizal is ${\mathbf{6}}$ steps behind Anagha. Where are Sushant and Faizal? The total number of steps to the hill top is ${\mathbf{3}}$ steps less than ${\mathbf{8}}$ times what Anagha has reached. Express the total number of steps using p.

Ans: If Anagha is at step ${\text{p}}$ and Sushant is $10$ steps ahead of Anagha.

So, he is at the step $= {\text{p}}{\text{ + }}{\text{10}}$.

Also, Faizal is $6$ steps behind Anagha. So is, he is at step$= {\text{p}} - 6$

total number of steps to the hill top is $3$ steps less than $8$ times what Anagha has reached then,

$8$ times of ${\text{p}} = 8{\text{p}}$

$3$ less than $8{\text{p}} = 8{\text{p}}-3$

Therefore, the total number of steps = $8{\text{p}}-3$

In examples 9 and 10, change the statements, converting expressions

into statements in ordinary language.

Example 9: Cost of a pencil is Rs ${\text{x}}$A pen costs Rs $6{\text{x}}$.

Ans: Cost of a pen is $6$ times the cost of a pencil.

Example 10: Manisha is ${\text{z}}$ years old. Her uncle is $5{\text{z}}$ years old and her aunt is $\left( {{\mathbf{5z}}-{\mathbf{4}}} \right)$ years old.

Ans: Manisha’s uncle is five times Manisha's age. Her aunt is $4$ years younger than her uncle.

In questions 1 to 23, out of the four given options, only one is correct. Write the correct answer.

1.If each match box contains ${\mathbf{50}}$ matchsticks, the number of matchsticks required to fill ${\mathbf{n}}$ such boxes is

(A) ${\mathbf{50}} + {\mathbf{n}}$

(B) ${\mathbf{50n}}$

(C) ${\mathbf{50}} \div {\mathbf{n}}$

(D) ${\mathbf{50}}-{\mathbf{n}}$

Ans: (B)

Given, number of matchsticks in a box are $= 50 \times 1$

Then, for n box $= 50 \times {\text{n}}$

${\text{i}}{\text{.e}}{\text{.}}{\text{50n}}$

2. Amulya is ${\text{x}}$ years of age now. ${\mathbf{5}}$ years ago her age was

(A) $\left( {{\mathbf{5}}-{\mathbf{x}}} \right)$years 

(B) $\left( {{\mathbf{5}} + {\mathbf{x}}} \right)$years

(C) $\left( {{\mathbf{x}}-{\mathbf{5}}} \right)$years

(D) $\left( {{\mathbf{5}} \div {\mathbf{x}}} \right)$years

Ans: (C) 

Given, that the present age of Amulya is $= {\text{x}}$ 

Then,

$5$ year ago $= \left( {{\text{x}}-5} \right)$ year.

3. Which of the following represents ${\mathbf{6}} \times {\mathbf{x}}$

(A) ${\mathbf{6x}}$

(B) $\dfrac{{\mathbf{x}}}{{\mathbf{6}}}$

(C) ${\mathbf{6}} + {\mathbf{x}}$

(D) ${\mathbf{6}}-{\mathbf{x}}$

Ans: (A)

As $6 \times {\text{x}} = 6{\text{x}}$.

4. Which of the following is an equation?

(A) ${\mathbf{x}} + {\mathbf{1}}$

(B) ${\mathbf{x}}-{\mathbf{1}}$

(C) ${\mathbf{x}}-{\mathbf{1}} = {\mathbf{0}}$

(D) ${\mathbf{x}} + {\mathbf{1}} > {\mathbf{0}}$

Ans: (C) 

As we know, expression with variable, constant and equal sign is a form of simple equation.

$\therefore {\text{x}}-1 = 0$

5. If ${\mathbf{x}}$ takes the value ${\mathbf{2}}$, then the value of ${\mathbf{x}} + {\mathbf{10}}$is

(A) ${\mathbf{20}}$

(B) ${\mathbf{12}}$

(C) ${\mathbf{5}}$

(D) ${\mathbf{8}}$

Ans: (B) 

Given, that ${\text{x}} = 2$,

Putting the value of ${\text{x}}$

then 

$= {\text{x + 10}}$

${\text{ = 2 + 10}}$

${\text{ = 12}}$

6. If the perimeter of a regular hexagon is ${\mathbf{x}}$ meters, then the length of each of its sides is 

(A) $\left( {{\mathbf{x}} + {\mathbf{6}}} \right)$ meter 

(B) $\left( {{\mathbf{x}} \div {\mathbf{6}}} \right)$meters

(C) $\left( {{\mathbf{x}}-{\mathbf{6}}} \right)$meters

(D) $\left( {{\mathbf{6}} \div {\mathbf{x}}} \right)$meters

Ans: (B) 

Perimeter of a hexagon is given by $= 6 \times {\text{sides}}$

Then,

${\text{x}} = 6 \times {\text{side}}$

${\text{side  =  }}\dfrac{{\text{x}}}{6}$ 

7. Which of the following equations has ${\mathbf{x}} = {\mathbf{2}}$ as a solution?

(A) ${\mathbf{x}} + {\mathbf{2}} = {\mathbf{5}}$

(B) ${\mathbf{x}}-{\mathbf{2}} = {\mathbf{0}}$

(C) ${\mathbf{2x}} + {\mathbf{1}} = {\mathbf{0}}$

(D) ${\mathbf{x}} + {\mathbf{3}} = {\mathbf{6}}$

Ans: (B) 

$\because {\text{x}} - 2 = 0$

${\text{x}} = 2$

Hence, the solution of the given equation ${\text{x}} = 2$

8. For any two integers ${\mathbf{x}}$ and ${\mathbf{y}}$, which of the following suggests that the operation of addition is commutative? 

(A) ${\mathbf{x}} + {\mathbf{y}} = {\mathbf{y}} + {\mathbf{x}}$

(B) ${\mathbf{x}} + {\mathbf{y}} > {\mathbf{x}}$

(C) ${\mathbf{x}}-{\mathbf{y}} = {\mathbf{y}}-{\mathbf{x}}$

(D) ${\mathbf{x}} \times {\mathbf{y}} = {\mathbf{y}} \times {\mathbf{x}}$

Ans: (A) 

${\text{x}} + {\text{y}} = {\text{y}} + {\text{x}}$ is a fundamental property.

9. Which of the following equations does not have a solution in integers? 

(A) ${\mathbf{x}} + {\mathbf{1}} = {\mathbf{1}}$

(B) ${\mathbf{x}}-{\mathbf{1}} = {\mathbf{3}}$

(C) ${\mathbf{2x}} + {\mathbf{1}} = {\mathbf{6}}$

(D) ${\mathbf{1}}-{\mathbf{x}} = {\mathbf{5}}$

Ans: (C)

$\because 2{\text{x + 1}}{\text{ = }}{\text{6}}$

$\Rightarrow {\text{x}} = \dfrac{{6 - 1}}{2} = \dfrac{5}{2}$

Which is not an integer.

10. In algebra, ${\mathbf{a}} \times {\mathbf{b}}$ means ${\mathbf{ab}}$, but in arithmetic ${\mathbf{3}} \times {\mathbf{5}}$ is

(A) 35

(B) 53 

(C) 15 

(D) 8

Ans: (C)

Because, ${\text{a}} \times {\text{b}} = {\text{ab}}$ then, $3 \times 5 = 15$.

11. In algebra, letters may stand for

(A) Known quantities 

(B) unknown quantities

(C) Fixed numbers

(D) none of these

Ans: (B)

In algebra, letters may stand for unknown quantities which we call variable.

12. “Variable” means that it

(A) Can take different values

(B) Has a fixed value

(C) Can take only 2 values 

(D) Can take only three values

Ans: (A) 

“Variable” means that it has unknown values and can take different values.

13. ${\mathbf{10}}-{\mathbf{x}}$ means

(A) ${\mathbf{10}}$ is subtracted ${\mathbf{x}}$ times 

(B) ${\mathbf{x}}$ is subtracted ${\mathbf{10}}$ times

(C) ${\mathbf{x}}$ is subtracted from ${\mathbf{10}}$

(D) ${\mathbf{10}}$ is subtracted from ${\mathbf{x}}$

Ans: (C)

${\text{x}}$ is subtracted from $10$.

14. Savitri has a sum of Rs ${\mathbf{x}}$. She spent Rs ${\mathbf{1000}}$ on grocery, Rs ${\mathbf{500}}$ on clothes and Rs ${\mathbf{400}}$ on education, and received Rs ${\mathbf{200}}$ as a gift. How much money (in Rs) is left with her?

(A) ${\mathbf{x}}-{\mathbf{1700}}$

(B) ${\mathbf{x}}-{\mathbf{1900}}$

(C) ${\mathbf{x}} + {\mathbf{200}}$

(D) ${\mathbf{x}}-{\mathbf{2100}}$

Ans: (A) 

Given, Total amount spent by Savitri $= \left( {1000 + 500 + 400} \right) = 1900{\text{Rs}}{\text{.}}$ + amount of gift = Rs. $200$

$= {\text{Rs }}2100$

If total amount Savitri has $= {\text{x}}$

Therefore, Left amount $= {\text{Rs}}\left( {{\text{x}}-2100} \right)$

15. The perimeter of the triangle shown in Fig. 7.1 is

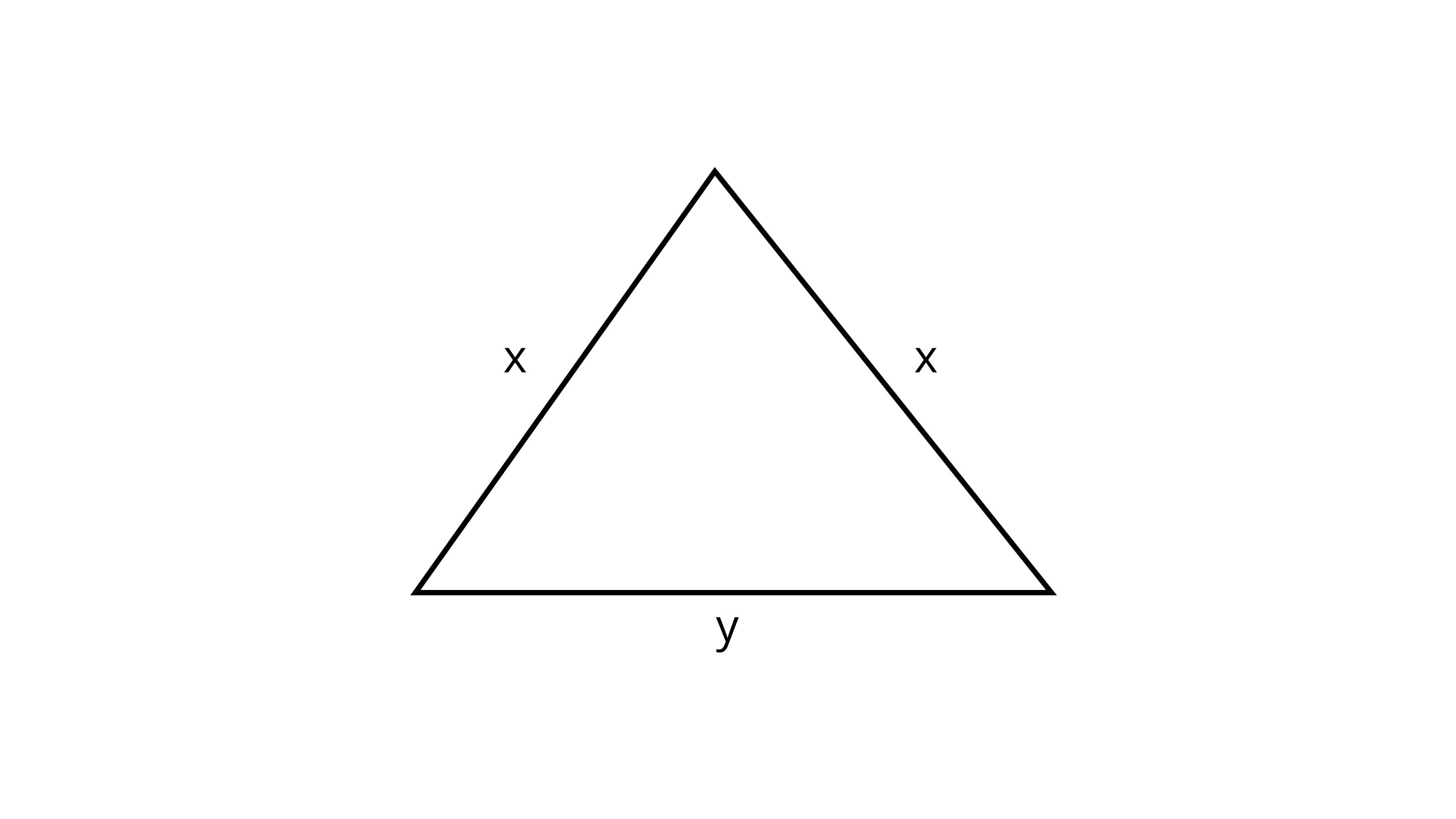
(A) 2x + y 

(B) x + 2y

(C) x + y

(D) 2x – y

Ans: (A) 

Addition of all Sides is called the perimeter of a given figure.

Perimeter of triangle $= {\text{x}} + {\text{x}} + {\text{y}} = 2{\text{x}} + {\text{y}}$.

16. The area of a square having each side x is 

(A) x × x 

(B) 4x 

(C) x + x

(D) 4 + x

Ans: (A)

Given, side of a square $= {\text{x}}$

We know, area of square 

$= {\text{side}} \times {\text{side}}$

${\text{ =  x}} \times {\text{x}}$

${\text{ = }}{{\text{x}}^2}$

17. The expression obtained when x is multiplied by 2 and then subtracted from 3 is 

(A) 2x – 3 

(B) 2x + 3

(C) 3 – 2x

(D) 3x – 2

Ans: (C)

When ${\text{x}}$ multiply by $2$ $= 2{\text{x}}$

And subtracted from $3 = 3-2{\text{x}}$

18. $\dfrac{{\mathbf{q}}}{{\mathbf{2}}} = {\mathbf{3}}$has a solution 

(A) 6 

(B) 8 

(C) 3

(D) 2

Ans: (A) 

$\because \dfrac{{\text{q}}}{2} = 3$

$\Rightarrow {\text{q}} = 3 \times 2 = 6$

19. x – 4 = – 2 has a solution

(A) 6 

(B) 2

(C) – 6 

(D) – 2

Ans: (B)

As 

$\Rightarrow {\text{x}} - 4 =  - 2$

$\Rightarrow {\text{x}} =  - 2 + 4$

$\Rightarrow {\text{x}} = 2$

20. $\dfrac{{\mathbf{4}}}{{\mathbf{2}}} = {\mathbf{2}}$ denotes a 

(A) Numerical equation

(B) algebraic expression

(C) Equation with a variable 

(D) false statement

Ans: (A)

It denotes a numerical equation.

21. Kanta has p pencils in her box. She puts more pencils in the box. The total numbers of pencils with her are

(A) p + q

(B) pq

(C) p – q

(D) $\dfrac{{\mathbf{p}}}{{\mathbf{q}}}$ 

Ans: (A)

Kanta has ${\text{p}}$ pencils in a box and she puts ${\text{q}}$ more pencils in the box. 

Hence, total pencils $= {\text{p}} + {\text{q}}$

22. The equation 4x = 16 is satisfied by the following value of x

(A) 4 

(B) 2

(C) 12

(D) –12

Ans: (A)

Solving: $4{\text{x = 16}}$

$\Rightarrow 4{\text{x}} = 16$

$\Rightarrow {\text{x}} = \dfrac{{16}}{4} = 4$

$\Rightarrow \therefore {\text{x}} = 4$

23. I think of a number and on adding 13 to it, I get 27. The equation for this is

(A) x – 27 = 13

(B) x – 13 = 27

(C) x + 27 = 13

(D) x + 13 = 27

Ans: (D)

If the number is ${\text{x}}$

Then according to the question:

$\Rightarrow {\text{x + 13 = 27}}$

$\Rightarrow {\text{x}} = 27 - 13$

$\Rightarrow {\text{x}} = 14$

In question 24 to 40 fill in the blanks to make the statements true:

24. The distance (in km) travelled in ${\mathbf{h}}$ hours at a constant speed of 40km per hour is __________. 

Ans:  $40{\text{km}}$

We know, Distance = speed $\times $time

$= \left( {40\dfrac{{{\text{km}}}}{{{\text{hour}}}} \times {\text{h hour}}} \right)$

$= 40{\text{km}}$

25. P kg of potatoes is bought for Rs 70. Cost of 1kg of potatoes (in Rs) is __________. 

Ans: $\dfrac{{70}}{{\text{P}}}{\text{kg}}$

Given, ${\text{P}}$ kg of potatoes is bought for $70{\text{Rs}}$. 

Cost of $1{\text{Kg}}$ of potatoes $= \dfrac{{70}}{{\text{P}}}$${\text{kg}}$ 

26. An auto rickshaw charges Rs 10 for the first kilometer then Rs 8 for each such subsequent kilometer. The total charge (in Rs) for d kilometers is __________. 

Ans: $2 + 8{\text{d}}$

Charges for first kilometer $= 10{\text{Rs}}$

Charges for subsequent kilometers $= 8{\text{Rs}}$

Charge for ${\text{d}}{\text{km}}$:

$= 10 + \left( {{\text{d}} - 1} \right) \times 8$

$= 10 + 8{\text{d}} - 8$

$= 2 + 8{\text{d}}$ 

27. If ${\mathbf{7x}} + {\mathbf{4}} = {\mathbf{25}}$, then the value of x is __________. 

Ans: $3$

Solving the given equation:

$\Rightarrow 7{\text{x  + }}{\text{4  = }}{\text{25}}$

$\Rightarrow {\text{7x  =  25}} - 4$

$\Rightarrow 7{\text{x  =  21}}$

$\Rightarrow {\text{x  = }}\dfrac{{21}}{7} = 3$

$\Rightarrow {\text{x  = }}{\text{3}}$

28. The solution of the equation ${\mathbf{3x}} + {\mathbf{7}} = -{\mathbf{20}}$ is __________. 

Ans: $ - 9$

On solving the given equation:

$\Rightarrow 3{\text{x  + }}7{\text{  = }} - {\text{20}}$

$\Rightarrow 3{\text{x  =  }} - 20 - 7$

$\Rightarrow 3{\text{x  =  }} - {\text{27}}$

$\Rightarrow {\text{x  = }} - \dfrac{{27}}{3} =  - 9$

$\Rightarrow {\text{x  = }} - 9$

29. „X exceeds y by 7‟ can be expressed as __________. 

Ans: ${\text{x}}{\text{ = }}{\text{y + 7}}$

If ${\text{X}}$ exceeds ${\text{Y}}$ by $7$ then 

$\Rightarrow {\text{x = }}{\text{y + 7or}}{\text{x}} - {\text{y}}{\text{ = 7}}$

30. „8 more than three times the number x‟ can be written as __________. 

Ans: $8 + 3{\text{x}}$

$8$ more than three times the number ${\text{x}}$ than it is $= 8 + 3{\text{x}}$ 

31. Number of pencils bought for Rs x at the rate of Rs 2 per pencil is __________.

Ans: $\dfrac{{\text{x}}}{2}$

Given: Rate of each pencil $= 2{\text{Rs}}$

number of pencils bought for ${\text{x}}{\text{Rs}}$$= \dfrac{1}{2} \times {\text{x  = }}\dfrac{{\text{x}}}{2}$

32. The number of days in w weeks is __________.

Ans: $7{\text{w}}$

Number of days in a week $= 7$

Number of days in ${\text{w}}$ week $= 7{\text{w}}$

33. Annual salary at r rupees per month along with a festival bonus of Rs 2000 is __________.

Ans: $12{\text{r}}{\text{ + }}{\text{2000}}$

Salary per month $= {\text{r}}{\text{Rs}}$

We know, $1$ year $= 12$ months

Therefore, annual salary $= 12{\text{r}}$

Annual salary in addition to festival bonus $= 12{\text{r}}{\text{ + }}{\text{2000}}{\text{Rs}}$.

34. The two digit number whose ten’s digit is “t‟ and unit’s digit is “u‟ is __________. 

Ans: $10{\text{t + u}}$

If two-digit number which have ‟ten’s digit “t‟ and unit’s digit “u‟ is $10{\text{t + u}}$

35. The variable used in the equation ${\mathbf{2p}} + {\mathbf{8}} = {\mathbf{18}}$ is __________. 

Ans:  ${\text{p}}$

Variable used in the equation $2{\text{p}} + 8 = 18$ is ${\text{p}}$

36. x meters = __________ centimeters.

Ans: $100{\text{x}}$

As we know that, $1{\text{m}} = 100{\text{ cm}}$

Therefore, 

${\text{x}}{\text{cm}} = 100 \times {\text{x cm}} = 100{\text{x}}{\text{cm}}$.

37. P liters = __________ milliliters.

Ans: $1000{\text{p}}$milliliters

As we know that, $1{\text{l}} = 1000{\text{ ml}}$

Therefore, 

${\text{pl}} = 1000 \times {\text{p ml}} = 1000{\text{p ml}}$.

38. R rupees = __________ paisa.

Ans: $100{\text{R}}$ paisa

As we know that, $1{\text{Rupee}} = 100{\text{ paisa}}$

Therefore, 

${\text{R}}{\text{rupee}} = 100 \times {\text{R paisa}} = 100{\text{R}}{\text{paisa}}$.

39. If the present age of Ramandeep is n years, then her age after 7 years will be __________. 

Ans: ${\text{n + 7}}$ years

Given that:

Present age of Ramandeep $= {\text{n}}$ year 

Ramandeep age after $7$ years $=$${\text{n + 7}}$ year.

40. If I spend f rupees from 100 rupees, the money left with me is __________ rupees.

Ans: $100 - {\text{f}}$

Total amount $= 100{\text{Rs}}$

Spent amount $= {\text{f Rs}}$

So, If f rupees spent from 100 rupees, the money left $=$$100 - {\text{f}}$${\text{Rs}}$.

In question 41 to 45, state whether the statements are true or false.

41. 0 is a solution of the equation ${\mathbf{x}} + {\mathbf{1}} = {\mathbf{0}}$

Ans: False 

$\because {\text{x + 1 = }}{\text{0}}$

${\text{x}} =  - 1$

42. The equations ${\mathbf{x}} + {\mathbf{1}} = {\mathbf{0}}$ and ${\mathbf{2x}} + {\mathbf{2}} = {\mathbf{0}}$ have the same solution. 

Ans: True

As on multiplying ${\text{x + 1}}{\text{ = }}{\text{0}}$ by $2$ we have:

$2{\text{x + 2 = 0}}$

43. If m is a whole number, then 2m denotes a multiple of 2. 

Ans: True

$\because 2{\text{m}}{\text{ = }}{\text{2}} \times {\text{m}}$

44. The additive inverse of an integer ${\text{x}}$ is $2{\text{x}}$.

Ans: False 

Additive inverse of ${\text{x}}$$=  - {\text{x}}$

45. If x is a negative integer, – x is a positive integer. 

Ans: True

$\because  - \left( { - {\text{x}}} \right) =  + {\text{x}}$

The Addition of a negative integer is always a positive integer. 

46. ${\mathbf{2x}}-{\mathbf{5}} > {\mathbf{11}}$ is an equation. 

Ans: False

Because, a simple equation is formed with variable, constant and equal sign and in this equation equality is absent.

47. In an equation, the LHS is equal to the RHS. 

Ans: True

48. In the equation ${\mathbf{7k}}-{\mathbf{7}} = {\mathbf{7}}$, the variable is $7$. 

Ans: False

Variable is ${\text{k}}$

49. ${\mathbf{a}} = {\mathbf{3}}$ is a solution of the equation ${\mathbf{2a}}-{\mathbf{1}} = {\mathbf{5}}$

Ans: True

If ${\text{a}}{\text{ = }}{\text{3}}$ then:

Putting the value of ${\text{a}}$ in equation we have:

$\Rightarrow 2{\text{a}} - 1 = 5$

$\Rightarrow 2\left( 3 \right) - 1 = 5$

$\Rightarrow 6 - 1 = 5$

$\Rightarrow 5 = 5$

$\therefore {\text{LHS = RHS}}$

Hence, verified.

50. The distance between New Delhi and Bhopal is not a variable. 

Ans: True

Because it’s a defined distance between two cities.

51. t minutes are equal to 60t seconds. 

Ans: True

As, $1{\text{min}} = 60{\text{ sec}}$

${{\text{t min }} = 60}$

$\therefore$

${{\text{ t}}{\text{min}} = 60{\text{t sec}}.}$ 

52. ${\mathbf{x}} = {\mathbf{5}}$ is the solution of the equation ${\mathbf{3x}} + {\mathbf{2}} = {\mathbf{20}}$.

Ans: False

Putting the value of ${\text{x}}{\text{ = }}{\text{5}}$in given equation:

$\Rightarrow 3{\text{x}}{\text{ + }}{\text{2  =  20}}$

$\Rightarrow 3\left( 5 \right) + 2 = 20$

$\Rightarrow 15 + 2 = 20$

$\Rightarrow 17 \ne 20$

$\therefore {\text{LHS}} \ne {\text{RHS}}$ 

53. ‘One third of a number added to itself gives 8’, can be expressed as $\dfrac{{\mathbf{x}}}{{\mathbf{3}}} + {\mathbf{8}} = {\mathbf{x}}$

Ans: False

If the number is ${\text{x}}$ then,

One third of a number is $= \dfrac{{\text{x}}}{3}$

And if it is added to itself then $= \dfrac{{\text{x}}}{3} + {\text{x}}$ and it gives $8$ then it is expressed as $\Rightarrow \dfrac{{\text{x}}}{3} + {\text{x}}{\text{ = }}{\text{8}}$

54. The difference between the ages of two sisters Leela and Yamini is a variable.

Ans: False

No, it is a number.

55. The number of lines that can be drawn through a point is a variable

Ans: False

A line is the distance between two points which is not variable.

In questions 56 to 74, choose a letter x, y, z, p etc...., wherever necessary, for the unknown (variable) and write the corresponding expressions:

56. One more than twice the number.

Ans: $1 + 2{\text{y}}$

Let, the number be $= {\text{y}}$

and twice of the number is $= 2{\text{y}}$

According to the question,

$1$ more than twice of the number $= 1 + 2{\text{y}}$

57. ${\mathbf{20}}^\circ C$ less than the present temperature. 

Ans: ${\text{t}} - 20^\circ {\text{C}}$

If the present temperature is $= {\text{t}}^\circ {\text{C}}$ then,

$20^\circ {\text{C}}$ less than ${\text{t}}^\circ {\text{C}}= {\text{t}}^\circ {\text{C}} - 20^\circ {\text{C}}{\text{ = }}\left( {{\text{t}}^\circ  - 20^\circ } \right){\text{C}}$

58. The successor of an integer. 

Ans: We know that the successor of an integer is an integer.

if the integer is $1$ and its successor is $= \left( {1 + 1} \right) = 2$

59. The perimeter of an equilateral triangle, if the side of the triangle is m.

Ans: The perimeter of an equilateral triangle $= 3 \times {\text{side}}$

And given side $= {\text{m}}$

Therefore, perimeter of an equilateral triangle $= 3 \times {\text{m}}{\text{ = }}{\text{3m}}$

60. Area of the rectangle with length k units and breadth n units.

Ans: Given: length $= {\text{k}}{\text{unit}}$

Breadth $= {\text{n unit}}$

Area of rectangle $= {\text{length}} \times {\text{breadth}}$

Therefore,

$\Rightarrow {\text{k}}{\text{unit}} \times {\text{n}}{\text{unit}}{\text{ = }}{\text{kn}}{\text{uni}}{{\text{t}}^2}$

61. Omar helps his mother 1 hour more than his sister does.

Ans: If Omar`s sister helps for ${\text{h}}$hours to his mother and Omar helps his mother $1$ hour more.

Then,

Omar helps his mother $= \left( {{\text{h}} + 1} \right)$ hour

62. Two consecutive odd integers.

Ans: $\left( {2{\text{n}} + 1} \right)$ and $\left( {2{\text{n}} + 3} \right)$

63. Two consecutive even integers.

Ans: If, ${\text{n}}$ is an integer then $\left( {{\text{n + 2}}} \right)$ and $\left( {{\text{n + 4}}} \right)$

64. Multiple of 5. 

Ans: If, ${\text{n}}$ is an integer,

Then as a multiple of $5 = 5{\text{n}}$.

65. The denominator of a fraction is 1 more than its numerator. 

Ans: If numerator of a fraction is ${\text{N}}$

Then denominator will be $= {\text{N + 1}}$

So, the fraction is $= \dfrac{{\text{N}}}{{{\text{N + 1}}}}$

66. The height of Mount Everest is 20 times the height of the Empire State building. 

Ans: If the height of the Empire =${\text{E}}$

Then,

Height of the Mount Everest will be =$20{\text{E}}$

67. If a note book costs Rs p and a pencil costs Rs 3, then the total cost (in Rs) of two note books and one pencil. 

Ans: Given: a note book costs $= {\text{P}}{\text{Rs}}{\text{.}}$

And a pencil costs $= 3{\text{Rs}}$

Then,

Cost of two pencils $= 2{\text{P}}{\text{Rs}}{\text{.}}$

Now, total cost $= 2{\text{p + 3}}{\text{Rs}}$.

68. z is multiplied by –3 and the result is subtracted from 13. 

Ans: As per question, 

$\Rightarrow {\text{z}} \times \left( { - 3} \right){\text{ = }} - {\text{3z}}$

$\Rightarrow 13 - ( - 3{\text{z}}) = 13 + 3{\text{z}}$

69. p is divided by 11 and the result is added to 10. 

Ans: As per question:

$\Rightarrow \dfrac{{\text{p}}}{{11}}$

$\Rightarrow \dfrac{{\text{p}}}{{11}} + 10$

70. x times of 3 is added to the smallest natural number. 

Ans: As we know, smallest natural number is $1$

Therefore, according to question:

${\text{x}}$ times of $3$ \[ = 3{\text{x}}\]

Now, $3{\text{x}}$added to $1$ \[ = 3{\text{x}} + 1\].

71. 6 times q is subtracted from the smallest two-digit number. 

Ans: As asked in question:

$6$times ${\text{q}}$$= 6{\text{q}}$

subtracted from the smallest two-digit number $= 10 - 6{\text{q}}$.

72. Write two equations for which 2 is the solution.

Ans: Required equations for which $2$ is a solution are ${\text{x}} - 2 = 0$ and $2{\text{x}}-4 = 0$.

73. Write an equation for which 0 is a solution. 

Ans: Required equations for which $0$ is a solution are ${\text{x}} - 2 =  - 2$.

74. Write an equation whose solution is not a whole number.

Ans: For equation

$2{\text{x}} - 4 = 2$

$\Rightarrow {\text{x}} =  - 2$

$- 2$ is not a whole number.

In questions 75 to 84, change the statements, converting expressions into statements in ordinary language:

75. A pencil costs Rs p and a pen costs Rs 5p. 

Ans: Given: a pencil costs =${\text{p}}{\text{Rs}}$

And a pen costs $= 5 \times {\text{p}}$

Therefore, we can say, the cost of one pen is $5$ time the cost of one pencil.

76. Leela contributed Rs y towards the Prime Minister‟s Relief Fund. Leela is now left with Rs $\left( {{\mathbf{y}} + {\mathbf{10000}}} \right)$

Ans: 

According to the given condition it can be said that the amount left with Leela is Rs. 10,000 more than the amount she contributed towards the Prime Minister‟s Relief Fund.

77. Kartik is n years old. His father is 7 years old.

Ans: According to the given condition it can be said that Kartik’s father is 7 times the age of kartik.

78. The maximum temperature on a day in Delhi was ${\mathbf{p}}^\circ {\text{ }}{\mathbf{C}}$. The minimum temperature was $\left( {{\mathbf{p}}-{\mathbf{10}}} \right)^\circ {\mathbf{C}}$. 

Ans: According to the given condition it can be said that the minimum temperature on a day in Delhi was $10^\circ {\text{C}}$ less than the maximum temperature.

79. John planted t plants last year. His friend Jay planted ${\mathbf{2t}} + {\mathbf{10}}$ plants that year. 

Ans: According to the given condition it can be said that John`s friend Jay planted $2$ time more than $10$ plants of John.

80. Sharad used to take ${\text{p}}$ cups of tea a day. After having some health problems, he takes $\left( {{\mathbf{p}}-{\mathbf{5}}} \right)$ cups of tea a day.

Ans: According to the given condition it can be said that due to the health issue Sharad reduces the $5$ cup of tea per day.

81. The number of students dropping out of school last year was m. Number of students dropping out of school this year is ${\mathbf{m}}-{\mathbf{30}}$.

Ans: According to the given condition it can be said that the number of students dropping out this year is $30$ less than last year.

82. Price of petrol was Rs p per liter last month. Price of petrol now is Rs $\left( {{\mathbf{p}}-{\mathbf{5}}} \right)$ per liter.

Ans: According to the given condition it can be said that the price of petrol decreases by ${\text{Rs 5}}$ per liter than last month. 

83. Khader’s monthly salary was Rs ${\mathbf{P}}$ in the year 2005. His salary in 2006 was Rs $\left( {{\mathbf{P}} + {\mathbf{1000}}} \right).$

Ans: According to the given condition it can be said that in 2006 Khader`s monthly salary is 1000 more than the last year's monthly salary.

84. The number of girls enrolled in a school last year was g. The number of girls enrolled this year in the school is ${\mathbf{3g}}-{\mathbf{10}}$. 

Ans: According to the given condition it can be said that the number of girls enrolled this year is $3$ time less than $10$ girls last year.

85. Translate each of the following statements into an equation, using ${\mathbf{x}}$ as the variable: 

(a) 13 subtracted from twice a number gives 3. 

(b) One fifth of a number is 5 less than that number.

(c) Two-third of the number is 12. 

(d) 9 added to twice a number gives 13. 

(e) 1 subtracted from one-third of a number gives 1. 

Ans: 

(a) Let, the number be $= {\text{x}}$

Now, $13$ subtracted from twice a number gives $3$ then: $2{\text{x}} - 13 = 3$

(b) Let, the number be $= {\text{x}}$

Now, one fifth of a number is $5$ less than that number 

$\therefore \dfrac{{\text{x}}}{5} = {\text{x}} - 5$

(c) Let, the number be $= {\text{x}}$ 

Now, Two-third of number is $12$ $\Rightarrow \dfrac{{2{\text{x}}}}{3} = 12$

(d) If the number is \[ = {\text{x}}\] 

Now, according to question:

\[2{\text{x}} + 9 = 13\]

(e) If the number is $= {\text{x}}$

Now, according to question:

$\Rightarrow \dfrac{{\text{x}}}{3} - 1 = 1$

86. Translate each of the following statements into an equation:

(a) The perimeter (p) of an equilateral triangle is three times of its side (a). 

(b) The diameter (d) of a circle is twice its radius (r).

(c) The selling price (s) of an item is equal to the sum of the cost price (c) of an item and the profit (p) earned. 

(d) Amount (a) is equal to the sum of principal (p) and interest (i).

Ans: 

(a) Let the side be ${\text{x}}$

Then perimeter of an equilateral triangle is 

${\text{P}}$$= 3 \times {\text{x}}{\text{ = }}{\text{3x}}$

(b) Given:  diameter ${\text{d}}$ of a circle is twice its radius ${\text{r}}$.

$\therefore {\text{d}}{\text{ = }}{\text{2r}}$

(c) Given that the selling price (s) of an item is equal to the sum of the cost price (c) of an item and the profit (p) earned then,

Selling price = cost price + profit 

$\therefore {\text{s}}{\text{ = }}{\text{c}}{\text{ + }}{\text{p}}$

(d) Given that amount (a) is equal to the sum of principal (p) and interest (i)

Amount = principal + interest

${\text{a}} = {\text{p}} + {\text{i}}$

87. Let Kanika’s present age be x years. Complete the following table, showing ages of her relatives:

Ans: If the age of Kanika is ${\text{x}}$ years then expressions under each situation is:

88. If m is a whole number less than 5, complete the table and by inspection of the table, find the solution of the equation ${\mathbf{2m}}-{\mathbf{5}} = -{\mathbf{1}}$:

Ans: 

If ${\text{m}}$ is a whole number then

At ${\text{m}} = 0$

$2{\text{m}} - {\text{5}} \Rightarrow 2\left( 0 \right) - 5 =  - 5$

At ${\text{m}} = 1$

$2{\text{m}} - {\text{5}} \Rightarrow 2\left( 1 \right) - 5 =  - 3$

At ${\text{m}} = 2$

$2{\text{m}} - {\text{5}} \Rightarrow 2\left( 2 \right) - 5 =  - 1$

At ${\text{m}} = 3$

$2{\text{m}} - {\text{5}} \Rightarrow 2\left( 3 \right) - 5 = 6 - 5 = 1$

At ${\text{m}} = 4$

$2{\text{m}} - {\text{5}} \Rightarrow 2\left( 4 \right) - 5 = 8 - 5 = 3$

Therefore, the solution of $2{\text{m}}-5 =  - 1$ at ${\text{m}} = 2$

89. A class with p students has planned a picnic. Rs 50 per student is collected, out of which Rs 1800 is paid in advance for transport. How much money is left with them to spend on other items? 

Ans: Given:

Number of students in class $= {\text{p}}$

Collected amount from p students $= {\text{Rs }}50{\text{p}}$

Paid in advance for transport $= {\text{Rs 1800}}$

Now, Left amount to spend on other items $= {\text{Rs }}\left( {50{\text{p}}-1800} \right)$

90. In a village, there are 8 water tanks to collect rain water. On a particular day, x litres of rain water is collected per tank. If 100 litres of water was already there in one of the tanks, what is the total amount of water in the tanks on that day? 

Ans: Given: Rain water collected by each tank of water $= {\text{x}}$

Number of water tank in a village $= {\text{ }}8$

Rain water collected by $8$ tanks $= 8{\text{x}}$

But if $100$ liter of water was already there in tank then total amount of water in the tank $= \left( {8{\text{x}} + 100} \right)$ liters.

91. What is the area of a square whose side is m cm?

Ans: We know, area of square $= {\text{side}} \times {\text{side}}$

Given side $= {\text{m cm}}$

Area of square is:

$\therefore$

$= {\text{m}}{\text{cm}} \times {\text{m}}{\text{cm}}$

${\text{ = }}{{\text{m}}^2}{\text{c}}{{\text{m}}^2}$

92. Perimeter of a triangle is found by using the formula ${\mathbf{P}} = {\mathbf{a}} + {\mathbf{b}} + {\mathbf{c}}$, where a, b and c are the sides of the triangle. Write the rule that is expressed by this formula in words. 

Ans:  Perimeter of a triangle is the addition of all sides.

93. Perimeter of a rectangle is found by using the formula ${\mathbf{P}} = {\mathbf{2}}\left( {{\mathbf{l}} + {\mathbf{w}}} \right)$, where l and w are respectively the length and breadth of the rectangle. Write the rule that is expressed by this formula in words.

Ans: Two times the sum of its length and breadth is called the perimeter of a rectangle.

94. On my last birthday, I weighed 40kg. If I put on m kg of weight after a year, what is my present weight?

Ans: Given that,

Present weight = Last year weight + weight put on after a year 

Last year weight $= 40{\text{ kg}}$

Put on weight is ${\text{m kg}}$then

${ = 40{\text{kg}} + {\text{m kg}}}$

${ = \left( {40 + {\text{m}}} \right){\text{kg}}}$ 

95. Length and breadth of a bulletin board are r cm and t cm, respectively.

(i) What will be the length (in cm) of the aluminum strip required to frame the board, if 10cm extra strip is required to fix it properly. 

(ii) If x nails are used to repair one board, how many nails will be required to repair 15 

such boards? 

(iii) If 500sqcm extra cloth per board is required to cover the edges, what will be the total area of the cloth required to cover 8 such boards?

(iv) What will be the expenditure for making 23 boards, if the carpenter charges Rs x per board.

Ans: Given: length of a board $= {\text{r}}{\text{cm}}$ and breadth $= {\text{t}}{\text{cm}}$

(i)  Strip required to frame the board = perimeter of the board 

$= 2\left( {{\text{r}}{\text{ + }}{\text{t}}} \right){\text{cm}}$

But $10{\text{cm}}$ meters extra strip reacquired therefore,

Total length of aluminum strip $= \left\{ {2\left( {{\text{r}}{\text{ + }}{\text{t}}} \right) + 10} \right\}{\text{cm}}$.

(ii) Nails required to repair 1 board $= {\text{x}}$

Then number of nails required to repair $15$ board 

$= 15 \times {\text{x}}$

${\text{ = }}{\text{15x}}$

(iii) Cloth required to cover the edges of one board $= 500{\text{c}}{{\text{m}}^2}$

Area of the cloth required of one board = Area of the board = length x breadth

$= \left( {{\text{r}}{\text{cm }} \times {\text{t cm}}} \right)$

$= {\text{rt}}{\text{c}}{{\text{m}}^2}$

Area of the cloth required of $8$ board $= 8 \times 500{\text{c}}{{\text{m}}^2} = 4000{\text{c}}{{\text{m}}^2}$

Therefore, total area of the cloth required of $8$ board $= \left( {8{\text{rt}} + 4000} \right){\text{ c}}{{\text{m}}^2}$

(iv) Charges per board $= {\text{x}}{\text{Rs}}$

Then, the charges for 23 boards $= 23 \times {\text{x}}{\text{Rs}}{\text{ = }}{\text{23x}}$${\text{Rs}}$.

96. Sunita is half the age of her mother Geeta. Find their ages

(i) After 4 years? 

(ii) 3 years?

Ans: 

Let, the present age of Geeta $= {\text{x}}$year

Then the age of Sunita $= \dfrac{{\text{x}}}{2}$year

(i) After $4$ years 

$\left( {{\text{x + 4}}} \right) =$ Geeta’s age in years

Sunita’s age $= \left( {\dfrac{{\text{x}}}{2} + 4} \right)$ years

(ii) Before 3 years 

Geeta’s age $= \left( {{\text{x}} - 3} \right)$ years

Sunita’s age $= \left( {\dfrac{{\text{x}}}{2} - 3} \right)$ years

97. Match the items of Column I with that of Column II:

Ans:

(i) Corners of a quadrilateral is $4$ which is a constant. Therefore B

(ii) The variable in the equation $2{\text{p}} + 3 = 5$ is ${\text{p}}$. Therefore, E

(iii) The solution of the equation ${\text{x}} + 2 = 3$ is  $1$ therefore, C

(iv) Solution of the equation $2{\text{p}} + 3 = 5$

$\Rightarrow 2{\text{p}} + 3 = 5$

$\Rightarrow 2{\text{p}}{\text{ = }}{\text{5}} - 3$

$\Rightarrow {\text{p}}{\text{ = }}\dfrac{2}{2} = 1$

$\therefore {\text{p}}{\text{ = }}{\text{1}}$

(v) A sign used in an equation is “=” hence, A

NCERT Exemplar Class 6 Maths Algebra

NCERT exemplar consists of questions different from the textbook to give students more sums for practice. It helps you to test your learning and prepare well for the exams. Class 6 Algebra is an important topic considering from an exam point of view, and exemplar problems benefit you to secure a good rank.

Algebra Chapter 7 Class 6 NCERT

Algebra uses letters and other general symbols to represent formulas or any quantities. It has variables, operators, and constants. Letters represent variables, symbols represent operators, and the remaining constants are numbers. Letters stand for numbers, and operation performs on numbers, e.g. addition, subtraction, multiplication and division.   

E.g. 2x+3=7 

In the above example, ‘X’ is variable, and numbers are constants. An arithmetic operation of addition is performed. Consider algebra as a helper to show problems in the mathematical expression.

How To Download Class 6 Chapter 7 Algebra Exemplar Solutions

Download the solution of problems from NCERT Exemplar from the link. All you need to do is sign in. NCERT doesn’t provide answers to the exemplar sums students need to solve them under the guidance of their teachers to get an in-depth understanding of the concepts. You can find other helpful resources like textbook solutions on our website and Vedantu mobile app. Experts crafted the answer in a detailed fashion to explain all questions and the topic related to them.