NCERT Exemplar for Class 6 Maths Solutions Chapter 2 Geometry

Solved Examples

In examples 1 and 2, write the correct answer from the given four options. 

Example 1: The number of diagonals of a pentagon is 

(A) 3 

(B) 4 

(C) 5 

(D) 10 

Ans: Correct option – C

Because we know that the pentagon is a five sided polygon.

And number of diagonals =$n\times \dfrac{(n-3)}{2}$

= $5\times\dfrac{(5-3)}{2}$

=$5\times 1$=5

Example 2: The number of diagonals of a triangle is 

(A) 0 

(B) 1 

(C) 2 

(D) 3 

Ans: Correct option – A

Because we know that a triangle is a three sided polygon.

And number of diagonals =$n\times$$\dfrac{(n-3)}{2}$

= $3\times$ $\dfrac{(3-3)}{2}$

=$3\times 0$=0

In examples 3 and 4, fill in the blanks to make the statements true: 

Example 3: A polygon of six sides is called a ______. 

Ans: A polygon of six sides is called a Hexagon.

Example 4: A triangle with all its sides of unequal lengths is called a ______ triangle. 

Ans: A triangle with all its sides of unequal lengths is called a  Scalene triangle.

In examples 5 to 7, state whether the statements are true or false. 

Example 5: Two non-parallel line segments will always intersect. 

Ans: False 

Because they will intersect only when they are produced. 

Example 6: All equilateral triangles are isosceles also. 

Ans: True

Because a triangle with all three equal sides is called equilateral and if two of its sides are equal, then a triangle is called isosceles.  

Example 7: Angle of 0° is an acute angle. 

Ans: False 

Because we know that the measure of acute angle is between 0° and 90°. 

Example 8: In Fig. 2.1, PQ ⊥ AB and PO = OQ. Is PQ the perpendicular bisector of line segment AB? Why or why not? 

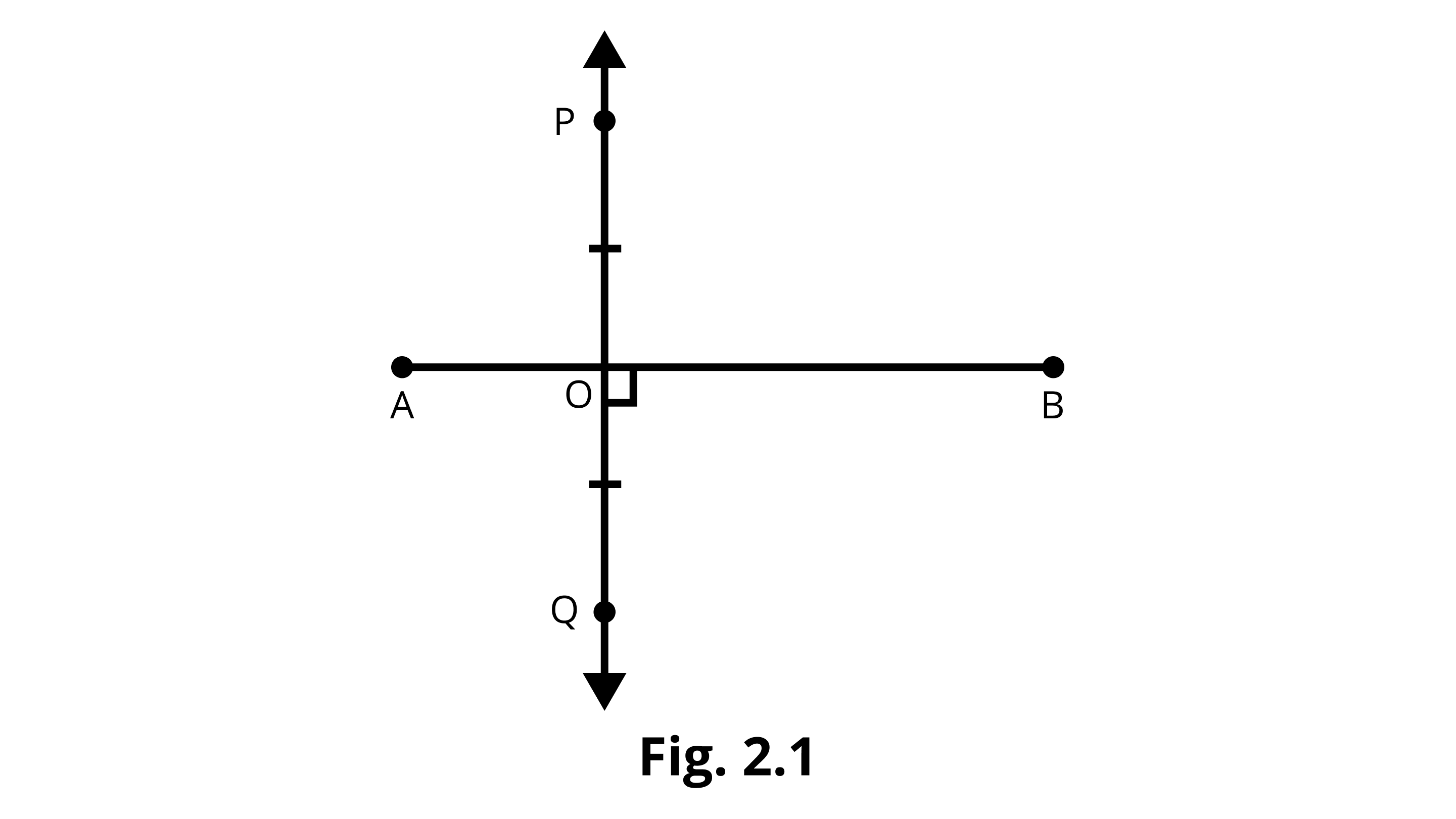
Ans: No, PQ is not the perpendicular bisector of a given line segment AB, because here AO ≠ BO. 

Example 9: In Fig. 2.2, if AC⊥BD, then name all the right angles. 

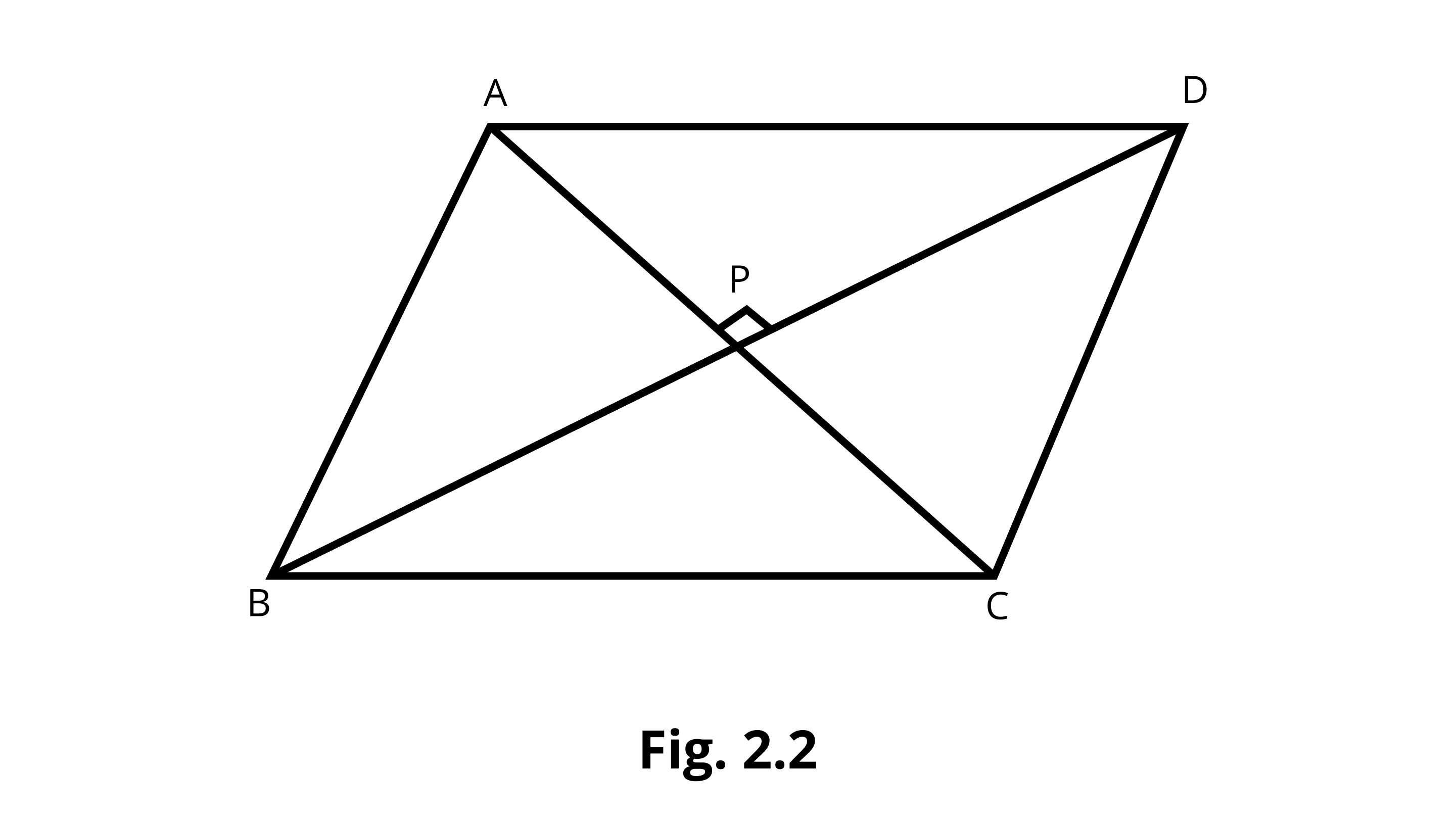
Ans: 4 right angles are: ∠APD, ∠APB, ∠BPC, and ∠CPD.

Example 10: Is ABCD of Fig. 2.3 a polygon? If yes, what is the special name for it? 

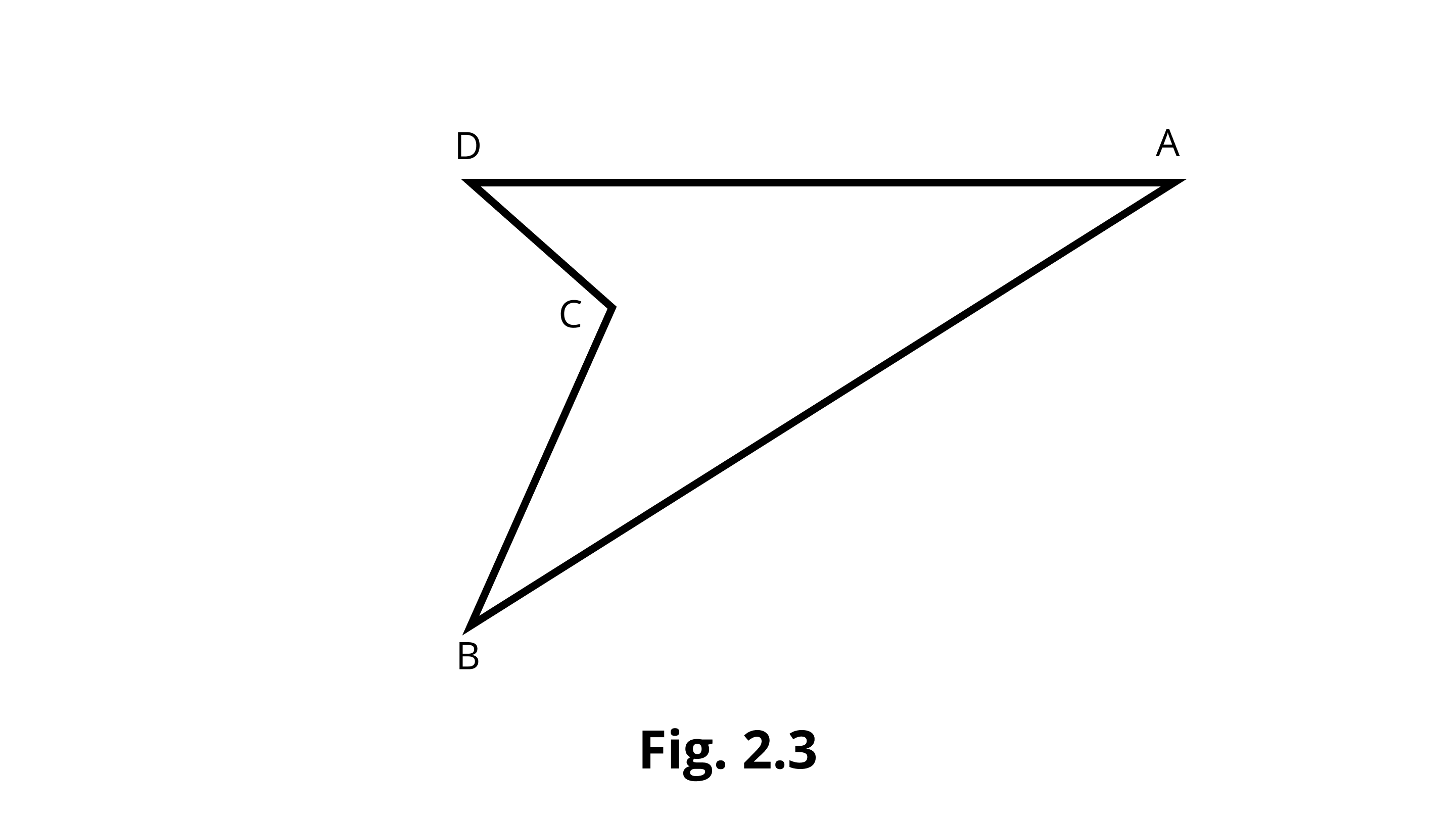
Ans: Yes, in the given figure, ABCD is a polygon, because it is a simple closed figure made of line segments only. It is a quadrilateral. 

Example 11: In Fig. 2.4, BCDE is a square and a 3D shape has been formed by joining the point A in space with the vertices B, C, D and E. Name the 3D shape and also its (i) vertices, (ii) edges and (iii) faces. 

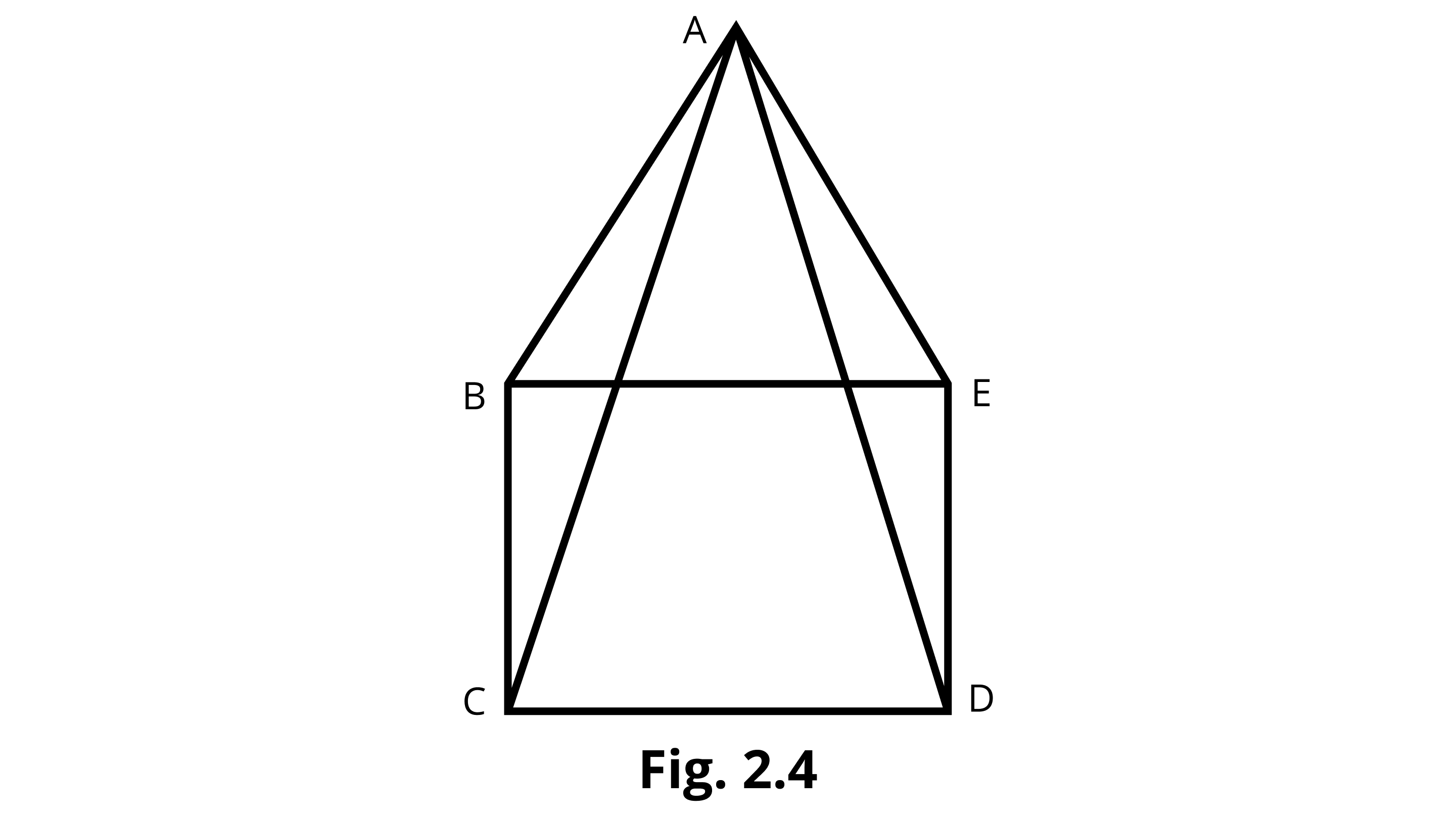
Ans: The name of the 3D shape formed is a square pyramid. 

i) Vertices - A, B, C, D, and E. 

ii) Edges - AB, AC, AD, AE, BC, CD, DE, and EB. 

iii) Faces - square BCDE and triangles ABC, ACD, ADE, and ABE. 

Example 12: Write the measure of the smaller angle formed by the hour and the minute hands of a clock at 7 O'clock. Also, write the measure of the other angle and also state what types of angles these are. 

Ans: Required angle = 30° + 30° + 30° + 30° + 30° = 150° 

This type of angle is called an obtuse angle.

Required other angle = 360° – 150° = 210° 

This type of angle is called a reflex angle.

Exercise

In each of the questions 1 to 16, out of four options, one is correct. Which is given with a solution.

1. Number of lines passing through five points such that no three of them are collinear is

(A) 10

(B) 5

(C) 20

(D) 8

Ans: Correct option - A 

There are five points out of which no three are collinear.

We know that number of lines = selecting 2 points out of given points

We know that number of lines = $\dfrac{5 \times 4}{2}$

So,number of lines = $5 \times 2=10$ 

2. The number of diagonals in a septagon is

(A) 21

(B) 42

(C) 7

(D) 14

Ans: Correct  option - D 

We know that number of diagonals =$\dfrac{n(n-3)}{2}$ ,where n=number of sides

Septagon has 7 sides so n=7

Then number of diagonals =$\dfrac{7(7-3)}{2}$

$=\dfrac{7 \times 4}{2}$

$7 \times 2=14$

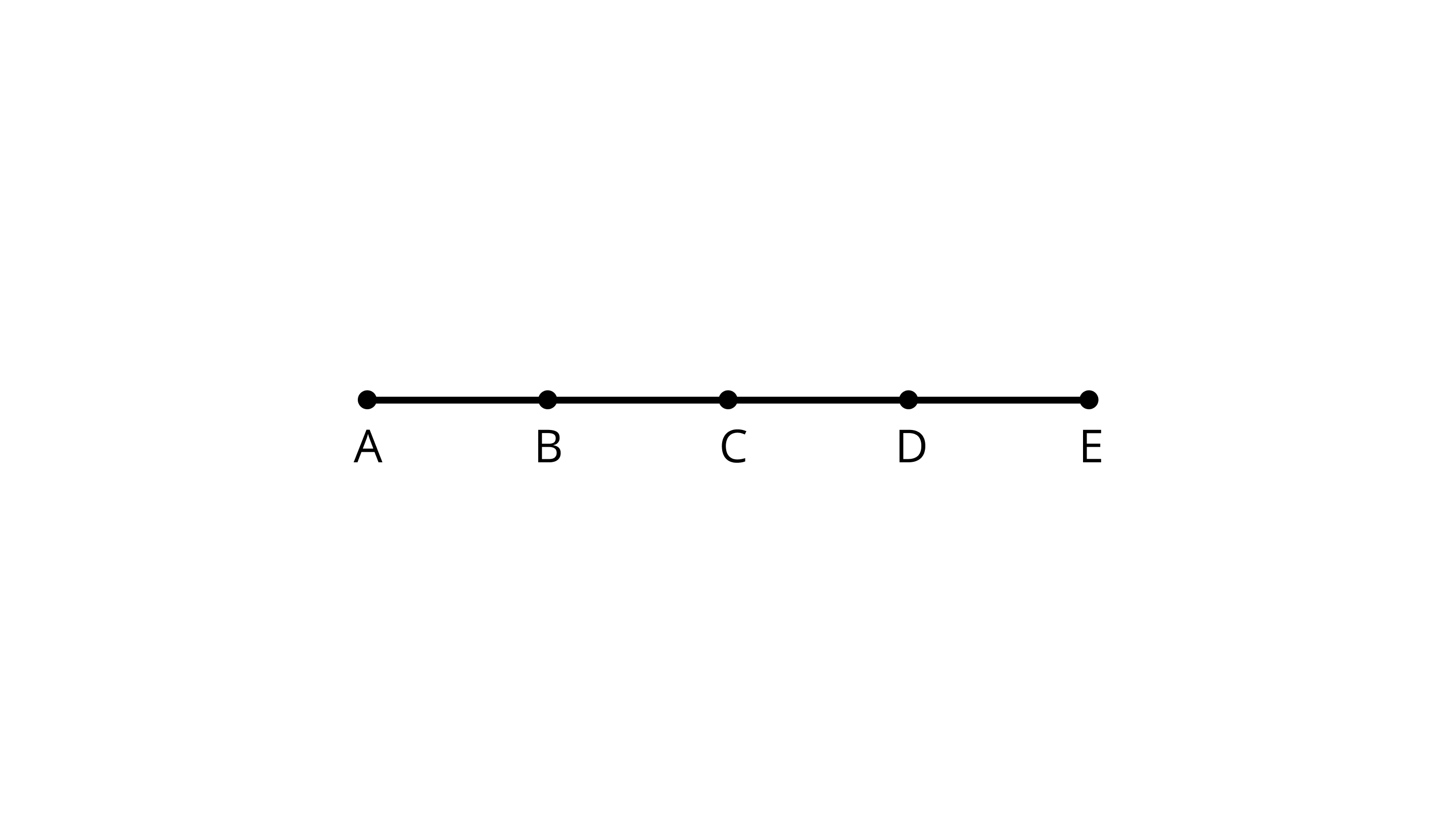
3. Number of line segments in the figure is

(A) 5

(B) 10

(C) 15

(D) 20

Ans: Correct option - B 

In the given line, there is five points A, B, C, D, and E

We know that number of lines = selecting 2 points out of given points

We know that number of lines = $\dfrac{5 \times 4}{2}$

Number of lines=$2\times 5=10$ 

4. Measures of the two angles between an hour and minute hands of a clock at 9 o'clock are

(A) $60^{\circ}, 300^{\circ}$

(B) $270^{\circ}, 90^{\circ}$

(C) $75^{\circ}, 285^{\circ}$

(D) $30^{\circ}, 330^{\circ}$

Ans: Correct option - B

We know that the total clock is $360^{\circ}$

At 9 o'clock, the hour hand is at 9:00 and the minute hand is at 12:00

In between 9:00 and 12:00 angle is $90^{\circ}$ 

Then remaining angle= $360^{\circ}$-$90^{\circ}$ =$270^{\circ}$ 

5. If a bicycle wheel has 48 spokes, then the angle between a pair of two consecutive spokes are

(A) $\left(5 \dfrac{1}{2}\right)$

(B) $\left(7 \dfrac{1}{2}\right)$

(C) $\left(\dfrac{2}{11}\right)$

(D) $\left(\dfrac{2}{15}\right)$

Ans: Correct option - B  

Given, number of spokes=48 and a complete angle in a circle = $360^{\circ}$

So, the angle between a pair of two consecutive spokes=$\dfrac{360}{48}=7 \dfrac{1}{2}$

6. In the given figure, $\angle X Y Z$ cannot be written as

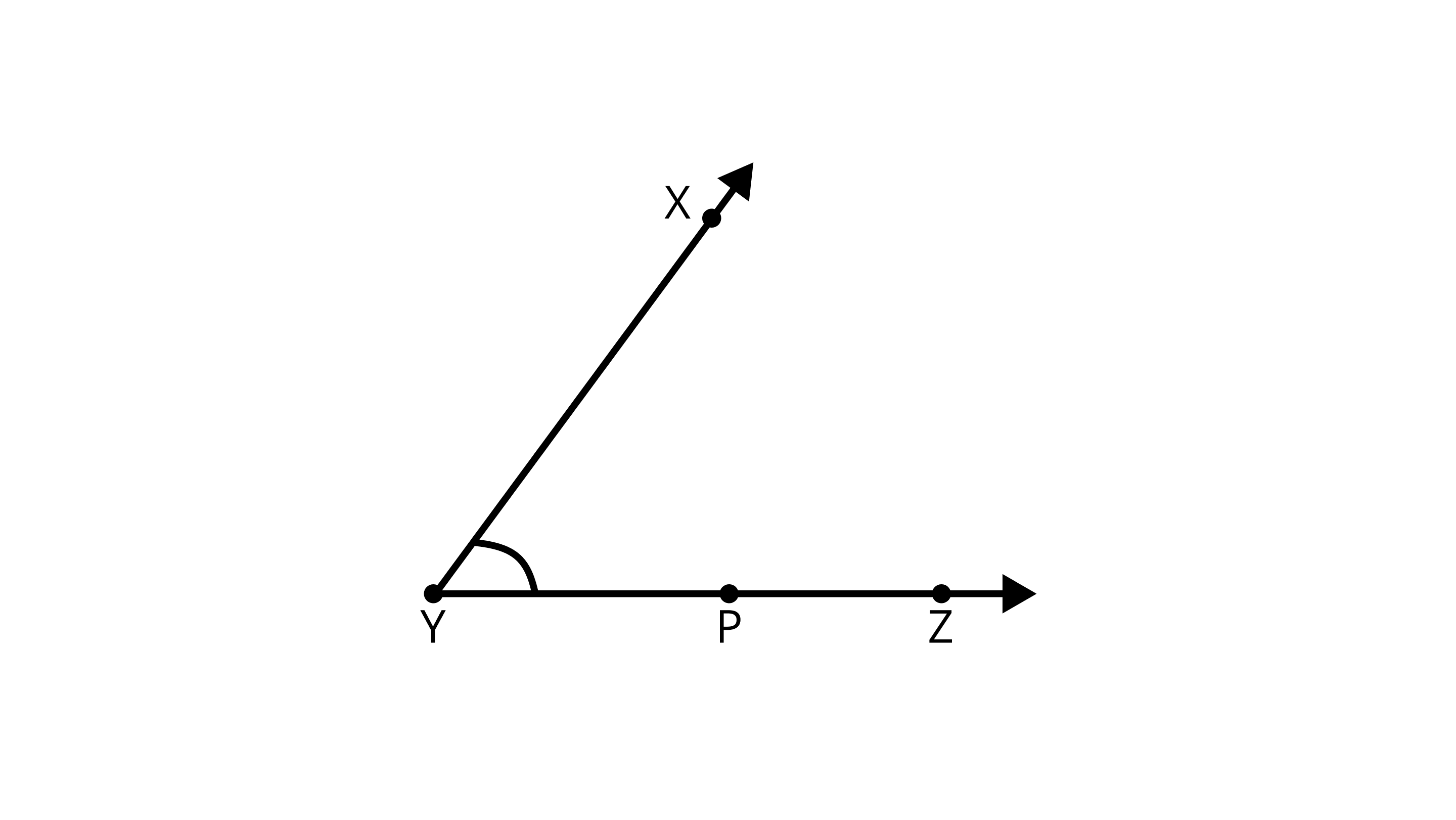
(A) $\angle Y$

(B) $\angle ZXY$

(C) $\angle ZYX$

(D) $\angle X Y P$

Ans: Correct option -B 

since possible angles are = $\angle Y$,$\angle XYP$ , $\angle ZYX$ and $\angle PYX$.

So,$\angle X Y Z$ cannot be written as $\angle ZXY$.

7. In Fig, if point $A$ is shifted to point $B$ along with the ray PX such that $PB =2 PA$, then the measure of $\angle BPY$ is

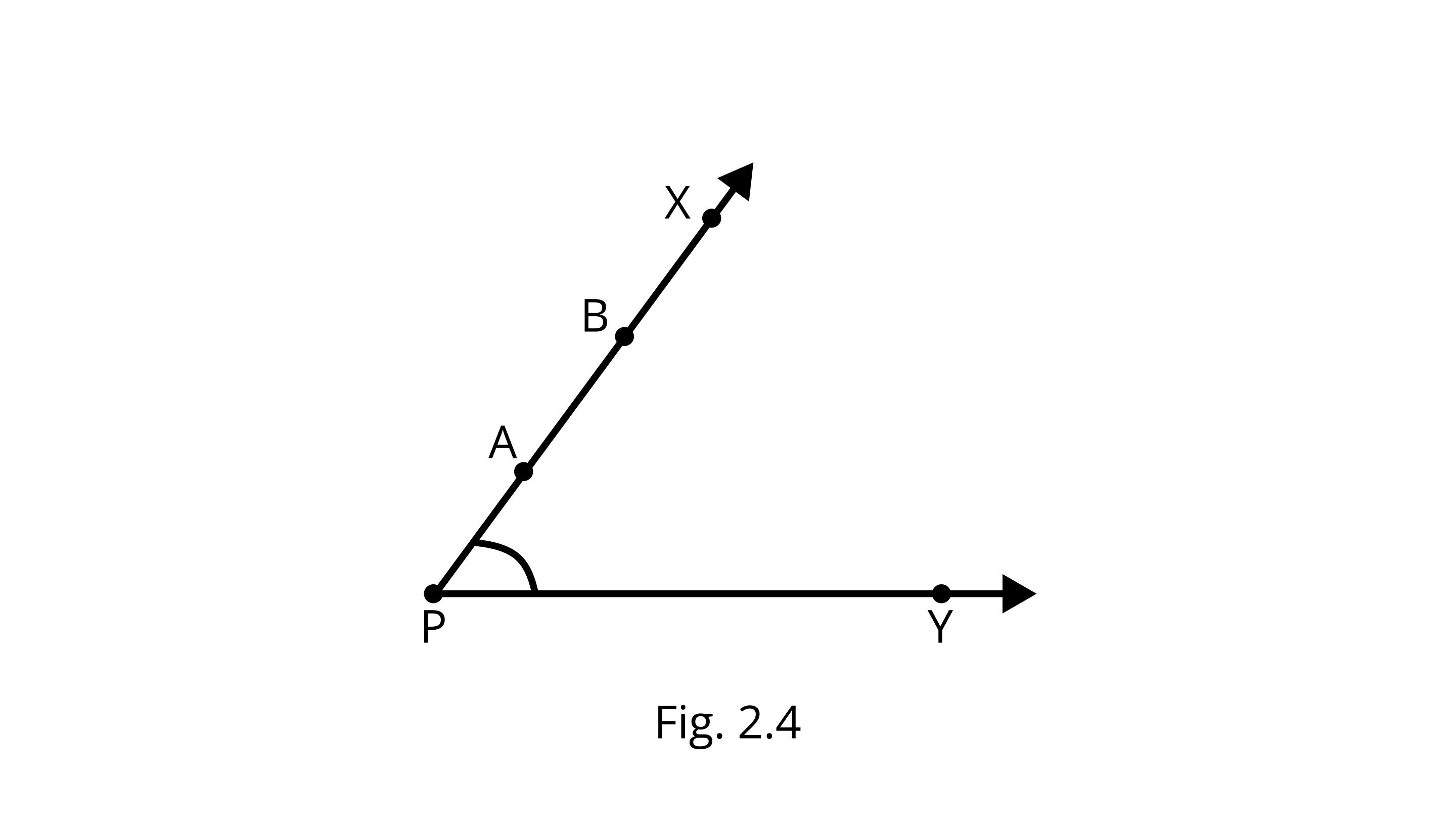
(A) Greater than $45^{\circ}$

(B) $45^{\circ}$

(C) Less than $45^{\circ}$

(D) $90^{\circ}$

Ans: Correct option -B 

There will be no change in the measure of $\angle BPY$. 

8. The number of angles in the Figure is

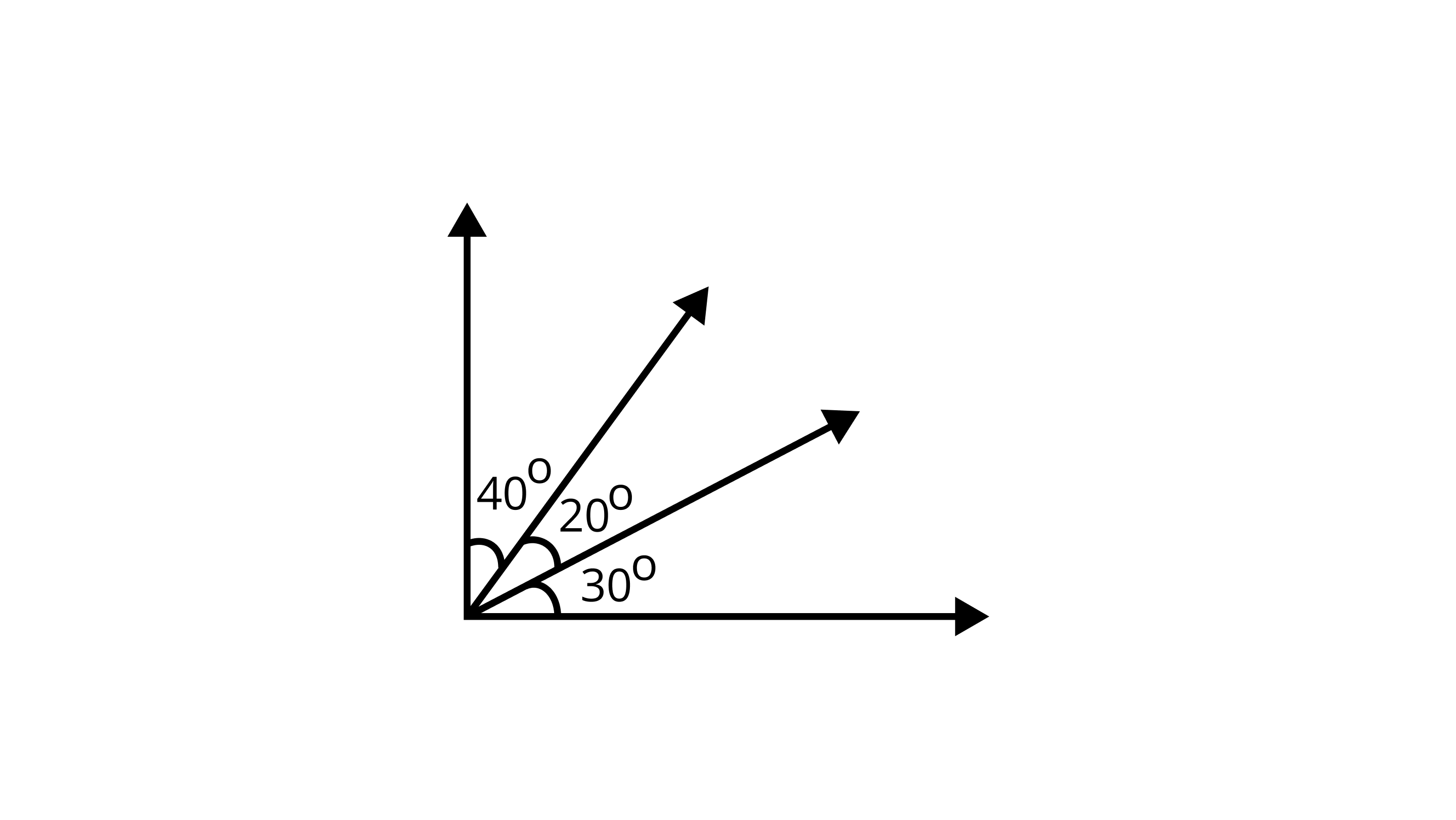
(A) 3

(B) 4

(C ) 5

(D) 6

Ans: Correct option - D

Angles shown in the figureare$40^{\circ}$,$30^{\circ}$,$20^{\circ}$,$60^{\circ}$,$90^{\circ}$,$50^{\circ}$\. So, number of angles=6

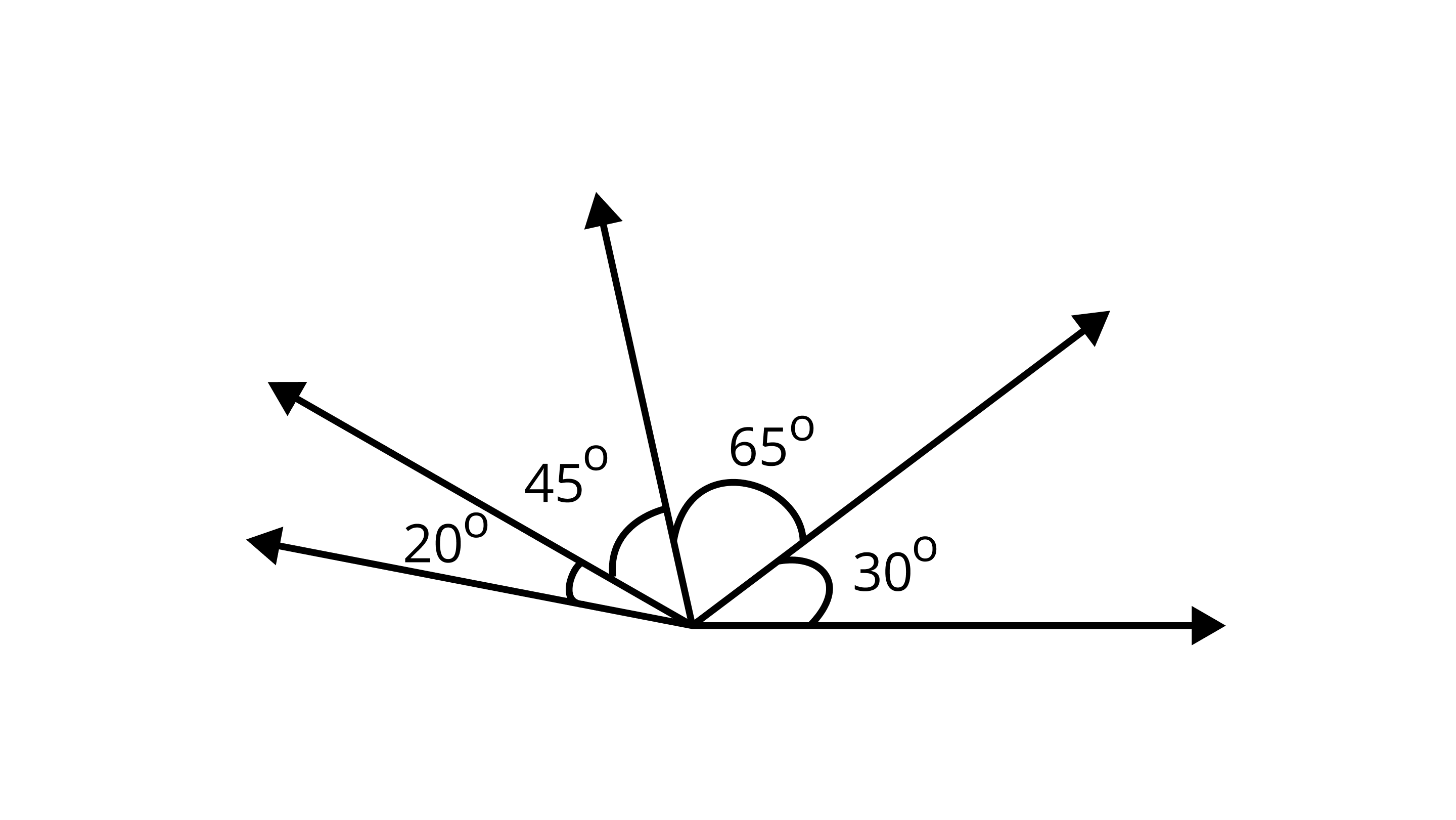
9. The number of obtuse angles in the figure is

(A) 2

(B) 3

(C ) 4

(D) 5

Ans: Correct option - C

We know that the obtuse angle is always greater than $90^{\circ}$ and less than $180^{\circ}$.

Then $65^{\circ}+30^{\circ}$=$95^{\circ}$

$45^{\circ}+65^{\circ}$=$110^{\circ}$

$45^{\circ}+30^{\circ}+65^{\circ}$=$140^{\circ}$

$45^{\circ}+65^{\circ}+20^{\circ}$=$130^{\circ}$

So,number of obtuse angles=4

10. The number of triangles in fig. Is

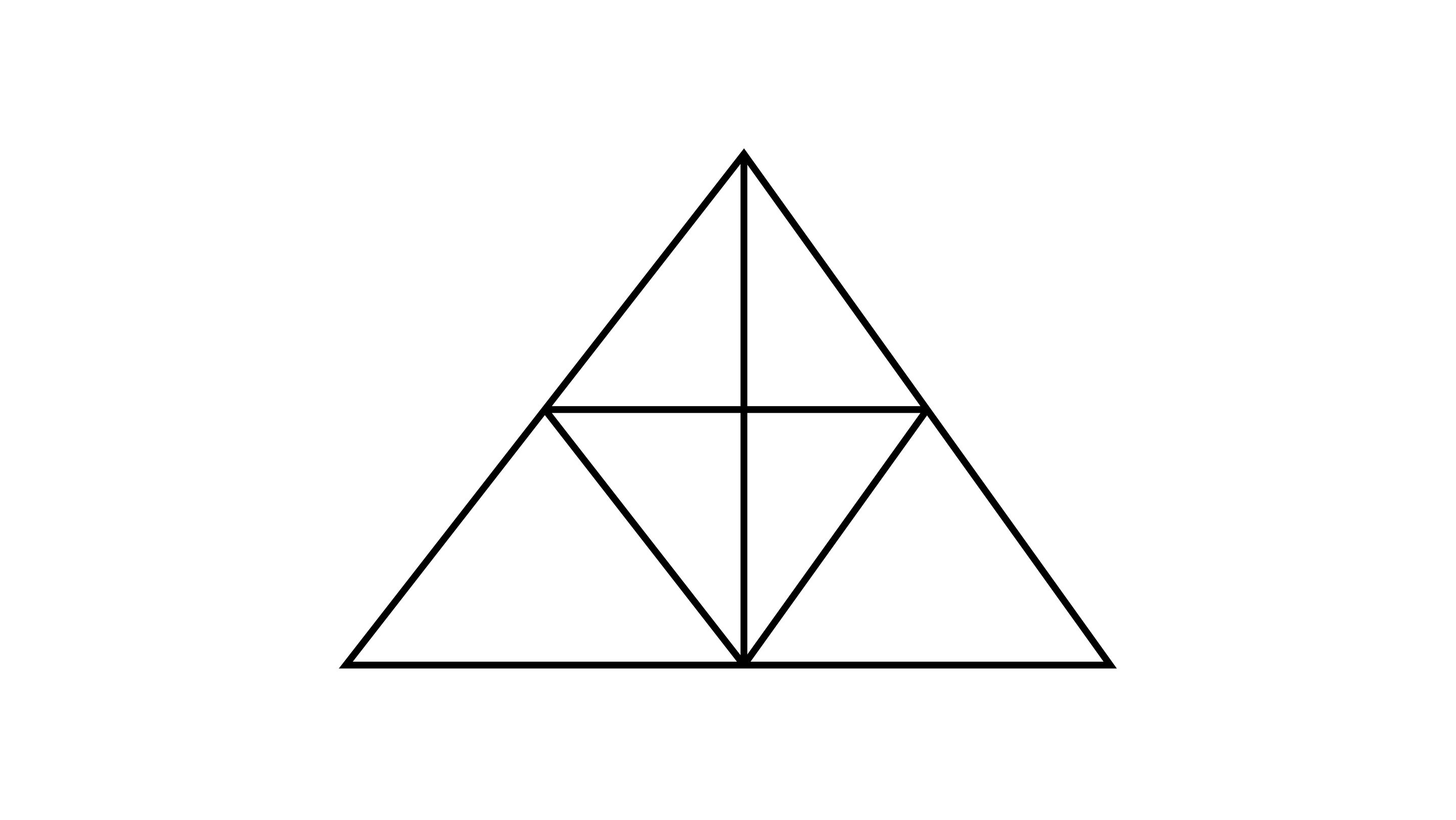
(A) 10

(B) 12

(C ) 13

(D) 14

Ans: Correct option - C

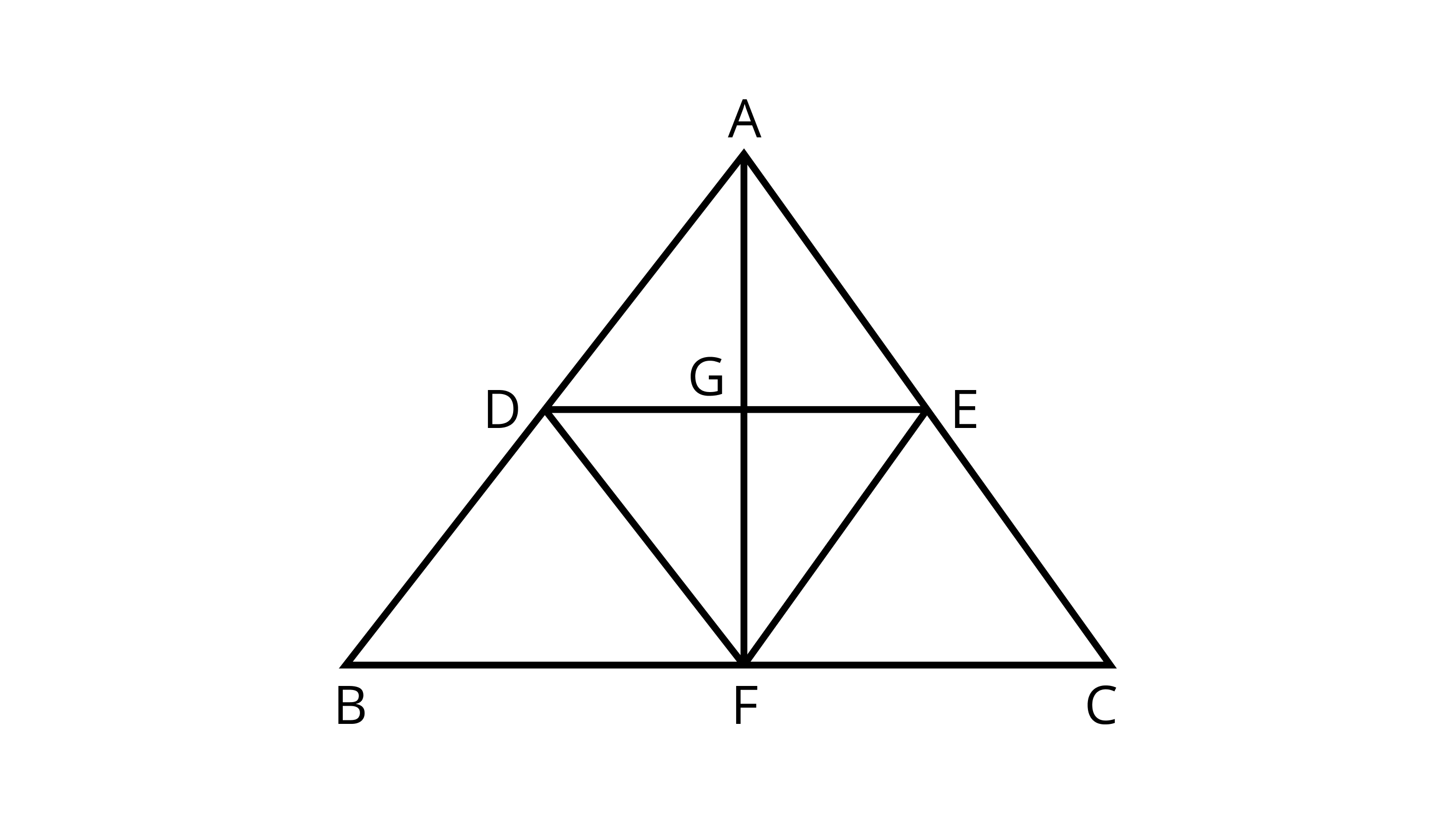
By observing the figure, triangles are - $\triangle ABC$,$\triangle ABF$, $\triangle AFC$, $\triangle AGD$, $\triangle AGE$, $\triangle ADE$, $\triangle DEF$, $\triangle DGF$, $\triangle GEF$, $\triangle ADF$, $\triangle AEF$, $\triangle DBF$, $\triangle EFC$

So, number of triangles=13

11. If the sum of two angles is greater than $180^{\circ}$, then which of the following is not possible for the two angles?

(A) One obtuse angle and one acute angle

(B) One reflex angle and one acute angle

(C) Two obtuse angles

(D) Two right angles

Ans: Correct option- D 

Because we know that the sum of two right angles is equal to $180^{\circ}$.

12. If the sum of two angles is equal to an obtuse angle, then which of the following is not possible? 

(A) One obtuse angle and one acute angle 

(B) One right angle and one acute angle

(C) Two acute angles

(D) Two right angles

Ans: Correct option- D 

Because we know that the sum of two right angles is equal to $180^{\circ}$ which is not an obtuse angle.

13. A polygon has a prime number of sides. Its number of sides is equal to the sum of the two least consecutive primes. The number of diagonals of the polygon is 

(A) 4 

(B) 5 

(C) 7

(D) 10

Ans: Correct option- B 

We know two least consecutive primes are 2 and 3.

Given, number of sides = sum of the two least consecutive primes number of sides(n)=2+3=5. 

So, number of diagonals=$\dfrac{n(n-3)}{2}$ ,where n=number of sides

Number of diagonals =$\dfrac{5(5-3)}{2}$

$=\dfrac{5 \times 2}{2}$

$=5$

14. In the given figure AB=BC and AD=BD=DC. The number of isosceles triangles in the figure is

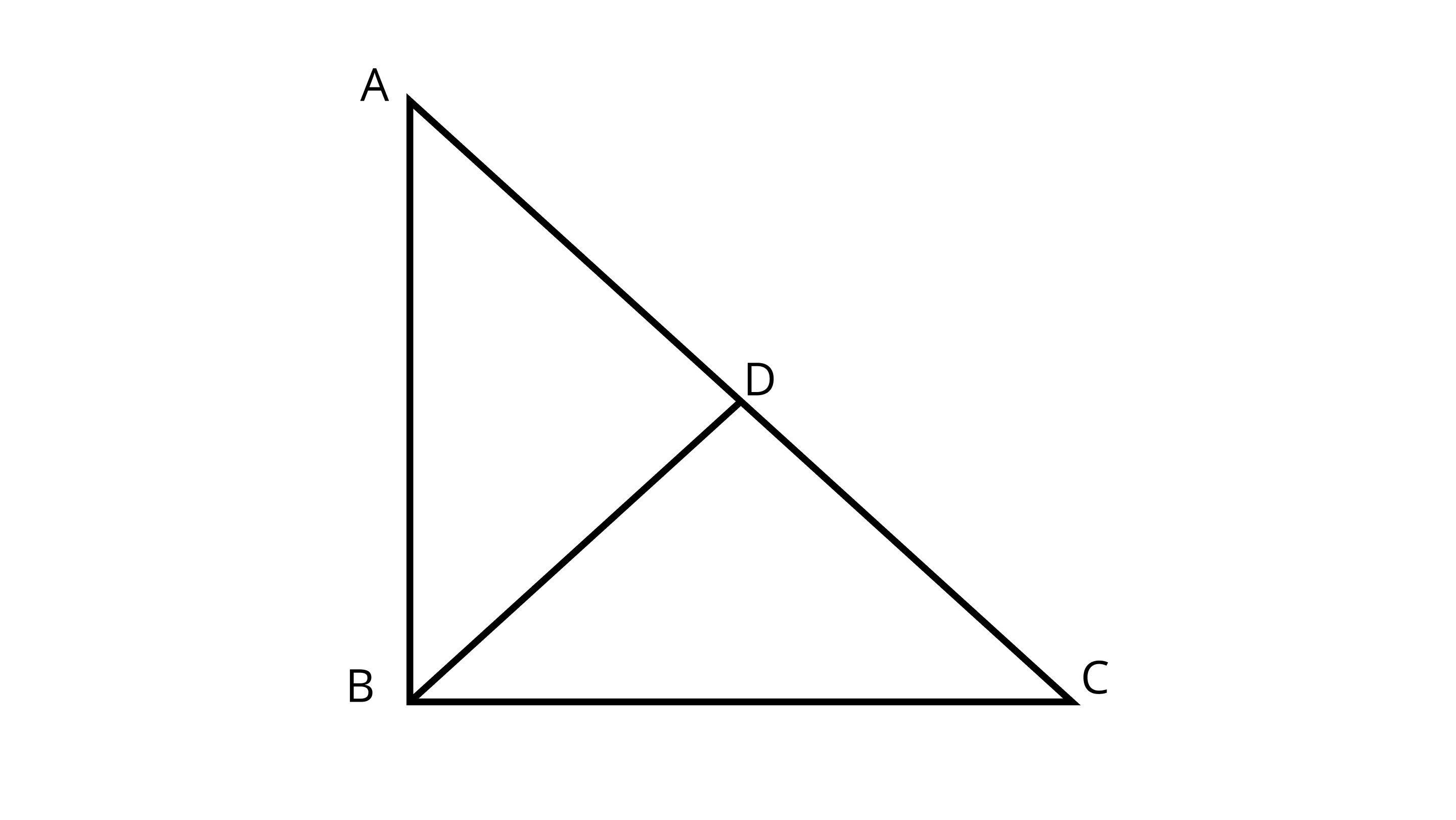
(A) 1

(B) 2

(C) 3

(D) 4

Ans: Correct option- C

Because AB=BC,AD=DB,BD=DC respectively in $\triangle ABC$,$\triangle ABD$ and $\triangle BDC$ So, number of isosceles triangles is =3

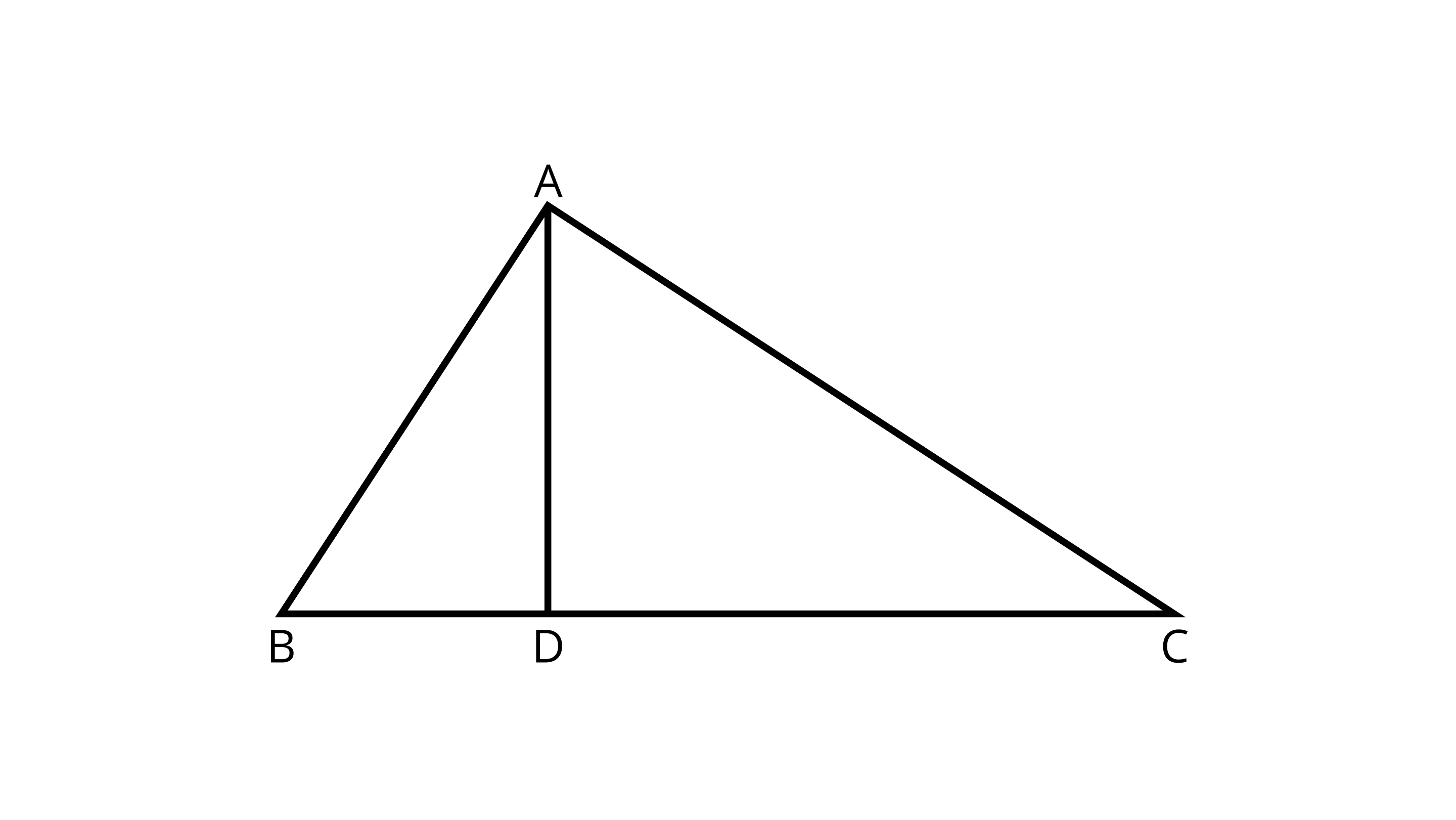
15. In Figure, $\angle BAC$ = $90^{\circ}$ and AD$\perp$BC. The number of right-angle triangles in the figure is

(A) 1

(B) 2

(C) 3

(D) 4

Ans: Correct option- C

We know a triangle, in which one angle is equal to  $90^{\circ}$,is called a right angle triangle.

$\angle{BAC}$ = $90^{\circ}$ ,so $\triangle{BAC}$ is a right angle triangle. 

Also,given AD$\perp$BC,so  $\angle ADB$= $\angle ADC$=$90^{\circ}$.Hence $\triangle ADB$ and  $\triangle ADC$ are also right angle triangles.

Number of right-angle triangles=3   

16. In Figure, PQ $\perp$RQ, PQ = 5 cm and QR = 5 cm. Then $\triangle PQR$ is

(A) A right-angle triangle but not isosceles

(B) An isosceles right angle triangle

(C) Isosceles but not a right-angle triangle

(D) Neither isosceles nor right angle triangle

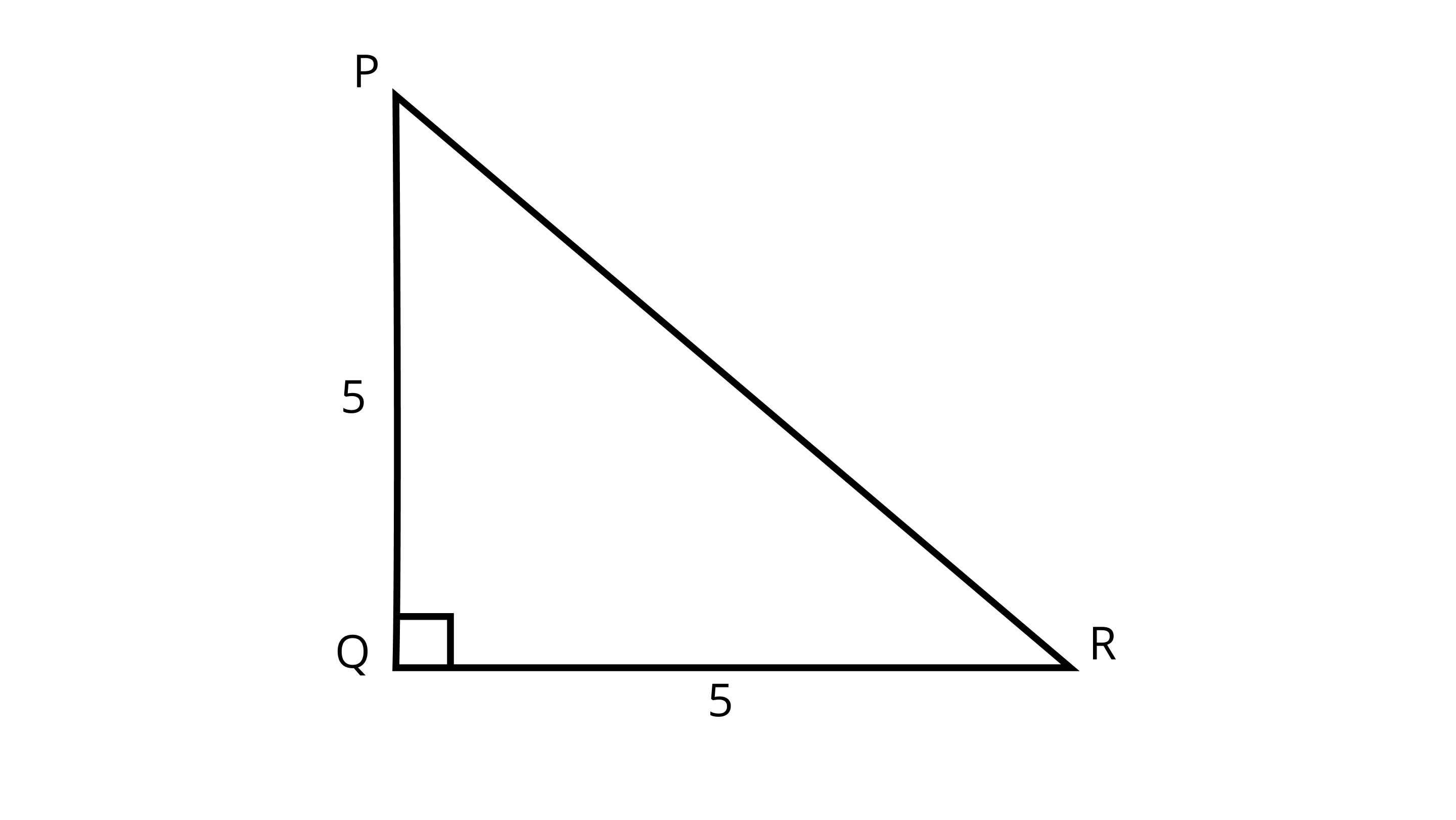
Ans: Correct option- B

Given, PQ $\perp$RQ so,$\angle PQR$=$90^{\circ}$ and PQ=QR=5cm SO,$\triangle PQR$ is an isosceles.

Hence $\triangle PQR$ is an isosceles right-angled triangle.

In questions 17 to 31, fill in the blanks to make the statements true:

17. An angle greater than $180^{\circ}$ and less than a complete angle is called……….

Ans: An angle greater than $180^{\circ}$ and less than a complete angle is called Reflex angle.

18. The number of diagonals in a hexagon is  ____.

Ans: The number of diagonals in a hexagon is 9.

Number of sides in hexagon(n)=6

So, number of diagonals =$\dfrac{n(n-3)}{2}$ ,where n=number of sides

Number of diagonals =$\dfrac{6(6-3)}{2}$

$=\dfrac{6 \times3}{2}$

$=9$

19. A pair of opposite sides of a trapezium is ____.

Ans: A pair of opposite sides of a trapezium is Parallel.

20. In Figure, points lying in the interior of the triangle $PQR$ are……. that in the exterior are……... and that on the triangle itself are……..

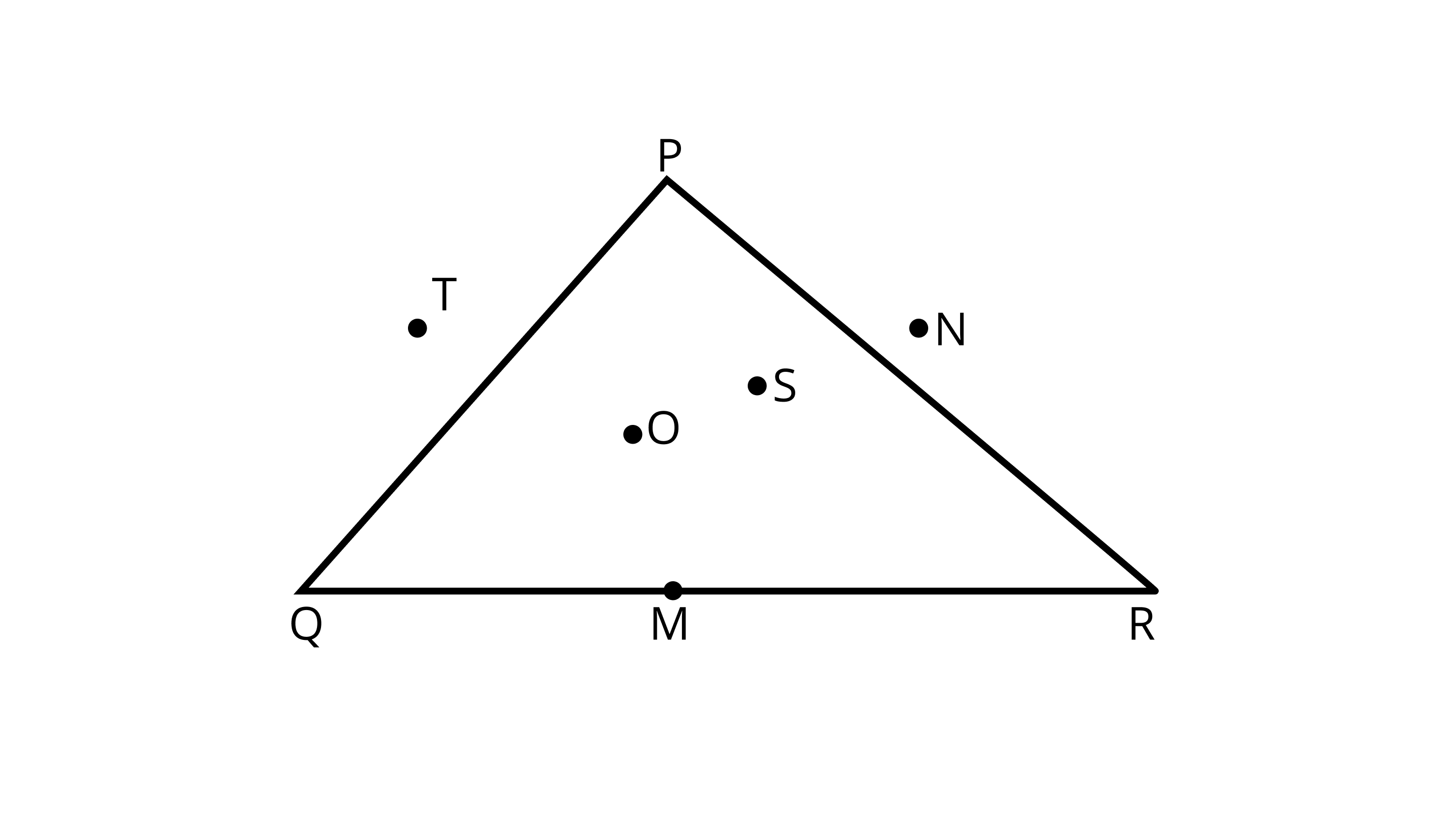
Ans: Points lying in the interior of the triangle $PQR$ are $O$ and $S$ that in the exterior are $T$ and $N$ and that on the triangle itself are $P, Q, R$, and $M$.

21. In Figure, points A, B, C, D and E are collinear such that AB = BC = CD = DE. Then

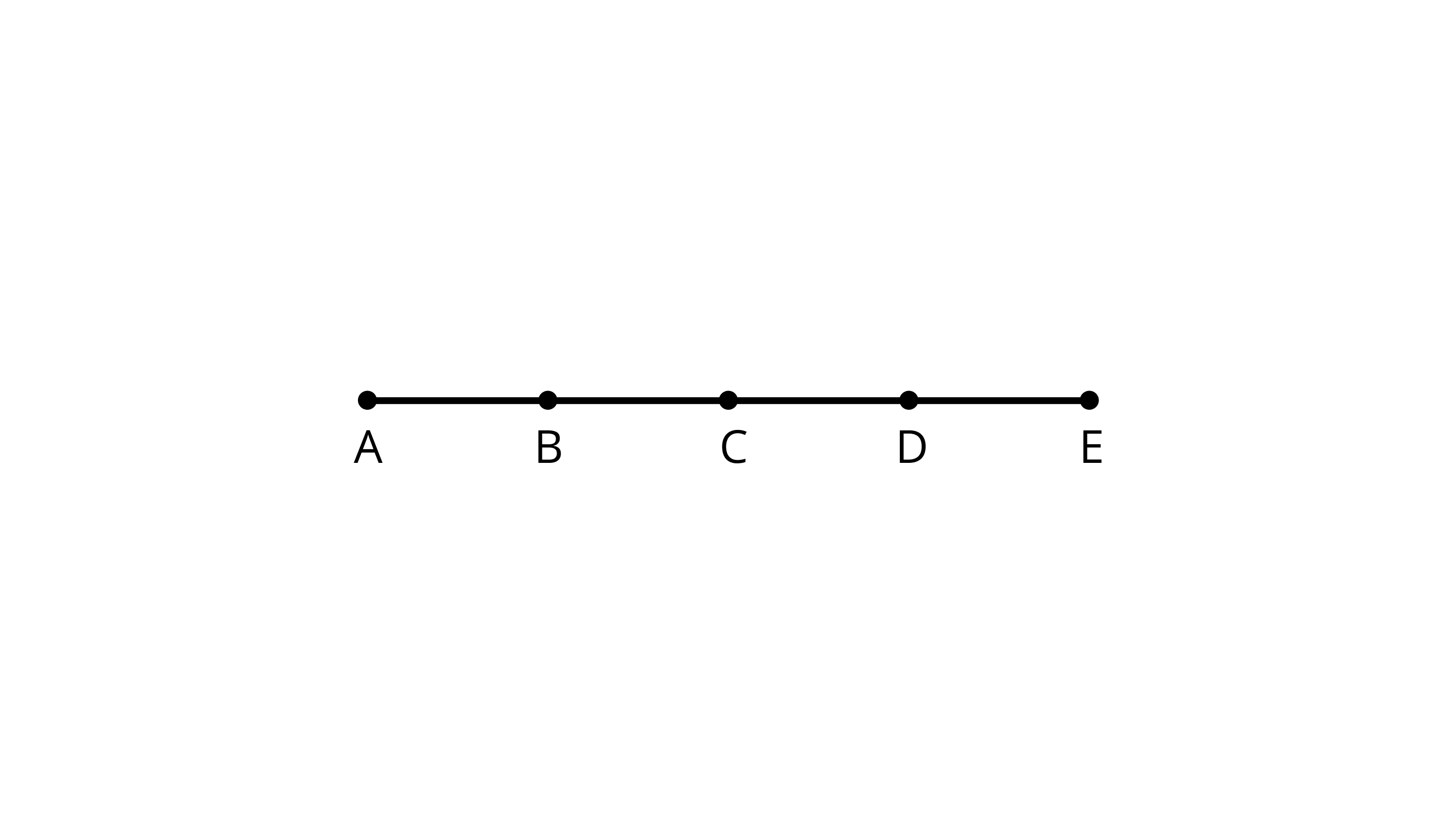
(a) AD = AB +_____

Ans: AD = AB +BD 

Because, AD = AB + BC + CD=AB+BD

(b) AD = AC +_____

Ans: AD = AC +CD 

Because, AD = AB + BC + CD=AC+CD

(c) Midpoint of AE is_____

Ans: Midpoint of AE is C.

Given,AB = BC = CD = DE

Then AE=AC+CE so, the Midpoint of AE is C.

(d) Midpoint of CE is_____

Ans: Midpoint of CE is D.

Given, AB = BC = CD = DE

Then CE=CD+DE so, the Midpoint of CE is D.

(e) AE = ______AB.

Ans: AE =4AB.

Or AE=AB+BC+CD+DE

Or AE=AB+AB+AB+AB

So, AE=4AB

22. In Figure,

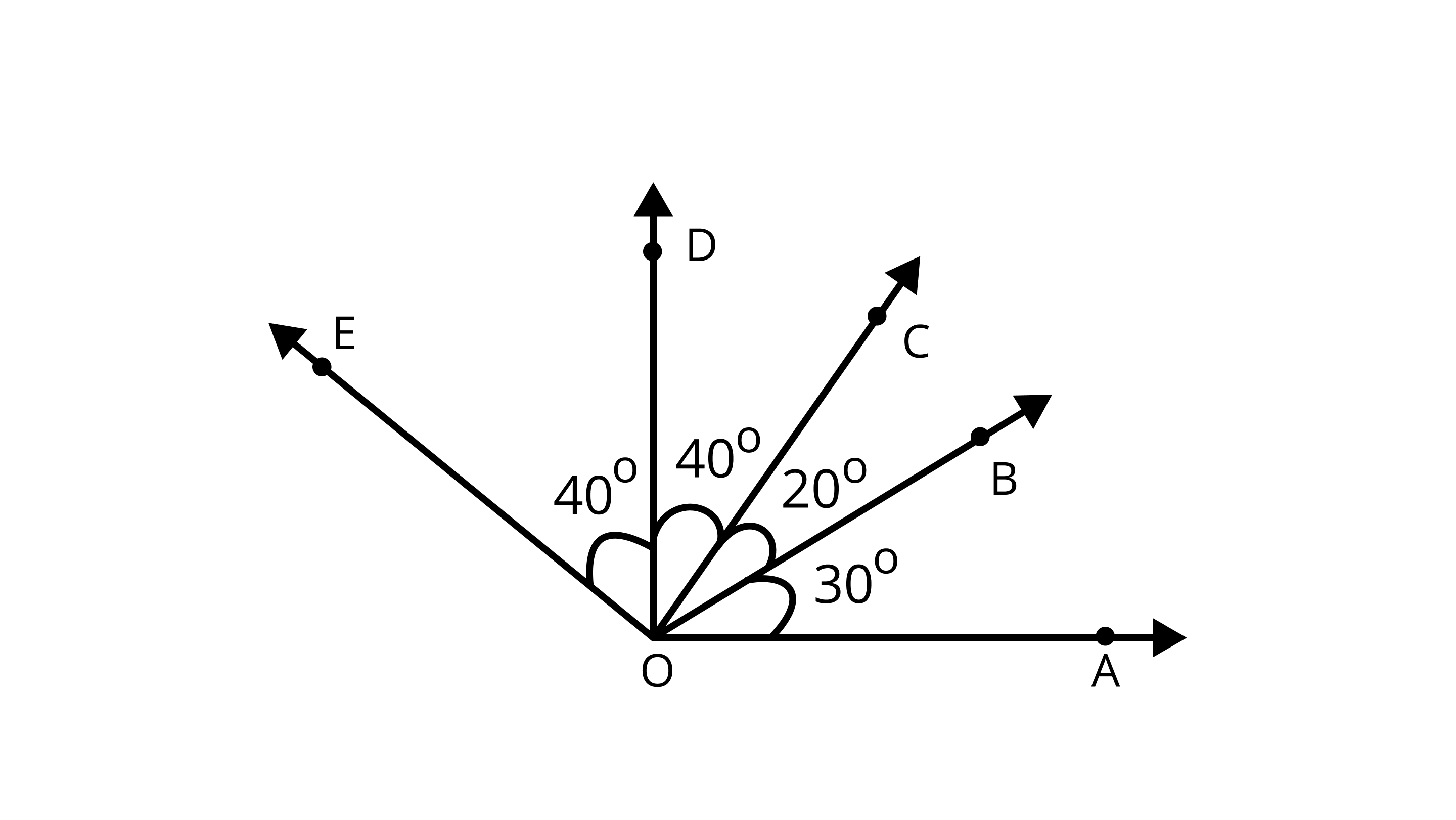
(a) $\angle AOD$ is a/an____ angle.

Ans: $\angle AOD$ is a Right angle.

$\angle AOD$=$\angle AOB$+$\angle BOC +\angle COD$

So, $\angle AOD$=$30^{\circ}+20^{\circ}+40^{\circ}=90^{\circ}$

(b) $\angle C O A$ is a/an_____ angle.

Ans: $\angle C O A$ is an acute angle.

$\angle COA$=$\angle COB$+$\angle BOA$

So, $\angle COA$=$20^{\circ}+30^{\circ}=50^{\circ}$

(c) $\angle AOE$ is a/an____ angle.

Ans:  $\angle AOE$ is an Obtuse angle.

$\angle AOE=40^{\circ}+40^{\circ}+20^{\circ}+30^{\circ}=130^{\circ}$

23. The number of triangles in Figure is____

Their names are____

Ans: The number of triangles in Figure is 5.

Their names are $\triangle ABC , \triangle ACD , \triangle AOB , \triangle AOC$ and $\triangle COD$.

24. Number of angles less than $180^{\circ}$ in Figure is and their names are

Ans: The number of angles less than $180^{\circ}$  in Figure is 12.

And their names are $\angle ABO, \angle BAO, \angle AOB, \angle BOD, \angle COD, \angle ODC, \angle OCD, \angle OCA$, $\angle CAO, \angle AOC, \angle BAC$ and $\angle ACD$.

25. The number of straight angles in Figure is______.

Ans: The number of straight angles in Figure is  4

The straight angles are - Both side angles of line AD and Both side angles of line BC.

26. The number of right angles in a straight angle is____ and that is a complete angle is___.

Ans: The number of straight angles is 2 and in a complete angle, the number of straight angles is 4.

27. The number of common points in the two angles marked in Figure is_____.

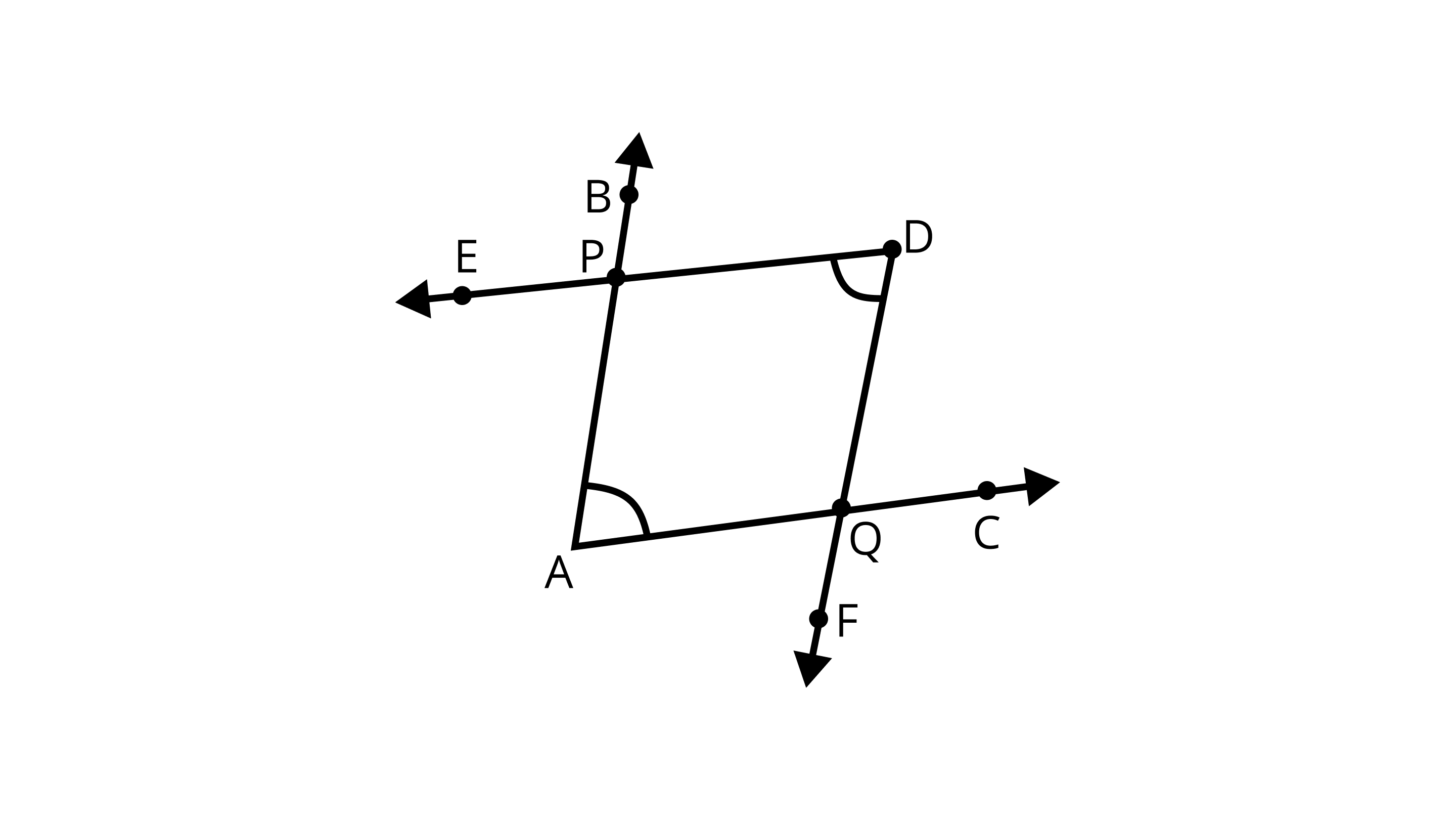
Ans: There are two common points marked in an angle is 2.

The common points in the $\angle PAQ$ and $\angle PDQ$ are $P$ and $Q$.

28. The number of common points in the two angles marked in Figure is____.

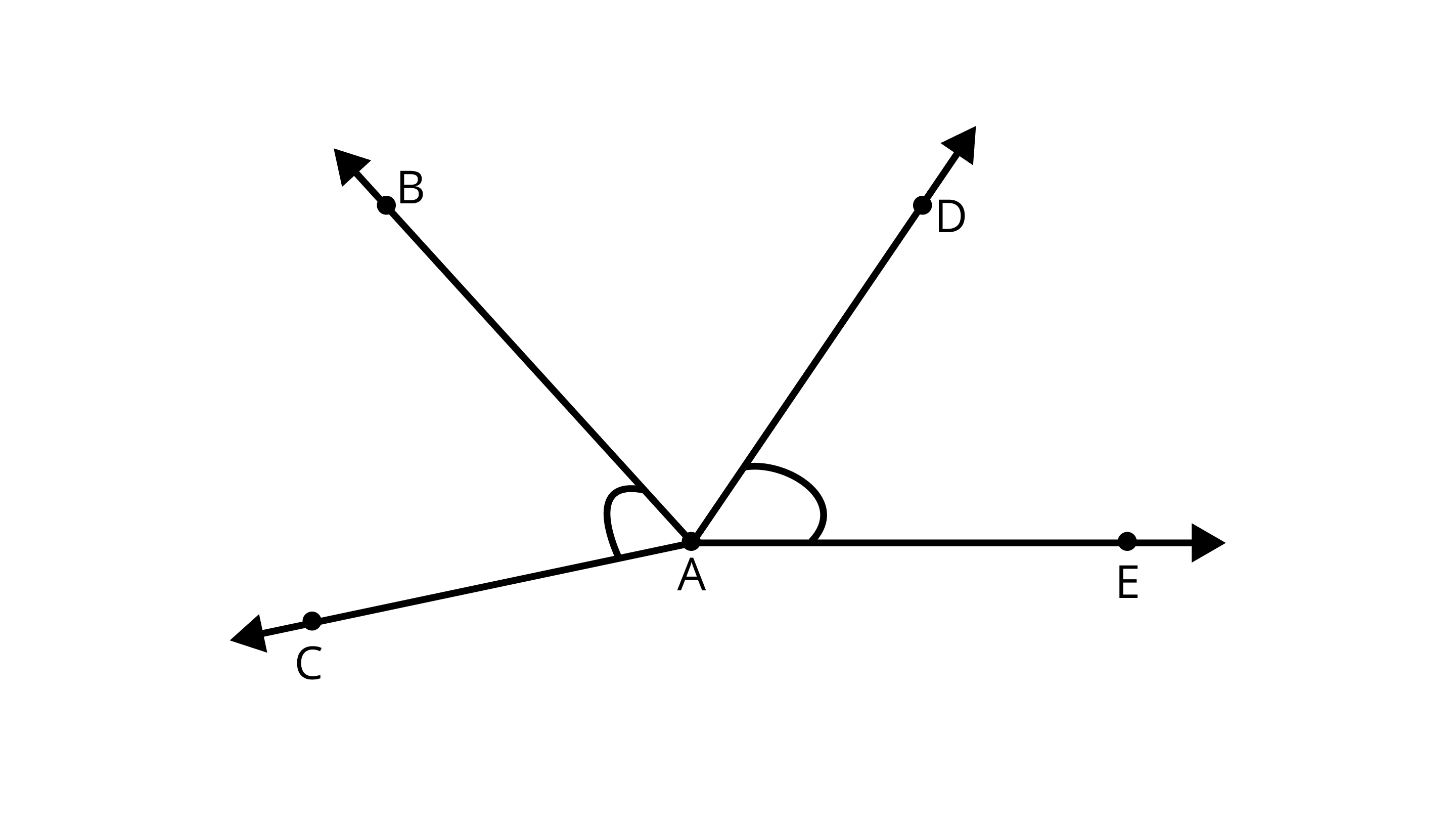
Ans: The number of common points is 1.

The common point in $\angle CAB \text { and } \angle DAE$ is A.

29. The number of common points in the two angles marked in Figure is_____.

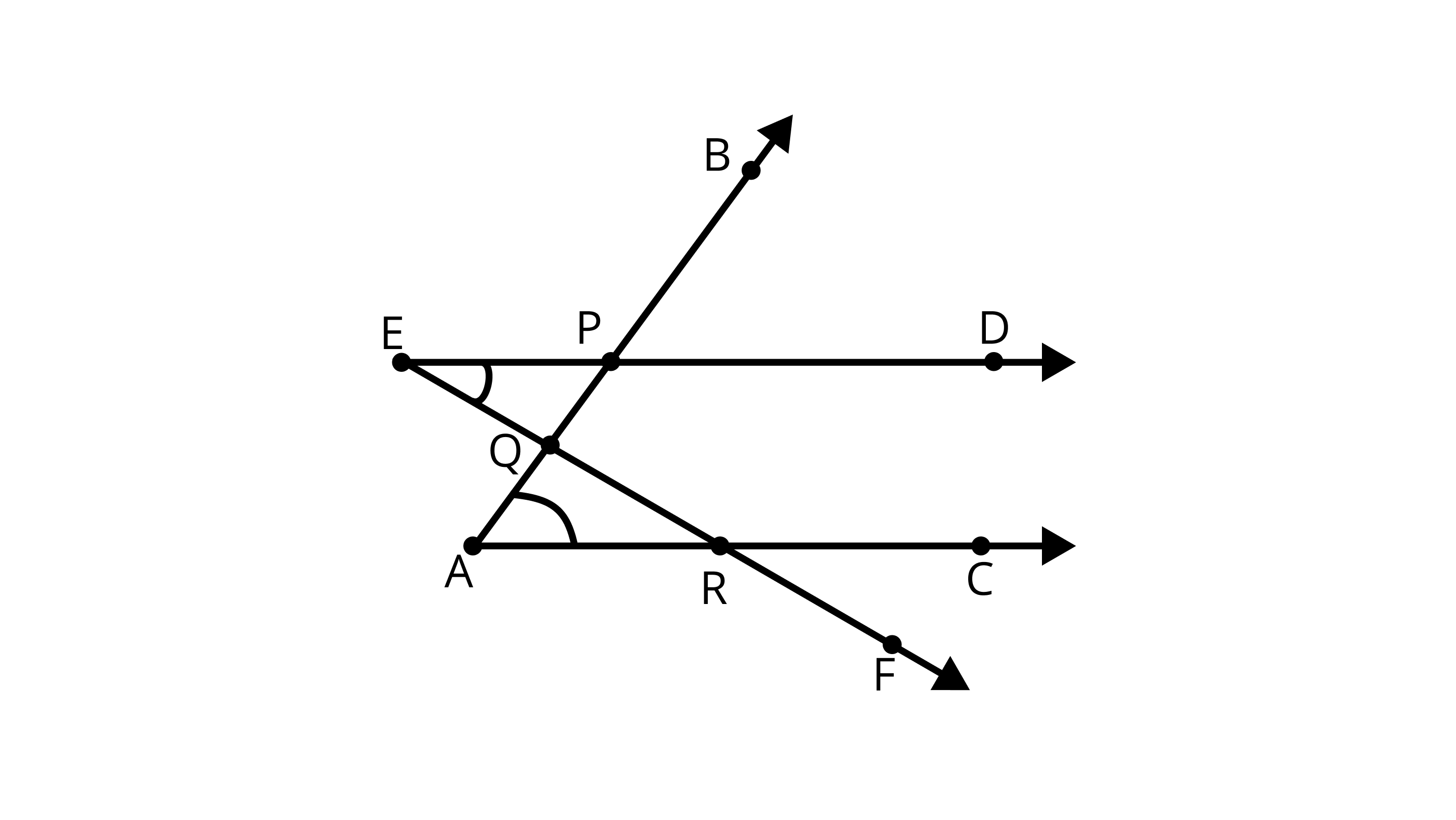
Ans:  The number of common points in the two angles is 3.

The common points in the $\angle DEF$ and $\angle BAC$ are $P$, $R$, and $Q$.

30. The number of common points in the two angles marked in Figure is______.

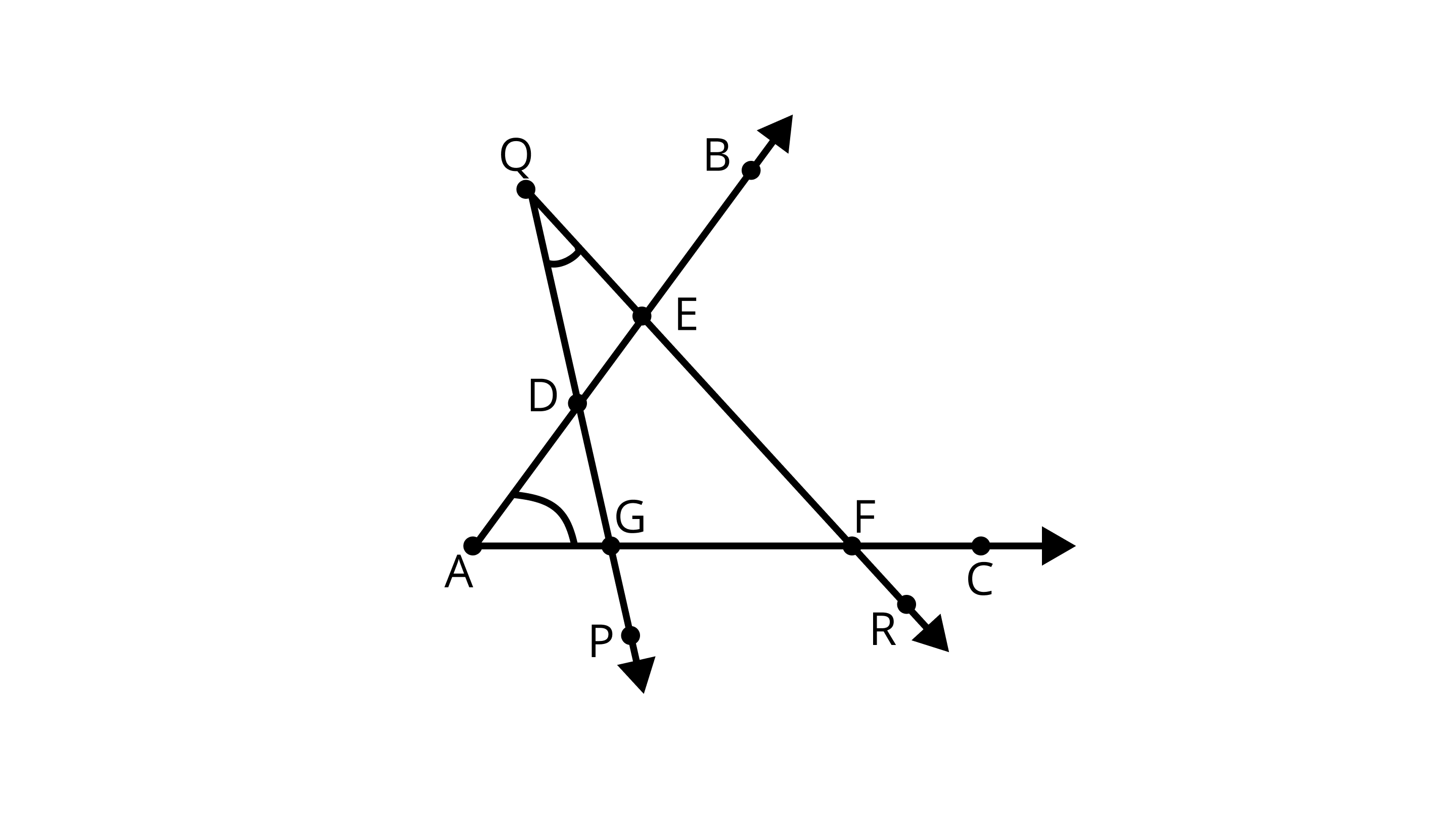
Ans:  The number of common points in the two angles is 4.

The common points in the $\angle PQR$ and $\angle BAC$ are $D$, $E$, $F$, and $G$.

31. The common part between the two angles BAC and DAB in Figure is_____.

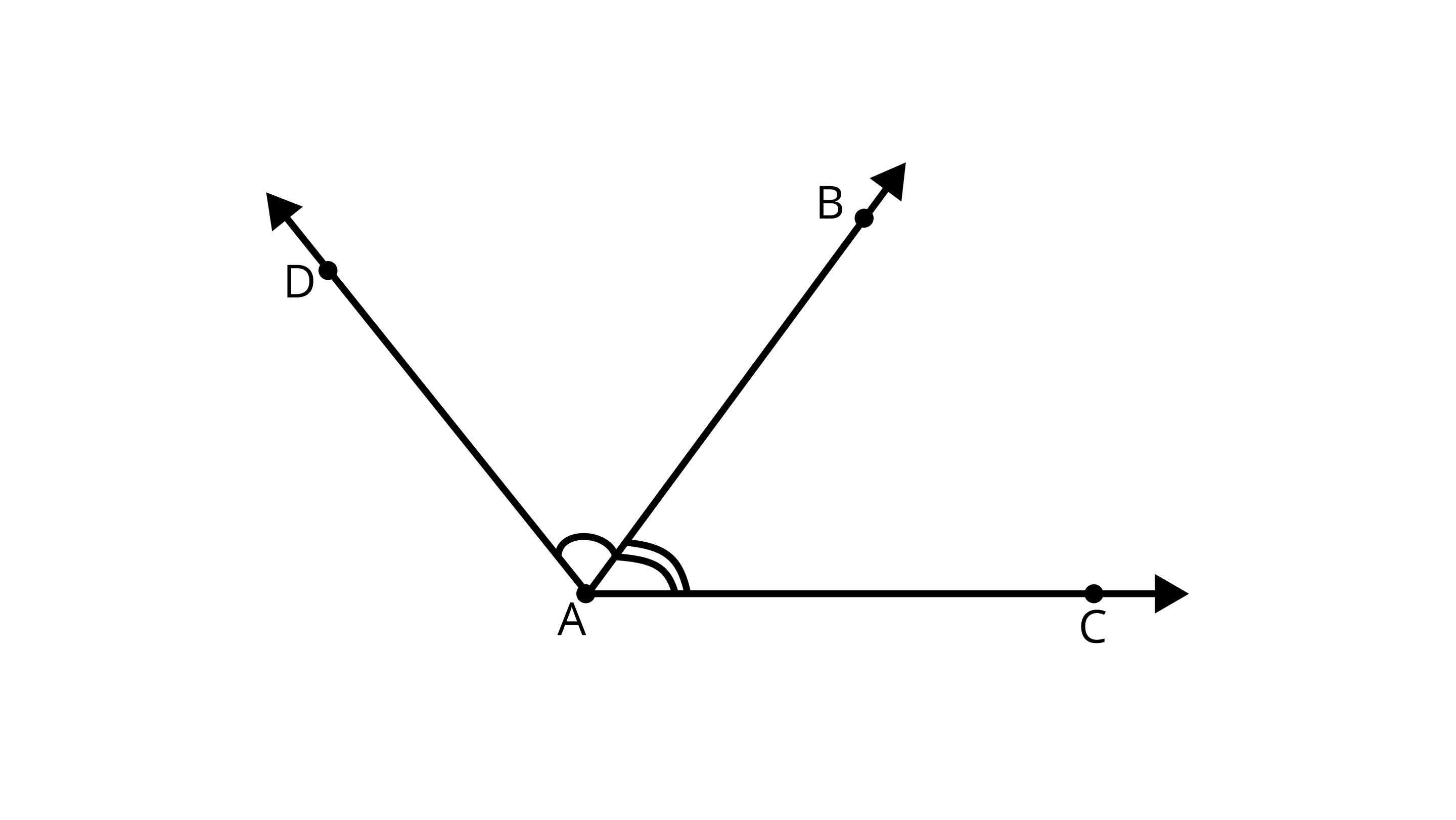
Ans:  The common part between the two angles BAC and DAB is ray AB.

The common part between angles $\angle BAC$ and $\angle DAB$ is Ray $ AB$.

State whether the statements given in questions 32 to 41 are true (T) or false (F):

32. A horizontal line and a vertical line always intersect at right angles.

Ans: True

33. If the arms of an angle on the paper are increased, the angle increases.

Ans: False

If the size of the arms changes, there will be no change in the angle.

34. If the arms of an angle on the paper are decreased, the angle decreases.

Ans: False

If the size of the arms changes, there will be no change in the angle.

35. If line $PQ \|$ line $m$, then line segment $PQ \| m$

Ans: True

If the line is parallel to another line, then line segments are also parallel.

36. Two parallel lines meet each other at some point.

Ans: False

We know two parallel lines never intersect.

37. Measures of $\angle ABC$ and $\angle CBA$ in Figure are the same.

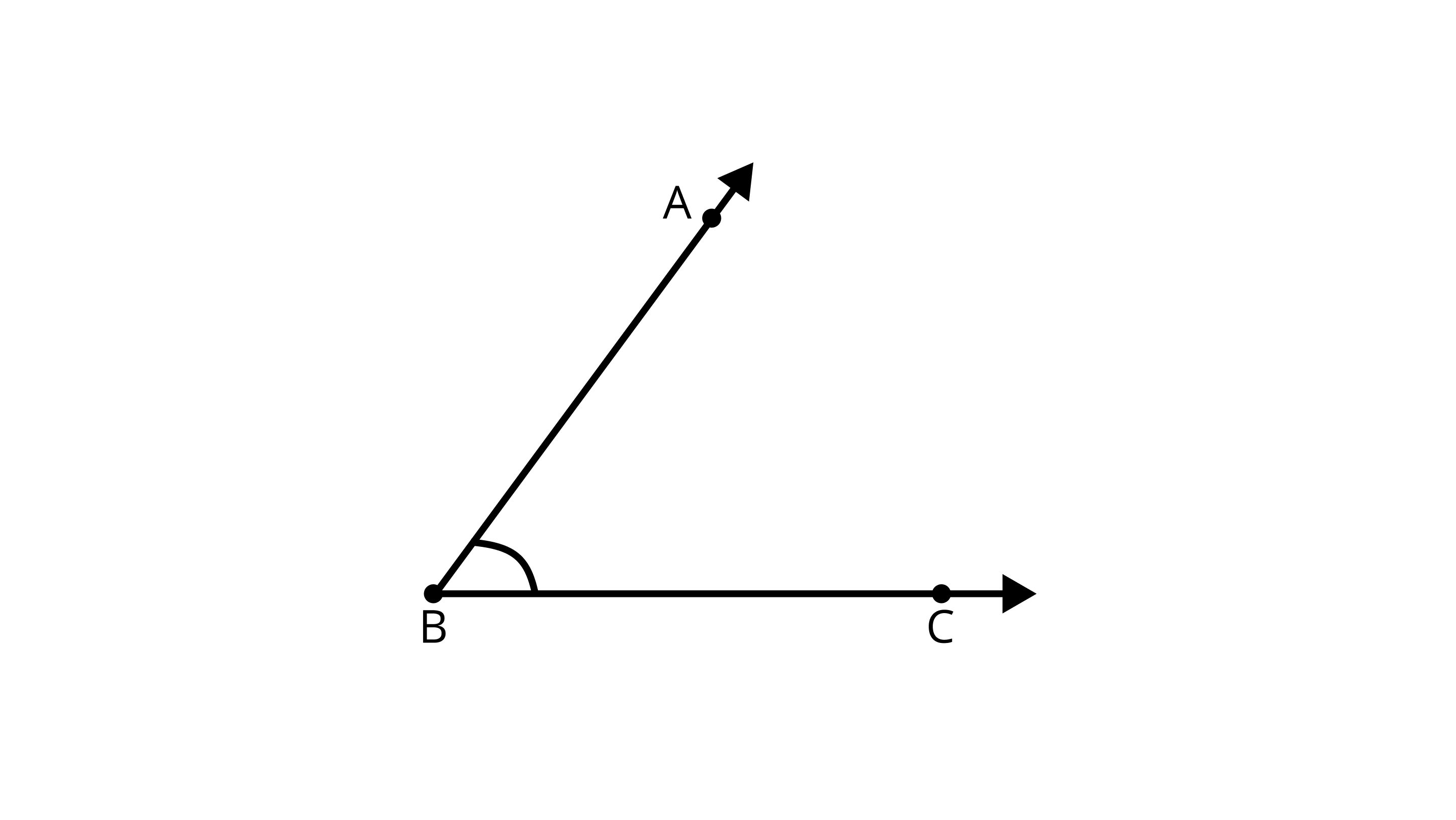
Ans: True

In $\angle ABC$ and $\angle CBA$ common angle is B.

38. Two line segments may intersect at two points.

Ans: False

Two line segments may intersect at only one point. 

39. Many lines can pass through two given points. 

Ans: False

We know that only one line can pass through two given points. 

40. Only one line can pass through a given point.

Ans: False

Many lines can pass through a given point.

41. Two angles can have exactly five points in common.

Ans: False 

We know two angles can have one or two points in common.

42. Name all the line segments in Figure.

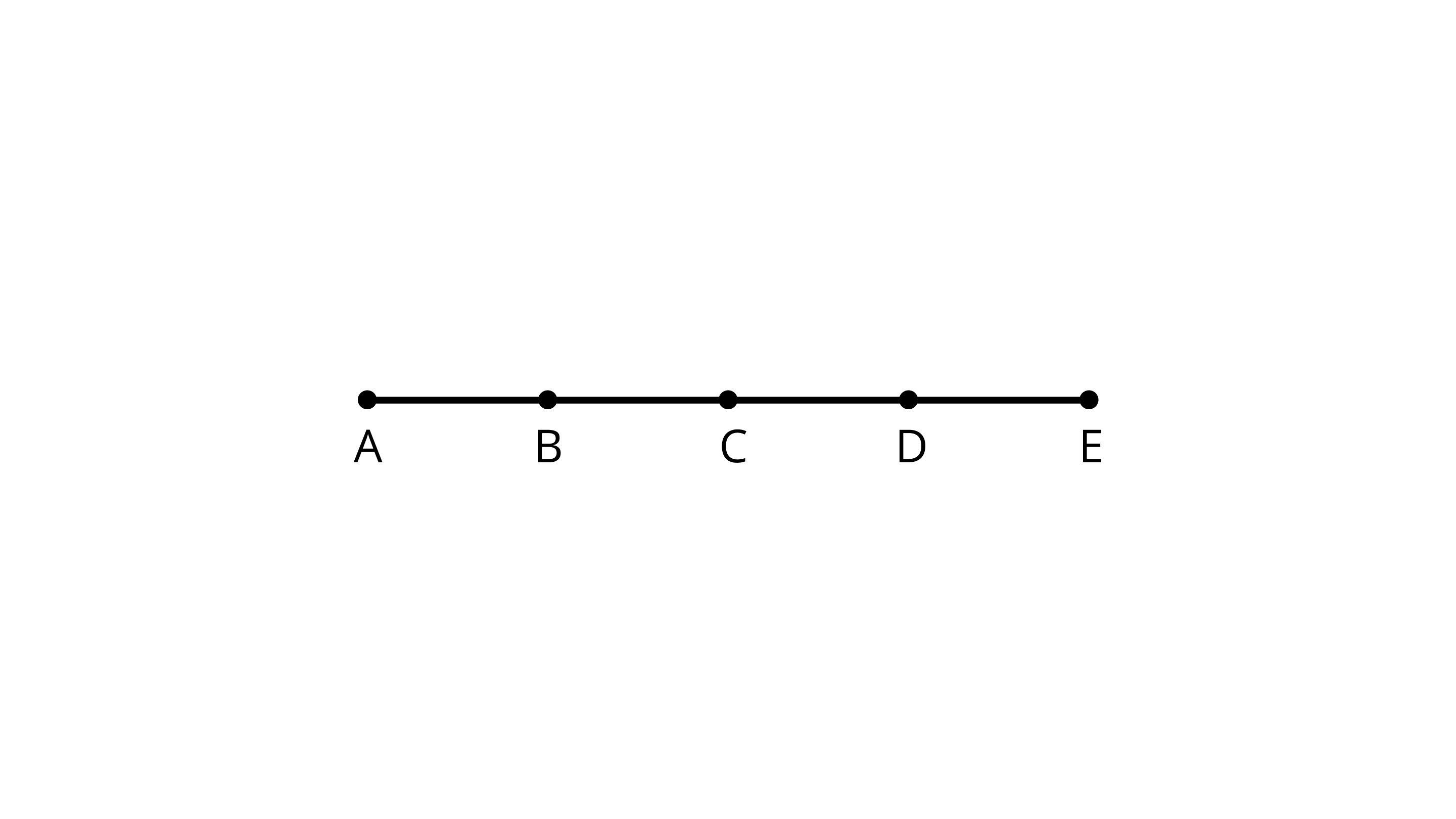
Ans: Line segments shown in the figure are AB, AC, CD, DE, BC, AD, BD, BE, CE, and AE.

43. Name the line segments shown in Figure.

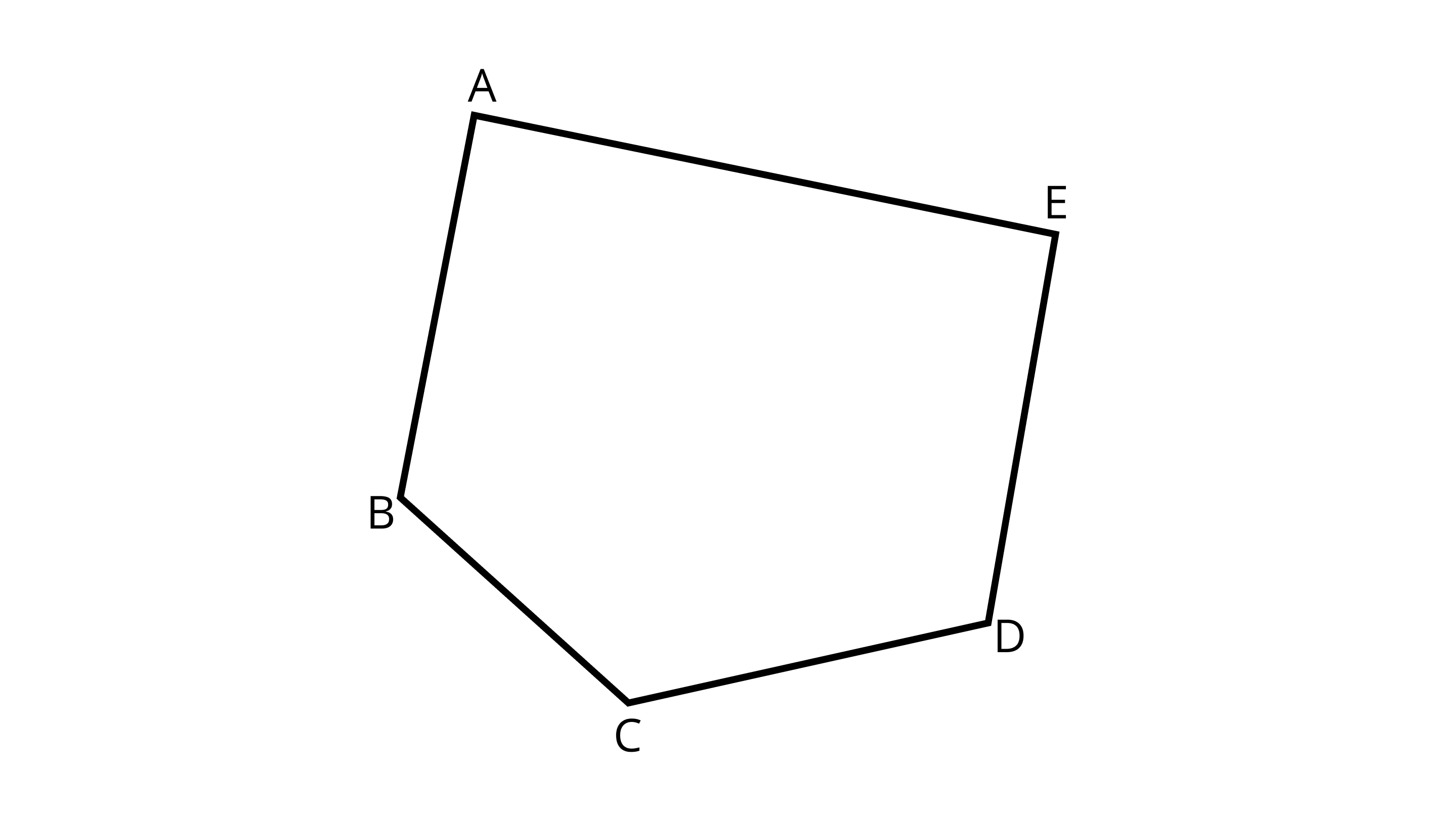
Ans: There are five line segments - AB, BC, CD, DE, and EA.

44. State the midpoints of all the sides of Figure.

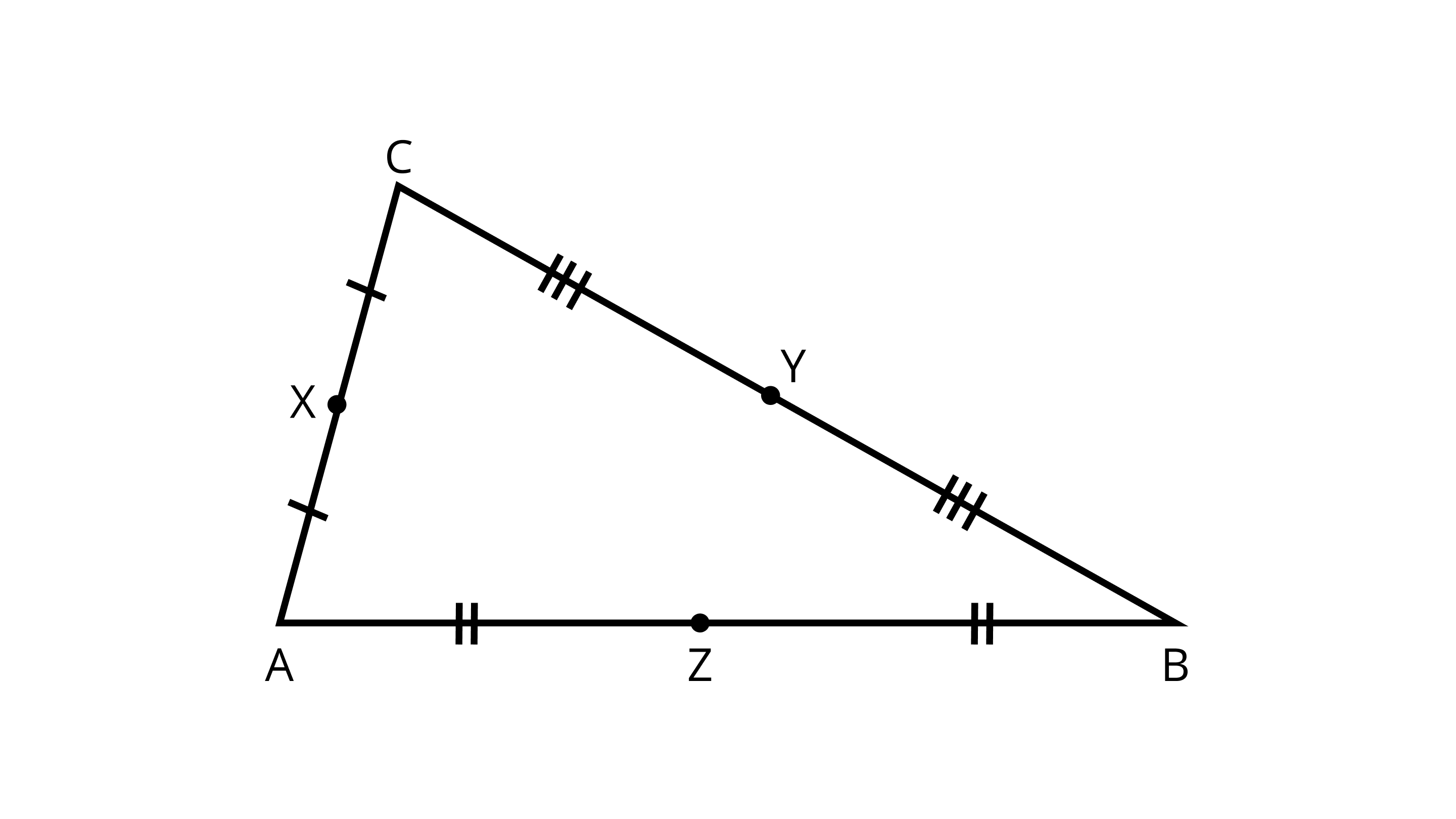
Ans: We know that the midpoint of a line divides it into two equal parts.

So, here Y, the midpoint of CB.

X, the midpoint of AC.

Z, the midpoint of AB.

45. Name the vertices and the line segments in Figure.

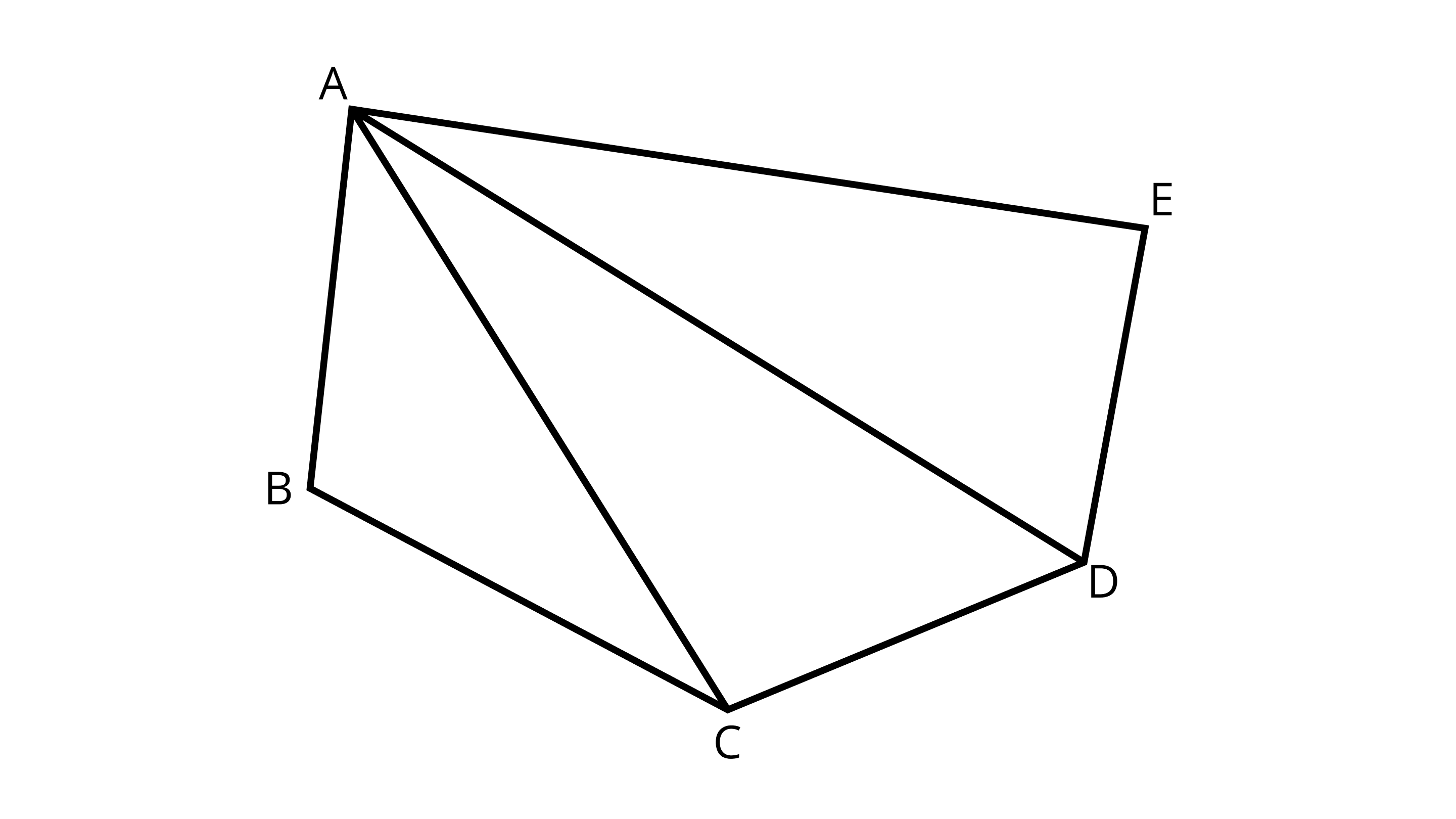
Ans: There are five vertices-A, B, C, D, and E.

There are seven line segments-  AB, BC, CD, DE, EA, AC, and AD.

46. Write down fifteen angles (less than $180^{\circ}$) in Figure.

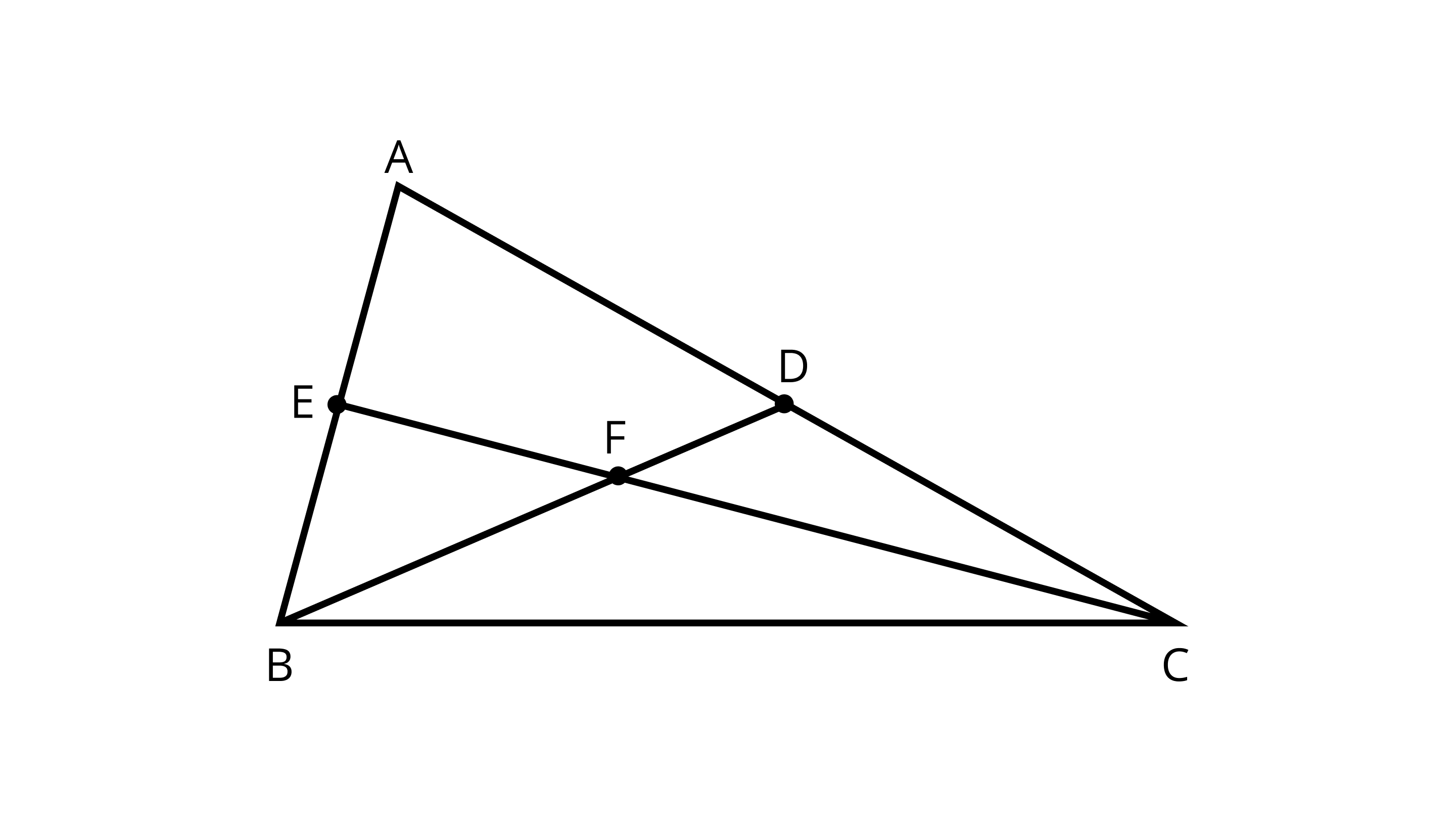
Ans: The fifteen angles- $\angle EAD$ ,$\angle AEF$,$\angle EFD$,$\angle ADF$,$\angle DFC$,$\angle DCF$,$\angle CDF$,$\angle BFE$,$\angle BEF$,$\angle EBF$,$\angle FCB$,$\angle FBC$,$\angle BFC$,$\angle ABC$ and $\angle ACS$.

47. Name the following angles of Figure, using three letters:

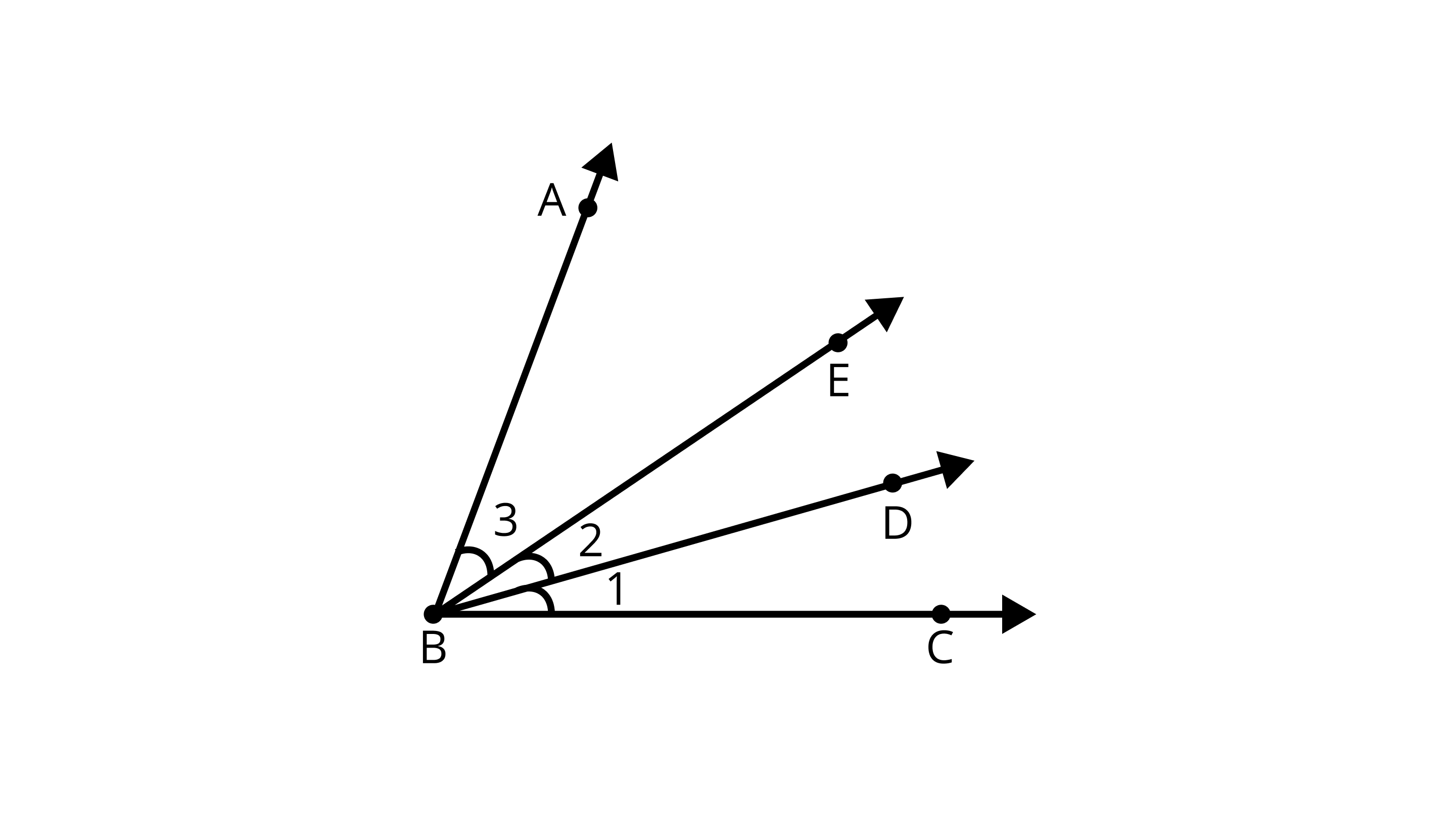
(a) $\angle 1$

Ans: $\angle 1$ = $\angle CBD$

(b) $\angle 2$ 

Ans: $\angle 2$ = $\angle DBE$

(c) $\angle 3$ 

Ans: $\angle 3$ = $\angle EBA$

(d) $\angle 1$ +$\angle 2$ 

Ans: $\angle 1$ +$\angle 2$= $\angle CBD$+$\angle DBE$=$\angle CBE$

(e) $\angle 2$ + $\angle 3$ 

Ans: $\angle 2$ +$\angle 3$= $\angle DBE$+$\angle EBA$=$\angle DBA$

(f)$\angle 1$ + $\angle 2$ + $\angle 3$ 

Ans: $\angle 1$ +$\angle 2$ + $\angle 3$ = $\angle CBD$+$\angle DBE$+ $\angle EBA$=$\angle ABC$

(g) $\angle CBA$ - $\angle 1$

Ans:  $\angle CBA$ - $\angle 1$= $\angle CBA$ - $\angle CBD$= $\angle ABD$

48. Name the points and then the line segments in each of the following figures (Figure)

Ans: Points are A, B, and C. 

Line Segments are AB, BC, and CA.

(ii)

Ans: Points are A, B, C, and D. 

Line segments are AB, BC, CD, and DA.

(iii)

Ans: Points are  A, B, C, D, and E. 

Line segments are  AB, BC, CD, DE, and EA.

(iv)

Ans: Points are  A, B, C, D, E, and F.

Line segments are  AB, CD, and EF.

49. Which points in the Figure, appear to be midpoints of the line segments? When you locate a midpoint, name the two equal line segments formed by it.

(i)

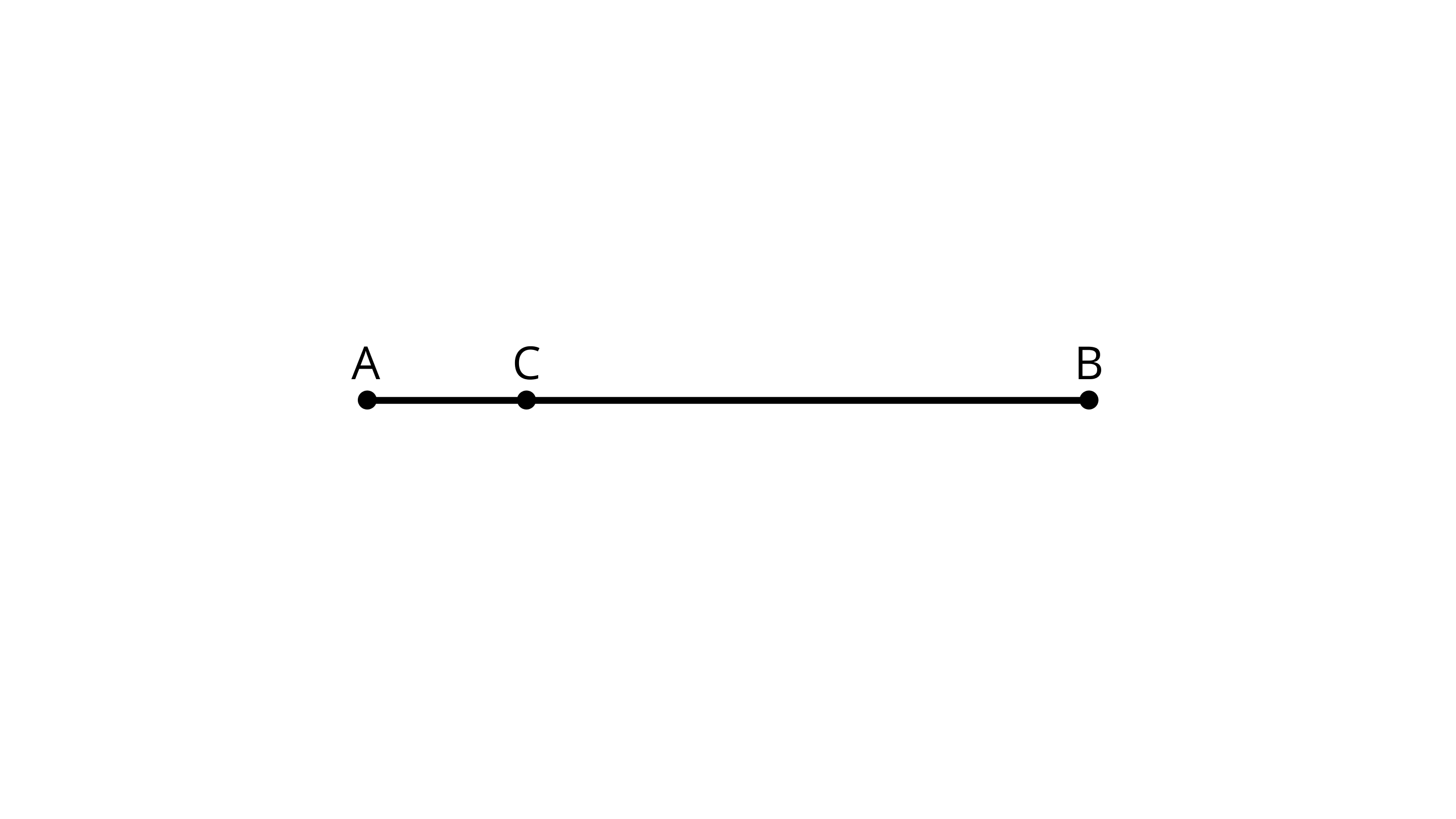
Ans: In this figure, there is no midpoint.

(ii) 

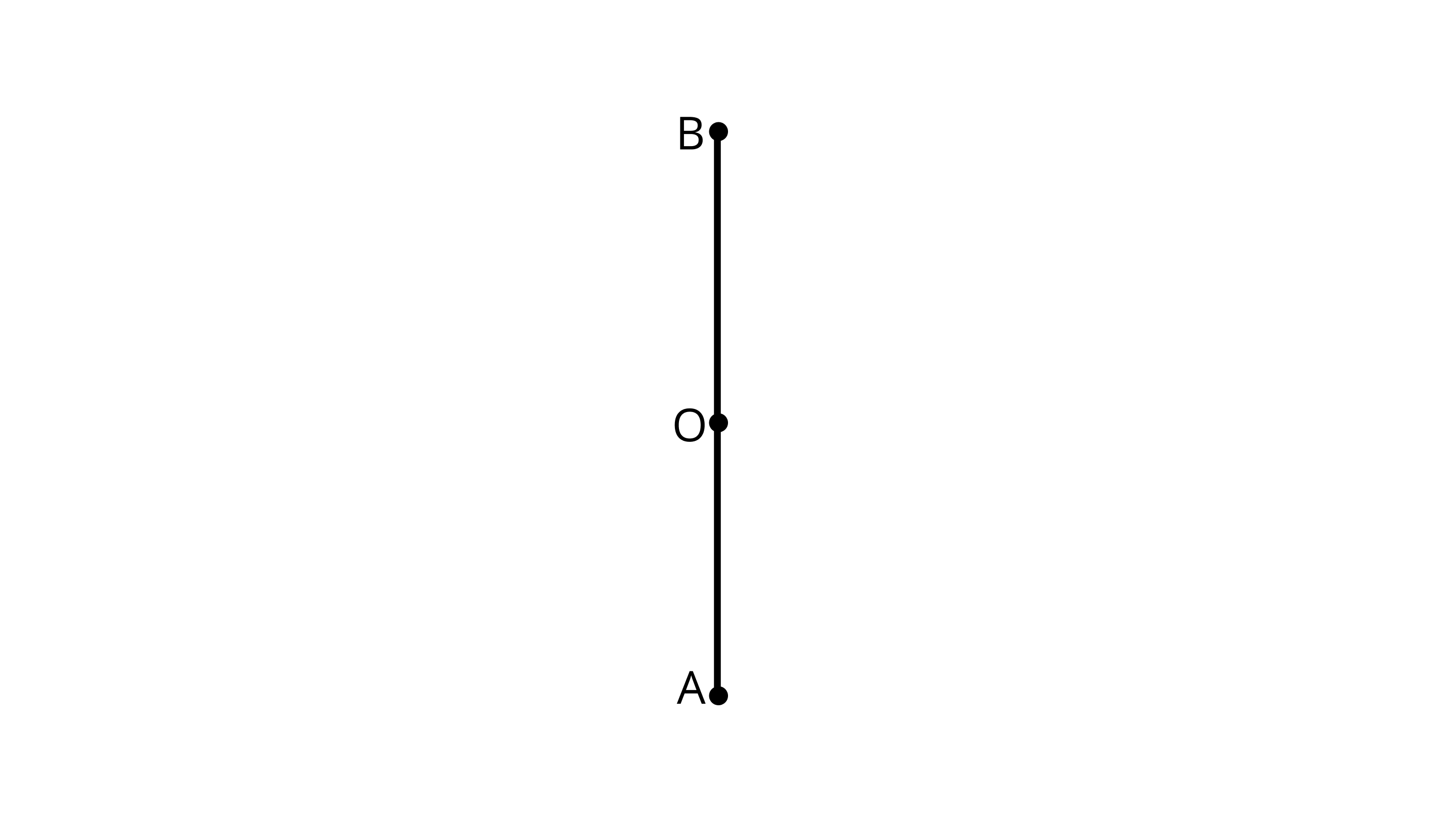
Ans: In this figure point O is the midpoint. 

Line sediments are OA and OB.

(iii)

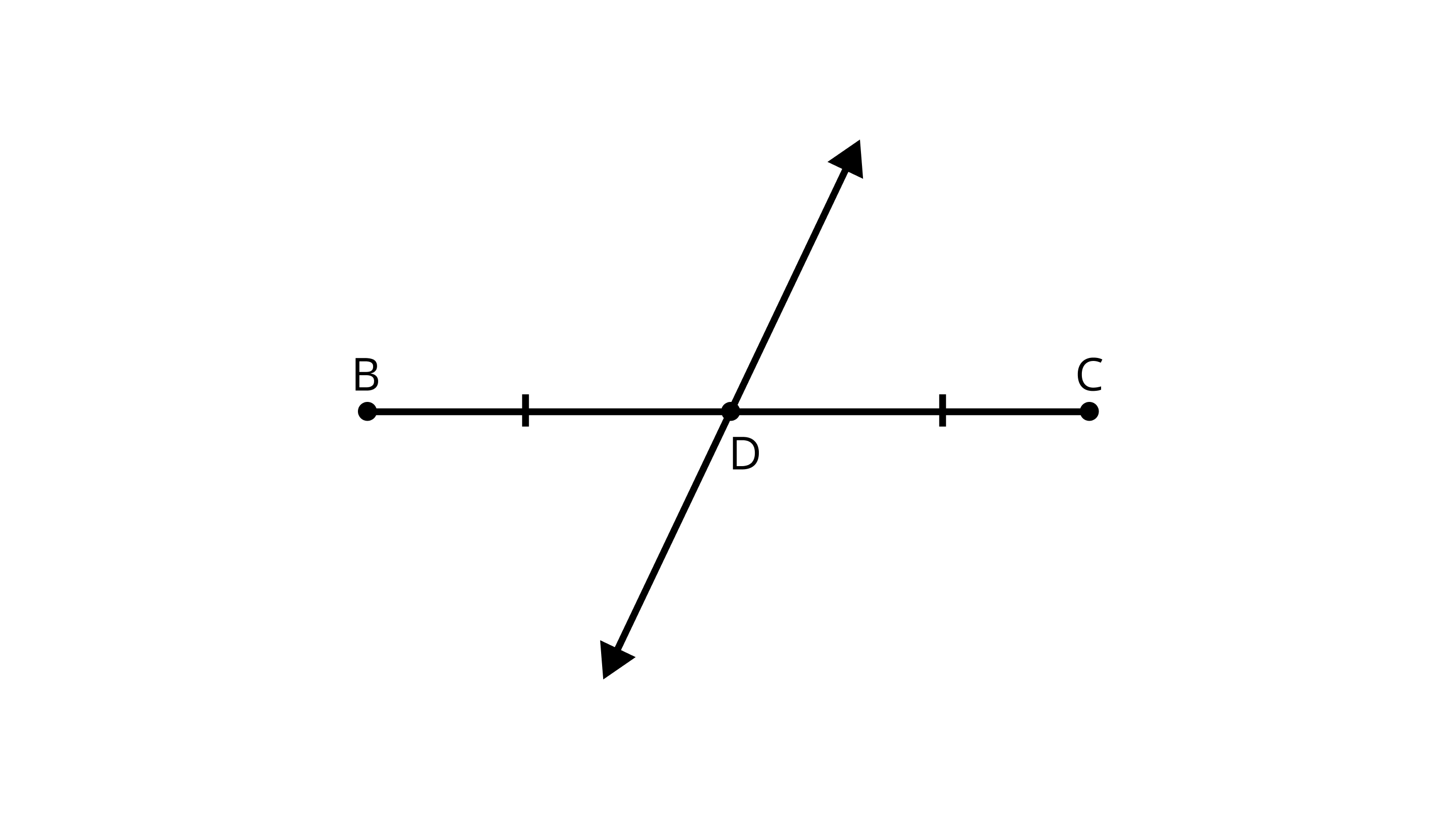
Ans: In this figure point  D is the  midpoint

Line segments are BD and DC. 

50. Is it possible for the same

(a) Line segment to have two different lengths?

Ans:  No, it is not possible that the same line segments have two different lengths.

(b) Angle to have two different measures?

Ans:  No, it is not possible that the same angles have two different measures.

51. Will the measure of $\angle ABC$ and of $\angle CBD$ make the measure of $\angle ABD$  in Figure.

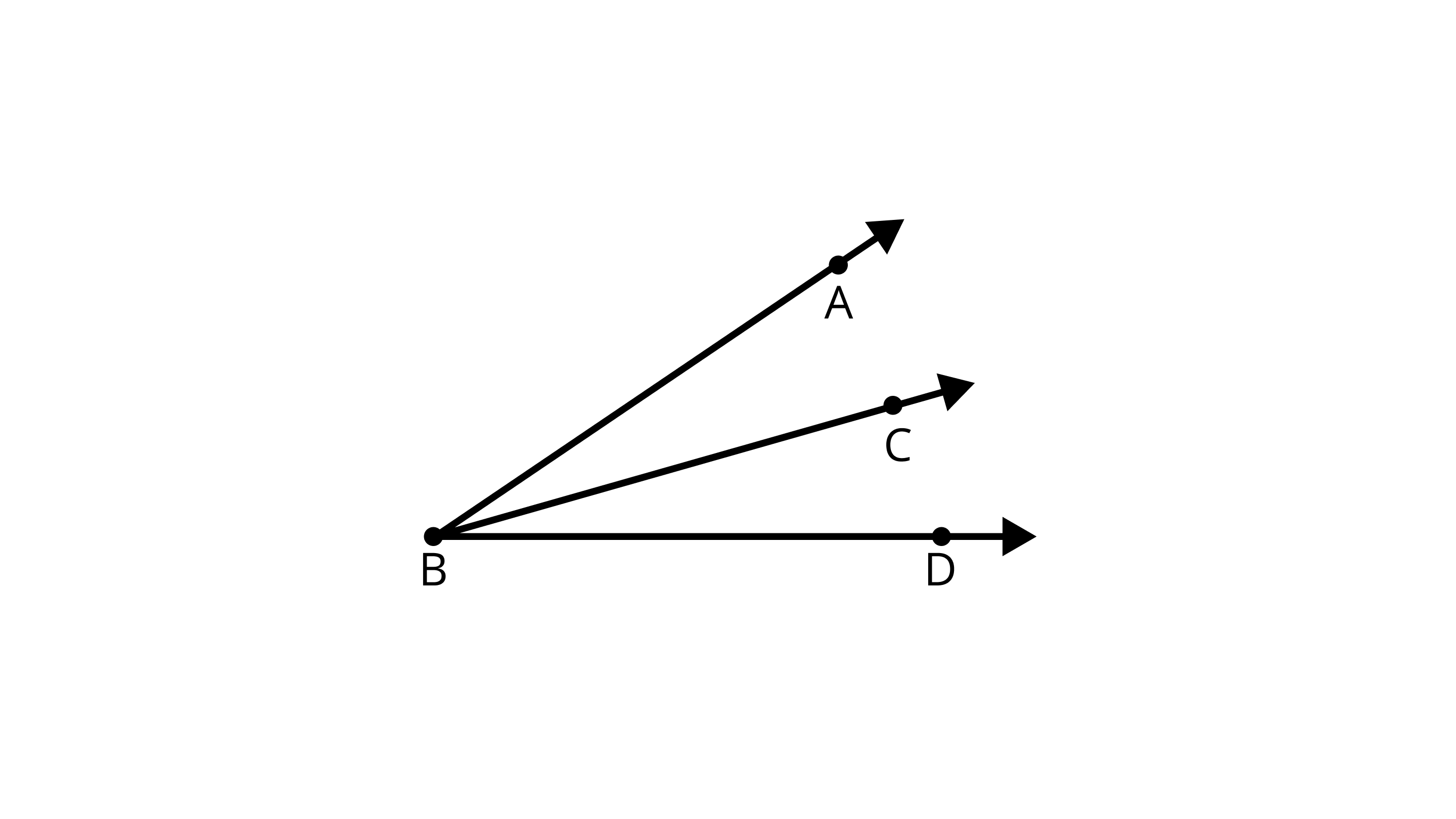
Ans: Yes, because $\angle ABD$ = $\angle ABC$ + $\angle CBD$

 $\angle ABC$  and $\angle CBD$ together form $\angle ABD$.

52. Will the lengths of line segment AB and line segment BC make the length of line segment AC in Figure?

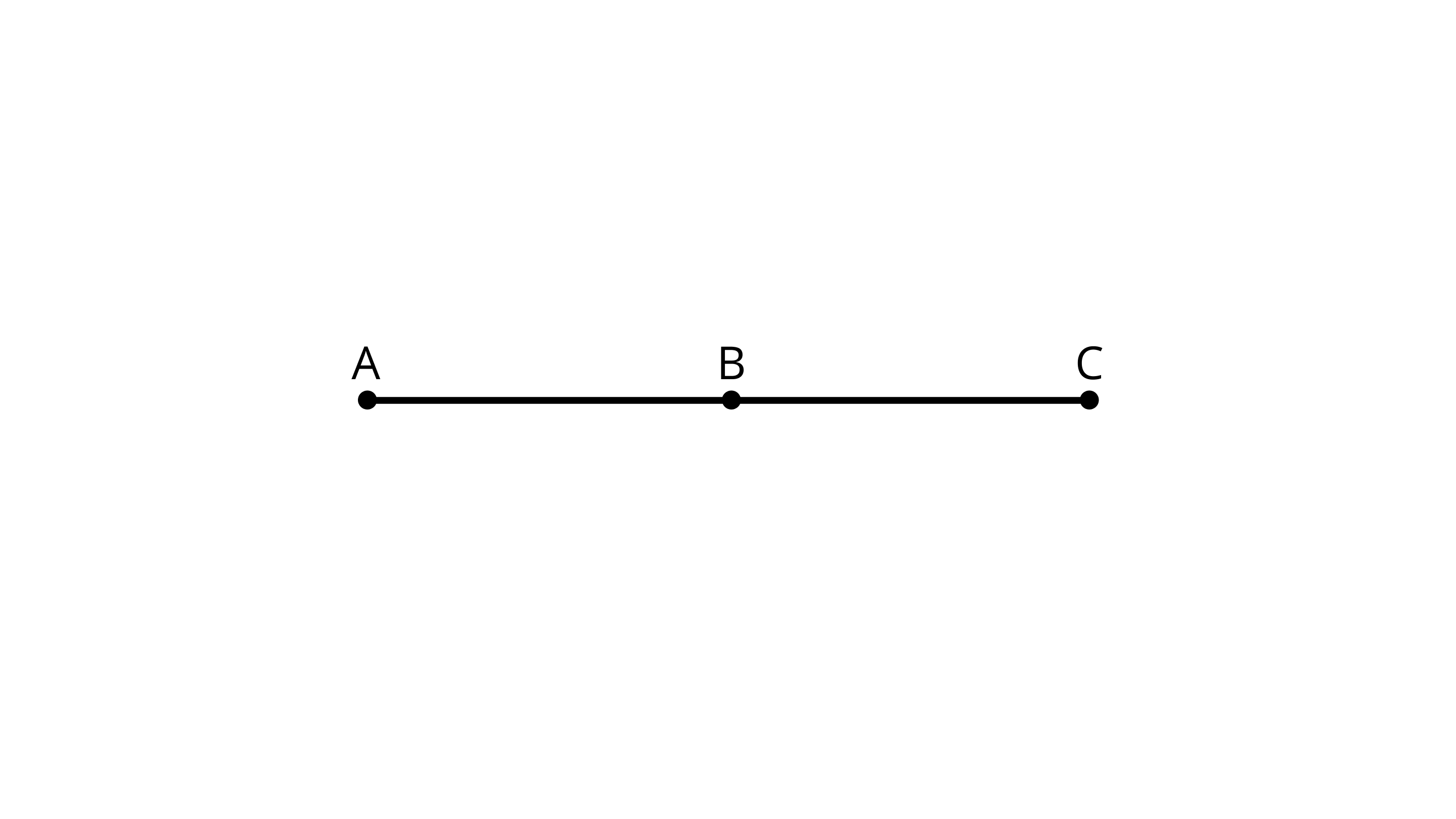
Ans: Yes, because AC=AB + BC

AB and BC together form the length of line segment AC

53. Draw two acute angles and one obtuse angle without using a protractor. Estimate the measures of the angles. Measure them with the help of a protractor and see how much accurate is your estimate?

Ans: Two acute angles are-

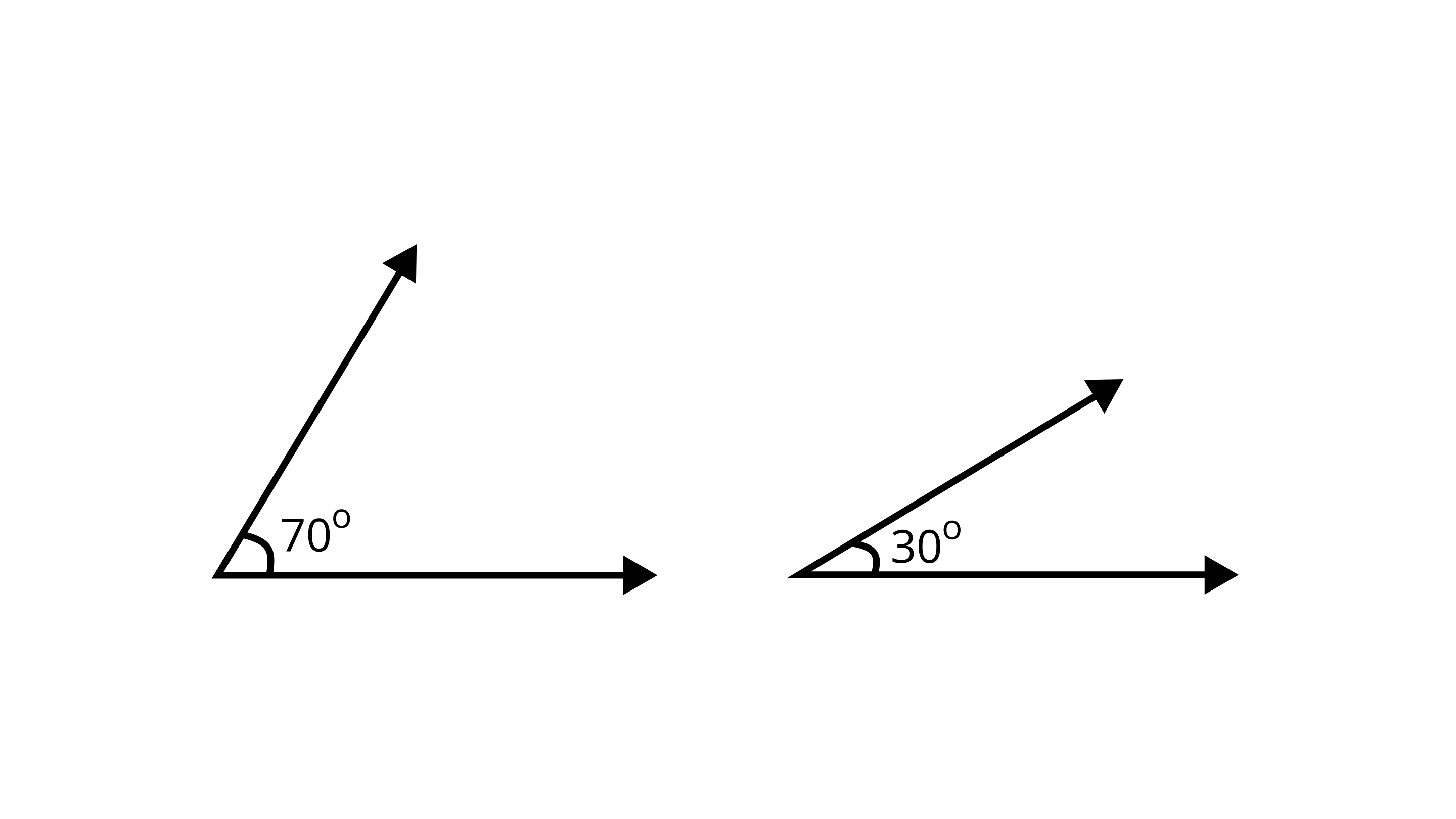
One obtuse angle is-

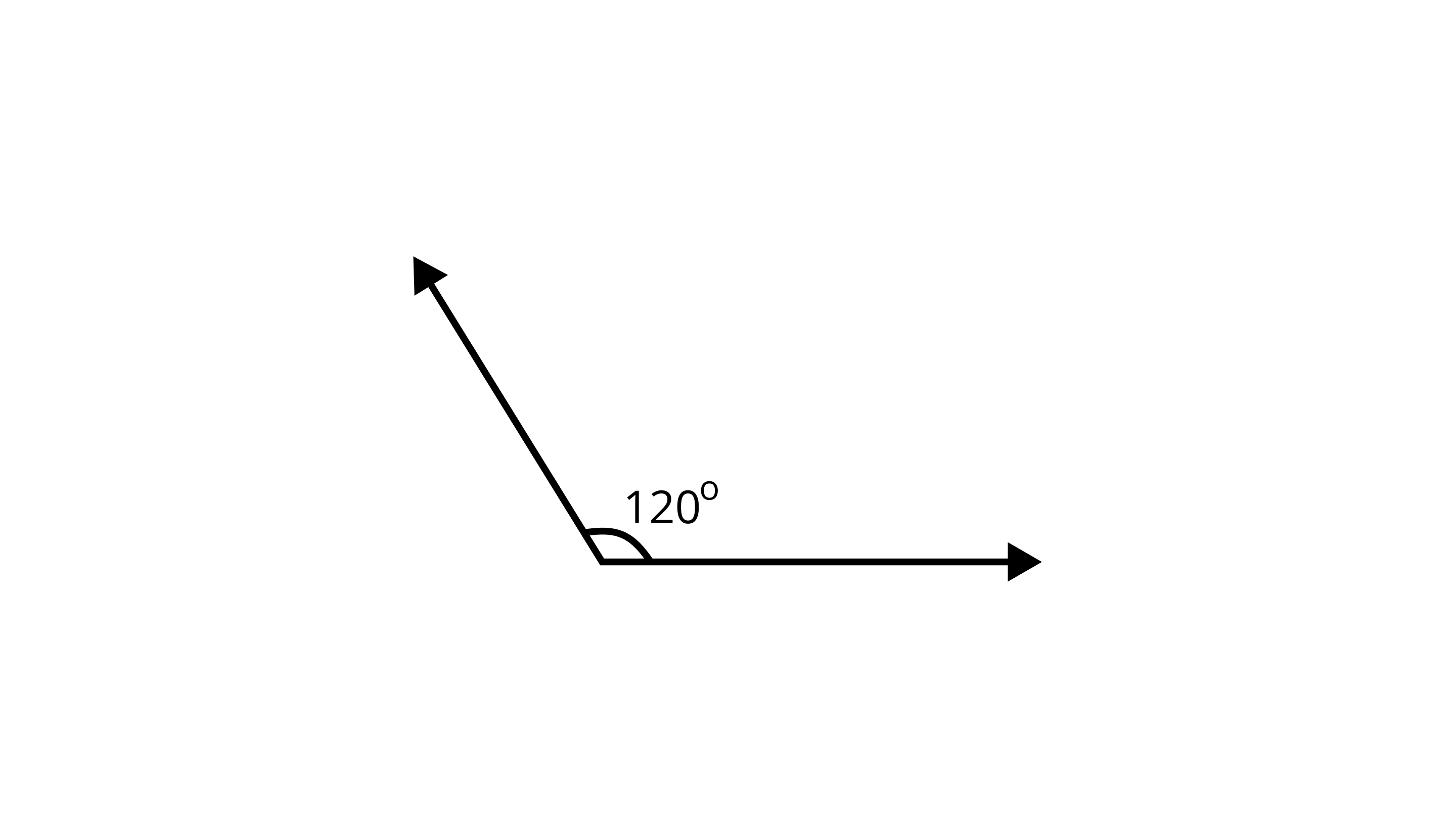
When measured with the help of a protractor, two acute angles are - $70^{\circ}$,$30^{\circ}$ and the obtuse angle is- $120^{\circ}$.

54. Look at Figure Mark a point

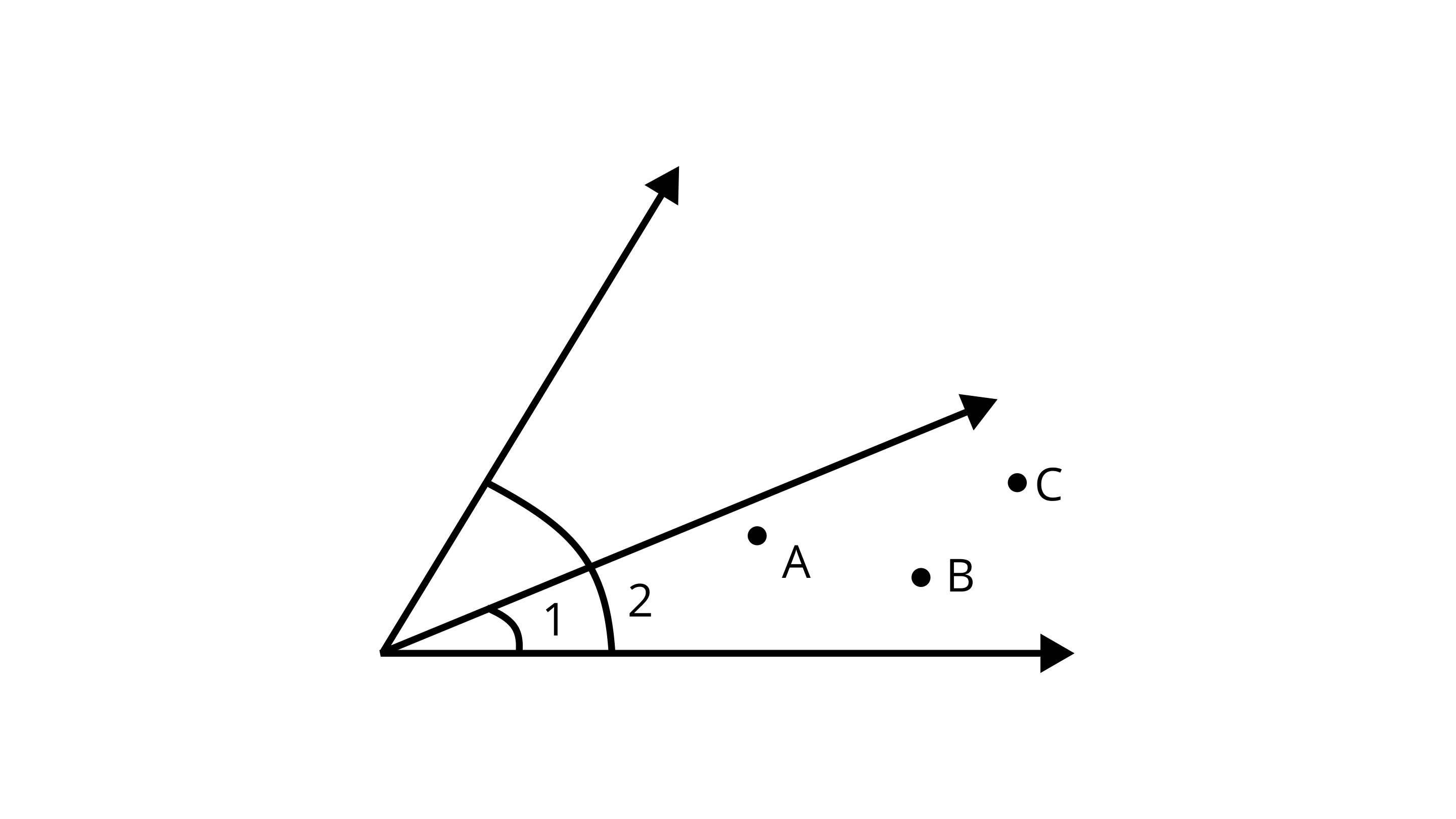
(a) A which is in the interior of both $\angle 1$  and $\angle 2$.

(b) B which is in the interior of only $\angle 1$.

(c) Point C in the interior of $\angle 1$.

Now, state whether points B and C lie in the interior of $\angle 2$ also.

Ans: Yes, because $\angle 1$ is in the interior of  $\angle 2$.Points B and C lie in the interior of $\angle 2$ also.

55. Find out the incorrect statement, if any, in the following:

An angle is formed when we have

(a) Two rays with a common end-point

Ans: Correct. Two rays with a common endpoint form an angle.

(b) Two line segments with a common end-point

Ans: Incorrect.

(c) A ray and a line segment with a common end-point

Ans: Incorrect.

56. In which of the following figures (Figure).

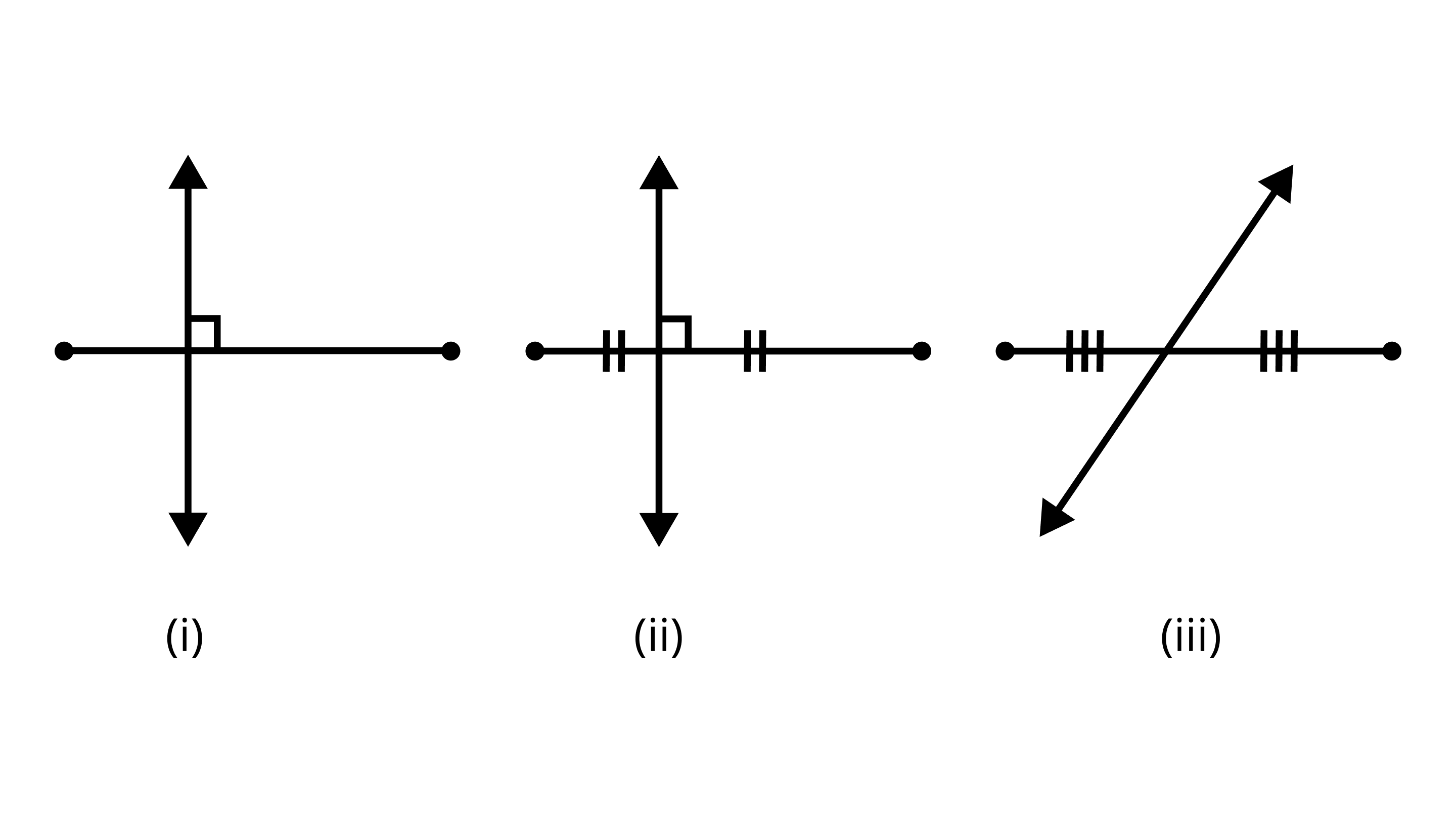
(a) A perpendicular bisector is shown?

Ans: Figure (ii) represents a perpendicular bisector.

(b) The bisector is shown?

Ans: Figure (ii) and (iii) represent bisectors.

(c) The only bisector is shown?

Ans:  Figure (iii) represents only the bisector.

(d) The only perpendicular is shown?

Ans: Figure (i) represents only perpendicular.

57. What is common in the following figures (i) and (ii)?

Is Figure (i) that of the triangle? If not, why?

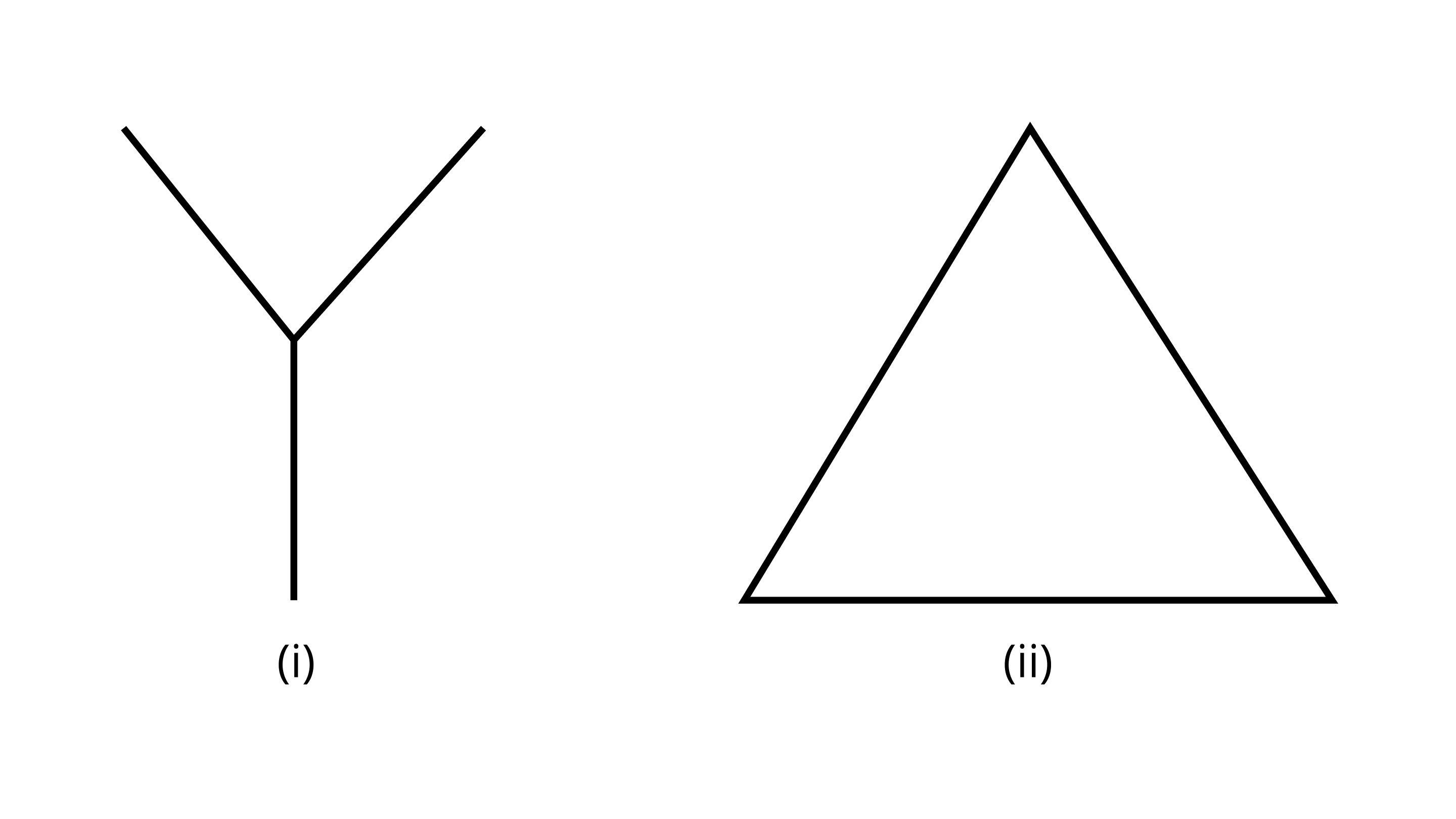
Ans: Figure (i) and (ii) have 3 line segments.

Figure (i) is not a triangle because it is not a closed figure.

58. If two rays intersect, will their point of intersection be the vertex of an angle of which the rays are the two sides?

Ans: Yes, If two rays intersect, their point of intersection will be the vertex of an angle. 

59. In Figure.

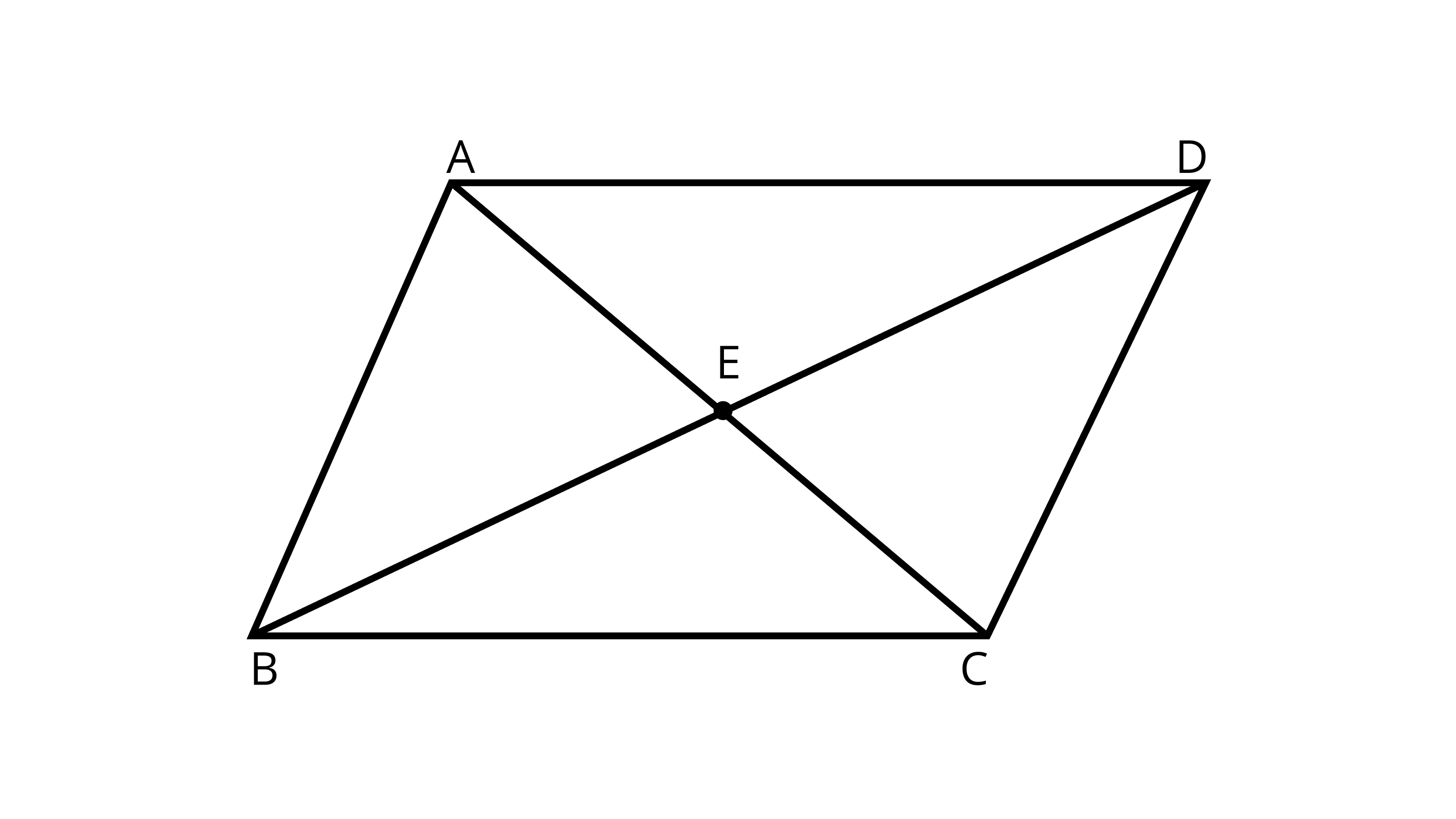
(a) Name any four angles that appear to be acute angles.

Ans: 4 acute angles - $\angle EDA$,$\angle EAD$, $\angle ABE$  and $\angle EBC$.

(b) Name any two angles that appear to be obtuse angles.

Ans: Obtuse angles - $\angle BAD$ and $\angle BCD$ .

60. In Figure.

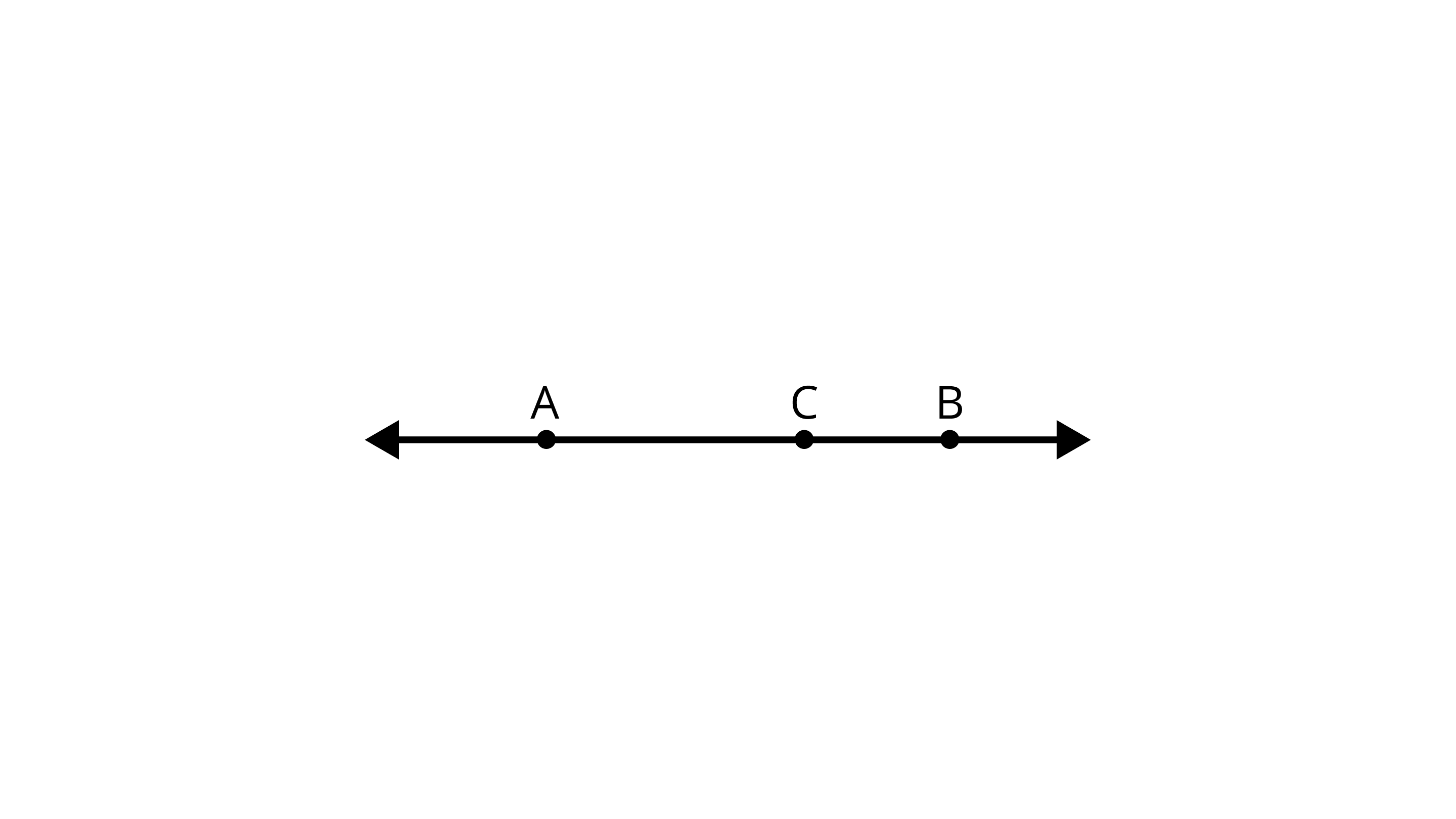
(a) Is AC + CB = AB?

Ans: Yes, it is possible.

(b) Is AB + AC = CB?

Ans: No, it is not possible.

(c) Is AB + BC = CA?

Ans: No, it is not possible.

61. In Figure.

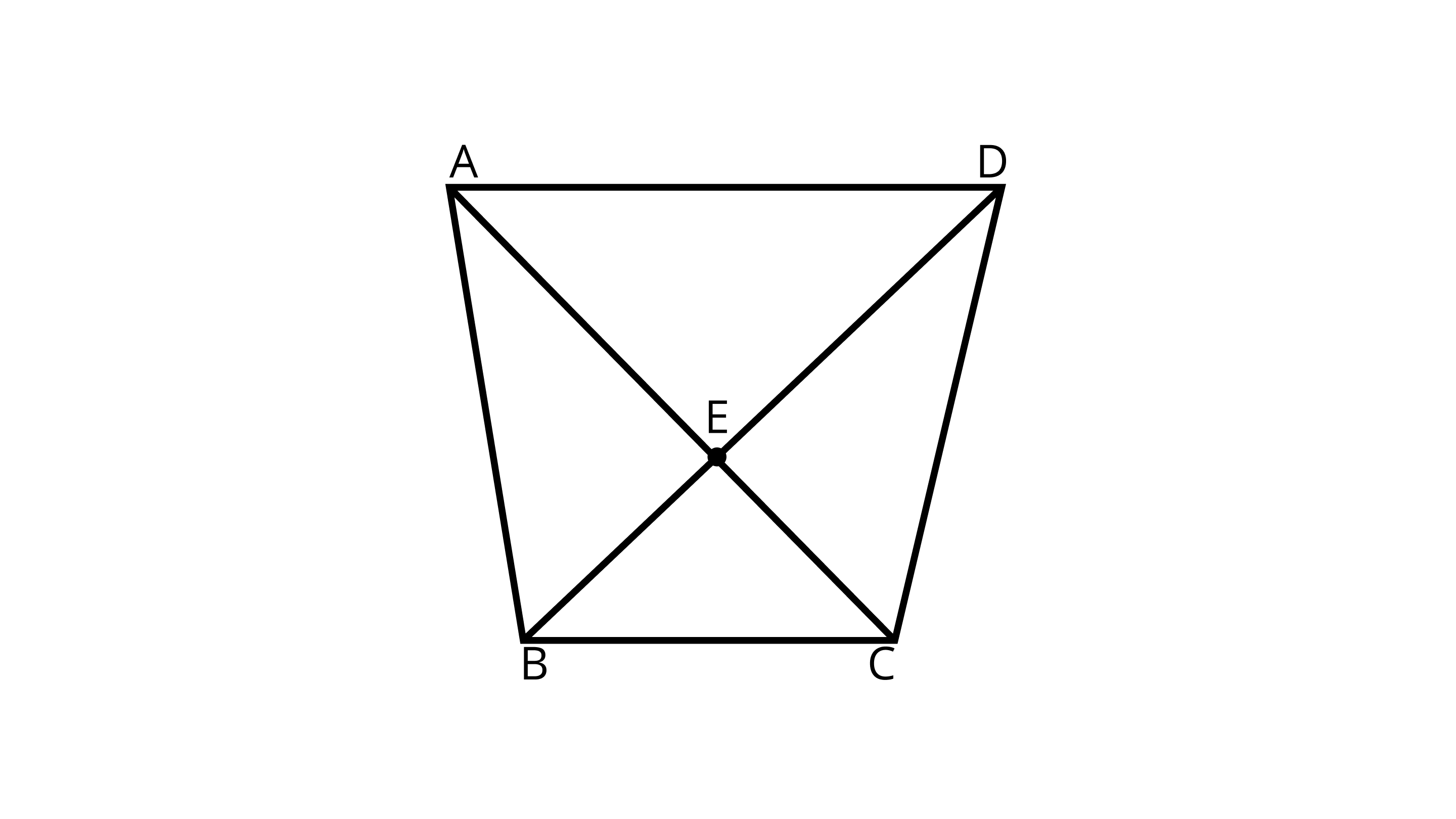
(a) What is AE+ EC? 

Ans: AE+EC = AC

(b) What is AC-EC?

Ans: AC-EC = AE

(c) What is BD - BE?

Ans: BD-BE = ED

(d) What is BD-DE?

Ans: BD-DE = BE

62. Using the information given, name the right angles in each part of Figure.

(a) BA$\perp$ BD

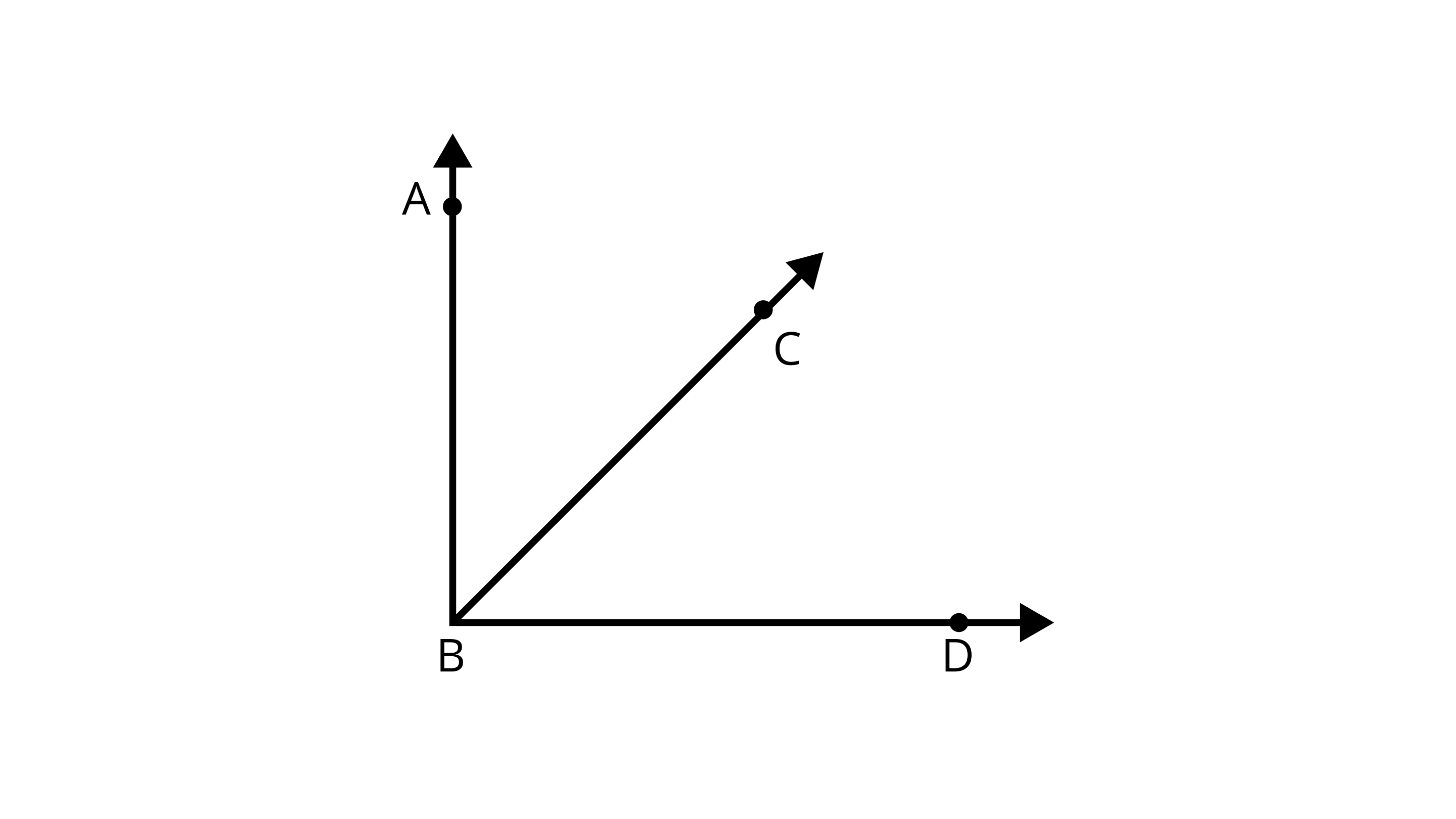
Ans: $\angle ABD$ because of BA$\perp$ BD.

(b) RT$\perp$  ST

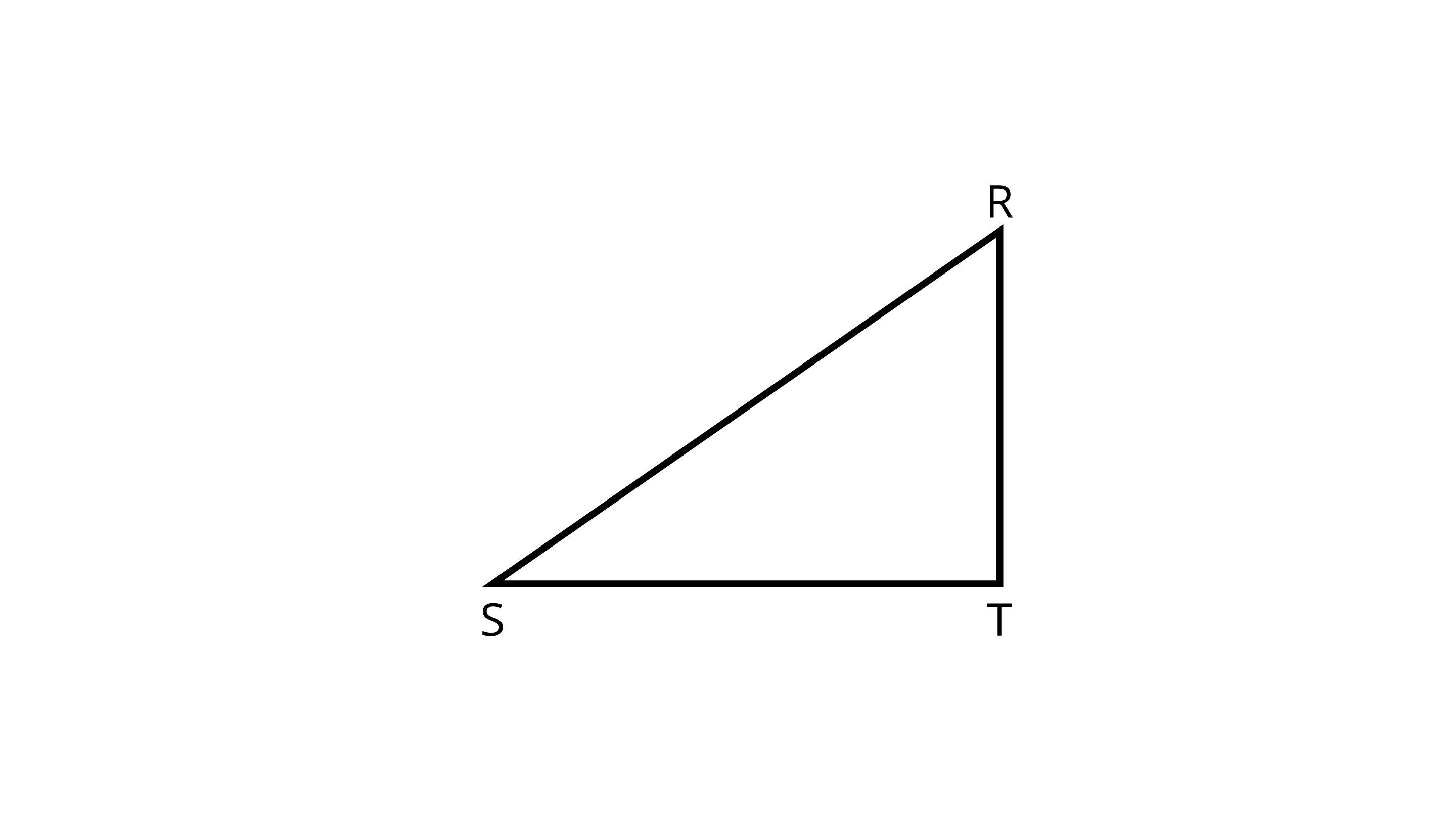
Ans: $\angle RTS$ because  RT$\perp$ ST.

(c) AC$\perp$  BD

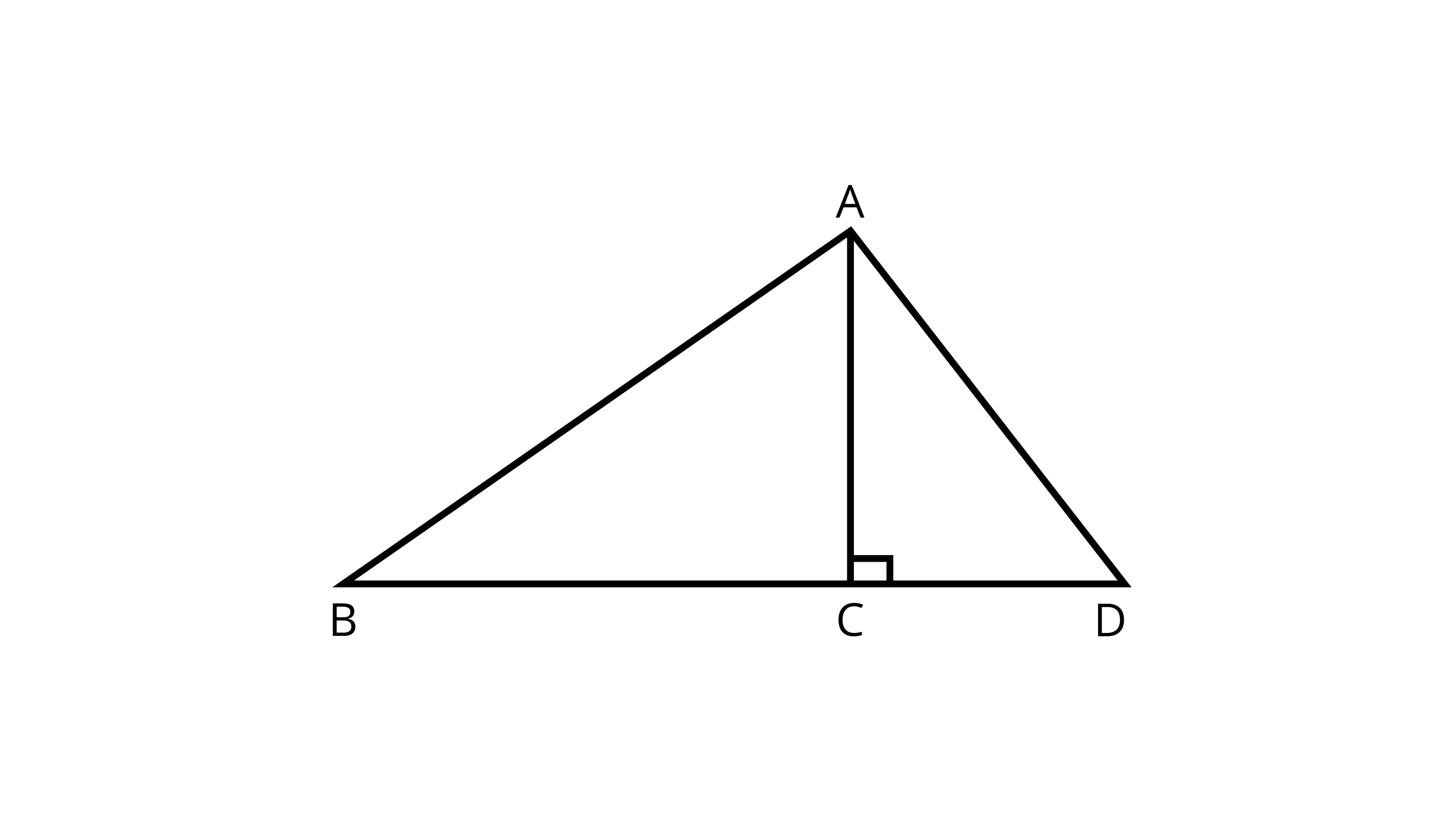
Ans:$\angle ACD$ because of AC$\perp$ BD.

(d) RS$\perp$  RW

Ans: $\angle RTW$ and $\angle RTS$ because of RT$\perp$ SW.

(e) AC $\perp$  BD

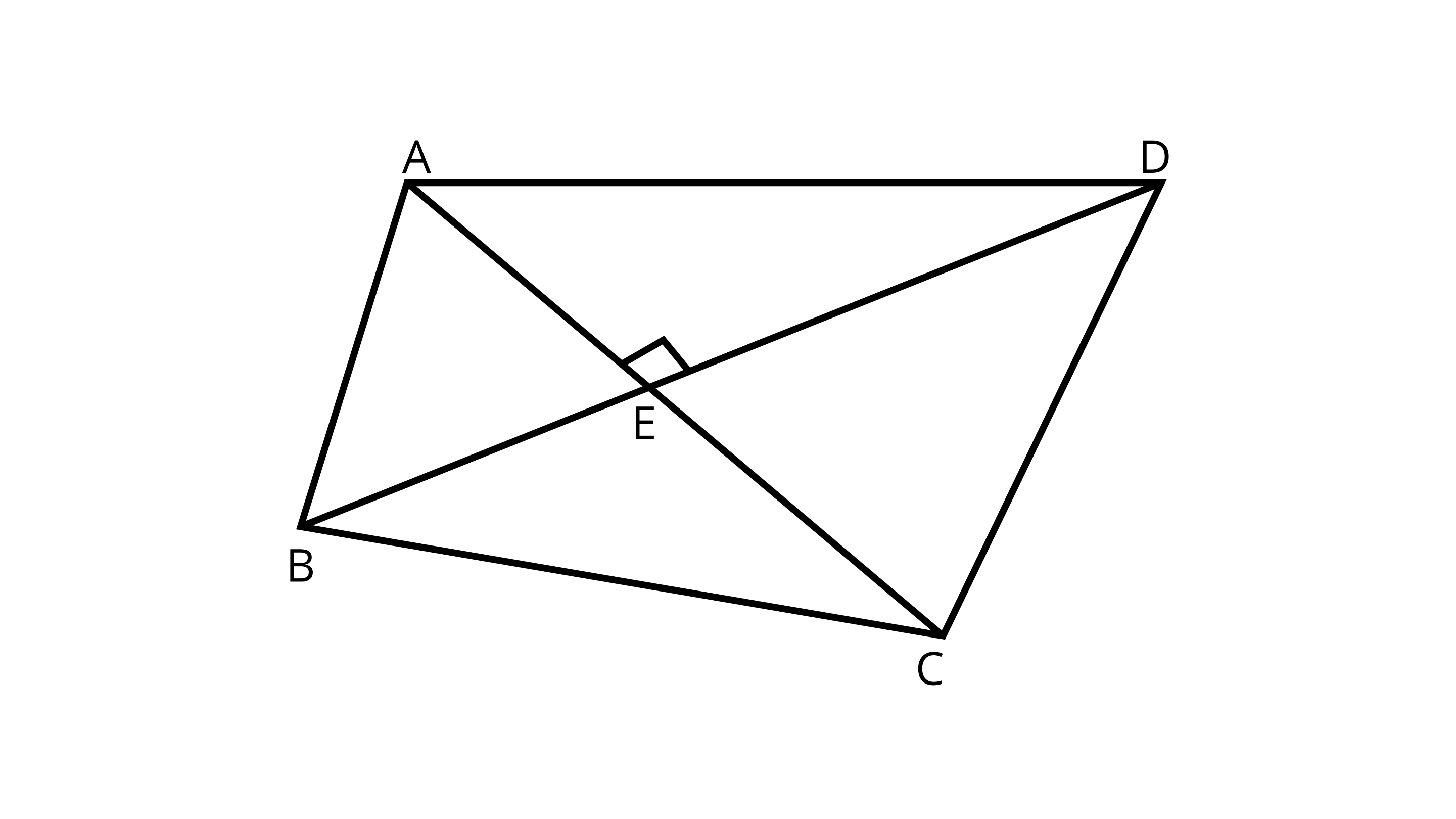
Ans: $\angle AED$,$\angle AEB$,$\angle BEC$ and $\angle DEC$  because of AC$\perp$ BD.

(f) AE $\perp$ CE

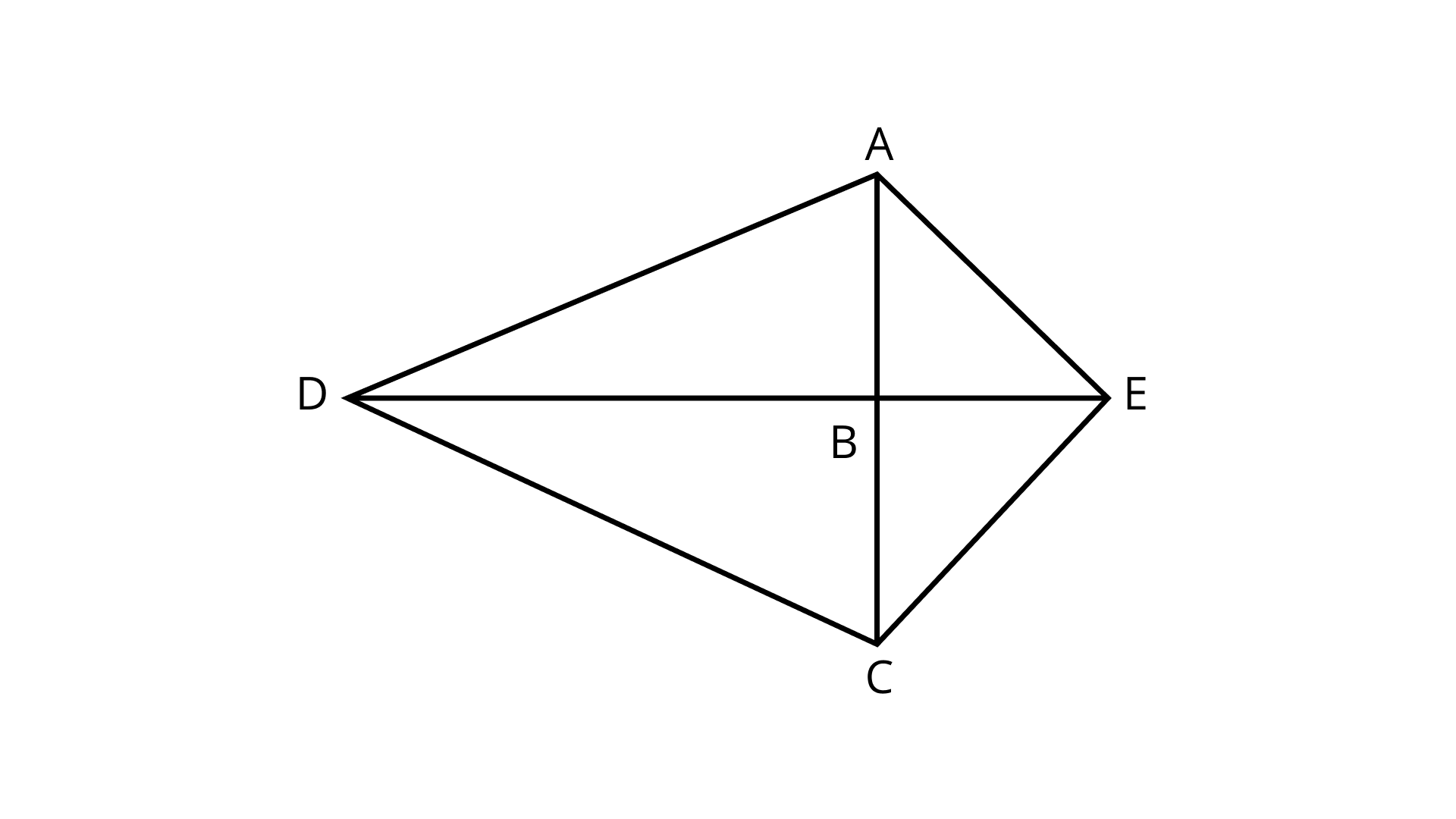
Ans: $\angle AEC$ because of AE$\perp$ CE.

(g) AC $\perp$  CD

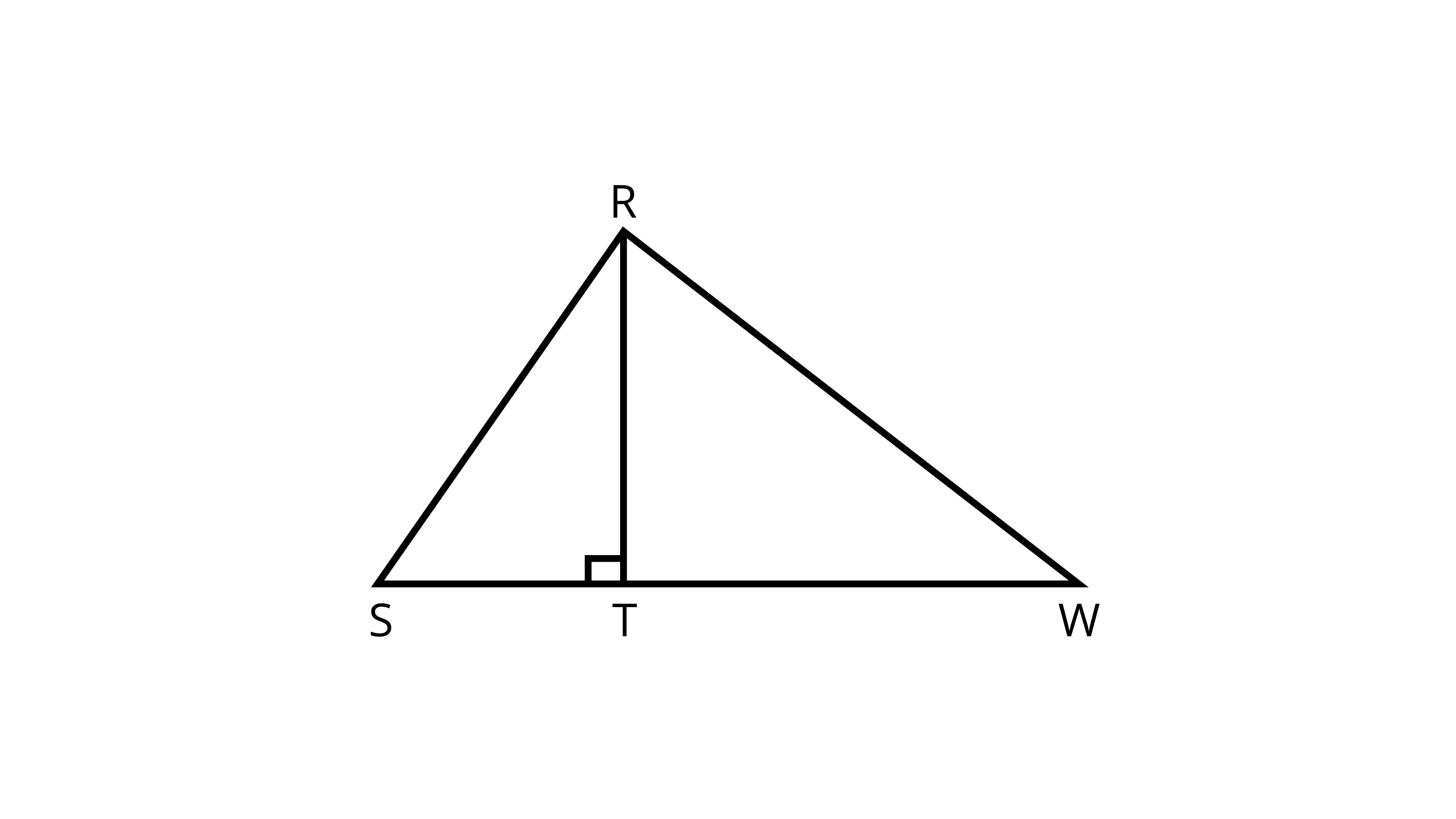
Ans: $\angle ACD$ because  AC$\perp$ CD.

(h) OP $\perp$  AB

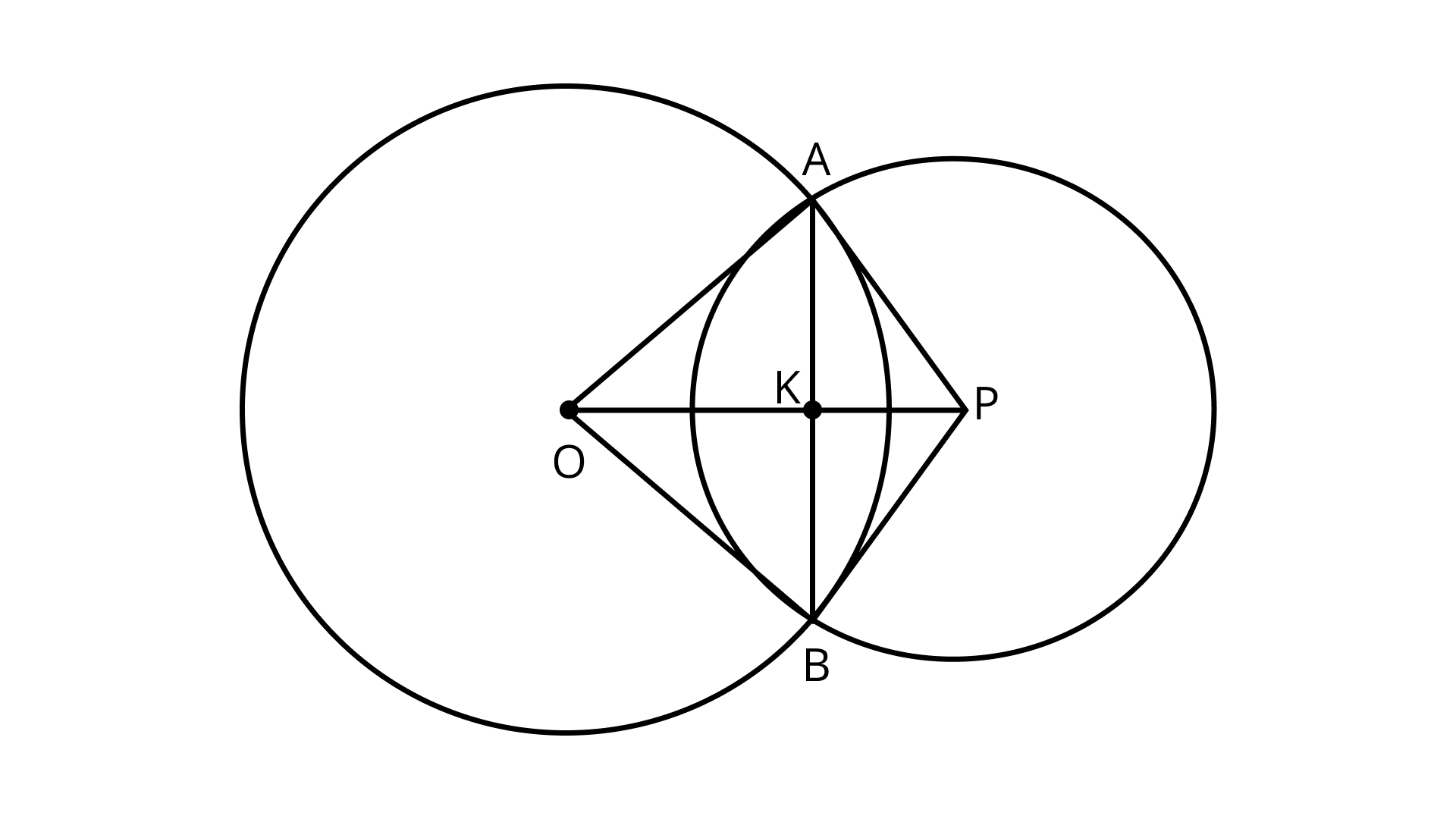
Ans: $\angle AKO$, $\angle AKP$, $\angle BKO$ and $\angle BKP$ because  OP$\perp$ AB.

63. What conclusion can be drawn from each part of the Figure.

(a) DB is the bisector of $\angle ADC$?

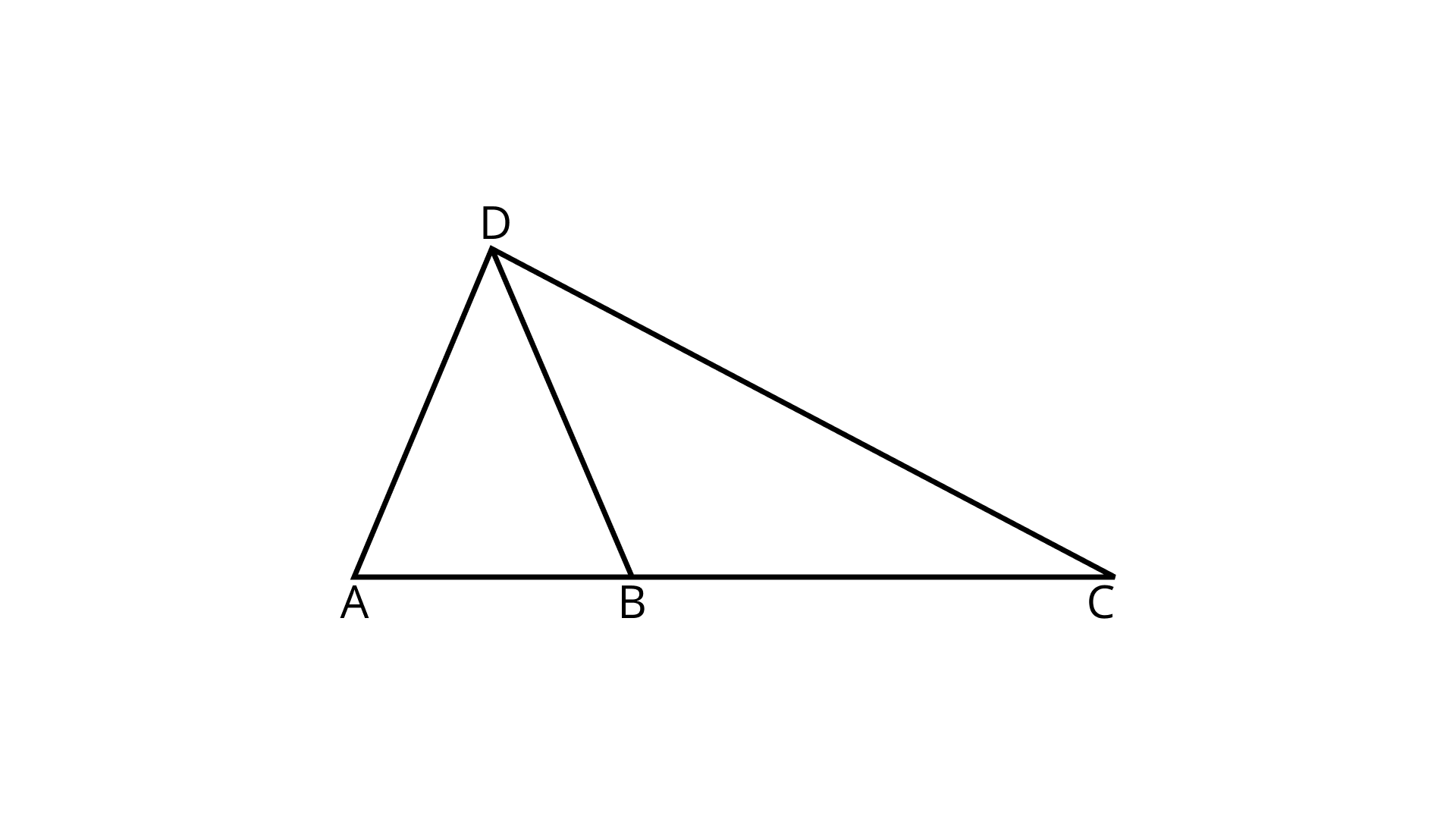
Ans: If DB is the bisector of $\angle ADC$,then $\angle ADB$ = $\angle CDB$.

(b) BD bisects $\angle ABC$?

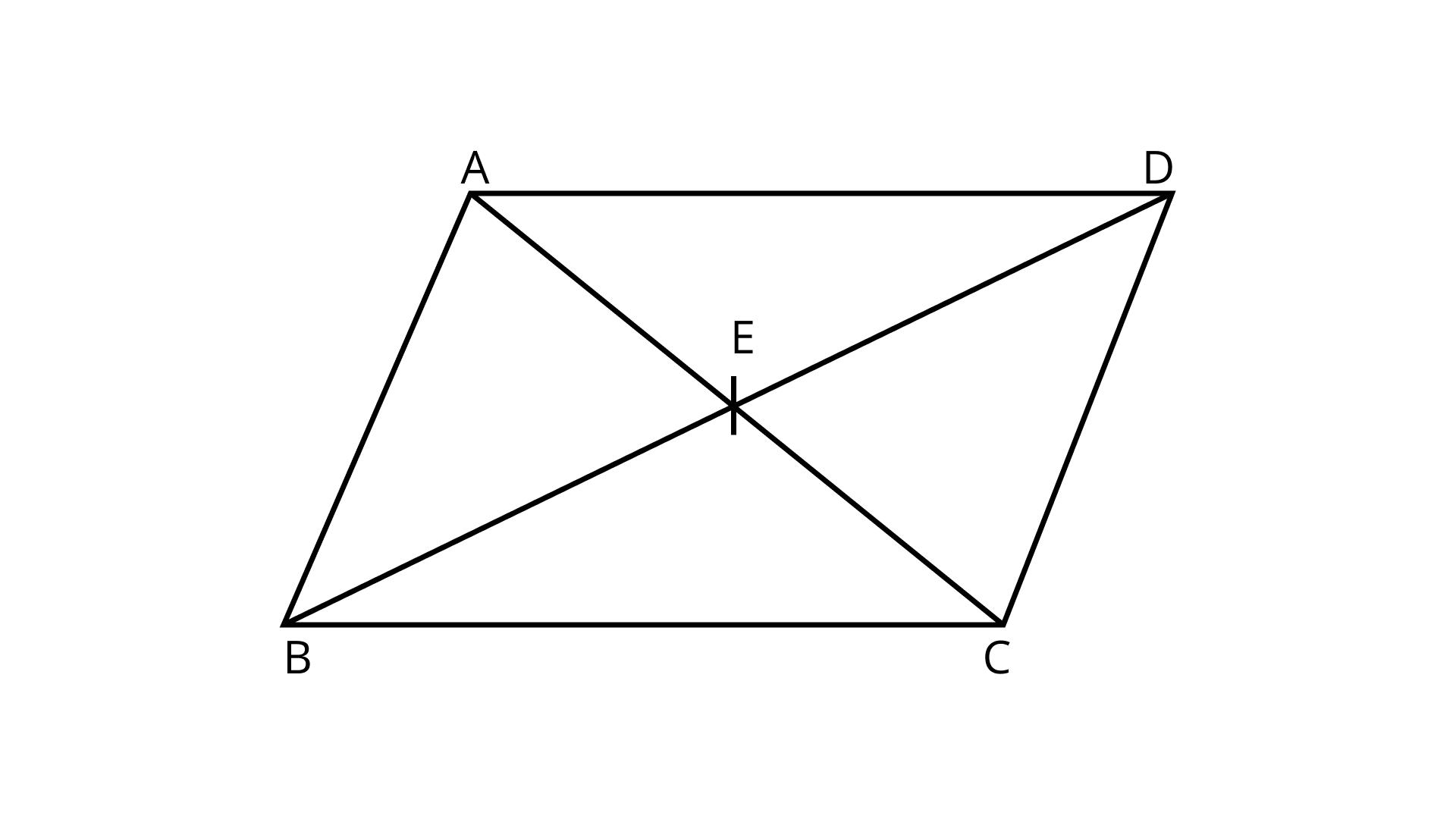
Ans: If BD is the bisector of $\angle ABC$,then $\angle ABD$ = $\angle CBD$.

(c) DC is the bisector of $\angle ADB$, CA $\perp$ DA, and CB $\perp$ DB?

Ans: If DC is the bisector of $\angle ADB$,then $\angle ADC$ = $\angle BDC$. Also 

$\angle CAD$=$\angle CBD$=$90^{\circ}$

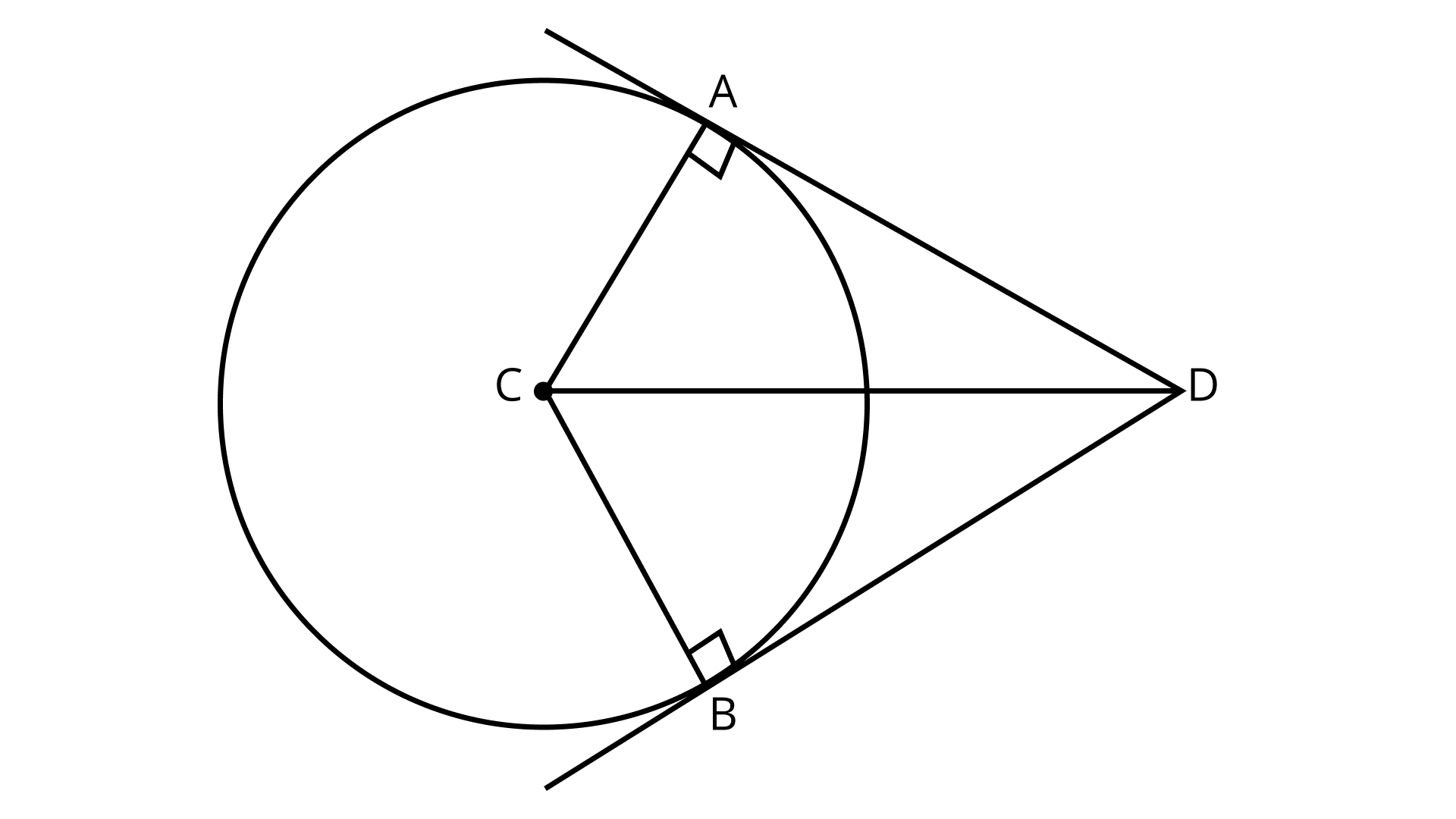
64. An angle is said to be trisected if it is divided into three equal parts. If in Figure.  $\angle BAC$ = $\angle CAD$=$\angle DAE$, how many trisections are there for $\angle BAE$?

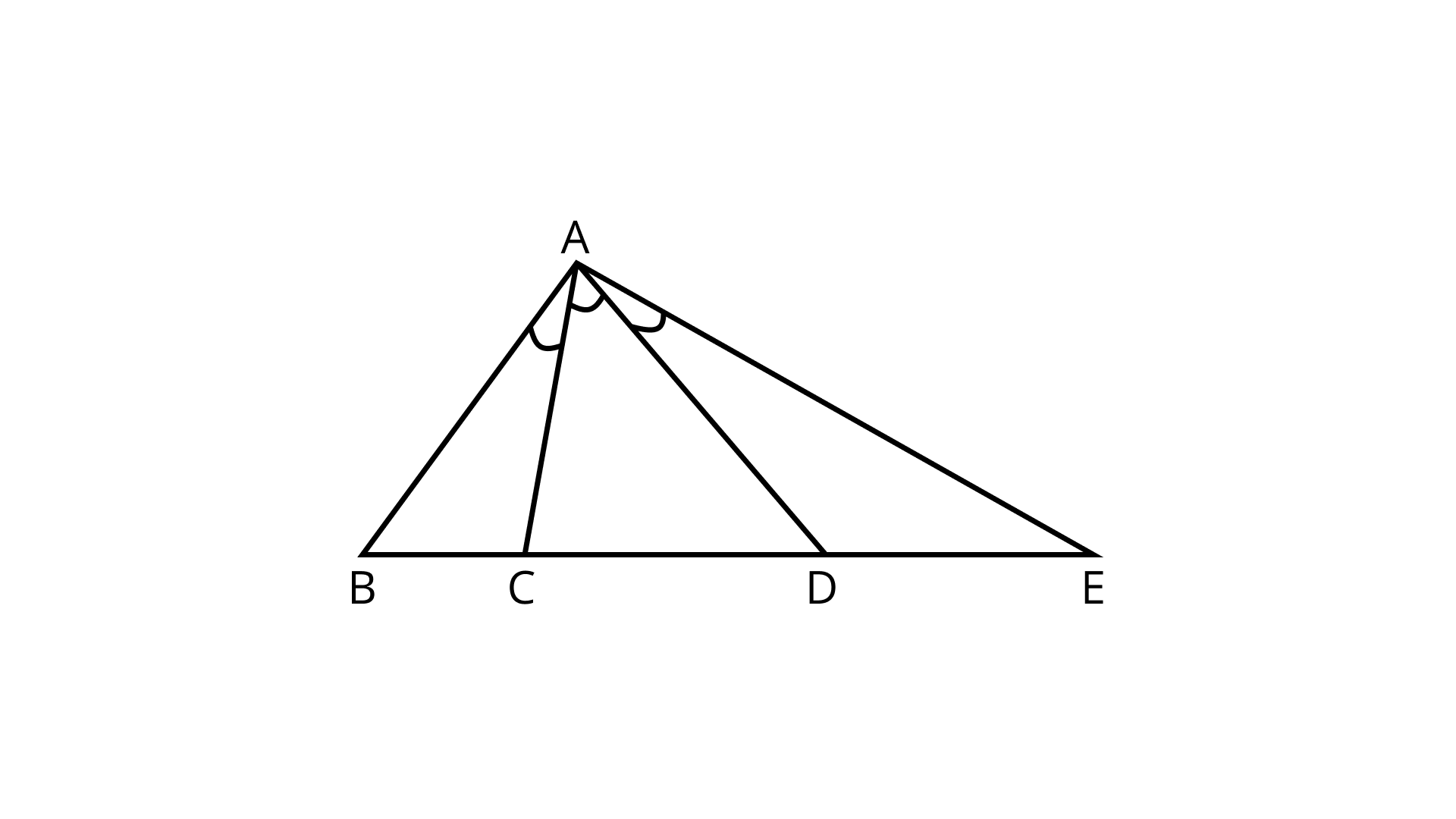
Ans: There are only two trisections namely - AC, AD.

65. How many points are marked in Figure?

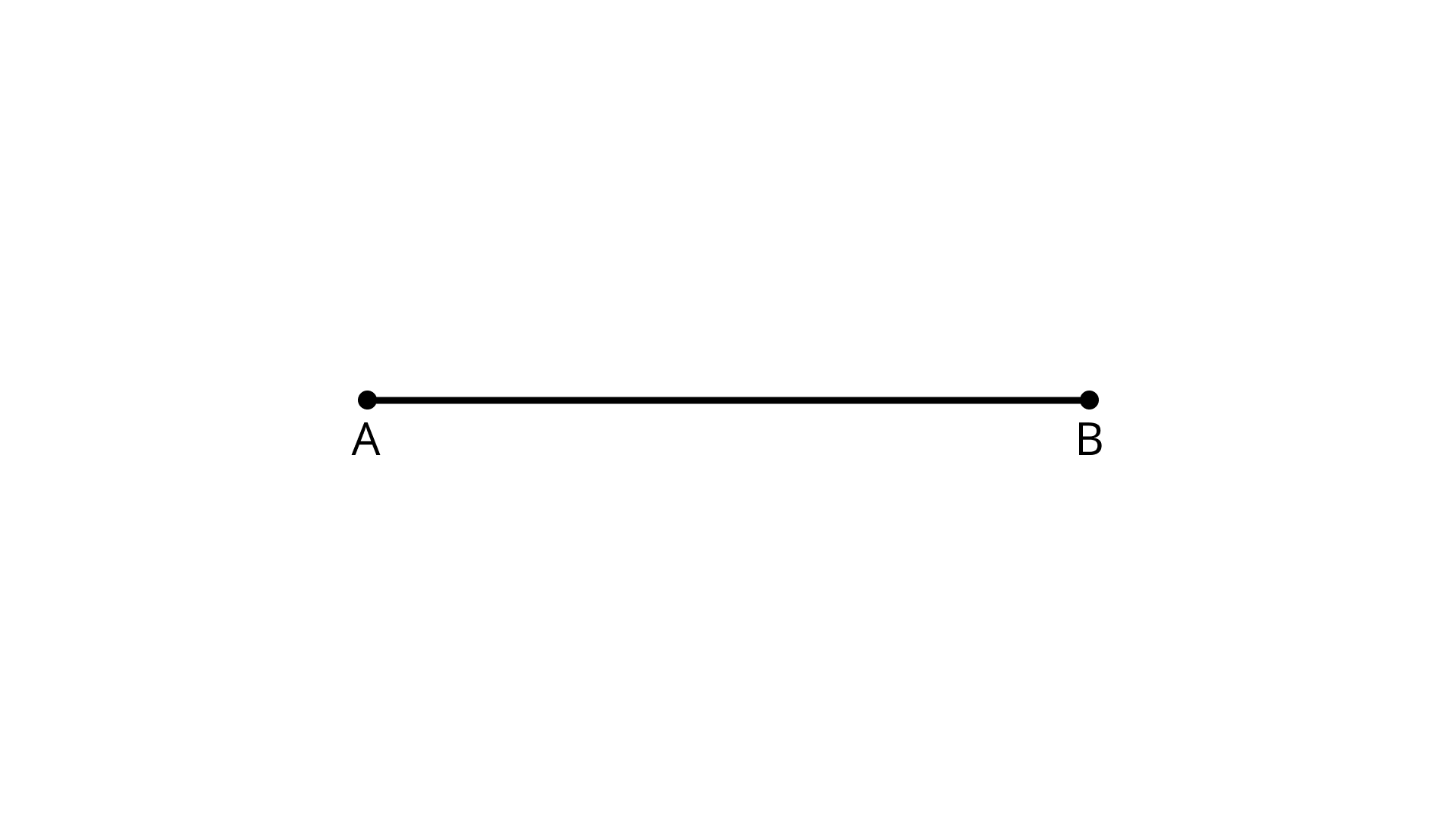
Ans: There are two points namely - A and B.

66. How many line segments are there in Figure?

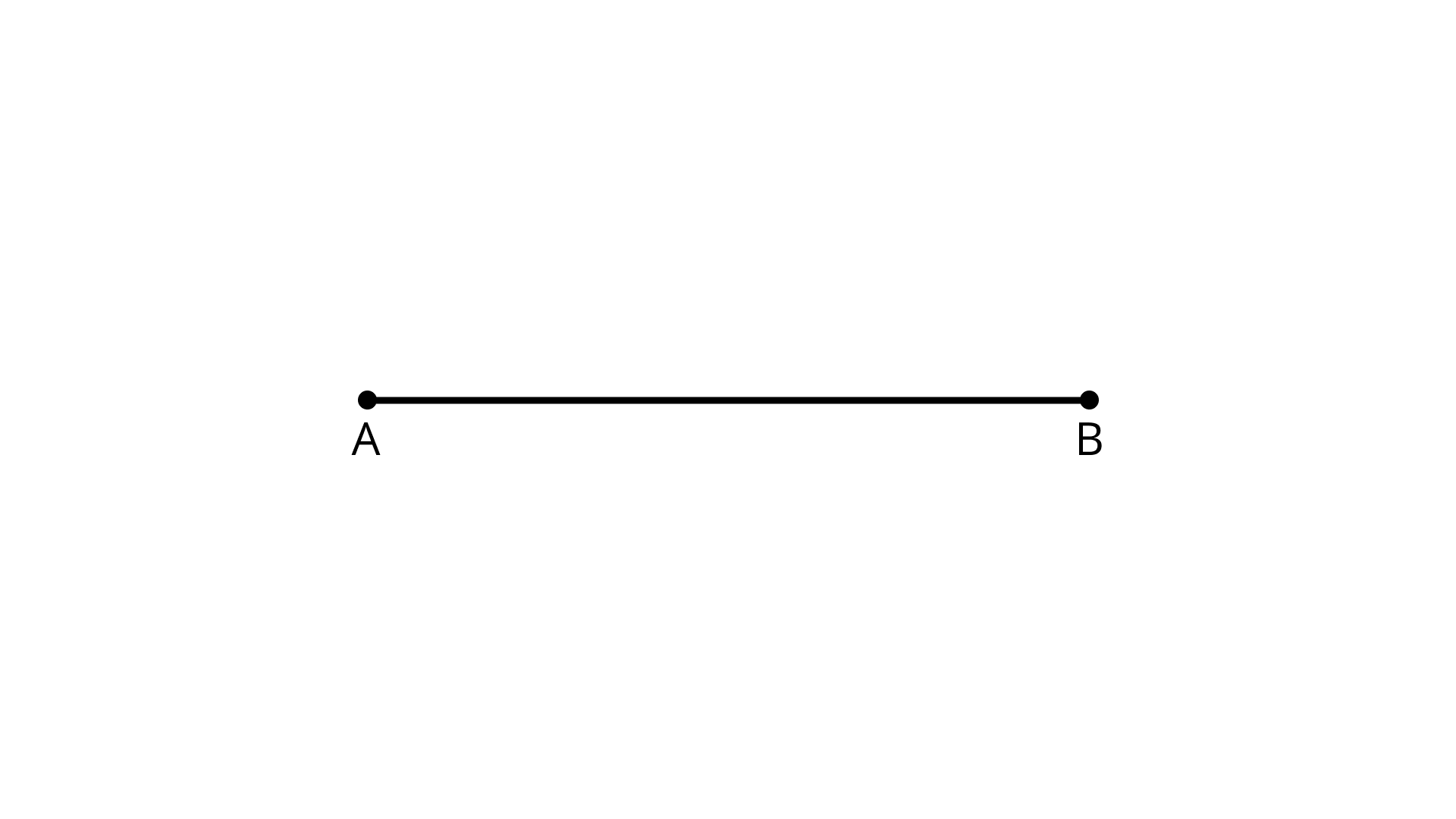
Ans: There is one line segment namely -  AB.

67. In Figure, how many points are marked?

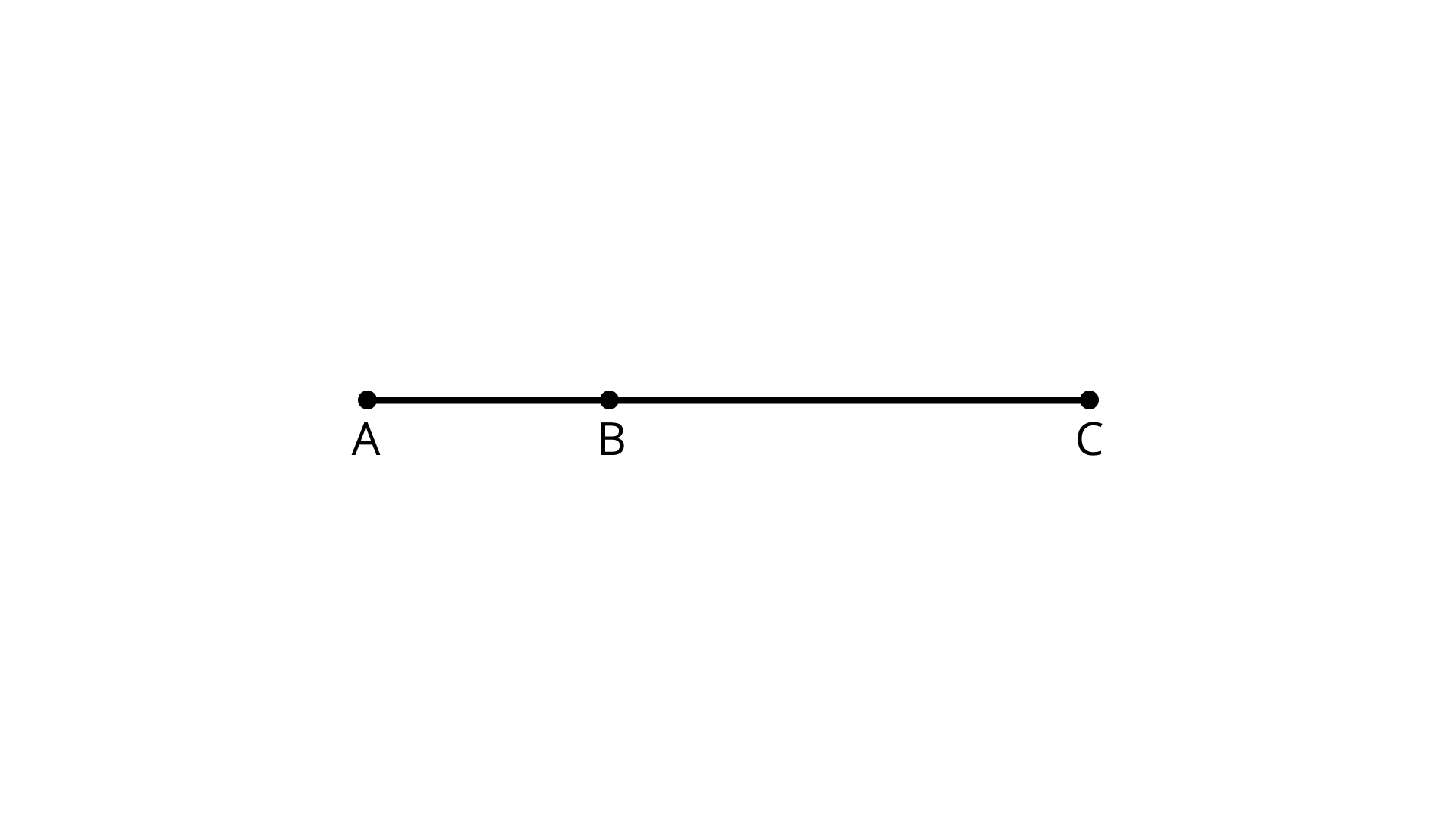
Ans: There are three points namely -  A, B and C.

68. How many line segments are there in Figure?

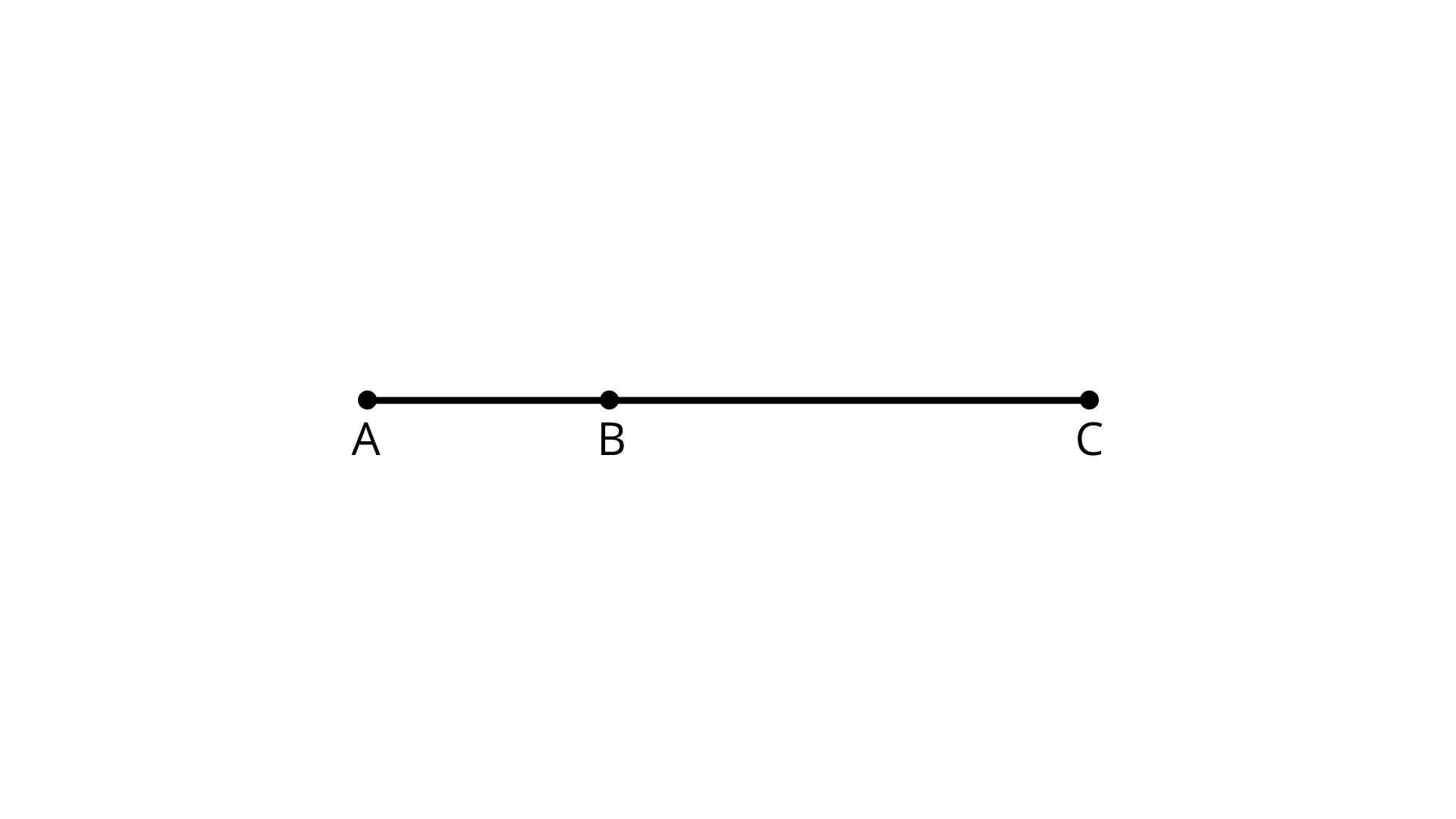
Ans: There are three line segments namely - AB, AC, and BC.

69. In Figure how many points are marked?

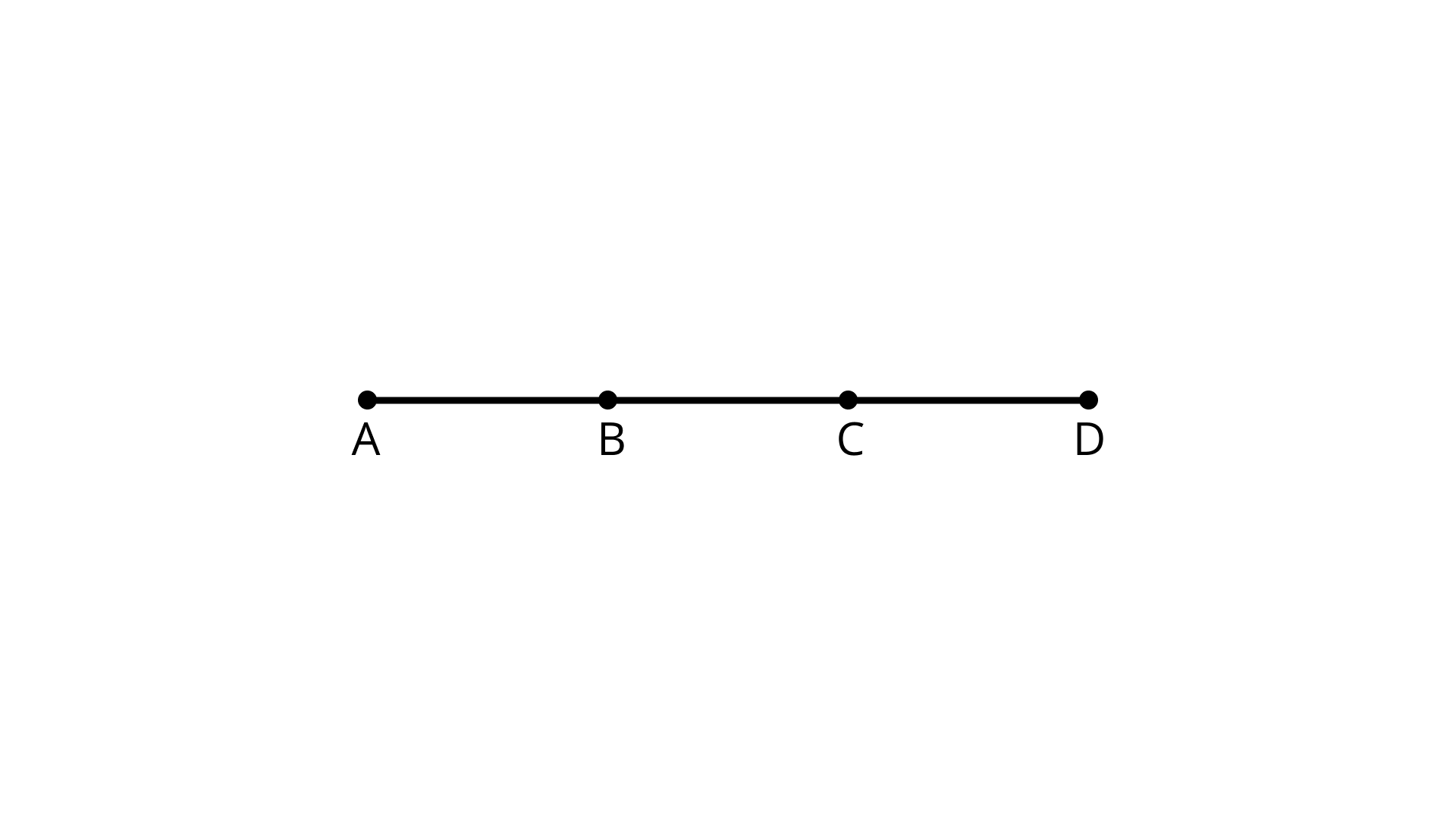
Ans: There are four points marked namely - A, B, C, and D.

70. In Figure, How many line segments are there?

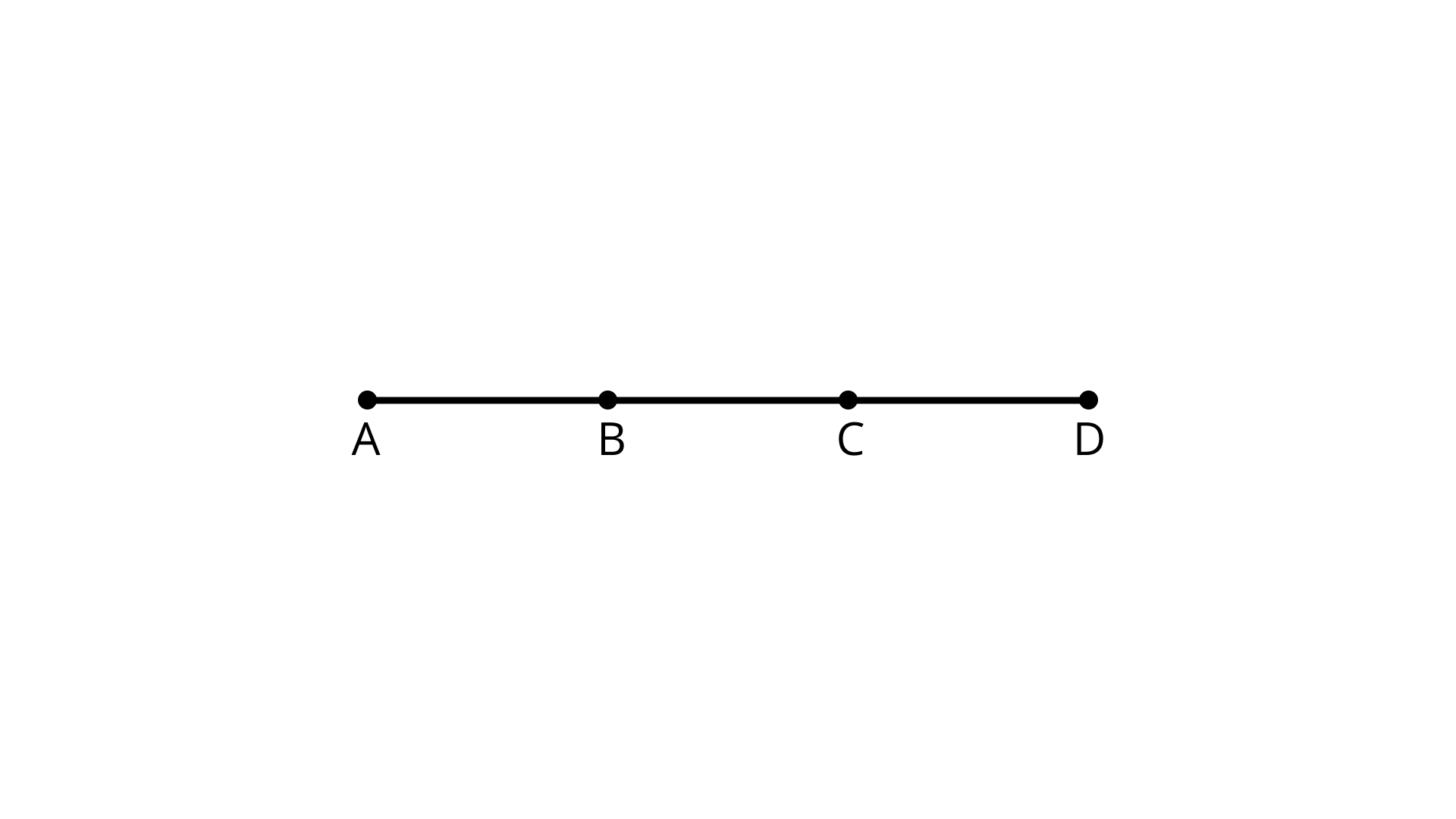
Ans: There are six line segments namely -  AB, BC, CD, AC, AD, and BD.

71. In Figure, how many points are marked?

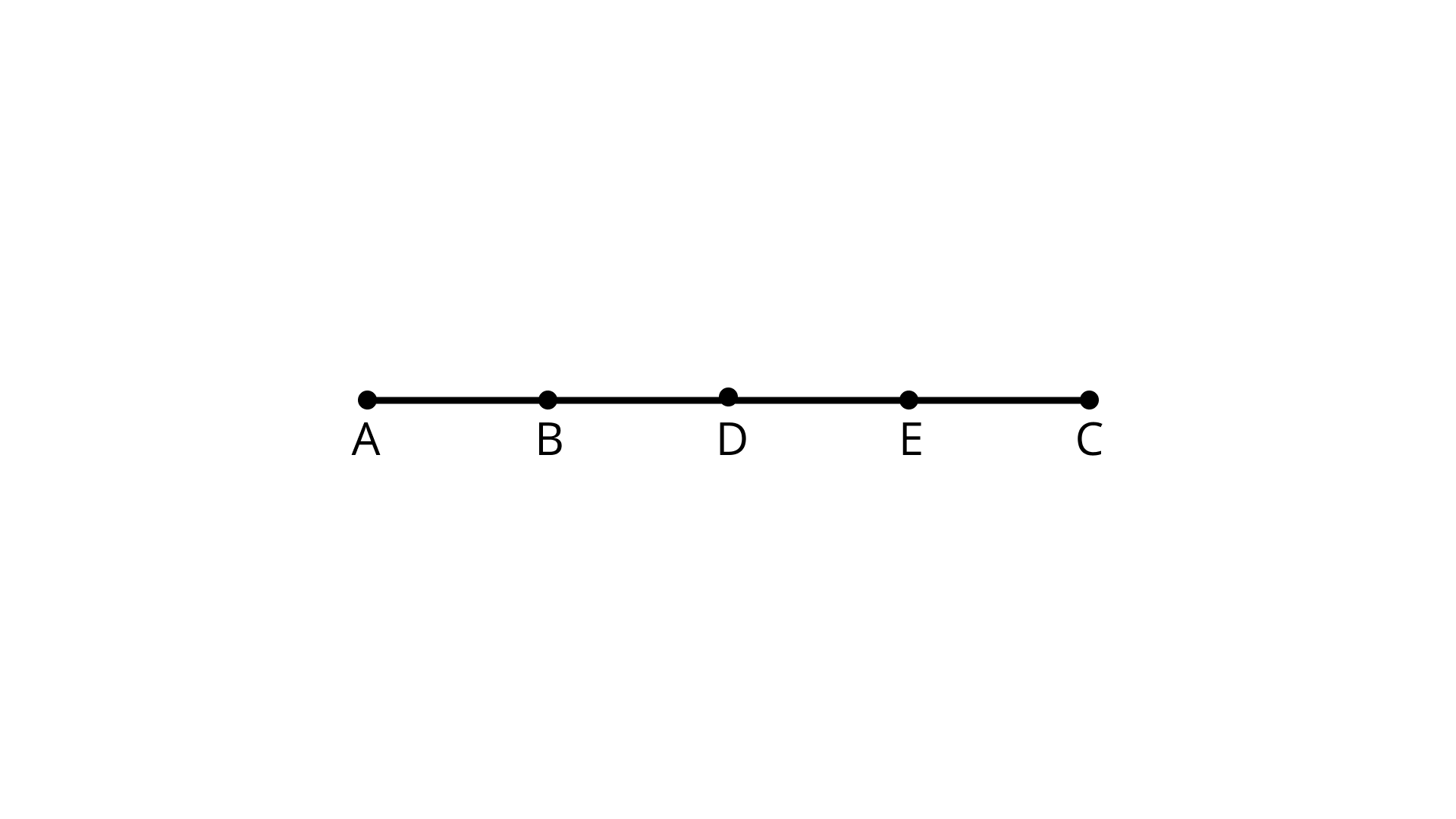
Ans: There are five points namely -  A, B, D, E, and C.

72. In Figure How many line segments are there?

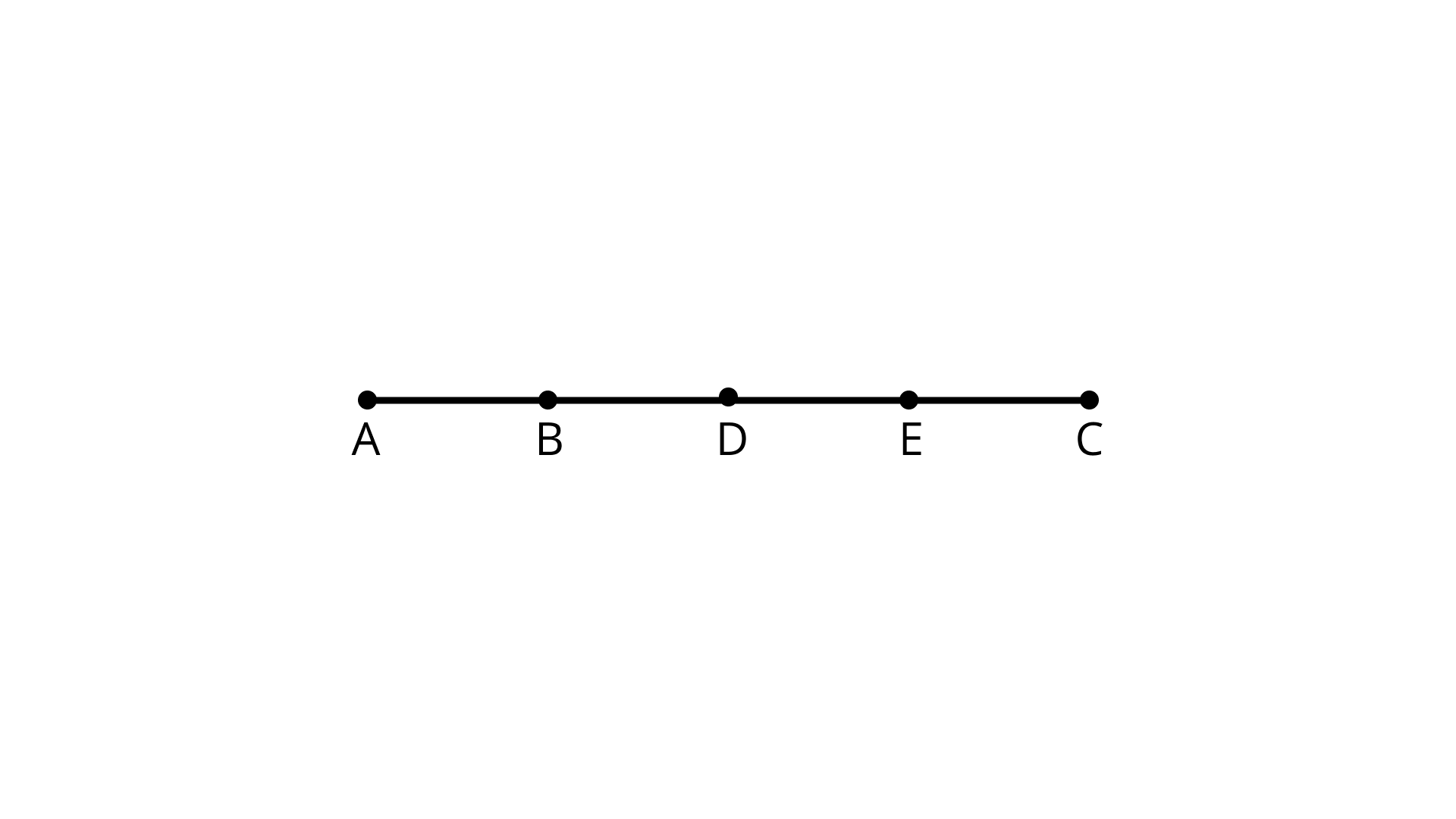
Ans: There are ten line segments namely -  AB, BD, DE, EC, AC, AE, AD, BC, BE, and DC.

73. In Figure, O is the center of the circle.

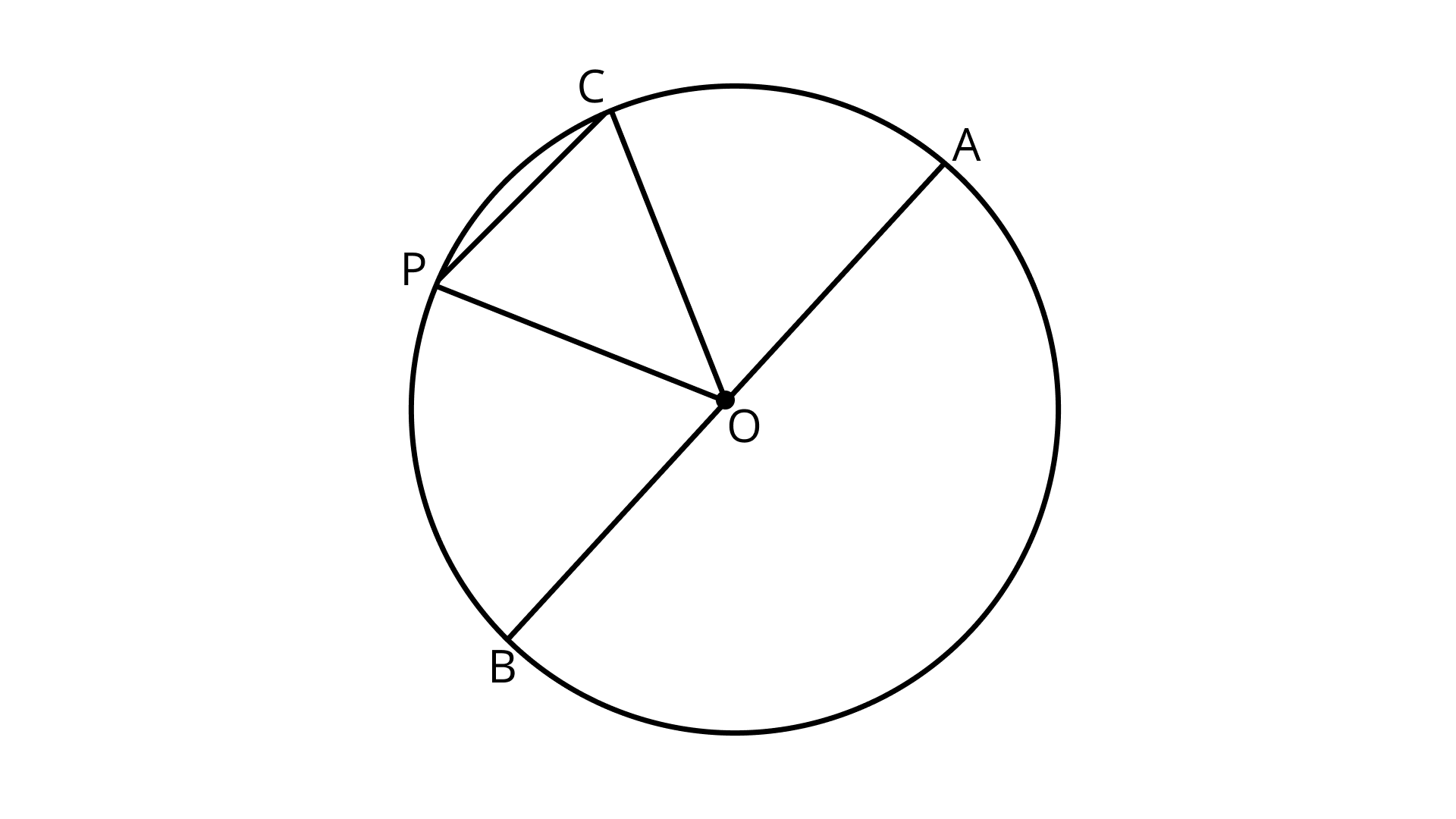
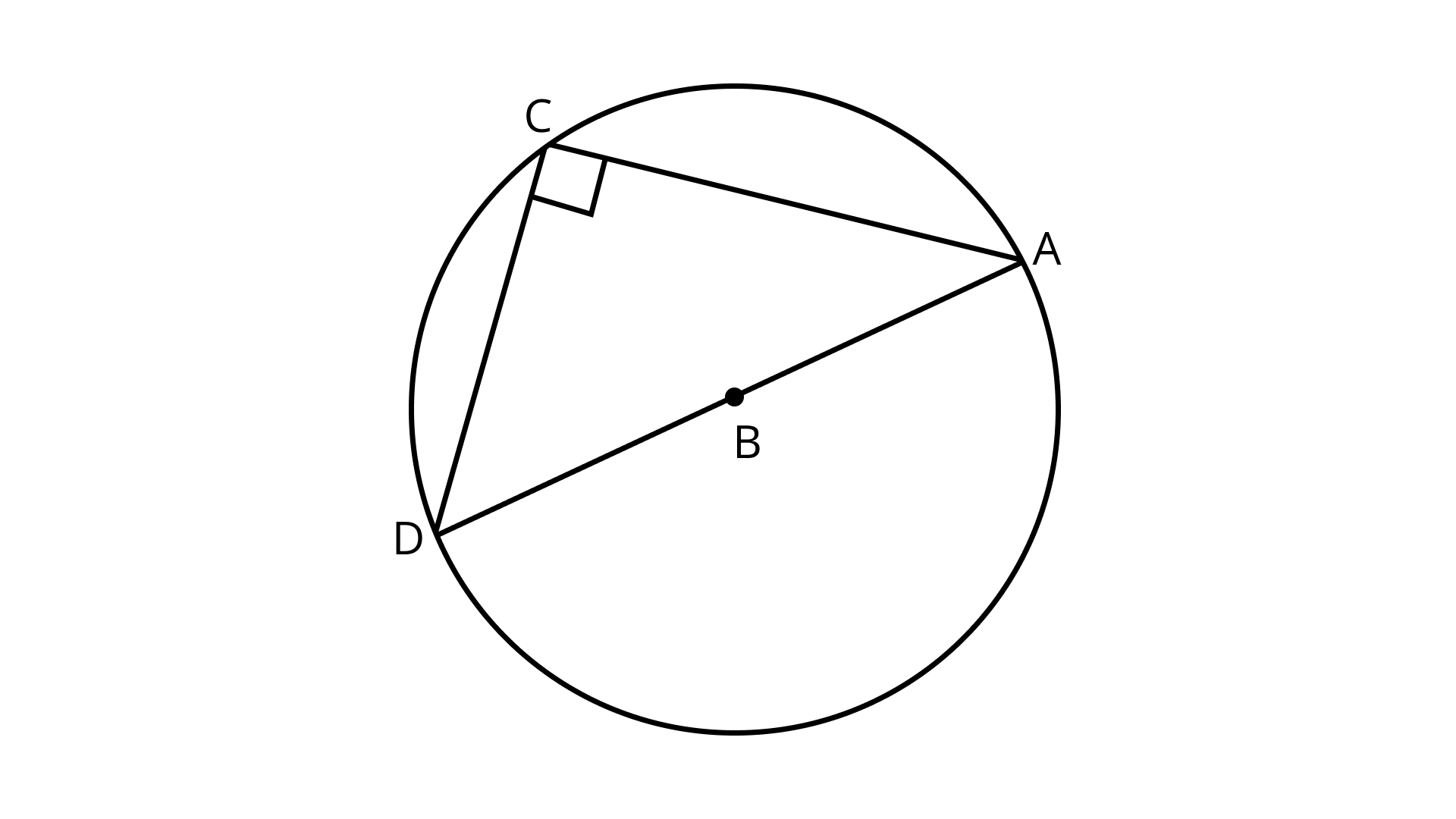
(a) Name all chords of the circle.

Ans: CP and AB are two chords.

(b) Name all radii of the circle.

Ans:  OP, OC, OB, and OA  are the radii of the circle. 

(c) Name a chord, which is not the diameter of the circle.

Ans: CP is a chord which is not the diameter of the circle.

(d) Shade sectors OAC and OPB.

Ans: Shaded sectors OAC and OPB are as:

(e) Shade the smaller segment of the circle formed by CP.

Ans: Shaded the smaller segment of the circle formed by CP is as:

74. Can we have two acute angles whose sum is

(a) An acute angle? Why or why not? 

Ans: Yes, the sum of the two acute angles may be less than a right angle.

e.g. $30^{\circ}$ and $45^{\circ}$ are acute and the sum of them $75^{\circ}$ is also an acute angle.

(b) A right angle? Why or why not?

Ans:  Yes, the sum of the two acute angles may be equal to a right angle.

e.g. $30^{\circ}$ and $60^{\circ}$ are acute and the sum of them is $90^{\circ}$.

(c) An obtuse angle? Why or why not?

Ans:  Yes, the sum of the two acute angles may be more than a right angle.

e.g. $60^{\circ}$ and $80^{\circ}$= $140^{\circ}$.

(d) A straight angle? Why or why not?

Ans:  No, the sum of the two acute angles is always less than a straight angle.

e.g. $89^{\circ}$ and $89^{\circ}$= $178^{\circ}$.

(e) A reflex angle? Why or why not?

Ans: No, the sum of the two acute angles is always less than a straight angle. So, their sum cannot be a reflex angle.

75. Can we have two obtuse angles whose sum is  

(a) A reflex angle? Why or why not?

Ans: Yes, the sum of two obtuse angles is always greater than $180^{\circ}$. So, the sum of them will be a reflex angle.

(b) A complete angle? Why or why not?

Ans: No, the sum of two obtuse angles cannot be $360^{\circ}$. It lies between $180^{\circ}$ to $360^{\circ}$.  

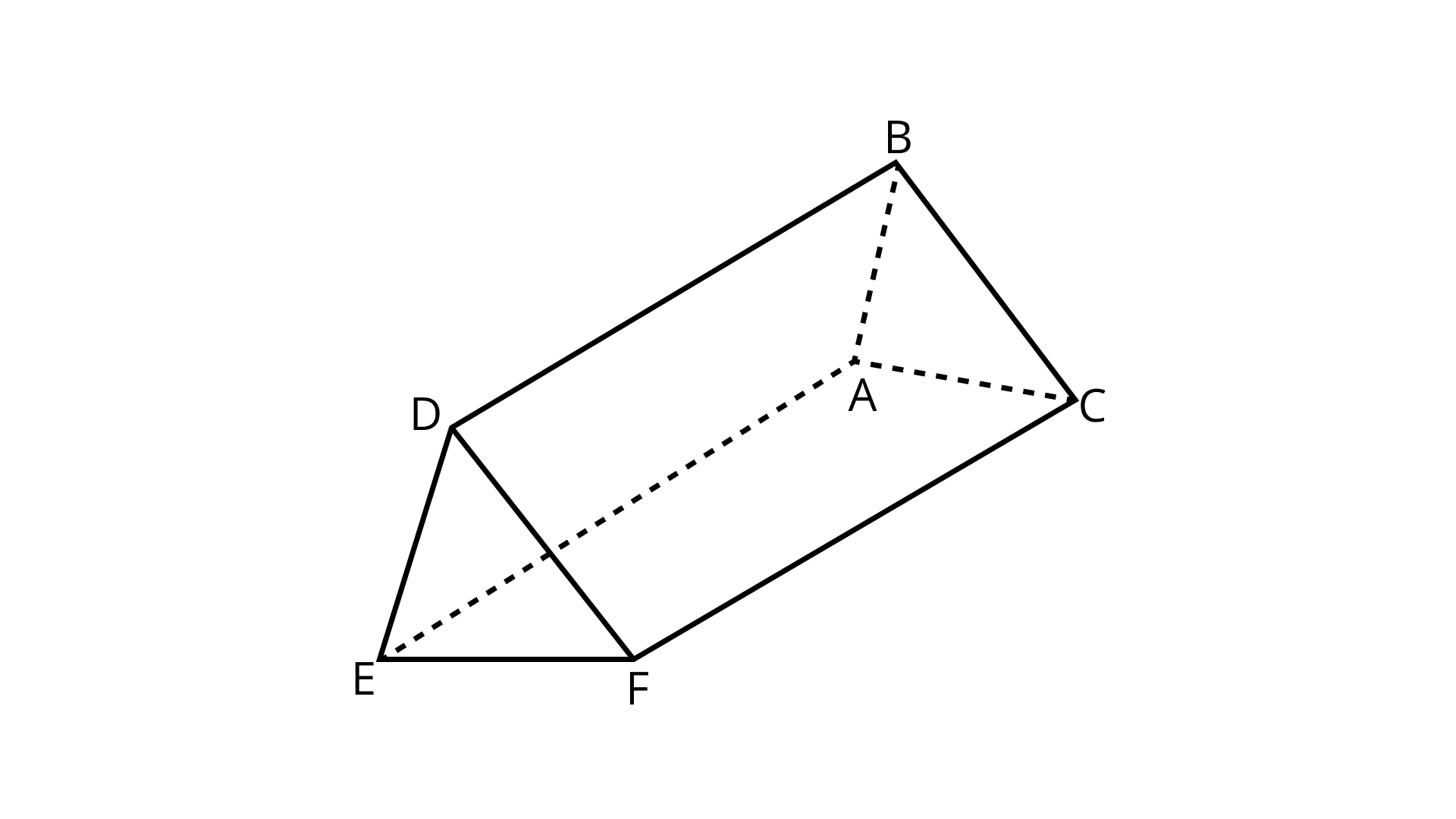
76. Write the name of

(a) Vertices

Ans:  Vertices in figure - A, B, C, D, E, and F.

(b) edges

Ans:  Edges in figure - AB, BC, AC,EF, AE, CF, DF, DE and BD.

(c) Faces of the prism shown in Figure.

Ans: Faces of prism - AEFC, AEDB, ABC, DEF, and BDCF.

77. How many edges, faces, and vertices are there in a sphere?

Ans: A sphere does not have any edges, faces, or vertices.

78. Draw all the diagonals of a pentagon ABCDE and name them.

Ans: 

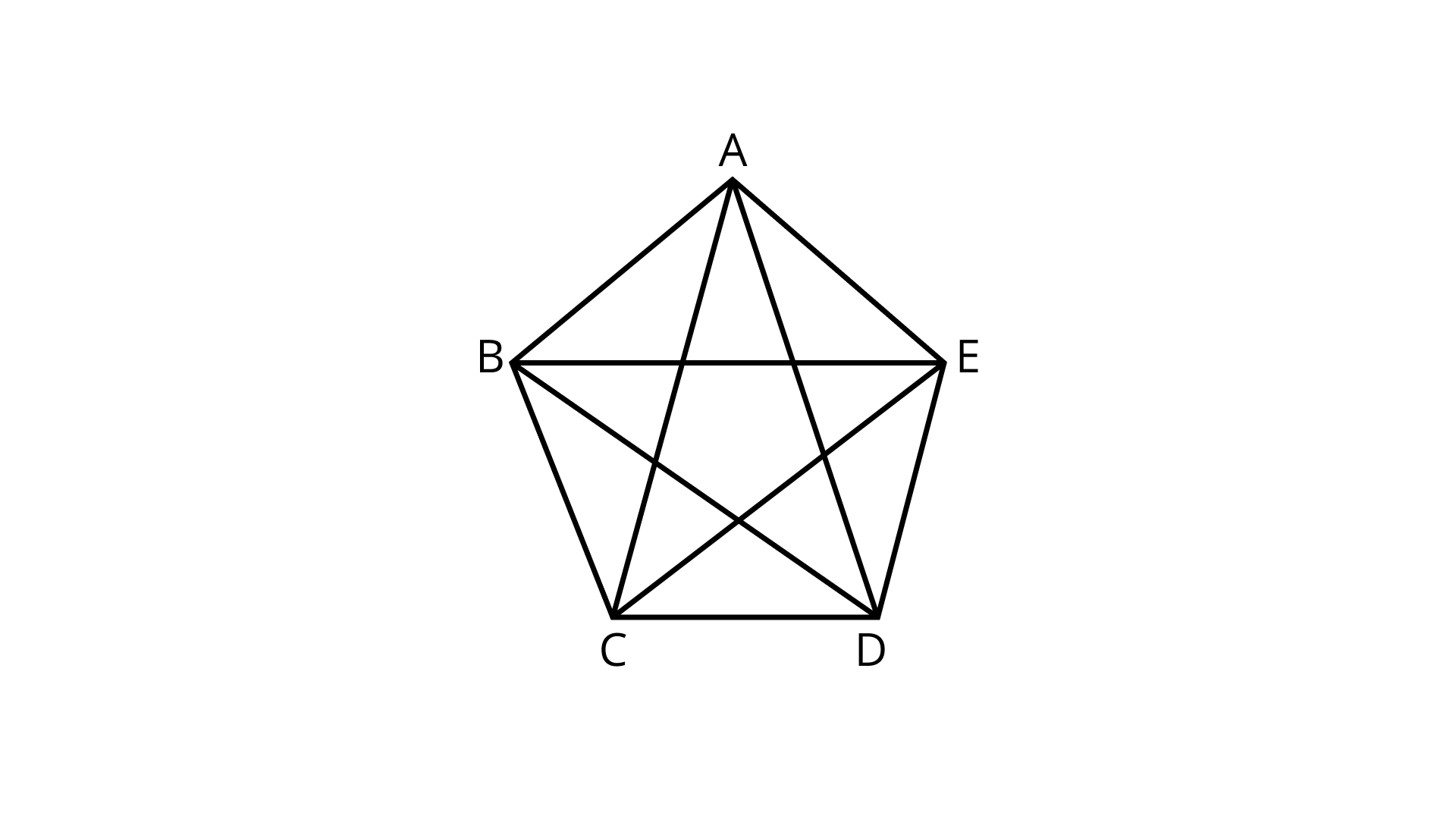
A pentagon has 5 sides and number of diagonals=5

The Diagonals - AC, AD, BE, BD and CE.

What Will We Learn in this Chapter?

In this chapter, Vedantu provides NCERT Exemplar Class 6 Maths Solutions for students, which will be of great help to every student in their tests. Students can download the latest NCERT Exemplar Problems Solutions for Pdf Class 6 Maths from the Vedantu website. The following PDF attached will give you a step-by-step solution to each question which may help you in preparation.

Geometry is a branch of mathematics that focuses on balance and the relationship of lines, angles, surface area, solid, and points. These NCERT Exemplar Class Mathematics Solutions Grade 6 Mathematics are available for download in pdf format and provide solutions to all questions provided in the NCERT Exemplar textbook. In this chapter, students will get assistance on the key themes, namely the line of the line, the cross line, the parallel lines, the angle, the polygon, the triangle, the four-dimensional polygon and the regular polygon.

Key Topics for NCERT Exemplar Solutions Class 6 Maths Chapter 2

• Parts of the Circle

The chapter talks about the different parts within the circle and their names. There is information about a chord, section, industry, radii, circle, and circle area. The concept of scope and breadth is also discussed in the chapter. 

• The Naming of Various Geometric Calculations

There is a detailed discussion of the various geometric figures and their names based on the number of their sides. Like triangle, polygon, hexagon, heptagon, octagon, etc. their properties are also briefly shared. 

• Angles of A Triangle and Other Geometric Figures

After the information about the words, there is a discussion about the angles in the whole geometric image and the basic concept of arithmetic based on their objects. For example, the total angular value of all three sides of a triangle is 180 degrees.

Some Important Questions:

Question 1. The number of lines exceeds five points so that none of them is collinear

1. 10

2. 5

3. 20

4. 8

Solution: (A): As the total number of points is 5 and we need two points to form a line.

∴ the total number of rows passing points is 5 × 2 = 10

Question 2. If the sum of the two angles is greater than 180 °, which of the following does not occur at two angles?

1. One obtuse angle and one sharp angle

2. One reflex angle and one sharp angle

3. Two angles thick

4. Two right angles

Solution: (D): As the sum of the two right angles is 180 °.

Question 3. If the sum of the two angles is equal to the obtuse angle, which of the following is impossible?

1. One obtuse angle and one sharp angle

2. One right angle and one sharp angle

3. Two sharp angles

4. Two right angles

Solution: (D): As, the sum of the two right angles is 180 °, which is a straight angle, not an obtuse angle.

Question 4. As the angles of the angle on the paper increase, the angle increases.

Solution:

False

If the angles of the angle on the paper increase or decrease, it does not affect the angle they made.

Question 5. When the angles of the angle on the paper are lowered, the angle decreases.

Solution:

False

If the angles of the angle on the paper increase or decrease, it does not affect the angle they made.

Question 6. Two parallel lines meet at some point.

Solution:

False

Two lines in a plane that do not connect even if permanently produced in any way, are known as parallel lines.

Question 7. The ∠ABC and ∠CBA ratings in the given figures are the same.

NCERT Exemplar Class 6 Maths Chapter 2 Geometry 82

Solution:

True

∵ ∠ABC is the same as ∠CBA.

Question 8. Two-line segments may meet at two points.

Solution:

False

The crossing point of any two-dimensional section is only one.

These are the sample questions and their difficulty levels you will find in the NCERT Exemplar. Download the file today from Vedantu and find out how to solve such conceptual questions. Understand the reasons behind using the particular concepts to answer these questions. It is then you will prepare this chapter better and can score more marks in the exams.