NCERT Exemplar for Class 11 Physics Chapter 2 - Units and Measurement (Book Solutions)

Multiple Choice Questions (MCQs)

1. The number of significant figures in $0.06900$ is 

(a) \[5\]

(b) $4$

(c) $2$

(d) $3$

Ans. Option (b) 

Here the zeroes which are present on the left of the non-zero number are not considered as significant figures and zeros which are on the right side are considered as significant figures. In $0.0\underline {6900} $, there are four significant figures. Thus, option (b) is correct.

2. The sum of the numbers $436.32$, $227.2$ and $0.301$ in appropriate significant figures is

(a) $663.821$

(b) $664$

(c) $663.8$

(d) $663.82$

Ans. Option (c) 

The sum of the given three numbers is $663.821$ but in the three numbers, the least number of places after the decimal is one thus the final significant figure is $663.8$ (rounding off up to one place). Thus option (c) is correct.

3. The mass and volume of a body are $4.237\;g$ and $2.5\;c{m^3}$, respectively. The density of the material of the body in correct significant figures is:

(a) $1.6048\;g\,c{m^{ - 3}}$

(b) $1.69\,g\;c{m^{ - 3}}$

(c) $1.7\;g\,c{m^{ - 3}}$

(d) $1.695\;g\;c{m^{ - 3}}$

Ans. Option (c) 

On multiplication or division, the final result should have the similar number of significant figures as vast as there are in the original number with the minimal significant figures. In the given numbers, $4.237\;g$ and $2.5\;c{m^3}$ there are four and two significant figures where the least significant figure is two.

$Density = \dfrac{{mass}}{{volume}}$

$ = \dfrac{{4.237}}{{2.5}}$

$density = 1.6948\;g\;c{m^{ - 3}}$

$ = 1.7\;g\;c{m^{ - 3}}$ (Rounding off up to two significant figures). Thus option (c) is correct.

4. The numbers $2.745$ and $2.735$ on rounding off to $3$ significant figures will give. 

(a) $2.75$ and $2.74$

(b) $2.74$ and $2.73$

(c) $2.75$ and $2.73$

(d) $2.74$ and $2.74$

Ans. Option (d) 

(a) if the digit to the instant right of the last sig fig is equal to five and is followed by a nonzero digit, round up.

(b) If the digit is an odd digit, round it up and if the digit is even digit, don’t round it up, leave it as it is.

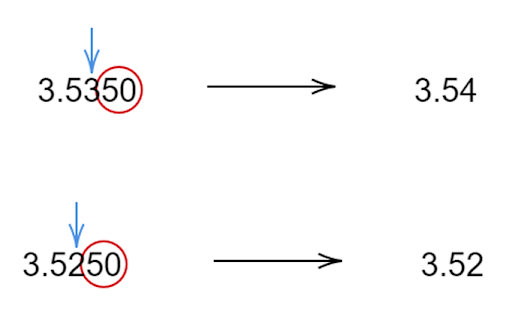
The given numbers are $2.745$, the instant preceding is an even number thus there will be no change, $2.74$ while $2.735$ the instant preceding is an odd number thus there will round up, $2.74$. Thus, option (d) is correct.

5. The length and breadth of a rectangular sheet are $16.2\;cm$ and $10.1\,cm$ respectively. The area of the sheet in appropriate significant figures and error is

(a) $164 \pm 3\;{cm}^{2}$

(b) $163.62 \pm 2.6\,{cm}^{2}$

(c) $163 \pm 6.2\;{cm}^{2}$

(d) $163.62 \pm 3\;{cm}^{2}$

Ans. Option (a) 

Here are two concepts used which are: first, the result of multiplying two significant figures is the minimal number of significant figures in given number and if $\Delta x$ is error then relative error or error is $\dfrac{{\Delta x}}{x}$. 

$l = 16.2\;cm$

$\Delta l = 0.1$

$l = 16.2 \pm 0.1$

$b = 10.1 \pm 0.1$

$A = Area$

$ = l \times b$

$ = 16.2 \times 10.1$

$ = 163.62\;c{m^2}$

$ = 164\;c{m^2}$ (In significant figures)

$\dfrac{{\Delta A}}{A} = \dfrac{{\Delta l}}{l} + \dfrac{{\Delta b}}{b}$

$ = \dfrac{{0.1}}{{16.2}} + \dfrac{{0.1}}{{10.1}}$

$\dfrac{{\Delta A}}{{164}} = \dfrac{{10.1 \times 0.1 + 16.2 \times 0.1}}{{16.2 \times 10.1}}$

$\Delta A = 164\left( {\dfrac{{1.01 + 1.62}}{{163.62}}} \right)$

$\Delta A = 2.63\;c{m^2}$

Now rounding off upto significant figures in $\Delta l$ and $\Delta b$ i.e., one 

$\Delta A = 3\;c{m^2}$

$A = \left( {164 \pm 3} \right)\;c{m^2}$

Thus, the option (a) is correct.

6. Which of the following pairs of physical quantities does not have the same dimensional formula?

(a) Work and torque

(b) Angular momentum and Planck’s constant

(c) Tension and surface tension

(d) Impulse and linear momentum

Ans. Option (c) 

In this question we will use dimensions of each term in the formula. 

In the first option i.e., (a) $work = Force \times displacement$

$\left[ {ML{T^{ - 2}}} \right]\left[ L \right] = \left[ {M{L^2}{T^{ - 2}}} \right]$

$Torque = Force \times distance$

$\left[ {ML{T^{ - 2}}} \right]\left[ L \right] = \left[ {M{L^2}{T^{ - 2}}} \right]$

Thus, both have the same dimension.

In the option (b), $angular\;momentum\;L = mvr$

$\left[ M \right]\left[ {L{T^{ - 1}}} \right]\left[ L \right] = \left[ {M{L^2}{T^{ - 1}}} \right]$

$Planck's\;constant\;h = \dfrac{{F.s}}{v}\;\left( {\therefore E = hv} \right)$

$\dfrac{{\left[ {ML{T^{ - 2}}} \right]\left[ L \right]}}{{\left[ {{T^{ - 1}}} \right]}} = \left[ {M{L^2}{T^{ - 1}}} \right]$

Here also the dimensions of $h$ and $L$ are equal.

In option (c), $Tension = force = \left[ {ML{T^{ - 2}}} \right]$

$surface\,tension = \dfrac{{\,force}}{l}$

$ \Rightarrow \dfrac{{\left[ {ML{T^{ - 2}}} \right]}}{{\left[ L \right]}} = \left[ {M{L^0}{T^{ - 2}}} \right]$

In this option the dimensions of both are not the same.

In option (d) $impulse = F \times t$

$\left[ {ML{T^{ - 2}}} \right]\left[ T \right] = \left[ {ML{T^{ - 1}}} \right]$

$Momentum = mv$

$ = \left[ {ML{T^{ - 1}}} \right]$

Both have the same dimension. So, option (c) is correct.

7. Measure of two quantities along with the precision of respective measuring instrument is $A = 2.5\,m{s^{ - 1}} \pm 0.5\,m{s^{ - 1}}$and $B = 0.10\;s \pm 0.01\;s$. The value of $AB$ will be:

(a) $\left( {0.25 \pm 0.08} \right)\;m$

(b) $\left( {0.25 \pm 0.5} \right)\;m$

(c) $\left( {0.25 \pm 0.05} \right)\;m$

(d) $\left( {0.25 \pm 0.135} \right)\;m$

Ans. Option (a) 

The resultant significant figure in multiplication and addition is equal to the minimal number of significant figures. 

$A = \left( {2.5 \pm 0.5} \right)\;m{s^{ - 1}}$

$B = \left( {0.10 \pm 0.01} \right)\,s$

$X = AB = 2.5 \times 0.10$

$ = 0.25\;m$

$\dfrac{{\Delta x}}{x} = \dfrac{{\Delta A}}{A} + \dfrac{{\Delta B}}{B}$

$\dfrac{{\Delta x}}{x} = \dfrac{{0.5}}{{2.5}} + \dfrac{{0.01}}{{0.10}}$

$\dfrac{{\Delta x}}{x} = \dfrac{{0.075}}{{0.25}},\,\Delta x = 0.007$

$ \cong 0.08$

$\therefore AB = \left( {2.5 \pm 0.08} \right)\,m$

Thus, option (a) is correct.

8. You measure two quantities as $A = \left( {1.0 \pm 0.2} \right)\;m$, $B = 2.0\;m \pm 0.2\;m$. We repot correct values of $\sqrt {AB} $ as:

(a) $1.4\;m \pm 0.4\;m$

(b) $1.41\,m \pm 0.15\;m$

(c) $1.4\;m \pm 0.3\,m$

(d) $1.4\;m \pm 0.2\,m$

Ans. Option (d) 

When we take significant figures of measured quantities, we also include zeros in significant figures. Here quantities $A$ and $b$ are the measuring quantities thus the number of significant figures in $1.0\;m$ and $2.0\,m$ are two. 

$\sqrt {AB}  = \sqrt {1.0 \times 2.0} $

$ = \sqrt 2 $

$ = 1.414\;\,m$

Here the minimal significant figure is two in the significant figures, $1.0\;m$ and $2.0\;m$. Thus,

$x = \sqrt {AB}  = 1.4$

$\dfrac{{\Delta x}}{x} = \dfrac{1}{2}\left[ {\dfrac{{\Delta A}}{A} + \dfrac{{\Delta B}}{B}} \right]$

$ = \dfrac{1}{2}\left[ {\dfrac{{0.2}}{{1.0}} + \dfrac{{0.2}}{{2.0}}} \right]$

$ = \dfrac{1}{2} \times 0.2\left[ {\dfrac{1}{{1.0}} + \dfrac{1}{{2.0}}} \right]$

$ = 0.1\left[ {\dfrac{{2.0 + 1.0}}{{1.0 \times 2.0}}} \right]$

$\dfrac{{\Delta x}}{{1.4}} = 0.1\left( {\dfrac{{3.0}}{{2.0}}} \right)$

$ = 2.1\;m$

$\Delta x = 0.2\,m$ rounding to one place of decimal.

$\therefore \sqrt {AB}  = \left( {1.4 \pm 0.2} \right)\;m$. Option (d) is correct.

9. Which of the following measurements is most precise?

(a) $5.00\;mm$

(b) $5.00\;cm$

(c) $5.00\;m$

(d) $5.00\;km$

Ans. Option (a) 

In this question the unit of measurement should be minimal. Here all the options have up to two places of decimal and in option (a) there is least unit i.e., $mm$. Thus, option (a) is the correct one.

10. The mean length of an object is $5\;cm$. Which of the following measurements is most accurate?

(a) $4.9\;cm$

(b) $4.805\,cm$

(c) $5.25\;cm$

(d) $5.4\,cm$

Ans. Option (a) 

For more accurate value there should be less absolute error $\left( {\overline a  - {a_i}} \right)$.

Error or absolute error

$\left| {\Delta {a_1}} \right| = \left| {5 - 4.9} \right|$

$ = 0.1\,cm$

$\left| {\Delta {a_2}} \right| = \left| {5 - 4.805} \right|$

$ = 0.195\,cm$

$\left| {\Delta {a_3}} \right| = \left| {5 - 5.25} \right|$

$ = 0.25\;cm$

$\left| {\Delta {a_4}} \right| = \left| {5 - 5.4} \right|$

$ = 0.4\;cm$

Thus here $\left| {\Delta {a_1}} \right|$ is minimum so option (a) is correct.

11. Young’s modulus of steel is $1.9 \times {10^{11}}\;N\;{m^{ - 2}}$. When expressed in CGS units of $dyne\,c{m^{ - 2}}$. It will be equal to ($1\;N = {10^5}\;dynes$, and $1{m^2} = {10^4}\,c{m^2}$).

(a) $1.9 \times {10^{10}}$

(b) $1.9 \times {10^{11}}$

(c) $1.9 \times {10^{12}}$

(d) $1.9 \times {10^{13}}$

Ans. Option (c) 

Here the Young’s modulus of steel is $1.9 \times {10^{11}}\,N\,{m^{ - 2}}$

$Y = \dfrac{{1.9 \times {{10}^{11}}\,N}}{{1\,{m^2}}}$

$ = \dfrac{{1.9 \times {{10}^{11}} \times {{10}^5}\,dynes}}{{{{10}^4}\,c{m^2}}}$

$Y = 1.9 \times {10^{11 + 5 - 4}}$

$Y = 1.9 \times {10^{12}}\,dyne\,c{m^{ - 2}}$, thus option (c) is correct.

12. If the momentum ($P$), area ($A$) and time ($T$) are taken to be fundamental quantities, then energy has a dimensional formula.

(a) $\left[ {{P^1}{A^{ - 1}}{T^1}} \right]$

(b) $\left[ {{P^2}{A^{ - 1}}{T^1}} \right]$

(c) $\left[ {{P^1}{A^{ - \dfrac{1}{2}}}{T^1}} \right]$

(d) $\left[ {{P^1}{A^{\dfrac{1}{2}}}{T^{ - 1}}} \right]$

Ans. Option (d) 

Let us consider in terms of fundamental quantities, the dimensional formula of energy be $P$, $A$ and $T$ be $\left[ {{P^a}{A^b}{T^c}} \right]$. Where $P$ is the momentum, whose dimensional formula is $\left[ {ML{T^{ - 1}}} \right]$, $A$ is the area whose dimensional formula is $\left[ {{L^2}} \right]$ and $T$ is time whose dimensional formula is $\left[ {{T^1}} \right]$

$\therefore Energy = F.s$

$ = \left[ {ML{T^{ - 2}}} \right]\left[ L \right]$

$ = \left[ {M{L^2}{T^{ - 2}}} \right]$

$\therefore \left[ {M{L^2}{T^{ - 2}}} \right] = {\left[ {ML{T^{ - 1}}} \right]^a}{\left[ {{L^2}} \right]^b}{\left[ T \right]^c}$

$\left[ {{M^1}{L^2}{T^{ - 2}}} \right] = \left[ {{M^a}{L^{a + 2b}}{T^{a + c}}} \right]$

Comparing the powers we get,

$a = 1$

$a + 2b = 2$

$1 + 2b = 2$

$2b = 2 - 1$

$b = \dfrac{1}{2}$

$ - a + c =  - 2$

$ - 1 + c =  - 2$

$c =  - 2 + 1$

$c =  - 1$

$\therefore $ dimensional formula of energy is $\left[ {{P^1}{A^{\dfrac{1}{2}}}{T^{ - 1}}} \right]$. So, option (d) is correct.

MULTIPLE CHOICE Question-II

13. On the basis of dimensions, decide which of the following relations for the displacement of particles undergoing simple harmonic motion is not correct.

(a) $y = a\;\sin \left( {\dfrac{{2\pi t}}{T}} \right)$

(b) $y = a\;\sin vt$

(c) $y = \dfrac{a}{T}\sin \left( {\dfrac{t}{a}} \right)$

(d) $y = a\sqrt 2 \left[ {\sin \dfrac{{2\pi t}}{T} - \cos \dfrac{{2\pi t}}{T}} \right]$

Ans. Options (b) and (c) 

According to the principle of homogeneity, the dimensions on both sides must be equal. Here displacement $y$ and amplitude $a$ have the same dimensions, angle of sin and cos is dimensionless. 

In option (a) and (d), here the dimensions of $y$ and $a$ is equal to $L$ in both L.H.S. and R.H.S. and in option (b) angle is $v.t$

$\therefore $dimension of $v.t$is $\left[ {L{T^{ - 1}}} \right]\left[ T \right] = \left[ L \right]$

Which means here angle is not dimensionless this option (a) is not correct. In option (c) dimension of amplitude $\dfrac{a}{T} = \dfrac{{\left[ L \right]}}{{\left[ T \right]}} = \left[ {L{T^{ - 1}}} \right]$. This is not equal to the dimension of $y$ i.e., $L$ and angle $\dfrac{t}{a} = \dfrac{{\left[ T \right]}}{{\left[ L \right]}} = \left[ {L{T^{ - 1}}} \right]$ is not dimensionless. Hence, option (b) and (c) are right answers to this question.

14. $P$,$Q$, Rare physical quantities, having different dimensions, which of the following combinations can never be a meaningful quantity?

(a) $\dfrac{{\left( {P - Q} \right)}}{R}$

(b) $\left( {PQ - R} \right)$

(c) $\dfrac{{PQ}}{R}$

(d) $\dfrac{{\left( {PR - {Q^2}} \right)}}{R}$

(e) $\dfrac{{\left( {R + Q} \right)}}{R}$

Ans. Options (a) and (e) 

In addition and subtraction, the same physical quantities are needed while in multiplication and division different physical quantities can also be possible. After multiplying or dividing two quantities, their dimension may be equal to third and can be added or subtracted. In the above options, options (a) and (e) there are term $\left( {P - Q} \right)$ and $\left( {R + Q} \right)$ in which different quantities are added and subtracted this option (a) and (e) can never be meaningful. While in option (b) the dimensions of both $PQ$and $R$ are the same. Thus, option (b) can be possible. 

Similarly dimensions of both $PR$ and ${Q^2}$ can be equal thus, option (d) can also be possible. In option (c) there is no subtraction or addition so option (c) is also possible. Thus, option (a) and (e) are correct.

15. Photon is a quantum of radiation with energy $E = h\nu $, where $\nu $ is the frequency and $h$ is Planck’s constant. The dimensions of $h$ are the same as that of:

(a) Linear impulse

(b) Angular impulse

(c) Linear momentum

(d) Angular momentum

Ans.  Options (b) and (d).

In this question we used dimensional formulae.

We know that, 

$E = h\nu $

$ \Rightarrow h = \dfrac{E}{\nu }$

$ \Rightarrow \dfrac{{\left[ {M{L^2}{T^{ - 2}}} \right]}}{{\left[ {{T^{ - 1}}} \right]}} = \left[ {M{L^2}{T^{ - 1}}} \right]$

(a) $Linear\;impulse = F \cdot t$

$ \Rightarrow \dfrac{{dp}}{{dt}} \cdot dt = dp$

$ \Rightarrow mv = \left[ {ML{T^{ - 1}}} \right]$

(b) $Angular\;impulse = \tau  \cdot dt$

$ \Rightarrow \dfrac{{dL}}{{dt}} \cdot dt$

$ \Rightarrow dL = mvr$

$ \Rightarrow \left[ M \right]\left[ {L{T^{ - 1}}} \right]\left[ L \right] = \left[ {M{L^2}{T^{ - 1}}} \right]$

(c) $Linear\,momentum = mv = \left[ {ML{T^{ - 1}}} \right]$

(d) $Angular\;momentum\;L = mvr = \left[ {M{L^2}{T^{ - 1}}} \right]$

Thus, angular impulse and angular momentum have the same dimensional formulae of $h$. So, the correct answer is option (b) and (d).

16.  If the Planck’s constant $\left( h \right)$ and the speed of light in vacuum $\left( c \right)$ are taken as two fundamental quantities, which one of the following can, in addition, be taken to express length, mass and time in terms of the three chosen fundamental quantities. 

(a) Mass of electron $\left( {{m_e}} \right)$

(b) Universal gravitational constant $\left( G \right)$

(c) Charge of electron $\left( e \right)$

(d) Mass of proton $\left( {{m_p}} \right)$

Ans. Options (a), (b) and (d) 

The dimension of Planck’s constant is 

$h = \dfrac{E}{\nu }$

$ \Rightarrow \dfrac{{\left[ {M{L^2}{T^{ - 2}}} \right]}}{{\left[ {{T^{ - 1}}} \right]}} = \left[ {M{L^2}{T^{ - 1}}} \right]$   ….eq(a)

dimension of speed of light in vacuum is

$c = \dfrac{s}{t}$

$ = \left[ {L{T^{ - 1}}} \right]$ …..eq(b)

(a) dimension of mass of electron $\left( {{m_e}} \right)$ is

${m_e} = \left[ M \right]$

On dividing equation (a) and (b) we get,

$\dfrac{h}{c} = \dfrac{{\left[ {M{L^2}{T^{ - 1}}} \right]}}{{\left[ {L{T^{ - 1}}} \right]}}$

$ = \left[ {ML} \right]$

$ \Rightarrow \dfrac{h}{c} = {m_e} \times \left[ L \right]$

$ \Rightarrow \left[ L \right] = \dfrac{h}{c} \times \dfrac{1}{{{m_e}}}$

$ = \left[ {{m_e}^{ - 1}h{c^{ - 1}}} \right]$

In eq (b)

$c = \left[ {L{T^{ - 1}}} \right]$

$ \Rightarrow c = \left[ {{m_e}^{ - 1}h{c^{ - 1}}{T^{ - 1}}} \right]$

$ \Rightarrow \left[ T \right] = \left[ {{m_e}^{ - 1}h{c^{ - 1 - 1}}} \right]$

$ \Rightarrow \left[ T \right] = \left[ {{m_e}^{ - 1}h{c^{ - 2}}} \right]$

(b) dimension of universal gravitational constant is

$G = \dfrac{{F{r^2}}}{{{M_1}{M_2}}}$      ….eq(c)

$ \Rightarrow \dfrac{{\left[ {M{L^3}{T^{ - 2}}} \right]}}{{\left[ M \right]\left[ M \right]}} = \left[ {{M^{ - 1}}{L^3}{T^{ - 2}}} \right]$     ….eq(i)

$hc = \left[ {M{L^2}{T^{ - 1}}} \right] \times \left[ {L{T^{ - 1}}} \right]$

$ = \left[ {M{L^3}{T^{ - 2}}} \right]$                 ….eq(ii)

On dividing both equation (i) and (ii) 

$\dfrac{{hc}}{G} = \dfrac{{\left[ {M{L^3}{T^{ - 2}}} \right]}}{{\left[ {{M^{ - 1}}{L^3}{T^{ - 2}}} \right]}}$

$ = \left[ {{M^2}} \right]$

$ \Rightarrow M = \sqrt {\dfrac{{hc}}{G}} $

$ = \left[ {{h^{\dfrac{1}{2}}}{c^{\dfrac{1}{2}}}{G^{ - \dfrac{1}{2}}}} \right]$

On dividing eq(a) and eq(b),

$\dfrac{h}{c} = \dfrac{{\left[ {M{L^2}{T^{ - 1}}} \right]}}{{\left[ {L{T^{ - 1}}} \right]}}$

$ \Rightarrow \left[ {ML} \right] = \sqrt {\dfrac{{hc}}{G}}  \times L$

$L = \dfrac{h}{c} \times \sqrt {\dfrac{G}{{hc}}} $

$ \Rightarrow \dfrac{{\sqrt {Gh} }}{{{c^{\dfrac{3}{2}}}}} = \left[ {{G^{\dfrac{1}{2}}}{h^{\dfrac{1}{2}}}{c^{ - \;\dfrac{3}{2}}}} \right]$

$c = \left[ {L{T^{ - 1}}} \right]$

$ = \left[ {{G^{\dfrac{1}{2}}}{h^{\dfrac{1}{2}}}{c^{ - \,\dfrac{3}{2}}}{T^{ - 1}}} \right]$

$T = \left[ {{G^{\dfrac{1}{2}}}{h^{\dfrac{1}{2}}}{c^{ - \;\dfrac{3}{2} - 1}}} \right]$

$ = \left[ {{G^{\dfrac{1}{2}}}{h^{\dfrac{1}{2}}}{c^{ - \;\dfrac{5}{2}}}} \right]$

(c) this option cannot be represented $L$, $M$ and $T$ in terms of the chosen fundamental quantities.

(d) dimension of mass of proton $\left( {{m_p}} \right)$ is

${m_p} = \left[ M \right]$

On dividing equation (a) and (b) we get,

$\dfrac{h}{c} = \dfrac{{\left[ {M{L^2}{T^{ - 1}}} \right]}}{{\left[ {L{T^{ - 1}}} \right]}}$

$ = \left[ {ML} \right]$

$ \Rightarrow \dfrac{h}{c} = {m_p} \times \left[ L \right]$

$ \Rightarrow \left[ L \right] = \dfrac{h}{c} \times \dfrac{1}{{{m_p}}}$

$ = \left[ {{m_p}^{ - 1}h{c^{ - 1}}} \right]$

In eq (b)

$c = \left[ {L{T^{ - 1}}} \right]$

$ \Rightarrow c = \left[ {{m_p}^{ - 1}h{c^{ - 1}}{T^{ - 1}}} \right]$

$ \Rightarrow \left[ T \right] = \left[ {{m_p}^{ - 1}h{c^{ - 1 - 1}}} \right]$

$ \Rightarrow \left[ T \right] = \left[ {{m_p}^{ - 1}h{c^{ - 2}}} \right]$

Thus, option (a), (b) and (d) can express $L$, $M$ and $T$ in terms of the chosen fundamental quantities.

17. Which of the following ratios express pressure?

(a) $\dfrac{{Force}}{{Area}}$

(b) $\dfrac{{Energy}}{{volume}}$

(c) $\dfrac{{Energy}}{{Area}}$

(d) $\dfrac{{Force}}{{Volume}}$

Ans. Options (a) and (b)

We can express the ratio as pressure $\left( P \right)$ if the dimension of the ratio is the same as that of pressure. 

So, we will check the dimension of each option whether it is equal to $P$ or not.

a) Dimension of $\dfrac{F}{A} = \dfrac{{\left[ {ML{T^{ - 2}}} \right]}}{{\left[ {{L^2}} \right]}}$

$ \Rightarrow \left[ {M{L^{ - 1}}{T^{ - 2}}} \right] = dimension\,of\,P$

b) Dimension of $\dfrac{E}{V} = \dfrac{{\left[ {M{L^2}{T^{ - 2}}} \right]}}{{\left[ {{L^3}} \right]}}$

$ \Rightarrow \left[ {M{L^{ - 1}}{T^{ - 2}}} \right] = dimension{\text{ }}of\,P$

c) Dimension of $\dfrac{E}{A} = \dfrac{{\left[ {M{L^2}{T^{ - 2}}} \right]}}{{\left[ {{L^2}} \right]}}$

$ \Rightarrow \left[ {M{L^0}{T^{ - 2}}} \right] \ne \;dimension\,\,of\,P$

d) Dimension of $\dfrac{F}{V} = \dfrac{{\left[ {ML{T^{ - 2}}} \right]}}{{\left[ {{L^3}} \right]}}$

$ \Rightarrow \left[ {M{L^{ - 2}}{T^{ - 2}}} \right] \ne dimension{\text{ }}of{\text{ }}P{\text{ }}$

$\therefore $ The correct answers are (a) and (b).

18. Which of the following are not units of time?

(a) Second

(b) Parsec

(c) Year

(d) Light year

Ans. options (b) and (d) 

The unit of time measured in second and year thus their dimension is $\left[ {{M^0}{L^0}{T^1}} \right]$. Whereas Parsec and light year give the measurement of distance and their dimensions are of distance i.e., $\left[ L \right]$ which is not equivalent to the dimension of time $\left[ T \right]$. So, option (b) and (d) are the correct answers to this question.

VERY SHORT ANSWER TYPE QUESTIONS

19. Why do we have different units for the same physical quantity?

Ans. To compute the different orders of the quantity; for the same physical quantity, we have different units. Let us take an example of speed, the speed of light is $3 \times {10^8}\;m{s^{ - 1}}$ whereas the speed of a person is ${10^0}\,cm{s^{ - 1}}$ and the speed of a train is $100\,km\;{h^{ - 1}}$. 

The above example verified that the same physical quantity can be expressed in different units depending upon the orders of quantity. 

20. The radius of the atom is of the order of $1\;\mathop A\limits^ \circ  $ and the radius of the nucleus is of the order of fermi. How many magnitudes higher is the volume of atoms as compared to the volume of the nucleus?

Ans. 

As shown in the figure the radius of atom $\left( R \right) = 1\;\mathop A\limits^ \circ   = {10^{ - 10}}\;m$

Radius of nucleus $\left( r \right) = 1\,fermi = {10^{ - 15}}\,m$

Ratio of volume of atom and nucleus is:

$ \Rightarrow \dfrac{{\dfrac{4}{3}\pi {R^3}}}{{\dfrac{4}{3}\pi {r^3}}} = \dfrac{{{R^3}}}{{{r^3}}}$

$ \Rightarrow {\left( {\dfrac{{{{10}^{ - 10}}}}{{{{10}^{ - 15}}}}} \right)^3} = {\left( {{{10}^5}} \right)^3}$

$ = {10^{15}}$

21. Name the device used for measuring the mass of atoms and molecules.

Ans. Charge particle’s deflection depends upon the magnitude of either magnetic or electric field. By using this principle, mass and charge of a particle can be measured by using a spectrograph or spectrometer which measures the mass of atoms and molecules. 

22. Express unified atomic mass unit in $kg$.

Ans. The unified atomic mass unit $\left( u \right)$ or Dalton $\left( {Da} \right)$ is described as one twelfth of the mass of carbon-12 $\left( {^{12}C} \right)$ atom which is unbind at rest and in its ground state. We know that by Avogadro’s number $6.023 \times {10^{23}}$, mass of $6.023 \times {10^{23}}$ atoms of carbon $_6{C^{12}}$ is equal to $12\;gm$.

So, mass of one atom of $_6{C^{12}} = \dfrac{{12}}{{6.023 \times {{10}^{23}}}}\,gm$

$1\,amu = \dfrac{1}{{12}}mass\;of\,one{\,_6}{C^{12}}$

$ = \dfrac{1}{{12}} \times \dfrac{{12}}{{6.023 \times {{10}^{23}}}}gm$

$ = 1.66 \times {10^{ - 24}}gm$

$1\;amu = 1.66 \times {10^{ - 27}}kg$

23. A function $f\left( \theta  \right)$ is defined as:

$f\left( \theta  \right) = 1 - \theta  + \dfrac{{{\theta ^2}}}{{2!}} - \dfrac{{{\theta ^3}}}{{3!}} + \dfrac{{{\theta ^4}}}{{4!}} - ........$

Why is it necessary for $f\left( \theta  \right)$ to be a dimensionless quantity?

Ans. Here the angle which is represented by $\theta $ is equal to $\dfrac{{arc}}{{radius}}$

$\theta  = \dfrac{{{L}}}{{{L}}} = no\,unit$

Thus, it is dimensionless physical quantity. In this expression, the first term is a constant i.e., numerical value which is dimensionless. The next term is $\theta $ that is dimensionless. Similarly, each term in R.H.S. expression is dimensionless which makes $f\left( \theta  \right)$ of L.H.S. dimensionless.

24.  Why length, mass and time are chosen as base quantities in mechanics?

Ans. The physical quantities, length, mass and time cannot be derived from any other physical quantities and all physical quantities of mechanics. That’s why length, mass and time are chosen as the base quantities in mechanics.

SHORT ANSWER TYPE QUESTIONS

25. (a) the earth-moon distance is about $60$ times the earth radius. What will be the diameter of earth (approximately in degrees) as seen from the moon?

Ans. (a) the angle is 

$\theta  = \dfrac{{arc}}{{radius}}$

$ \Rightarrow \dfrac{{{R_e}}}{{60{R_e}}} = \dfrac{1}{{60}}rad$

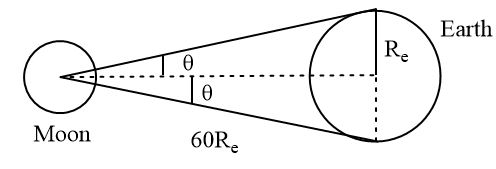
So, the angle from the moon to the diameter of the earth is

$2\theta  = 2 \times \dfrac{1}{{60}} \times \dfrac{{180}}{\pi }$

$ \Rightarrow \theta  = \dfrac{{{6^o}}}{\pi }$

$ \Rightarrow \dfrac{6}{{3.14}} = {2^o}$

(b) Moon is seen to be of ${\left( {\dfrac{1}{2}} \right)^0}$ diameter from the earth. What must be the relative size of the moon as compared to the earth?

Ans: Angle by which moon can be seen from earth (diametrically) = ${\dfrac{1}{2}^o}$

$\therefore \dfrac{{size\,of\,moon}}{{size(diameter)\,of\,earth}} = \dfrac{{\left( {\dfrac{1}{2}} \right)}}{{{2^o}}}$

$ = \dfrac{1}{4}$

$\therefore $ the size of the moon is one fourth of the size of earth.

(c) From parallax measurement, the sun is found to be at a distance of about $400$ times the earth-moon distance. Estimate the ratio of sun-earth diameters.

Ans: Let us take the distance between earth and moon ${r_{em}} = k\;m$

And the distance between the earth and the sun is

${r_{se}} = 400\;m$

In a solar eclipse the sun is covered by the moon fully. Thus, the angle formed by the diameter of moon and sun on earth are equal

$\therefore {\theta _m} = {\theta _s}$

Here, ${\theta _m}$ is the angle of the moon from earth and ${\theta _s}$ is the angle of sun from earth.

${\theta _m} = {\theta _s}$

$ \Rightarrow \dfrac{{{D_m}}}{{{r_{em}}}} = \dfrac{{{D_s}}}{{{r_{se}}}}$

$ \Rightarrow \dfrac{{{D_m}}}{x} = \dfrac{{{D_s}}}{{400x}}$

$ \Rightarrow \dfrac{{{D_s}}}{{{D_m}}} = \dfrac{{400{x}}}{{{x}}}$

$\therefore 4{D_m} = {D_e}$

Or ${D_m} = \dfrac{{{D_e}}}{4}$

$\therefore \dfrac{{{D_s}}}{{\dfrac{{{D_e}}}{4}}} = 400$

$ \Rightarrow \dfrac{{4{D_s}}}{{{D_e}}} = 400$

$\therefore \dfrac{{{D_s}}}{{{D_e}}} = \dfrac{{400}}{4}$

$ \Rightarrow \dfrac{{{D_s}}}{{{D_e}}} = 100$

$ \Rightarrow {D_s} = 100{D_e}$

26. Which of the following time measuring devices is most precise?

(a) a wall clocks

(b) a stopwatch

(c) a digital watch

(d) an atomic clock

Give reason for your answer.

Ans. To answer this question we have to know about the least count of the all clocks. The least count of a wall clock, stop watch, a digital watch and an atomic clock are $1\;\sec $, $\dfrac{1}{{10}}\;\sec $, $\dfrac{1}{{100}}\;\sec $ and $\dfrac{1}{{{{10}^{13}}}}\;\sec $ respectively. So, among these clocks, the atomic clock is most precise as it has the least least count than others.

27. The distance of the galaxy is of the order of ${10^{25}}\,m$. Calculate the order of magnitude of the time taken by light to reach us from the galaxy.

Ans. According to the question, distance travelled by light from galaxy to earth $ = \,{10^{25}}\,m$

Thus, the required time $ = \dfrac{{Distance}}{{speed}}$

$ \Rightarrow \dfrac{{{{10}^{25}}}}{{3 \times {{10}^8}}}\,\sec  = \dfrac{1}{3} \times {10^{17}}\,seconds.$

$required\,time = \dfrac{{10}}{3} \times {10^{16}}$

$ = 3.3\bar 3 \times {10^{16}}\;seconds.$

This is the required answer.

28. The Vernier scale of travelling microscope has $50$ divisions which coincide with $49$ divisions of main scale divisions. If each main scale division is $0.5\;mm$, calculate the minimum inaccuracy in measurement of distance.

Ans. The least count is the smallest reading on the main scale. To find the least count, we take the difference of one main scale division and one vernier scale division. When the $n$ parts of Vernier scale concur with the $\left( {n - 1} \right)$part of the main scale.

$L.C. = \dfrac{{L.C.\,\,of\,M.\,scale}}{n}$

In this question, parts on Vernier scale $ \Rightarrow n = 50\,parts$

And the number of divisions in M.S. concurring with $n$ parts of V.S.$ = \left( {n - 1} \right)$

$\therefore $L.C. of instrument $ = \dfrac{{L.C.\,\,of\;Mainscale}}{{No.\;of\,parts\,on\,V.S.}}$

$ = \dfrac{{0.5\;mm}}{{50}}$

Or minimum inaccuracy $ = 0.01\,mm$

29. During a total solar eclipse, the moon almost covers the sphere of the sun. write the relation between the distances and sizes of the sun and moon.

Ans.  As we know that${D_m} = 2{R_m}$             

And ${D_s} = 2{R_s}$

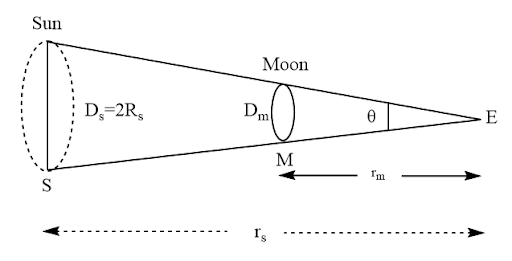
On the total eclipse, solid angle of sun and moon o the earth become equal 

$\therefore {\Omega _s} = {\Omega _m}$

$ \Rightarrow \dfrac{{\pi {{\left( {\dfrac{{{D_s}}}{2}} \right)}^2}}}{{r_s^2}} = \dfrac{{\pi {{\left( {\dfrac{{{D_m}}}{2}} \right)}^2}}}{{r_m^2}}$

$ \Rightarrow \dfrac{{D_s^2}}{{4r_s^2}} = \dfrac{{D_m^2}}{{4r_m^2}}$

$ \Rightarrow \dfrac{{{{\left( {2{R_s}} \right)}^2}}}{{4r_s^2}} = \dfrac{{{{\left( {2{R_m}} \right)}^2}}}{{4r_m^2}}$

$ \Rightarrow \dfrac{{{4}R_s^2}}{{{4}r_s^2}} = \dfrac{{{4}R_m^2}}{{{4}r_m^2}}$

On taking square root on both side

$ \Rightarrow \dfrac{{{R_s}}}{{{r_s}}} = \dfrac{{{R_m}}}{{{r_m}}}$

Or, $\dfrac{{{R_s}}}{{{R_m}}} = \dfrac{{{r_s}}}{{{r_m}}}$

Thus, the ratio of the size of sun to moon is equal to the ratio of the distances of sun to moon from earth. 

30. If the unit of force is $100\,N$, unit of length is $10\;m$ and unit of time is $100\,s$. What is the unit of mass in this system of units?

Ans. The dimension of force $ = \left[ {{M^1}{L^1}{T^2}} \right]$

$ = 100\,N$

Dimension of length $ = \left[ {{L^1}} \right]$

$ = 10\;m$

Dimension of time $ = \left[ {{T^1}} \right]$

$ = 100\;s$

$\because \left[ {{M^1}{L^1}{T^{ - 2}}} \right] = 100\,m$

$M \times \left( {10} \right) \times {\left( {100} \right)^{ - 2}} = 100$

$\dfrac{{10\,M}}{{100 \times 100}} = 100$

$M = {10^5}\;Kg$

$L = \;{10^1}\;m$

$F = {10^2}\,N$

$T = {10^2}\,\sec $

31. Give an example of: 

(a) A physical quantity which has a unit but no dimension

Ans. (a) the formula of plane angle is

$plane\,angle = \dfrac{{arc}}{{radius}}$

It has unit which is in radian but it does not have dimension because

$plane\,angle = \dfrac{{arc}}{{radius}}$

$ \Rightarrow \dfrac{{\left[ {{L}} \right]}}{{\left[ {{L}} \right]}} = \,no\,unit$

(b) A physical quantity which has neither unit nor dimension

Ans: strain is the ratio of the same physical quantity thus it doesn’t have any unit and dimension.

$strain = \dfrac{{\Delta L}}{L}$

Where, $\Delta L$ is the change in length and $L$is the original length.

(c) A constant which has a unit

Ans: Gravitational constant which is denoted by $G$ is a constant which has a unit i.e., $N\;{m^{2\,}}\,k{g^{ - 2}}$. Its value is $6.67 \times {10^{ - 11}}$.

(d) A constant which has no unit 

Ans: Avogadro’s number is the constant which has no unit. Its value is $6.022 \times {10^{23}}$.

32. Calculate the length of the arc of a circle of radius $31.0\;cm$ which subtends an angle of $\dfrac{\pi }{6}$ at the centre.

Ans. In this question,

$angle = \dfrac{{length\;of\,arc}}{{radius\,of\;arc}}$

Let the length of the arc be $x$.

According to the formula,

$\dfrac{\pi }{6} = \dfrac{x}{{31}}$

$ \Rightarrow x = \dfrac{{31 \times \pi }}{6}$

$ \Rightarrow x = \dfrac{{31 \times 3.14}}{6}$

$ \Rightarrow x = 16.22\;cm$

33. Calculate the solid angle subtended by the periphery of an area $1\;c{m^2}$ at a point situated symmetrically at a distance of $5\,cm$ from the area.

Ans. The formula of solid angle $\Omega  = \dfrac{{Area}}{{{{\left( {distance} \right)}^2}}}$ 

$ \Rightarrow \dfrac{{1\;c{m^2}}}{{{{\left( {5\,cm} \right)}^2}}} = \dfrac{1}{{25}}$

$ = 4 \times {10^{ - 2}}\,steradian.$

34. The displacement of a progressive wave is represented by $y = A\,\sin \left( {\omega t - kx} \right)$, where $x$ is distance and $t$ is time. Write the dimensional formula of 

(i) $\omega $

(ii) $k$

Ans.  by principal of homogeneity, the dimensional formula in L.H.S. and R.H.S. are equal. Thus, 

\[Dimension\;of\,y = Dimension\,of\,A\sin \,\left( {\omega t - kx} \right)\]

$\left[ L \right] = \left[ L \right] \times Dimension\,of\sin \left( {\omega t - kx} \right)$

Here $\omega t - kx$ is the angle of $\sin $ (trigonometric ratio)

$\omega t - kx$ has no dimension 

Or, \[dimension\;of\,\omega t = dimension\;of\;kx\]

$\therefore \dfrac{{2\pi }}{T}t = K \cdot x$

$ \Rightarrow \left[ {{M^0}{L^0}{T^0}} \right] = k\left[ L \right]$

Thus, dimension of k$ = \dfrac{{\left[ {{M^0}{L^0}{T^0}} \right]}}{{\left[ L \right]}}$

$ = \left[ {{M^0}{L^{ - 1}}{T^0}} \right]$

Whereas, $\omega $ is dimensionless.

35. Time for $20$ oscillations of a pendulum is measured as ${t_1} = 39.6\,s$; ${t_2} = 39.9\,s$ and ${t_3} = 39.5\,s$. What is the precision in the measurement? What is the accuracy of measurement?

Ans. Given,

${t_1} = 39.6\,s$;${t_2} = 39.9\,s$ and ${t_3} = 39.5\;s$

Number of oscillations $ = 20$

Least count of the instrument $ = 0.1\,s$

Thus, the precision $ = 0.1\;s$

Mean value of time for $20$ oscillations

$ \Rightarrow \dfrac{{39.6 + 39.9 + 39.5}}{3} = \dfrac{{119.0}}{3}$

$ = 39.7\;s$

In measurement, the absolute errors

$\left| {\Delta {t_1}} \right| = \left| {\bar t - {t_1}} \right|$

$ \Rightarrow \left| {39.7 - 39.6} \right| = \left| {0.1} \right|$

$ = 0.1\;s$

$\left| {\Delta {t_2}} \right| = \left| {\bar t - {t_2}} \right|$

$ \Rightarrow \left| {39.7 - 39.9} \right| = \left| { - 0.2} \right|$

$ = 0.2\;s$

$\left| {\Delta {t_3}} \right| = \left| {\bar t - {t_3}} \right|$

$ \Rightarrow \left| {39.7 - 39.5} \right| = \left| {0.2} \right|$

$ = 0.2\;s$

$\therefore $mean absolute error $ = \dfrac{{0.1 + 0.2 + 0.2}}{3}$

$ \Rightarrow \dfrac{{0.5}}{3} \cong 0.2\;s$

Thus, accuracy of measurement $ =  \pm 0.2\,s.$

LONG ANSWER TYPE QUESTIONS

36. A new system of units is proposed in which the unit of mass is $\alpha \;kg$ , unit of length $\beta \;m$ and unit of time $\gamma \;s$. How much will $5j$ measure in this new system?

Ans. The dimension formula of energy is

$energy = \left[ {M{L^2}{T^{ - 2}}} \right]$

${n_2}{u_2} = {n_1}{u_1}$

${n_2} = {n_1}\dfrac{{{u_1}}}{{{u_2}}}$

$ \Rightarrow {n_2} = {n_1}{\left[ {\dfrac{{{M_1}}}{{{M_2}}}} \right]^1}{\left[ {\dfrac{{{L_1}}}{{{L_2}}}} \right]^2}{\left[ {\dfrac{{{T_1}}}{{{T_2}}}} \right]^{ - 2}}$

Let the new system of unit be $x$

${n_2} = \,new\,system\,of\,unit = x$

${n_1} = S.I.\,system\,of\,unit = 5j\,$

${M_2} = \alpha \;kg$

${M_2} = 1\;kg$

${L_2} = \beta \,m$

${L_1} = 1\,m$

${T_2} = \gamma \;s$

${T_1} = 1\;s$

${n_2} = 5{\left[ {\dfrac{{1\;kg}}{{\alpha \;kg}}} \right]^1}{\left[ {\dfrac{{1\,m}}{{\beta \,m}}} \right]^2}{\left[ {\dfrac{{1\,\sec }}{{\gamma \,\sec }}} \right]^{ - 2}}$

${n_2} = 5\left[ {{\alpha ^{ - 1}}{\beta ^{ - 2}}{\gamma ^2}} \right]$

New system $ = \dfrac{{{\gamma ^2}}}{{\alpha {\beta ^2}}}$or $\left[ {{\alpha ^{ - 1}}{\beta ^{ - 2}}{\gamma ^2}} \right]$

37. The volume of a liquid flowing out per second from a pipe of length $l$ and radius $r$ is written by a student as $V = \dfrac{{\pi {{\Pr }^4}}}{{8\eta l}}$ where $P$ is the pressure difference between two ends of pipe and $\eta $ is coefficient of viscosity of the liquid having dimensional formula $\left[ {M{L^{ - 1}}{T^{ - 1}}} \right]$. Check whether the equation is dimensionally correct or not.

Ans. Dimension of volume per second is

$\dfrac{V}{T} = \left[ {{L^3}{T^{ - 1}}} \right]$

Dimension of Pressure $ = \dfrac{F}{A}$

$ \Rightarrow \dfrac{{\left[ {ML{T^{ - 2}}} \right]}}{{\left[ {{L^2}} \right]}} = \left[ {M{L^{ - 1}}{T^{ - 2}}} \right]$

Dimension of $r = \left[ L \right]$

Dimension of $\eta  = \left[ {M{L^{ - 1}}{T^{ - 1}}} \right]$ 

Dimension of $l = \left[ L \right]$ 

Dimension of R.H.S.$ = \dfrac{{\left[ {M{L^{ - 1}}{T^{ - 2}}} \right]\left[ {{L^4}} \right]}}{{\left[ {M{L^{ - 1}}{T^{ - 1}}} \right]\left[ L \right]}}$

$ = \left[ {{M^0}{L^3}{T^{ - 1}}} \right]$

Dimension of L.H.S. $V = \left[ {{M^0}{L^3}{T^1}} \right]$ 

We can see, dimensions of both sides are equal. Thus, the given equation is dimensionally correct.

38. A physical quantity $X$ is related to four measurable quantities $a$, $b$,$c$ and $d$ as follows:$X = {a^2}{b^3}{c^{\dfrac{5}{2}}}{d^{ - 2}}$. The percentage error in the measurement of $a$, $b$, $c$ and $d$ are $1\% $, $2\% $, $3\% $ and $4\% $ respectively. What is the percentage error in quantity $X$? If the value of $X$ calculated on the basis of the above relation is \[{\mathbf{2}}.{\mathbf{763}}\], to what value should you round off the result? 

Ans. The percentage error in the physical quantity 

$\dfrac{{\Delta X}}{X} \times 100 =  \pm \left[ {2\dfrac{{\Delta a}}{a} + 3\dfrac{{\Delta b}}{b} + \dfrac{5}{2}\dfrac{{\Delta c}}{c} + 2\dfrac{{\Delta d}}{d}} \right] \times 100$ 

$ \Rightarrow \dfrac{{\Delta X}}{X} \times 100 =  \pm \left[ {\dfrac{{2 \times 1}}{{100}} + \dfrac{{3 \times 2}}{{100}} + \dfrac{5}{2} \times \dfrac{3}{{100}} + \dfrac{{2 \times 4}}{{100}}} \right]100$

$ =  \pm \dfrac{{100}}{{100}}\left[ {2 + 6 + \dfrac{{15}}{2} + 8} \right]$

$\dfrac{{\Delta X}}{X} \times 100 =  \pm \left[ {16 + \dfrac{{15}}{2}} \right]$

$ =  \pm \left[ {\dfrac{{32 + 15}}{2}} \right]$

$ = \dfrac{{47}}{2}$

$ =  \pm 23.5\% $

$\therefore $Mean absolute error $ =  \pm \dfrac{{23.5}}{{100}}$

$ =  \pm 0.235$

= 0.24 (rounding off in significant figure)

On rounding off \[X{\text{ }} = {\text{ }}2.763\](again in two significant figures)\[ = 2.8\]

39. In the expression $P = E{l^2}{m^{ - 5}}{G^{ - 2}}$ , $E$, $l$, $m$ and $G$ denote energy, angular momentum, mass and gravitational constant respectively. Show that $P$ is a dimensionless quantity.

Ans. Dimensional formulas of $E$,$l$ and $G$:

$E = \left[ {M{L^2}{T^{ - 2}}} \right]$

$l = \left[ {M{L^2}{T^{ - 1}}} \right]$

$G = \left[ {{M^{ - 1}}{L^3}{T^{ - 2}}} \right]$

$\therefore $ dimension of $P = E{l^2}{m^{ - 5}}{G^{ - 2}}$ :

$\left[ P \right] = \dfrac{{\left[ E \right]\left[ {{l^2}} \right]}}{{\left[ {{m^5}} \right]\left[ {{G^2}} \right]}}$

$ = \dfrac{{\left[ {M{L^2}{T^{ - 2}}} \right]{{\left[ {M{L^2}{T^{ - 1}}} \right]}^2}}}{{{{\left[ M \right]}^5}{{\left[ {{M^{ - 1}}{L^3}{T^{ - 2}}} \right]}^2}}}$

$ = \left[ {{M^0}{L^0}{T^0}} \right]$

So, P is a dimensionless quantity.

40. If velocity of light $C$, Planck’s constant $h$ and gravitational constant $G$ are taken as fundamental quantities then express mass, length and time in terms of dimensions of these quantities.

Ans. dimension of Planck’s constant $h$$ = \dfrac{E}{\nu }$

$ = \dfrac{{\left[ {M{L^2}{T^{ - 2}}} \right]}}{{\left[ {{T^{ - 1}}} \right]}}$

$ = \left[ {M{L^2}{T^{ - 1}}} \right]$

Dimension of speed of light $C = \left[ {L{T^{ - 1}}} \right]$

Dimension of gravitational constant $G = N\,{m^2}\,k{g^{ - 2}}$

$ = \left[ {ML{T^{ - 2}}} \right]\left[ {{L^2}} \right]\left[ {{M^{ - 2}}} \right]$

$ = \left[ {{M^{ - 1}}{L^3}{T^{ - 2}}} \right]$

Let us first take mass $M$,

$M \propto {\left[ h \right]^a}{\left[ C \right]^b}{\left[ G \right]^c}$

$\left[ {{M^1}{L^0}{T^0}} \right] = k{\left[ {M{L^2}{T^{ - 1}}} \right]^a}{\left[ {L{T^{ - 1}}} \right]^b}{\left[ {{M^{ - 1}}{L^3}{T^{ - 2}}} \right]^c}$

$\left[ {{M^1}{L^0}{T^0}} \right] = k\left[ {{M^{a - c}}{L^{2a + b + 3c}}{T^{a - b - 2c}}} \right]$

Comparing the powers on the both sides,

$a - c = 1$

$ \Rightarrow a = c + 1$

$2a + b + 3c = 0$

$2\left( {c + 1} \right) + b + 3c = 0$ , putting the value of $a = c + 1$

$2c + 2 + b + 3c = 0$

$b + 5c =  - 2$   eq(i)

$ - a - b - 2c = 0$

$ - \left( {c + 1} \right) - b - 2c = 0$, putting the value of $a = c + 1$

$ - b - 3c = 1$    eq(ii)

Adding eq(i) and eq(ii),

$b + 5c - b - 3c =  - 2 + 1$

$c =  - \dfrac{1}{2}$

$\therefore a = c + 1$

$a =  - \dfrac{1}{2} + 1$

$a = \dfrac{1}{2}$

Put the value of $c$in the equation (i)

$ \Rightarrow b + 5\left( { - \dfrac{1}{2}} \right) =  - 2$

$b =  - 2 + \dfrac{5}{2}$

$b = \dfrac{1}{2}$, $a = \dfrac{1}{2}$and $c =  - \dfrac{1}{2}$

$\therefore M = k{h^{\dfrac{1}{2}}}{C^{ + \dfrac{1}{2}}}{G^{ - \dfrac{1}{2}}}$

$M = k\sqrt {\dfrac{{hC}}{G}} $

Let us first take length $L$,

$L \propto {\left[ h \right]^a}{\left[ C \right]^b}{\left[ G \right]^c}$

$\left[ {{M^0}{L^1}{T^0}} \right] = k{\left[ {M{L^2}{T^{ - 1}}} \right]^a}{\left[ {L{T^{ - 1}}} \right]^b}{\left[ {{M^{ - 1}}{L^3}{T^{ - 2}}} \right]^c}$

$\left[ {{M^0}{L^1}{T^0}} \right] = k\left[ {{M^{a - c}}{L^{2a + b + 3c}}{T^{a - b - 2c}}} \right]$

Comparing the powers on the both sides,

$a - c = 0$

$ \Rightarrow a = c$

$2a + b + 3c = 1$

$2\left( c \right) + b + 3c = 1$ , putting the value of $a = c$

$2c + b + 3c = 1$

$b + 5c = 1$   eq(i)

$ - a - b - 2c = 0$

$ - \left( c \right) - b - 2c = 0$, putting the value of $a = c$

$ - b - 3c = 0$    eq(ii)

Adding eq(i) and eq(ii),

$b + 5c - b - 3c = 1 + 0$

$c = \dfrac{1}{2}$

$\therefore a = c$

$a = \dfrac{1}{2}$

Put the value of $c$ in the equation (i)

$ \Rightarrow b + 5\left( {\dfrac{1}{2}} \right) = 1$

$b = 1 - \dfrac{5}{2}$

$b =  - \dfrac{3}{2}$, $a = \dfrac{1}{2}$and $c = \dfrac{1}{2}$

$\therefore L = k{h^{\dfrac{1}{2}}}{C^{ - \dfrac{3}{2}}}{G^{\dfrac{1}{2}}}$

$L = k\sqrt {\dfrac{{hG}}{{{C^3}}}} $

Let us first take time $T$,

$T \propto {\left[ h \right]^a}{\left[ C \right]^b}{\left[ G \right]^c}$

$\left[ {{M^0}{L^0}{T^1}} \right] = k{\left[ {M{L^2}{T^{ - 1}}} \right]^a}{\left[ {L{T^{ - 1}}} \right]^b}{\left[ {{M^{ - 1}}{L^3}{T^{ - 2}}} \right]^c}$

$\left[ {{M^0}{L^0}{T^1}} \right] = k\left[ {{M^{a - c}}{L^{2a + b + 3c}}{T^{a - b - 2c}}} \right]$

Comparing the powers on the both sides,

$a - c = 0$

$ \Rightarrow a = c$

$2a + b + 3c = 0$

$2\left( c \right) + b + 3c = 0$ , putting the value of $a = c$

$2c + b + 3c = 0$

$b + 5c = 0$   eq(i)

$ - a - b - 2c = 1$

$ - \left( c \right) - b - 2c = 1$, putting the value of $a = c$

$ - b - 3c = 1$    eq(ii)

Adding eq(i) and eq(ii),

$b + 5c - b - 3c = 0 + 1$

$c = \dfrac{1}{2}$

$\therefore a = c$

$a = \dfrac{1}{2}$

Put the value of $c$ in the equation (i)

$ \Rightarrow b + 5\left( {\dfrac{1}{2}} \right) = 0$

$b =  - \dfrac{5}{2}$

$b =  - \dfrac{5}{2}$, $a = \dfrac{1}{2}$and $c = \dfrac{1}{2}$

$\therefore T = k{h^{\dfrac{1}{2}}}{C^{ - \dfrac{5}{2}}}{G^{\dfrac{1}{2}}}$

$T = k\sqrt {\dfrac{{hG}}{{{C^5}}}} $

41. An artificial satellite is revolving around a planet of mass $M$ and radius $R$ in a circular orbit of radius $r$. From Kepler’s Third law about the period of satellite around a common central body, square of the period of revolution $T$ is proportional to the cube of the radius of the orbit $r$. show using dimensional analysis, that: 

$T = \dfrac{K}{R}\sqrt {\dfrac{{{r^3}}}{g}} $

Where $K$ is a dimensionless constant and $g$ is acceleration due to gravity?

Ans. By utilizing Kepler’s third law of planetary motion

${T^2} \propto {r^3}$

$T \propto {r^{\dfrac{3}{2}}}$

$T$also depends on radius $R$and $g$,

$T \propto {g^a}{R^b}{r^{\dfrac{3}{2}}}$

$T = K{\left[ {L{T^{ - 2}}} \right]^a}{\left[ L \right]^b}{\left[ L \right]^{\dfrac{3}{2}}}$

$\left[ {{M^0}{L^0}{T^1}} \right] = K\left[ {{M^0}{L^{a + b + \dfrac{3}{2}}}{T^{ - 2a}}} \right]$

On comparing the power on both sides

$a + b + \dfrac{3}{2} = 0$  eq (i)

$ - 2a = 1$

$ \Rightarrow a =  - \dfrac{1}{2}$

Putting this value in equation (i)

$ - \dfrac{1}{2} + b + \dfrac{3}{2} = 0$

$b + 1 = 0$

$b =  - 1$

$T = K{g^{ - \dfrac{1}{2}}}{R^{ - 1}}{r^{\dfrac{3}{2}}}$

$T = \dfrac{K}{R}\sqrt {\dfrac{{{r^3}}}{g}} $

Hence proved.

42. In an experiment to estimate the size of a molecule of oleic acid, \[{\mathbf{1}}\;{\mathbf{mL}}\] of oleic acid is dissolved in \[{\mathbf{19}}\;{\mathbf{mL}}\] of alcohol. Then \[{\mathbf{1}}\;{\mathbf{mL}}\] of this solution is diluted to \[{\mathbf{20}}{\text{ }}{\mathbf{ml}}\] by adding alcohol. Now \[{\mathbf{1}}\] drop of this diluted solution is placed on water in a shallow through. The solution spreads over the surface of water forming one molecule thick layer. Now, Lycopodium powder is sprinkled evenly over the film and its diameter is measured. Knowing the volume of the film, its diameter is measured. Knowing the volume of the drop and area of the film we can calculate the thickness of the film, which will give us the size of oleic acid molecules. 

Read the passage carefully and answer the following questions:

(a) Why do we dissolve oleic acid in alcohol? 

Ans. (a) After we lessen the concentration of oleic acid by dissolving it in a very correct solvent, we have a propensity to get to a molecular level. Oleic acid cannot be diffused in ionic solvent water as it is an organic compound. It can only be diffused in organic solvent alcohol.

(b) What is the role of lycopodium powder?

Ans: The part of Lycopodium is to forestall to merge oleic acid in water after we poured a drop of oleic acid on water. So, first on the surface of water, it has a tendency to spread Lycopodium powder and then a skinny layer of diluted oleic acid is formed on the surface of Lycopodium unfolding on water.

(c) What would be the volume of oleic acid in each ml of solution prepared. 

Ans: The amount of oleic acid (volume) within the solution is 

$\dfrac{1}{{20}} \times \dfrac{1}{{20}}V = \dfrac{1}{{400}}V\;ml$

If the quantity of $V$is $1\;ml$then the specified concentration in one $ml$solution $ = \dfrac{1}{{400}}\;ml$ as given in the question.

(d) How will you calculate the volume of drops of this solution of oleic acid?

Ans: To calculate the volume of the $n$ drop solution, we can use a burette. By dropping $1\;ml$ solution drop by drop in a beaker and count its number of drops. If there is $n$ drop in $1\;ml$ then volume of 

$1\;drop = \dfrac{1}{n}\;ml$

(e) What will be the volume of oleic acid in one drop of this solution?

Ans: The volume of a drop of solution is $\dfrac{1}{n}\;ml$ (if we have a tendency to measured $n$ drops in one $ml$ in partially (d) then concentration of oleic acid in $1$ drop solution) 

$ \Rightarrow \dfrac{1}{{400}}V = \dfrac{1}{{400}} \cdot \dfrac{1}{n}\;ml$ 

$ = \dfrac{1}{{400}}ml\,oleic\;acid$.

43. (a) How many astronomical units \[\left( {{\mathbf{A}}.{\mathbf{U}}} \right)\] make \[{\mathbf{1}}{\text{ }}{\mathbf{parsec}}\]? 

Ans. (a) The distance at which $1\,A.U.$ long arc subtends angle of $1\;s$or $1\,arc\,\sec $

$Angle\,1\,\sec  = \dfrac{{1A.U.}}{{1\,arc\,\sec }}$

$\therefore 1\;parsec = \dfrac{{1\,A.U.}}{{1\,arc\,\sec }}$

As we known,

$1\;arc\;\sec  = \dfrac{\pi }{{180 \times 3600}}radian$

$1\;parsec = \dfrac{{1 \times 180 \times 3600}}{\pi }A.U.$

$ = \dfrac{{7 \times 180 \times 3600}}{{22}}$

$ \Rightarrow 1\;parsec = \dfrac{{630 \times 3600}}{{11}}$

$ = \dfrac{{2268000}}{{11}}$

$ = 206181.8$

$1\;parsec = 2 \times {10^5}A.U.$

(b) Consider a sun like a star at a distance of\[{\mathbf{2}}{\text{ }}{\mathbf{parsec}}\]. When it is seen through a telescope with magnification, what should be the angular size of the star? Sun appears to be ${\left( {\dfrac{1}{2}} \right)^o}$ from the earth due to atmospheric fluctuations, eye cannot resolve objects smaller than \[{\mathbf{1}}{\text{ }}{\mathbf{arc}}\] minute.

Ans: Angle subtends by $1\;A.U.$ of sun’s diameter$ = {\left( {\dfrac{1}{2}} \right)^o}$

Because the distance from the sun rises the angle subtended in the same ratio.

Distant star ($2 \times {10^5}\;A.U.$) will form angle of

$\theta  = {\left( {\dfrac{{\dfrac{1}{2}}}{{2 \times {{10}^5}}}} \right)^o}$

$ = {\left( {\dfrac{1}{{4 \times {{10}^5}}}} \right)^o}$

So $1\;parsec$ subtended angle on earth of size (diameter of sun) is $\dfrac{1}{{4 \times {{10}^5}}}$ as the sunlike star’s diameter is same as sun. Suppose star be like sun is at $2\;parsec$ then angle at earth by star becomes

$ = \dfrac{1}{{4 \times {{10}^5}}} \times \dfrac{1}{2}$

$ = \dfrac{1}{8} \times {10^{ - 5}}$

$ = \left( {1.25 \times {{10}^{ - 6}}} \right)$

$angle = \left( {1.25 \times {{10}^{ - 6}}} \right)\;\min $

$ = \left( {75 \times {{10}^{ - 6}}} \right)\min $

(c) Mars has approximately half of earth’s diameter. When it is closest to earth, it is at about $\dfrac{1}{2}{\mathbf{A}}.{\mathbf{U}}.$ from the earth. Calculate what size it will appear when seen through the same telescope. (Comment: This is to illustrate why a telescope can magnify planets but not stars.)

Ans: When these star like sun glimpse by telescope of magnification$100$, then angle establish by sun like star becomes

$75 \times {10^{ - 6}} \times 100 = 75 \times {10^{ - 4}}$

=$7.5 \times {10^{ - 3}}\min $ is very less than $1\;\min $ as eyes cannot determine an object or image smaller than one minute. So cannot be perceived by a given telescope. 

44. Einstein’s mass energy relation emerging out from this famous theory of relativity relates mass ($m$) to energy ($E$) as $E = m{c^2}$ , where $c$ is speed of light in vacuum. At the nuclear level, the magnitude of energy is usually measured in $MeV$ where\[{\mathbf{1}}{\text{ }}{\mathbf{MeV}} = 1.6 \times {10^{ - 13}}{\text{ }}{\mathbf{J}}\]; the mass is measured in unified atomic mass unit\[\;\left( {\mathbf{u}} \right)\]where\[{\mathbf{1}}{\text{ }}{\mathbf{u}} = {\text{ 1}}{\text{.67}} \times {\text{1}}{{\text{0}}^{ - 27}}{\text{ K}}{\mathbf{g}}\]. 

(a) Show that energy equivalent of 1 u is 931.5 MeV 

The teacher points out that the relation is dimensionally incorrect. Write the correct relation.

Ans. (a) Given, 

$m = 1\;u$

$ = 1.67 \times {10^{ - 27}}kg$

$c = 3 \times {10^8}\,m{s^{ - 1}}$ 

According to mass energy relation given by Einstein 

$E = m{c^2}$

$E = 1.67 \times {10^{ - 27}} \times 3 \times {10^8} \times 3 \times {10^{8\;}}J$

$ = 1.67 \times {10^{ - 27 + 16}} \times 9\,J$

$ = \dfrac{{1.67 \times 9 \times {{10}^{ - 11}}}}{{1.6 \times {{10}^{ - 13}}}}MeV$

$ = \dfrac{{15.03 \times {{10}^{ - 11 + 13}}}}{{1.6}}MeV$

$E = \dfrac{{1503}}{{1.6}}$

$ = 939.4MeV$

$ \cong 931.5MeV$

(b) A student writes the relation as 1 u = 931.5 MeV 

Ans: Here, $1\;amu = 931.5\,MeV$

Is dimensionally not correct, but if we represent generally $931.5\,MeV$ energy will be released if $1\,u$ mass is converted totally into energy.

$E = m{c^2}$

$ \Rightarrow 1\,u\,{c^2} \cong 931.5MeV$

Is dimensionally correct.

NCERT Exemplar for Class 11 Physics Chapter 2 solutions

The NCERT Exemplar for Class 11 Physics Chapter 2 Units and Measurements is provided by Vedantu for the benefit of the student in their CBSE Class 11 examination and other competitive examinations. Chapter 2: Units and Measurements are basic to all future endeavours of the students, so it is very important that they understand and memorize every concept in this chapter thoroughly.

The NCERT exemplar Class 11 Physics Chapter 2 pdf provided on the Vedantu’s site with the solutions will help the students to get profound with the units and measurement as it consists of the questions from the NCERT exemplar book along with extra questions prepared by subject experts at Vedantu. The NCERT exemplar Class 11 physics Chapter 2 will also comprise the important questions from the previous year’s question papers and sample papers helping the student to get an idea of the exam pattern and prepare accordingly.

In chapter 2, Units and Measurement the measurement refers to the comparison of a standard unit of any physical quantity with a standard unit. Also, the laws of physics that are described in terms of the quantities whose measurements are necessary are titled physical quantities. A standard unit must be universally accepted and easily reproducible as a definite amount.

Some of the fundamental units of measurement are described below as follows:

1. Mass: Can be defined as the quantity of matter in a physical body.

2. Time: Can be defined as the interval over which any change occurs.

3. Temperature: Can be defined as the average kinetic energy of the particles in a particular system.

4. Length: It can be defined as the measurement of the physical quantity in distance.

5. Electric current: It can be defined as the flow of electric charge between two distinct points.

Download this solution file and work on your concepts for this chapter. Learn how the experts of Vedantu have compiled the answers to all the questions by following the NCERT syllabus and guidelines. Practice answering these questions and become more confident. You can also download the solutions for the other chapters of Class 11 and prepare for the board and competitive exams.