Question

You are given several identical resistors each of value of \[5\,\Omega \] and each capable of carrying a maximum current of \[2\,A\]. It is required to make a suitable combination of these resistances to produce a resistance of \[\,2.5\,\Omega \] which can carry current of \[4\,A\]. the minimum number of resistances required for this job is?

Answer 1

Hint: In series current remains the same and equivalent resistance is greater than the individual resistances. In parallel combination the current gets divided and the equivalent resistance is lesser that the individual resistances.

Complete answer:
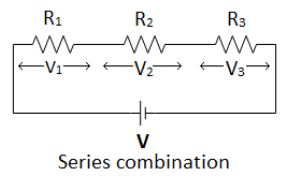
Series combination:
-The resistors are in series combination when same current passes through each of
the resistors present in the combination.
-Voltage across each resistance is directly proportional to its value
Hence, \[{V_1}\, = \,I \times {R_1}\] ,\[{V_2}\, = \,I \times {R_2}\], \[{V_3}\, = \,I \times {R_3}\]
-Sum of voltage across each individual resistor is equal to the Voltage applied across the whole combination.
\[V\, = \,{V_1} + {V_2} + {V_3}\,\]
\[ \Rightarrow I \times R\,\, = \,I \times {R_1} + I \times {R_2} + I \times {R_3}\]
\[ \Rightarrow \,R\, = \,{R_1} + {R_2} + {R_3}\]
where \[R\] is equivalent resistance of the combination.

Parallel combination:
-The resistors are in parallel when each of the resistors present in the combination has the same voltage difference across them.
-Current in each resistance is inversely proportional to the value of resistance.
\[{I_{1\,}}\, = \,\dfrac{V}{{{R_1}}}\], \[{I_2}\, = \,\dfrac{V}{{{R_2}}}\], \[{I_3}\, = \,\dfrac{V}{{{R_3}}}\].

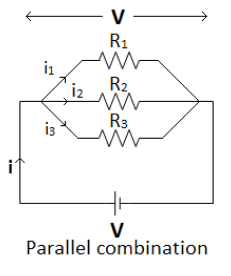
Current flowing in the circuit is sum of the
currents in individual resistance.
\[I\, = \,\,{I_1} + {I_2} + {I_3}\,\]
\[ \Rightarrow \dfrac{V}{R} = \,\dfrac{V}{{{R_1}}}\, + \,\,\dfrac{V}{{{R_2}}}\, + \,\,\dfrac{V}{{{R_3}}}\]
\[ \Rightarrow \dfrac{1}{R} = \,\dfrac{1}{{{R_1}}}\, + \,\,\dfrac{1}{{{R_2}}}\, + \,\,\dfrac{1}{{{R_3}}}\].
To get maximum resistance, resistance must be connected in series and in series the resultant is greater than the individual. To get minimum resistance, resistance must be connected in parallel and the equivalent resistance of parallel combination is lower than the value of lowest resistance in the combination.

As the equivalent resistance of the combination is lower than the individual resistances taken so from above two statements it is clear that the combination is a parallel combination. Also, as the current has increased (doubled) so the combination can’t be series as the same current flows through each of the resistance in series combination.Hence, it is clear that the combination of resistances in parallel combination.

Let the number of resistances used be \[x\].
Given resistance of the resistors = \[5\,\Omega \]
\[\therefore \,\,\dfrac{1}{{{R_{eq}}}}\, = \,\dfrac{1}{{{R_1}}}\, + \,\dfrac{1}{{{R_2}}}\, + \,\,\dfrac{1}{{{R_3}}}.......\]
Here all resistors are of same resistance (\[5\,\Omega \])
\[\therefore \,\,\dfrac{1}{{{R_{eq}}}}\, = \,\dfrac{1}{5}\, + \,\dfrac{1}{5}\, + \,\,\dfrac{1}{5}.......\,x\,times\]
\[ \Rightarrow \,\,\dfrac{1}{{2.5}}\, = \,\dfrac{x}{5}\,\]
\[ \Rightarrow \,\,x\,\, = \,\,2\]
Hence two resistances in parallel make the desired combination.

Verifying this combination with current. As we know that current gets divided in the inverse ratio of current. Hence, here the current will get halved. So, if \[4\,A\] is passed through the combination. Each resistance will have \[2\,A\] of current through them, which is inside their capacity. The required combination is two \[5\,\Omega \] resistance in parallel as shown in diagram.

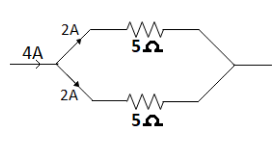
Note: Current is constant in series combination whereas voltage is constant in parallel combination. In our home parallel combinations are there to avoid short circuits and to not operate all the appliances simultaneously.