Question

Write the inclination of a line parallel to the y-axis.

Answer 1

Hint: To measure the inclination, we should try to find out the angle made by the line with the x-axis. This angle $\theta $ will be the inclination of the line.

Complete step-by-step answer:

It is given that the line is parallel to the y axis. Now, from the figure below(in which the points A and C lie on the line), we find that angle $\angle ACB$ is a corresponding angle of alpha (as the y-axis and the line are parallel).

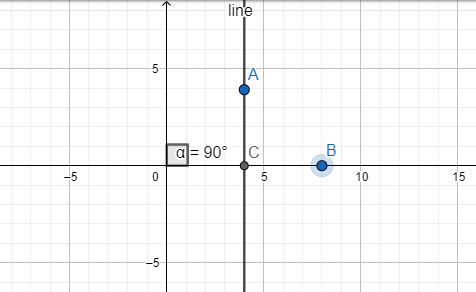
Also, by the rule of geometry, we should have that corresponding angles should be equal.

Also, in the figure, the angle of the line with the x-axis is equal to $\angle ACB$.

Therefore, we find that the slope of the line, given by the angle $\angle ACB$ will be equal to $\alpha ={{90}^{\circ }}$ and thus the inclination of the line w.r.t. the x-axis should be equal to ${{90}^{\circ }}$. Also, as the line and y-axis are parallel to each other, the inclination w.r.t. the y-axis should be zero.

Note: We can also use the equation of the line to find the slope. Two parallel lines will have the same slope. Thus as the y-axis can be represented by the equation $y=mx+c$where $m=\infty $ and thus equivalently as $x=0$, we find that the line parallel to it should also have $m=\infty $and thus its slope should be infinity. The angle with x-axis can be found from the slope using the formula $angle={{\tan }^{-1}}(m)$. And thus $angle={{\tan }^{-1}}\left( \infty \right)={{90}^{\circ }}$ which is the which we had obtained earlier.