
Write a rational number and its opposite in the decimal form. How do you know that these are opposite rational numbers? Write a rational number and its opposite in the fraction form.
Answer
578.1k+ views
Hint:Rational numbers are the numbers which can be expressed as \[\dfrac{p}{q}\] ratio, where \[p\], \[q\] are integers and \[q \ne 0\]. The opposite of a number is the same distance from 0 as the number itself, but on the other side of 0 on a number line.
Complete step-by-step answer:
We need to first write a rational number.
Also we have to find its opposite in the decimal form.
Let us the take the rational number \[\dfrac{1}{2}\] (It is a rational number because we can expressed it as \[\dfrac{p}{q}\] ratio, where \[p\], \[q\] are integers and \[q \ne 0\]).
The decimal form of this number is \[0.5\] .
It’s opposite in the decimal form is \[ - 0.5\].
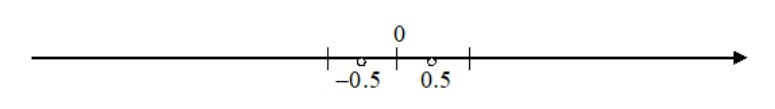
In the diagram, \[0.5\] is the opposite of \[ - 0.5\], and \[ - 0.5\] is the opposite of \[0.5\]. The distance from \[0.5\] to \[0\] is \[0.5\], and the distance from\[ - 0.5\] to \[0\] is \[0.5\]; this distance to \[0\] is the same for both \[0.5\] and \[ - 0.5\]. The absolute value of a number is its distance from \[0\] on a number line.
Let us take the rational number \[\dfrac{3}{5}\] , it’s opposite in the fraction form is \[ - \dfrac{3}{5}\].
Note:
Whole numbers: Whole numbers are simply the numbers \[0,\;{\text{ }}1,{\text{ }}2,\,{\text{ }}3,{\text{ }}4,{\text{ }}5,\,{\text{ }}6,\;....\]
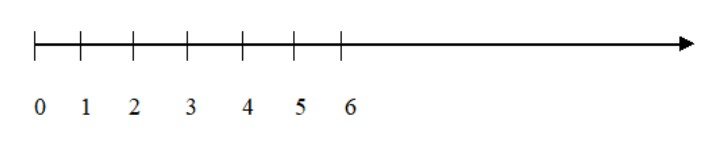
Integers: Integers are like whole numbers, but they also include negative numbers but still no fractions allowed.
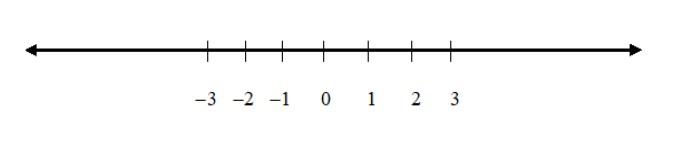
So integers can be negative {\[ - 1, - 2, - 3, - 4, - 5, - 6,....\]}, positive {\[1,2,3,4,5,6,....\]} or zero {\[0\]}.
Rational number:Rational numbers are the numbers which can be expressed as \[\dfrac{p}{q}\] ratio, where \[p\], \[q\] are integers and \[q \ne 0\].
Complete step-by-step answer:
We need to first write a rational number.
Also we have to find its opposite in the decimal form.
Let us the take the rational number \[\dfrac{1}{2}\] (It is a rational number because we can expressed it as \[\dfrac{p}{q}\] ratio, where \[p\], \[q\] are integers and \[q \ne 0\]).
The decimal form of this number is \[0.5\] .
It’s opposite in the decimal form is \[ - 0.5\].
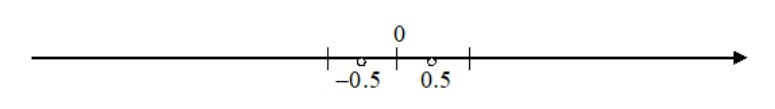
In the diagram, \[0.5\] is the opposite of \[ - 0.5\], and \[ - 0.5\] is the opposite of \[0.5\]. The distance from \[0.5\] to \[0\] is \[0.5\], and the distance from\[ - 0.5\] to \[0\] is \[0.5\]; this distance to \[0\] is the same for both \[0.5\] and \[ - 0.5\]. The absolute value of a number is its distance from \[0\] on a number line.
Let us take the rational number \[\dfrac{3}{5}\] , it’s opposite in the fraction form is \[ - \dfrac{3}{5}\].
Note:
Whole numbers: Whole numbers are simply the numbers \[0,\;{\text{ }}1,{\text{ }}2,\,{\text{ }}3,{\text{ }}4,{\text{ }}5,\,{\text{ }}6,\;....\]
Integers: Integers are like whole numbers, but they also include negative numbers but still no fractions allowed.
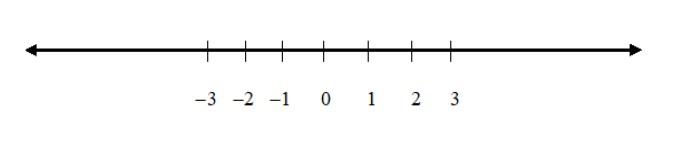
So integers can be negative {\[ - 1, - 2, - 3, - 4, - 5, - 6,....\]}, positive {\[1,2,3,4,5,6,....\]} or zero {\[0\]}.
Rational number:Rational numbers are the numbers which can be expressed as \[\dfrac{p}{q}\] ratio, where \[p\], \[q\] are integers and \[q \ne 0\].
Recently Updated Pages
Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Biology: Engaging Questions & Answers for Success

Master Class 12 Physics: Engaging Questions & Answers for Success

Master Class 8 Maths: Engaging Questions & Answers for Success

Class 8 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
Write a letter to the principal requesting him to grant class 10 english CBSE

Which of the following does not have a fundamental class 10 physics CBSE

State and prove the Pythagoras theorem-class-10-maths-CBSE

What is the full form of POSCO class 10 social science CBSE

State BPT theorem and prove it class 10 maths CBSE

A Gulab jamun contains sugar syrup up to about 30 of class 10 maths CBSE




