Question

Volume of a hollow sphere is $\dfrac{{11352}}{7}{\text{ c}}{{\text{m}}^3}$ . If the outer radius is 8cm, find the inner radius of the sphere. (Take $\pi = \dfrac{{22}}{7}$ )

Answer 1

Hint- If the hollow sphere has its outer radius as R and inner radius as small r then volume of the sphere is given as $V = \dfrac{4}{3}\pi ({R^3} - {r^3})$ . Using this formula we will find our solution.
Let $R$ and $r$ be the outer and inner radii of the hollow sphere respectively.
Let $V$ be the volume of the hollow sphere.

Complete step-by-step answer:

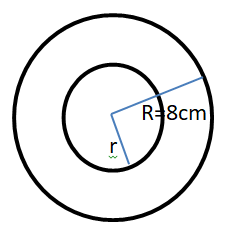
Given that volume of the sphere is
$V = \dfrac{{11352}}{7}{\text{ c}}{{\text{m}}^3}$
And outer radius is
$R = 8cm$
Now substituting these values in the formula of volume of sphere, we obtain
$
   \Rightarrow V = \dfrac{4}{3}\pi ({R^3} - {r^3}) \\
   \Rightarrow \dfrac{{11352}}{7} = \dfrac{4}{3} \times \dfrac{{22}}{7}({8^3} - {r^3}) \\
 $
On simplifying above equation for the value of $r$ , we obtain
\[
   \Rightarrow \dfrac{{11352 \times 3}}{{22 \times 4}} = {8^3} - {r^3} \\
   \Rightarrow 387 = 512 - {r^3} \\
   \Rightarrow {r^3} = 512 - 387 \\
   \Rightarrow {r^3} = 125 \\
   \Rightarrow r = 5cm \\
 \]
Hence, the inner radius of the hollow sphere is, \[r = 5cm\]

Note- To solve these types of questions formulas of volumes of shapes must be remembered. Here we have to calculate the volume of a hollow sphere and both the radii are given. We have calculated the volume of the hollow part with a small radius and volume of the whole sphere; then we subtracted the volume of the hollow sphere from the volume of the whole sphere. In this question we have the formula but the question can be solved using this approach also.