Question

Using theorem 6.1, prove that a line drawn through the midpoint of one side of the triangle parallel to the other side bisects the third side. (Recall that you have proved it in class IX).
Theorem 6.1: If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio.

Answer 1

Hint: Think about what we have given and what we can conclude from it. Write down what exactly we need to prove in this problem and use basic proportionality theorems.

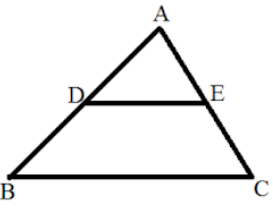
In $\vartriangle ABC$, we have given that, D is midpoint of AB and DE is parallel to BC. $\therefore AD = DB$.

We need to prove that AE=EC. Since, $DE\parallel BC$. By basic proportionality theorem, $\dfrac{{AD}}{{DB}} = \dfrac{{AE}}{{EC}}$.
Also, AD=DB so $\dfrac{{AE}}{{EC}} = 1 \Rightarrow AE = EC$. Hence proved.

Note: In theorems unlike the other mathematical problems, we need to think logically. What we have given and how we can use it in order to reach our goal.