Question

Using ruler and compasses only, draw an angle of measure of ${135^ \circ }$

Answer 1

Hint- This question can be solved by knowing that ${135^ \circ } = {90^ \circ } + {45^ \circ }$ .

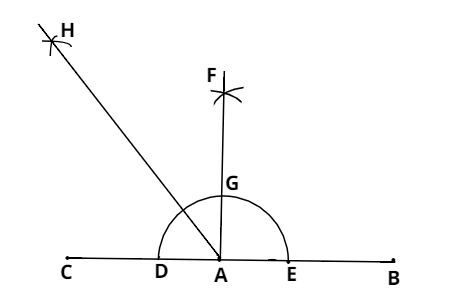
We have to draw an angle of the measure ${135^ \circ }$.
Steps of construction: -
$\left( 1 \right)$ Draw a line segment $AB$ and produce $BA$ to point $C.$
$\left( 2 \right)$ With centre $A$ and any radius draw an arc which intersects$AC$ at $D$ and $AB$ at $E$ .
$\left( 3 \right)$ With centres $D$ and $E$ and radius more than $\frac{1}{2}DE$ ,draw two arcs which intersect each other at $F$ .
$\left( 4 \right)$ Join $FA$ which intersects the arc in $\left( 2 \right)$ at $G$ .
$\left( 5 \right)$ With centres $G$ and $D$ and radius more than $\frac{1}{2}GD$ ,draw two arcs which intersect each other at $H$ .
$\left( 6 \right)$ Join $HA$.
$\therefore \angle HAB = {135^ \circ }$
Note- Whenever we face such types of questions the key concept is that we should construct a straight angle and then draw its perpendicular bisector as we did and then we get, ${90^ \circ } + {90^ \circ }$ but, we need${90^ \circ } + {45^ \circ }$ i.e. ${135^ \circ }$ so, we draw the angle bisector of one right angle and we get $\angle HAB = {135^ \circ }$ .