Question

Using a protractor, draw an angle of measure ${108^ \circ }$. With this angle as given, draw an angle of ${54^ \circ }$.

Answer 1

Hint: Start by drawing the given angle of ${108^ \circ }$ using protractor, the next step is to analyse the next angle they have given us to draw, in this question they have given us ${54^ \circ }$ which is just the half of ${108^ \circ }$, so we can bisect the angle. To bisect the angle, we take radius in the compass and draw the arc from x axis and y axis, the point at which they intersect is the point where ${54^ \circ }$ is obtained, from the origin extending a line to that point.

Complete step-by-step answer:

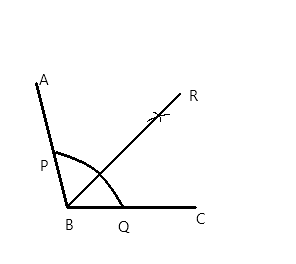
Step #1: Using protractor, draw an angle ABC of measure ${108^ \circ }$
Step #2: With centre B, and taking any radius, draw an arc, intersecting the ray BA and the ray BC at point D and E respectively.
Step #3: With centre D and radius greater than half of DE, draw an arc inside the angle.
Step #4: With centre E and taking the same radius as in step 3, draw an arc intersecting the arc drawn in step 3, at F.
Step #5: Draw the ray BF. This is the angle bisector of angle ABC. So $\angle FBC = {54^ \circ }$
Step #6: With centre B and taking any radius, draw an arc intersecting the ray BF and the ray BC at G and H respectively.
Step #7: Draw a ray MN.
Step #8: With a centre M and taking the same radius as in step 6, draw an arc intersecting the ray MN at point P.
Step #9: With centre P and taking radius equal to HG, draw an arc intersecting the arc drawn in step 8, at point L.
Step #10: Draw the ray ML.
Angle LMN is the desired angle of measure ${54^ \circ }$

Note: The main motive in this question should be o understand the relation between the angles given to draw, like in this question one of the angle was half the angle that was given, therefore we bisected it once, similarly if they had given us an angle one-third the given angle then we should have bisected it thrice, and so on.