Question

Two trains are moving in the same direction at 50km/hr. and 30km/hr. The faster train crossed a man in the slower train in 18 seconds. Find the length of the faster train?
a)80m
b)90m
c)100m
d)Can’t be determined

Answer 1

Hint: Use the relation $\text{speed = }\dfrac{\text{distance}}{\text{time}}$ to solve the problem.

Complete step by step answer:
Take man as a point with no width and a faster train crosses him if the endpoint of the train and man will lie on line. So, calculate distance travelled by men and faster train in 18sec and hence find the length using the difference of them.

As we know the relation among speed, distance and time is

$\text{speed = }\dfrac{\text{distance}}{\text{time}}$ …………….. (i)

So, we have two trains with the speed 50km/hr and 30km/hr and faster is crossing a man in slower train in 18 seconds and hence we need to determine the length of the faster train.

Therefore, let the faster train is crossing the man in the second train in time ‘t’ hours and covering a distance d, km, and let the man in the slower train cover distance $'{{d}_{2}}'$ km in time ‘t’ hours.

As we can observe that a faster train is crossing the man, not the train, so man will act as a point object. So, if the faster train just cross the man in second train, then diagram could be like:

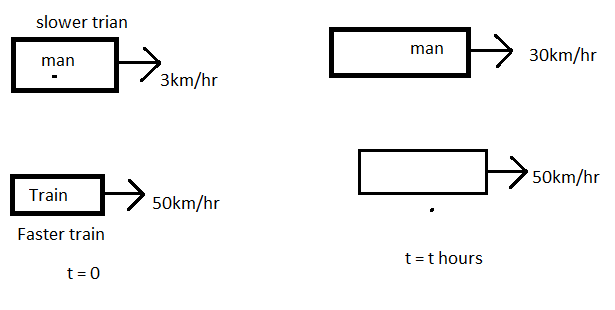
Now, it is given that the faster train is crossing the second train in 18 seconds. So, we need to convert it to hours and hence put it equal to t. We know,

60 seconds = 1 minute

$\text{1 second = }\dfrac{\text{1}}{\text{60}}\text{ minute}$

18 second = $\dfrac{18}{60}$ minute = $\dfrac{3}{10}$minute

And we also have relation:

60 minutes = 1 hour

$\dfrac{3}{10}$Minutes = $\dfrac{1}{60}\times \dfrac{3}{10}=\dfrac{1}{200}$hours.

Hence, the value of t is $\dfrac{1}{200}$ hr.

Now, we know that slower train is covering a distance $'{{d}_{2}}'$ km in t hours and faster train is covering distance $'{{d}_{1}}'$ km in ‘t’ hours. So, we can put these values to the equation (i).

For slower train

$30=\dfrac{{{d}_{2}}}{t}$

Put $t=\dfrac{1}{200}$ and we get on cross-multiplying the above equation as

$30\times \dfrac{1}{200}={{d}_{2}}$

${{d}_{2}}=\dfrac{3}{20}km$………………….. (iii)

And hence, distance $'{{d}_{1}}'$ can be calculated from the relation (i), using the speed, distance and time for faster trains. So, we get

$\begin{align}

  & 50=\dfrac{{{d}_{1}}}{t} \\

 & 50\times \dfrac{1}{200}={{d}_{1}} \\

\end{align}$

${{d}_{1}}-\dfrac{1}{4}km$………………….. (iv)

Now, we know that faster train will cross the man if train covers the distance that is covered by man and the length of its own (faster train) i.e. man will cover distance ${{d}_{2}}$ then train should cover ${{d}_{2}}$ + length of the train as shown in the diagram. It is shown in the diagram that man has covered $'{{d}_{2}}'$ in time ‘t’ and the faster train covered distance $\left( {{\text{d}}_{\text{2}}}\text{ + length} \right)$ at the just crossing point.

It means the difference between the distances ${{d}_{1}},{{d}_{2}}$ will give the length of the train. Hence, we get

$\begin{align}

  & \text{length = }{{\text{d}}_{\text{1}}}\text{- }{{\text{d}}_{\text{2}}}\text{ =
}\dfrac{\text{1}}{\text{4}}\text{=}\dfrac{\text{3}}{\text{20}} \\

 & \text{= }\dfrac{\text{5 - 3}}{\text{20}}\text{ = }\dfrac{\text{2}}{\text{20}}\text{ =
}\dfrac{\text{1}}{\text{10}}\text{ km} \\

\end{align}$

We can convert length in km to ‘m’ by multiplying it by 1000 as we know there are 1000m in
1 km. hence, we get

$\text{length = }\dfrac{\text{1}}{\text{10}}\text{ }\!\!\times\!\!\text{ 1000m = 100m}$

So, option (c) is the correct answer.

Note: One may go wrong with the relation of speed, distance, time. He/she may use formula as $\text{speed = }\dfrac{\text{distance}}{\text{time}}\text{, speed = distance }\!\!\times\!\!\text{ time}$,
Which is wrong. So, remember the exact formula to get the answer$\left( \text{speed = }\dfrac{\text{distance}}{\text{time}} \right)$.
One may think another approach using the concept of relative velocity. So, both are moving in the same direction (train and man). Hence, if we go by relative velocity, then the speed of the faster train will become (50 – 30) and time taken to reach the man will be 18 seconds (as men will be in rest position). Hence. We get
$\begin{align}
  & s=\dfrac{d}{t}=\dfrac{d}{\left( \dfrac{18}{60\times 60} \right)}=20 \\
 & \text{d = 20 }\!\!\times\!\!\text{ }\dfrac{\text{18}}{\text{60 }\!\!\times\!\!\text{
60}}\text{ km = }\dfrac{\text{20 }\!\!\times\!\!\text{ 18}}{\text{60 }\!\!\times\!\!\text{
60}}\times \text{ 1000m} \\
\end{align}$
d = 100m.