Question

Two poles are 10 m and 20 m high. The line joining their tips makes an angle of \[15^\circ \] with the horizontal. The distance between the poles is approximately equal to
(a) \[36.3\]m
(b) \[37.3\]m
(c) \[38.3\]m
(d) \[39.3\]m

Answer 1

Hint:
Here, we need to find the distance between the two poles. We will use the formula for tangent of an angle to form an equation. Then, we will use trigonometric identities and algebraic identities to simplify the equation, and obtain the required distance between the two poles.

Formula Used:
We will use the following formulas:
1) The tangent of an angle \[\theta \] in a right angled triangle is given by \[\tan \theta = \dfrac{{{\rm{Perpendicular}}}}{{{\rm{Base}}}}\].
2) The tangent of the difference of two angles is given by the trigonometric identity \[\tan \left( {A - B} \right) = \dfrac{{\tan A - \tan B}}{{1 + \tan A\tan B}}\].

Complete step by step solution:
First, we will draw the diagram using the information given in the question.

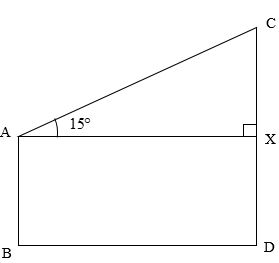
Here, AB is the first pole of height 10 m. CD is the second pole of height 20 m. The angle of elevation from the horizontal AX to the top of the pole CD is \[\angle CAX = 15^\circ \].
Now, since the poles are standing perpendicular to the ground, \[BD\] and \[AX\] are the shortest straight distances between the two houses.
Therefore, we can observe that \[BD\] and \[AX\] are equal and parallel.
Thus, we can conclude that the quadrilateral ABDX is a rectangle.
Therefore, we get
\[AB = XD = 10\]m
From the figure, we can observe that CD is the sum of the lengths CD and XD.
Therefore, we get
\[CD = CX + XD\]
Substituting \[XD = 10\]m and \[CD = 20\]m, we get
\[ \Rightarrow 20 = CX + 10\]
Subtracting 10 from both sides of the equation, we get
\[ \Rightarrow 20 - 10 = CX + 10 - 10\]
Therefore, we get
\[ \Rightarrow CX = 10\]m
Now, we will use the formula for tangent of an angle of a right-angled triangle to find the distance between the two poles.
We know that the tangent of an angle \[\theta \] in a right angled triangle is given by \[\tan \theta = \dfrac{{{\rm{Perpendicular}}}}{{{\rm{Base}}}}\].
Therefore, in triangle \[CAX\], we have
\[ \Rightarrow \tan \angle CAX = \dfrac{{CX}}{{AX}}\]
Substituting \[\angle CAX = 15^\circ \] and \[CX = 10\]m, we get
\[ \Rightarrow \tan 15^\circ = \dfrac{{10}}{{AX}}\]
The tangent of the difference of two angles is given by the trigonometric identity \[\tan \left( {A - B} \right) = \dfrac{{\tan A - \tan B}}{{1 + \tan A\tan B}}\].
Substituting \[A = 45^\circ \] and \[B = 30^\circ \] in the trigonometric identity, we get
\[ \Rightarrow \tan \left( {45^\circ - 30^\circ } \right) = \dfrac{{\tan 45^\circ - \tan 30^\circ }}{{1 + \tan 45^\circ \tan 30^\circ }}\]
Simplifying the expression, we get
\[ \Rightarrow \tan 15^\circ = \dfrac{{\tan 45^\circ - \tan 30^\circ }}{{1 + \tan 45^\circ \tan 30^\circ }}\]
The tangent of the angle measuring \[45^\circ \] is equal to 1.
The tangent of the angle measuring \[30^\circ \] is equal to \[\dfrac{1}{{\sqrt 3 }}\].
Substituting \[\tan 45^\circ = 1\] and \[\tan 30^\circ = \dfrac{1}{{\sqrt 3 }}\] in the expression, we get
\[ \Rightarrow \tan 15^\circ = \dfrac{{1 - \dfrac{1}{{\sqrt 3 }}}}{{1 + 1 \times \dfrac{1}{{\sqrt 3 }}}}\]
Simplifying the expression, we get
\[\begin{array}{l} \Rightarrow \tan 15^\circ = \dfrac{{\dfrac{{\sqrt 3 - 1}}{{\sqrt 3 }}}}{{1 + \dfrac{1}{{\sqrt 3 }}}}\\ \Rightarrow \tan 15^\circ = \dfrac{{\dfrac{{\sqrt 3 - 1}}{{\sqrt 3 }}}}{{\dfrac{{\sqrt 3 + 1}}{{\sqrt 3 }}}}\end{array}\]
Simplifying the terms, we get
\[ \Rightarrow \tan 15^\circ = \dfrac{{\sqrt 3 - 1}}{{\sqrt 3 + 1}}\]
Rationalising the denominator by multiplying and dividing the expression by \[\sqrt 3 - 1\], we get
\[ \Rightarrow \tan 15^\circ = \dfrac{{\sqrt 3 - 1}}{{\sqrt 3 + 1}} \times \dfrac{{\sqrt 3 - 1}}{{\sqrt 3 - 1}}\]
Therefore, we get
\[ \Rightarrow \tan 15^\circ = \dfrac{{{{\left( {\sqrt 3 - 1} \right)}^2}}}{{\left( {\sqrt 3 + 1} \right)\left( {\sqrt 3 - 1} \right)}}\]
Using the algebraic identities \[{\left( {a - b} \right)^2} = {a^2} - 2ab + {b^2}\] and \[\left( {a + b} \right)\left( {a - b} \right) = {a^2} - {b^2}\], we get
\[ \Rightarrow \tan 15^\circ = \dfrac{{3 + 1 - 2\sqrt 3 }}{{3 - 1}}\]
Adding and subtracting the terms, we get
\[ \Rightarrow \tan 15^\circ = \dfrac{{4 - 2\sqrt 3 }}{2}\]
Factoring out 2 from the numerator, we get
\[\begin{array}{l} \Rightarrow \tan 15^\circ = \dfrac{{2\left( {2 - \sqrt 3 } \right)}}{2}\\ \Rightarrow \tan 15^\circ = 2 - \sqrt 3 \end{array}\]
Substituting \[\tan 15^\circ = 2 - \sqrt 3 \] in the equation \[\tan 15^\circ = \dfrac{{10}}{{AX}}\], we get
\[ \Rightarrow 2 - \sqrt 3 = \dfrac{{10}}{{AX}}\]
Rewriting the expression, we get
\[ \Rightarrow AX = \dfrac{{10}}{{2 - \sqrt 3 }}\]
Substituting the approximate value \[\sqrt 3 = 1.732\], we get
\[ \Rightarrow AX = \dfrac{{10}}{{2 - 1.732}}\]
Subtracting the terms in the denominator, we get
\[ \Rightarrow AX = \dfrac{{10}}{{0.268}}\]
Simplifying the expression, we get
\[ \Rightarrow AX \approx 37.3\]m
Therefore, the distance between the two poles is approximately \[37.3\] metres.

Thus, the correct option is option (b).

Note:
Most of the time, the value of \[\sqrt 3 \] is given in the question, but in this question it is not given. You should remember the approximate value of \[\sqrt 3 = 1.732\] to simplify the final equation. A common mistake is to use \[1.414\], which is the value of \[\sqrt 2 \], and not \[\sqrt 3 \]. Using \[\sqrt 3 = 1.414\], you will get the incorrect answer.
Since quadrilateral ABDX is a rectangle, we concluded \[AB = XD = 10\]m. This is because the opposite sides of a rectangle are equal.