Question

Two particles A and B of masses 1 kg and 2 kg respectively are projected in the directions shown in figure with speed $ {{{u}}_{{A}}} $ =200m/s and $ {{{u}}_{{B}}} $ =50m/s. Initially they were 90m apart. They collide in mid-air and stick with each other. Find the maximum height attained by the centre of mass of the particles. Assume acceleration due to gravity to be constant (Take $ {{g = 10m/}}{{{s}}^{{2}}} $ ).

Answer 1

Hint: We need to calculate the maximum height attained by the centre of mass. First, we should find out the height of the centre of mass and then the velocity of the centre of mass to further get the maximum height of the centre of mass.

Formula used: We will start by solving equations for the height of the centre of mass.
For that we would be using the basic formula of centre of mass:
Height of centre of mass $ {{ = }}\dfrac{{{{{m}}_{{1}}}{{{H}}_{{1}}}{{ + }}{{{m}}_{{2}}}{{{H}}_{{2}}}}}{{{{{m}}_{{1}}}{{ + }}{{{m}}_{{2}}}}} $
Velocity of centre of mass $ {{ = }}\dfrac{{{{{m}}_{{1}}}{{{V}}_{{1}}}{{ + }}{{{m}}_{{2}}}{{{V}}_{{2}}}}}{{{{{m}}_{{1}}}{{ + }}{{{m}}_{{2}}}}} $
Also, equation of motion:
 $ {{{v}}^{{2}}}{{ = }}{{{u}}^{{2}}}{{ + 2as}} $

Complete step by step solution:
Here, we already know the mass and height of individual bodies of masses 1kg and 2 kg.

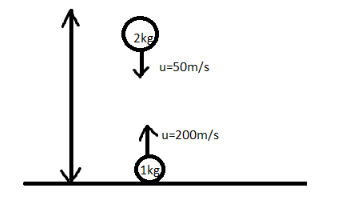
Also, there initial velocities are given
 $ {{{u}}_{{A}}} $ =200m/s
 $ {{{u}}_{{B}}} $ =50m/s
Initial distance between them is 90 m.
Now, Height of centre of mass $ {{ = }}\dfrac{{{{{m}}_{{1}}}{{{H}}_{{1}}}{{ + }}{{{m}}_{{2}}}{{{H}}_{{2}}}}}{{{{{m}}_{{1}}}{{ + }}{{{m}}_{{2}}}}} $
 $ \Rightarrow \dfrac{{{{200}} \times {{0 + 90}} \times {{2}}}}{{{{2 + 1}}}}{{ = }}\dfrac{{{{180}}}}{{{3}}}{{ = 60m}} $
Also, Velocity of centre of mass $ {{ = }}\dfrac{{{{{m}}_{{1}}}{{{V}}_{{1}}}{{ + }}{{{m}}_{{2}}}{{{V}}_{{2}}}}}{{{{{m}}_{{1}}}{{ + }}{{{m}}_{{2}}}}} $
 $ \Rightarrow \dfrac{{{{200}} \times {{1 - 50}} \times {{2}}}}{{{{2 + 1}}}}{{ = }}\dfrac{{{{100}}}}{{{3}}}{{m/s}} $
Now using the equation of motion,
 $ {{{v}}^{{2}}}{{ = }}{{{u}}^{{2}}}{{ + 2as}} $
It is already given that: $ {{a = g = 10m/}}{{{s}}^2} $
 $ \Rightarrow {0^2}{{ = }}{\left( {\dfrac{{{{100}}}}{{{3}}}} \right)^{{2}}}{{ - 2}} \times {{10}} \times {{h}} $
Since, the final velocity has to be 0 to attain maximum height.
 $ \Rightarrow {{h = }}\dfrac{{{{100 \times 100}}}}{{{{9 \times 2 \times 10}}}}{{ = 55}}{{.55m}} $
Thus, the total height obtained by the centre of mass= (60+55.55) m
The maximum height attained by the centre of mass =115.55 m

Additional information:
While studying about collisions we will know, There are three different kinds of collisions, however, elastic, inelastic, and completely inelastic. Just to restate, momentum is conserved in all three kinds of collisions. What distinguishes the collisions is what happens to the kinetic energy.

Note:
The common mistake during the evaluation is not taking the note that the particles stick together. Also, maximum height is always attained when the final velocity becomes 0.
Take the value of $ \left( {{g}} \right) $ to be $ {{9}}{{.8m/}}{{{s}}^{{2}}} $ if not mentioned in the question. Generally, the value is considered to be $ {{10m/}}{{{s}}^{{2}}} $ for the sake of calculation.