Question

Two circles of equal radii $ r $ cuts orthogonally. If their centres are $ \left( {2,3} \right) $ and $ \left( {5,6} \right) $ then $ r $ =
A. $ 1 $
B. $ 2 $
C. $ 3 $
D. $ 4 $

Answer 1

Hint: Since the two circles cut orthogonally it follows the formula that sum of the square of the first radius and square of the second radius is equal to the square of the distance between the centres of the circle. Use the property that the radius is equal for both circles.

Complete step-by-step answer:
Given that the circles cut orthogonally.
Given that the radius of the circles are equal.
Given the centres of the circles are $ \left( {2,3} \right) $ and $ \left( {5,6} \right) $ .

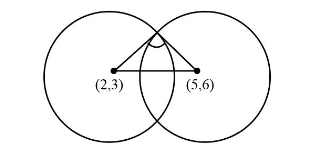
Now if the two circles are orthogonal to each other then the tangent of the first circle at the intersection point of the circle touches the other circle. So the tangents of the two circles form the right angled triangle where the base is the radius of one circle and height is the radius of the other circle and hypotenuse is equal to the distance between the centres of the circles.
Since the triangle is right angle triangle it follows Pythagoras theorem,
 $ \Rightarrow {\left( {base} \right)^2} + {\left( {height} \right)^2} = {\left( {hyp} \right)^2} $ ……(1)
Let us consider base as $ {r_1} $ .and height as $ {r_2} $ .
So after substituting (1) we get,
 $ \Rightarrow {r_1}^2 + {r_2}^2 = {\left( {hyp} \right)^2} $ ……(2)
We know the radius is equal then we will take $ {r_1} = {r_2} = r $ .
On substitute the value in (2) we get,
 $ \Rightarrow 2{r^2} = {\left( {hyp} \right)^2} $ ……(3)
The hypotenuse is equal to the distance of the two centres.
To find the distance between two points as $ \left( {{x_1},{y_1}} \right) $ and $ \left( {{x_2},{y_2}} \right) $ .
We know the distance between the two points is,
 $ \Rightarrow \sqrt {{{\left( {{x_1} - {x_2}} \right)}^2} + {{\left( {{y_1} - {y_2}} \right)}^2}} $
The distance between $ \left( {2,3} \right) $ and $ \left( {5,6} \right) $ is,
 $
\Rightarrow \sqrt {{{\left( {2 - 5} \right)}^2} + {{\left( {3 - 6} \right)}^2}} = \sqrt {{3^2} + {3^2}} \\
 = 3\sqrt 2
 $
Hence, the hypotenuse is $ 3\sqrt 2 $ .
Then on substitute the values in (3) we get,
 $
\Rightarrow 2{r^2} = {\left( {3\sqrt 2 } \right)^2}\\
\Rightarrow 2{r^2} = 9 \times 2\\
\Rightarrow\Rightarrow {r^2} = 9\\
\Rightarrow r = \pm 3
 $
Hence, we get the value of radius as $ r = 3 $ .
Therefore, the radius of the circle is $ 3 $ .
So, the correct answer is “ $ 3 $ ”.

Note: Here, in this problem we have taken radius as $ 3 $ instead of -3 because the radius of the circle will never be negative. The triangle formed is right angled only when the circle is orthogonal but in other cases it differs.