
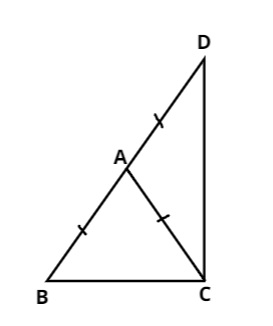
Triangle $ABC$ is an isosceles triangle in which $AB = AC$ , side $BA$ is produced to $D$ such that $AD = AB$ .Show that $\angle BCD$ is a right angle.

Answer
605.7k+ views
Hint: In order to solve this question, we will use angle sum property and the property of isosceles triangle according to which angles opposite to equal sides are equal.
Complete step-by-step answer:
Now, given that triangle\[\] is an isosceles triangle.
Also, $AB = AC$ and $AD = AB$.
And we have to prove that $\angle BCD$ is a right angle.
Now,
In triangle $ABC$
It is given that,
$AB = AC$
$ \Rightarrow \angle ACB = \angle ABC - - - - - - \left( i \right)$
(Because angles opposite to equal sides are equal)
Now,
$AB = AC$ (Given)
And $AD = AB$ (Given)
$ \Rightarrow AC = AD$
Now, in triangle $ACD$
$AC = AD$ (Given)
$ \Rightarrow \angle ADC = \angle ACD - - - - - - \left( {ii} \right)$ (Angles opposite to the equal sides are equal)
Angle sum property- In a Euclidean space, the sum of angles of a triangle equals the straight line i.e. \[{180^ \circ }\] ,$\pi $ radians, two right angles, one at each vertex, bounded by a pair of adjacent sides.
In triangle $BCD$
$\angle ABC + \angle BCD + \angle ADC = {180^ \circ }$ (Angle sum property of a triangle)
From $\left( i \right)$ and $\left( {ii} \right)$
$\angle ACB + \angle BCD + \angle ACD = {180^ \circ }$
Now It is clearly visible from the figure that $\angle BCD = \angle ACB + \angle ACD$
Or $\angle BCD + \angle BCD = {180^ \circ }{\text{ }}\left( {\because \angle BCD = \angle ACB + \angle ACD} \right)$
Or $2\angle BCD = {180^ \circ }$
Or $\angle BCD = {90^ \circ }$
Hence Proved.
Note: Whenever we face such types of questions the key concept is that we should write what is given to us then apply the basic properties of triangles like we did in this question. Here, we simply apply the property of the isosceles triangle that angles opposite to equal sides are equal and then we apply Angle sum property of a triangle and we get our answer.
Complete step-by-step answer:

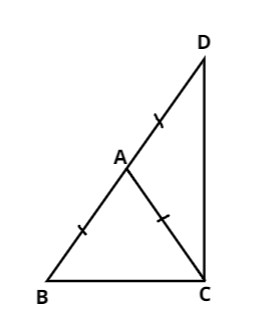
Now, given that triangle\[\] is an isosceles triangle.
Also, $AB = AC$ and $AD = AB$.
And we have to prove that $\angle BCD$ is a right angle.
Now,
In triangle $ABC$
It is given that,
$AB = AC$
$ \Rightarrow \angle ACB = \angle ABC - - - - - - \left( i \right)$
(Because angles opposite to equal sides are equal)
Now,
$AB = AC$ (Given)
And $AD = AB$ (Given)
$ \Rightarrow AC = AD$
Now, in triangle $ACD$
$AC = AD$ (Given)
$ \Rightarrow \angle ADC = \angle ACD - - - - - - \left( {ii} \right)$ (Angles opposite to the equal sides are equal)
Angle sum property- In a Euclidean space, the sum of angles of a triangle equals the straight line i.e. \[{180^ \circ }\] ,$\pi $ radians, two right angles, one at each vertex, bounded by a pair of adjacent sides.
In triangle $BCD$
$\angle ABC + \angle BCD + \angle ADC = {180^ \circ }$ (Angle sum property of a triangle)
From $\left( i \right)$ and $\left( {ii} \right)$
$\angle ACB + \angle BCD + \angle ACD = {180^ \circ }$
Now It is clearly visible from the figure that $\angle BCD = \angle ACB + \angle ACD$
Or $\angle BCD + \angle BCD = {180^ \circ }{\text{ }}\left( {\because \angle BCD = \angle ACB + \angle ACD} \right)$
Or $2\angle BCD = {180^ \circ }$
Or $\angle BCD = {90^ \circ }$
Hence Proved.
Note: Whenever we face such types of questions the key concept is that we should write what is given to us then apply the basic properties of triangles like we did in this question. Here, we simply apply the property of the isosceles triangle that angles opposite to equal sides are equal and then we apply Angle sum property of a triangle and we get our answer.
Recently Updated Pages
Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Biology: Engaging Questions & Answers for Success

Master Class 12 Physics: Engaging Questions & Answers for Success

Master Class 8 Maths: Engaging Questions & Answers for Success

Class 8 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
Write a letter to the principal requesting him to grant class 10 english CBSE

Which of the following does not have a fundamental class 10 physics CBSE

State and prove the Pythagoras theorem-class-10-maths-CBSE

What is the full form of POSCO class 10 social science CBSE

State BPT theorem and prove it class 10 maths CBSE

A Gulab jamun contains sugar syrup up to about 30 of class 10 maths CBSE




