Question

To divide a line segment AB in the ratio p: q, draw a ray AX, so that $\angle $BAX is an acute angle and then mark points on ray AX at equal distances such that the minimum number of these points is:
(a) Greater of p and q
(b) p+q
(c) p+q-1
(d) pq

Answer 1

Hint: To solve this problem, we need to be aware about the basic construction concepts related to dividing a line into equal parts. Thus, in case of line segment AB, to get the ratio of p: q, we divide the line segment into a certain number of points such that we are able to divide AB into the desired ratio p: q.

Complete step-by-step answer:

To solve this problem, we start with drawing a line segment AB. We then draw ray AX such that it should make an acute angle with line segment AB and then mark p+q points at equal units on the ray AX. To explain, we draw and mark these p+q points in the following manner with the help of arcs as shown (in the figure there are 5 points, in our case, there will be p+q points). In the below figure, ${{A}_{pq}}$represents ${{A}_{\begin{smallmatrix}
 p+q \\

\end{smallmatrix}}}$.

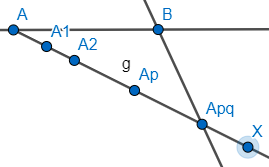
Thus, in our case, the points would be ${{A}_{1}},{{A}_{2}},....,{{A}_{p+q}}$. We will then draw a line segment from point ${{A}_{p+q}}$ to B. Our next step would be to draw a parallel line segment to line segment XB from the point ${{A}_{p}}$. Thus, we get,

Thus, line segment ${{A}_{p}}C$ divides AB in ratio p:q.
Hence, the minimum number of points required are p+q. Thus, the answer is (b) p+q.

Note: While solving the problem, where the line segment is to be divided by a ratio (say a: b), the number of points to be marked on the ray making an acute angle with the line segment should be a multiple of a+b. Thus, we can mark a+b, 2(a+b), 3(a+b) and so on. However, for a minimum number of points, we have to mark a+b number of points. Thus, in case of this problem, to have a ratio of p: q, we have to mark p+q number of points. Another point to keep in mind is that we can get the same result with BAX to be any angle less than 180 and greater than 0. However, in the problem we have taken an acute angle since it is mentioned in the question to take an acute angle.